1 Introduction
During the investigation of ternary diagrams Na2CO3–YbF3–H2O [1] and Na2CO3–YF3–H2O [2] at T = 190 °C, we have found four new fluoride carbonate families, Na2REE(CO3)2F (REE = Y, Yb), Na3Y(CO3)2F2, Na3Yb(CO3)2F2, Na4Y(CO3)2F3
In this paper, the synthesis, the crystal structure, the thermal behaviour and the vibrational analysis of Na3Y(CO3)3
2 Experimental
Crystals of Na3Y(CO3)3
Volume weight was measured with a pycnometer AccuPyc 1330 V3.03. The experimental value ρexp = 2.25 (5) g cm–3 is consistent with the calculated value ρcalc = 2.24 g cm–3.
Thermal analyses were performed with a DTA–TGA TA Instrument 2960 (heating rate 10 °C min–1, argon atmosphere) in the temperature range 25–1000 °C.
Single crystal diffraction data were obtained on a Siemens AED2 four-circle diffractometer. The conditions of intensity measurement are reported in Table 1.
Crystallographic data of Na3Y(CO3)3
| Crystal system | Hexagonal |
| Space group | P63 (No. 173) |
| a (Å) | 11.347(5) |
| c (Å) | 5.935(5) |
| V(Å3), Z | 661.8(5), 2 |
| μ(Mo Kα) (mm-1) | 4.62 |
| ρcalc(g cm-3) | 2.24 |
| ρexp(g cm-3) | 2.25(5) |
| Temperature (K) | 298 |
| Four-circle diffractometer | Siemens AED2 |
| Monochromator | graphite |
| 2θ range (°) | 2–55 |
| (hkl) limits (two sets) | |h| ≤ 12; |k| ≤ 14; |l| ≤ 7 |
| Scan mode | ω–2θ |
| Absorption correction | Gaussian |
| Reflections measured/unique/used (I > 2 σ(I)) | 1132/983/692 |
| Parameters refined (on F2) | 75 |
| R(int)/R(sigma) | 0.07/0.11 |
| a R/Rw | 0.058/0.161 |
| Goodness of fit | 1.05 |
| Weighting scheme (P = [F02 + 2 Fc2]/3) | 1/[σ2(F02) + (0.08 P)2] |
| Secondary extinction coefficient | 0.5(6) × 10-5 |
a R = Σ||Fo| – |Fc||/Σ|Fo| ; Rw = Σ[w(|Fo|2 – |Fc|2)2/Σw(Fo2)2]1/2.
The infrared spectrum of Na3Y(CO3)3
The Raman scattering study was performed in the backscattering geometry, under microscope (×50 objective), on a powder (without polarisation analysis). The spectrum was collected with a T64000 Jobin-Yvon multichannel spectrometer (in triple substractive configuration with 1800 lines/mm grating), using the 514.5 nm radiation of an argon–krypton laser as excitation, with 8 mW power on the sample in the range 40–4000 cm–1. The typical spectral resolution was better than 0.7 cm–1.
3 Structure determination
The systematic existing conditions of reflections 000l (l =2n) led to the P63 and P63/m space groups. Owing to a positive second harmonic generation test, the non-centrosymmetric P63 space group was chosen. The positions of yttrium atoms were obtained using the Patterson method (option PATT in SHELXS-86 [10]). Analysis of successive Fourier difference maps allowed the location of the remaining atoms. Na, C, and O were distinguished from distance criteria and from valence bond analysis. The refinement (SHELXL-97 [11]) of the atomic coordinates and anisotropic displacement parameters after absorption correction (Gauss method in SHELX-76 [12]), decreased the reliability factors to R = 0.058 and Rw = 0.161.
The final atomic coordinates with isotropic displacement parameters and bond valence analysis, the anisotropic displacement parameters and selected bond distances and angles are given in Tables 2, 3 and 4, respectively.
Atomic coordinates, equivalent isotropic displacement parameters and valence bond sums in Na3Y(CO3)3
| Atom | Site | x | y | z | Beq (Å2) | Σsa | Σsexpected |
| Y | 2b | 1/3 | 2/3 | 0.9023(4) | 1.31(4) | 3.12 | 3 |
| Na | 6c | 0.3749(5) | 0.3634(5) | 0.6788(8) | 2.12(8) | 1.1 | 1 |
| C | 6c | 0.120(1) | 0.436(1) | 0.676(2) | 1.6(2)b | 3.9 | 4 |
| O(1) | 6c | 0.0313(9) | 0.3382(7) | 0.563(1) | 1.8(1) | 1.7 | 2 |
| O(2) | 6c | 0.2505(9) | 0.4869(9) | 0.634(2) | 1.8(2) | 1.8 | 2 |
| O(3) | 6c | 0.0914(8) | 0.4929(8) | 0.841(1) | 1.8(1) | 1.9 | 2 |
| Ow(1) | 6c | 0.158(1) | 0.179(1) | 0.555(3) | 6.6(4) | ||
| Ow(2) | 6c | 0.493(1) | 0.216(1) | 0.674(2) | 2.3(2) | ||
| H(11) | 6c | 0.08(1) | 0.10(1) | 0.47(2) | 4.0 | ||
| H(12) | 6c | 0.12(2) | 0.25(2) | 0.52(2) | 4.0 | ||
| H(21) | 6c | 0.47(1) | 0.20(1) | 0.85(3) | 4.0 | ||
| H(22) | 6c | 0.54(2) | 0.17(2) | 0.68(3) | 4.0 |
a The results refer to the equation s = exp[(r0 – r)/0.37] with r0 = 2.014, 1.80 and 1.39 for Y–O, Na–O, and C–O, respectively.
b Isotropic displacement.
Anisotropic displacement parameters in Na3Y(CO3)3
| Atome | U11 | U22 | U33 | U23 | U13 | U12 |
| Y | 0.0157(5) | U11 | 0.0184(7) | 0 | 0 | U11/2 |
| Na | 0.028(3) | 0.030(3) | 0.025(2) | 0.006(2) | 0.006(2) | 0.016(2) |
| O(1) | 0.023(4) | 0.014(4) | 0.028(4) | –0.014(3) | –0.003(4) | 0.007(3) |
| O(2) | 0.020(4) | 0.021(4) | 0.030(5) | –0.006(4) | –0.006(4) | 0.010(4) |
| O(3) | 0.025(4) | 0.025(4) | 0.021(4) | –0.005(3) | –0.003(3) | 0.013(3) |
| Ow(1) | 0.046(7) | 0.044(7) | 0.16(1) | –0.018(8) | –0.023(8) | 0.025(6) |
| Ow(2) | 0.030(5) | 0.033(5) | 0.025(4) | –0.006(4) | 0.002(4) | 0.017(4) |
Selected inter-atomic distances (Å) and angles (°) in Na3Y(CO3)3
| 3 × Y–Ow(2) | 2.37(1) | Na–O(3) | 2.329(9) |
| 3 × Y–O(2) | 2.380(9) | Na–O(1) | 2.347(9) |
| 3 × Y–O(3) | 2.479(8) | Na–Ow(1) | 2.41(1) |
| Na–O(2) | 2.45(1) | ||
| Na–O(3) | 2.508(9) | ||
| Na–Ow(2) | 2.61(1) | ||
| <Y–O> | 2.41 | <Na–O> | 2.44 |
| C(1)–O(1) | 1.26(1) | O(2)–C–O(3) | 116(1) |
| C(1)–O(2) | 1.30(1) | O(1)–C–O(2) | 121(1) |
| C(1)–O(3) | 1.31(1) | O(1)–C–O(3) | 123(1) |
| <C–O> | 1.29 | <O–C–O> | 120 |
| Ow(1)–H(11) | 1.0(1) | Ow(2)–H(22) | 1.1(2) |
| Ow(1)–H(12) | 1.1(1) | Ow(2)–H(21) | 0.9(2) |
4 Structure description
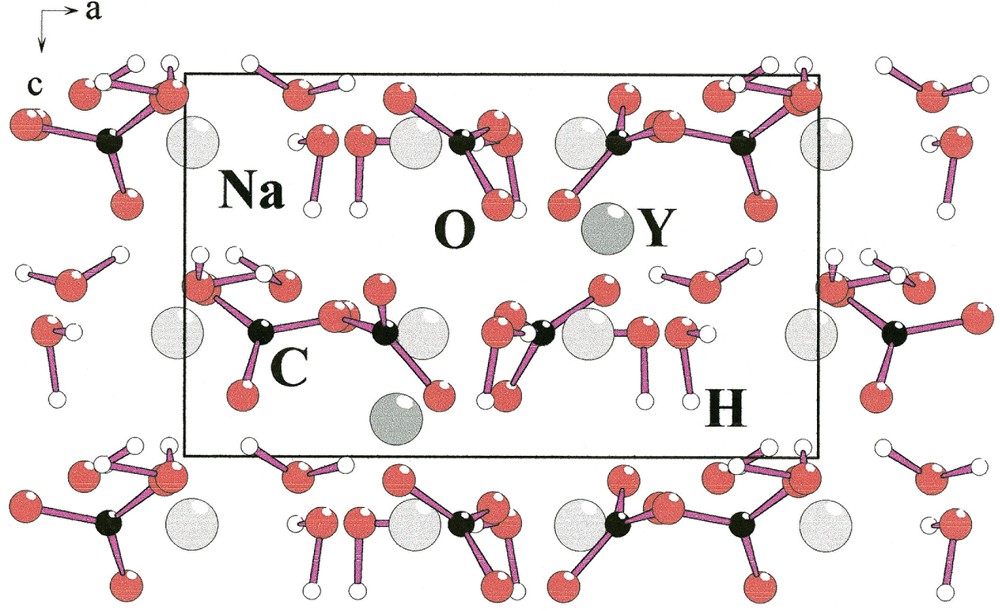
In the structure of Na3Y(CO3)3
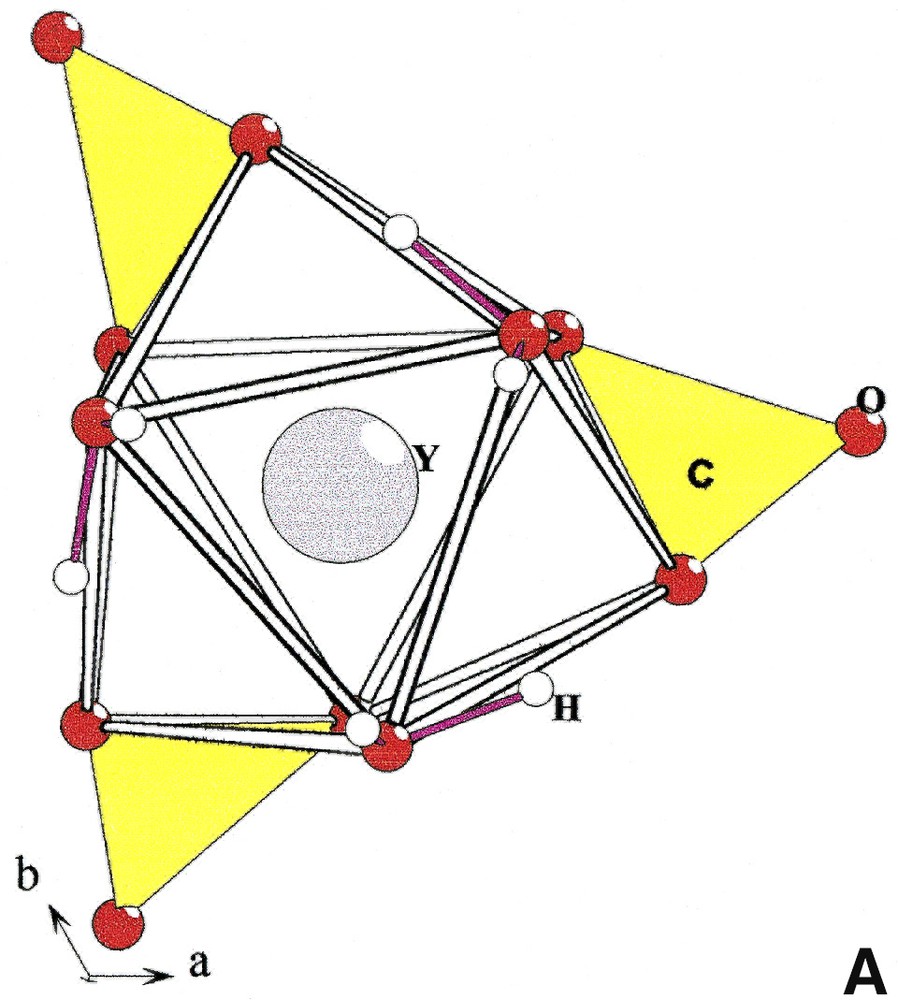

[YO3+3+3] and [(Y, Ln)O3+3+3] polyhedra in Na3Y(CO3)3
The distorted [NaO4(H2O)2] octahedra build infinite [001] corrugated chains [NaO4O2/2]∞ (Fig. 2, left). Each [YO3+3(H2O)3] polyhedron is connected by edges to six [NaO4(H2O)2] octahedra that belong to three independent [NaO4O2/2]∞ chains (Fig. 2 right). Two adjacent [YO3+3(H2O)3] polyhedra located at z = 0.4 and z = 0.9 share a unique [NaO4O2/2]∞ chain. Six chains form cavities in which hydrogen atoms of water molecules point (Fig. 3). Water molecules H2Ow(1) and H2Ow(2) establish hydrogen bonds with O(1) and O(2), respectively (Table 5).
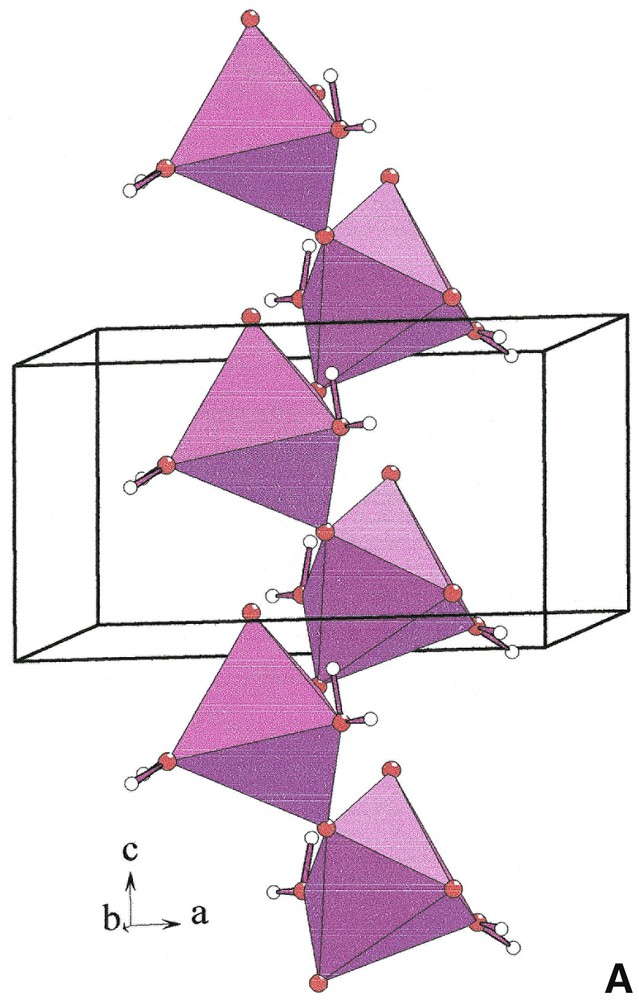
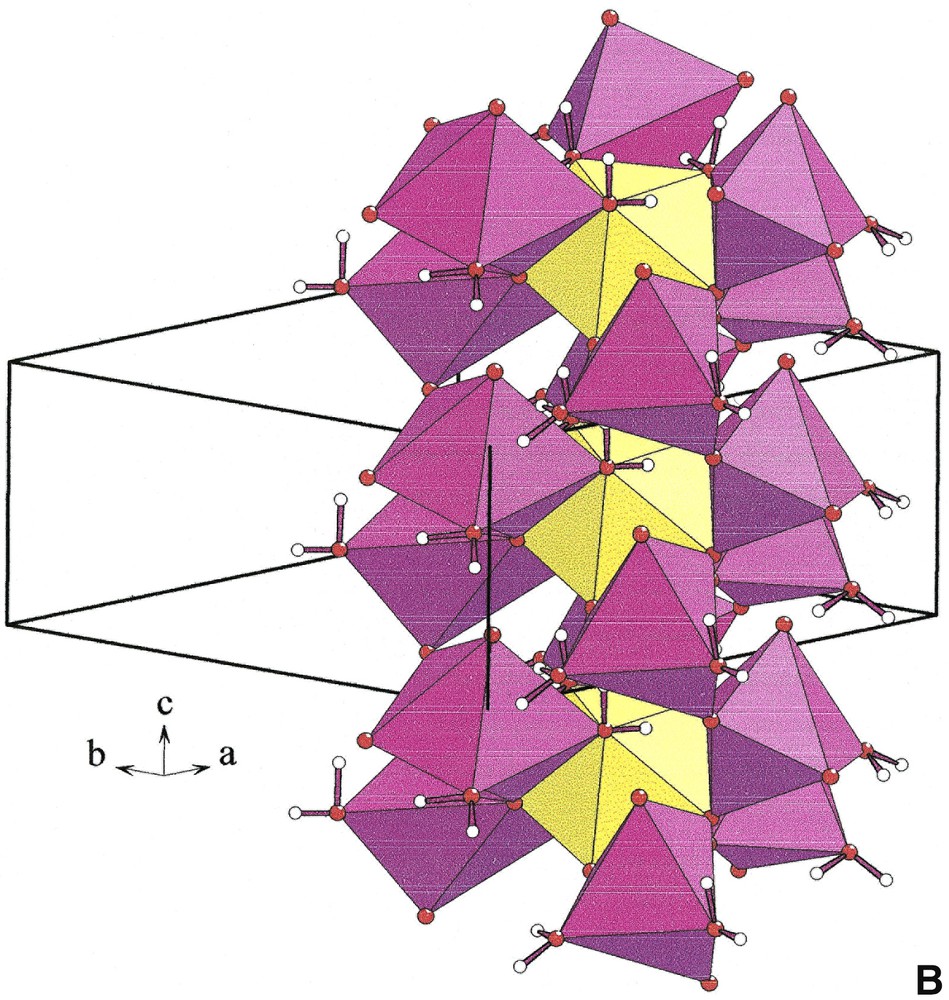
[001] chains [NaO4O2/2]∞ (left) and connection of [YO3+3(H2O)3] polyhedra (yellow) and [NaO4(H2O)2] octahedra (violet) in Na3Y(CO3)3
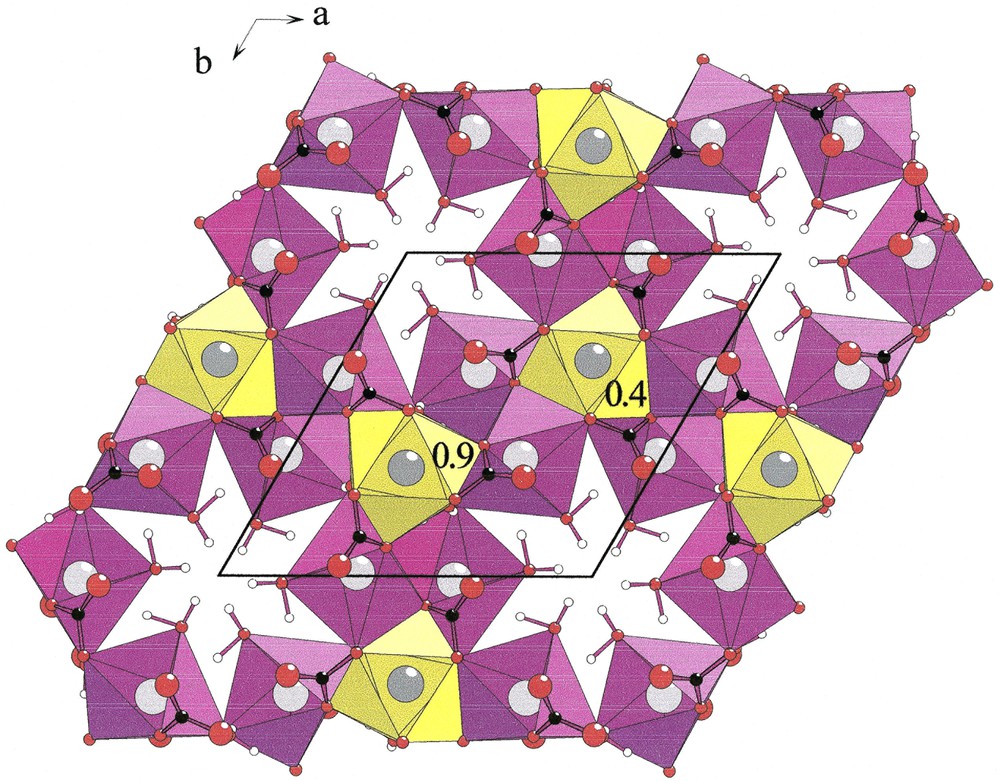
[0001] projection of Na3Y(CO3)3
Hydrogen bonds in Na3Y(CO3)3
| O–H | H | Ow | OwHO (°) |
| Ow(1)–H(12) | 1.8 | 2.8 | 172 |
| Ow(1)–H(12) | 2.5 | 3.2 | 160 |
| Ow(2)–H(21) | 1.9 | 2.7 | 174 |
| Ow(2)–H(22) | 2.3 | 2.6 | 155 |
| Ow(2)–H(22) | 2.1 | 3.0 | 164 |
Carbon atoms lie at z = 0.176 and z = 0.676 (Fig. 4); with O(1), O(2) and O(3) atoms, they form infinite layers of carbonate groups in which the shortest C–C distance is 4.37 Å. In one layer, it is remarkable that carbon atoms are approximately located at the nodes of a two-dimensional hexagonal network with
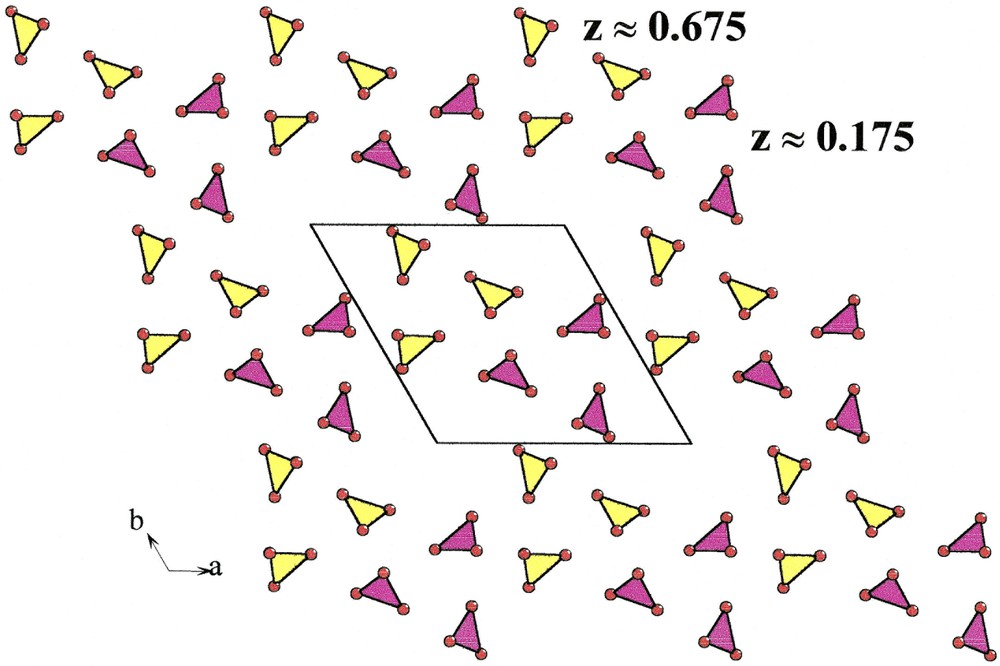
Layers of carbonate groups at z ≈ 0.175 and z ≈ 0.675 in Na3Y(CO3)3

Lacunar hexagonal network of carbonate groups in Na3Y(CO3)3
A relationship between the structures of Na3Y(CO3)3
[Na(CO3)
Structural relationship between Na3Y(CO3)3
| Y and Na polyhedra | cell parameters | space group | |||
| Na3Y(CO3)3 | Na[6] Y[9] | 11.347 | 5.935 | P63 | |
| Shomiokite | Na[6] Y[9] | 10.042 | 17.349 | 5.948 | Pbn21 |
| Adamsite | Na[6] Y[9] | 6.2592 | 13.0838 | 13.2271 | |
| 91.130 | 103.554 | 90.188 |
5 Characterization
5.1 Thermal behaviour
On heating, Na3Y(CO3)3
The second step corresponds to the departure of 1.5 mol of CO2 gas per mole of Na3Y(CO3)3 (exp./th. = 14.1/14.8%); the decomposition reaction is:
The third step is due to the decomposition of Na2CO3 and occurs above 850 °C.
5.2 Vibration analysis
In Na3Y(CO3)3
Vibrational analysis of Na3Y(CO3)3
| Factor group C6 | External modes | Internal modes | Activity | ||||||||||||||
| CO3 | H2O | ||||||||||||||||
| N | A | TCO3 | RCO3 | TY | TNa | TH2O | RH2O | ν1 | ν2 | ν3 | ν4 | ν | δ | γ | IR | Raman | |
| A | 34 | –1 | 3 | 3 | 1 | 3 | 6 | 6 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | z | αxx + αyy ; αzz |
| B | 34 | 0 | 3 | 3 | 1 | 3 | 6 | 6 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | – | – |
| E1 | 34 | –1 | 3 | 3 | 1 | 3 | 6 | 6 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | (x, y) | (αxx, αyz) |
| E2 | 34 | 0 | 3 | 3 | 1 | 3 | 6 | 6 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | – | (αxx – αyy, αxy) |
The acoustic modes are: Γacous = A ⊕ E1. The A and E1 modes are Raman and IR actives, while E2 modes are only Raman actives. B modes are inactive.
Free CO22– anion has the D3h symmetry and exhibits four normal vibrations ν1(A1′ ), ν2(A2′ ′ ), ν3(E′) and ν4(E′). E′ modes are IR and Raman actives, while A1′ is only Raman active and A2′ ′ is only IR active. ν1 (1000–1100 cm–1) and ν3 (1400–1500 cm–1) represent the symmetric and asymmetric stretching vibrations, respectively. ν2 (650–800 cm–1) and ν4 (800–1000 cm–1) correspond to out of plane and in plane deformation vibrations, respectively. The crystal modes (and the macroscopic geometry of observation) can be related to the previous modes by the so-called site method. In Na3Y(CO3)3
Correlation scheme for the internal vibration modes of CO3 groups in Na3Y(CO3)3
Fig. 7 shows the Raman spectrum. One line at 1065 cm–1 and two lines at 715 and 680 cm–1 are attributed to the ν1 and to the ν4 modes, respectively. Theoretically, three lines are expected for the ν1 mode and six lines for the ν4 mode (Table 7). Though no polarisation analysis was possible, these lines can be unambiguously assigned to the A mode as a reason of the diagonal form of the polarisability tensor. The ν2 and ν3 modes around 820 cm–1 and 1500 cm–1 are very weak. For the ν2 mode, this feature can be explained by the fact that ν2 derives from (A2′ ′ ), Raman inactive in D3h symmetry.

Raman spectrum of Na3Y(CO3)3
The observed bands at low frequencies are very large. They are attributed to external modes of Na+ and Y3+ translations and H2O or CO32– translations and librations.
The IR spectrum is given in Fig. 8. The band around 1065 cm–1 and the shoulder observed at 1045 cm–1 are assigned to the symmetric stretching modes ν1 of CO32–. The two bands located at 890 and 875 cm–1 are attributed to the out-of-plane deformation modes ν2. In the region 1200–1550 cm–1, two large bands, around 1375 and 1485 cm–1, correspond to the asymmetric ν3 stretching. For the out-of-plane ν4 deformation, four bands predicted in the region 800–650 cm–1 are observed at frequencies 680, 715, 755 cm–1 and 760 cm–1 (shoulder). Then, it is noted that the number of theoretical and observed bands is identical for ν2 and ν4.
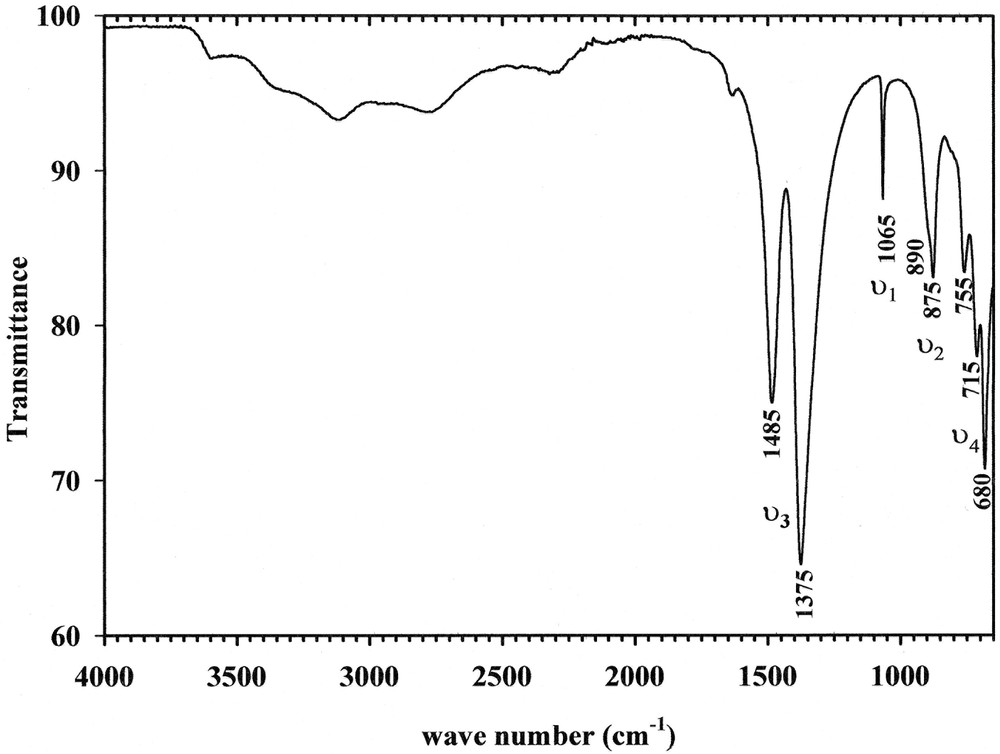
IR spectrum of Na3Y(CO3)3
H2O vibration modes, attributed to antisymmetric stretching, symmetric stretching, in plane β-OH deformation and out of plane γ-OH deformation, are expected in the intervals 3600–2000, 1700–1550, 1300–1200 and 800–700 cm–1, respectively. Experimentally, only five very large bands in the region 3600–2000 cm–1, together with one small band at 1635 cm–1, are observed.
6 Conclusion
The crystal structure of a new hydrated carbonate, Na3Y(CO3)3
It must be noted that shomiokite-(Y) mineral was found in association with an alteration yttrium carbonate. This silky white carbonate was too fine grained and the material quantity was too small; consequently, the structure is still unknown (J.D. Grice, personal communication). It should be interesting to collect X-ray diffraction and/or spectroscopic data of this carbonate, which could be compared with Na3Y(CO3)3
Acknowledgements
The authors are very indebted to Pr. A. Bulou (LPEC, Univ. Le Mans) for his help in the analysis of vibrational spectra and to Dr P. Aschehoug (LCAES, ENSC Paris) for the SHG test.


