1 Introduction
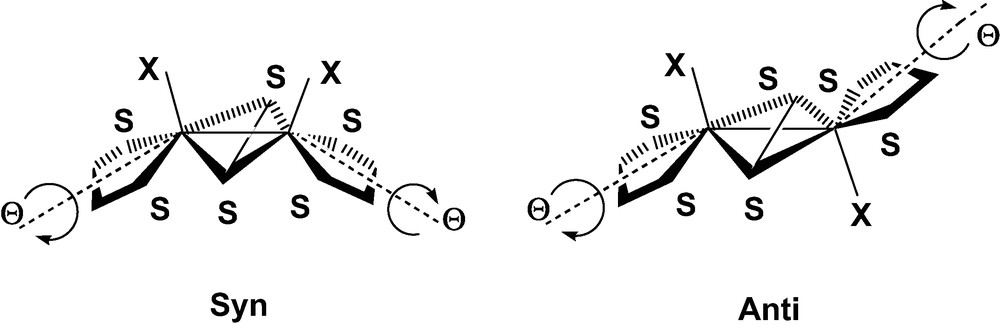
The reaction of tetraoxothiometalates [MSnO4–n]x– (M = V, Mo, Re, W) with electrophiles has been widely used in the last decade to produce a variety of sulfur-rich complexes of transition metals [1–8]. More specifically, the use of unsaturated substrates like alkynes as electrophilic agents has led to the preparation of new dithiolene ligands, eventually attached to metal cores with various nuclearities. Beyond mononuclear species [9–14], this synthetic pathway has contributed to enlarge and diversify the series of dianions organized around the (μ-S2)M2 metallacycle, and completed with two monoatomic ligands, either oxo or sulfido [7,8,15–21]. The position of these two M=X bonds with respect to the metallacycle gives rise to the classical syn/anti isomerism, illustrated in Fig. 1 [20,21]1.
Most structures involving the (η-X)2[(μ-S2)M2] core have been characterized in the syn form only [7,8,16–19]. Both the syn and the anti isomers have been isolated and characterized for the first time on a MoV dianionic complex with symmetric dithiolene ligands, [Mo2S4(S2C2H4)2]2– (1) [20]. Since then, various complexes have been characterized with both structures, including MoV complexes similar to 1 in which sulfido ligands have been replaced by oxo [8], and the series of bi- and tetranuclear compounds derived from ReS4– and synthesized by Goodman and Rauchfuss [15]. A theoretical analysis of the bonding in the syn and anti isomers of 1 was given by Chandler, Lichtenberger and Enemark (CLE) in 1981 [22], based upon Hall and Fenske [23] and extended Hückel (EHMO) [24–26] calculations. This study assigned the diamagnetism observed in both isomers to the presence of a metal–metal bond, “not large, but sufficient” to stabilize a closed-shell ground state [22]. The syn form was also predicted to be the most stable one, based on the calculated total energies and on the relative strength of the Mo–Mo bonding, estimated from the total Mo–Mo 4d overlap populations. A third, hypothetic form, the “closed” isomer, topologically equivalent to the syn form, but with a planar Mo2S2 metallacycle, was also investigated [22]. Even though the study by CLE was state of the art in 1981, its conclusions can hardly go beyond the qualitative aspects of the bonding, due to the lack of geometry optimization and to the crude estimates of total energies obtained from the above-mentioned semi-empirical methods. Quite recently, the bifunctional dithiolene S2C2[C(O)OMe]2 was grafted on a (η-X)2[(μ-S2)W2] core (X = O, S) by the group of Sécheresse, and resulted in complexes only displaying the anti conformation [27]. A subtle illustration of the syn/anti problem was also evidenced by the same group through the synthesis and X-ray characterization of a monovacant heteropolytungstate dimer in which the (PW11O39)7– monomers are coupled through two {(η-O)2(η-OH2)2 [(μ-S2)Mo2]}2+ bridges [28]. The metal–oxo bonds of the bridges are subject to the syn/anti isomerism, but the presence of a disorder in the structure has prevented to support one arrangement over the other. The goal of the present work is therefore to obtain by means of Density Functional Theory (DFT) a reliable estimate of the energy difference between the syn and anti isomers in standard dithiolene complexes of MoV, and then to vary the models and the electronic configurations in order to obtain a detailed analysis of the electronic and electrostatic factors conditioning the relative stability of both isomers.
2 Computational details
Most calculations and all geometry optimizations reported in the present work have been carried out using the DFT formalism by means of the 1999 release of the ADF program, based upon the use of Slater basis sets [29–32]. The exchange-correlation functional is the so-called Becke–Perdew/86 (BP86) functional [33–35], which belongs to the family of functionals referring to the generalized gradient approximation (GGA). The atomic basis sets used in the present calculations are referred to in the User’s Guide as TZP for H, C, O and S atoms, and TZ2P for Mo and W. These basis sets are to be used in conjunction with the Zero Order Regular Approximation (ZORA) to the relativistic effects with appropriate description of the inner shells, an option that was adopted throughout the present calculations. The atomic description consists in a core (He core for first-row atoms, Ne core for S, Kr and Xe cores for Mo and W, respectively) described by means of frozen double-ζ Slater functions. The valence shells are triple-ζ and supplemented either with one d-type polarization function (non-metal atoms) or with an extra p-type function and a f-type polarization function (Mo, W). Some calculations were also carried out with EHMO [24–26] in order to obtain qualitative orbital interaction diagrams.
3 Discussion
3.1 The case of [Mo2S4(S2C2H4)2]2– (1) and [Mo2S2O2(S2C2H4)2]2– (2)
Complex 1 has been the subject of the theoretical investigation carried out by CLE [22]. Not surprisingly, EHMO calculations carried out on 1 and on its oxo counterpart 2 reproduce the sequence of frontier MOs obtained by CLE from the Fenske–Hall method. Fig. 2 displays the EHMO interaction diagram constructing the orbitals of the syn form of 2 from the molecular fragments [Mo2O2(S2C2H4)2]2+ and (μ-S2)4–. The HOMO of 2 results from the σ-bonding combination of the two ML3 fragments. This orbital is somewhat destabilized due to a 4-electron interaction with μ-S2, but the energy increase remains moderate (Fig. 2). By contrast, electron donation from μ-S2 to the other metal levels significantly raises the energy of these unoccupied levels and generates a conspicuous HOMO–LUMO gap (1.35 eV). More specifically, the presence of the S2 bridge raises by 50% the energy gap between the σ-bonding and the σ-antibonding Mo–Mo levels (Fig. 2). These donation interactions globally stabilize the set of six valence orbitals of μ-S2 and ensure the stability of the complex. The frontier orbitals of the anti isomer can be deduced from those of Fig. 2 by a 180° rotation of one Mo–oxo–dithiolene fragment. The energy difference between the σ and the σ* levels is reduced by ~30% in the anti Mo2L6 fragment, but the donation from μ-S2 restores an important energy gap and the sequence of frontier MOs is eventually quite similar to that of the syn isomer, with a slight raise of the HOMO energy (0.15 eV).
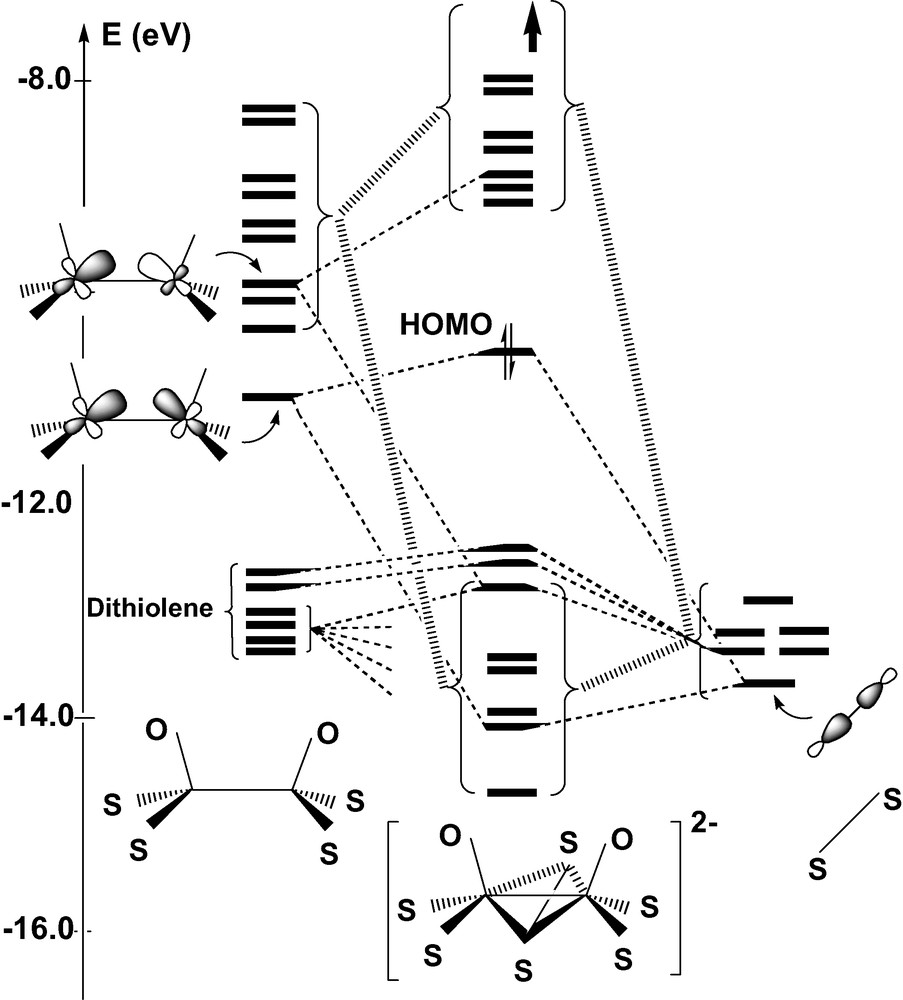
Orbital interaction diagram for the syn form of [Mo2(μ-S2)O2(S2C2H4)2]2– from EHMO calculations.
In view of these qualitative results, one might conclude in agreement with CLE that the relative stability of the syn and anti isomers should be correlated with a difference in the strength of the metal–metal bond, the relative orientation of the metal σ orbitals being more favorable in the syn conformation. This explanation seems in keeping with the slightly longer Mo–Mo distances observed for the anti forms, when both isomers are available [8,20]. However, one could also argue that the shortening of the Mo–Mo bond in the syn form is a mere consequence of the butterfly folding of the metallacycle rather than the parameter monitoring the relative stability of the system. Indeed, the Mo-(μ-S) distances, either observed or computed, remain quite similar in the bent metallacycle of the syn form, and in the planar core of the anti isomer (Table 1). One should also consider that the network of repulsive interactions developed among the highly charged ligands represents another factor that might influence the relative stability of the isomers. These repulsive contacts are partly accounted for by the EHMO interaction diagram in the form of repulsive 4-electron interactions occurring between the fragment orbitals of dithiolene and those of μ-S2 (Fig. 2). It is clear however that the Pauli and electrostatic components of this L–L repulsion are severely underestimated by EHMO. An opposite twist of the two dithiolene groups induced by a Θ rotation around their local symmetry axis is observed in some structures, the two forms of 1 [20] as well as in some other members of the same family of compounds [8]. This distortion reduces the molecular symmetry from C2v to C2 in the syn form, and from C2h to Ci in the anti form (Fig. 3). A particular emphasis should be given to the anti isomer of 1, a strongly distorted structure in which the twist angle reaches the relatively high value of 11.1° (Table 1). This deviation from ideal symmetry does not seem to be related to any specific interaction involving the frontier orbitals and could therefore be assigned either to the crystal forces, or to ligand–ligand repulsive interactions. One of the goals of the DFT calculations reported in the present work was to provide evidence for these interactions and to quantitatively assess their role in the energy balance between the syn and anti forms.
Relative energies (ΔE, kcal mol–1), selected bond lengths (Å), dihedral and twist angles (°) calculated for 1 and 2 and observed for 1. Calculations carried out with symmetry constraints are also reported, together with the relative energies calculated in the constrained and unconstrained geometries for the [Mo2X2(S2C2H4)2]2+ fragments
| 1 syn | 1 anti | 2 syn | 2 anti | |||||||
| Calc. | Obs. | Calc. | Obs. | Calc. | Calc. | |||||
| C2 | C2v | Ci | C2h | C2 | C2v | Ci | C2h | |||
| Dianion | ||||||||||
| Mo–Mo | 2.907 | 2.911 | 2.863 | 2.947 | 2.944 | 2.878 | 2.894 | 2.902 | 2.961 | 2.962 |
| Mo–X | 2.160 | 2.164 | 2.098a | 2.171 | 2.170 | 2.129a | 1.708 | 1.710 | 1.712 | 1.712 |
| Mo-μS | 2.350a | 2.352 | 2.320a | 2.345a | 2.349 | 2.321a | 2.363a | 2.366 | 2.361a | 2.365 |
| Mo–Sdith | 2.448a | 2.430 | 2.406a | 2.445a | 2.427 | 2.401a | 2.470a | 2.451 | 2.466a | 2.445 |
| Θb | 6.3 | 0.0 | 2.0 | 6.4 | 0.0 | 11.1 | 4.7 | 0.0 | 7.4 | 0.0 |
| Πc | 144.5 | 147.8 | 146.9 | 180.0 | 180.0 | 180.0 | 143.6 | 145.8 | 180.0 | 180.0 |
| ΔE | 0.0 | +7.3 | +3.4 | +11.5 | 0.0 | +8.3 | +3.9 | +12.8 | ||
| Dicationic fragment | ||||||||||
| ΔE | +0.1 | 0.0 | +3.8 | +4.9 | +0.05 | 0.0 | +2.7 | +3.1 |
a Average distance.
b Twist angle measuring the rotation of each Sdith–Mo–Sdith with respect to the position of perfect symmetry (Fig. 3).
c Dihedral angle between the two M-(μ-S2) planes.
Distortion of the dithiolene ligands downgrading the molecular symmetry of the syn and anti forms of [Mo2(μ-S2)X2(S2C2H4)2]2–.
Table 1 displays the relative energies obtained for both isomers of 1 and 2 after gradient optimization of the geometries, together with the observed and calculated values of selected structural parameters. These calculations have been carried out assuming the C2 symmetry for the syn form and the Ci symmetry for the anti form. The geometry of the same systems have also been optimized with the more severe constraints of the C2v and C2h point groups, respectively, in order to provide a first estimate of the effects of L–L repulsion. Finally, single-point calculations have been carried out on the dimetallic complex without μ-S2, assuming either the unconstrained or the constrained geometry for the [Mo2X2(S2C2H4)2]2+ fragments (Table 1).
DFT calculations confirm that the syn isomers of 1 and 2 are more stable than their respective anti counterparts. The computed energy difference is of the order of 3.5 kcal mol–1 (Table 1). The observed geometrical parameters of 1 syn and 1 anti are well reproduced by the calculations, accounting for the slight overestimation (0.03–0.06 Å) of the metal–metal and metal–ligand bond lengths generally encountered with the GGA functionals. All distances are quite similar in the two isomers, except for the Mo–Mo bond length, which is found shorter in the syn form by 0.04 and 0.07 Å in 1 and 2, respectively (Table 1). The butterfly folding of the metallacycle observed in 1 syn is well reproduced in the computed structure. Finally, the calculations show that the deviation from full symmetry induced by the twist of the dithiolene rings is an intrinsic character of the isolated molecule and contributes to its stability by as much as 7–9 kcal mol–1 for both isomers of 1 and 2 (Table 1). Note that the calculated interatomic distances are quite similar in the real and in the ideal symmetry, except for the average Mo–Sdith bond length which displays a small, but systematic contraction (~0.02 Å) in the most symmetric structure. In order to assess the role of ligand–ligand repulsive interactions in the dithiolene distortion, the energy of the [Mo2X2(S2C2H4)2]2+ fragments obtained by removing (μ-S2)4– from 1 and 2, was computed by means of single-point calculations. The geometries were taken from those optimized for both isomers of 1 and 2, assuming either the real, or the ideal symmetry (Table 1). Contrary to the case of the full complexes, the stability of the dicationic fragments is practically insensitive to the dithiolene twist. For both fragments, the syn form remains energetically favored by about the same amount (3–4 kcal mol–1) as for the full complex (Table 1).
It can therefore be concluded that a relatively important repulsion develops between (μ-S2)4– and the rest of the coordination sphere of sulfur-rich dimetallic complexes. This repulsion is smoothed by downgrading the molecular symmetry as represented in Fig. 3, possibly at the expense of a slight decline in the strength of the Mo–Sdith bond. However, it eventually appears that the ligand–ligand repulsion does not significantly affect the energy balance between the syn and trans isomers. The relative stability of the isolated dianionic structures, as that of the related dicationic fragments, therefore, remains ultimately conditioned by the different strength of the metal–metal σ-bond, either bent, in the syn form, or lateral, in the trans isomer (Fig. 4) [22].

The metal–metal bonding in the syn and anti forms of [M2(μ-S2)X2(S2R)2]2–.
3.2 Complexes of functionalized dithiolenes: [M2S2X2(S2C2R2)2]2– (R = C(O)OMe; M = Mo, W)
More recently, the use of alkynes, and more specifically of dicarbomethoxyacetylene as reducing agent resulted in the synthesis of functionalized dithiolenes as ligands of the (η-X)2[(μ-S2)M2] core. Coucouvanis et al. [8] reported the structure of both the syn and the anti isomers of [Mo2S2O2(SCC(O)OMe)2]2– (3). Very recently, the group of Sécheresse characterized similar compounds with M = W; X = O (4) and S (5), but the anti form only could be isolated and characterized up to now [27].
Calculations show that the syn form of the molybdenum oxo compounds 3 is again more stable than the anti isomer, although the energy difference is reduced to ~1 kcal mol–1 (Table 2). The structural parameters of the coordination sphere are not significantly different from those of the parent compound 2, except for a more pronounced folding of the metallacycle. This folding contracts the Mo–Mo distance, which is computed shorter than in the anti form by 0.086 Å. This difference is the largest computed in the whole series of investigated complexes. The observed gap between the Mo–Mo bond lengths in the syn and anti forms of 3 amounts 0.051 Å, which is also much larger than observed for 1 (0.015 Å). However, no conspicuous correlation shows up in the series of complexes 1–5 between the relative stability of the syn form and the shrinkage of the metal–metal bond length in this isomer. Indeed, the contraction of the M–M distance is a purely geometrical consequence of the folding angle Π between the two M-(μ-S2) planes and does not necessarily imply a better σ overlap between the metal atoms.
Relative energies (ΔE, kcal mol–1), selected bond lengths (Å), dihedral and twist angles (°) calculated and observed for {M2X2S2[S2C2–(COOMe)2]2}2– (3: M = Mo, X = O; 4: M = W, X = S; 5: M = W, X = O)
| 3 syn | 3 anti | 4 syn | 4 anti | 5 syn | 5 anti | |||||
| Calc.d | Obs. | Calc.d | Obs. | Calc. | Calc. | Obs. | Calc. | Calc. | Obs. | |
| M–M | 2.858 | 2.853 | 2.944 | 2.904 | 2.925 | 2.956 | 2.869 | 2.921 | 2.956 | 2.870 |
| M–X | 1.703 | 1.675 | 1.708 | 1.684 | 2.166 | 2.170 | 2.090 | 1.729 | 1.726 | 1.820 |
| M-μSa | 2.362 | 2.331 | 2.353 | 2.328 | 2.350 | 2.350 | 2.314 | 2.363 | 2.363 | 2.322 |
| M–Sditha | 2.456 | 2.425 | 2.456 | 2.419 | 2.436 | 2.433 | 2.395 | 2.458 | 2.451 | 2.402 |
| Θb | 5.8 | 3.9a | 5.2 | 1.0 | 5.3 | 3.1 | 1.3 | 7.8 | 1.8 | 0.7 |
| Πc | 138.0 | 148.0 | 180.0 | 180.0 | 153.6 | 180.0 | 180.0 | 153.5 | 180.0 | 180.0 |
| ΔE | 0.0 | +1.1 | 0.0 | +3.6 | 0.0 | +2.2 |
a As in Table 1.
b As in Table 1.
c As in Table 1.
d Calculations on 3 have been carried out on models in which the methoxy groups have been replaced by OH.
The replacement of MoV by WV hardly modifies the M–S and M–X bond lengths, but opens the wings of the syn butterfly. The Π angle is calculated larger by 10 to 15° for the syn isomers of 4 and 5 than for the Mo complexes 1–3 (Tables 1 and 2). An immediate consequence is the reduction to ~0.035 Å of the M–M distance gap calculated between the syn and anti isomers. The geometrical origin of this wing opening is a less pronounced bending of the dithiolene rings with respect to the metal–metal axis. Even though no folding can occur in the anti form, a similar leveling of the square pyramid M–S4 basis is observed and computed in the isomers with Ci symmetry. In keeping with this evolution of the molecular geometry, the ligand–ligand repulsion, as estimated by the twist angle Θ, tends to decrease, at least for the anti isomers. It is interesting to compare the computed values of Θ with the observed ones, when available in either form of complexes 1–5 (Table 2). With the notable exception of anti-1, the observed values of Θ are significantly lower than the computed ones. In the anti forms of 3, 4 and 5, the observed distortion even becomes almost negligible (~1°) when the computed values are comprised between 1.8° and 5.2°. It can be inferred that the crystal forces and more specifically the influence of the counter-ions tend in this case to oppose the repulsive interactions, whereas they seem to be enhanced in anti-1.
As for complexes 1 and 2 the syn form of 4 and 5 is more stable than the anti conformation by a few kcal mol–1, as long as they are considered isolated (Table 2). At variance with the structures displayed in Table 1, the computed distortion of the dithiolene ligands is consistently more important in the syn form than in the anti form of 4 and 5. This might influence the relative stability of the isomers: a secondary energy minimum, less distorted then the structure reported in Table 2, had been first characterized for 5 syn with an energy slightly higher than that calculated for 5 anti (+0.35 kcal mol–1). Besides, the geometry optimization of the anti forms of 4 and 5 has been carried out starting from the little distorted X-ray structure as trial geometry. Therefore, it cannot be totally excluded that a more severe distortion of dithiolene provides further stabilization to the anti forms of these isolated complexes.
4 Summary and conclusion
DFT calculations carried out on binuclear di-anionic complexes of MoV or WV with a square-pyramidal XMS4 coordination environment provides some new information about the syn/anti isomerism, characteristic of these molecules. Rather surprisingly, the structures with maximal symmetry, namely C2v for syn and C2h for anti do not correspond to the equilibrium geometry of the isolated molecules in either form. A distortion occurs in the dithiolene ligands, which are twisted away from their symmetric position. This type of distortion is present in the X-ray structures, when available, but the twist angles observed in the crystals are generally weaker than computed in the isolated molecules, with the notable exception of anti-[Mo2(μ-S2)S2(S2C2H4)2]2–. Since this type of distortion is neither predicted, nor explained by means of frontier orbital interactions, but nevertheless contributes to the molecular stability by as much as 7–9 kcal mol–1, it should be assigned to the relief of the strong electrostatic and Pauli repulsive interactions occurring within the coordination spheres of the two metals. Removing the (μ-S2)4– ligand abolishes the repulsive contacts and indeed restores the full symmetry. The magnitude of the repulsive interactions appears to be similar in the syn and anti forms of the same complex and do not significantly influence the energy balance. The ultimate factor conditioning the relative stability of the isomers, assumed isolated, is the overlap between the metal σ orbitals. As proposed by CLE [22], the bent σ bond characteristic of the syn form is eventually slightly more favorable than the lateral σ overlap encountered in the anti isomers and leads in most cases to a marginal stabilization of the syn form, comprised between 1 and 4 kcal mol–1. However, the important and somewhat erratic differences noted between the observed and computed values of the dithiolene twist angle Θ suggest that the crystal environment and more specifically the closest shell of counterions might play a prominent role in the management of the intramolecular electrostatic interactions and in the selection of the preferred isomer.
Acknowledgments
Most calculations have been carried out at the IDRIS computer center (Orsay, France), through a grant of computer time from the CNRS, and at the CURRI (ULP, Strasbourg). We are also pleased to acknowledge support from the GdR DFT.
1 Note that the crystal atomic coordinates provided for the anti isomer of 1 are in error for the dithiolene sulfur atoms S3 and S4. Crystal parameters consistent with the rest of the structure are as follows: S3: x = 0.6603; y = 1.1454; z = 0.2015, S4: x = 0.4963; y = 0.9895; z = 0.3043.


