1 Introduction
The trivalent lanthanide and actinide cations can bind with as many as nine ligand donor sites in their coordination sphere. In the formation of the binary 1:1 complex [M(DTPA)]2−, DTPA (diethylenetriaminepentaacetate), the ligand occupies eight coordination sites of metal cations. The X-ray diffraction studies of the [Ln(DTPA)]2− (Ln3+ = Nd, Gd, Dy, Ho and Yb) in solid [1,2] and the luminescence decay measurements in solution [3,4] indicate the presence of one water molecule in the inner coordination sphere of [Ln(DTPA)]2− for a total coordination number of 9.0. In principle, the coordinated water molecule can be displaced by a small ligand resulting in the formation of a ternary complex. Such ternary complexes of Ln3+ with EDTA (ethylenediaminetetraacetate) and HEDTA (N-hydroxyethylethylenediaminetriacetate) as the primary ligands have been studied extensively [5–10]. Because of the presence of a single water of hydration, the [Ln/An(DTPA)]2− complexes have a lesser tendency to form a ternary complex than the corresponding [Ln(EDTA)]− and [Ln(HEDTA)]0 complexes. The ternary complexes investigated include ligands such as IDA2− (iminodiacetate) [11], F− (fluoride) [12], CO32− (carbonate) and PO43− (phosphate) [13]. Larger multidentate ligands such as cit3− (citrate) do not form a ternary complex with [Ln(DTPA)]2− [13].
Currently, large volumes of nuclear wastes from weapon processing and from reprocessing of spent fuel are stored in underground tanks. These tanks have solutions which contain highly radioactive Cs, Tc, Am, Cm, etc., nuclides and high concentrations of nonradioactive salts such as NaNO3, Na2CO3, etc., as well as organic ligands (carboxylate and aminopolycarboxylates) [14,15]. Due to the radioactive decay, the temperatures of the tank solutions are significantly higher than the ambient temperature. The organic ligands present in the nuclear waste increase the solubility of the actinides by complexation. As a result, data on the complexation thermodynamics of lanthanides and actinides at the ionic strength and temperatures of the wastes are necessary to understand their behavior in the wastes media. Such studies have broadened the existing database for actinides and lanthanides, which are dominated by information on the binary systems. Studies on the ternary system are of fundamental interest as they offer the possibility to assess the steric interactions between ligands, the binding preference of various ligand donor groups and the coordination number of the cations.
The present investigation reports the complexation thermodynamics of the binary complexes of Am3+, Cm3+, and Eu3+ with DTPA and of their ternary complexes with DTPA + IDA at I = 6.60 m (NaClO4) and temperatures of 0 to 60 °C. The NMR (1H and 13C) spectra of the diamagnetic La3+/Y3+ complexes were studied to establish the coordination modes and structural aspects of the ligands in these binary and the ternary complexes. The luminescence lifetime measurements with Eu3+ were performed to provide knowledge on the hydration number of these cations in these complexes.
2 Experimental
All chemicals were of reagent grade or higher and distilled, deionized water (E-pure, Barnstead) was used in the preparation of solutions. Aqueous solutions of 6.60 m NaClO4 (>98%, Sigma–Aldrich, ACS certified) were prepared and filtered through 0.45 μm membrane. Solutions of DTPA (Fisher Scientific) and IDA (Fluka) were prepared in 6.60 m (NaClO4) and their concentrations were determined by pH-titration with standard NaOH. The Eu(ClO4)3, La(ClO4)3 and Y(ClO4)3 solutions were prepared from oxides (99.99%, Aldrich) in perchloric acid (60%, Fisher Scientific), followed by dilution to the desired concentrations. The concentrations of these solutions were determined by titration with solution of EDTA [16]. Di-(2-ethylhexyl) phosphoric acid, HDEHP (Sigma–Aldrich) and heptane (Fisher Scientific) were used as received.
The radioactive tracers 241Am, 244Cm and 152, 154Eu (Oak Ridge National Laboratory) were purified and their purity checked by α- and/or γ-spectrometry. The working stock of each tracer was prepared in HClO4 solution of pH ∼3.0 such that a 10.0 μL of the solution has a count rate of ca. 50,000 cpm. The concentration of metal ions was ca. ∼1 × 10−6 M. The activities of 241Am, 244Cm and 152, 154Eu were measured in a Beckman Liquid Scintillation Counter (LSC) using Ecolite cocktail (ICN, Research Product Division).
An Accumet 950 (Fisher Scientific) pH meter was used with a glass electrode (Corning semi-micro combination) to measure the pH values. The KCl solution in the salt bridge was replaced with saturated NaCl solution as the low solubility of the KClO4 at high ionic strengths resulted in erratic readings. The electrode was calibrated with 4.00 ± 0.01 and 7.00 ± 0.01 pH buffer. The meter readings (pHr) were converted to pH values using calibration curves obtained from a series of HClO4 and NaOH solutions of known [H+] in I = 6.60 m (NaClO4) and T = 0–60 °C as described in Ref. [17].
2.1 TRLFS
The 7F0–5D0 excitation spectra of Eu3+ were measured at room temperature in 1.00 cm quartz fluorimeter cells using an instrumental setup similar to that described in Ref. [17]. The [Eu3+] was fixed at ∼1 × 10−4 M in all solutions. Solutions of the complexes were prepared by mixing the Eu(ClO4)3 and the corresponding ligand solutions in 6.60 m (NaClO4). For the binary systems the ratios of Eu:IDA varied from 1 to 10 and that of Eu:DTPA from 1:1 to 1:2, while for the ternary system the ratios of Eu:DTPA:IDA varied between 1:1:1 to 1:1:5 and 1:10:10. The pH of these solutions was varied from 3.60 to 13.0 with dilute HClO4 or NaOH. To avoid precipitation of Eu3+, a constant ionic strength of I = 6.60 m (NaClO4) was not maintained in the Eu–IDA studies. The coordination number, CNC, of the complexes was calculated using the correlation CNC = 0.237Δν + 0.628 [18], where Δν is the peak shift of Eu3+(aq) upon complexation. The water of hydration
2.2 1H and 13C NMR
For NMR measurements, solutions of La(ClO4)3 and Y(ClO4)3 and the ligands were prepared in D2O. The solutions of La(ClO4)3 and Y(ClO4)3 after dissolution in perchloric acid were evaporated several times in D2O to eliminate water followed by dilution. Due to precipitation of La3+/Y3+, a constant ionic strength of I = 6.60 m (NaClO4) was not maintained in these solutions. The concentrations of La3+ were ca. 0.05 M, while that of Y3+ were maintained at ca. 0.04 M. Samples for La/Y–IDA, La/Y–DTPA and La/Y–DTPA–IDA in D2O were prepared by dropwise addition of La3+ to the IDA or DTPA and/or to the mixture of DTPA + IDA, followed by mixing to prevent precipitation of metal hydroxide. The pH of the solutions was adjusted with DCl or NaOD in D2O. The 1H and 13C spectra were obtained for solutions of (1) DTPA (0.50 M), pH = 9.60 (2) La:DTPA (1:1), pH = 9.60 and (3) La:DTPA:IDA (1:1:1–1:1:4, pH ∼10.00). The values reported are direct pH meter reading and no corrections for D2O were made. All spectra were recorded at room temperature on a Bruker AC300 at 300.13 MHz for 1H and at 75 MHz for 13C NMR and were referenced externally to spectra of sodium trimethylsilanolate, δ = 0.00 ppm (±0.1 ppm).
2.3 Metal ion distribution measurements
The distribution of the metal ions (Am3+, Cm3+ and Eu3+) between aqueous and organic phases was determined by the radiotracer distribution technique. Volumes of 3.0 mL of the aqueous phase (with or without ligands) and of the pre-equilibrated organic phase (HDEHP in heptane) were mixed in glass vials at pH = 3.60 ± 0.05 and I = 6.60 m (NaClO4). Aliquots of 10.0 μL of 241Am, 244Cm or 152, 154Eu tracer, were added to the aqueous phase and the two phases were shaken for 60 min as described in Ref. [17]. For the measurements of binary constants, the concentration of DTPA was varied between 9.0 × 10−6 and 1.0 × 10−5 M and, for the ternary constants, the concentration of DTPA was fixed at 2.0 × 10−6 M for Am3+ and Cm3+ and at 1.0 × 10−7 M for Eu3+ while that of IDA was varied from 0.02 to 0.20 M. The details of the equilibrium experiments, counting procedures, equilibrium pHr measurements and conversion of pHr readings to pH at I = 6.60 m (NaClO4) and at four temperatures were as described in Ref. [17].
2.4 Data analysis
2.4.1 M–DTPA system
The extraction of trivalent Am, Cm and Eu by HDEHP solution can be expressed as:
| M3+(a) + 3H2A2(o) ⇌ M(HA2)3(o) + 3H+(a) | (1) |
| (2) |
| (3) |
| (4) |
| (5) |
2.4.2 M–DTPA–IDA system
The formation of the ternary complex with DTPA + IDA can be written as:
| (6) |
| (7) |
| (8) |
| (9) |
The stability constants of the complexes [M(DTPA)]2−, β101, and [M(DTPA)(IDA)]4−, β111, were evaluated by correlating D values with ligands concentrations. The associated thermodynamic parameters of the binary and the ternary complexes were determined from linear Van't Hoff plot of stability constants with temperature. The entropy values were calculated with the Gibbs–Helmoltz equation. The stability constant values in molarity were converted to values in molality using the equation [21]:
| (10) |
Protonation constants of IDA and DTPA at I = 6.60 m (NaClO4), T = 0–60 °C
| Temp (°C) | pK011 | pK021 | pK031 | pK041 | pK051 | |
| IDA (n = 1–2) | 0 | 9.22 ± 0.05 | 2.72 ± 0.08 | – | – | – |
| 25 | 9.87 ± 0.03 | 2.82 ± 0.05 | – | – | – | |
| 45 | 9.98 ± 0.05 | 2.86 ± 0.08 | – | – | – | |
| 60 | 10.39 ± 0.05 | 2.94 ± 0.06 | – | – | – | |
| DTPA (n = 1–5) | 0 | 9.12 ± 0.08 | 8.24 ± 0.09 | 4.21 ± 0.05 | 2.89 ± 0.08 | 2.21 ± 0.12 |
| 25 | 9.98 ± 0.07 | 8.62 ± 0.09 | 4.41 ± 0.07 | 2.94 ± 0.08 | 2.32 ± 0.09 | |
| 45 | 10.25 ± 0.04 | 8.81 ± 0.03 | 4.49 ± 0.06 | 2.98 ± 0.08 | 2.35 ± 0.08 | |
| 60 | 10.42 ± 0.02 | 9.03 ± 0.11 | 4.61 ± 0.08 | 302 ± 0.08 | 2.40 ± 0.12 |
3 Results and discussion
3.1 Complexation thermodynamics
Am3+, Cm3+ and Eu3+ in an aqueous solution of I = 6.60 m (NaClO4), pH = 3.60 and at temperatures of 0–60 °C have linear curves of 1/D vs [DTPA]2− which indicate the formation of the 1:1 complexes. The stability constants of their 1:1 complex was calculated using Eq. (5) and are listed in Table 2 with the constants reported for these metal cations at I ≤ 1.0 M. Our values for Am3+ Cm3+ and Eu3+ at I = 6.60 m (NaClO4) are ca. 2.0 log units lower than the corresponding values at I = 0.1 m, reflecting the effect of the ionic media. With temperature, the stability constants of the 1:1 complex increase. DTPA is the main component in the trivalent Actinide–Lanthanide Separation by Phosphorous Extractants and Aqueous Komplexes (TALSPEAK) process, because of their larger separation factors for actinides–DTPA complexes relative to that of the lanthanides–DTPA [23]. The decreased values of Δlog β101 (log β101, Am/Cm − log β101, Eu) with increasing ionic strength (Table 3) indicate that high concentrations of salt may hinder the separation of trivalent actinides from lanthanides by TALSPEAK process.
Stability constants of Am3+, Cm3+ and Eu3+ with DTPA (log β101) at I = 6.60 m (NaClO4), pH = 3.60, T = 0–60 °C
| Temp (°C) | I (m) | log β101 | Ref. | ||
| Am | Cm | Eu | |||
| 0 | 6.60 NaClO4 | 18.19 ± 0.16 | 18.25 ± 0.15 | 18.29 ± 0.12 | p.w. |
| 10 | 6.60 NaClO4 | – | – | 19.08 ± 0.13 | p.w. |
| 25 | 6.60 NaClO4 | 19.89 ± 0.13 | 19.98 ± 0.12 | 19.82 ± 0.15 | p.w. |
| 25 | 0.1 NH4ClO4 | 22.92 ± 0.02 | 22.99 ± 0.01 | 22.40 ± 0.07 | [42] |
| 25 | 0.1 KNO3 | – | – | 22.39 ± 0.08 | [43] |
| 25 | 0.5 NaClO4 | 21.14 | 21.26 | – | [44] |
| 0.5 NaClO4 | – | – | 20.87 ± 0.07 | [45] | |
| 35 | 6.60 NaClO4 | – | – | 20.09 ± 0.15 | p.w. |
| 45 | 6.60 NaClO4 | 20.35 ± 0.16 | 20.38 ± 0.17 | – | p.w. |
| 60 | 6.60 NaClO4 | 20.87 ± 0.14 | 20.95 ± 0.17 | – | p.w. |
Δlog β101 values (log β101, Am/Cm − log β101, Eu) at different ionic strengths
| I (m) | Δlog β101 | |
| log β101, Am − log β101, Eu | log β101, Cm − log β101, Eu | |
| 0.10 | 0.52 | 0.59 |
| 0.50 | 0.27 | 0.39 |
| 6.60 | 0.07 | 0.16 |
In a mixture of DTPA + IDA, a linear plot of 1/D vs [IDA]2− at a fixed concentration of [DTPA]5− and temperatures of 0–60 °C (Fig. 1 is a representative graph for Am3+, Cm3+ and Eu3+ at 25 °C) indicates the formation of a ternary complex. The stability constants, log β111 calculated using Eq. (9) are listed in Table 4 plus a ternary constant reported for Eu3+ at I = 0.2 M (NaClO4). A difference of ca. 1.1 log units between our value of log β111 for Eu3+ at 25 °C and those of the literature at I = 0.2 m reflects the effect of the ionic media and the different reactions viz. M3+ + DTPA5− + IDA2− = [M(DTPA)(IDA)]4− in our case and the reaction [M(DTPA)]2− + IDA2− used in the literature to evaluate the constants. For Am3+ and Cm3+, no such constants are reported. The stability order of the 1:1:1 ternary complexes: DTPA + IDA > CDTA + IDA > EDTA + IDA (Table 4) at I = 6.60 m (NaClO4) agrees with the stability order of these ternary complexes at lower ionic strengths and is consistent with the stability sequence of the 1:1 binary complexes of DTPA, CDTA and EDTA [24]. Fig. 2 illustrates the relationship between ΣpKa and log β111 of Eu3+ with EDTA, CDTA and DTPA as primary ligands and Ox, IDA and NTA as secondary ligands. Such linearity reflects the ionic nature of the bonding in these ternary complexes. The stability constant data for the ternary complexes of EDTA + NTA, IDA, Ox were taken from Refs. [25–27], for CDTA + IDA, NTA were from Ref. [28] and that of DTPA + IDA from the present study.
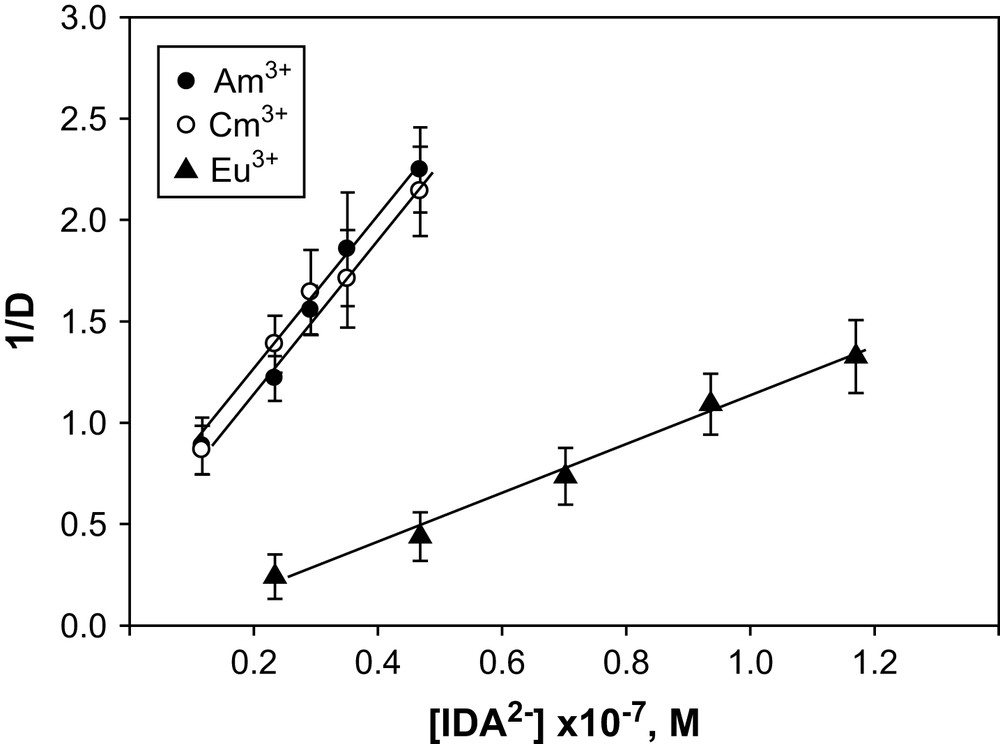
Plots of 1/D vs [IDA]2− for Am3+, Cm3+ and Eu3+ at I = 6.60 m (NaClO4); temp = 25 °C and pH = 3.60.
Stability constants of 1:1:1 ternary complexes of Am3+, Cm3+ and Eu3+ with DTPA + IDA (log β111) at I = 6.60 m (NaClO4), pH = 3.60, T = 0–60 °C
| Temp (°C) | I (m) | Am | Cm | Eu | Ref. |
| 25 | 6.60 NaClO4 | 27.98 ± 0.22 | 28.07 ± 0.25 | 27.62 ± 0.23 | p.w. |
| 25a | 6.60 NaClO4 | 23.95 ± 0.20 | 23.43 ± 0.19 | 22.95 ± 0.22 | [27] |
| 25b | 6.60 NaClO4 | 24.12 ± 0.24 | 23.96 ± 0.24 | 23.62 ± 0.23 | [28] |
| 25 | 0.2 NaClO4 | – | – | 26.50 ± 0.03 | [11] |
| 35 | 6.60 NaClO4 | 28.37 ± 0.23 | 28.53 ± 0.27 | 28.17 ± 0.22 | p.w. |
| 45 | 6.60 NaClO4 | 28.90 ± 0.25 | 29.01 ± 0.28 | 28.52 ± 0.24 | p.w. |
| 60 | 6.60 NaClO4 | 30.03 ± 0.27 | 30.16 ± 0.29 | 29.89 ± 0.28 | p.w. |
a log β111 for EDTA + IDA.
b log β111 for CDTA + IDA.
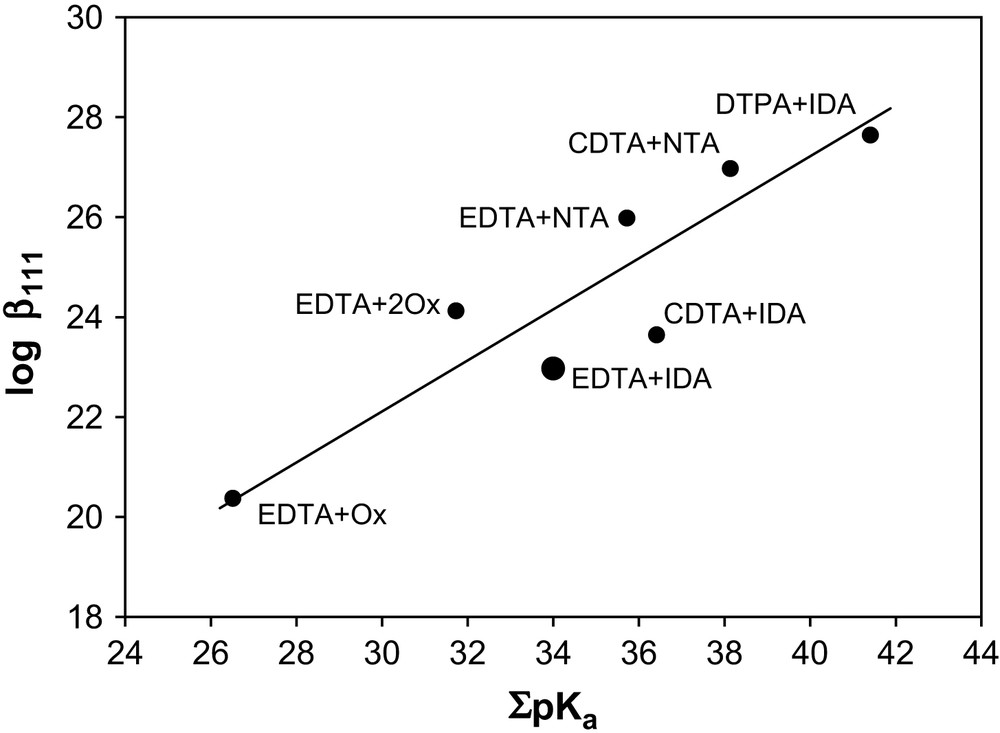
Relation of log β111 for the formation of the 1:1:1 ternary complex of Eu3+ and the acid constants, ΣpKa of the ligands.
The thermodynamic parameters for the formation of the 1:1 complexes in 6.60 m (NaClO4) (after corrections for the heat for deprotonation of the last three protons of DTPA due to the ionic media, 68.83 kJ mol−1 [17]) indicate that the complexation of M3+ with DTPA is accompanied by positive enthalpy and entropy contributions (Table 5). This is consistent with the greater dehydration of the metal cations at high ionic strength, as more energy is required to break the metal–water bonds than the energy released in the formation of the metal–ligand bonds. The net effect is endothermic enthalpies at high ionic strengths. By contrast, the exothermic enthalpy for these metal ions at lower ionic strength reflects that the metal–ligand interaction contribution is larger than that of the dehydration contribution. However, the dehydration dominates the entropy term at all ionic strengths.
Thermodynamics of complexation of Am3+, Cm3+ and Eu3+ with DTPA at 25 °C
| I (m) | ΔG101 (kJ mol−1) | ΔH101 (kJ mol−1) | ΔS101 (J K−1 mol−1) | Ref. | |
| Am | 6.60 NaClO4 | −113.5 ± 0.7 | 6.8 ± 2.2 | 404 ± 15 | p.w. |
| 0.5 NaClO4 | −120.6 ± 0.3 | −39.5 ± 1.0 | 272 ± 5 | [29] | |
| 0.5 NaClO4 | −120.6 ± 0.3 | −16.0 ± 2.0 | 350 ± 9 | [29] | |
| Cm | 6.60 NaClO4 | −114.0 ± 0.7 | 7.2 ± 2.3 | 407 ± 16 | p.w. |
| 0.5 NaClO4 | −121.3 ± 0.6 | −14.0 ± 2.0 | 360 ± 9 | [29] | |
| Eu | 6.60 NaClO4 | −113.1 ± 0.9 | 15.4 ± 4.4 | 431 ± 21 | p.w. |
| 0.5 NaClO4 | −119.1 ± 0.4 | −39.8 ± 1.5 | 266 ± 5 | [29] | |
| 0.5 NaClO4 | −119.1 ± 0.4 | −47.8 ± 0.4 | 239 ± 2 | [29] |
The complexation thermodynamics for the formation of the ternary complexes with DTPA + IDA (Table 6, values are corrected for the heat of deprotonation of the second proton of IDA (31.40 kJ mol−1) [22] and of the last three protons of DTPA for the ionic media)) also reflects the predominant effect of the cation dehydration over the metal–ligand interaction effect, which is in agreement with the formation of corresponding ternary complexes with EDTA + IDA and EDTA + NTA at I = 6.60 m (NaClO4) [25,27]. However, the cation dehydration and the rigid structure of CDTA contribute towards the endothermic values of enthalpy for the formation of the ternary complexes M(CDTA)(NTA)4− and M(CDTA)(IDA)3− [28].
Thermodynamics of complexation of Am3+, Cm3+ and Eu3+ with DTPA + IDA at 25 °C, I = 6.60 m (NaClO4)
| ΔG111 (kJ mol−1) | ΔH111 (kJ mol−1) | ΔS111 (J K−1 mol−1) | |
| Am–DTPA–IDA | −159.65 ± 1.25 | 10.06 ± 3.3 | 570 ± 48 |
| Cm–DTPA–IDA | −160.16 ± 1.42 | 11.01 ± 4.2 | 574 ± 51 |
| Eu–DTPA–IDA | −157.60 ± 1.35 | 18.48 ± 6.1 | 590 ± 56 |
In Fig. 3, the enthalpies of complexation of Am3+ with aminopolycarboxylates are plotted vs the total number of ligand coordination sites (carboxylate + nitrogen) at I = 0.5 and 6.60 m (NaClO4) [29]. The straight line plot supports the participation of the carboxylate and nitrogen donors in the bond formation with Am3+. The deviation of CDTA from the straight line reflects extra dehydration of metal ions due to cyclohexane ring. However, the value for CDTA conforms to the straight line after correction for the excess ligand dehydration. The excess entropy for Am(CDTA)− relative to that of Am(EDTA)− due to the cyclohexane ring is calculated to be ca. 120 J K mol−1 (ΔS101, CDTA − ΔS101, EDTA = 120 J K mol−1) [28]. The calculated endothermic enthalpy has a value of ca. 35.76 kJ mol−1 (using the relation ΔH = TΔS). The corrected enthalpy for Am(CDTA)− is 47.74 − 35.76 = 11.98 kJ mol−1, which is close to the enthalpy value of 14.7 kJ mol−1 for the Am(EDTA)− at I = 6.60 m (NaClO4) [17]. The complexation enthalpy for the [Am(Ac)]2+ (Ac = acetate, with no metal–nitrogen bond) is endothermic; however, the values become more exothermic with increasing number of metal–nitrogen bonds from one in [Am(IDA)]+ to three in [Am(DTPA)]2− formation. This confirms the exothermic enthalpic contribution of the metal–nitrogen interactions at I = 0.5 m [29]. However, at I = 6.60 m, the values of Am3+ are endothermic. The smaller endothermicity of [Am(DTPA)]2− complexation (with three metal–nitrogen bonds) compared to that of the [Am(IDA)]+ complexation (with one metal–nitrogen bond) suggests that the positive dehydration contributions overcome the negative metal–nitrogen interactions at high ionic strength. The enthalpy value of the ternary complex of [Am(DTPA)(IDA)]4− is close to that of the [Am(DTPA)]2−, each with three metal–nitrogen bonds, and the data point for [Am(DTPA)(IDA)]4− falls on the straight line, indicating that the nitrogen of IDA is not involved in the bonding.
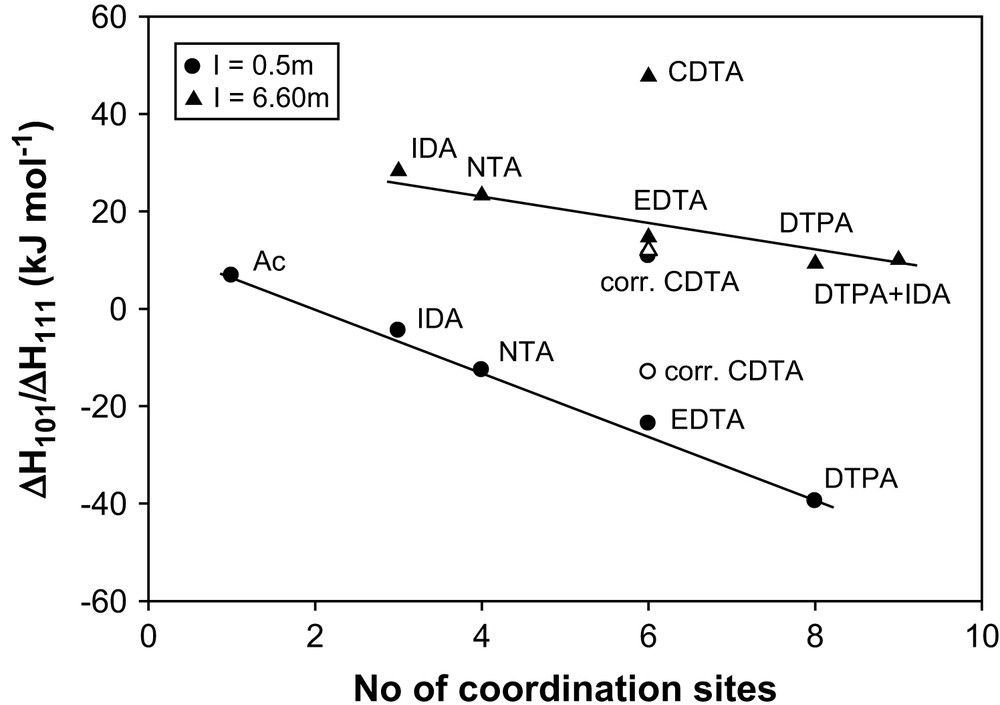
The relation between the entropy of complexation of Am3+ and the number of coordination sites (carboxylates + nitrogen) of aminocarboxylates.
3.2 TRLFS study
3.2.1 Eu(aq), Eu–IDA and Eu–DTPA systems
The 7F0–5D0 excitation spectra of Eu3+ at various metal-to-ligand concentration ratios and pH are shown in Fig. 4 and the peak positions; luminescence lifetimes and the calculated values of
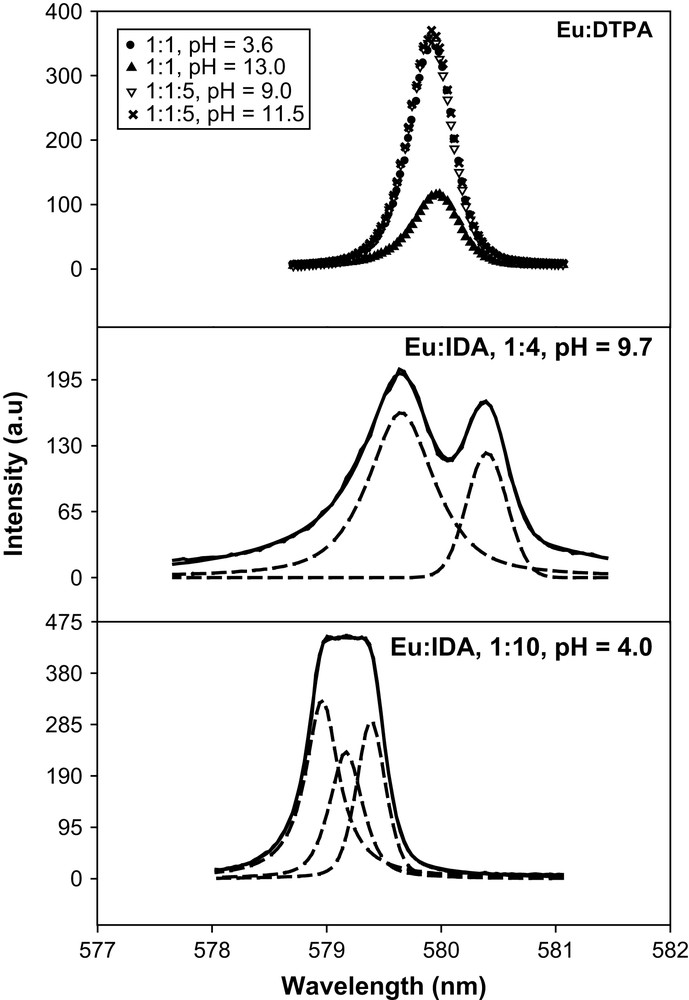
The 7F0–5D0 excitation spectra of Eu(III) in the binary, Eu–IDA, Eu–DTPA and the ternary Eu–DTPA–IDA systems; I = 6.60 m (NaClO4); T = 25 °C (expt., —) and (fitted, - - -).
Distribution of the species formed and spectral characteristics of Eu3+ complexes with IDA, DTPA and DTPA + IDA, I = 6.60 m (NaClO4), T = 25 °C
| Species | pH | % Species (L = IDA) | Peak position (nm) | Lifetime (μs) | Ref. | |||||
| Eu | EuL | EuL2 | EuHL | EuL3 | ||||||
| Eu3+(aq) | 2.21 | – | 578.90 | 116 ± 3 | 8.4 | p.w. | ||||
| Eu3+(aq) | 2.00 | – | 578.84 | 111 ± 2 | 9.0 | [4] | ||||
| Eu(IDA)+a, 1:1 | 4.50 | 95.0 | 4.5 | – | – | – | 579.17 | 144 ± 1 | 6.6 | p.w. |
| Eu(IDA)+, 1:1 | 6.00 | 36.0 | 63.2 | – | – | – | 579.14 | 161 | 5.8 | [46] |
| Eu(IDA)+, 1:1 | 8.48 | 20.2 | 67.4 | 12.2 | – | – | – | 158 ± 1 | 6.3 | [31] |
| Eu(IDA)2−a, 1:4 | 9.70 | – | 2.4 | 39.4 | – | 58.2 | 579.60 | 273 ± 3 | 3.1 | p.w. |
| Eu(IDA)33−a, 1.4 | 9.70 | – | 2.4 | 39.4 | – | 58.2 | 580.21 | 299 ± 2 | 2.8 | p.w. |
| Eu(IDA)2− | 6.00 | – | – | – | – | – | 579.64 | 274 | 3.0 | [46] |
| Eu(IDA)+a, 1:10 | 4.00 | 95.1 | 1.5 | – | 3.2 | – | 579.14 | 143 ± 2 | 6.6 | p.w. |
| Eu(IDA)33−a, 1:10 | 11.00 | – | – | 9.4 | – | 90.5 | 580.28 | 303 ± 15 | 2.7 | p.w. |
| Eu(IDA)33− | – | – | – | – | – | – | 580.28 | 375 | 2.1 | [33] |
| Eu(DTPA)2−, 1:1 | 3.60 | – | 579.91 | 657 ± 5 | 0.9 | p.w. | ||||
| Eu(DTPA)2− | 11.50 | – | 579.91 | 657 ± 5 | 0.9 | p.w. | ||||
| Eu(DTPA)(OH)3− | 13.00 | – | 579.98 | 549 ± 5 | 1.2 | p.w. | ||||
| Eu(DTPA)2− | 5.50 | – | 580.05 | 680 | 1.1 | [4] | ||||
| Eu(DTPA)2− | 4.00 | – | 580.05 | 627 | 1.2 | [3] | ||||
| Eu(DTPA)2−, 1:1:1 | 3.6–9.0 | – | 579.91 | 624 ± 8 | 1.0 | p.w. | ||||
| Eu(DTPA)2−, 1:1:5 | 3.60 | – | 579.91 | 606 ± 6 | 1.0 | p.w. | ||||
| Eu(DTPA)(IDA)4− | 9.00 | – | 579.91 | 775 ± 5 | 0.6 | p.w. | ||||
| Eu(DTPA)(IDA)4− | 11.50 | – | 579.91 | 757 ± 10 | 0.7 | p.w. | ||||
| Eu(DTPA)(IDA)4−, 1:10:10 | 3.60 | – | 579.91 | 763 ± 6 | 0.7 | p.w. |
a No NaclO4, p.w. = present work.
For Eu–IDA at a ratio of 1:1 and pH = 4.50 a broad peak at 579.17 nm was resolved into two peaks at 578.94 and 579.17 nm. The peak at 578.94 nm corresponds to the free Eu3+ and that at 579.17 nm, with a lifetime of 144 ± 1 μs and
At Eu:IDA of 1:4 and pH = 9.7, two peaks at 579.64 and 580.21 nm are due to the complexes Eu(IDA)2− and Eu(IDA)33−. At Eu:IDA of 1:10 and pH = 11.0, an asymmetric peak at 580.28 nm was resolved into two peaks at 580.28 and 579.98 nm, indicating the formation of the complexes Eu(IDA)33− and Eu(IDA)2−. These results indicate that at low pH values of 4–5, the complex most likely formed is [Eu(IDA)]+, while the complexes [Eu(IDA)2]− and [Eu(IDA)3]3− become dominant at pH > 8.0, which is consistent with the potentiometric and calorimetric studies of the formation of complexes [Ln(IDA)n]3−2n (n = 1–3) [32]. In the present study although the peak shift of the 7F0–5D0 band is consistent with the formation of the [Eu(IDA)3]3− (CNC = 9.6), the
Eu–DTPA at a ratio of 1:1 and pH = 3.60 shows a peak at 579.91 nm with a lifetime of 657 ± 5 μs and
3.2.2 Eu–DTPA–IDA system
The excitation spectra of Eu–DTPA–IDA at a ratio of 1:1:1 and pH = 3.60–9.00 and at a ratio of 1:1:5 and pcH = 3.60 have a peak at 579.91 nm. The lifetime and
3.3 1H and 13C NMR
The NMR spectra of diamagnetic La3+ and Y3+ with IDA, DTPA and DTPA + IDA were recorded to further substantiate the results of TRLFS and complexation thermodynamics. The 1H NMR spectra of La–DTPA and the La–DTPA–IDA systems are shown in Fig. 5 and the assigned chemical shift values are given in Table 8. The spectrum of IDA shifts from HIDA− (3.52 ppm, pH = 3.60) to IDA2− (3.04 ppm, pH = 10.0), reflecting the effect of proton removal [36]. No N–H resonance is observed, presumably because of rapid N–H proton exchange with the solvent. At low pH of ∼ 4.10, the spectra of La–IDA at ratios of 1:1 and 1:3 consist of a broad peak at 3.52 ppm for methylene protons of IDA. With increase of pH to 9.50, the broad peak is shifted downfield and appears at 3.31 ppm indicating the formation of La–IDA. The broadness of the peak at lower pH value is due to the slow exchange between free IDA and bound IDA. At pH = 9.50 most of the IDA is bound to La3+, which gives rise to a sharp signal for methylene protons of IDA. The large downfield shifts of this peak relative to free IDA reflect the coordination of the nitrogen atom to La3+.
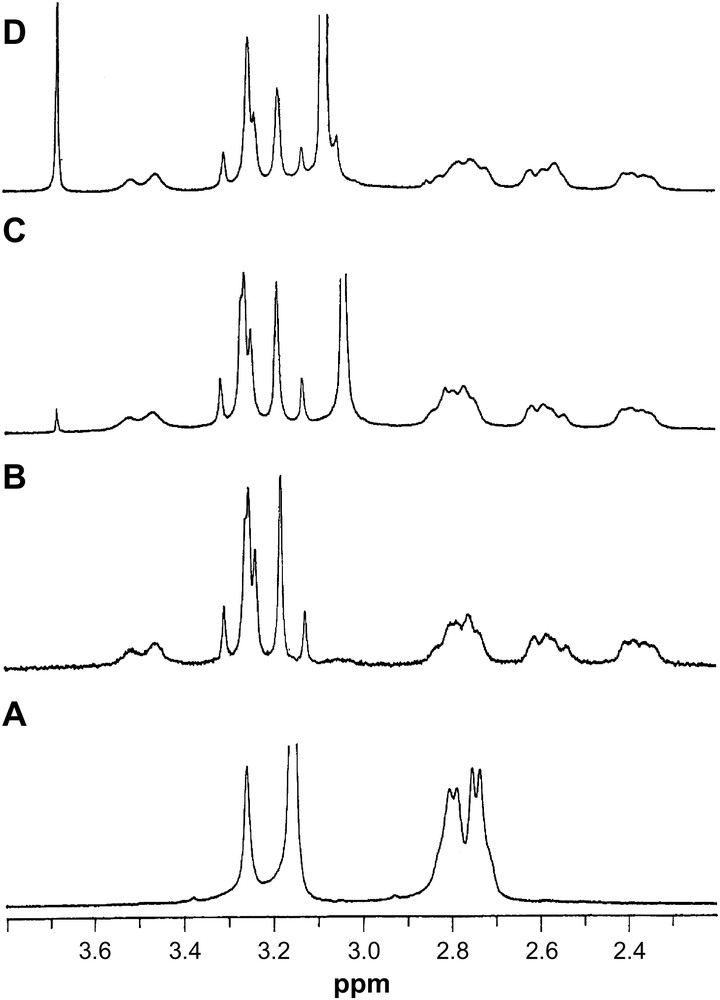
1H NMR spectra of (A) DTPA, pH = 9.60; (B) La–DTPA, 1:1, pH = 9.60; (C) La–DTPA–IDA, 1:1:2, pH = 10.12; (D) La–DTPA–IDA, 1:1:4, pH = 10.20.
Assigned chemical shifts and species proposed in the 1H and 13C NMR spectra of La3+ and Y3+ with IDA, DTPA and DTPA + IDA in D2O
| Species | pH | Chemical shifts δ (ppm) | ||||
| 1H | 13C | |||||
| Acetate proton | Backbone protons | CO | CH2COO | NCH2CH2 | ||
| IDA | 3.60 | 3.52 | – | 170.8 | 48.4 | – |
| 10.00 | 3.04 | – | 179.5 | 52.0 | – | |
| DTPA | 9.60 | 3.25, 3.15(s) | 2.80, 2.78(d) | 178.5 | 58.6(4), 57.0(1) | 51.7, 51.0 |
| 2.75, 2.73(d) | ||||||
| La:IDA (1:1) | 4.10 | 3.51 | 173.0(w) | 50.0(w) | ||
| 1:9 | 9.50 | 3.31 | 178.8 | 51.1 | ||
| Y:IDA (1:7) | 4.09 | 3.49 | 171.7 | 49.5 | ||
| 1:7 | 9.50 | 3.11, 3.68 (N–H) | 185.9 | 52.27 | ||
| La:DTPA (1:1) | 9.60 | 2 AB(q)(4) | 2.78–2.75, 2.61–2.53 | 181.4, 180.7(4) | 63.4(4) | 57.7, 56.4 |
| 3.25(s)(1) | 2.39–2.28 | 181.2(1) | 65.4(1) | |||
| Y:DTPA (1:1) | 9.60 | 2 AB(q)(4) | 2.82–2.78, 2.58–2.54 | 181.49, 180.36(4) | 66.1, 63.6 | 58.03, 56.07 |
| 3.26(s)(1) | 2.40–2.35 | 180.52(1) | 63.1 | |||
| La:DTPA:IDA (1:1:2) | 10.12 | 2 AB(q)(4) | 2.81–2.77, 2.61–2.59 | 180.4, 180.7(4) | 65.1, 63.4 | 57.7, 56.4 |
| 3.25(s)(1) | 2.39–2.34 | 181.2(1), 179.5 | 51.8 | |||
| La:DTPA:IDA (1:1:4) | 10.20 | 2 AB(q)(4) | 2.84–2.71, 2.61–2.55 | 181.3, 180.6(4), 181.2(1) | 64.7, 63.4 | 58.8, 57.5, 56.4 |
| 3.25(s)(1) | 2.40–2.36 | 179.5, 178.5 | 51.7, 51.5 | |||
| Y:DTPA:IDA (1:1:2–1:1:4) | 10.12 | 2AB(q)(4) | 2.80–2.76, 2.59–2.57 | 181.7, 180.6 | 66.2, 63.8 | 58.2, 56.2 |
| 3.25(s)(1), 3.03(s) | 2.39(b) | 180.7, 179.4 | 63.3 | 51.8 |
The 1H NMR spectra of unbound DTPA consist of two peaks at 3.15 ppm and 3.25 ppm for the four terminal acetate and the middle acetate, respectively, and the two groups of peak at 2.80–2.79 and 2.75–2.73 ppm for the ethylene protons. This is in contrast to that of singlet pattern observed for the ethylene protons in Ref. [37]. The difference in splitting pattern of the ethylene protons in these two studies is due to the differences in the resolution of spectra at 90 MHz in Ref. [37] and at 300 MHz in our study. In the complex [La(DTPA)]2−, two different AB patterns for the four terminal acetate protons and a singlet for the middle acetate protons were observed, which is consistent with the earlier report [37]. The two different AB patterns for the acetate protons are indicative of long-lived metal–nitrogen but with differing distances among the Ln–donor bonds. Nonequivalence of the Ln–donor bonds also have been observed for the Ln–HEDTA and MEDTA (N-methylethylenediaminetriacetate) complexes [38]. The singlet pattern for the middle acetate proton is due to the exchange averaging, while the multiplet for the ethylene protons is due to the existence of two different ethane conformations, which interconvert by wagging via an eclipsed transition state [39].
Similar chemical shifts were observed for the [Ln(DTPA)]2− (Ln3+ = La, Lu and Y), but a heptadentate structure with unbound middle acetate group has been proposed [37]. 139La NMR studies are also consistent with the heptadentate structure for the [Ln(DTPA)]2− complex [40]. However, crystal structures of [Ln(DTPA)]2− and the 2D-NMR techniques (1H-COSY and 2D-exchange spectroscopy) of some paramagnetic lanthanides (Pr3+, Eu3+ and Yb3+) suggested octadentate coordination for the DTPA, binding via five carboxylate groups and three nitrogen [1,2,39]. Our 1H NMR and the TRLFS studies are consistent with the octadentate coordination for the DTPA.
The 1H NMR spectra of the La–DTPA–IDA at ratios of 1:1:1–1:1:2 and pH = 10.20 have peaks that are also in the 1:1 La–DTPA system plus an additional peak at 3.04 ppm, which is the chemical shift value of the free IDA protons at this pH, indicating no formation of the ternary complex at these concentration ratios. With an increase in concentration of IDA, as in a solution ratio of 1:1:4 (Fig. 5) although the La–DTPA part of the spectrum shows similar chemical shift, a new broad peak between 3.08 and 3.05 ppm indicating the formation of the ternary complex [La(DTPA)(IDA)]4−. It is difficult to detect the peak for the free IDA because the resonance for free IDA falls under the resonance for the complexed IDA. No significant shift of DTPA signals in the formation of the ternary complex [La(DTPA)(IDA)]4− reflects that there is no additional steric crowding around the La3+ cation on formation of the ternary complex. The AB pattern of the acetate protons of DTPA implies that the metal–nitrogen bond remain long-lived in the ternary complex, which is consistent with the formation of corresponding ternary complexes [Ln(EDTA)(IDA)]3− (Ln3+ = Pr, Eu and Yb) [6]. By contrast, the long-lived metal–nitrogen bond becomes short-lived with the formation of the ternary complex [Lu(EDTA)(IDA)]3− [41], indicating two different modes of formation of the ternary complexes across the series. A small peak at ca. 3.68 ppm is due to the slow exchange of N–H proton with the solvent.
The 1H NMR spectra of Y3+, which usually has a CN of 8.0, show expected shift of signals on complexation with the IDA and DTPA (Table 8). The spectra of Y–DTPA–IDA at ratios of 1:1:2 and 1:1:4 have in addition to the existence of the usual peaks for the Y–DTPA, a broad peak at 3.03 ppm due to the free IDA and a peak at 3.68 ppm, due to the slow exchange of the N–H proton with the solvent. No peak for the complexed IDA in the spectra of Y–DTPA–IDA indicates that the Y(DTPA)2− does not form ternary complex with IDA.
The 13C spectra of unbound DTPA show a carboxylate peak at 178.5 ppm, two methylene carbon peaks at 51.0 (2C α-position to middle N) and 51.7 (2C α-position to terminal N) and the two peaks at 57.0 (1C CH2COO) and 58.6 (4C CH2COO) ppm (Fig. 6). On complexation with La3+ the five equivalent carboxylate groups are split into three peaks at 181.4 and 181.7 ppm for the terminal acetate and at 181.2 ppm for the middle acetate with an intensity ratio of ca. 2:1:2, consistent with the binding of all five carboxylate groups. The spectra of La–DTPA–IDA at ratios of 1:1:1–1:1:2 (Fig. 6) show no peaks for the complexed IDA, indicating no formation of the ternary complex at these concentration ratios. The spectrum of La–DTPA–IDA at a ratio of 1:1:4 has three peaks at 181.3, 181.2 and 180.6 ppm with an intensity ratio of ca. 2:1:2 for the binding of five carboxylate groups of DTPA and a new broad peak at 178.5 ppm, which is due to the formation of the ternary complex [La(DTPA)(IDA)]4−. The broadness of the peak indicates weakly coordination of the carboxylate groups of IDA to the metal cation, so that the one arm of the ligand coordinated to and detached from the metal rapidly. An additional peak at 179.5 ppm in the spectrum is due to the unbound carboxylate group of IDA.
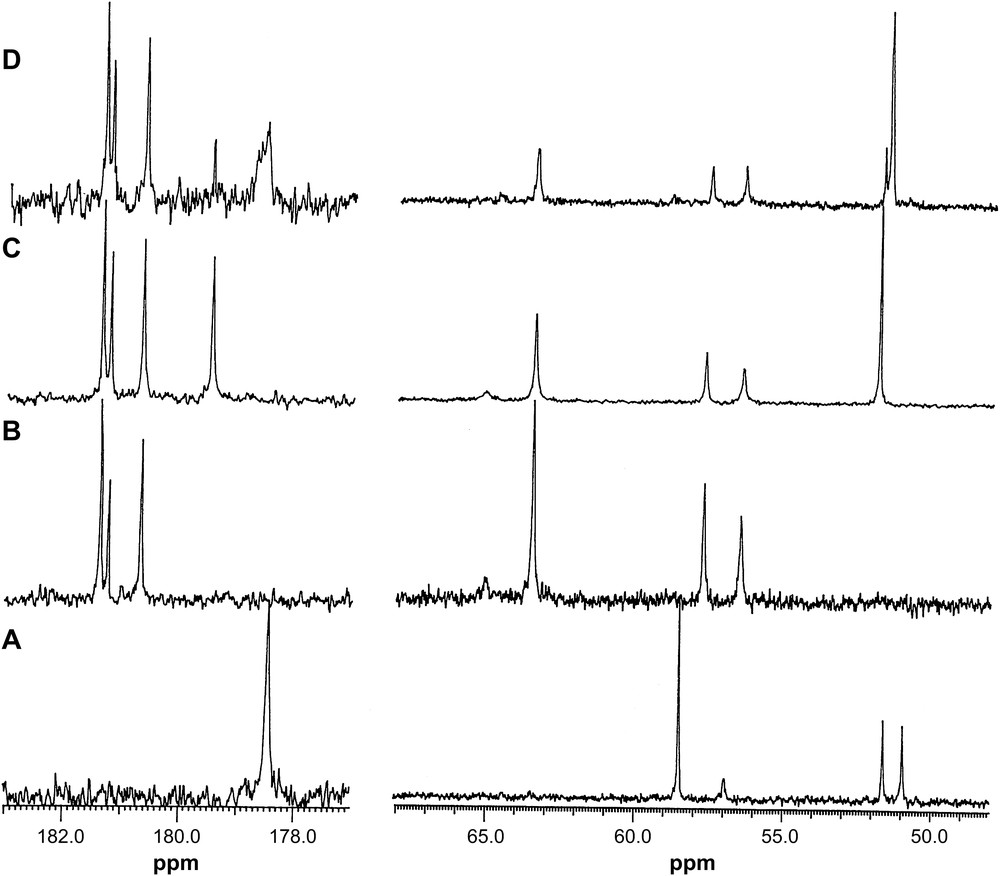
13C NMR spectra of (A) DTPA, pH = 9.60; (B) La–DTPA, 1:1, pH = 9.60; (C) La–DTPA–IDA, 1:1:2, pH = 10.12; (D) La–DTPA–IDA, 1:1:4, pH = 10.20.
The 13C NMR spectra of Y–IDA, Y–DTPA and the Y–DTPA–IDA complexes also support the finding of the TRLFS and 1H NMR studies. The species formed and the assigned chemical shifts are given in Table 8. The 13C NMR spectra of IDA and DTPA show the expected shifts of signal downfield on complexation. The absence of complexed IDA peak in the spectra of Y–DTPA–IDA at ratios of 1:1:2–1:1:4 is consistent with no ternary complex formation for Y3+. The proposed structure of the ternary complex Eu(DTPA)(IDA)4− showing the binding modes of the DTPA and IDA is given in Fig. 7.
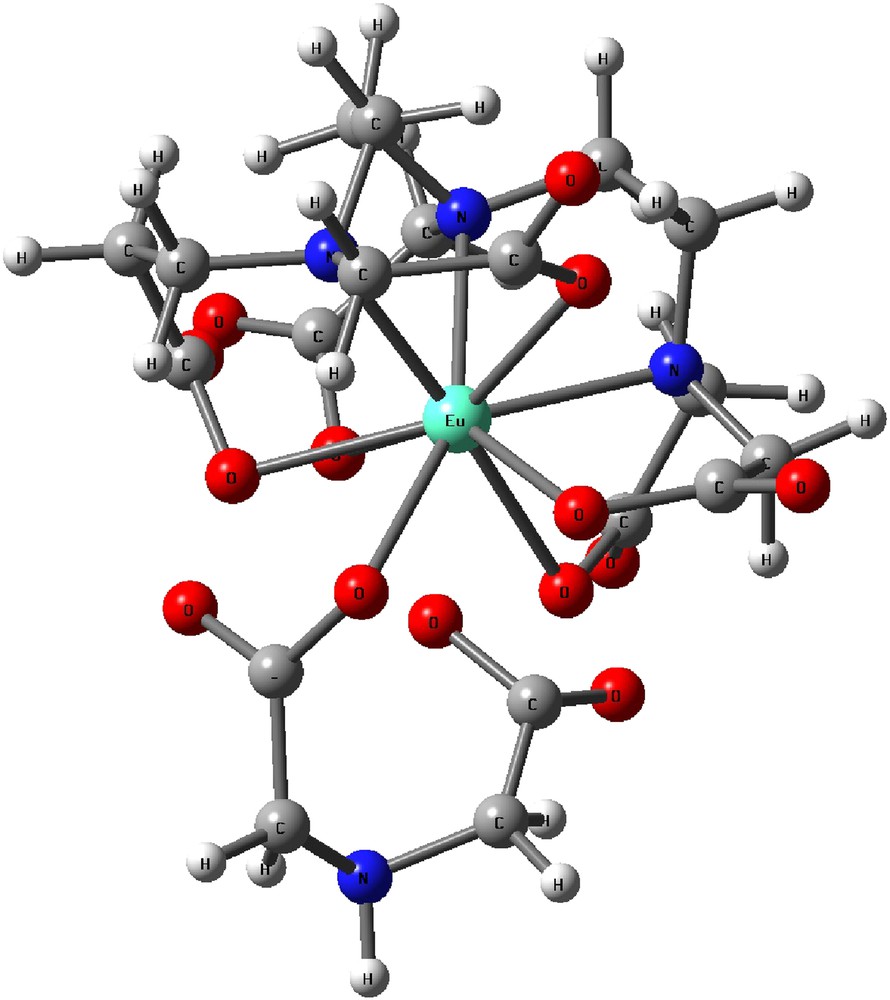
Proposed structure showing the binding of DTPA and IDA in the formation of the ternary complex Eu(DTPA)(IDA)4−; atoms: nitrogen – blue; oxygen – red; europium – green; carbon – grey. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
4 Conclusion
The present studies establish the formation and the coordination modes of the binary and of the ternary complexes of trivalent lanthanides and the actinides with DTPA and DTPA + IDA. The size of the metal cations and the steric requirement of the ligands seem to play an important role in the formation of these ternary complexes. In the binary 1:1 complex, the DTPA binds via five carboxylates and three nitrogen atoms, while in the ternary 1:1:1 complex, DTPA does not undergo any structural change and binds by the same eight coordination sites with IDA binding weekly via one carboxylate group. The metal–nitrogen bond is found to be remained long-lived in the formation of these complexes. The smaller lanthanides do not form ternary complexes with DTPA + IDA. The residual water of hydration of ca. 1.0 ± 0.5 for the binary and ca. 0.7 ± 0.5 for the ternary complexes are consistent with the results of the NMR study (1H and 13C).
The distribution measurement studies of Am3+, Cm3+ and Eu3+ (tracer concentrations) with DTPA and IDA in 6.60 m (NaClO4) also support the formation of the ternary complex, [M(DTPA)(IDA)]4− in the temperature range 0–60 °C. The complexation thermodynamics of these complexes reflected the significant contributions of a cation dehydration over that of the metal–ligand interaction contributions at such high ionic strengths. The high stability constant value of the ternary complex [M(DTPA)(IDA)]4− indicates that the ternary species plus the mixed chelate hydroxyl species can increase the solubility of the trivalent lanthanides and actinides in the waste tanks.
Acknowledgements
This research was supported by a USDOE, Office of Basic Energy Sciences contract. We gratefully acknowledge Dr. Bert Van De Burgt and Dr. Thomas Gedris for their assistance in data accumulations.


