1 Introduction
Molecular chemistry provides a “bottom-up” approach to produce new magnetic materials with interest for basic science as well as with promising applications [1–3]. From these materials, the ever-growing family of single-molecule magnets (SMMs) [3–5] stands out for its appeal to the research on the foundations of Quantum Physics. Single-molecule magnets are metal-organic clusters made of a magnetic core surrounded by a shell of organic ligands. One of the most studied SMM is Mn12 [6], whose core contains eight Mn3+ and four Mn4+ ions strongly coupled by oxygen ions giving rise to a spin S = 10. SMM are neutral entities that form molecular crystals bound by weak van der Waals interactions. Their basic magnetic properties (ground-state spin and magnetic anisotropy) are, however, characteristic of the isolated clusters. Indeed, they appear to be preserved in solution [7–9] even when they are deposited onto solid substrates [10–12]. In this respect, SMM can be seen as a close analogue to magnetic nanoparticles, with the advantageous difference of being monodisperse in size. The analogy was strengthened by the discovery, made in 1994 by Sessoli and co-workers [13], that Mn12 SMM shows magnetic hysteresis, i.e. magnetic memory, at liquid helium temperatures. The magnetic hysteresis does not result from long-range magnetic order induced by intermolecular interactions. Instead, it is the signature of the superparamagnetic blocking or freezing of the molecular spins by the anisotropy energy barriers that hinder, and therefore, slow-down, the spin-flip (see Fig. 1). These clusters are, therefore, potential candidates to store information at the molecular level. Achieving this technological goal requires, however, that memory be preserved above room temperature, which in its turn depends on our understanding of the basic principles that rule the magnetic relaxation in these materials. Hysteresis in SMM turns out to be rather unconventional though.

Semi-classical picture of the spin reversal. At finite temperatures, the process involves the thermal population of excited spin states. Quantum tunneling via intermediate states, having the same energy at zero field, provides a short-cut of the energy barrier separating spin-up from spin-down states. As shown in the right-hand schematic picture, the molecular spin, once in an excited state, undergoes the classical Larmor precession at frequency ωL around the anisotropy axis or tunnels to the spin-down state having the same energy at a tunneling frequency Δ/ħ. In addition, it can decay towards lower lying states via the emission of lattice phonons, a process that determines the lifetime τ0 of the excited level. The interaction of the spin with its surroundings (phonons, nuclear spins, other molecular spins, etc.) perturbs and eventually destroys the coherent spin precession and tunneling. The “classical” contribution to the nonlinear dynamical susceptibility depends on the number of precession turns that the spin is able to make after being excited, thus providing a method to determine the decoherence time τΦ in units of the precession time 2π/ωL.
In the case of macroscopic magnets, hysteresis can be fully understood in terms of classical physical laws, which describe the dynamics of domain walls [14]. The same applies to nanosized magnetic particles [15] as well, at least at not too low temperatures (but see e.g. Ref. [16] for an exception to this statement). The hysteresis and, in general, the spin dynamics of SMM reveal by contrast signatures of fascinating quantum phenomena, which result from their very small size and the discreteness of their magnetic energy level scheme. In this respect, these systems are ideally suited to investigate the fuzzy borderline between the classical and quantum worlds [17,18]. In 1996, it was found that the magnetization reversal of Mn12 clusters becomes faster at magnetic fields where magnetic states with opposite spin orientation (i.e. spin-up and spin-down states) become degenerate in energy [19–21]. At these fields, the possibility of crossing the energy barrier by quantum tunneling (QT) provides a kind of short-cut to the magnetic relaxation process [22–25].
In the last decade, a great variety of experimental and theoretical tools have been applied to study quantum tunneling in SMM [3]. The dynamical or frequency-dependent magnetic susceptibility χ(ω) deserves to be mentioned, since it has become a conventional characterization technique in Chemistry laboratories. In fact, the onset of a cusp in the imaginary component χ″ represents the fingerprint of the SMM behaviour [3]. It is for this reason rather surprising that the nonlinear component of χ has been virtually ignored in this research field, more so if one considers the relevance of this technique in the study of other magnetic materials, such as classical or quantum spin glasses [26–29] and magnetic nanoparticles [30–33] where important dynamical effects are also observed.
Furthermore, it was expected that the nonlinear susceptibility could provide unique information on some aspects of the magnetic relaxation process of SMM that remain rather obscure. In 1996, García-Palacios and Svedlindh [34] predicted that the nonlinear dynamical susceptibility of classical superparamagnets, such as magnetic nanoparticles, can become very large for some frequencies and, in sharp contrast to the linear susceptibility, quite sensitive to the coupling of spins to their environment (lattice vibrations, conduction electrons, nuclear spins, etc., usually referred to as the “bath”). One, therefore, hopes that the same information might be extracted from this quantity also in the case of superparamagnets, such as SMM, showing quantum dynamics. For these materials, the coupling to the bath acts as the main source of decoherence [17,35–37] (see Fig. 1 for a qualitative explanation of this term), an effect that not only limits the observation of quantum phenomena to microscopic bodies but also constitutes the main limitation to their applications (for e.g. quantum information processing) [38–40].
The present work reviews some of the work that the authors have recently done on the nonlinear magnetic response of SMM [41–43]. The basic concepts behind the nonlinear susceptibility and experimental techniques required to measure it are described in Section 2. A major result, described in Section 3, is that the nonlinear susceptibility is dominated by a very large contribution, hitherto unforeseen, with no analogue in classical Physics. This contribution is associated with the extreme sensitivity of QT to external magnetic fields, which detune energetically the initial and final states. Therefore, whereas the ac linear susceptibility senses one of the aspects of QT: the fact that it gives rise to faster relaxation than classical mechanisms, the nonlinear response senses, in addition, another one: its fragility to environmental perturbations. In Section 4, we discuss how experiments performed varying the orientation of the crystal axis with respect to the applied magnetic field provide the first estimate of the decoherence time for thermally assisted tunneling. In the final Section 5, we list some of the main points and conclusions of this work.
2 Definition and experimental determination of the nonlinear susceptibility: field-dependent linear susceptibility and its harmonics
2.1 Definition of the nonlinear susceptibilities
For sufficiently weak applied static magnetic fields H, the magnetization of any material is approximately proportional to H, i.e. M ≈ χ1H. This is the definition of the so-called linear regime and χ1 (usually referred to as simply χ) is the linear susceptibility for H = 0. As the field strength is increased, the magnetization curve deviates from its initial linear dependence as it gradually tends to saturation. To account for this deviation, one must then introduce new terms, containing higher-order powers of H:
| (1) |
The new coefficients, χ3, χ5, … are called nonlinear susceptibilities, again for H = 0. Since M ≤ χ1H, the third-order nonlinear susceptibility must be negative. The absence of even-order terms simply reflects the fact that M must change its sign when the applied magnetic field is reversed. Obviously, χ2, χ4, … do not need to be zero, and in fact they are not, for magnetic fields other than zero. Eq. (1) is then generalized as follows:
| (2) |
It is clear from Eq. (2), that χ2, χ3, … can be extracted from the second, third, … derivatives of the magnetization evaluated at H = H0.
A second typical nonlinear effect is connected with the response to oscillating magnetic fields h = h0 cos(ωt). If, in Eq. (2) we simply replace H by H0 + h0 cos(ωt), the magnetization contains then terms proportional to the harmonics of the ground frequency ω (i.e. terms that oscillate in time with frequency 2ω, 3ω, etc.).
| (3a) |
Keeping for each harmonic the lowest order powers of h0, this leads to:
| (3b) |
Since they contain powers of the amplitude h0, these terms are very small under the usual experimental conditions available at commercial magnetometers. However, as we shall see below, they can be detected if the corresponding nonlinear susceptibilities become sufficiently large.
The previous discussion assumes that the spins are in thermal equilibrium. However, the definitions of the nonlinear susceptibilities can be extended to the case when time-dependent phenomena are important. The coefficients χn depend then not only on temperature and magnetic field but also on frequency. It is also necessary to distinguish between the real χn′ and the imaginary χn″ components of the nonlinear susceptibilities. As we shall see in the following sub-section, the experimental methods used to determine these dynamical nonlinear susceptibilities are almost direct applications of the two definitions Eqs. (2) and (3).
2.2 Experimental determination of the nonlinear susceptibilities
In our experiments, we applied two well-known methods to determine the nonlinear susceptibilities as a function of temperature, frequency, and magnetic field. These methods are described next.
2.2.1 Field-dependent linear susceptibility
For sufficiently small values of h0, and according to Eq. (3), the magnetic response to an oscillating magnetic field provides an experimental determination of the first derivative of the magnetization. In particular, for H0 = 0 and applying Eq. (1) (or Eq. (2)), we can write
| (4) |
This expression can be generalized to the real χ′ and imaginary χ″ components of the experimental susceptibility with coefficients χn′ and χn″, respectively. By measuring e.g. with a SQUID magnetometer, the dependence of χ near H = 0, it is possible to extract the nonlinear frequency-dependent susceptibilities at zero field. The method is illustrated by the left-hand side plot in Fig. 2, which shows how at sufficiently low fields the decrease of χ with increasing H follows approximately a parabola, in agreement with Eq. (4).
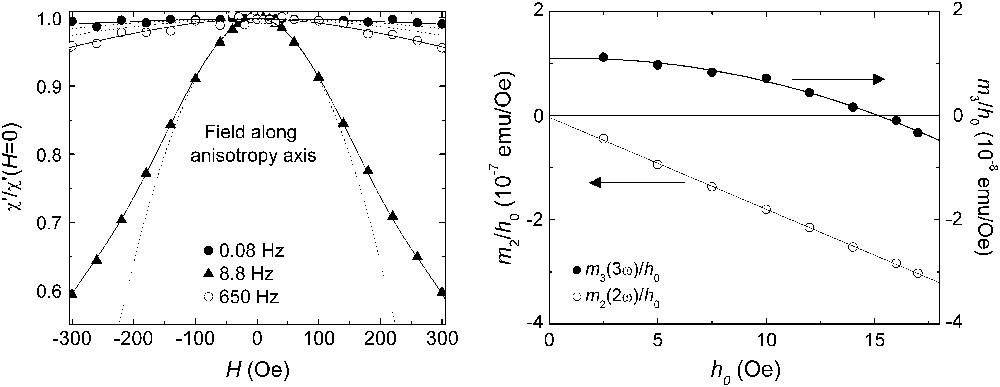
Two experimental methods to determine the nonlinear dynamical response of SMMs. Left-hand figure: real component of the magnetic ac susceptibility of a single crystal of Mn12Ac, normalized by its zero-field value, measured at T = 5 K under a dc longitudinal magnetic field and at several frequencies. Solid lines represent least-squares fits to polynomials, from which the nonlinear susceptibility χ3(H = 0,ω) is estimated. The parabolic approximation χ ≈ χ1 + 3χ3H2, which holds at sufficiently low fields, is shown by dashed lines. The figure on the right-hand side shows the amplitude of the second m2(2ω) and third m3(3ω) harmonics of the magnetic response of a sample of oriented Mn12Ac crystals, normalized by the amplitude h0 of the ac excitation magnetic field. Solid lines are least-square fits to second order polynomials. The nonlinear susceptibilities χ2(2ω) and χ3(3ω) are obtained from the slope of m2(2ω)/h0 vs h0 and from the quadratic coefficient of m3(3ω)/h0 vs h0, respectively.
2.2.2 Harmonics
This is by far the most broadly applied method to determine the nonlinear response of magnetic systems. The method is based on measuring the harmonics m2(2ω), m3(3ω), m4(4ω), etc. of the response to a strong oscillating magnetic field. This can be done on either “old-fashioned” hand-made susceptometers or by using, as it was our case, a commercial PPMS physical measuring platform. From Eq. (3b), it follows that the amplitudes of the different harmonics are m2(2ω) = (1/2)χ2(2ω) h02, m3(3ω) = (1/4)χ3(3ω)h03, and so on. Therefore, the analysis of harmonics provides a direct determination of the nonlinear susceptibilities.
Two words of caution are, however, to be mentioned here. First, usually the excitation signal also contains an harmonic “contaminations”. If, for instance, the excitation coil generates a field h0[(1 − δ)cos(ωt) + δ cos(2ωt)], with δ ≪ 1, the response m2(2ω) will contain an “spurious” term χ1(ω)h0δ cos(2ωt). In order to determine those signals arising solely from the sample, it is, therefore, necessary to measure m2 as a function of the amplitude h0 and to get from these data the term that is proportional to h02. The same applies to higher-order harmonics as well. An example of this experimental method is shown on the right-hand side of Fig. 2. This method also eliminates the contributions that higher-order susceptibilities of the sample might have on the lower order harmonic responses (compare the exact Eq. (3a) with the approximation (3b)).
The second aspect that should be mentioned is that the coefficients χ2(2ω), χ3(3ω), etc. that define the nonlinear susceptibilities measured by this method are not, in general, equal to χ2(ω), χ3(ω) obtained from the field-dependent linear susceptibility. They only coincide under conditions of thermal equilibrium but not when they depend on frequency. Nevertheless, the two can be easily calculated and the physical information they provide is very similar [42,43].
3 What is new? Quantum nonlinearity in single-molecule magnets
3.1 Linear ac susceptibility and resonant spin tunneling
As said in Section 1, the linear ac susceptibility χ1 has become a standard characterization technique in the field of molecular magnetism [3]. Here, we shall just recall the most fundamental aspects that characterize the linear response of SMM in order to help the reader in recognizing the new ingredients that are brought about by the study of the nonlinear components.
A typical measurement of χ1 as a function of frequency ω is shown in Fig. 3. As ω increases, a steep drop, or “blocking”, of the real susceptibility component χ1′ takes place, accompanied by the onset of a nonzero imaginary component χ1″. This behaviour can be approximated by the well-known Debye's laws.
| (5) |
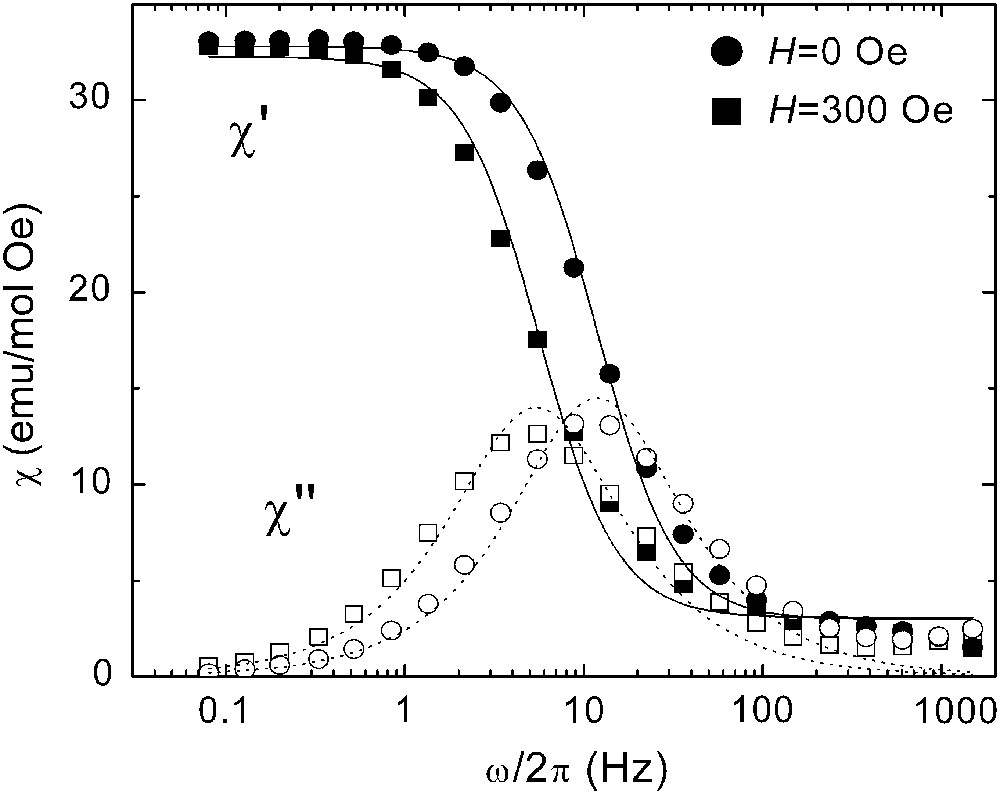
Magnetic susceptibility measured along the anisotropy axis of a single crystal of Mn12 acetate. Results are shown at zero bias (circles) and at H = 300 Oe (squares). Solid symbols correspond to the real component χ′ and open symbols to the imaginary component χ″. Lines are least-square fits to Debye's laws [Eq. (5)].
In a real sample, and despite the large uniformity in cluster size and stoichiometry that characterizes molecular crystals, there is always a certain distribution of relaxation times τ. Sources of these distributions are the dipolar interactions between the molecules [23] and the presence of crystalline defects [45] or disorder in the orientations of interstitial molecules [46]. In this context, an important advantage of ac susceptibility methods over other techniques, like time-dependent magnetization experiments, is that the magnetization of the sample remains stable and equals its thermal equilibrium value. This eliminates the influence of time-dependent demagnetizing fields, which usually lead to stretched exponential decays [47] and, therefore, contribute to broaden the distribution of relaxation times. Still, the susceptibility actually measured in the laboratory often deviates slightly from the pure Debye's laws given by Eq. (5). Therefore, when we refer to values of τ derived from this technique, we obviously mean averages over the clusters in a sample. By contrast, the theoretical description of the observed phenomena will mainly consider the situation of each of the clusters. Although the effect of the distribution can be easily introduced in any calculation, it adds little to understand the qualitative features observed, while adding a great deal of mathematical complexity. For this reason, we prefer to keep the discussion that follows to a simple level. In addition, samples of Mn12 contain always a fraction of the so-called “fast-relaxing” molecules [48], whose relaxation times are much shorter than those characteristic of the “standard” Mn12 clusters. In the temperature and frequency ranges of our experiments, these clusters contribute with their equilibrium susceptibilities (i.e. a flat response in χ′ and χ″ = 0, at least for frequencies below 600 Hz). The possibility of studying separately each type of molecule for a given crystal is another valuable feature of frequency-dependent susceptibility experiments. The experiments shown below refer only to the dynamical behaviour of the standard Mn12 clusters.
As it is already well-known, the variation of τ vs H (see Fig. 4) shows signatures of resonant spin tunneling [19–21]. Instead of a decrease of τ with increasing H, as predicted by classical laws of Physics, τ shows a series of minima centred at H = 0 and the other crossing fields for which quantum tunneling is allowed by the degeneracy of spin-up and spin-down states. Yet, we want to stress the fact that the overall shape of the χ vs ω curves are qualitatively the same in the quantum (H near 0) and classical limits (large H). The existence of QT is reflected only in the shift of this curve towards lower frequencies as H increases from zero. We shall next see that a very different situation arises in the case of the nonlinear response.

Magnetic relaxation time τ of Mn12 obtained from ac susceptibility measurements performed at T = 8 K. The solid line shows the behaviour expected for a classical spin [15]. The inset shows a close-up of the low-field region.
3.2 Nonlinear response of SMM: a new quantum phenomenon associated with QT
In order to better understand what makes the nonlinear response of SMM like Mn12 so singular, it is convenient to recall first how classical superparamagnets behave. Fig. 5(a) compares the variation with temperature of the linear χ1(ω) and nonlinear χ3(ω) susceptibilities of Co nanoparticles, with average diameter 1.4 nm (i.e. containing about 280 Co atoms each), self-organized in a matrix of alumina [49]. The linear component shows the familiar frequency-dependent blocking phenomenon we have discussed already, but now as a function of temperature. As can be seen in the lower panel of the same Fig. 5, the behaviour of the nonlinear counterpart is qualitatively similar: at high temperatures χ3′ attains its equilibrium limit, whereas below the blocking temperature it progressively tends to zero. As with the linear response, the blocking is marked also by the onset of a nonzero imaginary component χ3″. The only noticeable differences between the two are the reversed sign of χ3 with respect to χ1 and the sharper peak shown by the nonlinear susceptibility, which reflects the stronger temperature dependence of the equilibrium χ3T ∝ μ4/kB(T − θ)3, as compared to χ1T ∝ μ2/kB(T − θ). The main fact we would like to stress here is that, for these classical superparamagnetic nanoparticles, both χ1′ and χ3′ lie always below (in absolute values and within experimental uncertainties) their respective equilibrium limits.
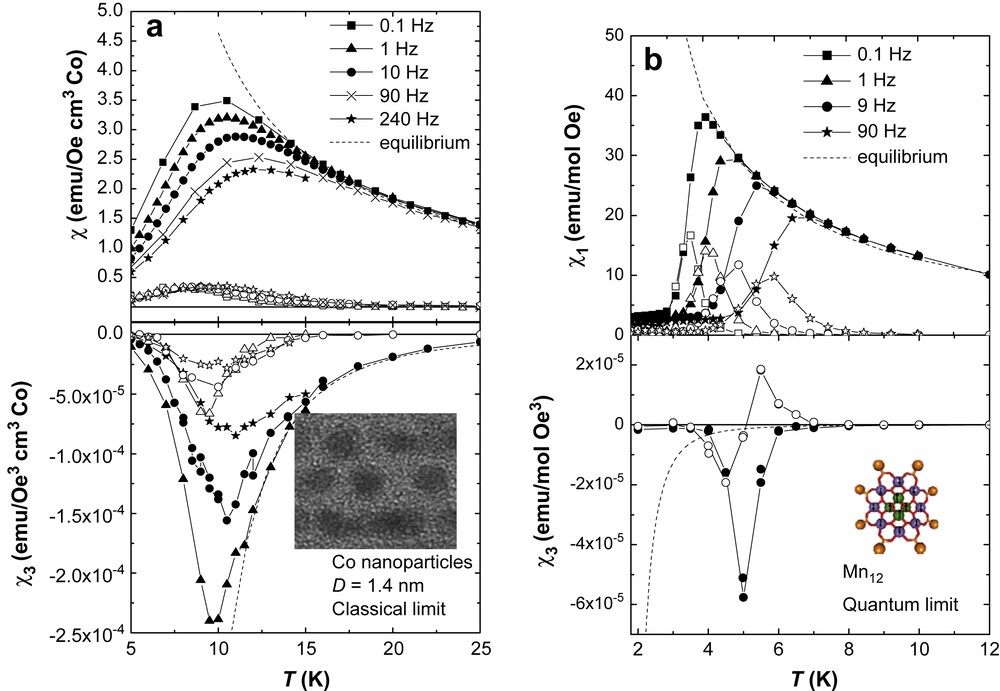
(a) and (b) show, respectively, the zero-field (i.e. for H0 = 0) ac susceptibility of 1.8 nm Co clusters and of Mn12 SMM. In both cases, the top panel shows the linear susceptibility data, whereas the lower panel shows the nonlinear susceptibility. Solid symbols are for the real component whereas the open ones represent the imaginary components.
Let us now turn our attention to SMM. In Fig. 5(b), we show the same χ1(ω) and χ3(ω) for Mn12 acetate as a function of temperature. As expected from the discussion following Eq. (5), the linear susceptibility differs very little with respect to that of classical superparamagnets. The blocking transition is just narrower on account of the very narrow distribution of relaxation times characteristic of SMM crystals. By contrast, the behaviour of the nonlinear susceptibility is markedly different. Near the blocking temperature (i.e. when τ ≈ 1/ω), the two components χ3′(ω) and χ3″(ω) attain very high values, crossing well above the equilibrium curve (dotted line). Clearly, an additional contribution, absent in the nanoparticles, becomes dominant in the case of SMM. We argue next that this contribution is directly associated with the existence of quantum tunneling of the spins.
To understand the origin of this additional nonlinearity of SMM, it is better to discuss data measured at fixed temperature, as a function of frequency, as we did for the linear susceptibility. These data are shown in the top panel of Fig. 6. The applied ac and dc magnetic fields were parallel to the anisotropy axis. We see that an enormous nonlinear response (about 65 times larger than χ3T) shows up in the neighbourhood of ωτ = 1. This contribution is furthermore unexpected in the framework of classical Physics. Indeed, classical predictions, shown in the bottom panel of Fig. 6, behave very differently, χ3′ decreasing monotonically from ≈χ3T for ωτ ≪ 1, to zero for ωτ ≫ 1. Interestingly, a nearly identical result is obtained when the experiments are performed on a powdered sample, provided of course that these results are normalized by the appropriate equilibrium limit [41].

Top panel: Zero-field nonlinear susceptibility χ3(ω) of an Mn12 acetate single crystal measured at T = 5 K along the c axis (easy axis for magnetization). The susceptibility data are normalized by the equilibrium χ3T and the frequency is multiplied by the relaxation time τ obtained at the same temperature from frequency-dependent linear susceptibility data [41]. Lines are theoretical predictions that include the presence of quantum tunneling [42]. Bottom panel: theoretical predictions for the classical case (i.e. no tunneling) [50].
What causes this enormous nonlinear response? To answer this question, we need to introduce a basic theoretical background for the nonlinear dynamical susceptibility. Appropriate expressions for χ3(ω) and χ3(3ω) can in fact be derived from the Debye equations that describe the linear response. We skip the details of the calculation (that can be found in Refs. [42,50]) and give just its final result. It looks as follows:
| (6) |
| (7) |
We see then that the magnitude of χ3 not only depends on τ, as the linear susceptibility does, but also on the magnitude and sign of its derivatives with respect to H. In other words, the nonlinear response senses how much the relaxation process is affected by the application of external magnetic fields. It is convenient to recall here that Eq. (6) applies only to the nonlinear susceptibility measured at zero field (i.e. for H0 = 0 in Eqs. (2) and (3a,b) that define the nonlinear susceptibilities).
Let us consider next what Eq. (6) gives for classical and quantum spins. For simplicity sake, we shall consider first a magnetic field parallel to the anisotropy axis, i.e. Ψ = 0. The effect of transverse magnetic fields will be considered with some detail in the following Section 4. For classical spins, ∂2τ/∂Hz2 is small and <0 (see the solid line in Fig. 4) because the magnetic field decreases the energy barrier separating spin-up and spin-down states. The variation of χ3 with frequency, shown in the bottom panel of Fig. 6, resembles then very much the curves obtained for the linear susceptibility. This is in agreement with the observations made for magnetic nanoparticles, for which a classical model seems appropriate indeed. For quantum spins, like that of SMM, the possibility of tunneling has to be taken into account. It leads to minima of the relaxation time τ near the crossing fields, in particular at H0 = 0, as shown by Fig. 4. For this reason, ∂2τ/∂Hz2 becomes >0. But in addition, it can be very large, since the external field detunes very effectively the two states between which quantum tunneling takes place. In other words, for magnetic fields of equal magnitude the changes in the relaxation rates are much larger for quantum spins than for classical spins. To make this argument quantitative: the experimental nonlinear response can be accounted for reasonably well (see the solid lines in Fig. 6(a)) by simply making g|| ≈ −260 in Eq. (6). This has to be compared with the classical prediction that gives [50] g|| = 1. The enormous sensitivity of tunneling probabilities to the energy tuning of states is, therefore, at the origin of the large nonlinear response of SMM. It is a pure quantum mechanical phenomenon, without classical analogue.
A simple way of checking the validity of this interpretation is by exploring how χ3 depends on Hz. Indeed, for sufficiently large bias, tunneling processes are suppressed and, therefore, a classical situation must be recovered. It is obviously necessary to revert to the method of measuring the harmonics χ3(3ω) of the magnetic signal (cf Section 2.2) since the dependence on the magnetic field can no longer be used to derive the nonlinear susceptibility. The disadvantage of this method is that the third-harmonic signals measured are rather small, yet as seen in Fig. 7, measurable. Near Hz = 0, χ3(3ω) is much larger than the equilibrium χ3T, showing the existence of the quantum contribution described in the preceding paragraph. With increasing Hz, the blocking of tunneling paths leads to an equally rapid decrease of χ3, which becomes smaller than our detection limit for Hz > 500 Oe, in agreement with the classical predictions.

Nonlinear susceptibility χ3(3ω) of a sample of oriented single crystals of Mn12 acetate as a function of the external bias at T = 8 K: •, χ3′(3ω) measured at ω/2π = 2 kHz; ×, equilibrium χ3T = (d2χ1T/dHz2)/6.
Obviously, the quantum nonlinear contribution must be recovered back when the magnetic field brings new magnetic states into degeneracy thus making tunneling possible again. To investigate experimentally this “switching-on and off” of the quantum nonlinearity, it is better to use the second harmonic χ2(2ω), which is considerably larger than χ3(3ω). This quantity is displayed in the lower panel of Fig. 8. The data neatly show how, at every crossing magnetic field, Hn = 0, H1, 2H1, with H1 ≈ 4100 Oe (marked by vertical dotted lines in Fig. 8), quantum tunneling becomes a “source” of magnetic harmonics [43].
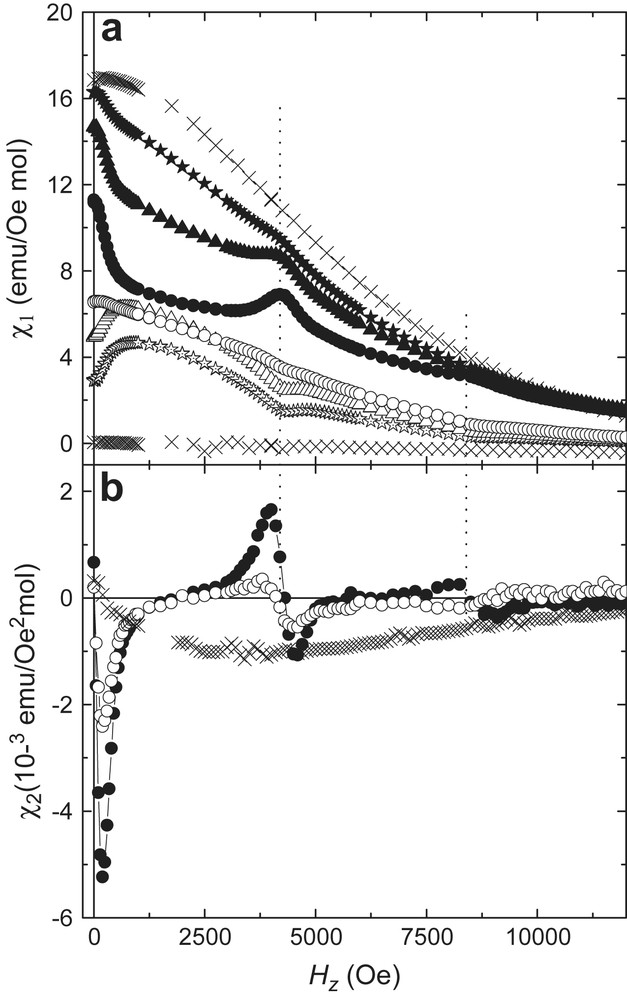
(a) Linear susceptibility of a sample of oriented Mn12 acetate single crystals measured at T = 8 K. ×, ω/2π = 1 Hz (equilibrium χ1T); ★, 500 Hz; Δ, 1 kHz; •, 2 kHz. Solid symbols represent the real component, open ones the imaginary component. (b) Second harmonic susceptibility measured at the same temperature. • and ○ are χ2′(2ω) and χ2″(2ω) at 2 kHz, respectively, whereas × is the equilibrium χ2T = (dχ1T/dHz)/2.
Concluding this section, the experiments show the existence of a purely quantum nonlinearity in SMM. This nonlinear phenomenon is associated with the strong sensitivity of quantum tunneling to the application of external magnetic bias fields. Its existence reflects also the subtle way in which the nonlinear susceptibility depends on the relaxation rates, very different to the case of the linear response. The nonlinear susceptibility depends not only on τ but also on its derivatives with respect to the applied magnetic fields. This quantity provides, therefore, a privileged tool to ascertain the existence of quantum tunneling in complex materials, like magnetic nanoparticles, where the distribution of sizes usually hinders a direct experimental determination of the relaxation times. As we shall see in the next section, the nonlinear response of SMM also contains information on how much the environment perturbs the quantum (and classical) spin dynamics.
4 Experimental determination of decoherence for thermally assisted tunneling
The term decoherence refers to the perturbation exerted by the “rest of the world” on the evolution with time that the state of quantum system would follow where it isolated [17,35–37]. For the particular case of an SMM flipping its spin via thermally activated QT, the situation is illustrated schematically in Fig. 1. Using a simple semi-classical picture, once the spin attains an excited magnetic state (say approximately +m) its dynamics would consist of the combination of two processes. The first, a classical precession around the anisotropy axis, is caused by the torque exerted on the spin by the effective magnetic field associated with the magnetic anisotropy, when the two are not parallel to each other (i.e. for states other than m = ±S). This is a very fast oscillation with a period τL = 2πħ/gμBHK ≈ 3 to 4 × 10−12 s, where HK is the anisotropy field. The second is the slower quantum tunneling coherent oscillation between the degenerate +m and −m states, with a period τT = ħ/Δm, where Δm is the tunnel splitting of the excited doublet. These processes are perturbed by the interaction with microscopic degrees of freedom, like phonons, giving rise eventually to the decay towards one of the two ground states, either +S or –S, for timescales longer than the lifetime τ0 of the excited states1.
The decoherence time τΦ sets the timescale in which these two dynamical processes are destroyed by the environment. If τΦ exceeds the period of tunneling τT then the spin undergoes some (approximately τΦ/τT) coherent tunnel oscillations before decaying to the ground state. Obviously, τ0 provides an upper bound to τΦ, but it is also possible that τΦ ≪ τ0. It is curious that different models proposed to describe the thermally assisted tunneling of SMM do not agree on the question of whether these quantum oscillations actually take place or not2. And, remarkably, that the relaxation time τ for the overall process depends little on the ratio τΦ/τ0: what actually determines τ is the fact that the spin has, just before decaying, nearly equal probabilities of pointing up or down. For the same reason, experiments that determine τ, for e.g. the frequency-dependent linear susceptibility, do not provide much information on τΦ. For clarity sake, let us emphasize that what we discuss here is the possibility that the spin undergoes coherent dynamics once it has reached an excited state with a very fast tunneling rate and just before it decays back to the ground state, and not the coherence of the spin reversal as a whole, which, being a phonon mediated relaxation process, is obviously incoherent.
As we argue next, and in contrast with the linear susceptibility, the nonlinear response turns out to be much more dependent on the behaviour of the spin during the intermediate steps of the relaxation process. Starting from the Landau–Lifshitz equation, which describes the evolution with time of the magnetization of classical superparamagnets, García-Palacios and Svedlindh showed that the nonlinear susceptibility strongly depends on the magnitude of the parameter λ that measures the damping of the Larmor precession by the environment [34,50,51]. This dependence is shown in Fig. 9 for the case of anisotropic axes oriented at random. A very large classical contribution to the dynamical nonlinear susceptibility is expected for underdamped (λ < 0.1) spins. It should be emphasized that this contribution has the sign reversed with respect to the quantum contribution discussed in the previous section: the quantum χ3′/χ3T > 0, whereas the classical χ3′/χ3T < 0, because quantum tunneling changes the sign of g|| with respect to the classical situation. The difference between the two can be appreciated by comparing the classical predictions for randomly oriented axes with experiments performed on a powdered sample of Mn12 clusters. The enormous quantum contribution fully dominates the experimental data near ωτ = 1, overshadowing the classical term that contains the information we seek on damping and decoherence.

(a) Nonlinear susceptibility of classical spins with anisotropy axes at random, calculated by the method described in Refs. [34,50] at U/kBT = 70/5 and for three different values of the damping parameter λ. (b) Nonlinear susceptibility of a powder sample of Mn12 acetate measured at T = 5 K. In the horizontal scale, the angular frequency ω is multiplied by τ = 1.31 × 10−2 s, obtained from frequency-dependent linear susceptibility data measured at the same temperature. Notice the reversed sign of these data with respect to the classical predictions.
Fortunately, it is still possible to separate the quantum and classical contributions by varying the angle Ψ between the applied magnetic field and the anisotropy axis. As we have seen in the previous section, the quantum contribution to χ3 arises from the strong dependence of tunneling on external bias, which leads to a very large g|| (remember Eqs. (6) and (7)). On the other hand, it is g⊥ that depends on the damping parameter [51]. As a result, the quantum contribution is maximum at Ψ = 0 (it is actually proportional to cos4Ψ) whereas the classical contribution peaks at around Ψ = π/4, as the results of numerical simulations show (see Fig. 10). Therefore, if the latter contribution was important in SMM, we would expect to see a change in the sign of χ3′ with increasing Ψ.
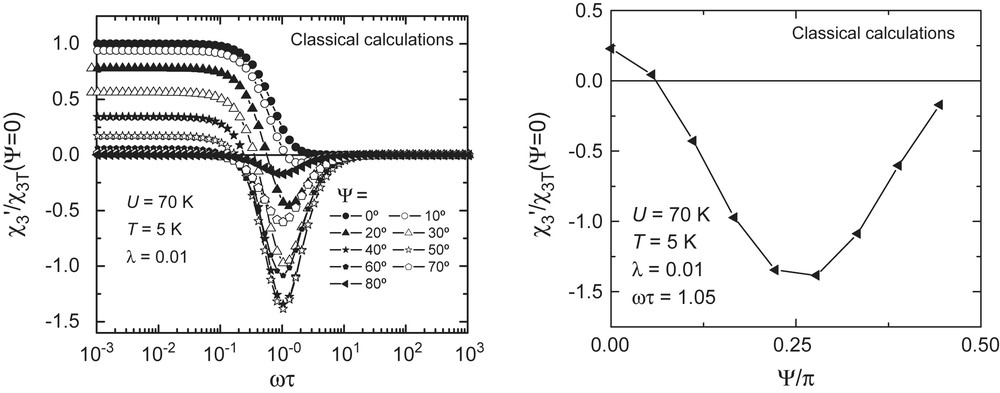
Left: Numerical calculations of the nonlinear susceptibility of classical spins [50] for different orientations of the magnetic field with respect to the anisotropy axis. The figure on the right shows that the reduced nonlinear susceptibility χ3′/χ3T (Ψ = 0) measured near the condition ωτ = 1 peaks (in fact it becomes most negative) at Ψ ≈ π/4.
Experimental results measured on a single crystal of Mn12 acetate are shown in Fig. 11. Increasing the angle Ψ leads indeed to a rapid decrease of the maximum χ3′/χ3(Ψ = 0). Yet, no change of sign is apparent. In fact, the data are proportional to cos4Ψ within the experimental uncertainties. The lack of any measurable classical contribution to χ3 is also supported by the fact that results obtained on powder samples are virtually identical to those measured on a single crystal for Ψ = 0 (compare Figs. 6 and 9). This provides an upper bound for the maximum |g⊥| or, equivalently, a lower bound for λ > 0.01.
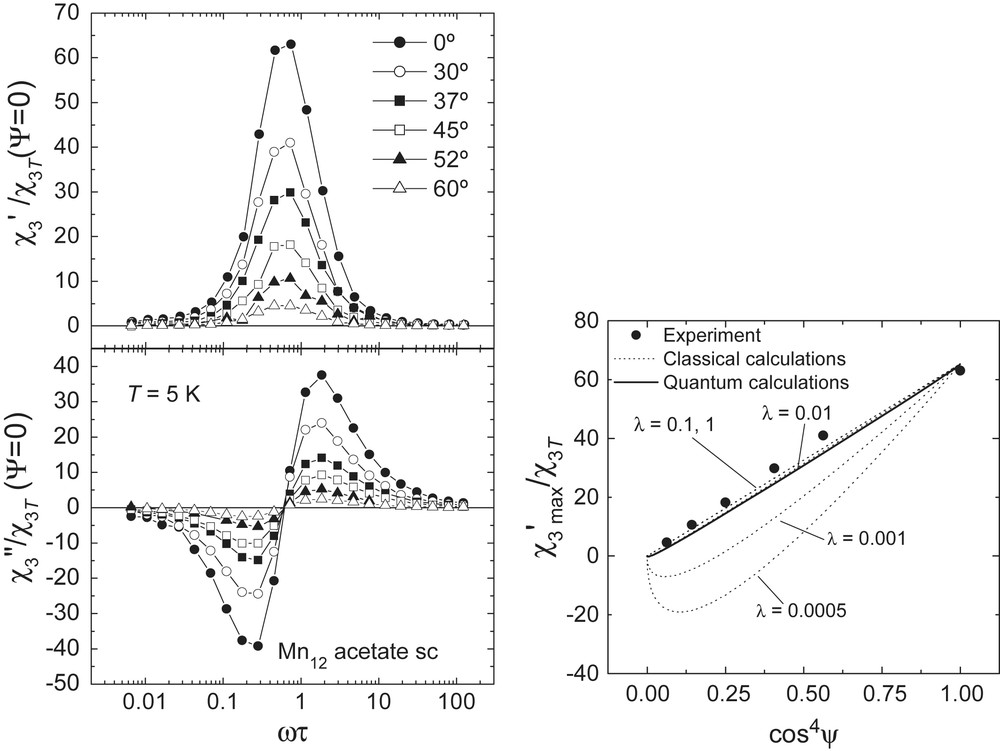
Left: Nonlinear susceptibility vs frequency at T = 5 K for a single crystal of Mn12 acetate. Results are shown for different angles Ψ between the applied field and the anisotropy axis. The data are normalized by the equilibrium χ3T measured at Ψ = 0. The relaxation time τ was obtained from linear susceptibility data at the same temperature (see Fig. 9). The solid lines are obtained using Eq. (6) with g|| = −260, to account for the existence of quantum tunneling, and g⊥ = 0. Right: evolution of the maximum of χ3′(ω) with Ψ at the same temperature. The dashed lines are calculated with Eq. (6) using g|| = −260 and g⊥ = F(λ)/2, where F is a function defined in Refs. [50,51]. The solid line corresponds to theoretical calculations with a Pauli quantum master equation (see Refs. [23,41] for details).
What these results tell us with respect to decoherence? In a pure classical picture of magnetic relaxation, the Larmor precession is limited by the lifetime τ0 of the excited magnetic states. Under these conditions, and for the parameters (temperature and activation energy) applicable to Mn12, λ ≈ 0.04 τL/τ0. We estimate [41,51] τ0 ≈ 3 × 10−8 s from the pre-factor of the Arrhenius law, whereas τL ≈ 3–4 × 10−12 s. This would then lead to λ ≈ 4 × 10−6 and, therefore, to a huge classical nonlinear response that we do not observe. The experiments indicate that the effective λ is not determined by τ0 but by another timescale τΦ that is much shorter than it. In fact, if we make λ ≈ 0.04 τL/τΦ and use the lower bound for λ > 0.01 estimated from the experiments, we get τΦ < 10−11 s. In other words, decoherence proceeds much faster than the decay towards lower energy states.
This “decoherence” time can be compared with the relevant tunneling times for Mn12. From the size of the activation energy, it follows that tunneling takes place predominantly via states with m ranging from ±4 to ±2 [20,21,52]. The tunneling time τT = ħ/Δm can be then calculated by using the tunnel splittings Δm determined by direct diagonalization of the spin Hamiltonian. For |m| = 2, 4, we find Δm ≈ 0.7–0.02 K, that is τT ≈ 10−11 to 4 × 10−10 s. Therefore, it seems that no coherent tunneling oscillations occur during the thermally activated relaxation process, despite the fact that the tunneling levels “live” much longer than the tunneling times. It is worth mentioning that decoherence rates of order τT (thus in agreement with our estimate) were predicted in the model of Ref. [23]. The fast decoherence of tunneling via thermally populated states follows in fact rather generally from the application of Heisenberg's uncertainty principle. For a more rigorous and detailed description of these issues we direct the reader to Refs. [23,42].
5 Conclusions
We have given a short overview of nonlinear magnetic phenomena found in SMM. Compared with the linear ac susceptibility, which has become the standard tool to investigate SMM behaviour, the nonlinear response offers additional information on how the relaxation times are affected by applied magnetic fields and, in this way, about the nature of the relaxation process. In particular, the existence of quantum tunneling and its strong sensitivity to external bias, gives rise to an enormous contribution to the dynamical χ3(ω), which has no classical analogue. This new quantum phenomenon, quantum nonlinearity, should not be restricted to SMM, but it could be observable in other systems, like magnetic clusters or nanoparticles, relaxing via QT. In this way, the measurement of χ3(ω) provides a relatively simple and unambiguous method to determine whether quantum tunneling plays a role in the magnetic relaxation of these materials, for which standard relaxation experiments do not always provide a definite answer [53].
In addition, we have shown that the nonlinear response provides also some information, albeit indirect, on decoherence times. In fact, we have derived the first, to the best of our knowledge, estimate for the decoherence time τΦ for thermally activated spin tunneling. Our data suggest that τΦ is several orders of magnitude shorter than the lifetime of the tunneling states. Compared with other techniques usually employed to directly measure τΦ, like spin-echo experiments with ESR [40], the nonlinear susceptibility has the advantage of its simplicity and of directly providing information on those states that contribute most to the relaxation process at zero field. Notice that, for H0 = 0, the excited states involved in the thermally activated tunneling process of Mn12 have m ≤ 4 (i.e. far from the ground-state doublet with m = ±10) and have energies of about 60–65 K (equivalent to 1.3 THz) above the ground state [20,21]. This means that the direct application of spin-echo experiments to this case can be very problematic if feasible at all. In this respect, the nonlinear susceptibility technique provides a poor man's tool to investigate decoherence phenomena in SMM at zero field.
The results described in this paper certainly do not exhaust the interesting possibilities offered by the study of nonlinear magnetic phenomena in SMM and other related magnetic materials. The evolution with the cluster size of the nonlinear susceptibility can be very useful to investigate the transition between the quantum and classical worlds [54]. As the number of atoms per cluster increases, the magnetic levels become more and more closely packed in energy. When they begin to overlap, the quantum nonlinear susceptibility should tend to vanish. The advantage of this technique is that it provides information for monodispersed clusters as well as for nanoparticles with a distribution of sizes. The same transition between the quantum and the classical limits can be observed by increasing the “damping” of the spins, i.e. the strength of the interaction between spins and the “bath”. Experimentally, this can be achieved by studying clusters having the same structure, spin, and anisotropy but different surroundings: diverse crystal structures, clusters embedded in conducting matrices, etc. Taking into account the results described in Section 4, it would also be of interest to investigate diluted samples of SMM, for which the energy of dipolar interactions might become smaller than the homogeneous broadening of the spin levels. Under the appropriate conditions (fast tunneling and weak dipolar interactions), tunneling via lower lying excited states should eventually give rise to even larger nonlinear responses and enable the observation of the classical contribution, overshadowed in Mn12 acetate by the quantum contribution, and its dependence on damping. Another interesting issue to be investigated is the behaviour of the nonlinear susceptibility of SMM crystals that undergo a phase transition to a long-range ordered magnetic phase [55–58]. As we have shown in Section 3, the dynamical nonlinear susceptibility can become very large at finite temperatures. This behaviour can be erroneously interpreted as the onset of a phase transition for e.g. a spin-glass phase. Our results, therefore, highlight the importance of carefully distinguishing dynamical effects from truly equilibrium phenomena. The information gained in model systems like SMM, can then help understanding the physical behaviour of more complex materials, such as arrays of interacting nanoparticles [31,32] as well as “classical” or “quantum” spin glasses [27–29]. Finally, these phenomena might also be relevant for applications of molecular nanomagnets in e.g. magneto-optical devices or as magnetic field sensors, for which the nonlinear effects can become important.
Acknowledgements
This work has been partly funded by projects CUNABI, from DGA, NAMESBI, from the Spanish “Acción Estratégica en Nanociencia”, and MAT2005/1272 from Spanish MCyT. Support from the European Network of Excellence MAGMANet is also acknowledged.
1 Notice that we refer here to the lifetime of the excited states through which tunneling takes place and not to the pre-factor of the Arrhenius law that describes the variation of τ with temperature. At sufficiently high temperatures, as those considered in the present work, the two are of the same order of magnitude. For a detailed definition of the pre-factor and its relationship with the lifetimes of excited levels. See e.g. Ref. [42].
2 More specifically, in Ref. [23] it is rigorously shown that “coherent” oscillations do not occur even in the most favourable situation of τT being much shorter than τ0.


