1 Introduction
Selective extractions of active pharmaceutical ingredients from plant-based materials have increased in recent years due to the high consumer demand. The world trading volume of phytopharmaceuticals was approximately 100 billion US Dollars in 2011 [1]. In other areas, such as the cosmetic and food industry, growth rates of up to 6 % for the coming years are expected [1]. Benefits of plant extracts compared to synthetic products are, in addition to the public acceptance, the opportunity to obtain complex compounds economically. One example is the production of secondary metabolites, such as mono-, di- and sesquiterpenes, which can either not be produced synthetically or not economically. Extraction of these valuable materials and the subsequent purification are not carried out target-oriented and are mostly empirically driven with only few experimental examinations [2]. Thus, there is no systematic procedure for the design of the overall processes.
To meet economic and environmental requirements for the production of herbal substances, also in future, needs optimized processing. Therefore, this publication will focus on the purification of plant extracts as representative for the efficient handling of complex mixtures.
In general, design and set up of industrial processes are divided into several development phases, like basic and detail engineering, equipment procurement, installation and start-up, and system operation [3]. The aim is to arrive at optimal process conditions at an early stage, since changes become more expensive the further development has progressed [3]. Therefore, an attempt is made using a conceptual process design (CPD) to arrive at an optimal process design for the separation sequence very early in process development, and in spite of still low information content (Fig. 1).
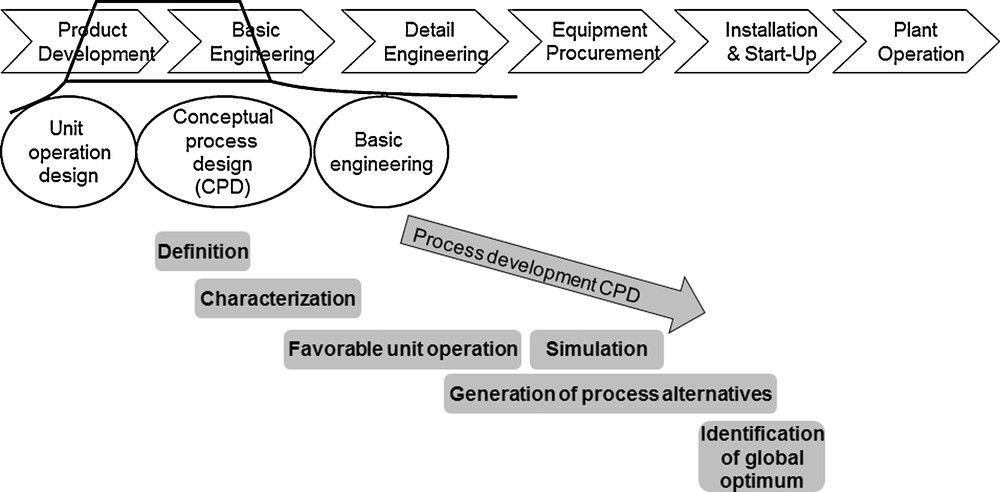
Conceptual process design according to Josch and Strube [3].
For this to happen, the process design has to be model-based, because this is the only way to find the process optimum fast and cost-effectively [4–6]. Depending on the modeling depth, either physicochemical properties or only separation factors are needed. These can either be retrieved from databases (e.g. Dortmunder Datenbank [DDB], DIPPR or Reaxys), calculated by means of thermodynamic theories (UNIFAC and COSMO-RS) or determined experimentally.
This approach has already been established for multicomponent mixtures with small molecules and is considered state of the art [7–9]. In this work, it will be assessed how this methodology can be transferred to complex mixtures with the objective to generate an optimal separation sequence relatively early in process design. This task is complicated by the fact that those multicomponent mixtures consist of many compounds from a variety of compound classes, for which at least in part neither substance data nor molecular structures are known. Therefore, a systematic approach is to be developed for characterization and determination of the required physical properties for complex mixtures. This systematic process for determination of physical properties will be performed on technical sample systems from industry. The sample systems including yew needles, fennel fruits and sage leaves were chosen to represent several industries in an optimal way. The target component from yew needles (10-deacetylbaccatin III) provides the starting material for semi-synthesis of the breast cancer drug taxol [10]. Fenchone and anethole are target components from the fennel fruit which are mainly used in the cosmetic and phytopharmaceutical industry. Most valuable substances in sage leaves are carnosol and carnosic acid, which are predominantly applied as antioxidants and preservatives in the food industry.
2 Materials for the determination of physicochemical properties
2.1 Raw materials
In this paper, the raw material systems yew needles, fennel fruits, and sage leaves were considered as examples, representing different parts of a plant as main sources and at the same time displaying different chemical classes (e.g. mono- and di-terpenoids, alkaloids or phenolic substances) for the determination of product properties for complex molecules.
In the following chapter the utilized raw materials yew, fennel and sage are defined and the compounds to be isolated from the individual plant matrix are shown in Table 1. The experimental methods for characterization of complex mixtures have been published in detail in earlier publication and are therefore not described in this work [2,3,11].
Sample systems.
| Fennel (Foeniculum vulgare) | Salvia (Salvia officinalis) | European yew (Taxus baccata) | |
| Localisation | Fruit | Leaf | Needle |
| Target component | Trans-anethol, fenchone | Carnosic acid, carnosol | 10-deacetylbaccatin III |
| Class of side components | Terpene: monoterpenoids Phenols: phenylpropanoids | Tricyclic diterpene, tannine | Various alkaloids |
| Industrial application | Cosmetics Nutraceuticals Phytopharmaceuticals | Nutraceuticals Phytopharmaceuticals | Phytopharmaceuticals |
2.1.1 European yew
Basically, yew represents a plant category containing a variety of yew species. Literature, for example, differentiates between the European, Pacific, Canadian, Japanese, Mexican, or Chinese yew [12]. All of them have in common to contain toxic components, like taxin B, or therapeutic compounds 10-deacetylbaccatin III and taxol [13]. Until 1990, the breast cancer therapeutic taxol was extracted from the bark of the pacific yew (Taxus brevifolia), where it can reach concentrations up to 0.1 mg/g [14]. As the tree grows slowly and does not survive the removal of the bark, this procedure is neither sustainable nor economic, as the demand for taxol cannot be satisfied that way. Therefore, today taxol is produced either biotechnologically or by partial synthesis from 10-deacetylbaccatin (10-DAB) or baccatin III [15]. Harvesting only the needles allows the tree to provide continuously raw material during each growing period.
This work focuses on the isolation of 10-deacetylbaccatin III (in the following abbreviated as 10-DAB) [13] from yew needles. 10-DAB belongs to the chemical class of taxanes. The yew's side component spectrum consists mainly of toxins, e.g. taxin A, B, C, or other terpenes, like cephalomannine and baccatin III.
2.1.2 Fennel
Fennel (Foeniculum officinalis) belongs to the family of Apiaceae [16] and is used as vegetable, spice plant and in therapy. Of special interest is its therapeutic use due to the high content on essential oil and here especially on components like anethole, fenchone and estragole. Fenchone and anethole have therapeutic use related to their mucolytic effect and digestive function against cold and stomach problems, however also their aromatic properties are used in soaps, perfumes, and in oral care. Therefore, these two substances are defined as main components of fennel. Other compounds, e.g. camphene, myrcene, pinene, phellandrene, terpinene, cymene, terpineol or estragole are considered as side components [16].
2.1.3 Salvia
Sage (Salvia officinalis) belongs to the family of Lamiaceae [17]. The plant acts as a strong antioxidant due to the radical-scavenging properties of the target compounds carnosic acid, carnosol and rosmarinic acid. In addition carnosic acid possesses antimicrobial properties. Therefore, sage extracts are often used to treat infections of oral and pharynx mucosa or gingivitis. Furthermore, it contains a number of side products, like thujone, camphor, cineol and oleanolic acid, with thujone and camphor being mainly responsible for the typical aromatic smell of sage leaves [18].
The valuable substances occurring in sage can be allocated to different chemical classes such as di- and tri-terpenes, or flavonoids. Carnosic acid and carnosol are diterpenes, whereas thujone, camphor and cineol represent monoterpenes and oleanic is a tripene substance. Besides the already mentioned antioxidant effect, sage also shows anti-inflammatory and antihydrotic properties, which is why sage extracts are used in e.g. mouthrinse, deodorants or creams. Also herbal teas are made from sage leaves to cure gastrointestinal tract diseases [19]. The target compounds carnosol and carnosic acid are widely used in food industry as antioxidants [20].
3 Approach to determine physicochemical properties of complex mixtures
As shown in Fig. 1, the challenge in conceptual process design (CPD) of complex molecules lies in correct determination of the product parameters required for a qualified process simulation. Therefore, in line with a systematic protocol, the approach laid out in Fig. 2 will be applied.

Process design complex mixtures.
Data generation for the process simulation can be conducted in two ways:
- • feed characterization;
- • product parameter determination of single compounds, where parameter determination is segmented into:
- ∘ data base search,
- ∘ calculation of product parameters,
- ∘ experimental parameter measurements.
The feed characterization includes the measurement of characteristic values for the various unit operations, e.g. boiling curves, distribution coefficients, hydrophobicity, etc. for the complete complex mixture. As shown in previous publications [3], the feed characterization can be used to conduct thermodynamic equilibrium assessments of individual unit operations with relatively small amounts of starting material relatively fast and effectively. For example, the boiling curve of a mixture is determined to assess the feasibility of a distillation, distribution coefficients are measured for a liquid-liquid extraction, chromatography requires hydrophobicities and isoelectric points, and crystallization or precipitation need solubility properties of mixtures, as can be taken from Table 2. It is not necessary to determine the equilibrium parameters for all unit operations, because it can be estimated on the basis of available product parameters, which unit operations are at all thermodynamically feasible for product separation/purification. For example, the determination of boiling curve is hardly necessary, if the desired compound is a solid. In the same way, solubility experiments for liquids are useless, as is the determination of partition coefficients for gases.
Feed characterization.
| Unit operation | Equipment | Measuring parameters | |
| Distillation | Boiling curve | ||
| Liquid-liquid extraction | Partition Coefficient | ||
| Reversed/normal phase chromatography | Hydrophobicity | ||
| Crystallization | Solubility |
For the experimental parameter determination of single components, it has to be checked first whether the structures of the target and side components of the extract are known. If that is not the case, a qualified amount of extract has to be prepared via solid-phase extraction, which then allows one to produce fractions of the pure compounds by multidimensional chromatography. In a first step the extract is pre-purified on a preparative column. Following that, pure compounds can be isolated by further chromatographic fractionation, as is schematically depicted in Fig. 3 [2–4].
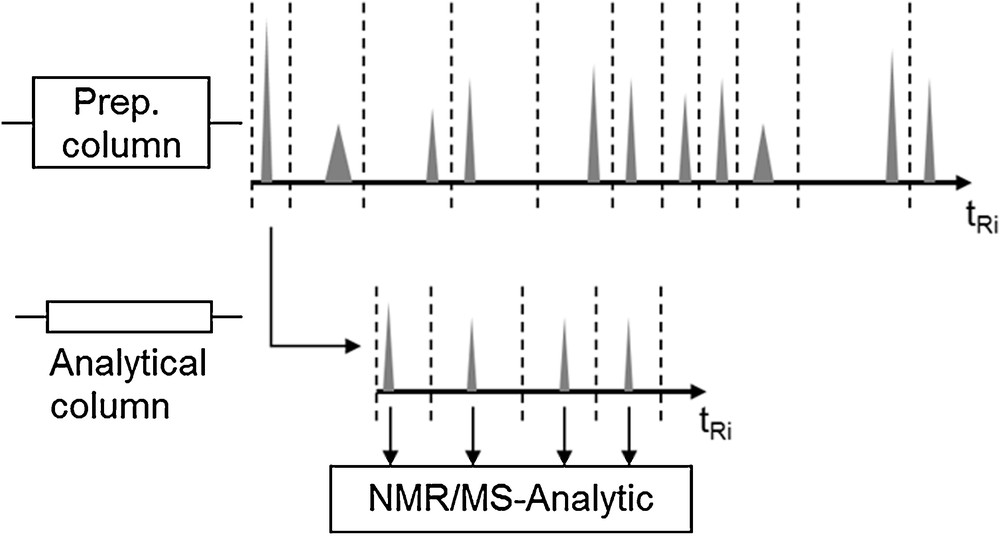
Multidimensional chromatography, according to [5].
These fractions can then be structurally identified via MS, Raman, IR and NMR spectroscopy [21].
In case the compounds are known, the accessible databases are searched for compound data. These can include databases like Reaxys, Dortmunder Datenbank, or DIPPR [22–24]. If no compound data can be found, the next step is their calculation on the basis of available thermodynamic models. Typical examples used in this work are group contribution methods and the COSMO-RS model [25]. A prerequisite for experimental determination of physicochemical properties is access to sufficient amounts of pure target and side compounds. Methods for determination of some important product parameters and required amounts are listed in Table 3.
Methods for determining physicochemical properties.
| Physicochemical properties | Methods for determining properties | Required amount of substance |
| Melting temperature and enthalpy of fusion | Differential scanning calorimetry | 100–500 mg |
| Solubility measurements | Non-isothermal HPLC method | < 10 g |
| Partition coefficient of pure target component | Shake flask experiments | < 10 g |
| Boiling point | Differential scanning calorimetry Distillation process Ebulliometer | 10–15 mL |
| Enthalpy of evaporation | Differential scanning calorimetry | 1 mL |
| Relative density | Pycnometer | 5 mL |
| Vapour pressure | Isoteniscope | N/A |
| Viscosity | Capillary viscometer | 5 mL |
The data in Table 3 show that up to 50 g of a pure compound may be necessary for the determination of the physicochemical properties. As many compounds are not commercially available at all or very expensive with prices in the tens of thousands Euro range, an option is presented herewith to generate the reference material from the respective raw material. Starting point in each case is the solid-liquid extraction of the raw material with suitable solvents. From the extract, the required amounts of pure compound can be gained by preparative chromatography. Goal is to get access to the required amounts of high purity material more cost effectively than by purchase from commercial sources, which sometimes lack the necessary purity criteria. It is not the goal at this stage to arrive at an optimal industrial process, which is the purpose of the total development concept, but well executed, it provides an excellent starting base.
Target compound concentrations of 0.2–4% [5] in plant tissue require 20–30 kg raw material to provide the necessary amounts of the pure compounds for the determination of the product parameters. Efficient process design and execution clearly show their worth already at this initial stage.
In the following chapters, the systematic approaches for product parameter determination will be shown using yew, fennel, and sage as examples. In particular, the objective is to apply specifically the available databases and calculation methods for physicochemical properties on complex molecules, their comparison as well as pointing out their limitations.
The experimental determination of these properties will be described in future publications, to propose a common standard for other working groups, who are interested to contribute to expand physicochemical properties data bases.
4 Thermodynamic fundamentals
Physicochemical properties serve as a basis for the simulation of processes development [26]. The following chapter describes various methods for the calculation of these properties comparing the methods for their applicability with complex mixtures such as plant extracts. For the description of physicochemical properties, e.g density, viscosity etc. often the critical temperature Tc, the critical pressure Pc, the critical volume Vc and the acentric factor as characteristic constant of a compound are required [26]. As the calculation of these properties depends on these values, a reliable determination of the critical parameters is important. The options for experimental determination of these parameters are limited, as many compounds disproportionate or denature before they reach a critical point. This is why for the determination of critical points also suitable equations-of-state or group contribution methods are used. In this chapter, only a short overview is given. For more detailed information, the specific literature should be inspected [26]. Critical temperature, critical pressure, and the critical volume can be determined via group contribution methods like those from Lydersen [27], Ambrose [28], Joback and Reid [29] or Constantinou and Gani [30].
The approach by Joback and Reid only needs the molecular structure. The equations for the calculation of the critical parameters are as follows:
| (1) |
| (2) |
| (3) |
The acentric factor ω, being a measure for the deviation from the ideal spherical shape and describing orientation-dependent intermolecular interactions, is defined as
| (4) |
| (5) |
To narrow the margin of error, a similar compound with known boiling point can be used as reference. The calculation of melting point and melting enthalpy is difficult compared to other physicochemical properties, as they depend on crystal structure, molecular interactions and molecular symmetry. Melting enthalpy is always a function of the melting point. As group contribution methods lose the information on molecular symmetry, they cannot be applied. An approximation on melting enthalpy and melting point is possible via the Clausius–Clapeyron equation.
| (6) |
The standard Gibbs enthalpy and enthalpy of formation, which are required for calculating reaction enthalpies and chemical equilibria, can also be calculated with the Joback and Reid group contribution method. The necessary equations are as follows.
| (7) |
| (8) |
Other pure compound properties like vapour pressure, density, viscosity, polarity or mixed properties like vapour-liquid, liquid-liquid, solid-liquid equilibria can be determined with gE models like UNIFAC, NRTL, COSMO-RS or with equations of state like PS-SAFT and CPA EoS.
For the description of complex molecules in particular a modified UNIFAC model and a COSMO-RS model have shown their effectiveness [31]. With these models, it is also possible to describe thermodynamic properties of a multicomponent system. Therefore, these methods will be discussed in more detail in the following chapter.
4.1 UNIFAC and modified UNIFAC model
So far, systems for the assessment of thermodynamic properties based on the group contribution method, like the UNIFAC model, have proven themselves [26]. The UNIFAC model is based on the fact that the number of all chemical compounds is much larger than the number of different molecule groups, from which they are composed. Therefore, a large number of chemical compounds can be developed from a relatively small number of functional groups [32].
Fig. 4 shows the breakdown of ethanol molecule into a CH3, a CH2, and an OH-group. In the UNIFAC model, a compound mixture is not considered as a mixture of molecules, but a mixture of molecule groups. Interactions between molecule groups are treated in the same way. The type of interaction only depends on the functional group and not on the compound, in which it is contained. Analogous to the UNIQUAC model, the activity coefficient, which can be used to describe thermodynamic properties, consists of an entropic and an enthalpic term [31] and is defined as follows.
| (9) |
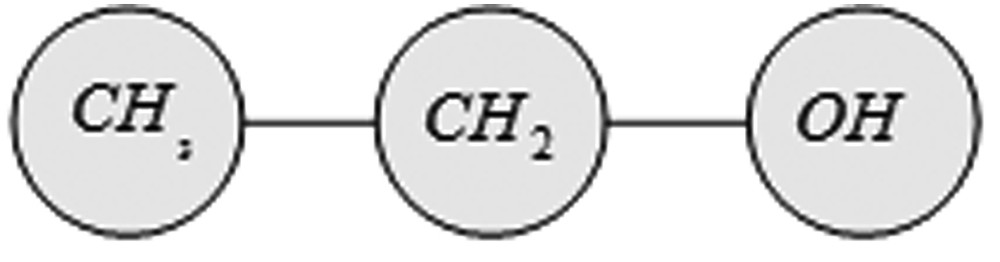
Breakdown of the ethanol molecule into its functional groups.
The entropic term sums up all effects, which relate to molecular size and shape and is described as combinatorial contribution . This combinatorial contribution can be calculated as follows.
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
Φi are the volume and Θi the surface contributions, ri the volume and qi the surface parameters, by which the volume and surface contributions can be calculated using a suitable bias. Volume and surface parameters can be generated from X-ray structural data or from simple geometric correlations and can be taken from the literature [33].
The enthalpic term sums up all effects resulting from energetic interactions between the functional groups and is called residual contribution. For its calculation, the following equation is needed.
| (15) |
By introducing the group activity coefficient it is possible to separate molecular interactions in the mixture from the interactions in the respective pure substances. It is defined as
(16)
| (17) |
| (18) |
Θm are the surface and Xm the molar contributions. By the definition of the interaction parameter (Ψnm) of the main groups,
| (19) |
The modified UNIFAC model builds on the same basic equations, however the volume part of the entropic term is modified to better describe strongly asymmetric and complex molecules.
(20)
(21)
The exponent ¾ was found empirically [31]. To better represent temperature dependencies, the interaction parameter is expanded by a polynomial extension.
| (22) |
A further improvement of the modified UNIFAC model over the conventional approach is the extension of the main- and side-group parameters. More than 1000 parameters are published in literature [34]. This large database is another advantage of the UNIFAC model. In particular, the extended group contribution methods provide good results for many terpenes and flavonoids. Nevertheless, in case of too complex molecules, they fail also. Therefore, one goal of this work is to check, for which main- and side components of the already mentioned compound systems the group contribution methods are still applicable.
4.2 COSMO-RS
The Conductor-like Screening Model for Real Solvents (COSMO-RS) Model belongs to the group of continuum solvation models. The model calculates properties of pure compounds and mixtures on the basis of quantum-mechanical calculations and statistical thermodynamics [35]. In the continuum solvent model, solvent molecules are substituted by a homogeneous dielectric continuum and the transfer of a molecule into a fixed position of the liquid phase is determined. The COSMO-RS model assumes that the solvent behaves like an ideal electrical conductor, and thereby the protective charges generated by electrostatic interactions between dissolved particle and solvent do not expand through the solvent, but are retained on the contact surface between the particle and the solvent. To calculate the behavior of real solvents, these protective charges are used for an approximation of the interaction energies. First in this process, a molecule geometry is generated and from that the protective charge density is determined, as can be seen in Fig. 5. For the COSMO-RS model it is necessary to average the charge densities of neighboring segments, because the calculation is performed with an effective contact area. This averaging of charge densities is called σ-profile and is characteristic for each molecule.
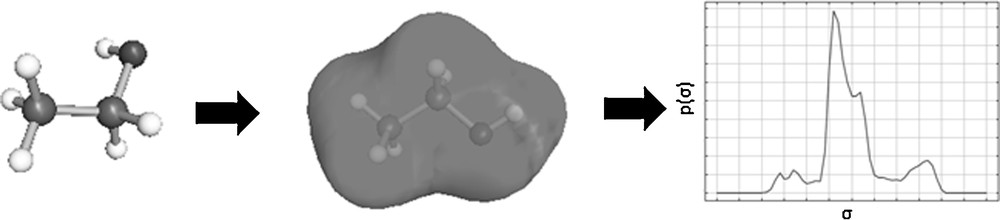
Procedure with COSMOS-RS according to [22].
Simplifying, it can be said that the COSMOS-RS model allows the calculation of the molecule properties on the basis of the characteristic distribution of its protective charges. For example, with this model, the chemical potential of a molecule can be determined by integrating the chemical potential of all surface segments via σ-profile and by adding it to an ideal and combinatorial contribution as can be seen in the following equation.
| (25) |
From here, activity coefficients can be calculated, which requires the chemical potential of the pure components and the component in the mixture as shown in the following equation.
| (26) |
5 Databased physicochemical properties
As described in the earlier chapters, physicochemical properties of target and side components are first searched in databases. In this work, the databases Reaxys, DIPPR und Dortmunder Datenbank are used, as can be seen in Fig. 6.
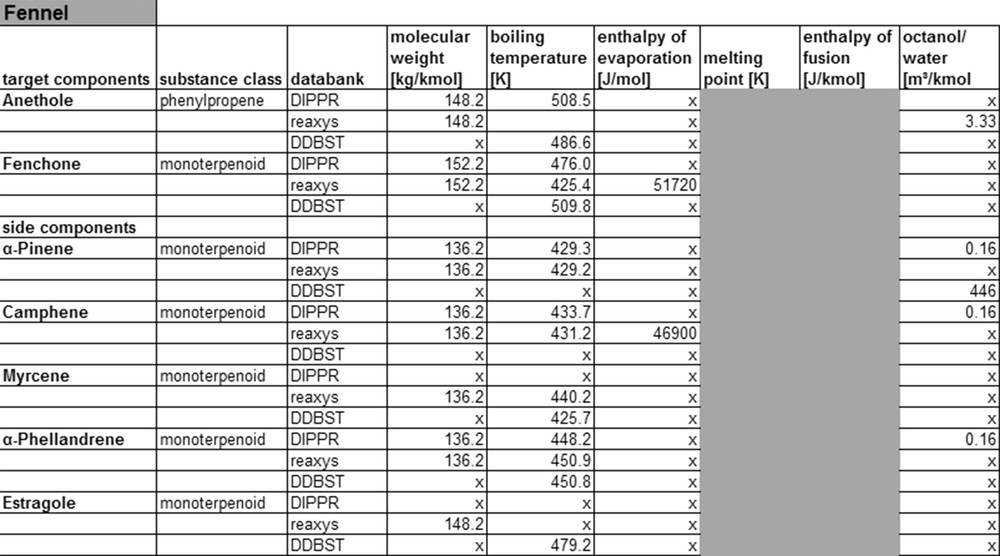
Fennel property data from data banks.
Generally molar mass, dynamic viscosity, critical temperature, critical pressure, critical volume, melting point, boiling point, freezing point, molecular volume of the liquid, polarity (relative as octanol/water-partition coefficient), enthalpy of formation, free Gibbs formation enthalpy, entropy, melting enthalpy, enthalpy of evaporation, combustion enthalpy, solubilities (in various solvents) and the virial coefficients were determined.
In order to reduce the number of compound data for the listing in the table, only molecular weight, boiling- and melting-temperature, evaporation and melting-enthalpy, and the octanol/water-partition coefficient are considered, as those data are relevant for the design of at least one unit operation, and they have somewhat similar behavior. The Kow value in this context is a measure for the polarity of a substance and is defined as the partitioning of a substance in an octanol and a water phase. The shaded areas indicate that melting enthalpies and temperature are determined only for solids, while boiling temperature and enthalpy of evaporation are only determined for liquids and gases.
As can be taken from Fig. 6, sufficient substance parameters exist for the main and side components of fennel. The databases Reaxys and DIPPR are larger and therefore allow to find more substance data than in the Dortmunder Datenbank. It should be noted that all three databases considered show little information on enthalpy of evaporation and the octanol/water-partition coefficient. Another deficiency of the databases is the lack of information on the experimental conditions applied during the measurements, as no common methods are used. Therefore, differing values exist in the different databases for the same compounds, as can be seen looking at boiling point data, for example.
For the main and side components of sage, less substance data are available than for fennel, see Fig. 7. This can be explained by the fact that the substances from sage belong to the class of diterpenoids, which are considerably more complex than mono-terpene substances. On the other hand, sage ingredients are less well researched in literature. The same applies when looking at the substance data for yew compounds.
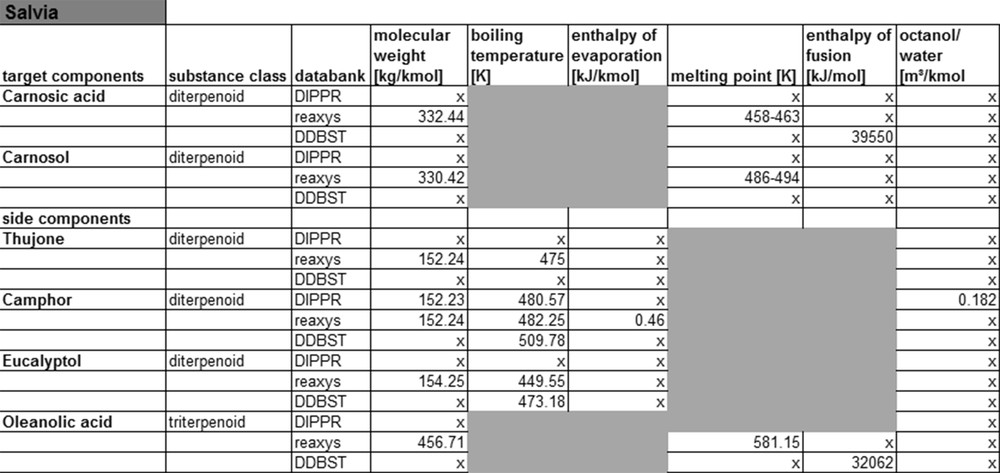
Salvia property data from data banks.
Fig. 8 shows that for this system, only the Reaxys database contains molar masses and melting points, all other substance data cannot be found there. Therefore, it can be concluded that for less complex monoterpenoids and phenylpropenes, the corresponding substance data may be found in databases. For more complex molecules like diterpenoids etc., little or no substance data exist, that means that currently not enough experimental data are available to expand the databases. In consequence, the compound data for such molecules either need to be calculated or experimentally determined. The following paragraph shows first results of such calculation of compound data applying different thermodynamic models.
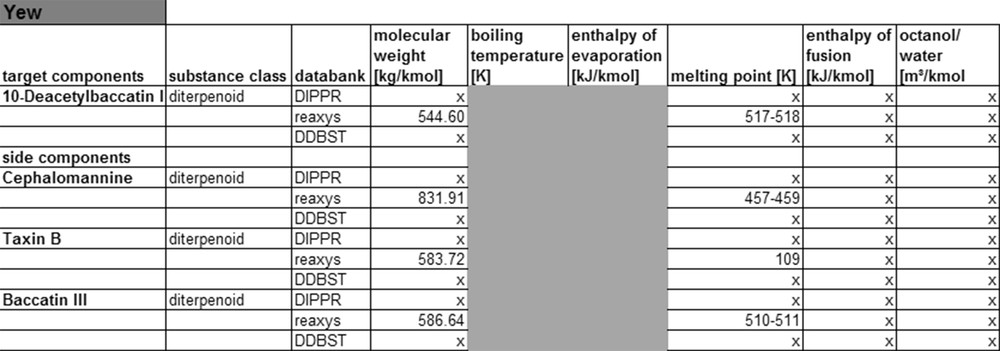
Yew property data from data banks.
Fig. 9 displays the possibilities for the calculation of substance parameters for fennel. For all target an, physicochemical properties can be calculated. With the group contribution method of Lyderson, Joback and Gani/Constantinou boiling points, enthalpy of evaporation, melting point and melting enthalpy are calculated. Comparing the calculated values with those from the database, DDB show that the calculated values coincide with the Joback model and the database DDB. Based on the missing information on the origin of the data in the DDB, it cannot be excluded, that the values have been calculated and have not been found experimentally. To decide in which of the three methods for the compound determination of target and side component of sage are better suited, they would also have to be experimentally verified. Due to the lack of comparable measurement techniques for compound data stored in databases, they cannot be referred to for judging the accuracy of a model.
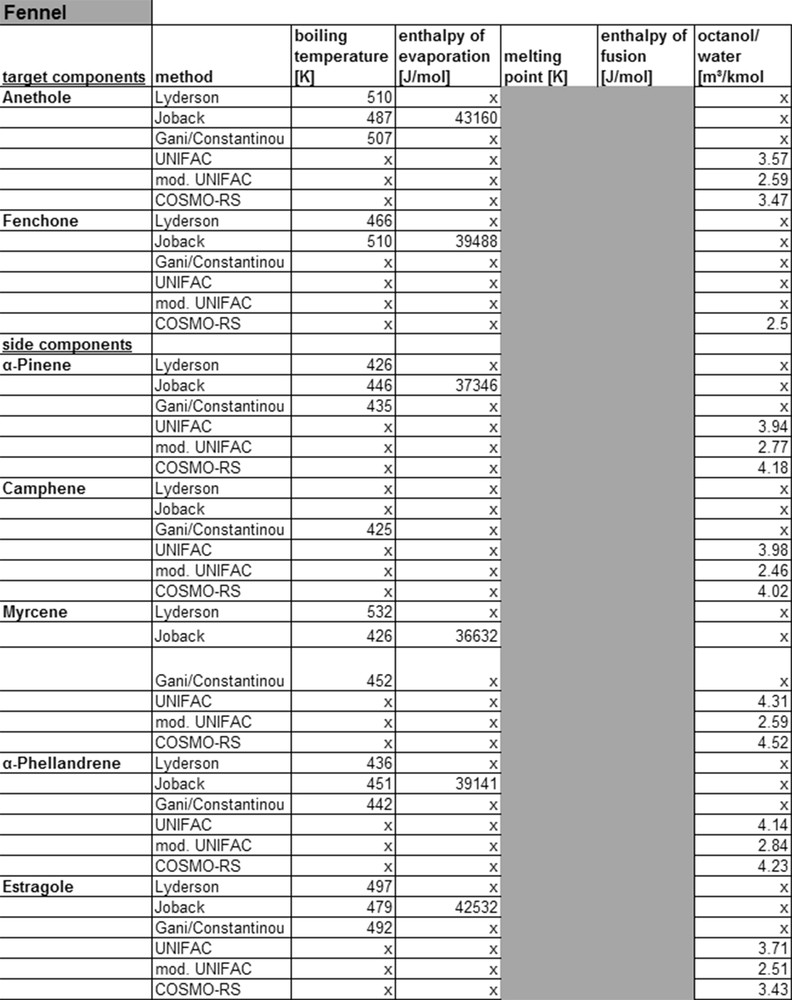
Calculated property data for fennel.
With the UNIFAC, modified UNIFAC and COSMO-RS model, octanol/water-partition coefficients are calculated. As described in chapter 4, group contribution methods, like e.g. the UNIFAC model, segment molecules into groups, which then permit the description of thermodynamic properties of a system. This step however requires interaction parameters, which for many molecule groups exist in databases. Simple monoterpenoids, with the isoprene as a core structure, can be calculated with UNIFAC. COSMO-RS can be applied here, as due to the simple molecular structure from the protective charges, activity coefficients and thereby physicochemical properties can be calculated. Thereby sufficient data for the simulation are available, which can be verified by Fig. 9.
In general, the determination of physicochemical properties for monoterpenoids with UNIFAC, modified UNIFAC, and COSMO-RS is possible. For a statement regarding the precision of models, the calculated and experimental data sets have to be compared. For anethole, KOW values in literature vary between 3.11 and 3.7 [37]. The comparison between calculated and literature data shows the best correlation for the COSMO-RS model. For α-pinene, camphene, myrcene, α-phellandrene and estragole, KOW values 4.49, 4.56, 4.50, 4.55 and 3.47 can be found in literature [38]. In all cases, COSMO-RS shows the highest accuracy. However it should be noted that different existing COSMO software, like ARTIST or COSMOtherm, leads to large deviation.
To compare the two gE models, the original UNIFAC shows better results than modified UNIFAC. The modified UNIFAC model requires other interaction parameters than the original model. In case of missing parameters, the use of those from the original model explains the large variations. As is known from literature [36], the quality of the COSMO-RS model depends on the precise capture of the molecule for the calculation of the protective charges. If the geometry of the molecule is not represented correctly, large deviations from reality result. This means that large molecules cannot be described this way.
Fig. 10 shows the target and side components of salvia with the corresponding calculated substance parameters. Also in this case, the parameters can be determined for the simple molecules of the monoterpenoid class. In addition, the data calculated with the Joback model can be compared with the DDB database. Limitations are found only for the target compounds carnosic acid and carnosol, and for the side component oleanolic acid.
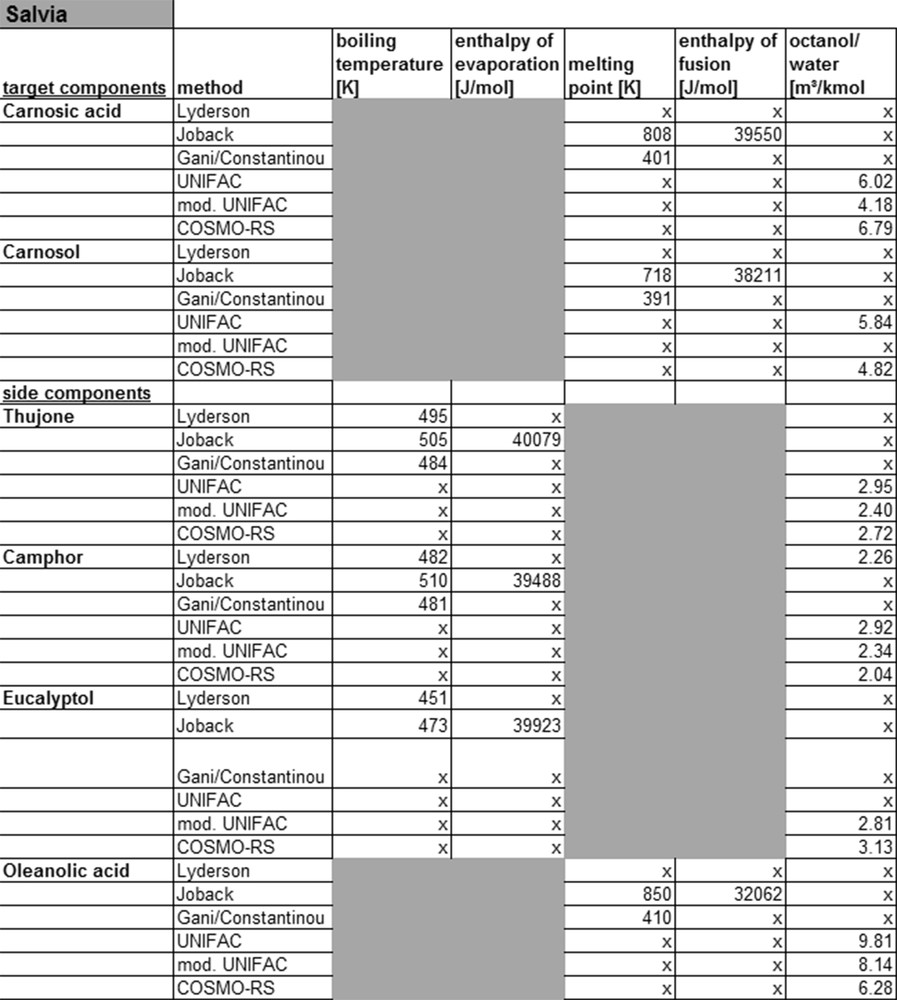
Calculated property data for salvia.
For these three compounds, belonging to the diterpenoid-class, parameters missing for sorting the molecules in groups. Only the Joback model can provide physicochemical properties also for these compound classes. The reason for this however is that the grouping for this method is kept very simple and therefore calculations are also possible for complex molecules. In addition, no interactions between groups are considered, making the method less precise and thereby not applicable to complex molecules. In general, COSMO-RS calculations for complex molecules are possible, but these are associated with high effort and low accuracy. For this reason, the applicability of COSMO-RS for detailed process simulation is limited.
The KOW value of carnosol and carnosic acid for example calculated by UNIFAC and modified UNIFAC shows a large deviation. For more complex molecules, like diterpenoids, the currently available models provide no physicochemical properties at all or only low accuracy data. This can also be shown on the example of yew, as listed in Fig. 11.
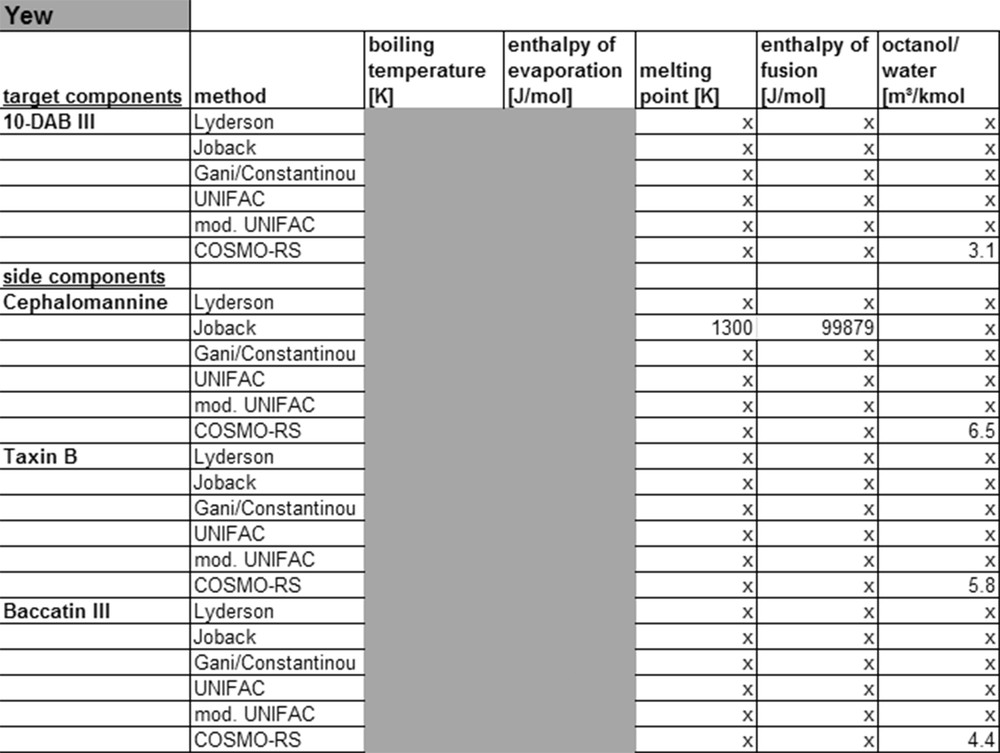
Calculated property data for yew.
For this system, data could only be calculated with the Joback and COSMO-RS model. Because of the low accuracy of the Joback method for complex molecules, the values cannot be used for the simulation. For the target compound 10-deacetylbaccatin III and other diterpenoids found in yew no properties can be calculated with UNIFAC or modified UNIFAC, because the group contribution methods lack the parameters required for the molecule groups. It is possible to calculate physico-chemical properties, like ocatanol–water partition coefficient with the COSMO-RS model. However, these values must be checked experimentally to draw a conclusion on the accuracy. Currently no thermodynamic models exist to describe such complex molecules with sufficient accuracy, because the required parameters are missing. These might be generated by fitting with experimental data.
This means that for such molecules, the physicochemical properties have to be determined experimentally. An advantage of the experimental determination would be that with the data for models like UNIFAC, additional parameters could be determined so that in future a calulation might be possible.
6 Conclusion
In this work, a systematic approach for the determination of physicochemical properties for complex molecules is presented. In particular, it was shown to what extent these properties can be obtained from databases or can be calculated using thermodynamic models. Selected sample systems have been fennel, salvia, and for the different target and side components of these systems boiling- and melting-temperatures, evaporation- and melting-enthalpies, and the octanol/water partition coefficients were determined. It could be shown that for all target and side components of fennel, physicochemical properties exist in databases. Only the octanol/water partition coefficients could not be found for all substances.
In case of salvia, less properties could be found for target and side components. Especially octanol/water partitioning data were lacking here, too. Also for the yew system, apart from melting temperatures in the Reaxys database, no additional physicochemical properties could be found. From this, it may be concluded that for simple molecules of the monoterpenoid class, physicochemical properties can be found in databases like Reaxys, DIPPR and the Dortmunder Datenbank.
For more complex molecules such as di- and triterpenoids, few or even no physicochemical properties can be found. A further disadvantage of the database lies in the lack of information on the measurement methods for the available properties, so that consistency in the measurements is not guaranteed. This is shown in the differing values of physicochemical properties from different databases, which limits their comparability somewhat.
The calculation of physicochemical properties showed that for monoterpenoids and phenylpropenes, these properties can be determined. The accuracy by comparison with databases could not be verified because the databases do not provide consistent material data. For the calculation of the KOW value, the COSMO-RS model and the original UNIFAC model performed well. Modified UNIFAC generated large deviations from literature data.
No consistent theory is currently available for diterpenoids, which allows an accurate calculation of properties. Group contribution methods like UNIFAC are missing the necessary interaction parameters. Due to low accuracy the COSMO-RS model is not applicable to complex molecules. Therefore, physicochemical properties for such molecules have to be determined experimentally. However, the calculated properties could be used for a reduction of the experimental determination, because some trends can be shown with the calculations. That way, data for comparison as well as for parameter determination of the models can be generated. The experimental determination will be the content of future publications to propose a standard for interested groups to jointly complete compound databases.
7 Symbols
| g | [J] | Gibbs enthalpy |
| h | [J] | Enthalpy |
| P | [bar] | Pressure |
| qi | [–] | Surface parameter |
| Qk | [–] | Surface of group |
| r | [–] | Volume parameter |
| R | [J/mol·K] | Gas constant |
| Rk | [–] | Volume of group |
| S | [–] | Dimensionless excess entropy |
| T | [K] | Temperature |
| v(i)K | [–] | Frequency of group k in molecule i |
| V | [cm3/mol] | Molar volume |
| x | [–] | Mole fraction |
| Xm | [–] | Mole fraction |
| z | [μm] | Spatial coordinate in the solid |
| Greek letters | ||
| γ | [–] | Activity coefficient |
| Θ | [–] | Surface fraction |
| Θm | [–] | Surface fraction |
| μ | J | Chemical potential |
| σ | [–] | Protective charge |
| Φ | [–] | Volume fraction |
| Ψmn | [–] | Adjustable parameter of UNIFAC |
| Indices | ||
| b | Boiling | |
| c | Critical | |
| C | Combinatorial | |
| f | Formation | |
| i | Component | |
| m | Melting | |
| R | Residual | |
| S | Saturation |
Acknowledgements
The authors would like to acknowledge Professors Jürgen Gmehling and Jürgen Rarey/University of Oldenburg as well as Professors Werner Kunz and Andreas Klamt/University of Regensburg for fruitful discussions and support calculating physical properties data.


