1 Introduction
Apatites are a large group of minerals whose main representative is fluoroapatite (Ca10Fap), crystallizing mainly in the hexagonal structure (space group P63/m), where the
Another class of apatites – rare-earth-based apatites – has gained great interest from researchers for over several decades given their appealing properties. For example, compounds with various compositions, Ln9.33(XO4)6O2, Ln10(XO4)6O3 and Ln10−xMx(XO4)6O3−x/2, where Ln is a rare-earth like La, Nd, etc., M is an alkaline earth like Ca, Sr, etc., and X is either Si or Ge, are extensively investigated thanks to their good ionic conductivity [14–18]. They are considered promising candidates to replace yttria-stabilized zirconia as solid oxide fuel cells (SOFCs) electrolytes at intermediate temperatures [19,20]. Also, oxyapatites doped with rare-earth ions, such as Eu3+, Tb3+, etc. have attracted the researchers’ attention for their luminescence properties [21,22]. On the other hand, the compounds with the general formula Ca10−xLnx(PO4)6−x(SiO4)xF2 (Ln = La, Nd) have been the subject of both theoretical and experimental studies, because of their potential use as confinement matrices for the minor actinides and long-lived fission products [23–31]. Ardhaoui et al. [32,33], studying the thermodynamic properties of the latter series of compounds, have shown that their enthalpy of formation increased with the increase of the substitution of the pair (Ln3+,
In order to get a better understanding of the evolution of their properties with the substitution degree, a systematic study of lanthanide-substituted fluoro- and oxyapatites has been undertaken in our laboratory [36–41]. In this paper, we investigate the ionic conductivity of the Ca6La4(PO4)2(SiO4)4F2 and Ca4La6(SiO4)6F2 samples using impedance spectroscopy.
2 Experimental procedure
2.1 Sample preparation
Samples with the chemical formula Ca10−xLax(PO4)6−x(SiO4)xF2, with x = 0, 4 and 6, were synthesized via a solid-state reaction from CaCO3, CaF2, La2O3, SiO2, and Ca2P2O7. The latter compound was obtained by heating a stoichiometric mixture of CaCO3 and (NH4)2HPO4 at 900 °C for 10 h. To avoid the deviation from stoichiometry, lanthanum oxide was calcined at 1000 °C for 24 h just before use, because it is very sensitive to moisture and carbon dioxide from the air [42]. The starting materials in suitable proportions were weighed and thoroughly ground in an agate mortar. Then, they were pressed into pellets, which were firstly heat-treated under a dynamic atmosphere of argon at 900 °C for 12 h, in order to remove the volatile species. After this heat treatment, the pellets were manually crushed and homogenized, and the resulting powders were again uniaxially pressed. According to their SiO2 content and until a pure phase was obtained, the compacts have undergone one or more heat treatments at a temperature between 1200 and 1400 °C for 12 h under the same atmosphere. The heating rate was 10 °C/min.
After heat treatment, the density (dex) of a compact was determined from its dimension and weight, and the relative density was calculated using the formula:
| (1) |
The theoretical density (dtheo) was calculated for each composition, taking into account its molecular weight (W), the number of units per unit cell (Z) and the volume of the unit cell, according to the following equation:
| (2) |
In the following sections, the compositions with x = 4 and 6 will be labelled as Ca6La4Fap and Ca4La6Fap, respectively.
2.2 Sample characterization
The X-ray diffraction (XRD) patterns of the samples were obtained on a Bruker D8 ADVANCE diffractometer operating with Cu Kα radiation. The samples were scanned in the 2θ range from 20 to 60° with a step size of 0.02° and a counting time of 10 s per step. The lattice parameters were refined by using the Rietveld method.
The MAS–NMR analyses were conducted on 31P and 29Si nuclei using a Bruker 300 WB spectrometer at resonance frequencies of 121.50 and 59.62 MHz, respectively. The spinning rate of the sample at the magic angle was 8 kHz. 31P and 29Si chemical shifts were referenced to external standards of an aqueous solution of 85% H3PO4 and tetramethylsilane (TMS), respectively.
Impedance measurements were carried out on samples with x = 4 and 6, whose relative density was about 77%, using a Hewlett-Packard 4192-A impedance analyzer, operating at frequencies ranging from 5 to 13 MHz. Silver electrodes were painted on the two faces of the pellets with a silver paste, and then the painted pellets were heated at 300 °C for 1 h.
3 Results and discussion
3.1 Phase identification
Fig. 1 shows the XRD patterns of samples for x = 0, 4 and 6. As seen, all the patterns exhibit only the reflections of an apatitic phase, indexed in the hexagonal system (space group P63/m) based on the fluoroapatite (JCPDS card #00-071-0880). No evidence of any second phase was found, indicating that the samples were single phased.
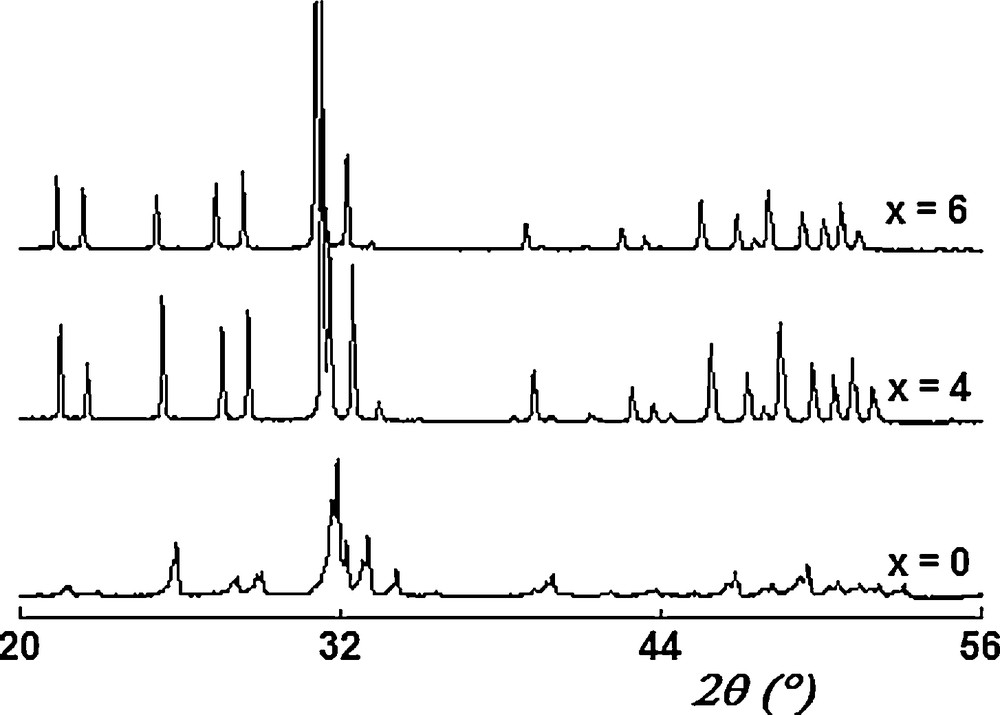
XRD patterns of Ca10 − xLax(PO4)6 − x(SiO4)xF2 samples.
The insertion of La3+ and
Unit cell parameters of Ca10−xLax(PO4)6−x(SiO4)xF2 samples.
| Lattice parameters | x = 0 | x = 4 | x = 6 |
| a (Å) | 9.389(6) | 9.562(7) | 9.638(4) |
| c (Å) | 6.886(6) | 7.040(4) | 7.113(2) |
| V (Å3) | 528.82(3) | 557.57(0) | 572.27(9) |
The conclusion drawn from the XRD analysis for the substitution of
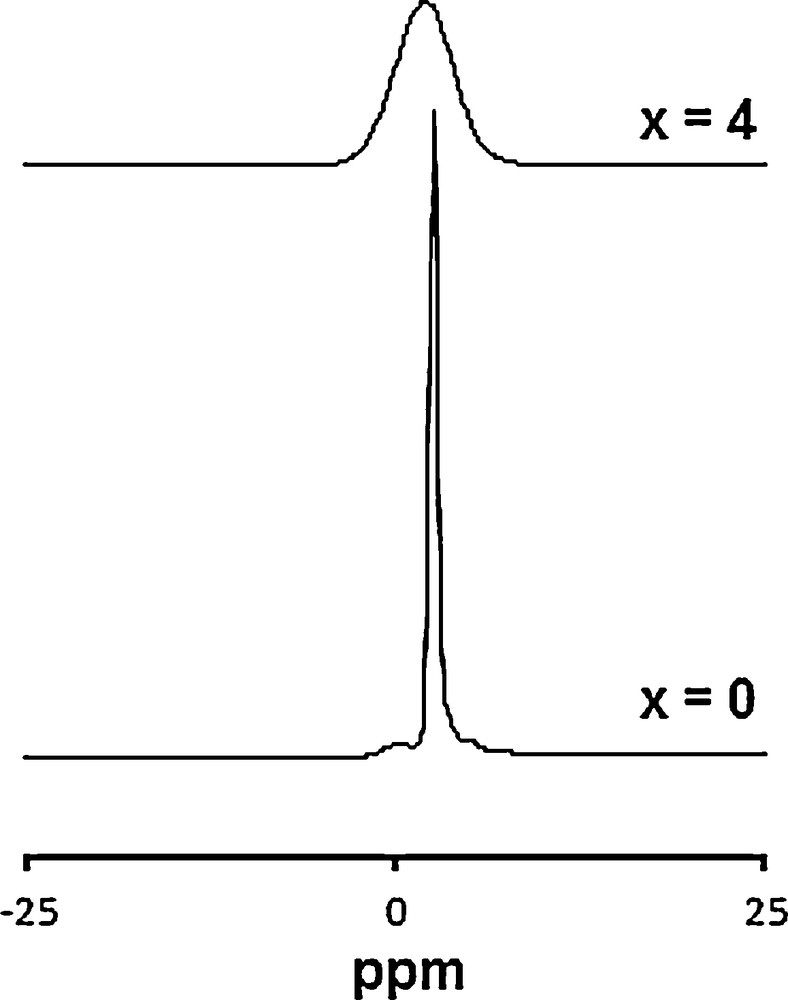
31P MAS–NMR spectra of Ca10−xLax(PO4)6−x(SiO4)xF2 samples.
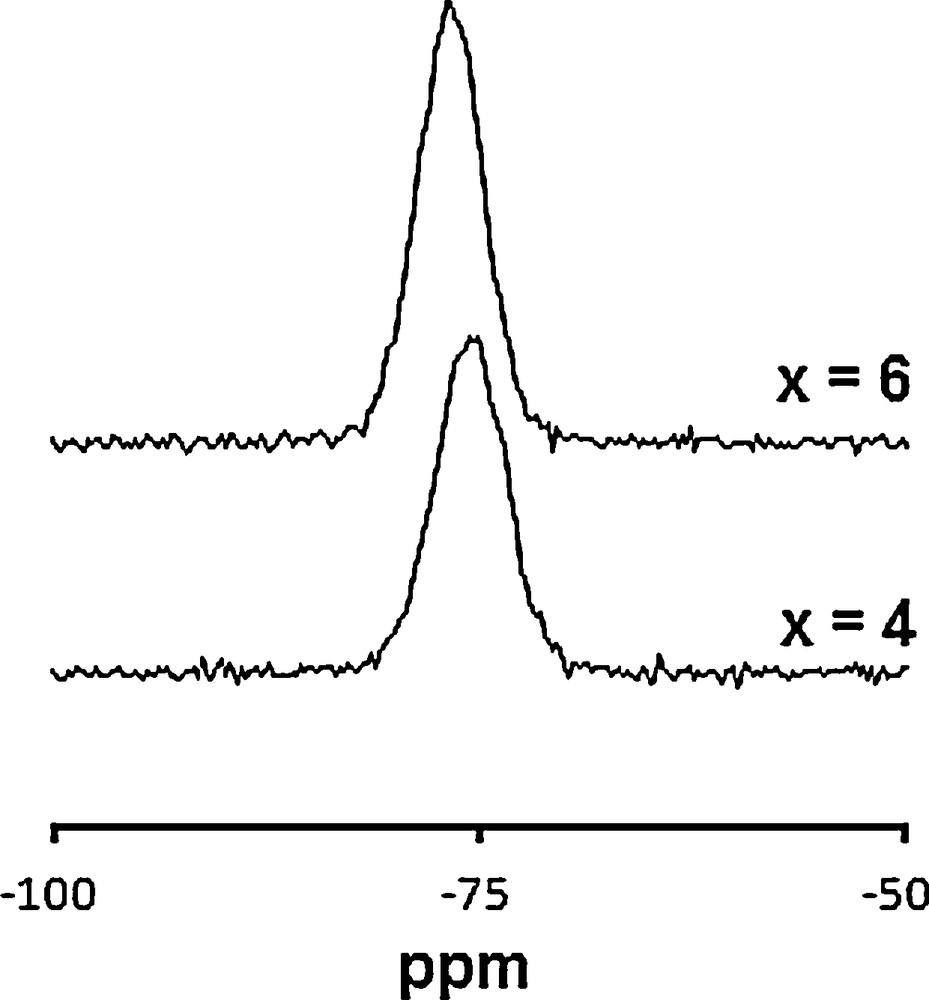
29Si MAS–NMR spectra of Ca10−xLax(PO4)6−x(SiO4)xF2 samples.
3.2 Ionic conductivity measurements
The complex impedance spectroscopy of the Ca6La4F and Ca4La6F samples was measured as a function of the frequency in the 400–800 °C temperature range. The complex impedance plane, Z′′ vs Z′, plots (not shown here) did not permit to resolve the bulk and boundary semicircles. The total resistance value was determined from the intercept of the semicircular arcs at high frequency with the real axis. Then, the ionic conductivity was deduced from the resistance data using the following relation:
| (3) |
In accordance with the conditions indicated above, the obtained values represent the total conductivity. The temperature dependence of the samples’ ionic conductivity is shown in Fig. 4 as an Arrhenius-type plot, Log(σT) vs. 1000/T. Just for comparison, the data of Ca10Fap [47] are also represented. It can be seen that with the substitution of (La3+,
- • the electrical conduction in the materials is a thermally activated process;
- • the conductivity increases and the activation energy decreases, Ca4La6F has the highest conductivity and the lowest activation energy (Table 2);
- • the samples exhibit a change in slope at 717 °C and 620 °C for Ca6La4F and Ca4La6F, respectively.
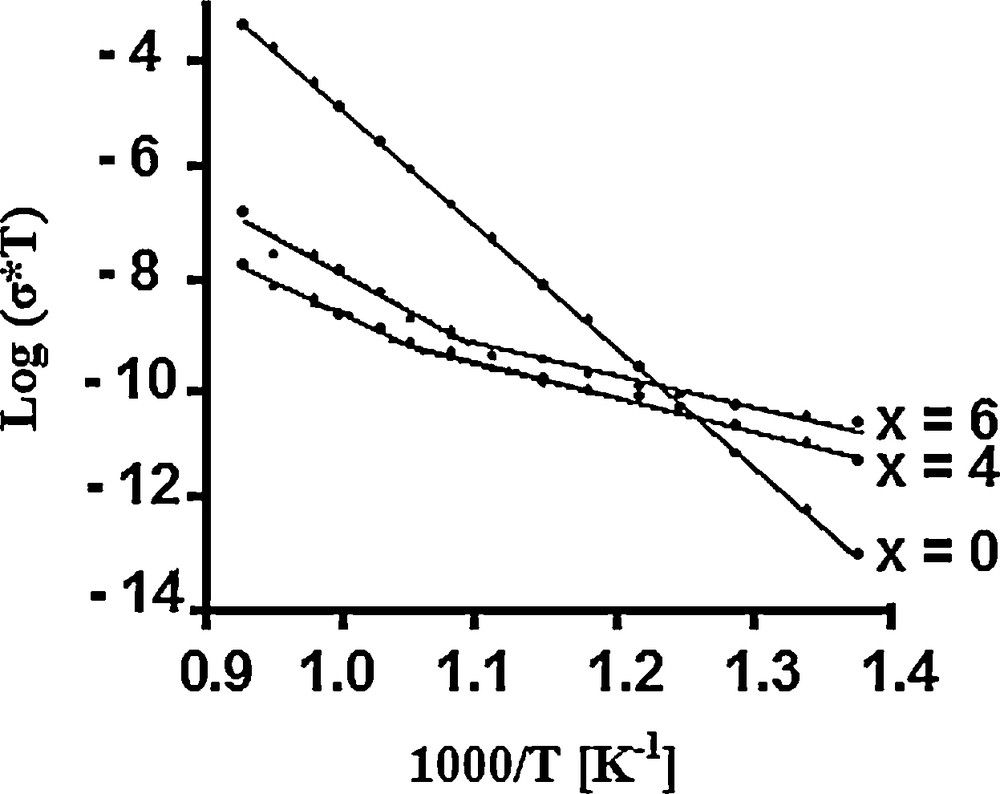
Plot of Log σT (S·K·cm−1) versus 1000/T (K−1) for Ca10−xLax(PO4)6−x(SiO4)xF2 samples: x = 0 [47]; x = 4 and 6 (present work).
Activation energy values of Ca10−xLax(PO4)6−x(SiO4)xF2 samples.
| Samples | x = 0 [47] | x = 4 | x = 6 |
| Ea (eV) | 1.86 | 1.07 0.54 | 1.01 0.46 |
However, the ionic conductivity values of 1.07 × 10−7 and 4.14 × 10−6 S·cm−1 determined at 800 °C for Ca6La4F and Ca4La6F, respectively, are lower than that reported for Ca10Fap by Laghzizil et al. (3.35 × 10−5 S·cm−1) [47]. This difference is probably due to the synthesis and sintering conditions used for the different materials. The relative density of our samples was only of about 0.77, while that of Ca10Fap prepared by Laghzizil et al. was 0.90 [47]. The activation energies for conduction were calculated from the slopes of the Arrhenius plots. As seen in Table 2, the activation energy decreases significantly with the substitution. It is worth noting that this decrease is similar to that of the chemical stability of the compounds. Indeed, their enthalpy of formation increases with the substitution degree [33]. Furthermore, according to the shape of the Arrhenius plots, the low-temperature domain is associated with the lowest activation energy. Studying the electrical properties of hydroxyapatites (M10(PO4)6(OH)2) and fluoroapatites (M10(PO4)6F2) (M = Ca, Pb, Ba), Laghzizil et al. observed that the break occurred only for lead apatites [48].
Like in Ca10Fap, the conduction mechanism in our materials should be related to the translational hopping of the fluoride ions along the c-axis of the lattice from ordinary sites to interstitial sites, as these ions are the only candidates for such a conduction process. Thus, the fluoride ions must be able to move to other positions by the formation of thermally activated defects, such as Schottky defects [47], especially as these materials were stoichiometric [36]. With the substitution of (Ca2+,
The break in the Arrhenius plots is usually related to a phase transition [52] or to a change in the conduction mechanism [53]. However, in the present case, no phase change was observed in the investigated temperature range, and no change in the conduction mechanism can be suspected, the F− ions being the only charge carriers in the absence of cationic vacancies [36]. Like for lead fluoroapatite, the break in the Arrhenius curve is related to the nature of the Ca/La–F bond, i.e. to the polarizability of the atoms located in the S(2) sites, as it has been suggested by Laghzizil et al. [47]. The decrease of the breakpoint temperature when x varied from 4 to 6 could be related to the increase in the conductivity. The same behavior was observed with Pb10Hap and Pb10Fap, the fluoride ions being more mobile than the protons. Indeed, the change of the temperature's slope occurs at 390 °C for Pb10Fap, while it occurs at 480 °C for Pb10Hap [48].
4 Conclusion
Ca6La4(PO4)2(SiO4)4F2 and Ca4La6(SiO4)6F2 were synthesized by a solid-state reaction. They were characterized by X-ray diffraction and nuclear magnetic resonance spectroscopy. Their ionic conductivity was measured by impedance spectroscopy. The obtained results indicated that:
- • the conduction is due to the mobility of F− ions along the c-axis of the lattice. The increase in conductivity with the substitution is caused by the widening of the tunnel and the weakening of the Ca/La–F bond;
- • the Arrhenius curves show a change in slope, which was related to the polarizability of the lanthanum. The decrease in the temperature at which the break occurs is attributed to the increase of the conductivity.


