Theoretical study of the inclusion processes of octopamine with β-cyclodextrin: PM6, ONIOM, and NBO analysis

Lachi Nadia; Khatmi Djameleddine; Djemil Rayenne

doi:10.1016/j.crci.2014.03.010

Theoretical study of the inclusion processes of octopamine with β-cyclodextrin: PM6, ONIOM, and NBO analysis

Lachi Nadia ¹ ; Khatmi Djameleddine ¹ ; Djemil Rayenne ¹

¹ Laboratory of Computational Chemistry and Nanostructures, Department of Materials Sciences, Faculty of Mathematical, Informatics and Material Sciences, University 08-Mai-1945, Guelma, Algeria

Comptes Rendus. Chimie, Volume 17 (2014) no. 12, pp. 1169-1175.

Résumé

The inclusion process involving β-cyclodextrin with octopamine (OA) was investigated by using PM6, HF/3-21G*, B3LYP/6-31G (d), WB97XD/6-31G (d) methods and several combination of ONIOM2 hybrid calculations. The obtained results clearly indicate the orientation in which the guest molecule penetrates into the hydrophobic cavity of β-CD with the aromatic ring is energetically preferred. The structures show the presence of several intermolecular hydrogen bond interactions that were studied on the basis of natural bonding orbital (NBO) analysis, employed to quantify donor–acceptor interactions between host and guest molecules. A study of these complexes in solution was carried out using the CPCM model to examine the influence of solvation on the stability of the octopamine/β-CD complex.

Métadonnées

Reçu le : 2013-11-30
Accepté le : 2014-03-10
Publié le : 2014-10-08

DOI : 10.1016/j.crci.2014.03.010

Mots clés : Octopamine, β-CD, Inclusion complex, PM6, DFT, ONIOM, NBO

Affiliations des auteurs :

Lachi Nadia ¹ ; Khatmi Djameleddine ¹ ; Djemil Rayenne ¹

¹ Laboratory of Computational Chemistry and Nanostructures, Department of Materials Sciences, Faculty of Mathematical, Informatics and Material Sciences, University 08-Mai-1945, Guelma, Algeria

@article{CRCHIM_2014__17_12_1169_0,
     author = {Lachi Nadia and Khatmi Djameleddine and Djemil Rayenne},
     title = {Theoretical study of the inclusion processes of octopamine with \ensuremath{\beta}-cyclodextrin: {PM6,} {ONIOM,} and {NBO} analysis},
     journal = {Comptes Rendus. Chimie},
     pages = {1169--1175},
     publisher = {Elsevier},
     volume = {17},
     number = {12},
     year = {2014},
     doi = {10.1016/j.crci.2014.03.010},
     language = {en},
}

TY  - JOUR
AU  - Lachi Nadia
AU  - Khatmi Djameleddine
AU  - Djemil Rayenne
TI  - Theoretical study of the inclusion processes of octopamine with β-cyclodextrin: PM6, ONIOM, and NBO analysis
JO  - Comptes Rendus. Chimie
PY  - 2014
SP  - 1169
EP  - 1175
VL  - 17
IS  - 12
PB  - Elsevier
DO  - 10.1016/j.crci.2014.03.010
LA  - en
ID  - CRCHIM_2014__17_12_1169_0
ER  -

%0 Journal Article
%A Lachi Nadia
%A Khatmi Djameleddine
%A Djemil Rayenne
%T Theoretical study of the inclusion processes of octopamine with β-cyclodextrin: PM6, ONIOM, and NBO analysis
%J Comptes Rendus. Chimie
%D 2014
%P 1169-1175
%V 17
%N 12
%I Elsevier
%R 10.1016/j.crci.2014.03.010
%G en
%F CRCHIM_2014__17_12_1169_0

Lachi Nadia; Khatmi Djameleddine; Djemil Rayenne. Theoretical study of the inclusion processes of octopamine with β-cyclodextrin: PM6, ONIOM, and NBO analysis. Comptes Rendus. Chimie, Volume 17 (2014) no. 12, pp. 1169-1175. doi : 10.1016/j.crci.2014.03.010. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2014.03.010/

Version originale du texte intégral

1 Introduction

Octopamine [OA, 2-amino-1-(4-hydroxyphenyl) ethanol], a biogenic amine that has functions analogous to those of the adrenergic system in vertebrates, is a well-established neurotransmitter, neurohormone, and neuromodulator in many invertebrate species [1,2]. Octopamine, present in trace amounts in mammalian brain [3] and human plasma [4], has long been hypothesized to play a role in different diseases, including hepatic encephalopathy [5,6], schizophrenia [7], and renal diseases [8]. To fully characterize the roles of octopamine in different diseases, the determination of octopamine in biological samples such as human plasma is required. It is also found naturally in numerous plants, including Citrus aurantium (bitter orange) [9–11].

Many analytical methods have been developed for the separation and quantification of biogenic amines including octopamine. Chromatographic and electrophoretic methods are the preferred analytical techniques, because of their highly efficient separation before detection of individual components [12]. Cyclodextrins (CDs) are used as chiral selectors in chromatographic separations of these amines in fruits, extracts, and herbal products of C. aurantium.

CDs are water-soluble compounds produced as a result of intramolecular transglycosylation reaction from degradation of starch by cyclodextrin glucanotransferase (CGTase) enzyme [13]. Mainly, three cyclic oligosaccharides are obtained: α-, β- and γ-cyclodextrin, consisting respectively of six, seven and eight α-d-glucopyranose units in the ⁴C₁ chair conformation. β-Cyclodextrin is the most accessible, the cheapest, and generally the most widely used. This macrocycle has the shape of a hollow truncated cone with a central hydrophobic cavity and hydrophilic exterior edges [14]. The primary hydroxyls of the glucose units are located at the narrow face of the cone and the secondary hydroxyls at the wide face [15]. These amphiphilic molecular structures of CDs form easily inclusion complexes with many organic, inorganic, and biological compounds without covalent bond. The resulting inclusion complexes can induce a modification of the physicochemical properties of the guest molecule. CDs have been used extensively in separation science because they have been shown to discriminate between positional isomers, functional groups, homologues, and enantiomers. This property makes them one of the most useful agents for a wide variety of separations [16].

Nowadays, because of the limitation of the experimental methods, molecular modeling is very popular in CD chemistry [17–24].

The aim of this work is to study the inclusion complex between OA and β-CD specifically to determine its optimum geometrical structure, to describe the conformational changes of OA inside the β-CD cavity, the stability of the complex and the principal intermolecular interactions between the guest molecule and the host CD.

In this paper, several levels of calculations were carried out. In the first part, we use PM6 semi-empirical method implemented in the MOPAC 2010 program [25] in order to localize the minimum energy structures, which are used as starting structures for subsequent optimizations. After that, the structures are subjected to higher-level calculations, such HF, DFT (single-point) and ONIOM2 [B3LYP/6-31G (d): HF/3-21G*, WB97XD/6-31G (d): HF/3-21G* and B3LYP/6-31G (d): B3LYP/3-21G*] methods to approach the ideal geometry and provide further insight into the complexation process of OA with β-CD. The natural bonding orbital (NBO) analysis is employed to quantify the donor–acceptor interactions between the host and the guest.

2 Computational method

All the calculations were performed using MOPAC 10 Software packages and Gaussian 09 [26]. The starting structures of β-CD and octopamine (OA) were built with the help of the Chembridge ChemBio 3D Ultra (version 11.0, Chembridge Software). OA was optimized with B3LYP method at the 6-31G* level, and β-CD was used without optimization, see Fig. 1.

Fig. 1
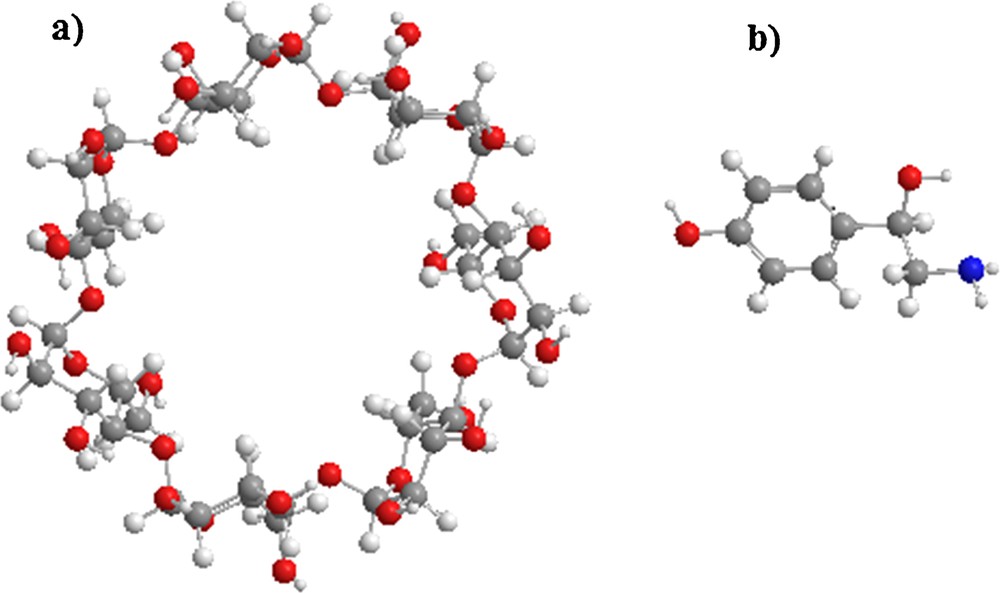
(Color online.) Molecular structure of: a: β-cyclodextrin; b: octopamine.

The coordinate system used to define the process of complexation is shown in Fig. 2. The construction method was reported in [27]. The glycosidic oxygen atoms of the cyclodextrin molecule were placed onto the XY-plane and their center was defined as the origin of the coordinate system. The secondary hydroxyl groups of β-CD were placed pointing toward the positive Z-axis. Then, the guest molecule, placed on the Z-axis was allowed to approach and pass through the β-CD cavity from −6A° to +6A° with a step of 1A°. The generated structures at each step were optimized with PM6 methods without imposing any symmetrical restrictions.

Fig. 2
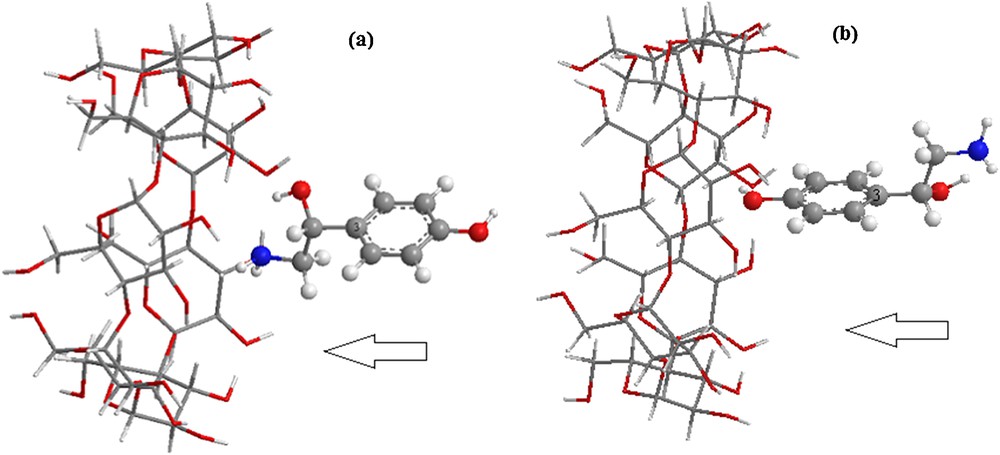
(Color online.) The proposed structures of the octopamine/β-CD complex for: a: orientation 1; b: orientation 2.

In order to find an even more stable structure of the complex, the guest molecule was rotated around the Z-axis at 20° intervals from 0° to 360°. Once the preliminary energy minima were determined, each derived complex was re-optimized, removing restraint on the β-CD and the reference atom (C3) of octopamine. Two possible orientations were considered (Fig. 2):

• the aliphatic ring oriented toward the center of mass of β-CD, namely orientation 1;
• the aromatic ring oriented toward the center of mass of β-CD, namely orientation 2.

Complexation energy upon complexes between OA and β-CD is calculated for the minimum energy structure according to eq. (1):

E_{complexation} = E_{complex} - (E_{host} + E_{guest})

(1)

where

E_{complex}, E_{β - CD}, E_{OA}

represent the energies of the complex, the free β-CD, and the free OA, respectively.

The deformation energy for each component, host and guest throughout the formation of the complex was defined as the difference between the energy of the totally optimized component compared and its energy in the complex (Eq. (2)) [28]:

E_{deformation} (component) = E {(component)}_{sp}^{opt} - E {(component)}^{opt}

(2)

The gas-phase full optimizations were carried out at PM6 and HF/3-21G*. To improve the precision of the theoretical results, we adopted ONIOM2 methods [29]. In our hybrid model study, we submitted the host molecule β-CD to the low level of quantum calculations HF/3-21G*and B3LYP/3-21G*, whereas the guest molecule is treated at a high level of calculation B3LYP/6-31G (d) and WB97XD/6-31G (d). The ONIOM energy is described as [30]:

E^{oniom} = E (high; model) + E (low; real) - E (low; model)

(3)

where:

E (high; model)

is the energy of OA at the high level of theory,

E (low; real)

is the energy of the complex at the low level of theory, and

E (low; model)

is the energy of β-CD at the low level of theory.

B3LYP/6-31G (d) and WB97XD/6-31G (d) single-point calculations were corrected for basis set superposition error (BSSE) using the counterpoise method.

Solvent effects on the conformational equilibrium have been taken into account using the CPCM model for water as a solvent. The solvation calculations were carried out using B3LYP/6-31G (d) and WB97XD/6-31G (d) single-point.

Finally, the natural bond orbital analyses (NBO) were applied to quantify the donor–acceptor interactions between host and guest.

3 Results and discussion

The graphical representation of the complexation energy involved during the inclusion process of octopamine into β-CD at different distances for the two orientations is displayed in Fig. 3.

Fig. 3
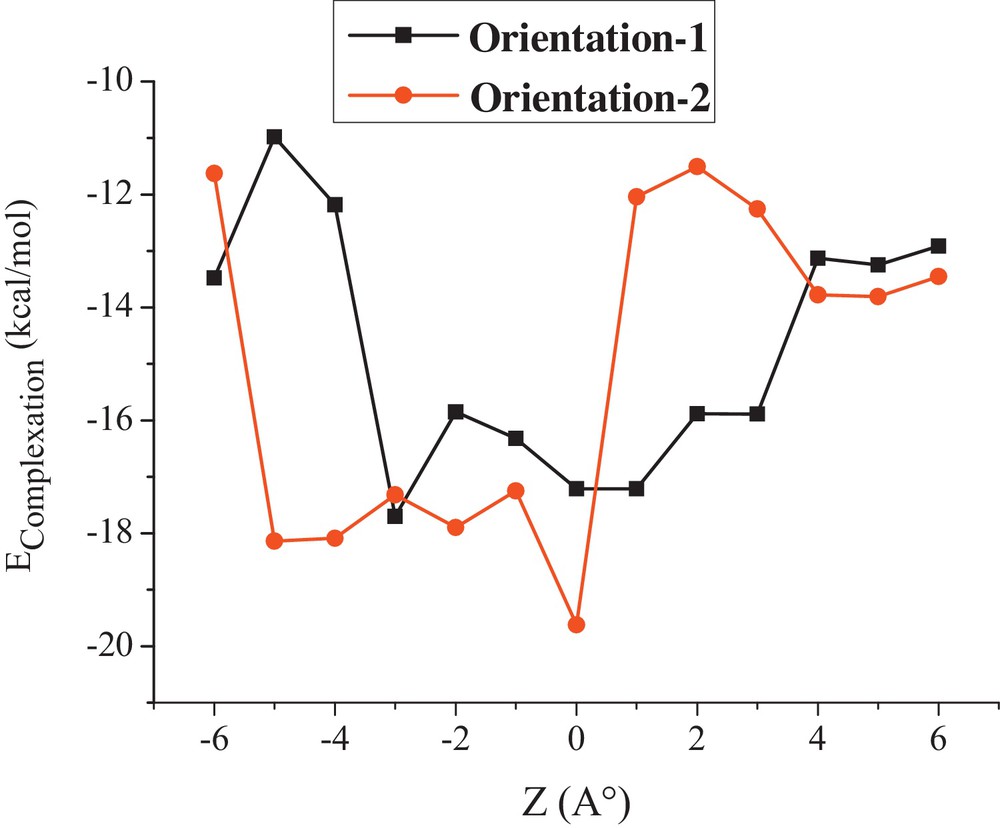
Complexation energies of the inclusion complexation of octopamine into β-CD at different positions (Z) for both orientations using PM6 method.

All the energetic values upon the complexation process are negative, which means that OA/β-CD complex is thermodynamically favorable. The most stable structure is located at −3 Ǻ and 0 Ǻ for orientations 1 and 2, respectively. At this point, complexation energies are −17.70 and −19.62 kcal/mol, as shown in Table 1. Orientation 2 is significantly more favorable than orientation 1 by an energy difference of 1.92 kcal/mol according to PM6 calculations.

Energies (kcal/mol)	Orientation 1	Orientation 2	ΔE
PM6
E_complexation	−17.70	−19.62	1.92
E_deformation (guest)	1.14	1.17	0.03
E_deformation (host)	1.41	1.86	0.45

HF/3-21G*
E_complexation	−13.36	−24.09	10.73

ONIOM
B3LYP/6-31G (d): HF/3-21G*
E_complexation	−13.62	−24.28	10.66
WB97XD/6-31G (d): HF/3-21G*
E_complexation	−13.99	−24.09	10.10
B3LYP/6-31G (d): B3LYP/3-21G*
E_complexation	−30.50	−56.41	25.91

The computed deformation energies given in Table 1 indicate that the guest needs only 1.14 kcal/mol for conformational adaptation inside the β-CD cavity for orientation 1, and 1.17 kcal/mol for orientation 2. On the contrary, the β-CD deformation energy is important. This deformation seems to be one of the driving factors leading to the formation of inclusion complexes. Indeed, complex 2 is more energy demanding than complex 1 by 1.86 kcal/mol.

Furthermore, the energetic gap between the two orientations is increased using HF/3-21G*, and ONIOM (B3LYP/6-31G (d): HF/3-21G*, WB97XD/6-31G (d): HF/3-21G* and B3LYP/6-31G (d): B3LYP/3-21G*) calculations, which confirms the preference for orientation 2. The energy difference between the two orientations in the four calculations varies considerably from 10.10 to 25.91 kcal/mol. These results indicate that the difference between the complexation energies in ONIOM methods is much larger than that in PM6 method, and the more stable complex is obtained with the [B3LYP/6-31G (d): B3LYP/3-21G*] level (Table 1).

The same result is also obtained with the B3LYP/6-31G (d) and WB97XD/6-31G (d) single-point calculations (Table 2), in which the energy difference becomes in vacuo and in water respectively 3.71 and 0.54 kcal/mol for B3LYP/6-31G (d), 7.36 and 4.23 kcal/mol for WB97XD/6-31G (d). The energy difference in solution becomes a little smaller than the calculated result in vacuo. The difference in E_complexation with BSSE correction in vacuo is 0.27 and 4.40 kcal/mol for B3LYP/6-31G (d) and WB97XD/6-31G (d), respectively. It can be seen that orientation 2 is more preferred than orientation 1, i.e., the interactions between octopamine in orientation 2 are stronger than those between the guest in orientation 1 and β-CD.

Energies (kcal/mol)	Orientation 1	Orientation 2	ΔE
In vacuo
B3LYP/6-31G (d)
E_complexation	−63.44	−67.15	3.71
E_complexation with BSSE correction	−52.84	−53.11	0.27
WB97XD/6-31G (d)
E_complexation	−82.87	−90.23	7.36
E_complexation with BSSE correction	−74.03	−78.43	4.40

In water
B3LYP/6-31G (d)
E_complexation	−52.45	−52.99	0.54
WB97XD/6-31G (d)
E_complexation	−70.74	−74.97	4.23

In vacuo
B3LYP/6-31G (d)
E_complexation	−63.44	−67.15	3.71
E_complexation with BSSE correction	−52.84	−53.11	0.27
WB97XD/6-31G (d)
E_complexation	−82.87	−90.23	7.36
E_complexation with BSSE correction	−74.03	−78.43	4.40

In water
B3LYP/6-31G (d)
E_complexation	−52.45	−52.99	0.54
WB97XD/6-31G (d)
E_complexation	−70.74	−74.97	4.23

As can be seen in Fig. 4, the structure of inclusion complexes obtained by ONIOM optimization shows that the guest is totally included in the hydrophobic cavity of the most favorable structure (complex 2); so there is a stronger hydrophobic interaction between the guest and β-CD. The NH₂ group points toward secondary hydroxyls and the reference atom C3 shifts upwards by 0.77 Å from the center of the coordination system. In complex 1 (orientation 1), we can see that the guest molecule is partially incorporated in the cavity, and the hydroxyl catechol of OA is left out of the wider rim.

Fig. 4
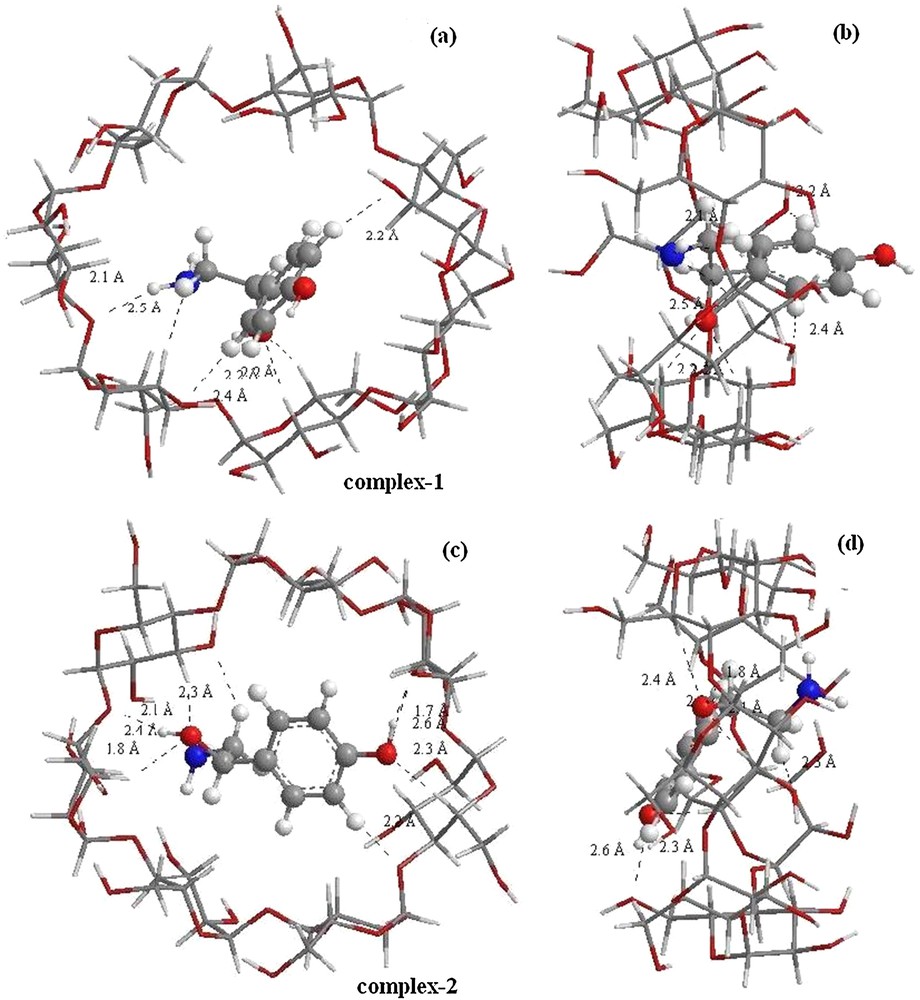
(Color online.) Geometric structures of octopamine/β-CD complexes optimized by ONIOM (B3LYP/6-31G (d): B3LYP/3-21G*); (a) and (c) seen from the secondary hydroxyl rim of the β-CD cavity correspond respectively to orientations 1 and 2, (b) and (d) seen from the side of the β-CD wall correspond respectively to orientations 1 and 2. Dotted lines represent the hydrogen bonds.

The B3LYP/6-31G (d): HF/3-21G* and WB97XD/6-31G (d): HF/3-21G* optimized structures (Fig. 5) are similar to those obtained by B3LYP/6-31G (d): B3LYP/3-21G*, where the aromatic ring is encapsulated in the cavity toward the smaller rim in orientation 2 (Fig. 5b and d), while in orientation 1, OA is partially included in β-CD. The aliphatic chain is embedded in the cavity and the aromatic ring is directed toward the wider rim (Fig. 5a and c).

Fig. 5
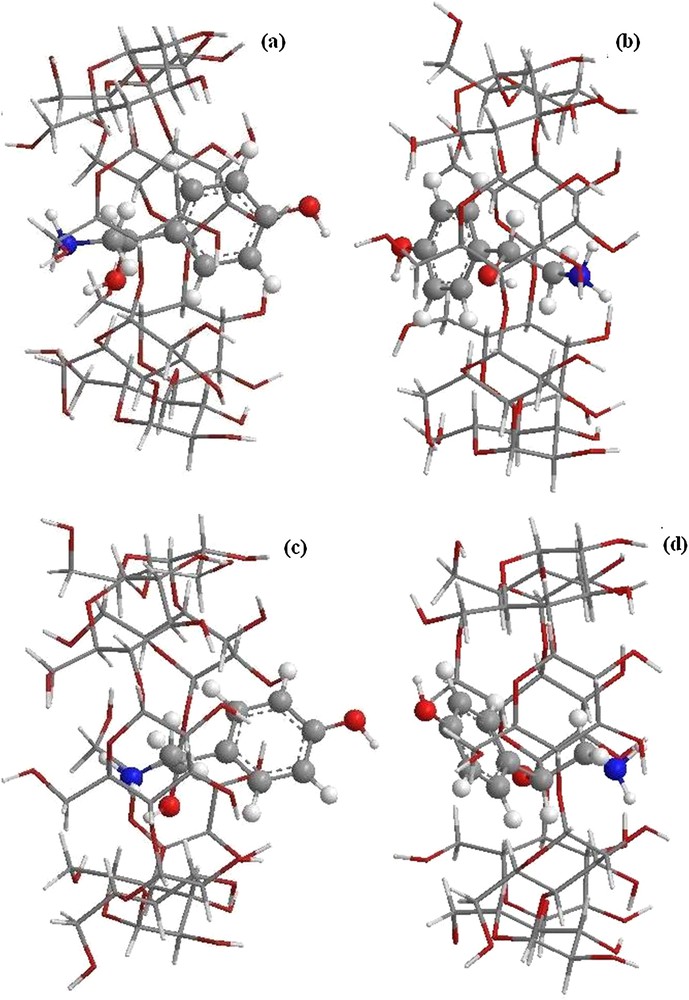
(Color online.) Structures of the optimized complexes obtained by ONIOM2; (a) structure of B3LYP/6-31G (d): HF/3-21G* for orientation 1, (b) structure of B3LYP/6-31G (d): HF/3-21G* for orientation 2, (c) structure of WB97XD/6-31G (d): HF/3-21G* for orientation 1, and (d) structure of WB97XD/6-31G (d): HF/3-21G* for orientation 2.

Natural bond orbital (NBO) analysis offers an efficient method for studying intra- and intermolecular bonding and interaction between bonds, and also provides a convenient basis for investigating charge transfer or conjugative interaction in molecular systems.

Some electron-donor orbitals, acceptor orbital and the interacting stabilization energy resulting from the second-order micro-disturbance theory are reported [31,32]. The second-order Fock matrix was calculated to evaluate the donor–acceptor interactions in NBO analysis [33]. For each donor (i) and acceptor (j), the stabilization energy E⁽²⁾ associated with delocalization i → j is estimated as:

E^{(2)} = Δ E_{i j} = q_{i} \frac{F (i, j)}{ε_{j} - ε_{i}}

(4)

where q_i is the donor orbital occupancy, ɛ_i and ɛ_j are diagonal elements and F(i, j) is the off-diagonal NBO Fock matrix element [34]. The delocalization of the electron density between occupied Lewis-type (bond or lone-pair) NBO orbitals and formally unoccupied (anti-bond or Rydgberg) non-Lewis NBO orbitals corresponds to stabilizing donor–acceptor interactions.

The geometrical parameters of the established H-bond in the inclusion complex and the stabilization energies E⁽²⁾, calculated using B3LYP/6-31G (d) and WB97XD/6-31G (d) single-point methods are presented in Table 3. The structure of the energy minimum obtained with ONIOM calculations shows the presence of several intermolecular hydrogen bond interactions, see Fig. 4.

Donor	Acceptor	E⁽²⁾ B3LYP/6-31G (d)	E⁽²⁾ WB97XD/6-31G (d)
Complex 1
Guest donor β-CD acceptor
LP O 8	σ*C 55–H 137	3.65 (2.2A°, 140.6°)	4.32 (2.2A°, 140.6°)
LP O 8	σ*C 57–H 139	2.45 (2.2A°, 141.0°)	2.83 (2.2A°, 141.0°)
β-CD donor guest acceptor
LP O 67	σ*N 10–H 20	6.02 (2.1A°, 158.0°)	7.23 (2.1A°, 158.0°)
LP O 81	σ*C 2–H 13	4.24 (2.2A°, 155.6°)	5.14 (2.2A°, 155.6°)
LP O 96	σ*C 5–H 14	3.24 (2.4A°, 178.0°)	3.95 (2.4A°, 178.0°)
LP O 97	σ*O 8–H 17	5.10 (2.1A°, 123.3°)	6.17 (2.1A°, 123.3°)

Complex 2
Guest donor β-CD acceptor
LP O 8	σ*C 37–H 115	6.02 (2.1A°, 102.7°)	7.22 (2.1A°, 102.7°)
LP O 8	σ*C 45–H 124	1.96 (2.4A°, 111.5°)	2.37 (2.4A°, 111.5°)
LP O 11	σ*C 63–H 145	2.32 (2.3A°, 107.5°)	2.83 (2.3A°, 107.5°)
β-CD donor guest acceptor
LP O 69	σ*O 11–H 22	27.79 (1.7A°, 164.6°)	32.60 (1.7A°, 164.6°)
LP O 77	σ*C 9–H 18	1.65 (2.3A°, 143.5°)	2.04 (2.3A°, 143.5°)
LP O 83	σ*O 8–H 17	9.63 (1.8A°, 147.1°)	11.59 (1.8A°, 147.1°)
LP O 87	σ*N 10–H 21	6.52 (2.2A°, 176.4°)	7.91 (2.2A°, 176.4°)
LP O 93	σ*C 1–H 12	1.00 (2.50A°, 163.9°)	1.27 (2.5A°, 163.9°)
LP O 98	σ*C 2–H 13	3.85 (2.2A°, 151.4°)	4.55 (2.2A°, 151.4°)

In complex 1, the guest molecule is partially incorporated in the cavity. In this structure, one strong (O···H–O) hydrogen bond is established between the glycosidic oxygen atom O 97 and the hydrogen atom H 17 of the O 8–H 17 bond located at 2.1 Ǻ with an angle equal to 123.3° with stabilization energy E⁽²⁾ equal to 6.17 kcal/mol.

Conversely, for complex 2, the guest is totally included in the β-CD cavity. In this disposition, two Hbonds (O···HO) are formed: the first one between the O 69 of β-CD and the H 22 of the hydroxyl group of the guest (O 69···H 22O 11) positioned at 1.7 Ǻ with an angle of 164.6°. The second one is (O 83···H 17O 8) located at 1.8 Ǻ, with an angle equal to 147.1°. The interaction energy for the second hydrogen bond (11.59 kcal/mol) is lower than that for the first one (32.60 kcal/mol).

At the same time, a great number of CH···O or NH···O hydrogen bonds occurs between the cavity and the guest molecule. We notice that when the guest acts as a donor, the acceptors are the anti-bonding σ* (CH) orbitals of β-CD. The important interaction is observed between LP O8 and σ* C 55–H 137 (4.32 kcal/mol) for complex 1 and between LP O8 and σ* C 37–H 115 (7.22 kcal/mol) for complex 2.

When β-CD acts as a donor, the greater interaction is formed between LP O 67 atom and σ*N 10–H 20 (7.23 kcal/mol) for complex 1; for complex 2, important interactions are established between donor orbital LP O 87 and acceptor orbital N 10–H 21 (7.91 kcal/mol). So, it can be deduced that the interactions in complex 2 are the strongest, suggesting that the complex is the most stable. As an overall conclusion, we can confirm that intermolecular hydrogen bond is the main driving force in the formation of the inclusion complex.

4 Conclusion

In this work, we investigated the structure of the complexes formed between β-CD and octopamine using quantum mechanics PM6, HF level theory with 3-21G* basis set and several combinations of hybrid calculations. These results clearly show that the orientation in which the aromatic ring of the guest molecule is oriented to the center of mass of β-CD (orientation 2) is preferred owing to complexation energy. ONIOM2 and NBO analysis reveals that intermolecular hydrogen bonds and hydrophobic interactions play an important role in the complexation process of the guest with β-CD. The study in solution using CPCM model follows the same trend as that in gas phase, thus favoring orientation 2.

Acknowledgements

This study was supported by the Algerian Ministry of Higher Education and Scientific Research and General Direction of Scientific Research as a part of projects CNEPRU (No. E01520080026).

Bibliographie

[1] A. Hirashima; E. Kuwano; M. Eto Internet Electron. J. Mol. Des., 2 (2003) no. 4, p. 274

[2] S.E. Cooper; B.J. Venton Anal. Bioanal. Chem., 394 (2009), p. 329

[3] D.P. Holschneider; K. Chen; I. Seif; J.C. Shih Brain Res. Bull., 56 (2001), p. 453

[4] G. D’Andrea; S. Terrazzino; D. Fortin; A. Farruggio; L. Rinaldi; A. Leon Neurosci. Lett., 346 (2003), p. 89

[5] K.K. Manghani; M. Lunzer; B.H. Billing Lancet, 2 (1975), pp. 943-946

[6] L. Capocaccia; C. Cangiano; A.F. Attili; M. Angelico; A. Cascino; F.R. Fanelli Clin. Chim. Acta, 75 (1977), pp. 99-105

[7] A.A. Boulton Can. J. Neurol. Sci., 7 (1980), pp. 261-263

[8] Q. Yu; S. Zhao; F. Ye; S. Li Anal. Biochem., 369 (2007), pp. 187-191

[9] F. Tang; L. Tao; X. Luo; L. Ding; M. Guo; L. Nie; S. Yao J. Chromatogr. A, 1125 (2006), p. 182

[10] R. Gatti; C. Lotti; R. Morigi; A. Andreani J. Chromatogr. A, 1220 (2012), p. 92

[11] F. Pellati; S. Benvenuti; M. Melegari; F. Firenzuoli J. Pharm. Biomed. Anal., 29 (2002), p. 1113

[12] F. Pellati; S. Benvenuti J. Chromatogr. A, 1161 (2007), p. 71

[13] J. Szetjli Chem. Rev., 98 (1998), p. 1743

[14] R. Challa; A. Ahuja; J. Ali; R.K. Khar AAPS. Pharm. Sci. Tech., 6 (2005) no. 2, p. 329

[15] E.M. Martin Del Valle Process Biochem., 39 (2004) no. 9, p. 1033

[16] E. Schneiderman; A.M. Stalcup J. Chromatogr. B, 745 (2000), p. 83

[17] H.J. Schneider; F. Hacket; V. Rüdiger; H. Ikeda Chem. Rev., 98 (1998), p. 1755

[18] L. Liu; X.S. Li; K.S. Song; Q.X. Guo J. Mol. Struct. (THEOCHEM), 531 (2000), p. 127

[19] E.C. Yang; X.J. Zhao; F. Hua; J.K. Hao J. Mol. Struct. (THEOCHEM), 712 (2004), p. 75

[20] C.L. Yan; Z.L. Xiu; X.H. Li; C. Hao J. Mol. Graph. Model., 26 (2007), p. 420

[21] F.O. Suliman; A.A. Elbashir J. Mol. Struct., 1019 (2012), p. 43

[22] R. Djemil; D. Khatmi Can. J. Chem., 89 (2011), p. 1519

[23] F. Madi; L. Largate; L. Nouar; D. Khatmi J. Taiwan Inst. Chem. Eng., 43 (2012), p. 868

[24] S. Benghodbane; D. Khatmi C.R. Chim., 15 (2012), p. 371

[25] J.J.P.J. Stewart MOPAC 2007, Stewart Computational Chemistry, Colorado Springs, CO, USA, 2007

[26] M.J. Frisch; G.W. Trucks; H.B. Schlegel; G.E. Scuseria; M.A. Robb; J.R. Cheeseman; J.A. Montgomery; T. Vreven; K.N. Kudin; J.C. Burant; J.M. Millam; S.S. Iyengar; J. Tomasi; V. Barone; B. Mennucci; M. Cossi; G. Scalmani; N. Rega; G.A. Petersson; H. Nakatsuji; M. Hada; M. Ehara; K. Toyota; R. Fukuda; J. Hasegawa; M. Ishida; T. Nakajima; Y. Honda; O. Kitao; H. Nakai; M. Klene; X. Li; J.E. Knox; H.P. Hratchian; J.B. Cross; C. Adamo; J. Jaramillo; R. Gomperts; R.E. Stratmann; O. Yazyev; A.J. Austin; R. Cammi; C. Pomelli; J.W. Ochterski; P.Y. Ayala; K. Morokuma; G.A. Voth; P. Salvador; J.J. Dannenberg; V.G. Zakrzewski; S. Dapprich; A.D. Daniels; M.C. Strain; O. Farkas; D.K. Malick; A.D. Rabuck; K. Raghavachari; J.B. Foresman; J.V. Ortiz; Q. Cui; A.G. Baboul; S. Clifford; J. Cioslowski; B.B. Stefanov; G. Liu; A. Liashenko; P. Piskorz; I. Komaromi; R.L. Martin; D.J. Fox; T. Keith; M.A. Al-Laham; C.Y. Peng; A. Nanayakkara; M.Z.L. Pople Gaussian 03, Revision E. 03, Gaussian Inc., Pittsburgh, PA, USA, 2003

[27] C.L. Yan; X.H. Li; Z.L. Xiu; C. Hao J. Mol. Struct. (THEOCHEM), 764 (2006), p. 95

[28] I. Matei; A. Nicolae; M. Hillebrand J. Incl. Phenom. Macrocycl. Chem., 57 (2007), p. 597

[29] O. Attoui Yahia; D.E. Khatmi J. Mol. Struct. (THEOCHEM), 912 (2009), p. 38

[30] G.S. Tschumper; K. Morokuma J. Mol. Struct. (THEOCHEM), 592 (2002), p. 137

[31] C. James; A. Amal Raj; R. Reghunathan; I.H. Joe; V.S. Jayakumar J. Raman Spectrosc., 37 (2006), p. 1381

[32] J.N. Liu; Z.R. Chen; S.F. Yuan; J. Zhejiang Univ. Sci. B, 6 (2005), p. 584

[33] M. Szafran; A. Komasa; E. Bartoszak-Adamska J. Mol. Struct., 82 (2007), p. 101

[34] E. Kavitha; N. Sundaraganesan; S. Sebastian; M. Kurt Spectrochim. Acta A Mol. Biomol. Spectrosc., 77 (2010), p. 612

Commentaires - Politique