1. Introduction
Nanotechnology makes it possible to create nanoscale structures that can be used to study the electronic properties and electronic structure of a macromolecule or biological nanoparticle (MM or BNP) [1, 2, 3]. In single-molecule electronics [4], it was proposed to use the Josephson junction (JJ) [5, 6, 7] to study the electronic properties of small organic molecules and for different versions of Andreev spectroscopy and molecular electronics methods and devices.
The purpose of this work is to show the possibility of the Josephson effect in a JJ based on an insulator barrier of MM or BNP. To do this, we propose to use special superconducting nanoscale devices including the studied MM or BNP. In this case, the barrier size is determined by that of the MM, 2–2000 nm. Nevertheless, if the coherence length of Cooper pairs in superconductors and the sizes of MMs or BNPs are of the same order of magnitude, the Josephson effect may take place. Realization of the Josephson effect let us to measure electrophysical parameters (tensors conductivity, electronic polarizability and magnetic susceptibility) of the MM and its resonance frequency. The use of a JJ to determine the electronic properties of single MMs or BNPs can be an additional approach to conventional structural analysis.
Al, Sn, Nb have stable oxide films on the surface due to interaction with atmospheric oxygen. Oxides of these metals are very often used in chemistry and biochemistry as adsorption, separation and bioconjugate media for chromatography of biological molecules and sorbents for a wide range of biochemical and chemical compounds. This makes it possible to use “Metal–Oxide–(MM or BNP)” structures to create a JJ. Types of chemical bonding between a BNP (protein, biological membrane, biological complex, DNA, RNA) at room temperature are electrostatic and hydrophobic interactions [8]. At room temperature the types of interactions between the metal oxide and the MM or BNP depend on the type and number of ionic, hydrophobic, and hydrophilic groups on the BNP surface.
For example, an aluminum oxide film on the surface of an aluminum electrode can be a good material to create a JJ based on a conjugate with a MM or BNP. For example, the coherence length is 1600 nm for aluminum in the superconducting state [9].
2. Materials and methods
2.1. JJ with protein-based insulation barrier
2.1.1. Preparation of JJ with protein on metal electrode surface
To prepare a protein–metal structure on the metal (Sn or Nb) electrode surface, we used a polyacrylamide gel (PAAG) bead with a single green fluorescent protein (GFP) molecule (28 kDa; length 4.2 nm; diameter ∼2.4 nm; Merck Catalog N 14-392) in an individual gel bead. We prepared an individual bead (diameter ∼1 μm) from PAAG with a single GFP molecule inside the bead using 10% PAAG and immobilines (pH = 9) [10]. Beads of 10% PAAG with immobilines (pH = 9) (PAAG with functional acidic and basic groups) were placed in contact with flat PAAG. Initially GFP molecules were located in the pores of the flat PAAG. The concentration of the GFP in the flat gel was 0.01 μg/mL. GFP was introduced into PAAG using electrophoresis. The distribution of GFP molecules in the gel pores and transfer of the GFP from the gel to the gel bead was controlled using a fluorescent microscope [10, 11, 12, 13]. The pore size of the 10% PAAG was ∼70 nm. A bead made from immobilines with a PAAG adsorbed (extracted) single GFP molecules from a flat PAAG. At pH = 9 in immobiline, the GFP protein is well transferred into the immobiline bead from a flat PAAG with pH = 7. We then transferred the immobiline beads from the individual GFP molecules to the surface of the Nb or Sn electrode. The gel bead transfer to the metal surface was carried out using a nanomanipulator.
Then we applied a 1 V electrical signal to transfer the GFP molecule from the immobiline gel bead to the surface of the Nb or Sn electrode (5 s period of electrophoresis). The counter electrode was another Nb (or Sn) electrode. After the transfer of the GFP to the surface of the Nb (or Sn) electrode, fluorescence was used to control the presence of the GFP on the surface of the Nb (or Sn) electrode. The presence of GFP fluorescence on the surface of the electrode indicated the transfer of a single GFP molecule to the electrode. The voltage for electrophoresis is less than the decomposition potential of water and therefore no chemical reactions should have occurred with the protein molecule when it was transferred from the gel bead to the metal (Nb or Sn) surface.
At room temperature the binding mechanism of the GFP to the Nb or Sn electrode is associated with electrostatic and hydrophobic interactions between the metal, metal oxide layer, and the protein molecule [8].
PAAG and other gels have been successfully used for fluorescence spectroscopy of individual (single) macromolecules, such as proteins. Gel pores with cell sizes commensurate with the size of macromolecules (proteins) fix the macromolecule well and facilitate the task of manipulation and transfer of the macromolecule during the manufacture of the experimental setup [10, 11, 12, 13]. The properties of GFP are well defined and it is a well observed single molecule, which facilitates the JJ assembly process and quality control.
We used the fluorescence microscopy method from [14, 15] to achieve the experimental conditions to work with a single GFP molecule. Isolation of single molecules in PAAGs is routinely and reliably used for the isolation and detection of single GFP molecules in single molecule fluorescence spectroscopy [16]. To monitor the formation of “single GFP molecule”–metal structure on the electrode surface, we measured the fluorescence of the GFP under a fluorescent microscope [10, 11, 12, 13, 15].
The GFP on the Nb or Sn electrode was dried at room temperature in a helium atmosphere. After drying the protein layer, the protein-coated Nb or Sn electrode was cooled. Then we assembled the JJ.
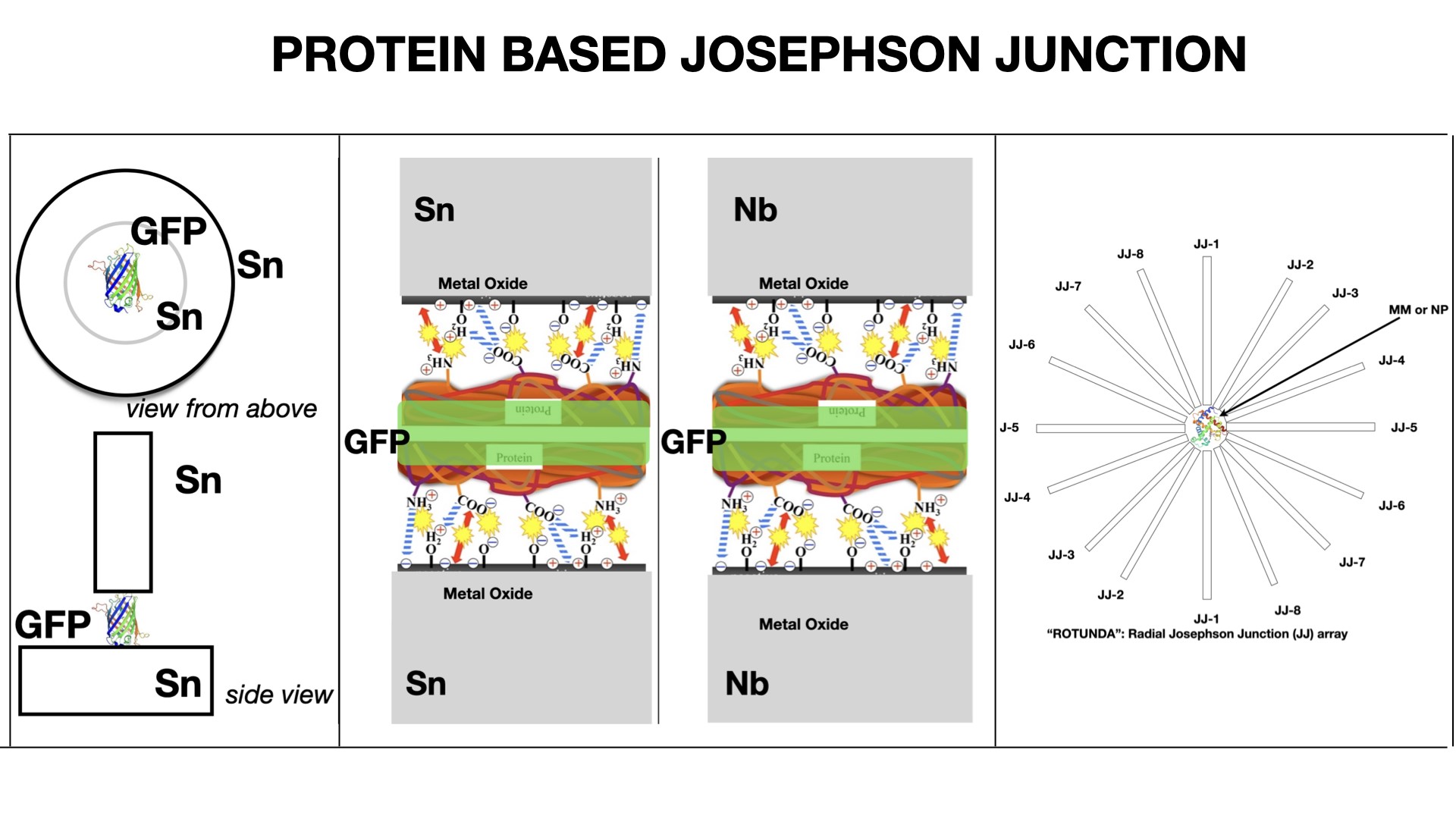
A top “needle” electrode covered with a GFP on a metal surface touched the lower metal electrode. The electrode with GFP was moved using a vertical nanomanipulator. The contact area was 10−4 μm2. The electrical circuit (JJ made from Sn–GFP–“needle” Sn electrode; or JJ made from Nb–GFP–“needle” Nb electrode) was closed and the voltmeter connected to the JJ for measurements (Figure 1).
(a) Scheme of Sn–GFP–Sn Josephson junction. (b) Nb or Sn metal surface bounding with GFP. Metal oxide layer electrostatic bounding with protein’s ionogenic groups.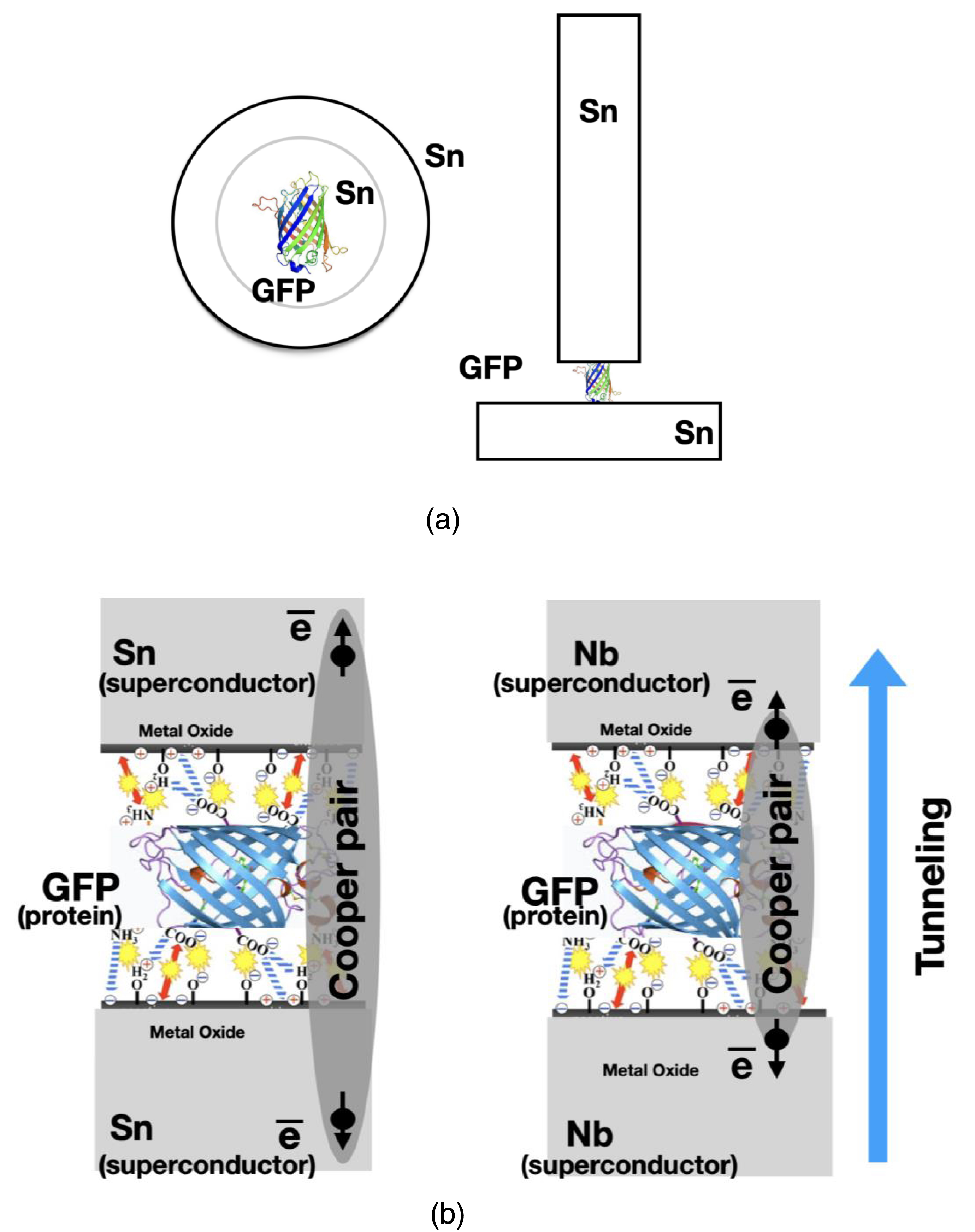
For control experiments, we prepared a JJ without GFP molecules. For this purpose, we used beads made from immobilines without GFP molecule. The immobiline beads were applied to the surface of the electrodes. Then the immobiline gel beads were removed and the final assembly of the control JJ was carried out.
2.2. JJ with GFP-based insulation barrier
We made measurements of low-temperature phenomena in the Me–MM–Me structure. The voltage (V) on the structures was measured by the 4-probe method using digital voltmeters of the HP 34401A type at a constant current set by a large load resistance. Temperatures below 4.2 K were obtained by evacuating helium vapor and fixed with a monostat with an accuracy of 0.01 K. The temperature above 4.2 K was obtained by heating helium vapor with a microheater, and controlled using an exemplary germanium thermometer of the TSG-1 type. Sn and Nb with a purity of at least 99.999% were used as electrodes (purity control made by X-ray photoelectron spectroscopy—XPS—analysis).
Figures 2 and 3 show the low-temperature dependences of the resistances (R) for the Nb–GFP–Nb (Figure 2) and Sn–GFP–Sn (Figure 3) structures. It is known that Sn passes into the superconducting state at Tc = 3.72 K, and Nb at Tc = 9.3 K. In our M–MM–M structures, upon cooling starting from Tc, a decrease in resistance is observed up to technical zero, determined by the resolution limit of the equipment used. For the Nb–GFP–Nb (Figure 2) and Sn–GFP–Sn (Figure 3) structures, the transition to technical zero is observed around 4.5 K and 3.65 K, respectively.
Low-temperature dependences of the resistances R for the Nb–GFP–Nb structure from temperature.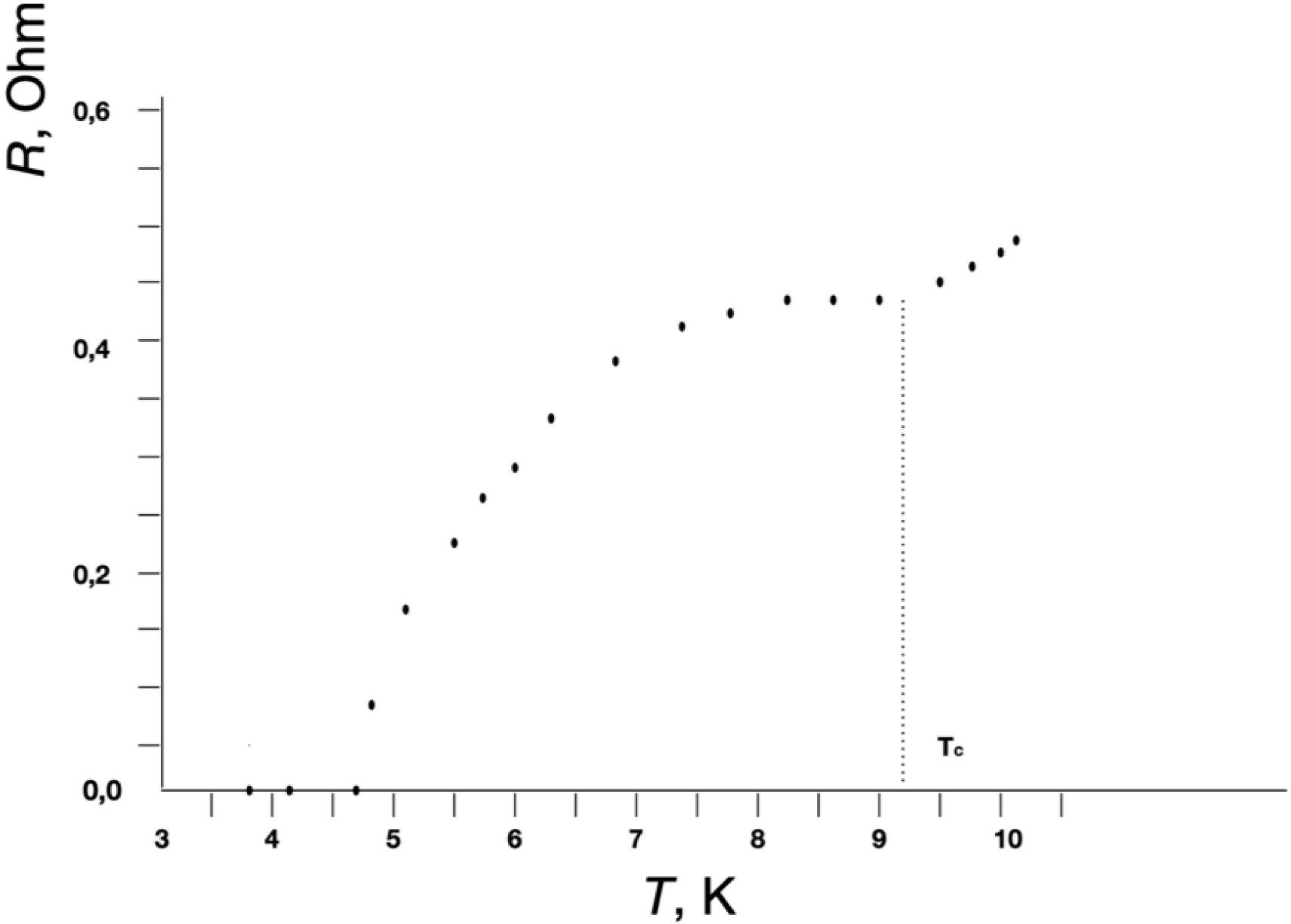
Low-temperature dependences of the resistances R from temperature for the Sn–GFP–Sn structure.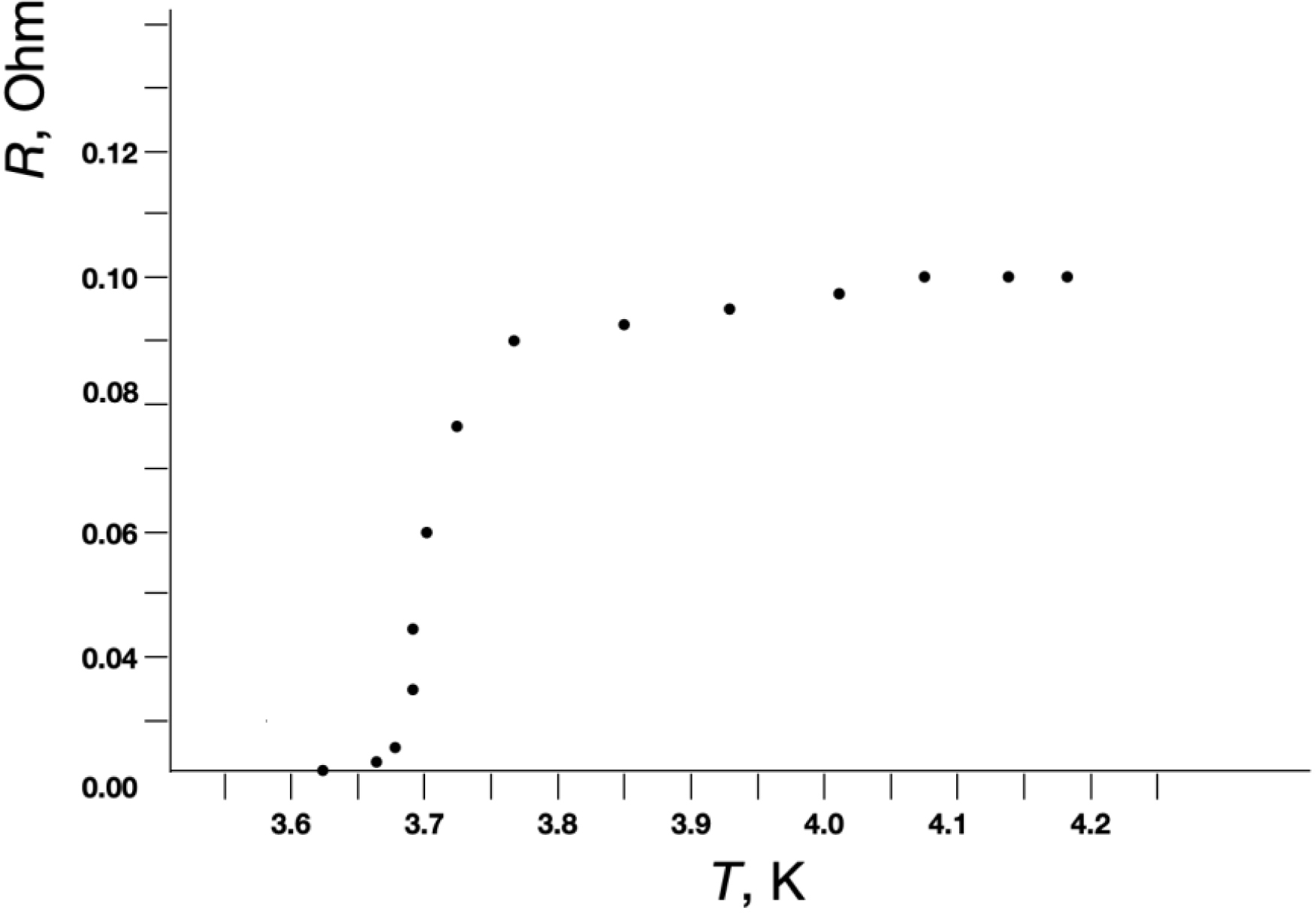
In the control M–M structure where there was no MM between the metal electrodes and the electrodes directly touched each other, the transition to technical zero resistance during cooling occurred very abruptly. XPS elemental analysis and electric resistance measurements as a function of temperature indicated a sufficiently high purity of the metals used as electrodes. The smearing of the transition may indicate fluctuation phenomena in the vicinity of the critical temperature Tc. In the vicinity of Tc, fluctuations of the order parameter cause the appearance of resistance in the superconducting state at T < Tc and superconducting electrons at T > Tc. In two-dimensional and one-dimensional superconductors, allowance for such fluctuations should lead to smearing of the temperature transition. In pure bulk superconductors, allowance for fluctuations does not noticeably affect the nature of the superconducting transition. In thin superconducting filaments and particles with diameter d ≪ 𝜉0 the coherence length (2300 Å [9] or 2100 Å [17] for Sn, 430 Å for Nb [18]), the influence of fluctuations on the temperature transition smearing is observed. In films these values are typically smaller.
Twenty GFP-based JJ devices were tested to assess device-to-device reproducibility. Current–voltage characteristics are given in the Supplementary Material. There is an oxidated film on the surface of Sn or Nb. The orientation and attachment (interaction) of the GFP molecule on oxide surfaces during the production of the JJ is carried out through certain ionogenic groups. GFP’s electrostatic charge distribution at the time of device production is not random [19]. There are references in the literature about the orientation of the GFP molecule on crystalline surfaces. The orientation of the MM or BNP inside the JJ insulator barrier can be controlled by fluorescence spectroscopy methods [20] or running electrostatic interactions control [21] at the time of GFP transfer to the electrode surface. It is also possible to check the degree of isotropy (or anisotropy) of the MM or BNP in this way [20].
3. Results
The electronic structure of MMs and BNPs is mostly often anisotropic in three-dimensional space. This anisotropy gives different profiles of the phase transition dependence on the normal to superconducting state for superconductor–MM contacts. Dependence of the “electrical resistance–temperature” (R–T) curve on direction or position of the MM or BNP inside the JJ may be a new characteristic for the MM or BNP. It is also possible to check the degree of isotropy (or anisotropy) of nanoparticles and MMs in this way.
For the Josephson effect, the protein molecule’s dielectric barrier thickness must be much smaller than the Cooper pair coherence length. Figures 4(a) and (b) show an example of the current–voltage characteristics (CVCs) of the Nb–GFP–Nb and Sn–GFP–Sn structures prepared by the method described above in the text.
Current–voltage characteristics of the following Josephson junctions: (a) Nb–GFP–Nb and Nb–Nb (without GFP), (b) Sn–GFP–Sn and Sn–Sn (without GFP), (c) Nb–mGFP–Nb with modified GFP, and (d) Sn–mGFP–Sn with modified GFP.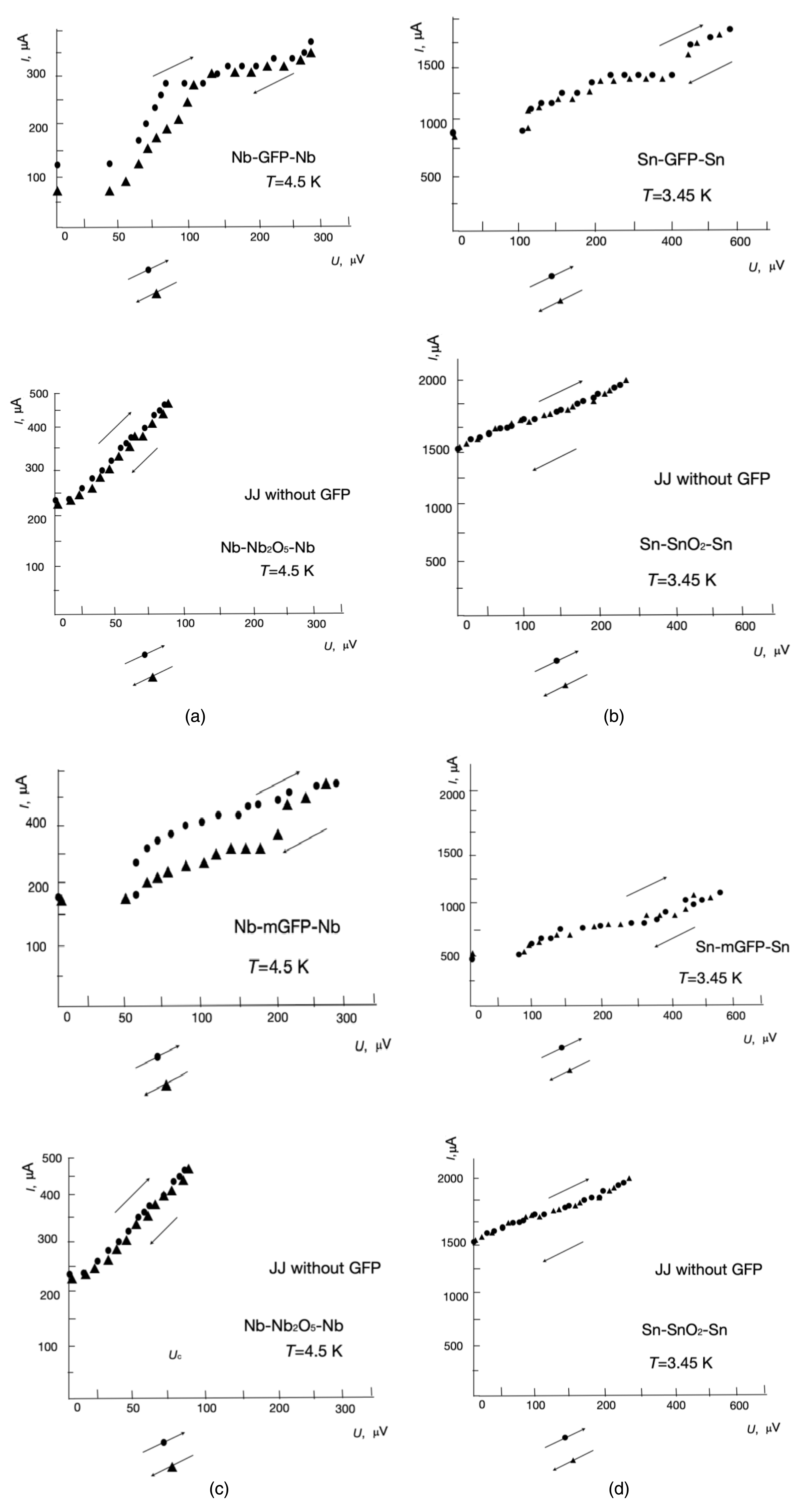
It is possible that the low critical current can be associated with induced superconductivity in the MM channel, as is the case in superconductor–normal metal–superconductor structures. In the presence of a “coupling”, the critical current should oscillate in weak magnetic fields [22]. The dependence Ic(H) was measured in weak magnetic fields at a current transverse to the magnetic field, flowing through the Sn–GFP–Sn structure, at which a voltage drop across the M–MM–M structure is recorded. Current–voltage characteristic for the Nb–GFP–Nb structure are presented in Figure 4(a). Measurement set-up was shielded from the Earth’s magnetic field.
Figures 4(c) and (d) show the CVCs for Nb–mGFP–Nb and Sn–mGFP–Sn with a modified GFP (mGFP) (another GFP structure). This modified GFP is eGFP His-tag from Cube Biotech (catalogue number 29901) [23]. The CVCs for GFP and mGFP are different. Figure 5 shows the observed dependence Ic(H), which clearly indicates an oscillation of the critical superconducting current. Thus, in the case of the transition of electrodes to the superconducting state in Me–MM–Me structures, the Josephson effect is observed.
(a) Sn–GFP–Sn and (b) Nb–GFP–Nb JJ critical current versus magnetic field applied in the plane of the substrate—perpendicular to the current direction.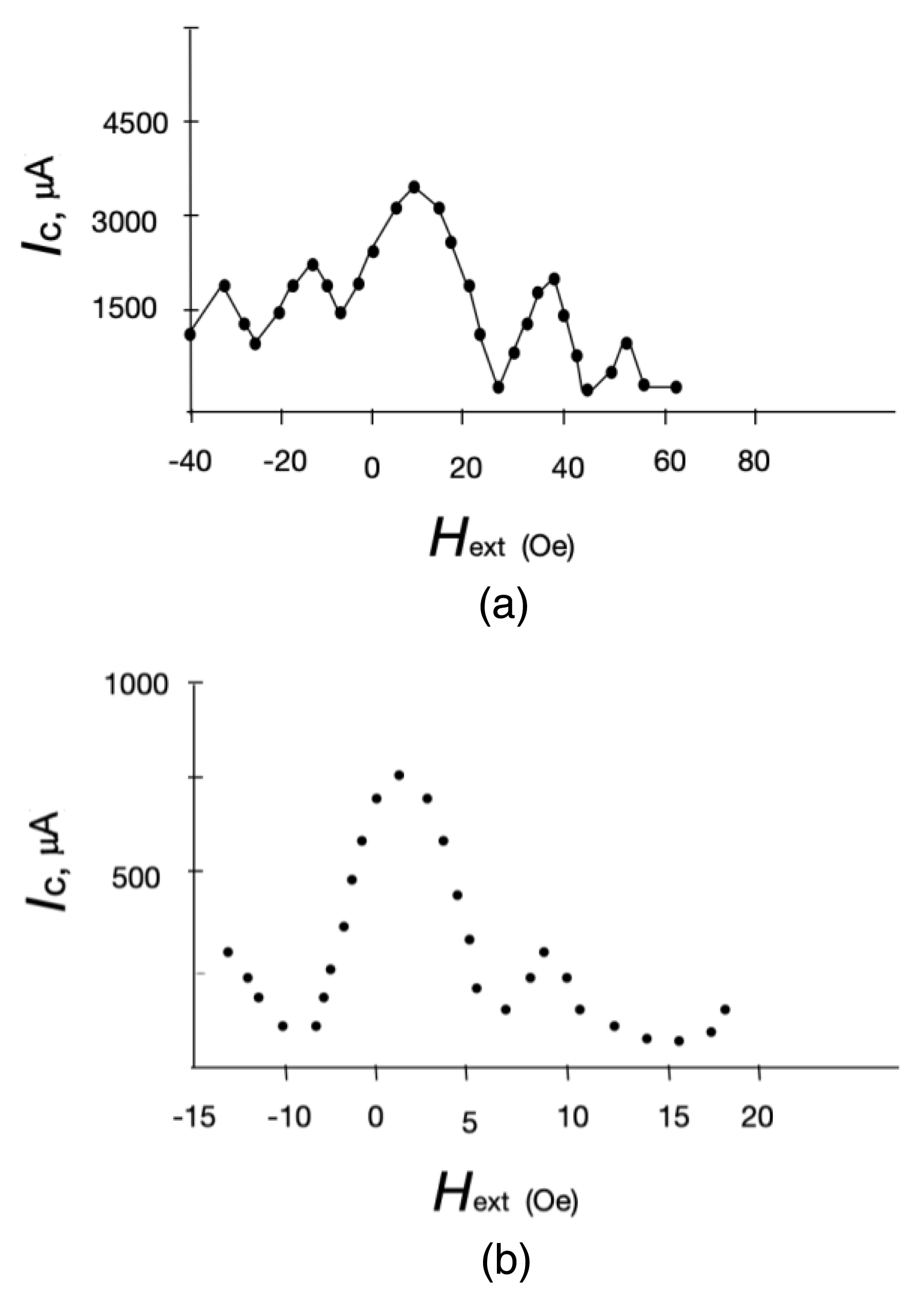
When analyzing the CVCs of a JJ, it is necessary to divide it into sections [24, 25]. At a voltage of 0 V, a superconducting current is observed in both JJs (Sn–GFP or Nb–GFP). The magnitude of the total step of the JJ’s superconducting current is equal to the sum of the steps from the elementary JJ contacts of the superconductor and the GFP subunits (amino acid or beta helix). These macromolecule’s subunits influence the formation of a path for superconducting current tunneling through the JJ. Thus, based on the height of the general stage of the JJ, one can find the number of subunits of the macromolecule. As the electrical voltage increases, the normal current component begins to appear. This normal current component occurs in addition to the superconducting current. The normal component of the current is carried out by electrons and not by Cooper pairs. Hysteresis on the CVC of the Nb–GFP JJ means that the JJ has a certain electrical capacity. In the CVC of the Sn–GFP JJ, the electrical capacitance is quite small. When an external electrical voltage is applied to a JJ, the current is carried by Cooper pairs and electrons. When the JJ’s internal energy (Ec) is exceeded, electromagnetic radiation is generated, determined by the formula
The electromagnetic radiation mode manifests itself in the form of a flatter CVC section, where excess JJ energy is emitted in the form of electromagnetic radiation. The radiation frequency is proportional to the voltage (potential difference) across the JJ. The greater the voltage, the greater the frequency of the emitted radiation. Measuring the radiation frequency in this section of the CVC provides information about the ohmic resistance of the JJ and the contributions of normal and superconducting currents. The magnitudes of the current steps are the sum of the contributions of steps from elementary contacts from the superconductor to the subunits of the macromolecules (amino acids). After increasing the electrical voltage to more than 450 μV for Sn–GFP and 280 μV for Nb–GFP, the main contribution is made by the normal component of the current (electrons). Differences in the CVCs of Nb–GFP and Sn–GFP appear due to different values of the elements in the circuit diagram (ohmic resistance, electrical capacitance and inductance). The critical level of the superconducting current and the normal electron current level when an electrical voltage is applied determine the type of superconductive electrodes CVC for each type of JJ. The CVC is determined by the electronic characteristics of the dielectric placed in the JJ gap.
4. Discussion
4.1. JJ with MMs or BNPs as device for detection of their electronic properties
The implementation of the Josephson effect on MMs or BNPs makes it possible to develop a method and device for determining the electronic properties of these particles. In the proposed device and method, only one single MM or BNP is required to determine its electronic properties and structure.
By placing a particle in a JJ, it is possible to measure the tensor components (tensor of the second rank) of the electric polarizability, magnetic susceptibility of the MM or BNP for different directions and magnitudes of the external electric or magnetic field’s strength vector. By measuring the “plasma frequency” of a superconducting resonator based on a JJ with a MM or BNP, in the dielectric layer (or “superconducting current—MM or BNP”), one can obtain projections of the electron density distribution of the MM or BNP. When measuring various (all) projections in space, one can obtain the volume distribution of the electron density of the MM or BNP placed in the JJ. A JJ-based superconducting resonator is preferred over a capacitor due to the absence of thermal fluctuations and the ability to exploit the unique properties of superconductors near the superconducting-to-normal transition.
To study the electrical properties of MMs or BNPs, the JJ has advantages over a conventional RLC circuit based on normal metals with normal electronic conductivity. These advantages are: (1) a higher quality factor of the JJ oscillatory circuit than that of an oscillatory circuit with normal conductivity; (2) the ability to record Josephson radiation when voltage is applied to the JJ’s electrodes (use this radiation for “Josephson” spectroscopy of MMs or BNPs); (3) the tunneling length of Cooper pairs in a JJ exceeds the length of electron tunneling from the surface of a normal metal electrode. Accordingly, superconducting current as a probe has advantages over the tunnel current of normal electrons. Low temperatures when measuring the electrical characteristics (electronic parameters—structure) of MMs or BNPs rigidly fixed in the superconducting resonator make it possible to avoid the influence of movement and reorientation of MMs or BNPs in the electromagnetic field of the superconducting resonator. To describe the operation of a JJ with a MM or BNP insulator layer, we can use a RCSJ model (Resistively & Capacitively Shunted Junction model) with an electric capacitance C.
When using a “thin” JJ, the measured characteristic is the magnitude of the superconducting current, which depends on the phase difference of the superconducting current on the JJ’s superconducting electrodes. When placing a dielectric MM or BNP in the gap between the JJ’s superconducting electrodes, the system becomes similar to a parallel connection of a superconducting shunt, capacitance and electrical resistance.
A JJ with a MM or BNP in the gap between the superconducting electrodes acts as a superconducting resonator. In contrast to the “thin” JJ implementations, we use a dielectric barrier (gap) between the superconducting electrodes to measure the main components of the electronic characteristics and electronic structure of the MM or BNP that is part of this barrier. The difference between such a device and a “thin” JJ is the presence of electrical resistance, capacitance, inductance when an external field (electric and/or magnetic) is applied. MMs or BNPs usually have certain chemical groups and types of chemical bonds (C–C, C–N, C–O, C–H, O–H, C=O, N–H, C=C, aromatic groups, indole, etc.). These chemical groups and bonds have certain dipole and magnetic moments, and dielectric constants. Dielectric constants, constants of magnetic susceptibility are tensors of the second rank.
A JJ with a single MM or BNP placed in a dielectric gap between the superconducting electrodes behaves like a very sensitive RLC oscillating circuit with effective capacitance, magnetic inductance and superconducting shunt. In such an oscillatory circuit, with the help of an external potential difference or a magnetic field, resonance frequencies are excited. The resonance frequencies of the circuit depend on the electronic structure of the MM or BNP placed in the dielectric gap of the superconducting resonator. Also, the resonance frequencies depend on the orientation of the MM or BNP relative to the JJ’s superconducting electrodes. A single MM or BNP must be fixed between the superconducting electrodes of the Josephson superconducting resonator (Figure 6). Superconducting electrodes are placed radially with the MM or BNP at the center and this device looks like a “rotunda”.
“JJ-ROTUNDA”—radial geometry of JJ’s array for 2 or 3D measurements of single molecule (or nanoparticle) electric polarization and magnetic susceptibility.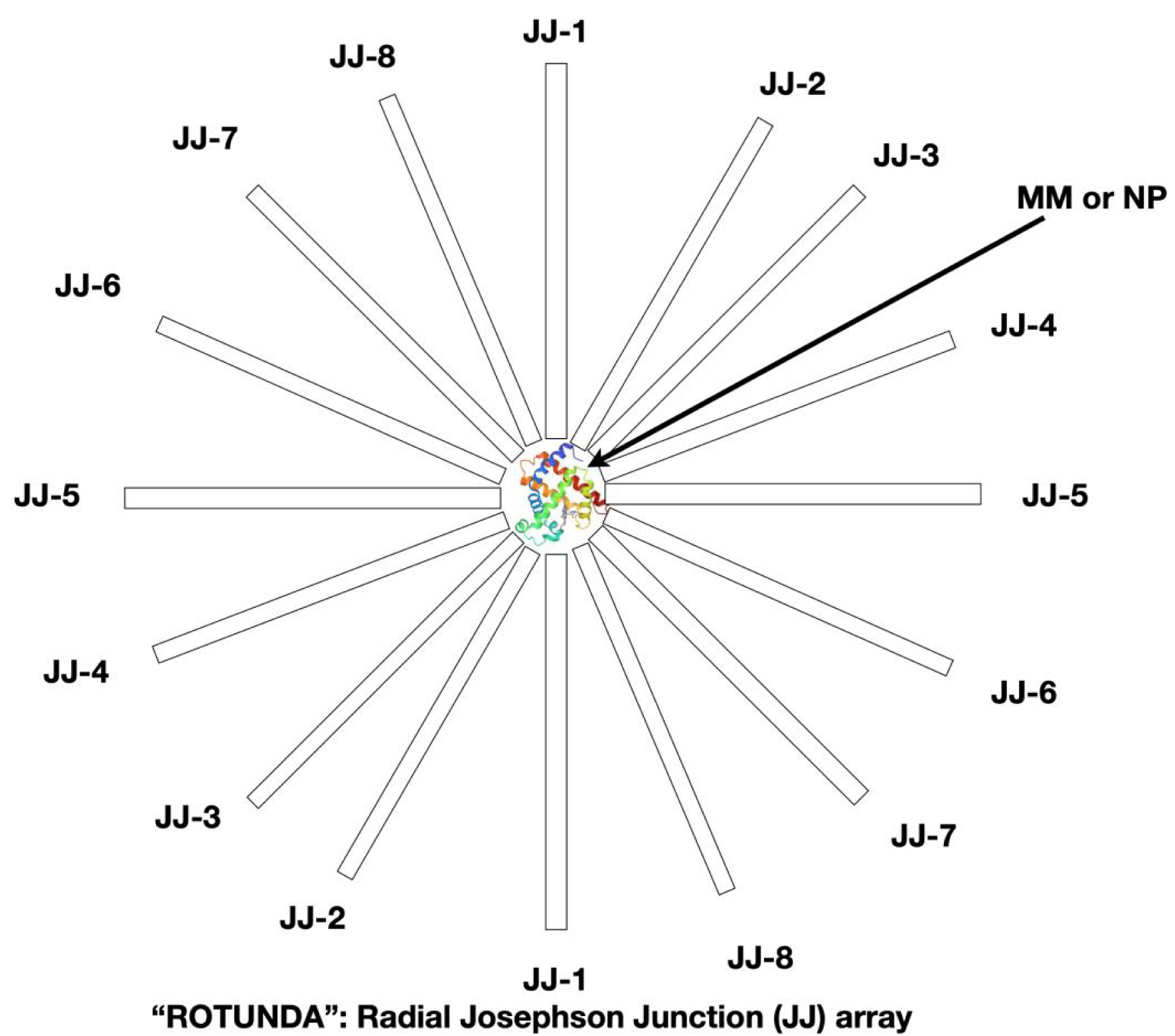
The presence of electric capacitance leads to the possibility of creating a circuit to measure the parameters of the dielectric layer. The JJ can be described as a nonlinear inductive element which stores energy when the current through it changes [26, 24, 27, 28, 29, 30, 31]. In the general case, within the framework of the resistive model, the equivalent circuit is supplemented by a capacitance C connected in parallel (Figure 7).
Schematic diagram of a resistive model with electric capacitance.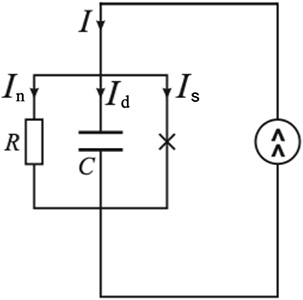
Accordingly, we can consider the natural resonance frequency of the circuit with capacitance C and “self-inductance” JJ:
From measurements of the JJ’s electric capacitance, it is possible to determine the MM or NP’s polarizability tensor components. The components of the magnetic susceptibility tensor are determined from measurements of the inductance. The measurements from each pair of JJ electrodes correspond to certain tensor components. To determine the three parameters of electronic polarizability, conductivity, and magnetic susceptibility, it is sufficient to measure the normal current, superconducting current, and frequency.
Based on the experimental values of the current through the JJ on the CVC, the parameters of the circuit diagram of the modeling JJ (inductance, capacitance, conductivity) are determined. These parameters are the parameters of the molecule between the superconducting electrodes. Based on conductivity, inductance and capacitance, one can determine magnetic susceptibility, polarizability, dielectric constant, and electrical conductivity. These quantities are tensors of the second rank with 9 components. These components provide information about the spatial distribution of the electron density of the protein molecule.
To find the parameters of circuit diagram elements, it is necessary measure the response to an external magnetic or electric (applied voltage) field. By measuring the resonance frequency of current oscillations in the circuit, we can find the electric capacitance and magnetic inductance using the formula:
4.2. Some aspects of preparing a MM- or BNP-based JJ
For easy handling and preparation of the “rotunda” device, one can use MMs or BNPs inside gel beads. It is possible to use different types of gels (polyacrylamide, agarose, silica gel, etc.) with a pore size of tens or hundreds of nanometers to isolate a single protein molecule or other MMs or BNPs. The pore size of the gels is commensurate with the coherence length of the Cooper pairs. After evaporation of water from the gel, the volume of gel pores and the volume of gel pieces decrease tenfold. Therefore, for a simpler assembly of a MM-based JJ between superconducting electrodes, one can use submicron gel pieces (beads, other shapes) with single MMs (proteins, DNA, or BNP) inside the gel’s pore cells.
5. Conclusion
For the first time, a JJ was created on the basis of a biological molecule. A device is proposed that consists of a macromolecule or biological particle (MM or BNP) and a JJ. The MM or BNP is placed in the gap between the superconducting electrodes of the JJ. The choice of the JJ as a device for studying the properties of MMs or BNPs makes sense because the scales of the coherence length of Cooper pairs in superconductors and the sizes of MMs or BNPs coincide.
The Josephson effect manifests itself not only in tunnel junctions, but also when connecting two (or more) superconductors through a weak link of any kind. In this work study case the weak link is a protein molecule placed between superconducting electrodes.
The presence of oxide films on the surface of superconductors provides a good opportunity to create covalently bonded stable metal–oxide–(MM or BNP) structures (produced at room temperature). By varying the conditions for the synthesis of metal–oxide–(MM or BNP) structures, it is possible to selectively use ionic or hydrophobic groups in MMs or BNPs. The choice of superconducting electrode material allows one to vary different coherence lengths and for different types of MMs or BNPs (with different sizes). For each size of BNP it is proposed to select a specific superconductor material.
The proposed method could be used to study the mechanisms of interaction of drugs with membrane target proteins, or in virology, for example, to study the process of how a virus interacts with a cell. Note that endogenous viruses are very large formations. Their diameter reaches 25 nm and their mass can exceed 1 MDa. Viruses, even of the same species, are very heterogeneous. This may enable the detection of the fold and fill of DNA under the envelope of the virus.
It is discussed that conventional electrophysical measurements of the resulting JJ structure with MM or BNP (CVC, dependence of the critical current on the external magnetic field, and others) make it possible to obtain information about the distribution of electron density in the MM or BNP.
Prior to this work, no one had used a JJ to determine the structural and electronic properties of dielectrics and MMs or BNPs. Much remains to be understood in the Josephson effect itself in molecular compounds based on biological molecules and particles [32, 33, 34, 35].
Declaration of interests
The authors do not work for, advise, own shares in, or receive funds from any organization that could benefit from this article, and have declared no affiliations other than their research organizations.
Acknowledgements
We thank to Professor Matvey V. Entin from the Institute of Semiconductor Physics of the Russian Academy of Sciences (Novosibirsk) and Professor Pier Giorgio Righetti from Politecnico di Milano for interest in our work and very fruitful discussions.




 CC-BY 4.0
CC-BY 4.0