Détermination du tenseur des contraintes par inversion de mécanismes au foyer de séismes sans choix de plans nodaux

Jacques Angelier

doi:10.1016/S1631-0713(02)01712-1

Résumés

Français
Anglais

Il est possible de déterminer l'état de contrainte sismotectonique à partir de mécanismes au foyer de séismes de type double couple, sans devoir choisir entre les deux plans nodaux de chaque mécanisme. Il faut adopter pour critère d'inversion une fonction qui ne dépend pas de ce choix : la composante de glissement de la contrainte cisaillante, ou CGCC. Une méthode est donc construite autour de ce critère. Elle est analytique ; de ce fait, le temps de calcul requis par l'inversion, négligeable, est le même quel que soit le nombre de données.

The seismotectonic state of stress is determined using double couple focal mechanisms of earthquakes, without any need to choose among the nodal planes. As the inversion criterion, a function that does not depend on this choice is adopted: the slip shear stress component, or SSSC. A new method is built, based on this criterion. Because the inversion is carried out by analytic means, the runtime is negligible and does not depend on the number of data.

Abridged version

1 Introduction

After it had been proposed to carry out inversion of fault slip data to obtain the stress state [1,8], the same technique was applied to double couple focal mechanisms of earthquakes; a major limitation arose because of the apparent need to choose between the nodal planes [2,9,12]. Choosing the ‘best’ nodal plane of each mechanism through an iterative inversion process implies that 50 % of the data are retained simply, because they best fit the researched solution, a somewhat circular approach. If the inversion criterion does not depend on the choice among the nodal planes and is physically meaningful, such an arbitrary choice can be ignored. The slip shear stress component, or SSSC, adopted in this paper as a criterion, fulfils this requirement.

2 Mechanical significance of the inversion criterion

The SSSC is the component of the calculated shear stress along the observed slip. It is given by the scalar product $σ \cdot 𝐬$ , where $σ$ is the applied stress vector and $𝐬$ the unit slip vector (figure 1). The SSSC is positive if the stress acts in the same sense as the actual slip, negative otherwise. The SSSC is also the shear stress, τ, multiplied by the cosine of the angle, α, between observed slip and calculated shear stress (figure 1). The SSSC is an increasing function of τ and a decreasing function of α. Thus, with τ_max as the largest possible shear stress, the SSSC ranges from τ_max (largest slip-parallel shear stress) to −τ_max (largest slip-opposite shear stress).

Figure 1
Définition du critère d'inversion, la fonction CGCC (composante de glissement de la contrainte cisaillante). Le jeu de faille est défini par deux vecteurs unitaires: $𝐧$ , la normale au plan de faille (flèche blanche), et $𝐬$ , le vecteur glissement unitaire (flèche grise, montrant le mouvement du bloc inférieur par rapport au bloc supérieur). Les flèches noires décrivent la contrainte appliquée ( $σ$ ), la contrainte tangentielle ( $τ$ ) et le vecteur CGCC ( $τ_{s}$ ). L'angle entre la contrainte tangentielle calculée et le glissement observé est α. Deux définitions équivalentes de la fonction CGCC (τ_s) sont indiquées par les formules (remarquer que τ_s peut être négative, et donc n'est pas simplement le module du vecteur $τ_{s}$ ).
Definition of the inversion criterion, the SSSC (Shear Stress Slip Component) function. The direction and sense of fault slip are defined by two unit vectors: $𝐧$ , normal to fault plane (open arrow), and $𝐬$ , unit slip vector (grey arrow, indicating motion of lower block with respect to upper one). The black arrows describe the applied stress ( $σ$ ), the shear stress ( $τ$ ), and the SSSC vector ( $τ_{s}$ ). The angle between calculated shear stress and actual slip is α. Two equivalent definitions of the SSSC function (τ_s) are given as formulas (note that τ_s may be negative, and hence is not the simple modulus of the vector $τ_{s}$ ).

To determine the SSSC, one needs parameters to describe the orientations of the plane and the slip, and variables to describe the stress tensor. The mechanical significance of the SSSC is obvious regarding the angle α (figure 1); considering the shear stress (τ), the meaning is also clear, because increasing shear stress results in greater probability of slip occurrence. Thus, making the SSSC as large as possible is reasonable to reconstruct a stress state that accounts for the observed slip. On the other hand, the Tresca criterion (figure 2) poorly accounts for the activation of pre-existing discontinuities with various orientations, and using the SSSC is a raw approximation with respect to the adoption of the Mohr–Coulomb criterion [13]. However, not only would such an adoption require the choice between nodal planes, but also it would be necessary to give values to unknown or poorly constrained parameters like friction coefficients or fluid pressures. Using the SSSC criterion thus represents a compromise, in any case better than the simple use of the angle α, which would mean that fault activation does not depend on shear stress amount [5].

Figure 2
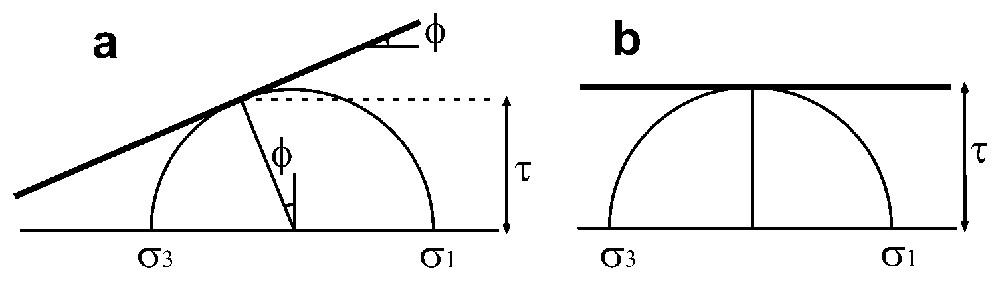
Critères de Mohr–Coulomb (a) et de Tresca (b). Diagrammes de Mohr avec la contrainte normale en abscisse et la contrainte tangentielle en ordonnée. Symboles définis dans le texte, sauf l'angle de frottement φ de la loi de Mohr–Coulomb.
Mohr–Coulomb (a) and Tresca (b) criteria, illustrated in Mohr's diagrams with normal stress as abscissas and shear stress as ordinates. Symbols defined in the text, except for the friction angle, φ, of the Mohr–Coulomb law.

3 The inversion criterion does not depend on the choice between nodal planes

As an interesting property, the SSSC value is identical for the two nodal planes of an earthquake mechanism. If a nodal plane is the fault, it does not follow that the shear stress virtually exerted on the inactive nodal plane is perpendicular to the fault plane: it may be oblique (figure 3). Thus, except in particular situations [2], a stress tensor does not simultaneously account for the two possible slips of a focal mechanism. However, the same SSSC is calculated for each nodal plane as a function of the stress tensor, $𝐓$ . If the fault plane is the nodal plane 1, with unit normal vector $𝐧_{1}$ , the stress vector $σ$ applied to the plane is $𝐓 𝐧_{1}$ . By essence, the unit slip vector on plane 1 and the unit vector normal to plane 2, $𝐧_{2}$ , are identical; the SSSC is thus given by the scalar product $(𝐓 𝐧_{1}) \cdot 𝐧_{2}$ . Likewise, if the fault plane is the nodal plane 2, the SSSC is ( $𝐓 𝐧_{2}) \cdot 𝐧_{1}$ . These two expressions are identical. It follows that for a focal mechanism consistent with the stress state, a single SSSC value exists, whatever the nodal plane activated as a fault.

Figure 3
L'ambiguı̈té du mécanisme au foyer des séismes de type double couple. Pour les deux situations possibles, mutuellement exclusives, les plans nodaux sont identiques, mais le plan nodal agissant comme faille (F) diffère. Une paire de flèches blanches indique le sens de cisaillement. Le plan de faille actif porte des stries parallèles au glissement réel, un fantôme indique le plan nodal inactif. La flèche blanche en trait continu désigne la normale ( $𝐧$ ) au plan de faille, la flèche noire désigne la contrainte cisaillante idéale ( $τ$ ). La flèche blanche en trait pointillé désigne la contrainte tangentielle théorique pour le plan nodal inactif. Si le glissement réel et la contrainte cisaillante idéale sur la faille F sont perpendiculaires au plan nodal inactif, la contrainte tangentielle virtuelle sur ce plan nodal inactif peut être oblique au plan de faille.
The double couple focal mechanism of earthquake and its ambiguity. The two possible, mutually exclusive, situations show identical nodal planes, but the nodal plane acting as the fault (F) differs. The shear sense is indicated by a couple of open arrows. The active fault plane bears striations parallel to actual slip, the inactive nodal plane is indicated by a ghost. The open arrow with solid line shows the normal ( $𝐧$ ) to the fault plane, the black arrow shows the shear stress on the fault ( $τ$ ). The open dotted arrow shows the theoretical shear stress on the inactive nodal plane. Whereas the actual slip and ideal shear stress on fault F are perpendicular to inactive nodal plane, the virtual shear stress on this inactive nodal plane may be oblique to fault plane.

As a consequence, the SSSC-based inversion does not require any choice between nodal planes. This property does not matter for geologists, who observe the fault plane and slickenside lineation, but is crucial for seismologists analysing focal mechanisms of earthquakes (figure 3).

4 Analytical resolution of the inverse problem

The stress state that best accounts for a set of K focal mechanism data can thus be determined without any choice of nodal planes. It suffices to search for the stress tensor giving the largest possible SSSC, for all mechanisms simultaneously. Two sums are considered:

S = \sum_{k = 1}^{k = K} τ_{s k} or S' = \sum_{k = 1}^{k = K} {(τ_{\max} - τ_{s k})}^{2}

(1)

where τ_sk refers to the SSSC number k. S ranges from

- K τ_{\max}

K τ_{\max}

, and should be made maximum. S′ ranges from 0 to

4 τ_{\max}^{2}

, and should be made minimum (in the least square sense). In practice, S results in more robust inversion than S′, because it is less sensitive to large misfits.

The stress tensor is written as follows, with the director cosines of the three principal axes as x_i,y_i and z_i (i=1, 3 in the east–north–up coordinate frame), and the principal stress magnitudes as σ₁⩾σ₂⩾σ₃ (pressure noted positive):

(\begin{matrix} T_{11} & T_{21} & T_{31} \\ T_{12} & T_{22} & T_{32} \\ T_{13} & T_{23} & T_{33} \end{matrix}) = (\begin{matrix} x_{1} & x_{2} & x_{3} \\ y_{1} & y_{2} & y_{3} \\ z_{1} & z_{2} & z_{3} \end{matrix}) \cdot (\begin{matrix} σ_{1} & 0 & 0 \\ 0 & σ_{2} & 0 \\ 0 & 0 & σ_{3} \end{matrix}) \cdot (\begin{matrix} x_{1} & y_{1} & z_{1} \\ x_{2} & y_{2} & z_{2} \\ x_{3} & y_{3} & z_{3} \end{matrix})

(2)

The nine director cosines are expressed as functions of three independent angles, θ,ζ and ξ. As for the three stress magnitudes, two unknowns cannot be determined with slip orientations and senses: $𝐓$ being solution of the problem, $m 𝐓 + n 𝐈$ is also solution (m being any strictly positive number, n any pressure or tension, $𝐈$ the unit matrix). To determine m and n, additional information is necessary [3]. As a consequence, the three principal stresses depend on a single variable, ψ [6], a function of the ratio of principal stress differences, Φ=(σ₂−σ₃)/(σ₁−σ₃). The reduced stress tensor is finally expressed as a function of independent variables, the four angles θ,ζ,ξ and ψ. The SSSC and the sum S are then calculated as indicated before. The extrema of the function S are obtained by setting the four partial derivatives to zero:

\frac{\partial S}{\partial θ} = 0, \frac{\partial S}{\partial ξ} = 0, \frac{\partial S}{\partial ζ} = 0, \frac{\partial S}{\partial ψ} = 0} .

(3)

This system is solved by analytical means as it was done before for fault slips [4]. A numerical comparison between the extrema indicates the largest sum D, and hence the four values of θ,ζ,ξ and ψ solution of the inverse problem.

5 A posteriori review of the data and stability of the inversion

A review of the results follows the inversion. Although the SSSC value is the same for the two nodal planes of a focal mechanism according to the a priori model, note that different a posteriori values may be obtained for the angle α between calculated shear stress and observed slip, and for the normalised shear stress (τ/τ_max) as well.

Three estimators, averaged or individual, enable one to evaluate the results of the inversion (table). The main estimator, Omega, is the normalised SSSC (divided by τ_max): it ranges from −100 % (full stress incompatibility) to +100 % (perfect fit). The two subsidiary estimators are Tau, the normalised shear stress (τ/τ_max), and Ang, the slip-shear stress angle (α). As the misfit increases, Tau decreases (from 100 % to zero) and Ang increases (from 0° to 180°).

Tableau

Inversion de 115 mécanismes au foyer de la séquence sismique de Chichi, Taiwan [10,11]: tenseurs des contraintes et estimateurs d'écarts. La première ligne se rapporte à une détermination en une seule étape avec le lot complet de données, les dix lignes suivantes résument un processus de purification avec une exigence croissante de bon accord. Le paramètre de contrôle ω_acc correspond à la plus petite valeur acceptable de la CGCC individuelle, en %. Le tenseur des contraintes obtenu est indiqué par les directions et les inclinaisons des axes principaux, $σ_{1}, σ_{2}$ et $σ_{3}$ , et par le rapport des différences des contraintes principales, Φ=(σ₂−σ₃)/(σ₁−σ₃) [1]. N_a: nombre de plans nodaux acceptables. N_r: nombre de plans nodaux rejetés. Estimateur principal Omega (CGCC moyenne): ω_m (%). Plus petite CGCC individuelle: ω_min (%). Estimateur auxiliaire Tau (contrainte tangentielle normalisée moyenne): $τ_{m}^{*}$ (%). Estimateur auxiliaire Ang (angle moyen contrainte tangentielle–glissement): α_m (degrés).

Inversions of 115 mechanisms of the Chichi earthquake sequence, Taiwan [10,11]: stress tensors and misfit estimators. Set of the first row refers to a single-step determination with the whole dataset, the next ten rows summarise refining experiments carried out with increasing demand for good fit. The control parameter ω_acc indicates the lowest acceptable value of the individual SSSC ω, in %. The stress tensor obtained is indicated by the trends and plunges of principal axes, $σ_{1}, σ_{2}$ and $σ_{3}$ , in degrees, and the ratio of the principal stress differences, Φ=(σ₂−σ₃)/(σ₁−σ₃) [1]. N_a, number of nodal planes accepted. N_r, number of nodal planes rejected. Main estimator, Omega (average SSSC): ω_m (%). Smallest individual SSSC: ω_min (%). Subsidiary estimator, Tau (normalised average shear stress): $τ_{m}^{*}$ (%). Subsidiary estimator Ang (average shear stress-slip angle): α_m (degrees).

ω _acc	σ ₁	σ ₂	σ ₃	Φ	N _a	N _r	ω _m	ω _min	$τ_{m}^{*}$	α _m
−100	301	9	40	44	203	44	0,31	230	0	50	−66	70	40
0	299	8	35	39	200	50	0,27	205	25	60	1	73	30
10	298	6	33	41	201	49	0,33	196	34	61	13	74	28
20	295	5	29	38	199	52	0,33	180	50	65	23	76	25
30	296	5	30	37	199	53	0,30	172	58	68	31	78	24
40	294	4	27	35	199	55	0,29	152	78	72	43	81	22
50	294	5	27	33	197	57	0,29	144	86	74	51	82	21
60	294	5	28	37	198	53	0,32	118	112	77	61	84	19
70	301	10	46	55	205	33	0,48	72	158	85	73	89	15
80	304	11	53	59	208	28	0,53	46	184	90	82	92	11
90	302	16	58	56	203	28	0,53	25	205	94	91	95	9

The SSSC-based inversion is used as a core in iterative processes that aim at separating [2] or selecting data. A refining algorithm enables one to determine series of stress states for increasing good fit demand. The main parameter is the smallest acceptable value of the SSSC, ω_acc (table). This value gradually increases from −100 % to the final bound; as the solution tensor varies when the data set changes, data can be eliminated and reincorporated. The interest of such a process is twin-fold. First, it allows one to determine the ω_acc that best corresponds to the uncertainties and dispersion of the data. Second, the comparison between the results obtained with increasing ω_acc values is an indicator of stability in the inversion (table). The relationship between ω_acc and the number of rejected data is a better quality criterion than the average SSSC and standard deviation, which show artificial improvement as soon as data are rejected.

6 Application to a seismic sequence as an example

Recently [10], the proposed method was applied to a set of 115 focal mechanisms [11] of the Chichi earthquake sequence, Taiwan (21 September 1999, M_w=7.6). A variety of mechanisms exists and although a simple graphical method [7] revealed dominating WNW–ESE, the result of the stress inversion was not obvious. The table shows the results obtained with increasing values of ω_acc; the average SSSC, ω_m, increases from 60 to 94 % and the number of rejected mechanisms increases from 12 to 102. The normalised shear stress ( $τ_{m}^{*}$ ) increases from 73 to 95 %, while the slip-shear stress angle (α_m) decreases from 30 to 9°.

The stress tensors obtained with these 11 experiments are similar, which reveals high level of stability of the inversion and suggests that in the first approximation a single state of stress well accounts for the data. The best value of ω_acc is chosen as a function of both the accuracy of the data (depending on measurements) and the natural dispersion (neglected by the assumption of homogeneous stress axes and Φ ratio). The angular uncertainty of focal mechanism determinations [11] averages 10°, and the angular dispersion of the data set, which depends on the heterogeneous response of volume of crust affected by these earthquakes, averages 12°. One thus adopts the solution obtained for a 40 % value of ω_acc, giving 22° for α_m (table).

7 Conclusion

The new SSSSC-based inversion provides the principal stress axes ( $σ_{1}, σ_{2}, σ_{3}$ ) and the ratio of principal stress differences (Φ), for a set of double couple focal mechanisms of earthquakes. No choice is made among nodal planes. Because of the analytical inversion, the number of data is unlimited and the runtime is negligible regardless of the size of the data set. As a counterpart, the inversion criterion, which aims at simultaneously obtaining small angles (α) and large shear stresses (τ), is an approximation. This is however preferable than introducing uncontrolled mechanical parameters or neglecting the influence of the amount of shear stress. To these respects, using the SSSC should be regarded as a realistic compromise. The smallest acceptable SSSC must be chosen according to the evaluation of both the technical uncertainties and the seismotectonic sources of data dispersion. The convergence of the results obtained with increasing fit demands provides the best criterion for stability and robustness.

1 Introduction

La principale limitation des déterminations de contraintes sismotectoniques par inversion de données de mécanismes au foyer de type double couple, apparues après celles portant sur les failles [1,8], mais suivant les mêmes principes, réside dans l'apparente nécessité d'un choix entre les plans nodaux [2,9,12]. Rares sont les cas où, pour chacun des mécanismes traités, le plan de faille est connu, grâce à la connaissance géologique ou à un alignement de foyers sismiques. Il est certes possible de choisir le « meilleur » plan nodal par un processus itératif d'inversion. Mais il est peu satisfaisant de sélectionner la moitié des données en fonction du tenseur vers lequel se dirige le processus d'inversion, ce qui revient à améliorer arbitrairement le résultat. Si le critère utilisé dans l'inversion pouvait être indépendant du choix entre les plans nodaux, et si ce critère avait une signification physique acceptable, le choix serait évité. Tel est le cas de la composante de glissement de la contrainte cisaillante, ou CGCC, décrite et utilisée dans la présente note.

2 Signification mécanique du critère d'inversion

La CGCC est la composante, suivant la direction du glissement observée, de la contrainte tangentielle calculée. Elle résulte donc du produit scalaire $σ \cdot 𝐬, σ$ étant le vecteur contrainte et $𝐬$ le vecteur glissement unitaire (figure 1). La CGCC est positive si la contrainte agit dans le sens du cisaillement réel, négative si elle agit dans le sens opposé. La CGCC est aussi le produit de la contrainte tangentielle τ par le cosinus de l'angle α entre le glissement réel et le cisaillement calculé (figure 1). Pour une contrainte tangentielle τ donnée, la CGCC décroı̂t continûment de τ à −τ lorsque α croı̂t de 0 à 180°. Pour un angle α donné, la CGCC varie proportionnellement à τ si l'angle est aigu, à −τ si l'angle est obtus. Algébriquement, la CGCC est donc une fonction croissante de τ et décroissante de α. Appelant τ_max la contrainte tangentielle maximum, demi-différence des contraintes principales extrêmes, les bornes de la CGCC sont τ_max (cisaillement maximum suivant le glissement) et −τ_max (cisaillement maximum opposé au glissement).

La CGCC est calculable en fonction de paramètres qui caractérisent l'orientation du plan ainsi que la direction et le sens du glissement, et de variables qui caractérisent le tenseur des contraintes. La signification de la CGCC vis-à-vis de l'angle α est claire (figure 1) ; sa signification vis-à-vis de la contrainte tangentielle τ l'est aussi dans la mesure où la probabilité de glissement augmente lorsque τ croı̂t. Rendre la CGCC algébriquement aussi grande que possible revient à déterminer un état de contrainte qui rend certainement compte du glissement réel. Toutefois, le critère de Tresca (figure 2) rend mal compte de l'activation de plans de défaut diversement orientés, et l'usage de la CGCC est une approximation par rapport au critère de Mohr–Coulomb [13]. Mais utiliser ce dernier dans l'inversion exigerait un choix entre plans nodaux, car il faudrait faire intervenir la contrainte normale, et forcerait à assigner des valeurs à des paramètres inconnus ou mal contraints, et de surcroı̂t variables d'un séisme à l'autre, comme le coefficient de frottement, la cohésion ou la pression de fluide qui régit la contrainte effective. À cet égard, l'utilisation de la CGCC constitue un compromis. Cette approximation est plus justifiée que l'approche classique consistant à minimiser l'angle α, ce qui revient à considérer que l'activation d'une faille ne dépend pas de la valeur de la contrainte tangentielle [5].

3 Un critère d'inversion qui ne dépend pas du choix entre les plans nodaux

Une propriété remarquable de la CGCC, en matière de mécanismes au foyer des séismes, est son identité pour les deux plans nodaux. Si un plan nodal est le plan de faille, il ne s'ensuit pas que la contrainte tangentielle virtuellement exercée sur le plan nodal inactif doit être perpendiculaire au plan de faille : elle peut être oblique (figure 3). Sauf cas particulier [2], un tenseur des contraintes ne rend donc pas compte simultanément des deux mouvements possibles, mutuellement exclusifs, d'un mécanisme au foyer. Mais la CGCC est la même pour ces deux jeux possibles, ce que l'on démontre pour tout tenseur des contraintes $𝐓$ . Si le plan de faille est le plan nodal 1, de normale unitaire $𝐧_{1}$ , le vecteur contrainte $σ$ exercé sur ce plan est $𝐓 𝐧_{1}$ . Par essence, le vecteur glissement unitaire sur le plan 1 est la normale unitaire à l'autre plan nodal, $𝐧_{2}$ ; la CGCC est donc le produit scalaire $(𝐓 𝐧_{1}) \cdot 𝐧_{2}$ . De même, si le plan de faille est le plan nodal 2, la CGCC calculée pour ce plan est le produit scalaire $(𝐓 𝐧_{2}) \cdot 𝐧_{1}$ . Les produits étant distributifs, ces deux expressions sont identiques. Si un mécanisme au foyer de séisme est conforme à l'état de contrainte, la CGCC est donc la même, quel que soit le plan nodal activé en cisaillement.

L'utilisation de la CGCC comme critère d'inversion permet donc de déterminer l'état de contrainte rendant compte au mieux d'un lot de mécanismes au foyer de séismes, sans qu'il faille choisir entre les deux plans nodaux de chaque mécanisme. Peu importe pour le géologue qui observe le plan de faille et ses stries, mais l'atout est majeur pour le sismologue qui analyse des mécanismes au foyer des séismes avec l'ambiguı̈té inhérente au calcul des plans nodaux (figure 3).

4 Résolution analytique du problème inverse

Afin de calculer l'état des contraintes rendant compte au mieux d'un lot de K données de mécanismes au foyer, sans choisir entre les plans nodaux, il faut donc rechercher le tenseur des contraintes qui rende la CGCC aussi grande que possible, pour tous les mécanismes simultanément. Cette recherche est faite en considérant l'une des deux sommes suivantes :

S = \sum_{k = 1}^{k = K} τ_{s k} ou S' = \sum_{k = 1}^{k = K} {(τ_{\max} - τ_{s k})}^{2}

(1)

où τ_sk désigne la CGCC de numéro k. Les bornes de S, qui doit être rendue maximum, sont

- K τ_{\max}

K τ_{\max}

. Les bornes de S′, qui doit être rendue minimum (au sens des moindres carrés), sont 0 et

4 τ_{\max}^{2}

. L'expérience prouve que l'utilisation de la première fonction, moins sensible à la présence de grands écarts entre données et calcul, conduit à des inversions plus robustes.

Le tenseur des contraintes est écrit sous la forme suivante, dans laquelle sont séparés les termes décrivant l'orientation des trois axes principaux (x_i,y_i,z_i, i=1, 3 dans le repère est–nord–haut) et ceux décrivant les contraintes principales (σ₁⩾σ₂⩾σ₃, pressions notées positives) :

(\begin{matrix} T_{11} & T_{21} & T_{31} \\ T_{12} & T_{22} & T_{32} \\ T_{13} & T_{23} & T_{33} \end{matrix}) = (\begin{matrix} x_{1} & x_{2} & x_{3} \\ y_{1} & y_{2} & y_{3} \\ z_{1} & z_{2} & z_{3} \end{matrix}) \cdot (\begin{matrix} σ_{1} & 0 & 0 \\ 0 & σ_{2} & 0 \\ 0 & 0 & σ_{3} \end{matrix}) \cdot (\begin{matrix} x_{1} & y_{1} & z_{1} \\ x_{2} & y_{2} & z_{2} \\ x_{3} & y_{3} & z_{3} \end{matrix})

(2)

Quelques transformations permettent d'exprimer les neuf cosinus directeurs en fonction de trois angles indépendants, θ,ζ et ξ. Quant aux magnitudes, comme les données ne décrivent que des sens et des orientations de cisaillement, si $𝐓$ est solution du problème, alors $m 𝐓 + n 𝐈$ l'est aussi (m est tout nombre strictement positif, n toute pression ou tension, $𝐈$ la matrice unité). Le tenseur est connu à un facteur d'échelle et à une pression près, qui ne peuvent être déterminés qu'avec des données supplémentaires [3]. Les magnitudes des contraintes sont donc exprimables en fonction d'une seule variable. Une solution simple consiste à utiliser les cosinus d'un angle ψ pris tel quel, augmenté de 120° et augmenté de 240° [6]. Cet angle ψ est lié au rapport des différences des contraintes principales, Φ=(σ₂−σ₃)/(σ₁−σ₃). En fin de compte, le tenseur réduit est exprimable en fonction de quatre variables indépendantes, les angles θ,ζ,ξ et ψ. Après développement de l'expression (2) en fonction de ces quatre inconnues du problème, la CGCC est calculée comme il a été expliqué précédemment, puis sommée suivant l'équation (1). Les extrema de la fonction S sont alors obtenus en résolvant le système d'équations différentielles :

\frac{\partial S}{\partial θ} = 0, \frac{\partial S}{\partial ξ} = 0, \frac{\partial S}{\partial ζ} = 0, \frac{\partial S}{\partial ψ} = 0} .

(3)

Bien que les transformations ne soient pas simples, ce système est résolu analytiquement d'une manière analogue à celle déjà adoptée pour les jeux de failles [4]. Les paramètres sont cinq sommes de fonctions simples des cosinus directeurs des normales aux plans nodaux. Une comparaison numérique désigne parmi les extrema le maximum de S et, par conséquent, les quatre valeurs θ,ζ,ξ et ψ caractérisant le tenseur solution du problème inverse. L'inversion étant analytique, le temps de calcul nécessaire à la résolution est celui mis à résoudre les quatre équations (3). Ce temps, très bref, est indépendant du nombre de données.

5 Examen a posteriori des données et stabilité de l'inversion

Après inversion, les résultats doivent être passés en revue. À cet égard, il faut distinguer les situations a priori et a posteriori. Si la CGCC est la même pour les deux plans nodaux d'un mécanisme au foyer, les valeurs a posteriori de l'angle entre glissement et contrainte tangentielle (α) et de la contrainte tangentielle normalisée (τ/τ_max) diffèrent d'un plan nodal à l'autre. Ces différences peuvent permettre de choisir un plan nodal, mais ce choix fait a posteriori n'a bien évidemment pu influer sur l'inversion.

Trois estimateurs, moyens et individuels, permettent de juger des résultats de l'inversion (tableau). Le principal estimateur, Omega, est la CGCC normalisée (divisée par τ_max) : il varie de −100 % (incompatibilité totale) à +100 % (accord parfait). Les estimateurs auxiliaires sont Tau, la contrainte tangentielle normalisée (τ/τ_max), et Ang, l'angle glissement–contrainte tangentielle (α). Lorsque l'écart aux données augmente, Tau décroı̂t (de 100 à 0 %) et Ang croı̂t (de 0 à 180°).

La brièveté de l'inversion analytique permet d'en faire le noyau de processus itératifs visant à séparer [2] ou à sélectionner les données. Un algorithme d'épuration permet de calculer des séries d'états de contraintes pour des exigences croissantes d'accord données–calcul. Le paramètre principal du processus épuratif est la plus petite valeur individuelle acceptable de la CGCC, ω_acc (tableau). Cette valeur augmente graduellement de −100 % à la valeur finale souhaitée ; comme le tenseur solution change quand le lot de données est modifié, des données éliminées à un stade peuvent être réintroduites lors d'un stade ultérieur. Un tel procédé présente deux avantages. Premièrement, il permet de déterminer la valeur ω_acc qui correspond le mieux aux incertitudes et à la dispersion réelles des données. Deuxièmement, la comparaison entre des résultats obtenus avec des seuils ω_acc croissants de la CGCC permet de juger de la stabilité de l'inversion (tableau). Pour un lot de données mécaniquement homogène, le tenseur change peu, alors qu'il varie significativement pour des lots hétérogènes. La relation entre ω_acc et le nombre de données rejetées est un critère de précision plus révélateur que la CGCC moyenne et l'écart type, qui sont artificiellement améliorés dès lors que des données sont rejetées.

6 Exemple d'application à une séquence sismique régionale

Un récent travail [10], qui ne sera pas repris ici, a illustré l'application de la méthode proposée ici à 115 mécanismes au foyer [11] de la séquence sismique du tremblement de terre destructeur de Chichi, à Taiwan (21 septembre 1999, M_w=7,6). Le tableau illustre les résultats de sélections successives effectuées à partir du lot complet. Les mécanismes au foyer sont de types inverse, décrochant, oblique et, pour quelques-uns, normaux. Bien qu'une méthode graphique simple [7] suggère un état de contrainte dominant en compression WNW–ESE, il est difficile de prévoir précisément le résultat de l'inversion. Un premier calcul brut est effectué sur le lot total. Les calculs suivants mettent en œuvre un processus d'élimination, avec des valeurs finales croissantes du seuil ω_acc, de 0 % (exigeant un simple accord en sens de cisaillement) à 90 %, une valeur exagérément sévère (tableau). Le nombre de mesures rejetées va de 12 à 102 mécanismes quand la CGCC moyenne (ω_m) augmente de 60 à 94 %. La contrainte tangentielle normalisée moyenne ( $τ_{m}^{*}$ ) croı̂t de 73 à 95 %, tandis que l'angle moyen glissement–contrainte tangentielle (α_m) décroı̂t de 30 à 9°. Un choix final a posteriori entre les plans nodaux réduirait considérablement ces angles moyens, à condition de retenir pour chacun des N mécanismes le plan nodal donnant l'angle le plus petit, soit une configuration parmi les 2^N cas possibles.

Les tenseurs des contrainte résultant des onze expériences sont similaires ; l'inversion est donc stable et, en première approximation, un état de contrainte unique rend compte des données. L'obtention d'une série continue de solutions montre que le choix du seuil ω_acc doit être fait suivant la précision des données (en fonction des mesures) et la dispersion naturelle (négligée avec l'hypothèse d'un état de contrainte homogène en termes d'orientation et de rapport Φ). L'incertitude angulaire des déterminations de mécanismes au foyer [11] vaut 10° en moyenne. La dispersion angulaire naturelle, qui dépend de l'hétérogénéité de la déformation cassante dans le volume de croûte affecté par les séismes, est de 12° en moyenne. On adopte donc la solution obtenue pour un seuil ω_acc de 40 %, donnant une valeur de 22° pour α_m (tableau).

7 Conclusion

La nouvelle méthode d'inversion fondée sur l'emploi de la CGCC fournit, pour une série de mécanismes au foyer de séismes de type double couple, les axes principaux des contraintes ( $σ_{1}, σ_{2}, σ_{3}$ ) et le rapport des différences des contraintes principales (Φ). Aucun choix de plans nodaux n'est effectué. L'inversion étant analytique, un nombre illimité de données peut être traité et le temps de calcul est négligeable, quelle que soit la taille du lot de données. En contrepartie, le critère d'inversion, qui associe la recherche d'un angle glissement–contrainte tangentielle aussi petit que possible et celle d'une contrainte tangentielle aussi grande que possible, n'est qu'une approximation. Mais ce choix vaut mieux que l'introduction de paramètres mécaniques incontrôlés ou l'indifférence à l'amplitude de la contrainte tangentielle. L'utilisation de la CGCC représente donc un compromis réaliste. La détermination de la plus petite CGCC individuelle acceptable doit être faite en fonction de la précision technique des données et de la dispersion sismotectonique des mécanismes. La convergence des résultats obtenus pour des tris de plus en plus sévères constitue le meilleur critère de stabilité et de robustesse de la détermination.

Remerciements

Cette recherche a été effectuée grâce au soutien de l'Institut universitaire de France. D'utiles commentaires ont été faits par le Dr François Cornet.