1 Introduction
Leukemia, a cancer of the white blood cells, is classified clinically on the basis of the character of the disease (acute or chronic), the type of cells involved (myeloid, lymphoid or monocytic), and the increase or constant nature in the number of abnormal cells (leukemic or aleukemic). The acute or chronic character of leukemia is based upon the rate of progression of the disease behavior in the sense that with no treatment, a patient with acute leukemia will die within months, while chronic leukemia will kill within years.
In this paper, we analyze chronic myelogenous (or myeloid) leukemia (CML), one of the most common types of leukemia. CML is usually diagnosed by the presence of a specific chromosomal abnormality, the Philadelphia chromosome. It is due to a reciprocal translocation between chromosome 9 and chromosome 22, which results in chromosome 9 longer than normal and one chromosome 22 shorter. This latter is called the Philadelphia chromosome. Associated with this transformation is the fusion of the proto-oncogene c-Abl carried by the removed part of the chromosome 9 and the gene Bcr contained in the break of the chromosome 22. This fusion results in the creation of a chimerical protein, the Bcr-Abl Tyrosine Kinase [1].
CML is believed to arise in the hematopoietic stem cell (HSC) compartment (the earliest stage of blood cell formation) from which all of the formed elements of the blood (white blood cells, red blood cells and platelets) are derived. Two lines of evidence lead to this hypothesis. First, in CML the Philadelphia chromosome is found in all of the hematopoietic lineages [2], which come from the hematopoietic stem cell. The second piece of evidence is derived from the observation of periodic oscillations in the three types of blood cells in one rare variant of CML. Thus, our investigations of the CML are concentrated on the dynamics in the stem cell compartment [3].
In [4], the authors using the same model as here, proved that it is theoretically possible to get the large difference observed experimentally between the short cell cycle duration in the HSC (on the order of one to two days) and the long period oscillations observed in periodic CML (PCML) – in the order of 40 to 80 days – (the experimental results are presented in [3]). Here we examine the role of each parameter in determining stem cell dynamics without going into the mathematical details. We then summarize some results presented in [4] (such as stability results), and refer the reader to this latter publication for the analytical work.
This paper is organized as follows. In Section 2, we present the mathematical model for the hematopoietic stem cells that is used to investigate the problem. In Section 3, we present some stability results for the HSC, and conditions for the Hopf bifurcation to occur. In Section 4, we transform the problem to compute the solutions analytically and study the role of each parameters involved in the model. We give a short conclusion in Section 5.
2 The stem-cell model
Because PCML is believed to arise in the stem cell compartment in the bone marrow, here we consider a stem cell model with a proliferating and a resting G0 phase [5]. A cell entering the proliferating phase can either die by apoptosis at a rate γ or divide a fixed time τ after entry (point of cytokinesis). Immediately after division, the two newly born cells, the daughter cells, enter the resting phase. They can either remain in this resting phase, or exit from this phase by differentiating into one of the committed cell lines (red cells, white cells, platelets) at a rate δ, or exit and re-enter the proliferating phase at a rate β.
If we denote the density of proliferating cells at time t by P(t), and the density of resting cells at time t by N(t), the conservation equations are given by (see [6–8] for further details)
| (1) |
| (2) |
| (3) |
Note that the solution to Eq. (2) is independent of the behavior of the solution to Eq. (1) but the converse is not true. Knowing the behavior of the solutions of Eq. (2) it is easy to obtain the behavior of the solutions of Eq. (1). Thus we concentrate our study on Eq. (2).
A solution to Eq. (2) is a continuous function , for all t>0. We denote the continuous function , φ(t)=N(t) for all t∈[−τ,0], as the initial condition for N. Using the method of steps, it is easy to prove (see [9]) that for every ϕ∈C([−τ,0]), there is a unique solution to Eq. (2), where C([−τ,0]) is the space of continuous functions on [−τ,0].
The purpose of this paper is to apply the technique used in [11] to this HSC model in order to study the effect of various parameter changes on the dynamics and to thereby hopefully obtain some insight into the HSC origin of PCML.
3 Stability results
Our objective is to derive some understanding of the possible mechanisms giving rise to the long-period oscillations seen in PCML by looking at the influence of each parameter in our HSC model on the stability of the steady states and the period of the solutions that result once stability is lost.
In this section, we briefly summarize the stability results analytically proved by Mackey and Pujo-Menjouet in [4]. Before analyzing the period of the solutions, it is necessary to give the regions where stability occurs and the ones where the solutions become unstable through the Hopf bifurcation. To that end, we determine the steady states of Eq. (2), and then simplify the problem using dimensionless variables and determine the regions of stability.
3.1 Steady states
When dN/dt≡0, the steady-state solutions of Eq. (2) satisfy either or
| (4) |
| (5) |
| (6) |
3.2 Local stability
Let x=N/θ, which is a dimensionless variable, so Eq. (2) becomes:
| (7) |
| (8) |
If we linearize Eq. (7) in the neighborhood of one of the steady states, and set and , then Eq. (7) becomes:
| (9) |
Take z(t)=eλt; so the characteristic equation corresponding to Eq. (9) is:
| (10) |
The regions of parameter space in which are easily determined (see [4] and [16] for the details of the computations), and can be summarized as follows:
- (1) if n∈[0,1], then the solutions are locally stable for τ∈[0,τmax];
- (2) if n>1, then we must consider two sub-cases:
- (a) if [n/(n−1)]δ⩾β0, then the solutions are locally stable for τ∈[0,τmax];
- (b) consider 0⩽[n/(n−1)]δ⩽β0, and let τn=−(1/γ)ln{1/2[(δ/β0)(1+1/{n−1})+1]}
- (i) if τ∈[0,τn], then we have stability if and only if (11)
- (ii) if 0⩽[n/(n−1)]δ<β0, then the solutions are locally stable for τ∈[τn,τmax].
- (i) if τ∈[0,τn], then we have stability if and only if (11)
Periodic solutions will appear through the Hopf bifurcation when the parameters B, δ, κ are such that τ≡τcrit. We therefore focus our attention on Case (2(b(i))). When there is a Hopf bifurcation, the eigenvalues are pure imaginary λ=iω, ω being a real number, and there is a periodic solution to Eq. (9) with Hopf period TH=2π/ω given by:
| (12) |
After this brief analysis, we now turn to a numerical investigation of the influence of each parameter in the HSC model on the stability and periodicity of the solutions. Simulations presented in 3D were done using WinPP, the Windows version of XPP (freeware created by Prof. B. Ermentrout), and the ones presented as two-dimensional graphs were carried out using MATLAB version 6.0. The figures in 3D are neither normalized nor shown from the same perspective because each case is different and we chose the best way to present the simulations. The reader should also note that since we are interested here only in periodic oscillations for PCML, we do not investigate the behavior of the blood cell population after this phase (acute leukemia) where a sudden expansion of abnormal cells occurs leading to the death of the patient [17]. The following sections are then focused only on the amplitude and period of the oscillations that could might be observed clinically during PCML. The parameters chosen for the simulations were taken from estimates in the literature [6,8].
3.2.1 Influence of the sensitivity n
When n varies from 1 to 10 (Fig. 1), we observe that oscillations appear (for n about 10), then increase in period and amplitude up to a ‘saturation’ limit (Fig. 2) due to the fact that the Hill function β given by (3) approaches the Heaviside step function when n→∞, as explained in Section 4. Consequently, to increase the oscillation period and amplitude in a larger way, the other parameters involved in the model play a crucial role.
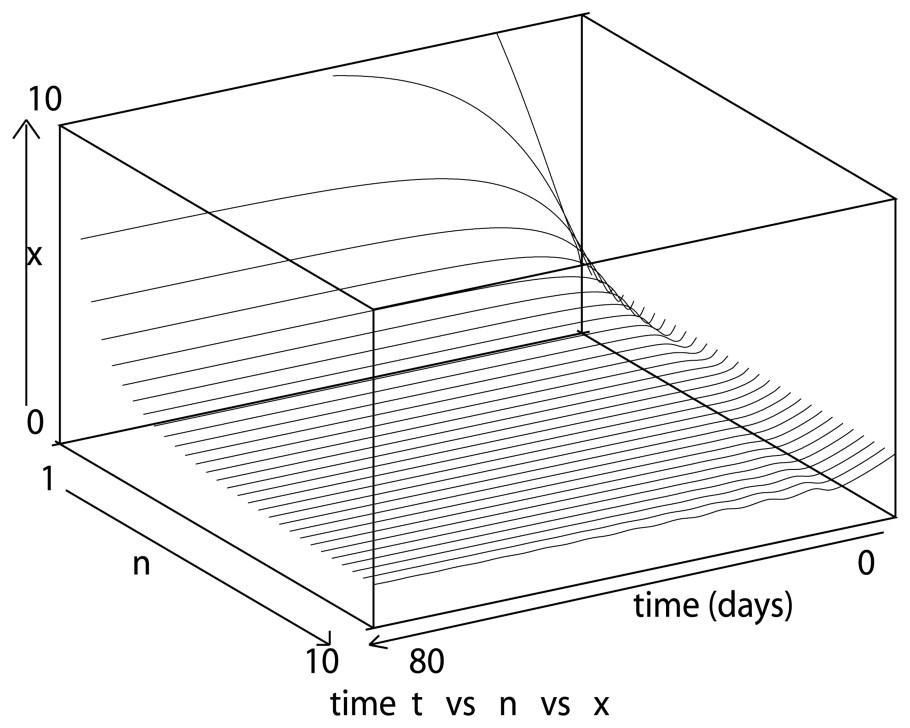
This figure illustrates the highly sensitive behavior of the solutions to Eq. (7) as n varies from 1 to 10, with δ=0.05 day−1, τ=1 day, β0=1.77 day−1 and γ=0.2 day−1. As n increases, the steady state decreases, as expected from Eq. (8), and for n=10 oscillations appear.
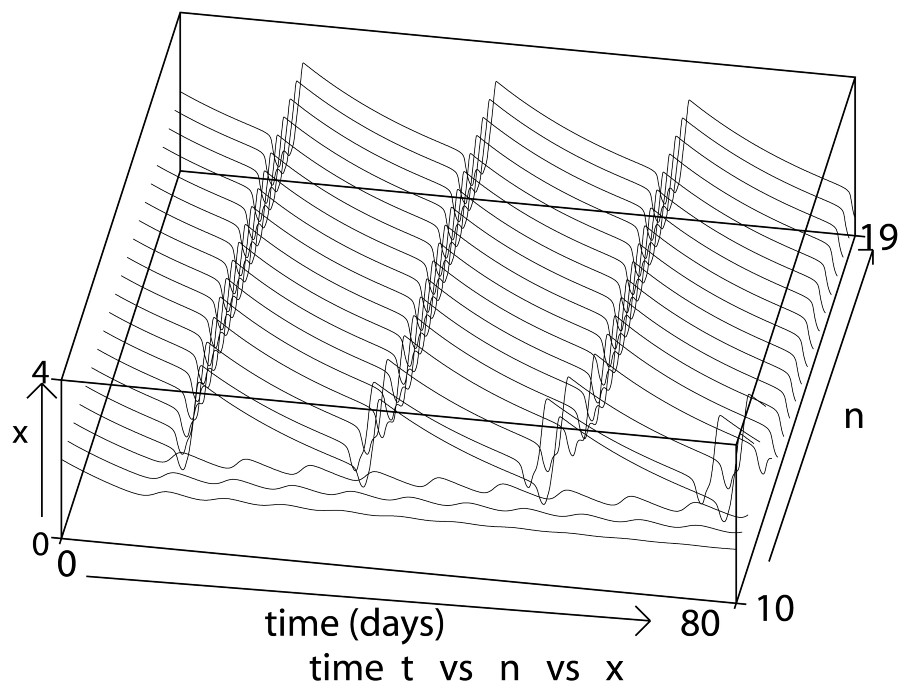
As n increases from 10 to 19 (with δ=0.05 day−1, τ=1 day, β0=1.77 day−1 and γ=0.2 day−1), the amplitude and period of the periodic solutions increase until they saturate.
Note that for the next simulations in this section, we choose n=12 not only because we are focused on long period oscillations but also because in Section 4 we are interested in the linear case where n tends to infinity. Due to the saturation effect, it is then sufficient to take n=12 as a good parameter value for comparison.
3.2.2 Influence of the loss rates δ and γ
Consider first the loss rate δ from the resting phase. One can observe five different stages as δ increases.
- 1. When δ=0, the solution converges rapidly to the nontrivial steady state (Fig. 3). Then as δ increases, small oscillations start to appear.
- 2. If we increase δ slightly, one notices an abrupt rise in the amplitude and period of the oscillations occurring in a narrow interval of change in δ. We denote by δg the value at which this transition occurs where the amplitude and period are at their maximum. From our calculations (shown in Fig. 3), this value is about δg≈0.46567 day−1.
- 3. Let δ become larger than δg. Then, the amplitude and period decrease slowly as δ continues to increase.
- 4. This phenomenon persists until the solution starts to exhibit a succession of small-amplitude oscillations just before a ‘big amplitude jump’. These big jumps are, however, smaller than the amplitudes seen in the previous case, and continue to decrease as δ increases. This behavior is shown in Fig. 4 when δ is close to 0.5. Due to this small oscillation effect the period again increases. We denote these solutions as having a ‘tail-jump’ shape.
- 5. When a too large value of δ is reached, the solutions converge to the trivial steady state x≡0 due to a high loss rate in the resting phase leading to the extinction of the cell population.
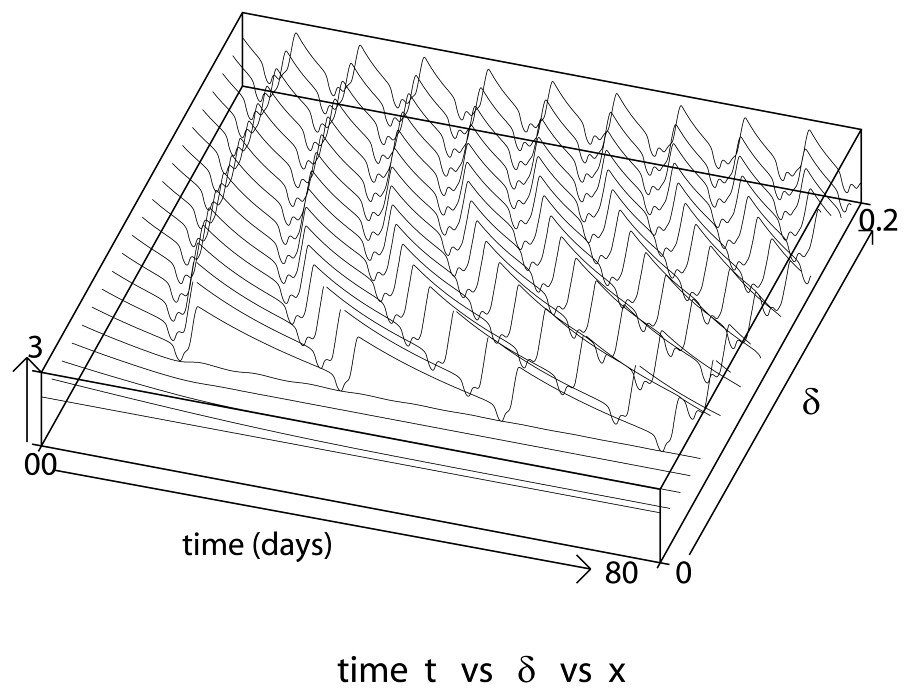
These numerical solutions illustrate the influence of the loss rate δ from the resting phase on the solutions of Eq. (7), with δ varying from 0 to 0.2 day−1 and taking τ=1 day, β0=1.77 day−1, γ=0.2 day−1 and n=12.

Here we show the sensitive dependence of the solution amplitude and period on the loss rate δ for δ varying from 0.5 to 1.4 day−1 and again taking τ=1 day, β0=1.77 day−1, γ=0.2 day−1 and n=12. δg≈0.04657.
This behavior is subtle. It is rather easy to observe the five different stages but it is more difficult to explain them by considering the nonlinear equation (7). However, if we transform this nonlinear equation (7) into a simpler linear system and if we consider the explicit expression of the Hopf period given by TH in (12), it is then possible to get a better understanding of what happens. This will be done in Section 4.
Consider next the influence of the apoptosis rate γ from the proliferating phase. Numerically, we found that γ influences the behavior of the solutions in the much same way as δ. Namely, as γ increases, the amplitude and period of the oscillations increase and again there is a transition point at which there is a sudden jump in both, and then a slight decrease in the amplitude and period. We have estimated the value at which this happens to be γ≈0.2 day−1 (Fig. 5). A succession of ‘tail-jump’-like shapes then occurs until finally the solution approaches the trivial steady state x≡0.
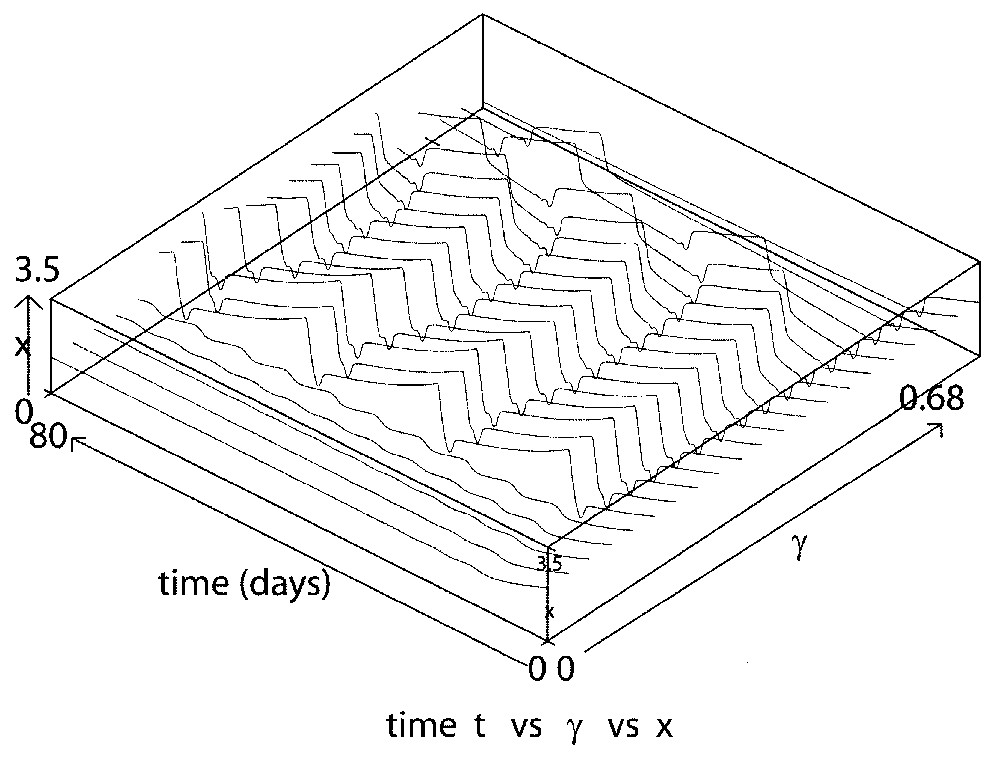
This figure illustrates the influence of the apoptosis (death) rate γ on solution behavior for γ varying from 0.58 to 0.68 day−1 and taking τ=1 day, β0=1.77 day−1, δ=0.05 day−1 and n=12. The behavior is qualitatively the same as for changes in the loss rate δ from the resting phase, as illustrated in Figs. 3 and 4.
3.2.3 Influence of the cell cycle time τ
The influence of τ on the behavior of the cell population corresponds to the predictions based on the local stability analysis in Section 3.2. Thus, when τ is small and close to 0 (so the cell cycle time is short and the cells rapidly proliferate), the solution is stable and rapidly converges to the nontrivial steady state. As τ increases, it reaches the point τ=τcrit, the nontrivial steady state becomes unstable and there is a Hopf bifurcation to limit cycle behavior. Further increases lead to complex solution behavior that are still under investigation and will be the object of future work. Finally, if τ is increased past the value τmax, the cell cycle time becomes so large that the population is extinguished and the nontrivial steady state ceases to exist. In this case the single remaining steady state is the trivial one and the cell population dies out. This is clearly due to the parameter , because as τ increases, κ tends toward 0 and so the right-hand side of Eq. (7) is ruled only by the negative term. The solution reaches then the trivial steady state. All these behaviors are shown in Fig. 6.

This figure illustrates the influence of the proliferating phase duration τ on the solutions of Eq. (7), with τ varying from 0 to 3 days and holding δ=0.05 day−1, β0=1.77 day−1, γ=0.2 day−1 and n=12. As proved analytically in Section 3.2, if τ is too small, the solutions approach the nontrivial steady state which is stable. After the critical value τcrit is exceeded, oscillations occur and these oscillations increase in period and amplitude as τ increases until τ=τmax at which point the solutions again approach the trivial steady state.
3.2.4 Influence of the maximal reentry rate β0
The maximal reentry rate β0 plays an important role in determining the amplitude and period of the periodic solutions. As shown in Fig. 7, when β0 is sufficiently large, the more β0 increases, the larger the amplitude and the period of the oscillations are. However, when β0 is close to 0, the behavior is more complicated. Indeed, in this case, one can observe from Eq. (7) that the behavior of the solutions is ruled by the two loss death rates γ and δ, and it is not so straightforward to understand what is happening by considering the full equation (7). To give a more accurate interpretation of this complex behavior we transform the nonlinear equation (7) into a piecewise linear one, by considering the extreme case of n→∞. This is the subject of the next Section 4.
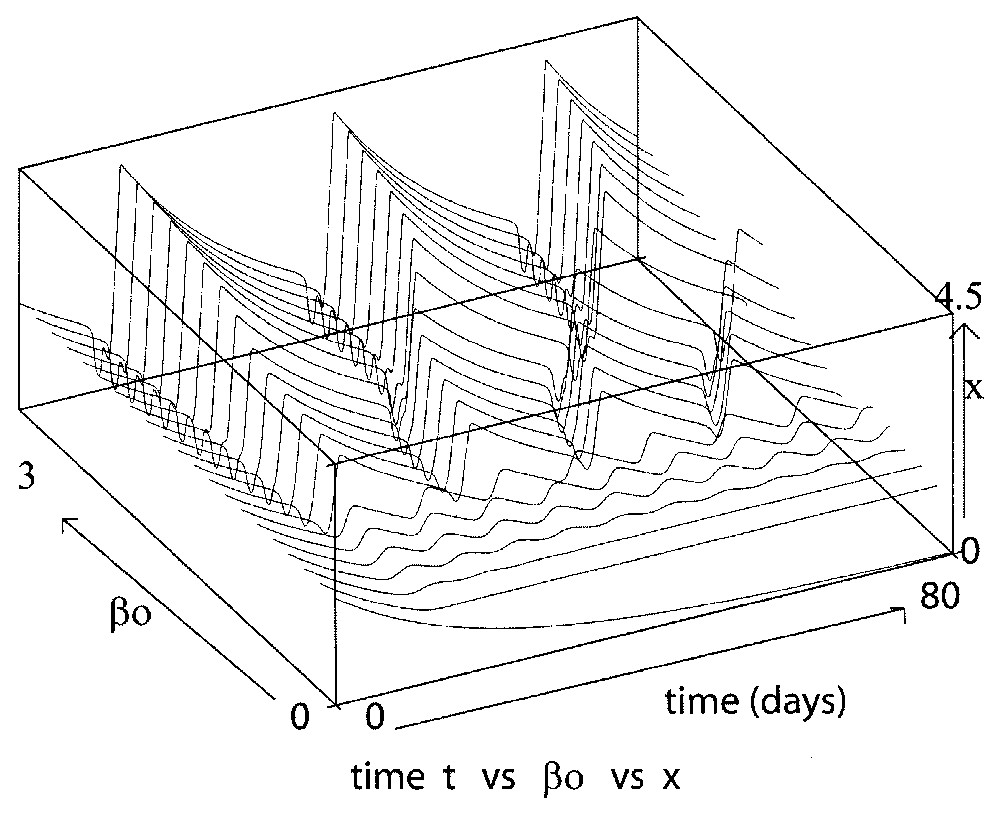
Here we show the influence of the maximal reentry rate β0 on the solution behavior (Eq. (7)), with β0 varying from 0 to 1 day−1 and taking τ=1 day, γ=0.2 day−1, δ=0.05 day−1 and n=12. The larger β0, the larger the oscillation amplitude and period.
4 Transformed problem
In [4], the explicit solution to Eq. (2) was computed for n→∞ to obtain the oscillation period and amplitude analytically. In this section we are not interested in the analysis of [4]. Our purpose is to go further in the interpretations of the numerical results presented in Section 3.2 and explain the complicated influence of the loss rates observed in the previous section.
Before showing the numerical results, note that when n→∞, the feedback function β can be approximated by the Heaviside step function β(xτ)=β0[1−H(xτ−θ)], where:
| (13) |
| (14) |
Since the numerical simulations in Section 3.2 were carried out for n=12, when n tends to infinity one observes only slight differences in the numerical simulation for the same set of parameters. As explained in Section 3.2.1, this is due to a ‘saturation’ limit influenced by the Hill function β. For this reason, we do not show the effect of τ in this section, as well as the effect of large values of β0. However, the transformed problem is useful in the sense that, thanks to its simplicity, we are able to interpret the different behaviors induced by the loss rates.
Indeed, concerning the loss rate δ from the resting phase, we can explain the five different stages shown in the previous section.
- (i) If δ is very low, i.e., δ≅0, the right-hand side of the first and second equations of the system (14) are close to 0 and the solution x does not oscillate, or does so only slightly, and rapidly reaches the non-trivial steady state.
- (ii) For larger values of δ, the amplitude and period in oscillations reach their maximum very rapidly; these maximum values are due to the fact that the difference between −αx and Γxτ (or −δx and Γxτ) in the right-hand side of the third (or fourth) equation of (14) is at its optimum. In other words, all the conditions are met to obtain the maximal amplitude and period oscillations. This value of δ is difficult to find analytically, but is approximated by δ≈0.46567 day−1 in Section 3.2.2. The rapid evolution in such a short interval of δ is not well understood analytically but is confirmed in [4]. Indeed, the authors were able to give an explicit but quite complicated form of the amplitude and to show numerically that in this interval the increase of the amplitude to its maximum is remarkably fast. However, because the explicit form found in [4] is complicated we were not able to provide any simple interpretation.
- 3. After this abrupt increase, the amplitude and period decrease slowly due to a smaller and positive difference between −αx or −δx and Γxτ. We can see this phenomenon if we study the Hopf period given by TH in (12). It is clear (even analytically) that TH decreases as δ increases (up to a critical value of δ as explained in the next case). This is shown in Fig. 8. Because the influence of τ and γ on the Hopf period TH is similar, we do not show the effect of the increase of γ in this figure. Thus, with our chosen parameters, to obtain maximal oscillations, δ has to be very close to an ‘optimal’ value that is neither too small nor too large and τ and γ have to also stay at a low level.
- 4. When δ is too large, the difference between −αx or −δx and Γxτ decreases, but is still positive. Then the solution x as well as xτ have some difficulty in going to 1. This means that some very small oscillations occur due to the fact that the difference −αx or −αx−Γxτ (or −δx−Γxτ) is positive, then negative following the different values taken by x and xτ. This phenomenon leads to very long period oscillations with very small amplitudes and the ‘tail-jump’-like shape. This period tends to infinity as δ tends to a value δcrit. In Fig. 8, if we increase τ with τ=1 day and τ=3 days), one can observe a shorter interval where oscillations occur, i.e. δcrit becomes smaller as τ gets bigger. The cell population tends to be extinguished for lower values of δ when τ is larger.
- 5. Then, when δ>δcrit, δ becomes too large, so the difference −αx−Γxτ (or −δx−Γxτ) remains negative and the oscillations vanish with the solution x converging to the trivial solution x≡0.
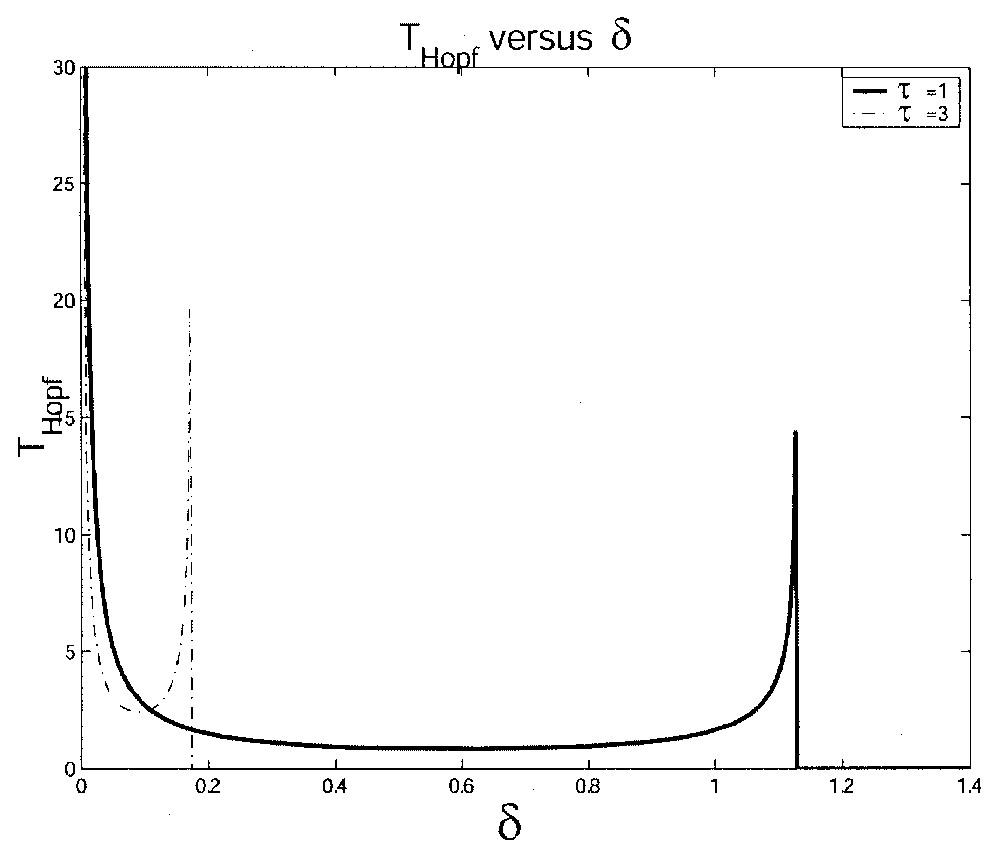
This figure illustrates the influence of the loss rate δ on the length of the Hopf period TH with δ varying from 0 to 0.05 day−1 and for two different values of τ: τ=1 day and τ=3 days.
A slightly similar interpretation can be given for the death rate γ related to the proliferating phase, and so we do not go into the details. However, the length of the Hopf period TH is more difficult to study analytically when γ varies. If we analyze it numerically one can note that the period length decreases as γ increases up to a certain value. Then due to the effect of the ‘tail-jump’ oscillations as explained above we can see that the period length will increase up to infinity when γ tends to a value we denote by γcrit. For γ>γcrit, the periodic solutions disappear, and the solution x converges to the trivial solution x≡0, which means that the cell population is extinguished.
We give two numerical illustrations of the Hopf period TH when γ varies. One figure is with two different values of δ and the other is with two different values of τ. In the first figure, we increase δ (Fig. 9 with δ=0.05 day−1 and δ=0.1 day−1), which implies an increase in the period length. In the second figure, which is similar to Fig. 8, if we increase τ (Fig. 10 with τ=1 day and τ=3 day), we can see a shorter interval where oscillations occur, i.e. γcrit becomes smaller as τ gets bigger. The cell population tends to be extinguished for lower values of γ when τ is larger.
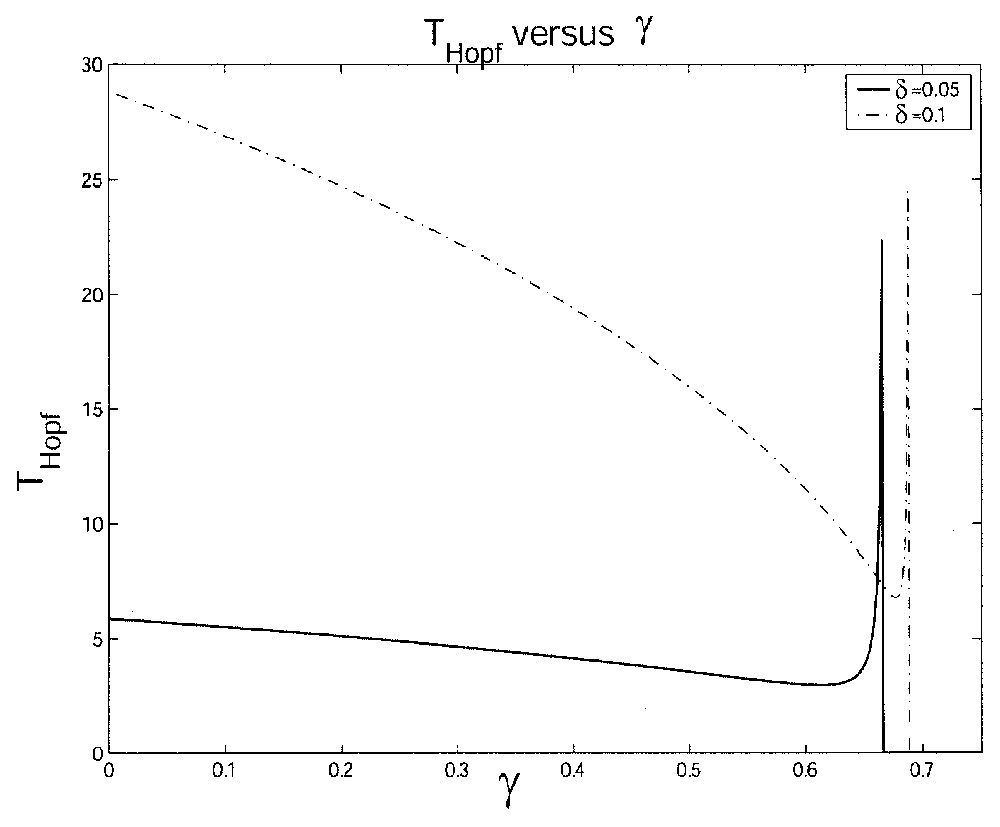
This figure illustrates the influence of the loss rate γ on the length of the Hopf period TH with γ varying from 0 to 0.7 day−1 and for two different values of δ: δ=0.05 day−1 and δ=0.1 day−1.
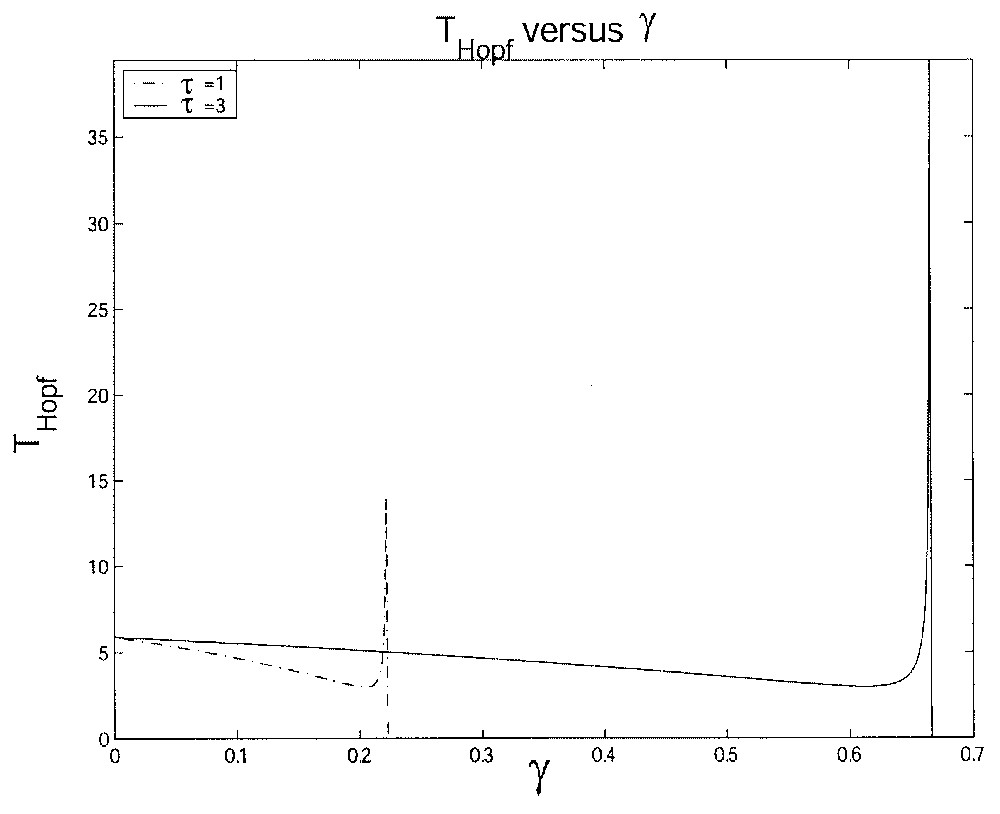
This figure illustrates the influence of the loss rate γ on the length of the Hopf period TH with γ varying from 0 to 0.7 day−1 and for two different values of τ: τ=1 day and τ=3 days.
The influence of the proliferating phase duration τ has been fully explained analytically in Section 3.2 and illustrated in Section 3.2.3. The transformed problem does not bring further insight.
However, the system (14) is very useful to interpret the influence of the maximal reintroduction rate β0. As noted in Section 3.2.4, when β0 is sufficiently large, then α∼β0 and Γ∼2β0 and the more β0 increases, the more the amplitude and period of the oscillations increase. However, when β0 decreases and is close to 0, α∼δ and . In that case, the population dynamics become more complicated and depend on δ and γ. The behavior is then under the influence of these loss rates and so it is similar as the one presented in Section 3.2.2 and above (see Figs. 11 and 12).
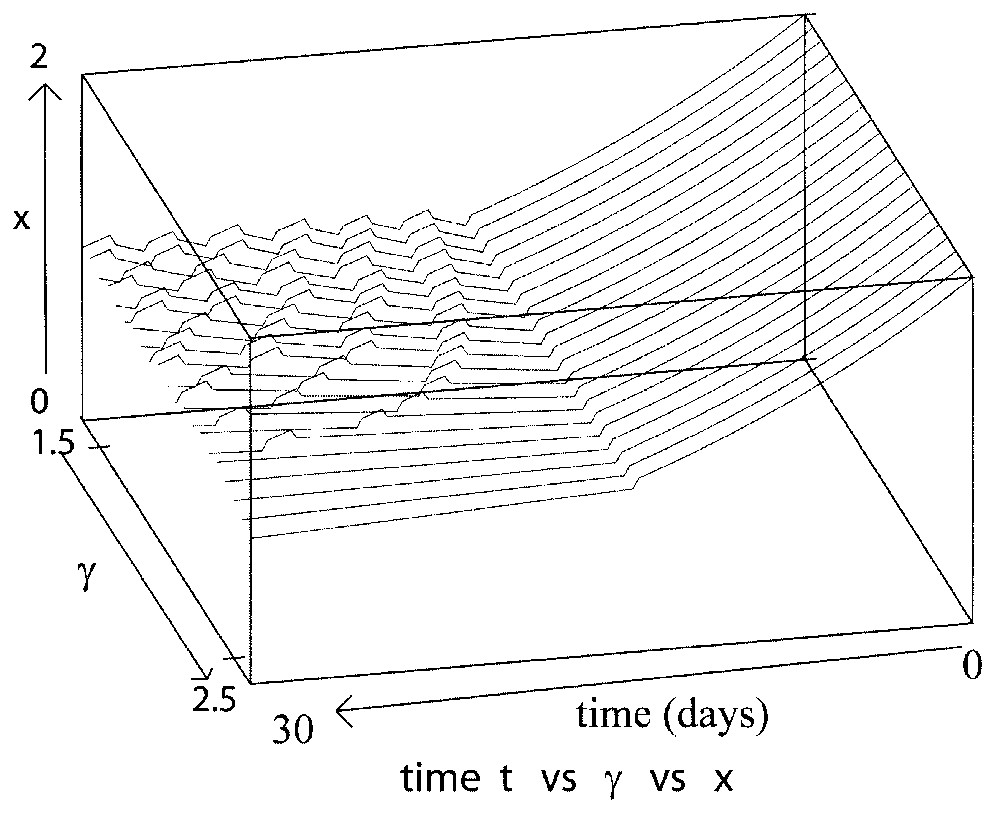
This figure illustrates the influence of γ when the reintroduction rate β0 is close to 0 in the proliferating phase of Eq. (9), with γ varying from 2.5 to 3 day−1 and τ=0.2 day, δ=0.05 day−1, β0=0.2 day−1.
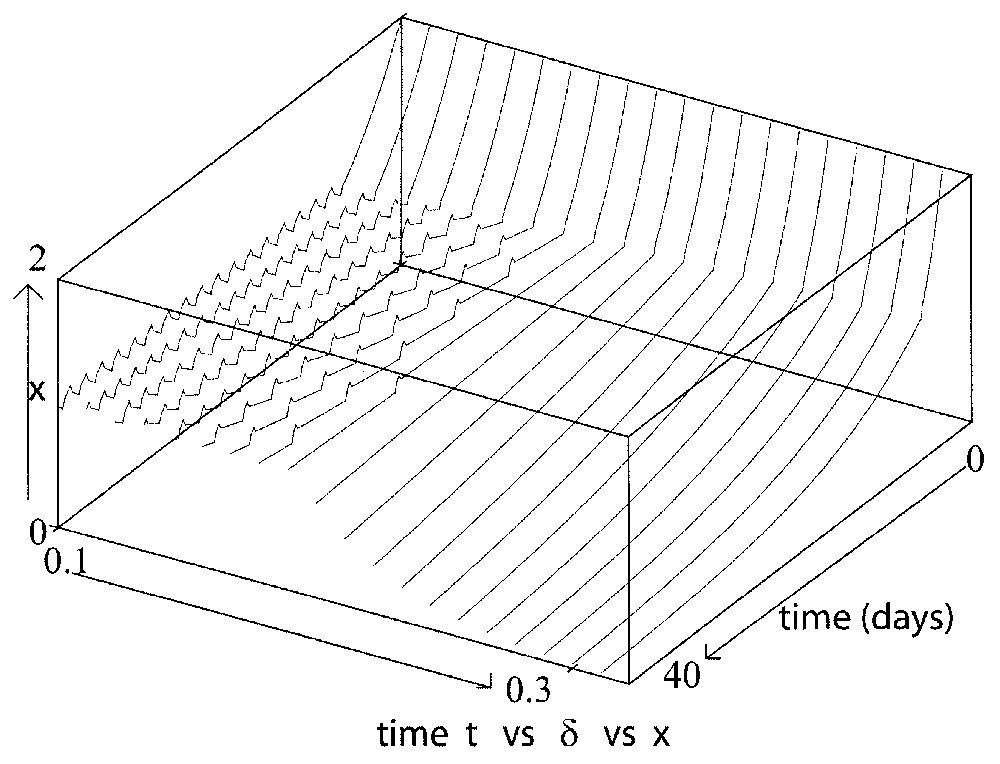
This figure illustrates the influence of δ when the reintroduction rate β0 is close to 0 in the proliferating phase of Eq. (9), with δ varying from 0.3 to 0.5 day−1 and taking τ=0.2 day, γ=0.2 day−1, β0=0.2 day−1.
5 Conclusion
The aim of this note was to show how short cell cycle durations in the HSC (order of one to two days) can give birth to long period oscillations (order of 40 to 80 days) as observed in the disease PCML. We also wanted to see how these oscillations could occur and in which way each of the five HSC parameters (n, β0, τ, γ, and δ) influence the oscillation amplitude and period.
Our analysis of Eq. (7) showed that instability occurs in a very small interval [0,τn] of τ. It is in this interval that our attention has been focused, and we showed analytically that periodic solutions can arise in this interval. We performed numerical investigations to see if large amplitude and long period oscillations could exist and under which circumstances. We observed three different groups in the parameters.
- • The first one consists of n and β0 and corresponds to the influence of the Hill function β(N). Changes in n and β0 can produce oscillations, but due to a saturation effect increases in n do not imply long period and large amplitude. However, if β0 is large, long period and large amplitude oscillations are possible.
- • The second group consists of the loss rates γ and δ. It appears that under changes in these parameters, it is possible to obtain large amplitude and long period oscillations. However, the evolution of these oscillations is very sensitive to slight changes in both γ and δ. We showed that the behavior can be totally different in small intervals of change of these parameters, and thus the HSC population seems to be highly sensitive to changes in its loss rates (mortality or differentiation).
- • The third group, consisting of τ, is interesting in the sense that this is the main focus of our study. Indeed, because our goal was to show that long period oscillations could occur when the cell cycle duration τ is small, our attention was concentrated only in small variations of τ (no more than 3 days). Like the loss rate, the behavior of the solution showed a high sensitivity to changes in τ, and we observed that the interval of τ over which we can obtain long-period oscillations with large amplitude is quite narrow, i.e. τ can be neither too small nor too large.
All these five parameters can be combined together to give rise to the maximal values of amplitude and period oscillations, but this optimum point is difficult to find due to the strong influence of each parameter.
Acknowledgements
This work was supported by the Mathematics of Information Technology and Complex Systems (MITACS, Canada), the Natural Sciences and Engineering Research Council (NSERC Grant No. OGP-0036920, Canada), the ‘Alexander von Humboldt Stiftung’, and the ‘Fonds pour la formation de chercheurs et l'aide à la recherche’ (FCAT Grant No. 98ER1057, Québec, Canada). We also would like to thank Samuel Bernard for his contribution in the numerical work on MATLAB.


