Algorithme de dénombrement des graphes chiraux et achiraux d’un cycloalcane monocyclique hétérosubstitué de formule brute CnHm1Xm2Ym3

Robert M. Nemba; Alphonse Emadak

doi:10.1016/S1631-0748(02)01400-5

Algorithme de dénombrement des graphes chiraux et achiraux d’un cycloalcane monocyclique hétérosubstitué de formule brute C_nH_m₁X_m₂Y_m₃

Robert M. Nemba ¹ ; Alphonse Emadak ¹

¹ Laboratoire de chimie théorique, section de topologie moléculaire, université de Yaoundé-1, faculté des sciences, BP 812, Yaoundé, Cameroun

Comptes Rendus. Chimie, Volume 5 (2002) no. 6-7, pp. 533-538.

Résumés

Français
Anglais

On propose une méthode générale de détermination directe du nombre de graphes chiraux et achiraux d’un cycloalcane monocyclique ayant une hétérosubstitution multiple de nature binaire X,Y et une formule brute C_nH_m₁X_m₂Y_m₃, avec m₁ + m₂ + m₃ = 2 n.

A general pattern inventory is given for the enumeration of chiral and achiral graphs of any monocyclic cycloalkane with a multiple heterosubstitution of binary type X and Y and an empirical formula C_nH_m₁X_m₂Y_m₃, where m₁ + m₂ + m₃ = 2 n.

Métadonnées

Reçu le : 2002-04-02
Accepté le : 2002-07-19
Publié le : 2002-06-01

DOI : 10.1016/S1631-0748(02)01400-5

Mot clés : graphes chiraux, graphes achiraux, cycloalcanes, hétérosubstitution binaire
Mots clés : chiral graphs, achiral graphs, cycloalkanes, binary heterosubstitution

Affiliations des auteurs :

Robert M. Nemba ¹ ; Alphonse Emadak ¹

¹ Laboratoire de chimie théorique, section de topologie moléculaire, université de Yaoundé-1, faculté des sciences, BP 812, Yaoundé, Cameroun

@article{CRCHIM_2002__5_6-7_533_0,
     author = {Robert M. Nemba and Alphonse Emadak},
     title = {Algorithme de d\'enombrement des graphes chiraux et achiraux d{\textquoteright}un cycloalcane monocyclique h\'et\'erosubstitu\'e de formule brute {<strong>\protect\emph{C}\protect\textsubscript{\protect\emph{\protect\emph{n}}}\protect\emph{H}\protect\textsubscript{\protect\emph{\protect\emph{m}\protect\textsubscript{<strong>1</strong>}}}\protect\emph{X}\protect\textsubscript{\protect\emph{\protect\emph{m}\protect\textsubscript{<strong>2</strong>}}}\protect\emph{Y}\protect\textsubscript{\protect\emph{\protect\emph{m}\protect\textsubscript{<strong>3</strong>}}}</strong>}},
     journal = {Comptes Rendus. Chimie},
     pages = {533--538},
     publisher = {Elsevier},
     volume = {5},
     number = {6-7},
     year = {2002},
     doi = {10.1016/S1631-0748(02)01400-5},
     language = {fr},
}

TY  - JOUR
AU  - Robert M. Nemba
AU  - Alphonse Emadak
TI  - Algorithme de dénombrement des graphes chiraux et achiraux d’un cycloalcane monocyclique hétérosubstitué de formule brute CnHm1Xm2Ym3
JO  - Comptes Rendus. Chimie
PY  - 2002
SP  - 533
EP  - 538
VL  - 5
IS  - 6-7
PB  - Elsevier
DO  - 10.1016/S1631-0748(02)01400-5
LA  - fr
ID  - CRCHIM_2002__5_6-7_533_0
ER  -

%0 Journal Article
%A Robert M. Nemba
%A Alphonse Emadak
%T Algorithme de dénombrement des graphes chiraux et achiraux d’un cycloalcane monocyclique hétérosubstitué de formule brute CnHm1Xm2Ym3
%J Comptes Rendus. Chimie
%D 2002
%P 533-538
%V 5
%N 6-7
%I Elsevier
%R 10.1016/S1631-0748(02)01400-5
%G fr
%F CRCHIM_2002__5_6-7_533_0

Robert M. Nemba; Alphonse Emadak. Algorithme de dénombrement des graphes chiraux et achiraux d’un cycloalcane monocyclique hétérosubstitué de formule brute C_nH_m₁X_m₂Y_m₃. Comptes Rendus. Chimie, Volume 5 (2002) no. 6-7, pp. 533-538. doi : 10.1016/S1631-0748(02)01400-5. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/S1631-0748(02)01400-5/

Version originale du texte intégral

1 Introduction

Dans un cycloalcane monocyclique hétéropolysubstitué de formule brute C_nH_m₁X_m₂Y_m₃, le quadruplet de nombres entiers positifs (n, m₁, m₂, m₃) qui désignent respectivement la taille du cycle, les nombres d’atomes H et de substituants de nature distincte X et Y vérifient la condition :

m_{1} + m_{2} + m_{3} = 2 n

Désignons par G, comme dans nos précédentes études 〚1–5〛, le stéréographe ou graphe tridimensionnel en symétrie D_nh du monocycloalcane parent C_nH_2n. Les positions des 2 n hydrogènes, qui sont des sites de substitution numérotés 1, 2,..., n et 1’, 2’,…, i’,…, n’ dans la Fig. 1 ci-dessous, sont permutées par les 4 n opérations de symétrie de D_nh.

Fig. 1
Stéréographe G d’un cycloalcane monocyclique C_nH₂_n en symétrie D_nh.

Les différents types de permutations des sites de substitution, engendrés par les classes d’opérations de symétrie de D_nh sont récapitulés dans le Tableau 1. L’ensemble P contenant les 4 n permutations des sites de substitution de G sous l’action de D_nh est défini comme suit :

D_nh, n impair	D_nh, n pair
Classes d’opérations de symétrie	Permutations engendrées	Classes d’opérations de symétrie	Permutations engendrées
E=Cⁿ_n	〚1²ⁿ〛	E=Cⁿ_n	〚1²ⁿ〛
C^r_n r et n premiers entre eux et r ≤ n – 1	〚n²〛	C^r_n, r et n premiers entre eux et r ≤ n – 1	〚n²〛
C^r_n=C^kj_kd=C^j_d, j ≤ d –1	$[d^{\frac{2 n}{d}}]$	C^r_n=C^kj_kd=C^j_d, j ≤ d – 1	$[d^{\frac{2 n}{d}}]$
S^{r^′}_n, r’ et n premiers entre eux	〚2n〛	S^{r^′}_n, r’ et n premiers entre eux	〚n²〛
S^{r^′}_n=S^{kj^′}_kd=S^{j^′}_d, d impair, j’ ≤ 2d – 1	$[{(2 d)}^{\frac{n}{d}}]$	S^{r^′}_n=S^{kj^′}_kd=S^{j^′}_d, d pair, j’≤ d – 1	$[d^{\frac{2 n}{d}}]$
		S^{r^′}_n=S^{kj^′}_kd=S^{j^′}_d, d impair, j’ ≤ 2d – 1	$[{(2 d)}^{\frac{n}{𝑑}}]$
σ_h	〚2ⁿ〛	σ_h, i, C₂	〚2ⁿ〛, 〚2ⁿ〛, 〚2ⁿ〛
$n σ_{ν}$	n 〚1²2ⁿ^–1〛	$\frac{n}{2} σ_{ν}$	$\frac{n}{2} [1^{4} 2^{n - 2}]$
nC^′₂	n 〚2ⁿ〛	$\frac{n}{2} C_{2}^{'}$ , $\frac{n}{2} C_{2}^{''}$ , $\frac{n}{2} σ_{d}$	$\frac{n}{2} [2^{n}]$ , $\frac{n}{2} [2^{n}]$ , $\frac{n}{2} [2^{n}]$

P = a_{1} [1^{2 n}], (n + 1) [2^{n}], . . ., a_{d} [d^{\frac{2 n}{d}}], . . ., a_{n} [n^{2}], a_{2 n} [2 n], n [1^{2} 2^{n - 1}] si n est impair

P = a_{1} [1^{2 n}], \frac{3}{2} (n + 2) [2^{n}], . . ., a_{d} [d^{\frac{2 n}{d}}], . . ., a_{n} [n^{2}], \frac{n}{2} [1^{4} 2^{n - 2}] si n est pair

Si on supprime dans P les permutations résultant des rotoréflexions et des plans de symétrie, on obtient l’ensemble P′ des permutations engendrées par les 2 n opérations de symétrie restantes, qui sont l’opération identité et les rotations propres ; ainsi :

P^{'} = a_{1}^{'} [1^{2 n}], n [2^{n}], . . ., a_{d}^{'} [d^{\frac{2 n}{d}}], . . ., a_{n}^{'} [n^{2}] si n est impair

P^{'} = a_{1}^{'} [1^{2 n}], (n + 1) [2^{n}], . . ., a_{d}^{'} [d^{\frac{2 n}{d}}], . . ., a_{n}^{'} [n^{2}] si n est pair

Dans les expressions (2)–(5), chaque terme du type 〚i^j〛 désigne j cycles de permutations de longueur i, tandis que les coefficients a_d et a^′_d sont obtenus à partir des formules (6)–(10) ci-après :

a_{d} = ϕ {(d)}_{rp}

a_{d} = ϕ {(d)}_{rp} + ϕ {(d)}_{ri} si d (pair parfait) \neq 2 μ (μ impair)

a_{d} = ϕ {(d)}_{rp} + ϕ {(d)}_{ri} + ϕ {(μ)}_{ri} si d = 2 μ (μ impair)

a_{d}^{'} = ϕ {(d)}_{rp} si d est pair ou impair

ϕ {(d)}_{rp} = ϕ {(d)}_{ri}

Les termes

ϕ {(d)}_{rp}

,

ϕ {(d)}_{ri}

et

ϕ {(μ)}_{ri}

sont les fonctions « totient » d’Euler 〚6〛 pour les nombres entiers d et μ lorsque l’opération de permutation est équivalente à une rotation propre C^j_d (voir indice rp) ou à une rotation impropre S^{j^′}_d ou S^{j^′}_μ(voir indice ri).

2 Conditions mathématiques de formation d’une polyhétérosubstitution de degrés (m₁, m₂, m₃) sur le squelette de G

Les polyhétérosubstitutions distinctes résultent des combinaisons avec répétition de (m₁, m₂, m₃) éléments H, X et Y parmi 2 n sites de substitutions de G, qui sont permutés par les opérations de symétrie de D_nh. Posons que le nombre de combinaisons avec répétition de (b, c, d) objets de type H, X et Y parmi a boîtes est déterminé à partir du coefficient multinomial $T (a; b, c, d) = \frac{a!}{b! c! d!}$ .

On note ainsi que le nombre de combinaisons avec répétition de H, X et Y sur G par les d-cycles de permutations du type $[d^{\frac{2 n}{d}}]$ est $T (\frac{2 n}{d_{c}}; \frac{m_{1}}{d_{c}}, \frac{m_{2}}{d_{c}}, \frac{m_{3}}{d_{c}})$ si d = d_c est le diviseur commun du quadruplet de nombres entiers non nuls (2n, m₁, m₂, m₃).

Le calcul du nombre de combinaisons avec répétition dans le cas des permutations de types 〚1² 2ⁿ^–1〛 ou 〚1⁴ 2ⁿ^–2〛, qui sont le produit de deux cycles unitaires et de n – 1 transpositions (2-cycles), lorsque n est impair, ou le produit de quatre cycles unitaires et de n–2 transpositions (2-cycles), lorsque n est pair, passe par la résolution des équations simultanées (11) et (12).

p_{1} + p_{2} + p_{3} = {\begin{matrix} 2 si n impair \\ 4 si n pair \end{matrix}

m_{1}^{'} + m_{2}^{'} + m_{3}^{'} = {\begin{matrix} n - 1 si n impair \\ n - 2 si n pair \end{matrix}

qui donnent k solutions, qui sont les choix des triplets de nombres entiers positifs ou nuls (p₁, p₂, p₃) et

(m_{1}^{'}, m_{2}^{'}, m_{3}^{'})

, dont les couples

(p_{i}, m_{i}^{'})

vérifient l’équation (13) :

m_{i}^{'} = \frac{m_{i} - p_{i}}{2} o \overset{̀}{u} 1 \leq i \leq 3

Ainsi, chaque solution (p₁, p₂, p₃) indique le choix du placement de deux ou quatre éléments de types H, X et Y sur deux ou quatre positions invariantes suivant la parité de n, tandis que $(m_{1}^{'}, m_{2}^{'}, m_{3}^{'})$ sont les nombres de couples d’éléments H, X et Y à placer parmi (n – 1) où (n – 2) boîtes contenant chacune deux positions de substitutions.

Le nombre de type de placements des éléments de nature H, X ou Y sur deux et quatre positions invariantes pour (p₁, p₂, p₃) donné est T(2; p₁, p₂, p₃) et T(4; p₁, p₂, p₃) si n est impair ou pair, respectivement. De même, les nombres de combinaisons avec répétition de $(m_{1}^{'}, m_{2}^{'}, m_{3}^{'})$ couples d’éléments de types H, X et Y parmi n – 1 ou n – 2 positions sont : $T (n - 1; m_{1}^{'}, m_{1}^{'}, m_{1}^{'})$ , si n est impair, et $T (n - 2; m_{1}^{'}, m_{1}^{'}, m_{1}^{'})$ , si n est pair.

Le nombre de polyhétérosubstitutions ou combinaisons avec répétition de degrés (m₁, m₂, m₃) en H, X et Y sur 2n sites de G obtenus à partir des permutations du type 〚1² 2ⁿ^–1〛 ou 〚1⁴ 2ⁿ^–2〛, pour un couple de triplets (p₁, p₂, p₃) et $(m_{1}^{'}, m_{2}^{'}, m_{3}^{'})$ , est déterminé à partir du produit des coefficients multinomiaux :

T (2; p_{1}, p_{2}, p_{3}) . T (n - 1; m_{1}^{'}, m_{2}^{'}, m_{3}^{'}) = (\begin{matrix} 2 \\ p_{1}, p_{2}, p_{3} \end{matrix}) (\begin{matrix} n - 1 \\ m_{1}^{'}, m_{2}^{'}, m_{3}^{'} \end{matrix}) si n est impair

T (4; p_{1}, p_{2}, p_{3}) . T (n - 2; m_{1}^{'}, m_{2}^{'}, m_{3}^{'}) = (\begin{matrix} 4 \\ p_{1}, p_{2}, p_{3} \end{matrix}) (\begin{matrix} n - 2 \\ m_{1}^{'}, m_{2}^{'}, m_{3}^{'} \end{matrix}) si n est pair

Si les propositions ci-dessus sont vérifiées, en cherchant la différences P’ – P et 2 P – P’ des contributions moyennes des 4 n permutations de P et 2 n permutations de P’, on obtient le couple de nombres entiers de graphes chiraux et A_ac(n, m₁, m₂, m₃) de graphes achiraux du stéréographe G d’un cycloalcane monocyclique polyhétérosubstitué de la série C_nH_m₁X_m₂Y_m₃ à partir des formules de récurrence (16)–(19). On donne dans la suite quelques exemples d’applications.

Si n est impair :

A_{c} (n, m_{1}, m_{2}, m_{3}) = \frac{1}{4 n} [\sum_{d_{c} \neq 2} (2 a_{d_{c}}^{'} - a_{d_{c}}) (\begin{matrix} \frac{2 n}{d_{c}} \\ \frac{m_{1}}{d_{c}}, \frac{m_{2}}{d_{c}}, \frac{m_{3}}{d_{c}} \end{matrix}) + (n - 1) (\begin{matrix} n \\ \frac{m_{1}}{2}, \frac{m_{2}}{2}, \frac{m_{3}}{2} \end{matrix})] - \frac{1}{4} \sum_{k} (\begin{matrix} 2 \\ p_{1}, p_{2}, p_{3} \end{matrix}) (\begin{matrix} n - 1 \\ m_{1}^{'}, m_{2}^{'}, m_{3}^{'} \end{matrix})

A_{ac} (n, m_{1}, m_{2}, m_{3}) = \frac{1}{2 n} [\sum_{d_{c} \neq 2} (a_{d_{c}} - a_{d_{c}}^{'}) (\begin{matrix} \frac{2 n}{d_{c}} \\ \frac{m_{1}}{d_{c}}, \frac{m_{2}}{d_{c}}, \frac{m_{3}}{d_{c}} \end{matrix}) + (\begin{matrix} n \\ \frac{m_{1}}{2}, \frac{m_{2}}{2}, \frac{m_{3}}{2} \end{matrix})] + \frac{1}{2} [\sum_{k} (\begin{matrix} 2 \\ p_{1}, p_{2}, p_{3} \end{matrix}) (\begin{matrix} n - 1 \\ m_{1}^{'}, m_{2}^{'}, m_{3}^{'} \end{matrix})]

Si n est pair :

A_{c} (n, m_{1}, m_{2}, m_{3}) = \frac{1}{4 n} [\sum_{d_{c} \neq 2} (2 a_{d_{c}}^{'} - a_{d_{c}}) (\begin{matrix} \frac{2 n}{d_{c}} \\ \frac{m_{1}}{d_{c}}, \frac{m_{2}}{d_{c}}, \frac{m_{3}}{d_{c}} \end{matrix}) + (\frac{n}{2} - 1) (\begin{matrix} n \\ \frac{m_{1}}{2}, \frac{m_{2}}{2}, \frac{m_{3}}{2} \end{matrix})] - \frac{1}{8} \sum_{k} (\begin{matrix} 4 \\ p_{1}, p_{2}, p_{3} \end{matrix}) (\begin{matrix} n - 2 \\ m_{1}^{'}, m_{2}^{'}, m_{3}^{'} \end{matrix})

A_{ac} (n, m_{1}, m_{2}, m_{3}) = \frac{1}{2 n} [\sum_{d_{c} \neq 2} (a_{d_{c}} - a_{d_{c}}^{'}) (\begin{matrix} \frac{2 n}{d_{c}} \\ \frac{m_{1}}{d_{c}}, \frac{m_{2}}{d_{c}}, \frac{m_{3}}{d_{c}} \end{matrix}) + (\frac{n}{2} + 2) (\begin{matrix} n \\ \frac{m_{1}}{2}, \frac{m_{2}}{2}, \frac{m_{3}}{2} \end{matrix})] + \frac{1}{4} [\sum_{k} (\begin{matrix} 4 \\ p_{1}, p_{2}, p_{3} \end{matrix}) (\begin{matrix} n - 2 \\ m_{1}^{'}, m_{2}^{'}, m_{3}^{'} \end{matrix})]

3 Applications

3.1 Exemple 1. Détermination du nombre de graphes chiraux et achiraux de C₃H₄XY

n = 3, m₁ = 4, m₂ = m₃ = 1; P = {〚1⁶〛, 4〚2³〛, 2〚3²〛, 2〚6〛, 3〚1²2²〛}, P’ = {〚1⁶〛, 3〚2³〛, 2〚3²〛}; D_c = D₆ ∩ D₄ ∩ D₁ = {1}; a₁=a^′₁=1. Les solutions des équations de partition p₁ + p₂ + p₃ = 2 et m^′₁+m^′₂+m^′₃=2 sont respectivement : (p₁, p₂, p₃) = (0,1,1) et $(m_{1}^{'}, m_{2}^{'}, m_{3}^{'}) = (2, 0, 0)$ . À partir de ces données, on obtient :

A_{c} (3, 4, 1, 1) = \frac{1}{12} (\begin{matrix} 6 \\ 4, 1, 1 \end{matrix}) - \frac{1}{4} (\begin{matrix} 2 \\ 0, 1, 1 \end{matrix}) (\begin{matrix} 2 \\ 2, 0, 0 \end{matrix}) = 2 et A_{ac} (3, 4, 1, 1) = \frac{1}{6} [3 (\begin{matrix} 2 \\ 0, 1, 1 \end{matrix}) (\begin{matrix} 2 \\ 2, 0, 0 \end{matrix})] = 1

3.2 Exemple 2. Détermination du nombre de graphes chiraux et achiraux de C₃H₂X₂Y₂

n = 3, m₁ = m₂ = m₃ = 2 ; P = {〚1⁶〛, 4〚2³〛, 2〚3²〛, 2〚6〛, 3〚1²2²〛}, P′ = {〚1⁶〛, 3〚2³〛, 2〚3²〛}; D_c = D₆ ∩ D₂ = {1, 2}; a₁=a^′₁=1. Les solutions des équations de partitions p₁ + p₂ + p₃ = 2 et m^′₁+m^′₂+m^′₃=2 sont respectivement :

(p_{1}, p_{2}, p_{3}) = (\begin{matrix} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2 \end{matrix}) et (m_{1}^{'}, m_{2}^{'}, m_{3}^{'}) = (\begin{matrix} 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \end{matrix})

À partir de ces données, on détermine :

A_{c} (3, 2, 2, 2) = \frac{1}{12} [(\begin{matrix} 6 \\ 2, 2, 2 \end{matrix}) + 2 (\begin{matrix} 3 \\ \frac{2}{2}, \frac{2}{2}, \frac{2}{2} \end{matrix})] - \frac{1}{4} [(\begin{matrix} 2 \\ 2, 0, 0 \end{matrix}) (\begin{matrix} 2 \\ 0, 1, 1 \end{matrix}) + (\begin{matrix} 2 \\ 0, 2, 0 \end{matrix}) (\begin{matrix} 2 \\ 1, 0, 1 \end{matrix}) + (\begin{matrix} 2 \\ 0, 0, 2 \end{matrix}) (\begin{matrix} 2 \\ 1, 1, 0 \end{matrix})] = 7

et

A_{ac} (3, 2, 2, 2) = \frac{1}{6} [(\begin{matrix} 3 \\ \frac{2}{2}, \frac{2}{2}, \frac{2}{2} \end{matrix})] + \frac{1}{2} [(\begin{matrix} 2 \\ 2, 0, 0 \end{matrix}) (\begin{matrix} 2 \\ 0, 1, 1 \end{matrix}) + (\begin{matrix} 2 \\ 0, 2, 0 \end{matrix}) (\begin{matrix} 2 \\ 1, 0, 1 \end{matrix}) + (\begin{matrix} 2 \\ 0, 0, 2 \end{matrix}) (\begin{matrix} 2 \\ 1, 1, 0 \end{matrix})] = 4

3.3 Exemple 3. Détermination du nombre de graphes chiraux et achiraux de C₄H₆XY

n = 4, m₁ = 6, m₂ = m₃ = 1 ; P = {〚1⁸〛, 9〚2⁴〛, 4〚4²〛, 2〚1⁴2⁴〛}, P′ = {〚1⁸〛, 5〚2⁴〛, 2〚4²〛,} ; D_c = D₄ ∩ D₆ ∩ D₁ = {1} ; a₁=a^′₁=1. Les solutions des équations de partitions p₁ + p₂ + p₃ = 4 et m^′₁+m^′₂+m^′₃=2 sont respectivement : (p₁, p₂, p₃) = (2,1,1) et $(m_{1}^{'}, m_{2}^{'}, m_{3}^{'}) = (2, 0, 0)$ . À partir de ces données, on obtient :

A_{c} (4, 6, 1, 1) = \frac{1}{16} [(\begin{matrix} 8 \\ 6, 1, 1 \end{matrix})] - \frac{1}{8} [(\begin{matrix} 4 \\ 2, 1, 1 \end{matrix}) (\begin{matrix} 2 \\ 2, 0, 0 \end{matrix})] = 2 et A_{ac} (4, 6, 1, 1) = \frac{1}{4} [(\begin{matrix} 4 \\ 2, 1, 1 \end{matrix}) (\begin{matrix} 2 \\ 2, 0, 0 \end{matrix})] = 3

3.4 Exemple 4. Détermination du nombre de graphes chiraux et achiraux de C₄H₄X₂Y₂

n = 4, m₁ = 4, m₂ = m₃ = 2 ; P = {〚1⁸〛, 9〚2⁴〛, 4〚4²〛, 2〚1⁴2⁴〛}, P′ = {〚1⁸〛, 5〚2⁴〛, 2〚4²〛,} ; D_c = D₄ ∩ D₂ = {1,2} ; a₁=a^′₁=1. Les solutions des équations de partition p₁ + p₂ + p₃ = 4 et m^′₁+m^′₂+m^′₃=2 sont respectivement les lignes des matrices :

(p_{1}, p_{2}, p_{3}) = (\begin{matrix} 2 & 2 & 0 \\ 2 & 0 & 2 \\ 0 & 2 & 2 \\ 4 & 0 & 0 \end{matrix}) et (m_{1}^{'}, m_{2}^{'}, m_{3}^{'}) = (\begin{matrix} 1 & 0 & 1 \\ 1 & 1 & 0 \\ 2 & 0 & 0 \\ 0 & 1 & 1 \end{matrix})

À partir de ces données, on obtient :

A_{c} (4, 4, 2, 2) = \frac{1}{16} [(\begin{matrix} 8 \\ 4, 2, 2 \end{matrix}) + (\begin{matrix} 4 \\ 2, 1, 1 \end{matrix})] - \frac{1}{8} [(\begin{matrix} 4 \\ 2, 2, 0 \end{matrix}) (\begin{matrix} 2 \\ 1, 0, 1 \end{matrix}) + (\begin{matrix} 4 \\ 2, 0, 2 \end{matrix}) (\begin{matrix} 2 \\ 1, 1, 0 \end{matrix}) + (\begin{matrix} 4 \\ 0, 2, 2 \end{matrix}) (\begin{matrix} 2 \\ 2, 0, 0 \end{matrix}) + (\begin{matrix} 4 \\ 4, 0, 0 \end{matrix}) (\begin{matrix} 2 \\ 0, 1, 1 \end{matrix})] = 23

A_{ac} (4, 4, 2, 2) = \frac{1}{2} [(\begin{matrix} 4 \\ 2, 1, 1 \end{matrix})] + \frac{1}{4} [(\begin{matrix} 4 \\ 2, 2, 0 \end{matrix}) (\begin{matrix} 2 \\ 1, 0, 1 \end{matrix}) + (\begin{matrix} 4 \\ 2, 0, 2 \end{matrix}) (\begin{matrix} 2 \\ 1, 1, 0 \end{matrix}) + (\begin{matrix} 4 \\ 0, 2, 2 \end{matrix}) (\begin{matrix} 2 \\ 2, 0, 0 \end{matrix}) + (\begin{matrix} 4 \\ 4, 0, 0 \end{matrix}) (\begin{matrix} 2 \\ 0, 1, 1 \end{matrix})] = 14

4 Conclusion

Le Tableau 2 récapitule les résultats du calcul des séquences de nombres entiers A_c(n, m₁, m₂, m₃) et A_ac(n, m₁, m₂, m₃) pour les systèmes monocycliques polysubstitués C_nH_m₁X_m₂Y_m₃, où n = 3, 4, 5, 6 et 8, tandis que les nombres entiers (m₁, m₂, m₃) varient conformément à la condition fixée par l’équation (1). On vérifie facilement avec les cycloalcanes substitués de petite taille (n = 3 et 4) que les résultats de ce modèle sont identiques à ceux obtenus par dessin et inventaire des différents graphes. Cette concordance est montrée pour les cyclopropanes disubstitués par les graphes de la Fig. 2a. Dans le cas des cyclobutanes tétrasubstitués de la série C₄H₄X₂Y₂, les calculs prévoient A_c(4, 4, 2, 2) = 23 et A_ac(4, 4, 2, 2) = 14. Les graphes de la Fig. 2b confirment cette prévision et montrent 23 couples d’énantiomères et 14 formes achirales. En fixant par exemple X = COOH et Y = C₆H₅, on dénombre les isomères de position et les stéréoisomères d’une famille de diacides organiques ayant la même formule brute C₄H₄(COOH)₂(C₆H₅)₂. Les composés les plus connus de cette série sont les acides truxuliques (avec deux groupements COOH en positions 1 et 3) et les acides truxiniques (avec deux groupements COOH en positions 1 et 2). Ces deux catégories de diacides existent à l’état naturel dans les feuilles de coca ou sont obtenues par photodimérisation topochimique des formes α et β de l’acide cinnamique 〚7〛. L’importance de cette étude est de montrer qu’on peut éviter la méthode classique de Polyà 〚8–13〛 et obtenir, par une approche combinatoire directe, des formules de récurrence permettant d’inventorier les squelettes chiraux et achiraux des cycloalcanes monocycliques hétéropolysubstitués par un binaire (X,Y). En outre, le présent modèle peut être généralisé aux systèmes ayant une polyhétérosubstitution de nature multiple. Il est à noter qu’en effectuant les sommes suivantes : A_c(n, m₁, m₂, m₃) + A_ac(n, m₁, m₂, m₃) = A_T(n, m₁, m₂, m₃) et 2 A_c(n, m₁, m₂, m₃) + A_ac(n, m₁, m₂, m₃) = A_E(n, m₁, m₂, m₃) à partir des données du Tableau 2 et pour des valeurs fixées n, m₁, m₂ et m₃, on obtient A_T(n, m₁, m₂, m₃) et A_E(n, m₁, m₂, m₃), qui sont respectivement les résultats des dénombrements topologique et énantiomérique de la méthode de Polyà.

n	3	4	5	6	8
m₁	m₂	m₃	A_c	A_ac	A_c	A_ac	A_c	A_ac	A_c	A_ac	A_c	A_ac
4	1	1	2	1
3	2	1	4	2
2	2	2	7	4
6	1	1			2	3
5	2	1			8	5
4	2	2			23	14
4	3	1			14	7
3	3	2			30	10
8	1	1					4	1
7	2	1					16	4
6	3	1					40	4
6	2	2					62	12
5	4	1					60	6
5	3	2					120	12
4	4	2					156	18
4	3	3					204	12
10	1	1							4	3
9	2	1							24	7
8	3	1							76	13
8	2	2							118	29
7	4	1							156	18
7	3	2							316	28
6	5	1							220	22
6	4	2							564	62
6	3	3							749	44
5	5	2							672	42
5	4	3							1 128	54
4	4	4							1 422	96
14	1	1									6	3
13	2	1									48	9
12	3	1									333	48
12	2	2									218	19
11	4	1									666	33
11	3	2									1 338	54
10	5	1									1 476	51
10	4	2									3 723	156
10	3	3									4 954	102
9	6	1									2 470	65
9	5	2									7 440	135
9	4	3									12 430	165
8	7	1									3180	75
8	6	2									11 205	270
8	5	3									22 410	225
8	4	4									28 065	414
7	7	2									12 780	180
7	6	3									2 900	260
7	5	4									44 880	330
6	6	4									52 430	560
6	5	5									62 868	390

Fig. 2
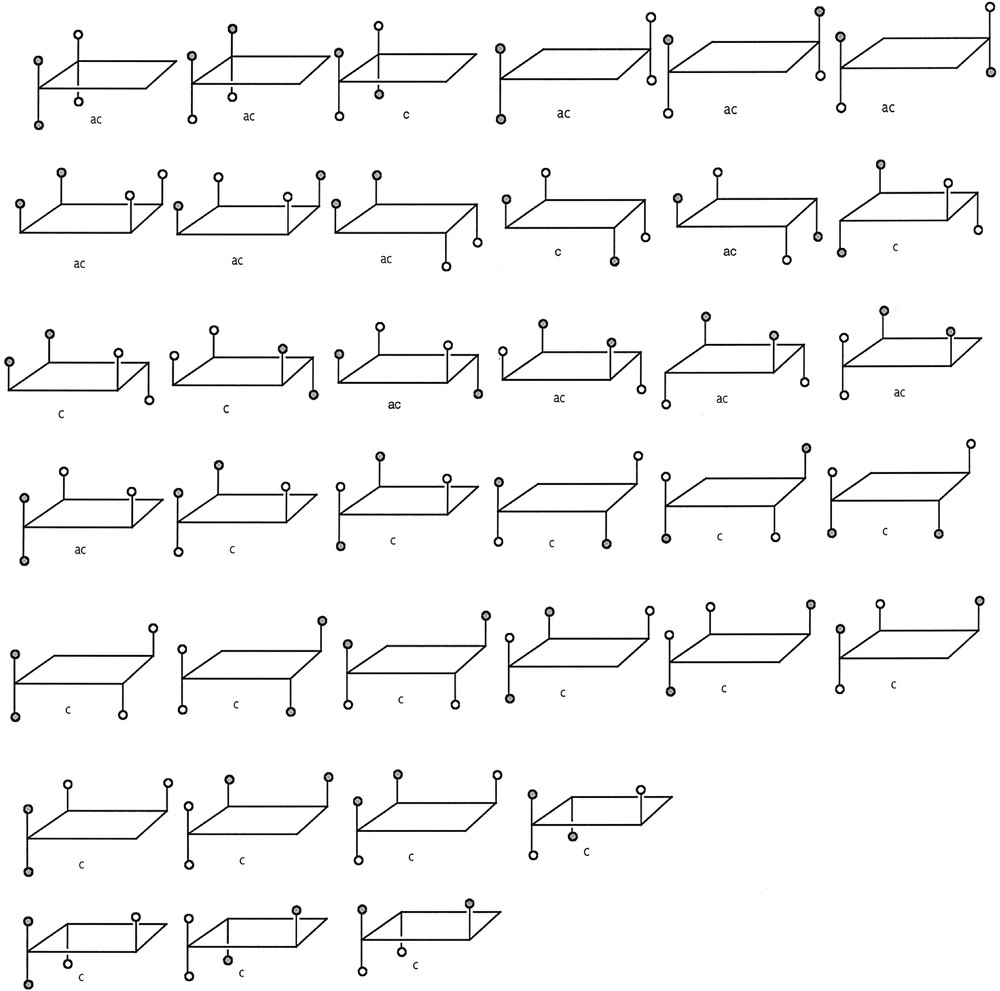
a. Formes chirales (c) et achirale (ac) de C₃H₄XY avec X = et Y = •. b. Formes chirales (c) et achirale (ac) de C₄H₄X₂Y₂ avec X = et Y = •.

Bibliographie

[〚1〛] R.M. Nemba; F. Ngouhouo Tetrahedron, 50 (1994), p. 6663

[〚2〛] R.M. Nemba; F. Ngouhouo New J. Chem, 18 (1994), p. 1175

[〚3〛] R.M. Nemba; M. Fah J. Chem. Inf. Comput. Sci, 37 (1997) no. 4, p. 722

[〚4〛] R.M. Nemba; A.T. Balaban J. Chem. Inf. Comput. Sci, 38 (1998), p. 1145

[〚5〛] R.M. Nemba C. R. Acad. Sci. Paris, Ser. IIb, 323 (1996), p. 773

[〚6〛] A. Kaufman Introduction à la combinatorique, Dunod, Paris, 1980, p. 84

[〚7〛] E.L. Eliel; S.H. Wilen; L.N. Mander Stereochemistry of organic compounds, Wiley Interscience, New York, 1994, p. 756

[〚8〛] G. Polyà Acta Math, 69 (1937), p. 145

[〚9〛] G. Polyà; R.C. Read Combinatorial Enumeration of Graphs, Groups and Chemical Compounds, Springer Verlag, New York, 1987, p. 58

[〚10〛] (a) G. Polyà, R.E. Tarjan, D.R. Woods, Notes in introductory combinatorics, Birhauser, Boston, 1983, p. 55 ; (b) A.T. Balaban, Croat. Chem. Acta 51 (1978) 35

[〚11〛] (a) F. Harary, E. Palmer, R.W. Robinson, R.C. Read, in : A.T. Balaban, Chemical Applications of Graph Theory, Academic Press, London, p. 11 ; (b) A.T. Balaban, J.W. Kennedy, L.V. Quintas, J. Chem. Educ. 65 (1988) 304; (c) R.W. Robinson, F. Harary, A.T. Balaban, Tetrahedron 32 (1976) 355

[〚12〛] A. Tucker Math. Mag, 47 (1974), p. 248

[〚13〛] D.H. Rouvray Chem. Soc. Rev, 3 (1974), p. 355

Commentaires - Politique

1 Introduction

2 Conditions mathématiques de formation d’une polyhétérosubstitution de degrés (m1, m2, m3) sur le squelette de G

3 Applications

3.1 Exemple 1. Détermination du nombre de graphes chiraux et achiraux de C3H4XY

3.2 Exemple 2. Détermination du nombre de graphes chiraux et achiraux de C3H2X2Y2

3.3 Exemple 3. Détermination du nombre de graphes chiraux et achiraux de C4H6XY

3.4 Exemple 4. Détermination du nombre de graphes chiraux et achiraux de C4H4X2Y2