Abridged version
1 Introduction
Most of the French gravity data were measured during the last 50 years and, in the same time, terrain correction (TC) computation techniques have significantly evolved. Originally, the TCs were determined manually with the help of charts [3] out to a maximum distance of 22 km from the gravity station (often less in practice). Today, they are generally computed numerically out to the radius of 167 km (based on the work by Bullard [1] concerning the effect of the Earth curvature), using appropriate algorithms and Digital Elevation Models (DEM). Moreover, the present widening of use of gravity data justifies our efforts for homogenising the French gravity database (BGF). From the local to the national scale, the disparity in the TC [2] can cause regional gravity artefacts. Also, in the context of the European Community building, an increased need for standardisation between the national gravity networks is expressed.
2 Procedure and computation of the terrain corrections
Among the 410 000 gravity stations in the BGF database, about 77 000, located in the Alps region, had their TC homogenised out to 167 km [6] in the framework of the GéoFrance 3D program. Contrary to that study, we decided to fully recompute the TC (not only complete it) for the remaining 330 000 stations, in order to simplify the computations and get a result as homogeneous as possible. In order to insure the best quality/computation time compromise, we performed several tests, based on different algorithms and different DEM [5] that led us to the following procedure: we compute terrain effects in three zones of increasing radius, 53 m/3 km, 3 km/10 km and 10 km/167 km, using three DEM, with grid sizes 50, 250 and 1000 m, respectively. In the inner zone, we use a flat-top-prism-based algorithm, while in the two outer zones, the topography is described as vertical mass lines. The 50 m DEM is provided by IGN and covers all the French metropolitan territory and Corsica Island. Beyond the borderlines, these data are extended out to 3 km, using a commercial 75 m DEM. The 250 m DEM is redrawn from the 50 m one and extended 10 km out of our borders. Accurate numerical marine data are not available yet for the entire French coast and we therefore have not computed the TC for all the stations within a 10 km coastal area. The 1000 m DEM is redrawn from the 50 m one and extended about 200 km out of our borders, using (1) a 1-arc minute bathymetry provided by SHOM, (2) the 30-arc second land GTOPO30 DEM. The Earth curvature is not taken into account in our computations, since its effect (1) can be easily determined independently, provided that the altitude of the station be known, (2) is relatively low and exists mainly for high elevation stations (∼1 mGal at an altitude of 1000 m), and (3) is generally not taken into account in foreign gravity databases.
3 Controlling the computed terrain corrections
Due to inaccurate altitude positioning of the gravity stations and DEM imprecision, altitude gaps Δz can arise between them. The bigger the gap is, the more erroneous the computed TC is. We show a map of these Δz in Fig. 1 for the 330 000 gravity stations. Most of the stations have a Δz smaller than 5 m (absolute value). However, about 10% of the stations have a higher Δz, some reaching 30 m or more, in the mountains especially. For a sample of 13 000 stations, Fig. 2 shows that to the first order, the TC has the same tendency as the topography, except in places where the station/DEM gap is significantly high. Therefore, for all the gravity stations scattered over the territory that have a Δz higher than 30 m, we have reduced the TC to the level of surrounding stations. The result is shown in blue in Fig. 2: where the Δz was low, the TC remains unchanged and where Δz⩾30 m, the TC looks much like the topography.
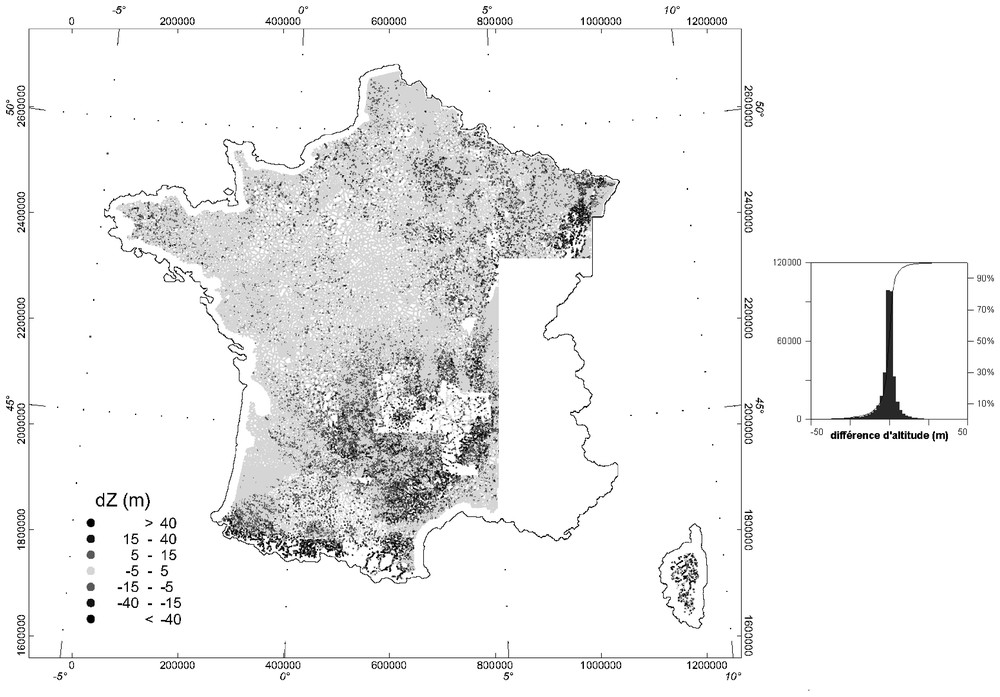
Répartition des Δz MNT/stations gravimétriques pour l'ensemble des points où les CT ont été recalculées (en blanc: la zone Alpes de GéoFrance 3D, les zones sans données et la frange côtière, où les nouvelles CT n'ont pas été recalculées). On observe que la majorité des stations (points gris très clair) se classent dans la tranche de Δz−5/5 m. Cependant, un nombre non négligeable de stations présentent un Δz supérieur à ±5 m par rapport au MNT. Environ 2,5% des stations, essentiellement sur les massifs montagneux, atteignent même des écarts de 30 m et plus avec le MNT (points gris à noirs).
Δz Map between gravity stations and the DEM (white areas correspond to the GéoFrance 3D study, to the 10 km-wide coastal fringe where TCs were not computed and to areas with no data). Most of the gravity stations (very light grey) are within ±5 m from the DEM. However, about 10% of the stations have a higher Δz, some reaching 30 m or more, in mountainous areas especially.

Influence du Δz MNT/stations sur le calcul de la CT proche. En haut (en blanc, partiellement recouvert par le noir), la CT proche (50 m/3 km), globalement corrélée à l'altitude de la station (au centre). Là où le Δz MNT/stations (en bas) s'écarte sensiblement de zéro, on constate que la CT est perturbée et ne suit plus la même tendance que l'altitude. Lorsque le Δz était supérieur à 30 m, la CT a été ramenée au niveau des stations environnantes (noir en haut); on constate qu'elle reproduit alors plus fidèlement les tendances de la variable altitude (au centre).
Influence of DEM/station Δz on the TCs. In the upper graph (in white, partially overlap by black), the inner TC (53 m/3 km) appears correlated to the altitude (central part), except where the DEM/station Δz (lower part) deviates from zero. When this Δz is higher than 30 m, we reduce the TC to the level of surrounding stations (black in upper graph); it then matches much better the topography tendencies.
In the Alps area, our computations partially meet the one performed in GéoFrance 3D. Fig. 3 shows the differences of CT that we observe at the 26 111 gravity stations that are common to both studies. Most of these differences are lower than 20 μGal (light grey dots), which indicates a fairly good agreement between both studies. Dots in dark grey and black in zones A and B correspond to gravity stations measured in 1966 and 1967 for which the TC were estimated manually out to a distance of 22 km. Since the TCs in the GéoFrance 3D study were completed (not fully recomputed), it is not surprising that differences arise between our results, especially in this mountainous area. Stations of zone C exhibit a TC difference higher than 0.1 mGal on a 10 km-wide band along the Swiss border. In their study, Masson et al. [6] did not have an accurate DEM on the Swiss side of the borderline; therefore, they could not compute the inner-terrain corrections in this zone.
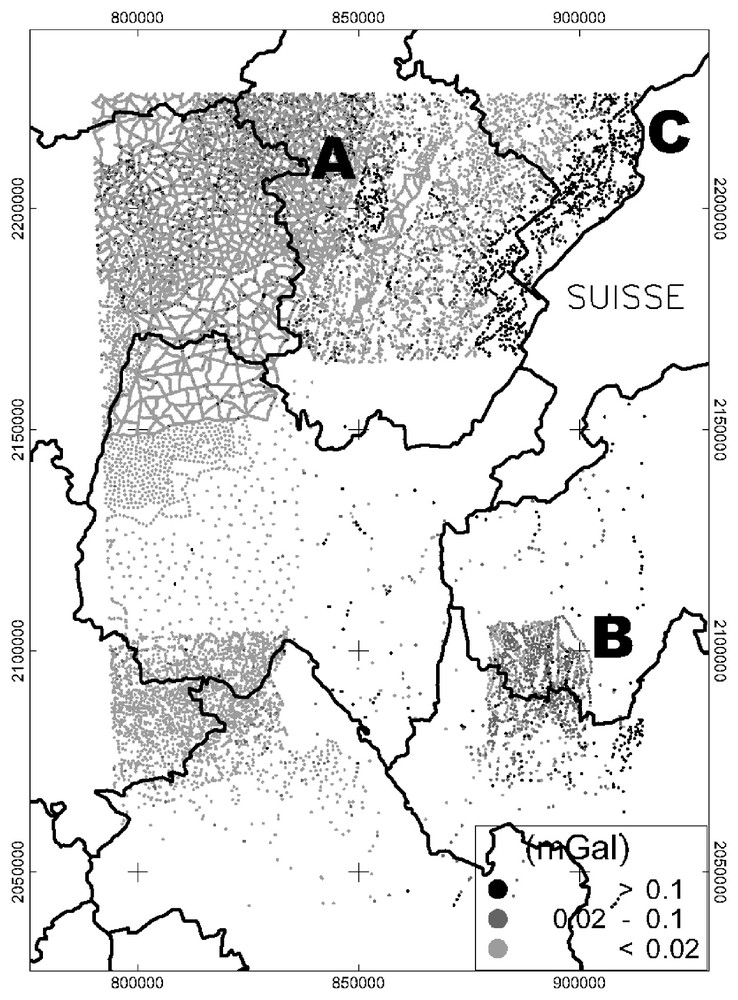
Carte des différences de CT obtenues aux 26 111 points communs à notre étude et à l'étude Alpes de GéoFrance 3D. Pour la majorité des stations gravimétriques, l'écart de CT est inférieur à 20 μGal, ce qui indique une très bonne cohérence entre les deux études. Pour les autres points, en particulier dans les zones A, B et C, on peut identifier la cause des écarts mis en évidence, en se référant à l'historique des études qu'elles concernent (voir détails dans le texte).
Map of the differences between TCs at the 26 111 stations that are common to this study and to the GéoFrance 3D study. Most differences are less than 20 μGal, showing a fairly good agreement between both studies. At other stations, especially in zones A, B and C, the stronger TC differences can be explained when referring to the concerned survey history (see text for details).
4 Discussion and conclusion
We present the map showing the TC recomputed between 53 m and 167 km, all over France, in Fig. 4. To the first order, the TC is correlated to the elevation and roughness of the topography. The TC is less than 10 mGal for 90% of the gravity stations, and reaches a maximum of about 40 mGal (see histogram in Fig. 4). In comparison to the old TC map (insert view in Fig. 4), the new one (1) does not exhibit any null TC, except in a 10 km-wide coastal fringe for which accurate bathymetric data were not available, and (2) is significantly increased, especially near and on the mountains. Errors in our results are mainly due to the lack of terrain corrections between 0 and 53 m (that represents about 1% of the total CT) and to computation errors: inaccuracies in the DEM and in the computation algorithm. We estimate the total error on the CT to be less than 1 mGal, with maximums located in mountainous zones. And we also remind than in the Alps area, comparison of our results with previous one leads to differences generally lower than 20 μGal.
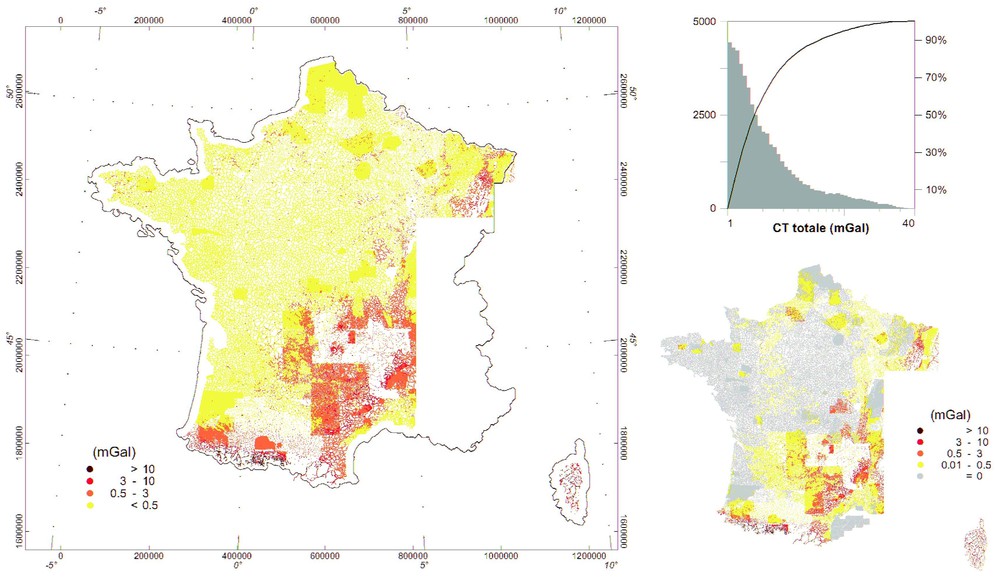
Carte des CT homogénéisées jusqu'à la distance de 167 km. Pour l'ensemble des stations, 90% des CT sont inférieures à 10 mGal. Elles croissent sur les reliefs et atteignent environ 40 mGal au maximum. En comparaison de la carte des CT qui existait au départ de cette étude (encart), la nouvelle carte (1) ne comporte plus de zones où la CT est nulle, (2) présente des valeurs de CT globalement légèrement rehaussées.
Map of the TCs homogenised out to a distance of 167 km. 90% of the gravity stations have TC lower than 10 mGal. The TC increases in mountainous areas, reaching a maximum of about 40 mGal. Compared to the old TC map (insert view), the new TCs do not exhibit zero values and are globally slightly higher, in particular in mountains.
1 Introduction
Au cours des 50 dernières années, parallèlement à l'acquisition de l'essentiel des données gravimétriques françaises, les techniques de calcul des corrections de terrain (CT) ont beaucoup évolué : réalisées à l'origine manuellement à l'aide des abaques de Hammer [3], elles sont aujourd'hui généralement calculées à l'aide de moyens informatiques. Le choix du rayon maximal de calcul des CT autour de chaque station gravimétrique a aussi varié au cours du temps, en fonction de l'utilisation projetée des données et des moyens dont on disposait lors du levé : classiquement 22 km (en pratique, souvent moins), tant que les CT étaient estimées manuellement à l'aide d'abaques, le plus souvent aujourd'hui par des moyens informatiques, jusqu'à 167 km (à la suite des travaux de Bullard [1] sur l'effet de courbure terrestre).
La diversification de l'utilisation des données gravimétriques nationales justifie à plusieurs titres les efforts d'homogénéisation de la Banque gravimétrique française (BGF), gérée au BRGM. À l'échelle locale et nationale, la disparité des CT [2] peut être la source d'artefacts apparentés à des effets régionaux. Plus largement, dans le cadre de la construction européenne et à l'échelle internationale, apparaı̂t le besoin d'une interconnexion accrue des réseaux gravimétriques nationaux entre eux.
2 Protocole et calcul des corrections de terrain
La BGF comprend près de 410 000 stations gravimétriques validées. Pour environ 77 000 d'entre elles, situées dans la région des Alpes, les CT avaient été complétées jusqu'à 167 km [6] dans le cadre du programme GéoFrance 3D. Cette solution présente deux inconvénients : une gestion assez complexe des calculs et, surtout, une perte d'homogénéité du résultat final, liée à la disparité de qualité des CT préexistantes. Pour nous affranchir de ces inconvénients et garantir la plus grande homogénéité possible aux nouvelles CT, nous avons, pour les 330 000 stations restantes, choisi de recalculer intégralement les CT entre 53 m et 167 km. Divers tests, avec plusieurs algorithmes et plusieurs grilles MNT, ont été réalisés [5], qui ont abouti au protocole de calcul décrit ci-après. L'espace compris entre 53 m et 167 km autour de chaque station gravimétrique a été découpé en trois couronnes de diamètres croissants (53 m/3 km, 3 km/10 km et 10 km/167 km), auxquelles on a associé des MNT à mailles de plus en plus larges (50, 250 et 1000 m, respectivement). Afin d'assurer le meilleur compromis précision/temps de calcul, deux algorithmes ont été utilisés : l'un pour la couronne proche, basé sur le principe des prismes à toits plats, l'autre pour les deux couronnes externes, en assimilant l'effet du relief à des lignes de masse. Le MNT au pas de 50 m est dû à l'IGN ; il couvre l'ensemble du territoire national, jusqu'à la côte et aux frontières, ainsi que la Corse. Aux frontières, il est complété par un MNT commercial au pas de 75 m, précisément calé et validé sur le MNT IGN [4]. Une frange d'un peu plus de 3 km de large a ainsi été ajoutée au MNT IGN sur les frontières nord-est, est et espagnole, de manière à réaliser proprement les CT proches pour les stations situées à moins de 3 km de ces frontières. Le MNT au pas de 250 m a été obtenu en sous-échantillonnant le MNT à 50 m, auquel on a cette fois ajouté une frange de 10 km de large au-delà de nos frontières. Sur les côtes, en revanche, il n'existe pas à l'heure actuelle de MNT de la bathymétrie de cette résolution. La digitalisation des données existant sous forme papier est en cours de réalisation au SHOM. Pour cette raison, nous avons, tout le long des côtes Atlantique et Méditerranée, laissé une bande de 10 km de large environ, pour laquelle les CT n'ont pas été recalculées. Enfin, le MNT au pas de 1000 m a été obtenu en sous-échantillonnant le MNT au pas de 250 m pour la zone du territoire national et en le complétant jusqu'à environ 200 km de nos frontières par (1) un MNT bathymétrique au pas de 1 minute d'arc (projeté en Lambert II, étendu et ré-interpolé à 1000 m), (2) le MNT GTOPO30, recouvrant l'ensemble des zones émergées, avec une maille de 30 secondes d'arc (projeté en Lambert II étendu et ré-interpolé à 1000 m).
On notera également que le terme correctif pour la rotondité de la Terre n'a pas été pris en compte, car (1) ce terme peut être facilement calculé de manière indépendante (seule l'altitude du point de mesure est alors nécessaire ; voir, par exemple, [7]), (2) son effet est relativement peu important, ressenti essentiellement pour les stations en altitude (∼1 mGal pour une station d'altitude 1000 m), et (3) ce terme correctif n'est généralement pas inclus dans les bases de données étrangères.
3 Contrôles des CT calculées
Un des paramètres clé dans la justesse des CT est la différence d'altitude entre la station gravimétrique et le MNT. En effet, lorsque la station gravimétrique s'écarte de la surface topographique (vers le haut ou vers le bas), en particulier pour les corrections proches, l'effet calculé du terrain est faussé. Plus l'écart d'altitude est important, plus la CT est erronée. Dans la pratique, on observe couramment des écarts d'altitude entre MNT et stations de mesure atteignant 5 à 10 m et, plus rarement, jusqu'à 50 m. Ces écarts ont plusieurs causes, qui toutes sont accentuées dans les zones de relief : (1) le MNT est une représentation numérique de la topographie, dont la précision n'est pas absolue, (2) l'altitude du MNT est connue aux nœuds d'une grille discrète – en dehors de ces nœuds, l'altitude est le résultat d'une interpolation – (3) selon le type de positionnement des levés, les erreurs sur l'altitude peuvent atteindre plusieurs mètres. La Fig. 1 présente le Δz MNT/stations gravimétriques pour l'ensemble des points où les CT ont été recalculées. Pour la très grande majorité de ces points (figurés en gris), le Δz reste inférieur à 5 m (en valeur absolue). Environ 10 % des stations présentent cependant un Δz avec le MNT supérieur à 5 m, certaines atteignant même 30 m et plus, dans les zones montagneuses en particulier. La Fig. 2 présente l'influence de ces Δz MNT/stations sur le calcul des CT : pour un échantillon de 13 000 stations, les trois paramètres altitude, CT proche et Δz avec le MNT ont été représentés. Au premier ordre, on observe que la CT croı̂t avec l'altitude. On constate également que, lorsque le paramètre Δz s'écarte sensiblement de zéro, la CT proche ne suit plus la même tendance que l'altitude. Pour l'ensemble des stations gravimétriques disséminées affectées par cet effet (Δz⩾30 m), à défaut d'identifier la cause du Δz, la CT a été ramenée au niveau des stations environnantes. Le résultat est présenté sur la Fig. 2 (figuré bleu) : on constate que là où le Δz était supérieur à 30 m, la CT est modifiée et qu'elle reproduit désormais plus fidèlement les tendances de la topographie.
Dans la zone des Alpes, nos calculs recoupent partiellement ceux réalisés dans le cadre de GéoFrance 3D, ce qui nous a permis de vérifier la cohérence des deux types de calculs. La Fig. 3 présente les différences de CT obtenues aux 26 111 points communs aux deux études. On constate que la grande majorité des écarts de CT sont inférieurs à 20 μGal (points gris clair), ce qui indique une excellente cohérence entre les résultats. Pour les autres points (gris moyen et noir), on a réalisé une étude plus fine des causes possibles de ces écarts. Il faut tout d'abord rappeler que, dans l'étude Alpes, à la différence de notre étude, les CT ont été complétées et non recalculées intégralement. Les écarts de CT observées en A et C sur la Fig. 3 en découlent directement : en A et B, les stations où apparaissent les écarts appartiennent aux levés ∗CM2074 et ∗CM2520, qui datent de 1966 et 1967 et pour lesquels les CT avaient été réalisées à la main jusqu'à 22 km. Ces levés sont situés en zone montagneuse ou proche de reliefs, et il n'est donc pas étonnant, selon l'opérateur qui a réalisé les CT à l'époque, que des écarts apparaissent par rapport à nos propres calculs. En C apparaı̂t nettement une bande d'une dizaine de kilomètres environ, parallèle à la frontière avec la Suisse, dans laquelle l'écart de CT est supérieur à 0,1 mGal. Cet écart correspond à un déficit de la CT calculée dans l'étude Alpes. En effet, lors de cette étude, un MNT précis n'avait pas pu être obtenu sur la Suisse [6] et les CT de la bande 53 m/10 km n'avaient pas été calculées le long de cette frontière. À cet endroit, nos CT sont donc plus pertinentes et devront remplacer celles de l'étude Alpes dans la BGF.
4 Discussion et conclusion
La carte des CT recalculées entre 53 m et 167 km sur la France est présentée sur la Fig. 4. Au premier ordre, la CT est corrélée à la rugosité et à l'altitude des reliefs. Les CT sont pour 90 % inférieures à 10 mGal et atteignent au maximum environ 40 mGal (histogramme de la Fig. 4). Comparée à la carte des CT qui existait au départ de cette étude (encart sur la Fig. 4), la nouvelle carte (1) ne comporte plus de zones où la CT est nulle, excepté dans une frange côtière de 10 km de large, où les CT n'ont pas été recalculées, faute d'un MNT assez précis, (2) présente une CT légèrement accrue par rapport à la carte préexistante (encart sur la Fig. 4), en particulier sur et au pourtour des reliefs. L'absence de corrections proches de 0 à 53 m (environ 1 % de la CT totale) et l'incertitude sur les calculs (imprécision du MNT et de l'algorithme de calcul) constituent les principales causes d'erreur sur la CT. Nous estimons cette erreur à 1 mGal au maximum, en zone montagneuse. Rappelons que dans la zone alpine, nos comparaisons avec les travaux de GéoFrance 3D montrent un excellent accord, généralement meilleur que 20 μGal.
Remerciements
Nous remercions F. Masson et G. Grandjean pour leur aimable collaboration à ce travail. Cette note a bénéficié des commentaires de M. Diament. Les données bathymétriques au pas de 1 min d'arc pour l'ensemble des côtes françaises ont été fournies par le SHOM dans le cadre de la convention BRGM–SHOM n∘ E32/2001. Cet article constitue la publication BRGM n∘ 02125, financée sur le projet DR Méthodes géophysiques au service de la cartographie numérique et 3D.



