Version abrégée
1 Introduction
Les systèmes colloı̈daux en milieu aqueux d'intérêt environnemental ou technologique sont dominés par leurs propriétés électriques à l'interface solide–eau. À l'échelle moléculaire, l'adsorption d'espèces ioniques (nutriments, polluants) détermine leur partition et leur transport, et modifie les propriétés interfaciales des particules. Ainsi, les tensioactifs ioniques sont utilisés, d'une part, dans le procédé de séparation des minerais métalliques par flottation et, d'autre part, dans la récupération assistée du pétrole. Dans les deux cas, une bonne connaissance des mécanismes d'adsorption et de leurs conséquences sont indispensables pour une application maı̂trisée. Les interactions interparticulaires contrôlent la stabilité des colloı̈des dans des phénomènes comme la dissémination des particules aériennes ou aquatiques, la stabilité des sols, la sédimentation, le transport des solutés. De nombreux procédés industriels font appel à ces interactions : la formulation des peintures, des cosmétiques, des matériaux composites, le traitement des eaux par coagulation–floculation, l'industrie agroalimentaire, la pharmacie.
L'objectif de cette contribution est de donner un aperçu des théories et méthodes majeures pour la compréhension de ces phénomènes et de leurs applications industrielles dans des procédés mettant en jeu la matière particulaire.
2 Origine de la charge de surface
La charge a trois origines :
- • des différences de stœchiométrie entre la surface et la solution, comme dans le cas des sels ;
- • des substitutions isomorphes dans le réseau cristallin, qui génèrent une capacité d'échange ionique, comme dans le cas des zéolites, de certains phyllosilicates et des hydroxydes lamellaires doubles ;
- • les coordinances libres des atomes de surface, comme dans le cas des oxydes métalliques.
La chimisorption de molécules d'eau dissociées sur les surfaces d'oxydes donne naissance à des groupes oxo ou hydroxo, dont la protonation–déprotonation confère à ces surfaces une charge amphotère, caractérisée par le point de charge nulle (PCN).
3 Propriétés électriques des surfaces chargées
3.1 Le modèle de la double couche
Le modèle le plus ancien est celui de Helmholtz [39], qui assimile l'interface chargée à un condensateur (équation (1)). En revanche, le modèle de Gouy [35] et Chapman [19] ne considère que le nuage ionique (équation (2)). Stern [76], puis Grahame [36] proposent une combinaison entre les deux modèles, alliant les deux couches ioniques (Fig. 1) : les ions immobilisés par complexation avec les groupes de surface et une couche diffuse d'ions mobiles, en interaction électrostatique avec la surface.
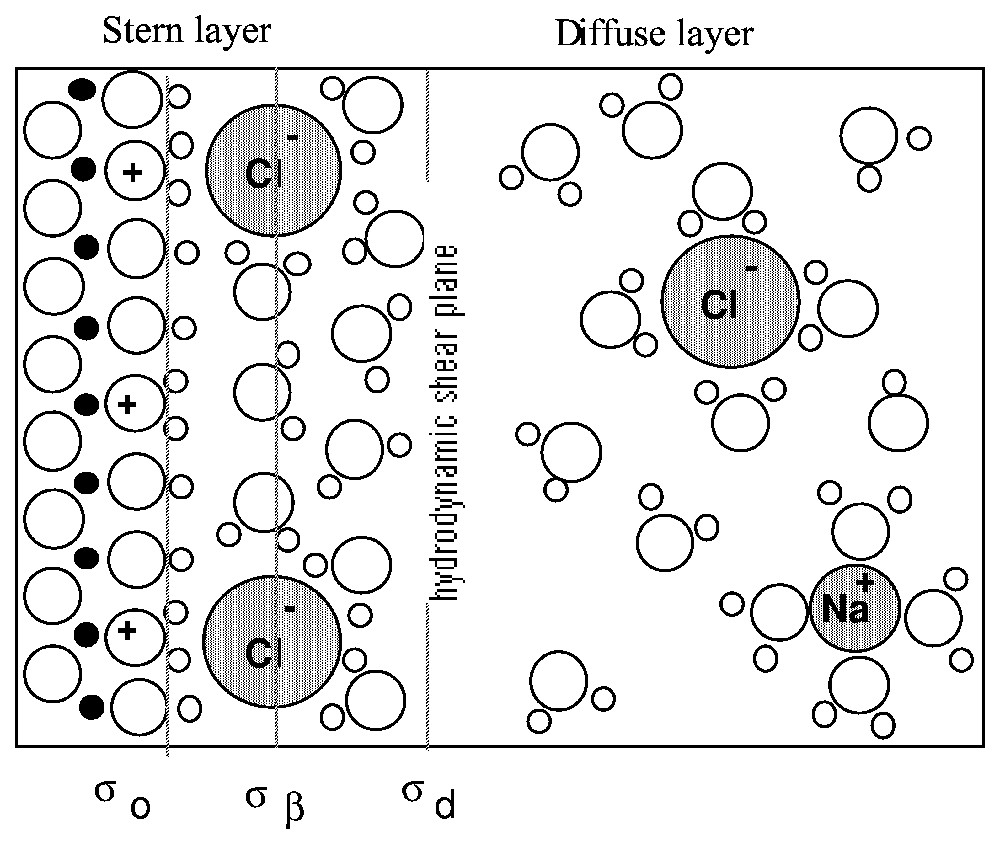
Schematic representation of the electrical double layer. Example of a positively-charged surface in an NaCl solution.
Représentation schématique de la double couche électrique. Exemple d'une surface chargée positivement dans une solution de NaCl.
3.2 Le potentiel électrocinétique et le plan de coupure hydrodynamique
Lors d'un mouvement relatif de la particule et du milieu créé mécaniquement (potentiel d'écoulement) ou électriquement (électrophorèse ou électro-osmose), un potentiel électrocinétique – ou potentiel ζ – localisé au plan de coupure hydrodynamique est mesuré. L'identification avec le plan externe de Helmholtz (Fig. 1) permet de calculer la charge au plan de coupure (équation (3)). Cette mesure est largement utilisée, par exemple pour déterminer le choix des tensioactifs ioniques en flottation des minerais : la Fig. 2 montre que la flottation de la zircone est optimale avec des tensioactifs de signe opposé à celui de la charge de surface.
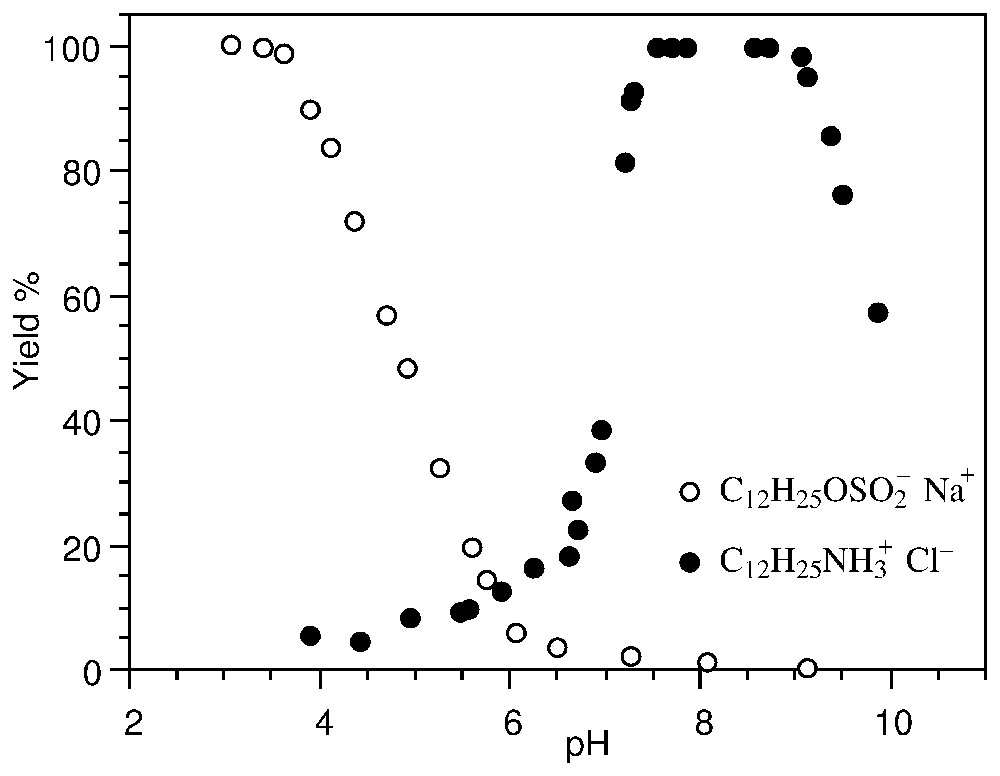
Evolution of the flotation yield of ZrO2 with two surfactants (10−4 M): dodecyl-sulfonate and dodecyl-ammonium (after [14]).
Évolution du rendement de flottation de ZrO2 avec deux tensioactifs (10−4 M) : dodécyl-sulfonate et dodécyl-ammonium (d'après [14]).
La coı̈ncidence du plan externe de Helmholtz (Fig. 1) et du plan de coupure hydrodynamique est suggérée par des mesures de microcalorimétrie d'immersion et de RMN du proton [16,34], qui montrent que deux à trois couches d'eau sont fortement structurées par la surface, les molécules au-delà possédant la mobilité de l'eau liquide. Cette discontinuité pourrait être à l'origine du plan de coupure hydrodynamique, qui se situerait alors à une distance finie de la surface. L'adsorption de macromolécules non ioniques sur des surfaces chargées repousse le plan de coupure à mesure que la couche adsorbée s'épaissit, et le potentiel ζ décroı̂t, alors que la charge de surface n'est pas modifiée [10]. Les conséquences de ces observations sont importantes pour les suspensions colloı̈dales : dans les pulpes concentrées et les boues, seule une faible proportion de l'eau est perturbée [22,74].
3.3 La couche diffuse et les interactions interparticulaires
La théorie DLVO [30,86] décrit les interactions interparticulaires comme la somme des interactions attractives réunies sous l'appellation de forces de Van der Waals et des interactions répulsives de double couche. Seules ces dernières dépendent des conditions du système (densité de charge, nature et concentration des ions), tandis que leur intensité détermine la distance d'approche entre surfaces chargées. Le potentiel électrocinétique est donc un paramètre déterminant pour comprendre et prédire la stabilité et l'écoulement de systèmes colloı̈daux (Fig. 3) : au point isoélectrique (IEP) où le potentiel ζ est nul, le surnageant d'une suspension de TiO2 est limpide et le seuil d'écoulement d'une suspension concentrée d'alumine est maximal. Ces deux résultats sont dus à l'état coagulé des suspensions. C'est ce phénomène qui est mis à profit, par exemple, dans la clarification de l'eau potable par coagulation–floculation.
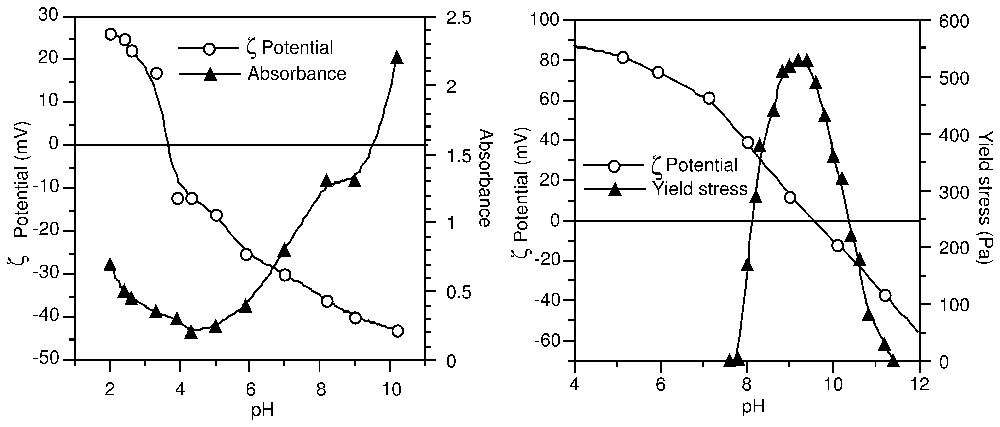
ζ-potential dependence: (a) of the absorbance in a diluted TiO2 suspension, and (b) of the yield stress in a concentrated Al2O3 suspension (after [21,47]).
Influence du potentiel ζ (a) sur l'absorbance dans une suspension diluée de TiO2 et (b) sur le seuil d'écoulement dans une suspension concentrée de Al2O3 (d'après [21,47]).
4 Mesure et modélisation de la charge de surface
4.1 Le titrage de surface
La charge de surface σ0 est calculée à partir de la quantité adsorbée du couple H+/OH−, mesurée par titrage potentiométrique d'une suspension (équation (4)).
4.2 Modèles de charge de surface
Les équilibres de protonation–déprotonation à l'interface sont exprimés à l'aide de la loi d'action de masse. Deux approches ont été décrites dans la littérature :
- • une approche globale [27,60,77], rendant compte de la propriété amphotère des surfaces chargées, par deux équations successives de protonation–déprotonation : le modèle à deux pK (équations (5) et (6)) ;
- • une approche locale, utilisant le concept de valence formelle de Pauling, qui attribue aux groupes oxo ou hydroxo des différentes faces d'un cristal un caractère mono-, di- ou tri-coordiné. Le modèle MUSIC [40,41] repose sur ce principe et utilise un seul équilibre de protonation–déprotonation (équation (7)).
4.3 La position du point de charge nulle (PCN)
Indépendamment des modèles de charge de surface, la PCN indique le pH d'inversion de charge où les propriétés des colloı̈des changent radicalement. Les modèles prédictifs recherchent des corrélations entre la position du PCN avec le potentiel d'ionisation ou l'électronégativité des cations métalliques dans les oxydes [13,80], les distances interatomiques dans le solide [40,60,91], ou la densité d'ions par maille [38]. Dans les silicates, il existe une corrélation entre les propriétés cristallochimiques et la position du PCN, fondée sur l'abondance et la coordinance des cations par rapport aux tétraèdres SiO4 (Fig. 4) [14,15].
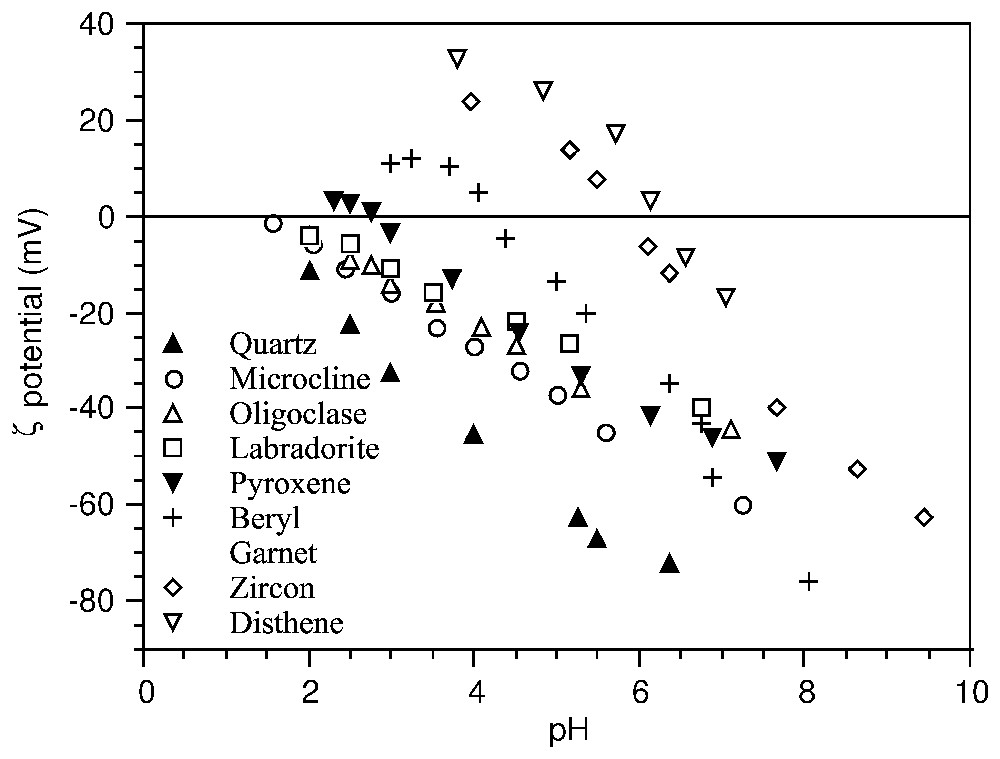
ζ potential–pH curves of silicates (after [14,15]).
Courbes potentiel ζ–pH de silicates (d'après [14,15]).
5 Mesure et modélisation de la complexation de surface
5.1 L'adsorption d'ions
La charge de la couche de Stern est déterminée à partir des isothermes d'adsorption de contre-ions ou des seuils d'adsorption en fonction du pH (équation (8)). La formation de complexes en surface est liée à la tendance à former des complexes hydroxo en solution (Fig. 5).
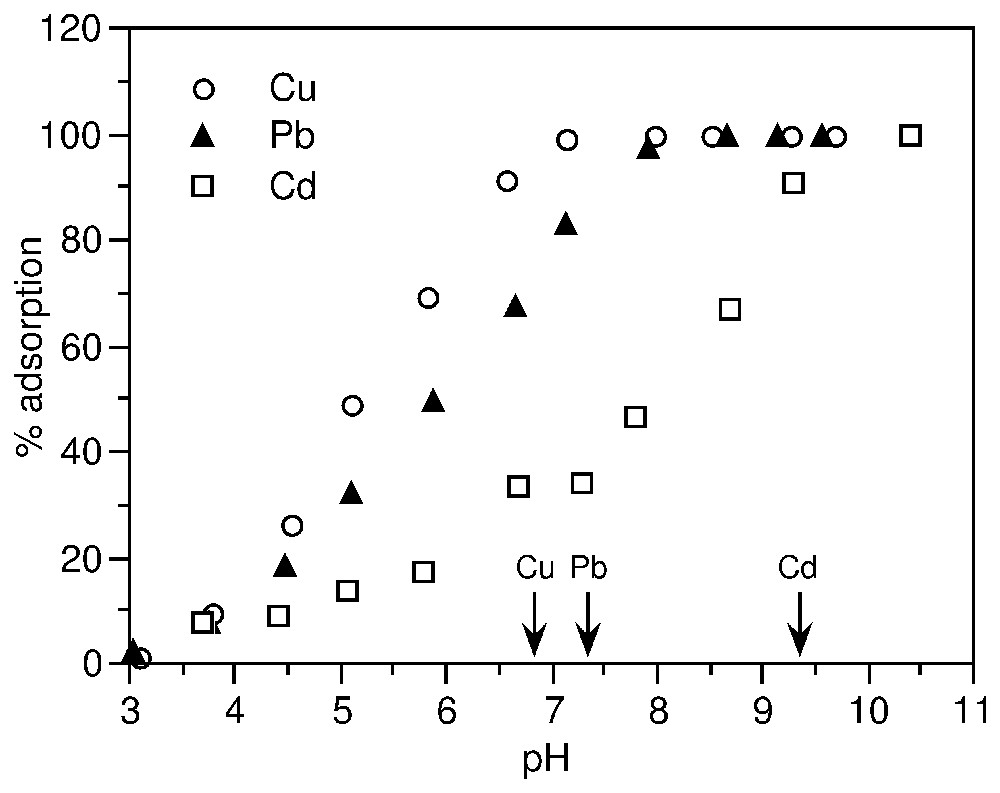
Adsorption edges of Cu2+, Pb2+ and Cd2+ (10−3 M) on synthetic goethite (after [63]). The arrows indicate the pH of hydrolysis of the metals.
Seuils d'adsorption de Cu2+, Pb2+ et Cd2+ (10−3 M) sur une gœthite de synthèse (d'après [63]). Les flèches indiquent le pH d'hydrolyse des métaux.
5.2 Modèles de complexation de surface
L'interaction chimique entre les groupes de surface chargés et les ions se traduit par la formation de complexes de surface (équations (9)–(12)). Les constantes intrinsèques sont calculées en prenant en compte le facteur coulombique et l'activité des espèces (équation (13)).
Les équations de complexation de surface sont combinées aux modèles électriques (Fig. 6). Le modèle à capacité constante (CCM) considère l'interface comme un condensateur [71]. Le modèle à couche diffuse (DLM) permet de rendre compte de l'influence de la force ionique sur la charge [43]. Le modèle de Stern (BSM) peut être considéré comme une combinaison des deux modèles précédents [76]. Enfin, le modèle à triple couche (TLM) intègre l'existence de complexes de surface de sphère externe et considère deux condensateurs en série. Le nombre croissant de plans caractéristiques introduits dans les modèles permet de rendre compte des conditions du milieu et des propriétés du solide, mais amène un nombre croissant de paramètres ajustables [55]. Par ailleurs, les courbes expérimentales utilisées pour la validation de ces modèles n'ont toujours pas une résolution suffisante pour permettre une discrimination univoque.
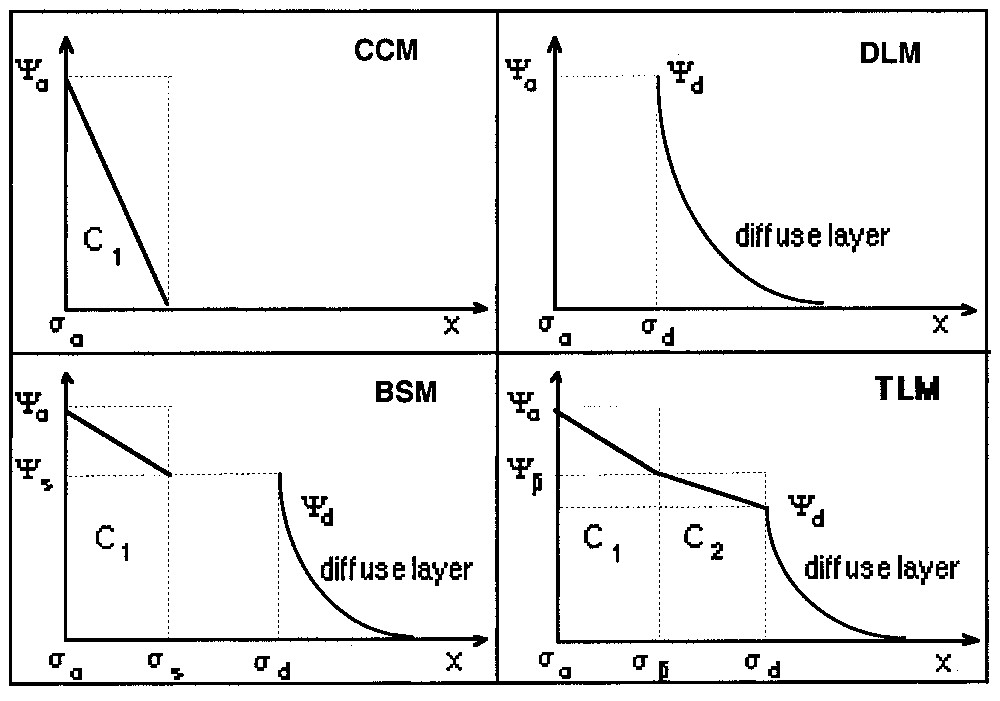
Schematic representation of the surface complexation models. CCM: Constant capacitance model; DLM: double layer model; BSM: basic Stern model; TLM: triple layer model. Notations are defined in the text.
Représentation schématique des modèles de complexation de surface. CCM : Modèle à capacité constante ; DLM : modèle à couche diffuse ; BSM : modèle de Stern ; TLM : modèle à triple couche. Les notations sont définies dans le texte.
5.3 Bilan des charges de surface
La quantification de la charge aux trois plans caractéristiques de la double couche (Fig. 7) permet non seulement une meilleure connaissance de l'interface solide–électrolyte, mais elle apporte aussi une contrainte forte dans les modèles théoriques [43,46,65].
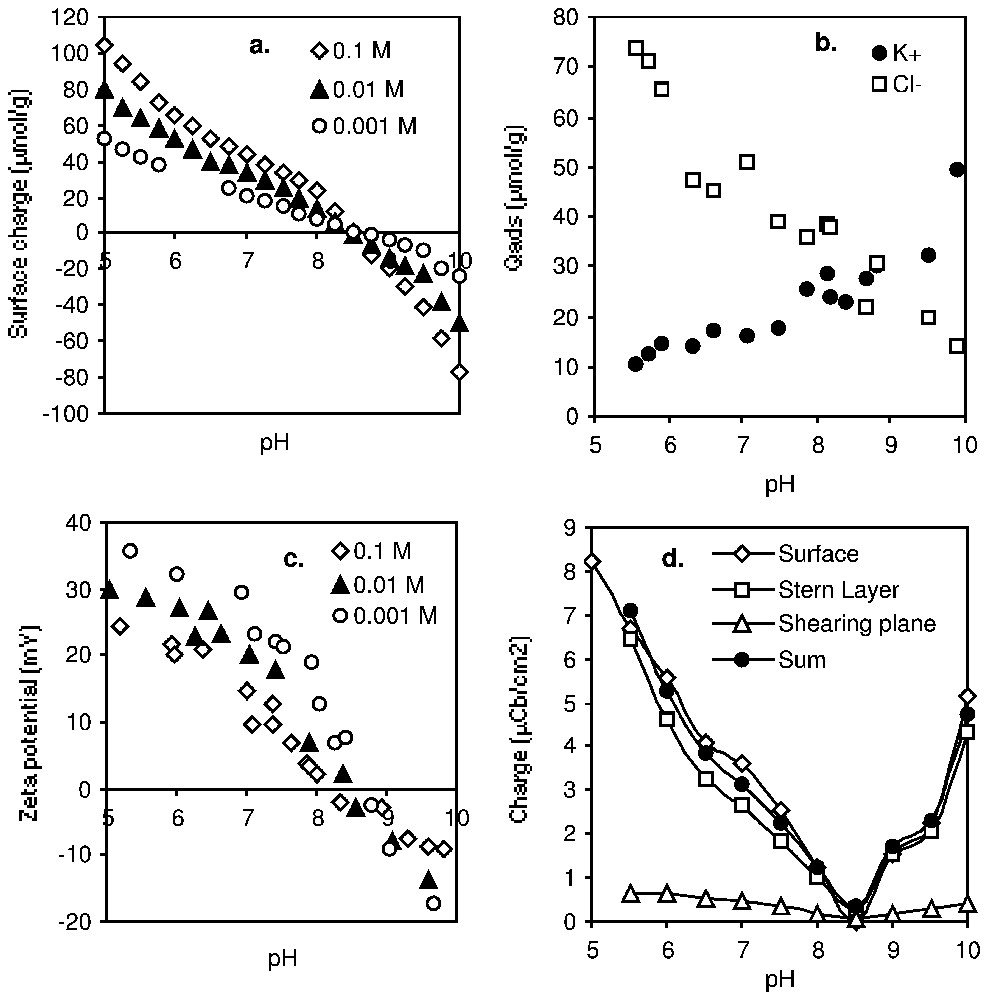
Charge at the characteristic planes of the EDL of δ-alumina (Degussa) versus pH and KCl concentration: (a) surface excess of H+ and OH−; (b) adsorption of counter-ions in 0.01 M KCl; (c) electrokinetic potential; (d) evolution of the charge (absolute value) and electroneutrality (σβ+σd=σ0) (after [82]).
Charge aux plans caractéristiques de la double couche d'une alumine δ (Degussa) en fonction du pH et de la concentration en KCl : (a) Excès de surface en H+ et OH− ; (b) adsorption de contre-ions dans KCl 0,01 M ; (c) potentiel électrocinétique ; (d) évolution de la charge (valeur absolue) et électroneutralité (σβ+σd=σ0) (d'après [82]).
6 Hétérogénéité de surface et double couche électrique
Ce n'est que dans les années 1980 que l'hétérogénéité énergétique des interfaces a été formellement prise en considération dans ce domaine. Le modèle le plus pertinent, MUSIC, a été proposé par Hiemstra et al. [40,41] sur la base de considérations cristallographiques et du principe de charge formelle de Pauling [62].
7 Distributions d'affinité protonique
La validation des modèles les plus récents a nécessité une évolution significative des méthodes expérimentales. Le concept de distribution d'affinité protonique, développé par Contescu et al. [23–26], permet une approche expérimentale de l'hétérogénéité à l'interface solide–électrolyte. Des développements dans ce domaine ont été récemment réalisés grâce au titrage potentiométrique haute résolution [63].
7.1 La procédure TDIS (Titration Derivative Isotherm Summation)
Le principe est celui développé pour l'adsorption des gaz [87–89]. Une courbe de titrage est considérée comme une isotherme d'adsorption de protons ou d'hydroxyles (selon le sens du titrage). L'interface est considérée comme composée de domaines indépendants, d'énergies différentes. La dérivée de l'isotherme expérimentale peut être analysée comme une somme d'isothermes dérivées théoriques locales d'adsorption sur les différents domaines énergétiques. L'isotherme locale utilisée est celle de Temkin, qui prend en compte les interactions latérales entre espèces adsorbées (équations (20) et (21)).
7.2 Application de la méthode TDIS : distributions d'affinité protonique sur l'anatase et la gœthite
Les courbes de titrage haute résolution de l'anatase et de la gœ thite (Fig. 8) sont caractérisées par des points de charge nulle situés respectivement à pH 5,7 et 6,8. Dans l'application de la méthode TDIS, les courbes d'adsorption d'ions hydroxo à 0,1 M d'électrolyte a été dérivée en fonction du pH. La distribution d'affinité ainsi obtenue est ajustée par une somme d'isothermes locales.
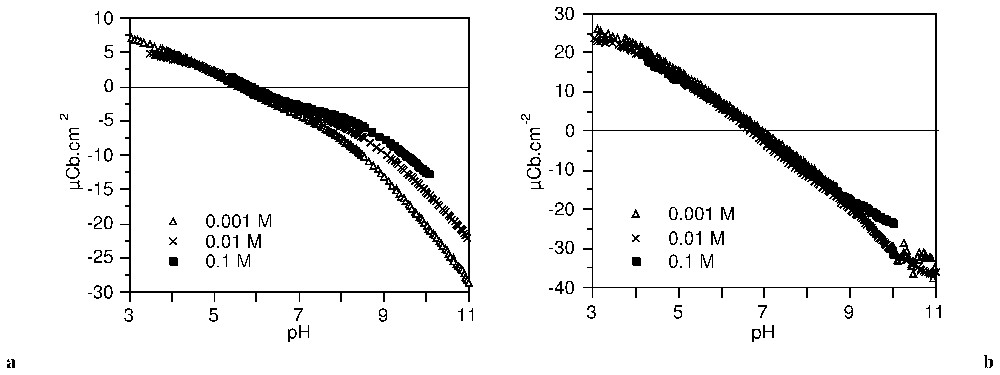
Surface charge density of anatase (a) and goethite (b) in NaClO4 (after [63]).
Densité de charge de surface sur l'anatase (a) et la gœthite (b) dans NaClO4 (d'après [63]).
La courbe dérivée pour l'anatase (Fig. 8) a été recomposée par 3 isothermes locales caractérisant 3 domaines centrés sur pK 5,2, 7,5 et 9,8. Une seule valeur correspond aux prédictions du modèle MUSIC : 5,3, −7,5 et 6,3 [41]. En revanche, l'analyse donnée par Ludwig et Schindler [53] se trouve entièrement confirmée par la Fig. 9. La distribution d'affinité sur la gœthite (Fig. 10) montre quatre modulations : trois domaines équivalents en quantité adsorbée à pK 4,5, 6,4 et 8,0 et une contribution majeure à pK 9,5. La confrontation de ces observations avec les prédictions successives du modèle MUSIC [40,41] ne permet d'attribuer que partiellement ces domaines.
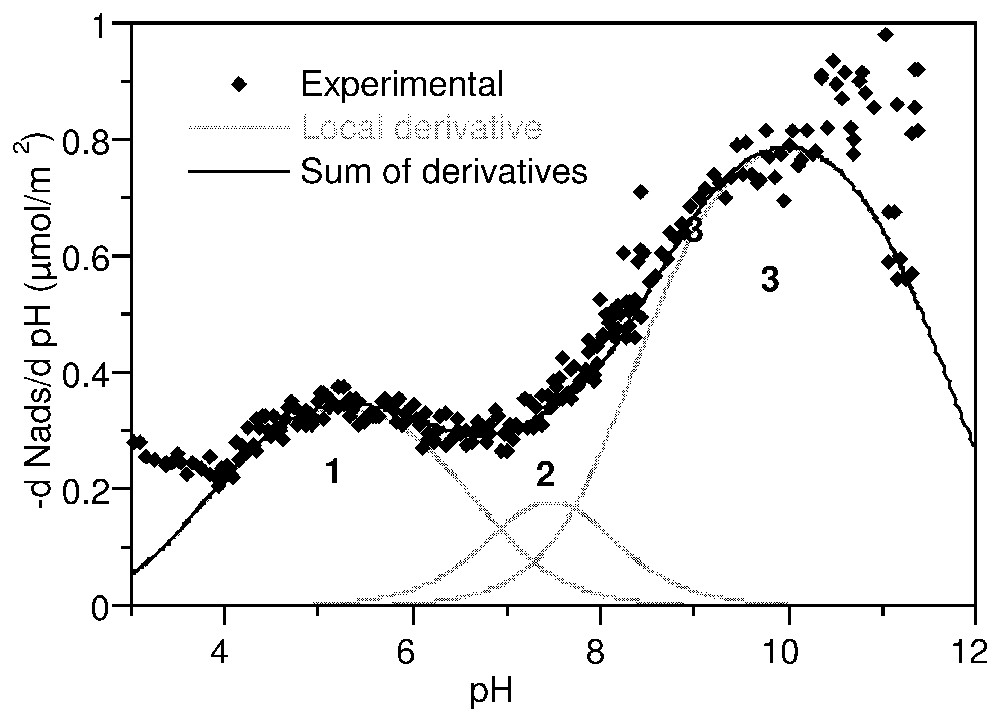
Proton affinity distribution on anatase in 0.1 M NaClO4, expressed as the derivative adsorption isotherm of OH− versus pH (after [63]).
Distribution d'affinité protonique sur l'anatase dans NaClO4 0,1 M, exprimée en dérivée de l'isotherme d'adsorption de OH− en fonction du pH (d'après [63]).
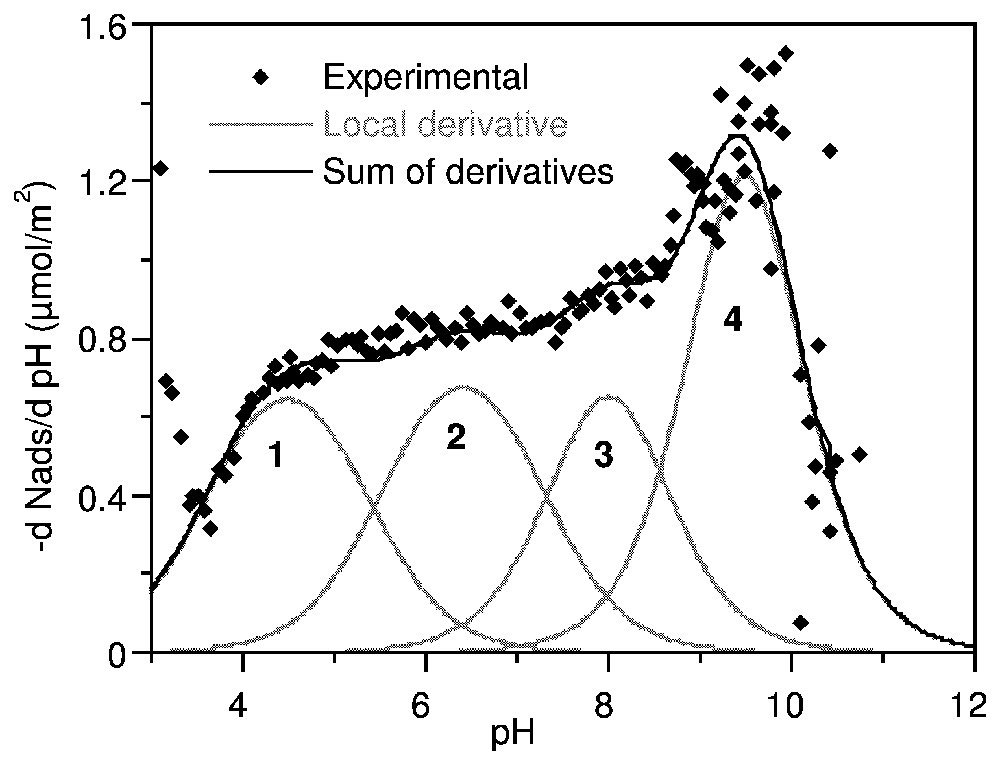
Proton affinity distribution on goethite in 0.1 M NaClO4, expressed as the derivative adsorption isotherm of OH− versus pH (after [63]).
Distribution d'affinité protonique sur la gœ thite dans NaClO4 0,1 M, exprimée en dérivée de l'isotherme d'adsorption de OH− en fonction du pH (d'après [63]).
Il n'existe donc pas d'attribution univoque des domaines énergétiques révélés par les distributions d'affinité uniquement à des faces cristallographiques. En effet, des fluctuations de composition ou de morphologie dans l'échantillon peuvent se traduire par des déplacements de bandes et des domaines énergétiques supplémentaires. Ces résultats montrent clairement la nécessité de prendre en compte l'hétérogénéité énergétique des surfaces dans les modèles de prédiction des équilibres géochimiques dans les milieux naturels.
8 Conclusion
La compréhension des mécanismes liés à l'existence d'une charge électrique à la surface des solides et de leurs conséquences sur les comportements macroscopiques de la matière divisée s'est bâtie par une évolution des théories et des méthodes expérimentales de plus en plus fines. La nécessaire prise en compte de l'hétérogénéité énergétique des solides est en voie de généralisation. Les nouveaux défis environnementaux, comme la maı̂trise de l'énergie, le stockage des déchets radioactifs ou industriels, comme les nanocomposites, rendent encore plus nécessaire la poursuite de la compréhension de ces phénomènes à l'échelle moléculaire. Pour cela, des informations locales doivent être obtenues au moyen de méthodes analytiques spécifiques. Des spectroscopies comme la microspectroscopie infrarouge, l'XPS, le Raman de champ proche, l'EXAFS sont particulièrement adaptées pour étudier la stœchiométrie et la structure des complexes locaux. Enfin, les derniers développements des techniques AFM devraient permettre de mesurer les forces interparticulaires locales.
1 Introduction
Electrical properties of the solid–water interface are a key feature for colloidal systems in aqueous media of environmental and technological significance. At the molecular level, the surface charge of colloidal particles induces adsorption of dissolved organic or inorganic ions, which influences their partitioning between solution and particulate matter. In natural media, adsorption controls the colloid-mediated dissemination of metallic or organic pollutants. Industrial applications of adsorption are common in many domains: for instance charged surface-active compounds are used at a very large scale as selective hydrophobing agents in the processes of froth flotation in metallic ore beneficiation. On the other hand, the use of the same surfactants in enhanced oil recovery is severely hindered by adsorption on the bedrocks. In both cases, accurate knowledge of the mechanisms and consequences of adsorption is required for proper technologic applications.
Electrostatic interparticle interactions control the stability of colloids, which is an important parameter for flow and sedimentation properties. Natural phenomena such as dissemination of atmospheric dust or aquatic suspended particles, colloidal behaviour of soils, sedimentation, colloid-mediated transport of solutes, are strongly dependent on electrical inter-particle interactions. Many industrial processes involving particulate matter take advantage of the charging properties of surfaces: formulation of paints, cosmetics, and composite materials. Environmentally important applications, such as water purification and waste water treatment, largely use coagulation-flocculation or filtration. In food industry, physical and gustative properties of aliments are inherently linked to proper stabilisation of the surface electrical properties of emulsions and macromolecules. Recent developments in pharmaceutical industry in controlled drug delivery are based on the use of charged colloids. In all these colloidal systems, properly controlling surface charging, surface complexation and electrostatic forces are of crucial economic and environmental importance.
The aim of the present paper is to show how major theoretical approaches and analytical methods allow investigation of these phenomena, and how industrial processes involving particulate matter can benefit from this knowledge.
2 Origin of the surface charge
In solid matter, strong coordinance bonds between the constituting atoms allow for cohesion in crystalline or amorphous lattices, but also result in decreased mobility of the atoms. Therefore, fluctuations in order or composition cannot be compensated by local rearrangements as it is the case in liquid or gaseous phase, where high mobility prevails. Such fluctuations are of three origins:
- • difference in stoichiometry between the surface and the bulk of the solid; this situation is encountered in systems such as Ag2S–water [33] or AgI–water [56], or in some trioctahedral phyllosilicates, in which edge structural cations are partially labile [92];
- • isomorphous substitutions in the crystalline lattice by ions with different valency; this is characteristic for zeolites [3] and many phyllosilicates in which substitution by cations of lower valency results in negative charge [12]; the opposite situation occurs in layered double hydroxides (LDH) which carry a net positive charge [32,57,66]; the resulting bulk charge determines an ion exchange capacity, which is independent of physicochemical conditions of the suspending medium [83,84];
- • incompletely saturated coordinances on the outermost atoms of the solid (a surface charge results from dissociation of water molecules on these coordinances); this type of surface charge is characteristic of metal oxides and salt minerals, and depends on the pH and ionic composition of the surrounding solution [61]; chemisorption and dissociation of water at the interface result in the formation of oxo and hydroxo groups, subjected to protonation–deprotonation reactions, which gives rise to an electric charge at the solid–water interface; charged surfaces exhibit amphoteric behaviour: with increasing pH, the sign of the charge is reversed from positive to negative; such a behaviour is characterised by the Point of Zero Charge (PZC), the pH at which the overall surface charge density equals zero.
3 Electrical properties of charged interfaces
3.1 The double-layer model
In the presence of an electrolyte solution, the surface charge is compensated by counter-ions from the solution. The spatial distribution of these counter-ions was historically first described using the formalism of electrical point charges. One of the very earliest models of charged interfaces is that of Helmholtz [39], in which the charged solid–electrolyte system is considered as a capacitor, the two plates of which being respectively the charged surface groups and the counter-ions accumulated at the interface. The plates are separated by a distance x and occur with a potential difference ΔΨ between them. The relation between the charge σ and the potential is given by the Helmholtz equation (1):
| (1) |
On the other hand, Gouy [35] and Chapman [19] considered that the counter-ions form a cloud around a charged particle, and described the spatial distribution of the potential on the basis of the Poisson–Boltzmann equation. In the case of a symmetrical electrolyte, the simplified equation for a flat interface is:
| (2) |
Inconsistencies in both above models were noted by Stern [76]. In the capacitor model, accumulation of the counter-ions as a rigid alignment is implausible because of thermal agitation, whereas the ion concentrations near the interface predicted by the Gouy–Chapman theory are unrealistically high if ions are no longer considered as point charges.
Therefore, Stern, and later Grahame [36], combined both models into the double-layer model (DLM), which is still recognised. It includes two layers of counter-ions compensating the surface charge σ0 (Fig. 1). Counter-ions interacting with surface groups by inner-sphere or outer-sphere complexation are immobilised on the surface and form the so-called Stern layer. The characteristic plane of the Stern layer is the mid-plane passing through the centre of the counter-ions, and is called the Inner Helmholtz Plane (IHP); the charge at the IHP is noted σβ. Several other planes may be defined within the Stern layer, according to the size of the counter-ions and the type of formed complex [27,28]. Beyond the Stern layer is located the Outer Helmholtz Plane (OHP) which carries the charge σd, the part of the surface charge which is not compensated by the ions in the Stern layer. Complete cancellation of the surface charge by Stern layer counter-ions is generally not achieved, due to electrostatic repulsion between ions, excepted in the case of inner-sphere complexes with multivalent ions or high electrolyte concentration. The charge at the OHP then electrostatically attracts a cloud of mobile counter-ions, which form the so-called diffuse layer, in which the potential decrease with distance is described by the Boltzmann equation (equation (2)).
3.2 The electrokinetic potential and the hydrodynamic shear plane
The electrokinetic potential – or ζ potential – is measured when a relative motion between the particles and the water is created using a mechanical flow (streaming potential) or an electric field (electrophoresis, electro-osmosis). The plane of the ζ potential is the hydrodynamic shear plane, which is identified with the OHP in order to calculate the value of σd from the ζ potential using the Gouy–Chapman equation (see equation (5) for symbols):
| (3) |
The measurement of the ζ potential is of great importance, for instance in the domain of metal ore beneficiation by the flotation process. Selective hydrophobation by surfactants is achieved by accurate knowledge of the surface charge. Fig. 2 shows that the flotation yield of ZrSiO2 is optimal with ionic surfactants whose charge is opposite to that of the surface [14]. The actual flotation conditions can then be chosen to be selective with respect to other minerals.
Whether the OHP coincides with the shear plane was answered by experimental evidences. Immersion microcalorimetry and 1H NMR [16,34] demonstrates that two to three water layers are strongly structured by the solid surface. Beyond this structured domain of approximately 1 nm thickness, water molecules possess bulk properties. Such physical discontinuity in water molecules structuring could be the location of the shear plane, and then coincide with the OHP. As a consequence, the hydrodynamic shear plane may be at quite fixed distance from the surface, and not at a distance depending on ion concentration. Experiments with adsorbed macromolecules tend to support this hypothesis [10]. The ζ potential of montmorillonite on which uncharged polyacrylamide is adsorbed progressively vanishes from −50 to 0 mV, according to the molecular weight and adsorbed amount of the macromolecules. Although the surface charge is not altered by interaction with polyacrylamide, the shear plane is moved away from its initial position towards the solution, according to the thickness of the adsorbed layer, i.e., the extension of loops and trains of the adsorbed macromolecules, which was measured by 13C NMR.
Such results bear important consequences as far as colloidal dispersions are concerned. In concentrated pulps or gels, most of the water has a bulk activity coefficient, and the proportion of ‘bound’ water is very small. This is an important factor in dewatering and drying processes. Sludge generally contains few grams per litre of solid matter, and the amount of bound water, quantified by dilatometry or differential thermal analysis, represents between one to four times the dry matter, the vast majority being mechanically retained within the aggregate or gel structure of the sludge [22,74].
3.3 The diffuse layer and interparticle interactions
The interparticle interactions are described by the Derjaguin, Landau, Verwey and Overbeek (DLVO) theory [30,86]. The theory is based on competition between two opposite contributions, an attractive Van der Waals force and a repulsive double layer force. Van der Waals interactions are non-covalent and non-electrostatic forces: universal dispersion (or London) interactions, permanent dipole–dipole (orientation) interactions, and dipole–induced dipole (induction) interactions. Non-DLVO forces should also be considered, such as the osmotic pressure, which originates from overlapping of the ion clouds around approaching interfaces [75]. These forces are significant at high ion concentration (or low water content) and strongly depend on the hydration properties of ions.
The Van der Waals force decays as 1/r6, where r is the separation between interacting surfaces. The repulsive double layer force, described by the Poisson–Boltzmann equation, decays as , where κ is the Debye length, and thus its profile strongly depends on the pH, ionic strength, ion valency, and surface charge density. The distance of closest approach between two charged surfaces is then governed by the physicochemical conditions in solution, via the double layer force.
The electrokinetic potential appears therefore as a key parameter for understanding and predicting the stability and flow behaviour of colloidal systems. This is illustrated in Fig. 3: at the Iso-Electric Point (IEP), where the ζ potential takes zero value, the supernatant of a TiO2 suspension is cleared from particles [21], and the yield stress of an alumina suspension is at maximum [47]. These observations result from coagulation of the suspensions when repulsive interparticle forces are screened by counter-ions. The drinking water process makes use of coagulants and flocculants that act by cancellation of the surface charge of natural colloids, and by bridging between particles. Aluminium salts are the most used in this industry, and their ability as coagulants and/or flocculants is adapted to the type of water to be treated by an accurate control of their hydrolysis prior to use [9]. Microbial adhesion to solid surfaces in aquatic media was also shown to be sensitive to electrostatic repulsion, which significantly retards the initial steps of surface colonisation [2].
4 Measuring and modelling the surface charge
4.1 Surface titration
The primary charge σ0 is determined from the adsorption of so-called potential-determining ions (PDI) H+ and OH− measured by potentiometric titration. The charge σ0 is calculated from the amount Q of PDI adsorbed:
| (4) |
A wide majority of the published titration curves were obtained with a limited number of oxides: TiO2 polymorphs anatase and rutile, aluminium (oxy) hydroxides ranging from hydroxides, mainly gibbsite γ–Al(OH)3 to corundum α–Al2O3, iron oxide hematite α–Fe2O3 or oxi-hydroxides goethite α–FeOOH, crystalline or amorphous SiO2, quartz and silica, respectively, and, more rarely, silicates. As a matter of fact, accurate experimental measurements require that the studied solid possesses several essential properties. The size and texture of the solid particles must be such as the surface area is high (above ) in order to produce significant surface consumption of protons or counter-ions, but devoid of porosity in order to minimise diffusion of soluble species. The studied solid must be sparingly soluble in aqueous medium in order to neglect consumption of protons and hydroxo ions from dissolution. Such requirements compel some limitation on the variety of solids that can be investigated for their surface charge.
4.2 Surface charging models
Thermodynamic parameters such as dissociation constants are derived from the titration curves. To that purpose pH dependent protonation–deprotonation equilibria of surface charging are expressed using the mass action law. Two types of approaches can be followed:
- • a global approach developed by Parks [60,61], Davis and co-workers [27–29], and Stumm and co-workers [77,78], accounting for the overall amphoteric property of charged surfaces:
(5)
where SO expresses a surface group composed of a metal ion linked to the solid lattice and an oxygen atom, and the subscript ‘s’ denotes the surface localisation of the species; this approach is commonly referred to the 2-pK model; the PZC is defined as ); it has been widely shown to model most of the titration curves obtained on metal oxides;(6) - • a local approach considering real individual charge on surface groups.
Pauling's concept of formal bond valency was applied [11,62,91] in order to take into account the mono-, di- and tri-coordinated character of the outermost surface oxo- and hydroxo-groups on the different crystal planes. Based on this principle, Hiemstra and co-workers [40,41] developed the Multi-Site Complexation (MUSIC) model. The proton affinity of a given surface group can be calculated from the summation of all valences of the bonds with underlying metal atoms. The formal valency of an ion is the ratio between its charge and its coordination number. It represents the level at which the charge of an ion is compensated by chemical bonds within a lattice. Surface oxo or hydroxo groups of metal oxides are mainly mono-, di- or tri-coordinated, and exhibit then a partial charge [7,85]. Charging of such surface sites then reduces to mere protonation–deprotonation of a monofunctional surface group:
| (7) |
4.3 Predicting the position of the PZC
Independently of surface charging models, there is a wide concern about the position of the Point of Zero Charge, the pH of charge reversal, where the colloidal behaviour of dispersed particles dramatically changes. If one refers to the successive models predicting the position of the PZC of metal oxides, it appears that three properties of the solid array were basically investigated. First, it has been shown that the value of the PZC is negatively correlated to intrinsic properties of the metal atom, such as ionisation potential or electronegativity [13,80]. Then, following Pauling's concept of formal bond valence [62], atomic distance parameters were combined with the charging properties of the metal ion to predict the position of the PZC of oxides. Parks [60] calculated the Z/R ratio with Z the ionic charge and R the distance parameter ( with ro and r+ the ionic radii of oxygen and metal). He found that the PZC of oxides is as higher as Z/R is lower. Further improvements concerned essentially the distance parameter. Yoon et al. [91] improved the model by using mean metal–oxygen distances instead of ionic radii. Such approach was also applied to amorphous and heterogeneous solids [13]. Bleam [6] proposed to use the Pauling bond valence s=Z/ν (with ν the coordination number of the metal) instead of Z/R, and improved the linear correlation with the PZC of oxides. Further refinement in lattice parameters was brought by Hiemstra et al. [40–42], using the metal–proton distance instead of the metal–oxygen distance as the distance parameter. Finally, Healy et al. [38] established a correlation between the PZC and the ability of the electrostatic field of the solid lattice to polarise and dissociate water molecules at the interface. They calculated the electrostatic field strength using as a lattice parameter the cation–anion spacing, and as a surface parameter the adsorbate–adsorbent ionic distance. They showed that the PZC of oxides is as higher as the interatomic distance decreases, which is in accordance with the results of the above models.
In silicates, a clear relationship between the crystallo-chemical properties and the position of the PZC, measured by electrophoresis in an indifferent electrolyte was observed (Fig. 4). This relationship is explained by the relative abundance and coordinance of metal cations versus oxygen atoms of the SiO4 tetrahedra on the cleavage planes [14,15]: the higher the valence and the lower the coordinance of the cations, the higher is the PZC.
5 Measuring and modelling surface complexation
5.1 Ion adsorption
The charge of the Stern layer σβ where counter-ions are complexed to surface sites (in the case of outer sphere complexes) is usually measured from ion adsorption isotherms, called adsorption edges in the case of hydrolysable metal ions. The charge σβ is calculated from the amount Q of counter-ions adsorbed:
| (8) |
Fig. 5 exemplifies adsorption edges of Cu2+, Pb2+ and Cd2+ on goethite. The relative positions of the edges show that there is a correlation between the tendency to form complexes on solid surface and to form hydroxo-complexes in solution; the slope of the edge corresponds to the affinity of the metal ion for the surface [63,73].
5.2 Surface complexation models
The interaction between charged sites and ions from the electrolyte solution (anions A− and cations C+) results in formation of surface complexes:
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
Surface complexation models (Fig. 6) combine these thermodynamic equilibria with the equations of the electrical theories (equations (1) and (2)). The constant capacitance model (CCM) was developed by Schindler and co-workers [71,72] for the study of the adsorption of metals ions in low ionic strength medium. In this simplified model, the inner-sphere complexed metal ions can be assimilated to a capacitor plate. The capacitance is then constant for a given ionic strength. The use of the CCM requires several parameters: dissociation–complexation constants, capacitance C, and site density. These parameters are conditional parameters [37], since they depend on experimental conditions.
Stumm and co-workers [43,77,78] developed the diffuse layer model (DLM) to account for variations in complexed amounts with the ionic strength. The interface is located at the OHP. This model does not need a capacitance to be defined. It can also be used to compute intrinsic constants by extrapolation of the results to zero ionic strength [27].
The combination between the above two models results in the basic Stern model (BSM), which can be considered as a generalised model. For high ionic strength, it reduces to the CCM, for low ionic strength or low surface potential it reduces to the DLM. A further refinement to the BSM was brought by Yates et al. [90] and Davis et al. [27–29] by considering external sphere complexes. This approach leads to the Triple Layer Model (TLM), and requires two capacitances (C1 and C2 in Fig. 6) to be defined in addition to the other parameters. Recently, a four-layer model was proposed in order to account for different positions of cations and anions in the Stern layer [20].
A thermodynamic approach has been proposed first by James and Healy [44,45] considering the free energy of adsorption as the sum of coulombic, chemical and solvation free energy. The importance of the solvation term lies in its prediction of a ‘solvation barrier’, which is greater as the charge of the sorbing ion increases. Sverjensky [79] combined the solvation theory with crystal chemistry to predict intrinsic protonation constants.
According to the number of characteristic planes taken into account, these models progressively took into account the characteristics of the medium and of the solid surface. However, they introduced an increasing number of arbitrary parameters. For instance, the TLM requires seven parameters: two dissociation constants, two complexation constants, two capacitances, and the site density [55]. Also, it must be recognised that almost any of these models is in fact able to fit reasonably well experimental data. This can be attributed to the poor resolution of conventional titration, ion adsorption or ζ potential experimental data: generally 1 or 2 points per pH unit. Validation of one selected model can only be improved by increasing resolution and accuracy of experimental data.
5.3 Surface charge balance
The electroneutrality of the system requires that σ0+σβ+σd=0. As an example, Fig. 7 shows the experimental data recorded for a δ-alumina sample (Degussa) [81,82]. Quantification of the charge at the three characteristic planes of the EDL is important, not only for a better knowledge of the solid–electrolyte interface, but also to validate theoretical approaches [43,46,65].
6 Surface heterogeneity and the EDL
Non-uniformity of the charge at the solid–electrolyte interface was first postulated by Kruyt [54]. More formal description of surface heterogeneity was initiated by Davis and Leckie [27,28] and Benjamin and Leckie [4], who suggested that differently coordinated surface groups should be taken into account in surface complexation models. It appeared since the mid-1980's that modelling the surface charge on real solids, which are in fact complex and heterogeneous, requires more adequate models. Among the models that appeared in that period, Cernik et al. [18] distinguished mechanistic and empirical binding models.
Mechanistic models imply the knowledge of the underlying molecular binding mechanism. Crystallographic considerations clearly indicate that site density and local charge are characteristic of a given crystal plane. In the case of goethite, the contributions of different planes have thus been identified by Evans et al. [31]. Such considerations were generalised in the MUSIC (MUlti SIte Complexation) model, developed by Hiemstra et al. [40,41]. The principle is based on the calculation of site densities and coordinations on the most probable crystal planes, and on the application of Pauling's formal charge principle. It allowed for predicting the pK and PZC of most metal (oxi-hydr)oxides. The major contribution of the MUSIC model was to show that various faces of a metal oxide crystal bear differently coordinated hydroxyles, which results in energetic heterogeneity at the solid–solution interface.
However, heterogeneity may also originate from disordered crystal lattices, imperfections in crystal planes, or local and chemical impurities, which is the case of most of the natural solids [59]. Empirical models, based on experimental data, are then requested [18]. Surface heterogeneity can be theoretically modelled from two fundamental types: random heterogeneity and patchwise heterogeneity [17,64,70]. Random heterogeneity occurs when different types of dissociable functions are available on the surface. Patchwise heterogeneity is related to defined crystal planes; if these are large enough, boundary interactions can be neglected, and no interactions between patches have to be considered; if the patches are small, boundary effects make the system tend towards random heterogeneity.
Charging equilibria on individual domains can basically be described by the 1-pK equilibrium:
| (14) |
| (15) |
| (16) |
Theories considering random heterogeneity are also based on the Langmuir isotherm, as for example the approach of Rudzinski and co-workers [67–69], which combines 2-pK equilibria, the Langmuir equation, and correlation between surface energies. Random-type surface heterogeneity was also described by analogy with the titration of polyelectrolyte macromolecules (humic acids or synthetic polyelectrolytes), considering successive monoprotic dissociations [8,11,58]. These authors use the Bragg–Williams mean-field approximation to calculate the strength of the mean energy of pair interactions due to the vicinity of ionic functions in macromolecules.
7 Proton affinity distributions (PADs)
Despite significant progress made in the last two decades in realistic theoretical description of surface charging, validation of the predicted results is still based on previously obtained experimental data, which were already used to validate simpler models. There is yet a need for new experimental approaches explicitly addressing surface heterogeneity. Only few attempts have been published so far to improve the resolution of experimental data. For instance, Kinniburgh et al. [48] constructed an automatic titrator able to deliver 20 to 30 titration points per pH unit. On the other hand, Contescu et al. [1,23–26] developed the concept of proton affinity spectra, which is based on the following considerations. A titration curve is in fact an adsorption isotherm of protons or hydroxo ions (according to the direction of titration, respectively basic-to-acid or acid-to-basic). Titration curves can then be converted into pK spectra by derivation, and decomposed into local derivative isotherms. The parameters revealed by the decomposition are then used to generate linear combinations of Langmuir-type isotherms. This procedure often requires smoothing of the experimental titration points by a spline function because of the low density of titration data, generally less than 10 points per unit pH [26]. Significant improvement was recently achieved in the determination of proton affinity distributions using high-resolution titration curves [63].
7.1 The TDIS procedure
The principle is that of the derivative isotherm summation (DIS) method developed for gas adsorption by Villiéras et al. [87–89]. It consists in analysing the derivative of the titration curve, which features different domains of characteristic proton affinity. The experimental derivative isotherm can then be fitted by a linear combination of theoretical local derivative charging equations. Therefore this method is referred to as the titration derivative isotherm summation (TDIS) method. The derivative of the Langmuir-type (equation (16)) is used:
| (17) |
| (18) |
| (19) |
It has also been shown that the gaussian term m may also express cooperative effect due to lateral interactions between adsorbed species [51]. However, lateral interactions are better described by the Temkin isotherm. With (ω is the lateral interaction), this equation is:
| (20) |
| (21) |
The parameters of the local derivative isotherms are then used to generate linear combinations of Langmuir or Temkin-type isotherms (equations (17) and (21)). The maximum of such curves is the pK of the local charging equilibrium, the area of the derivative curve corresponds to the proportion of charged groups, and the broadening represents the energy dispersion on the considered patch, and/or the energy of the lateral interactions.
7.2 Application of the TDIS method: proton affinity distributions on anatase and goethite
The high resolution charging curves on anatase and goethite at three background electrolyte concentrations (NaClO4) are shown in Fig. 8. They are characterised by the common intersection point which defines the PZC, respectively at pH=5.7 for anatase and 6.8 for goethite. It can be seen that the charging curves at various ionic strengths on goethite are not significantly different compared to those on anatase. This may be attributed to relatively low influence of counter-ions on the protonation–deprotonation of surface sites of goethite.
Each one of the curves in Fig. 8 can be considered as a hydroxo ion adsorption isotherm. In the present application of the TDIS method, the isotherms for the 0.1 M electrolyte were derived according to pH and fitted with a sum of local theoretical derivative adsorption isotherms (equation (21)).
The derivative curve for anatase (Fig. 9) was fitted with three local isotherms featuring three energetic domains centred at pK 5.2, 7.5 and 9.8, respectively. This distribution is in agreement with that determined in similar conditions by Contescu et al. [26]. However, it fits only to one of the pK values predicted by the MUSIC model: −7.5, 5.3 and 6.3, corresponding to tridentate oxo- (Ti3O), bidentate oxo (Ti2O), and monodentate hydroxo (TiOH) groups on the 110 plane [41]. Better agreement is found with the scheme proposed by Ludwig and Schindler [53] from the metal adsorption behaviour of anatase: pK=5.40, 7.75 and 9.46.
The affinity distribution curve on goethite displayed four modulations between pH 3 and 10.5 (Fig. 10). The energetic domains identified using the TDIS procedure were three domains approximately equivalent in adsorbed amount at pK 4.5, 6.4 and 8.0, respectively, and a major contribution at pK 9.5. Analysis by the MUSIC model [40,41] predicted four proton binding groups: bidentate oxo (Fe2O) at pK−0.1, bidentate hydroxo (Fe2OH) and pK 13.7, tridentate oxo (Fe3O) at pK 4.3 and monodentate hydroxo (FeOH) at pK 10.7. Again, the correspondence between measured and predicted values is very poor. This clearly shows that predictions made from perfect crystal structures can only give indications for the attribution of the energetic domains identified on PADs. Chemical and morphological fluctuations result in shifted protonation constants and in additional energetic domains. These results clearly show that energetic surface heterogeneity must be taken into account in the models of geochemical equilibria in natural media.
8 Conclusion
Understanding the mechanisms induced by the existence of a surface charge and the consequences on macroscopic behaviour of particulate matter was built on increasingly refined theories and experimental methods. It is also necessary to take into account the surface energetic heterogeneity of real solids, and to modify the existing theories accordingly. New challenges in the environmental domain such as the deposit of nuclear waste or energy saving, or in industrial processes such as nanocomposites, require further evolution of understanding towards the molecular scale.
Experimentally, information at local scale should be obtained from specific analytical tools. Spectroscopies such as IR microspectroscopy, XPS, near-field Raman spectroscopy, or EXAFS should allow describing the local stoichiometry and structure of surface complexes. Local energy distributions can be probed thanks to recent developments of AFM techniques.



