Understanding solubilisation using principles of surfactant self-assembly as geometrical constraints

Fabienne Testard; Thomas Zemb

doi:10.1016/S1631-0713(02)01803-5

Understanding solubilisation using principles of surfactant self-assembly as geometrical constraints
[Compréhension de la solubilisation par utilisation des principes d'auto-association des tensioactifs à partir des contraintes géometriques]

Fabienne Testard ¹ ; Thomas Zemb ¹

¹ Service de chimie moléculaire, DSM/DRECAM, CEA Saclay, Bât. 125, 91191 Gif-sur-Yvette, France

Comptes Rendus. Géoscience, Volume 334 (2002) no. 9, pp. 649-663.

Résumés

Anglais
Français

Our aim is to give a short introduction of the use of phase diagrams in order to rationalise general principles of surfactant self-assembly. These can be rationalised in terms of geometrical constraints: volume, surface and curvature. Binary (two components: surfactant and water) and ternary systems (surfactants, water, oil) are considered separately. Models for solubilisation, to be understood within the general principles and not as tabulated data, are presented. Finally, some examples of application of solubilisation in formulation are given.

Cet article présente une synthèse des principes généraux de l'auto-association des tensioactifs à partir des contraintes géométriques : surface, volume et courbures des hétérogénéités polaires/apolaires se formant spontanément. Les tensioactifs permettent de solubiliser dans un milieu des composés a priori insolubles. Les principes généraux sont présentés dans le but de donner une vue d'ensemble unifiée des diagrammes de phases binaires (deux composants : tensioactifs et eau ) et ternaires (tensioactifs, eau, huile). Ces mêmes principes généraux de l'auto-association des tensioactifs permettent d'établir des modèles prédictifs pour la solubilisation de composés dans des systèmes binaires ou ternaires.

Métadonnées

Reçu le : 2001-11-16
Accepté le : 2002-05-22
Publié le : 2002-01-01

DOI : 10.1016/S1631-0713(02)01803-5

Keywords: curvature, phase diagram, surfactant, solubilisation, formulation
Mot clés : courbure, diagramme de phase, tensioactifs, solubilisation, formulation

Affiliations des auteurs :

Fabienne Testard ¹ ; Thomas Zemb ¹

¹ Service de chimie moléculaire, DSM/DRECAM, CEA Saclay, Bât. 125, 91191 Gif-sur-Yvette, France

@article{CRGEOS_2002__334_9_649_0,
     author = {Fabienne Testard and Thomas Zemb},
     title = {Understanding solubilisation using principles of surfactant self-assembly as geometrical constraints},
     journal = {Comptes Rendus. G\'eoscience},
     pages = {649--663},
     publisher = {Elsevier},
     volume = {334},
     number = {9},
     year = {2002},
     doi = {10.1016/S1631-0713(02)01803-5},
     language = {en},
}

TY  - JOUR
AU  - Fabienne Testard
AU  - Thomas Zemb
TI  - Understanding solubilisation using principles of surfactant self-assembly as geometrical constraints
JO  - Comptes Rendus. Géoscience
PY  - 2002
SP  - 649
EP  - 663
VL  - 334
IS  - 9
PB  - Elsevier
DO  - 10.1016/S1631-0713(02)01803-5
LA  - en
ID  - CRGEOS_2002__334_9_649_0
ER  -

%0 Journal Article
%A Fabienne Testard
%A Thomas Zemb
%T Understanding solubilisation using principles of surfactant self-assembly as geometrical constraints
%J Comptes Rendus. Géoscience
%D 2002
%P 649-663
%V 334
%N 9
%I Elsevier
%R 10.1016/S1631-0713(02)01803-5
%G en
%F CRGEOS_2002__334_9_649_0

Fabienne Testard; Thomas Zemb. Understanding solubilisation using principles of surfactant self-assembly as geometrical constraints. Comptes Rendus. Géoscience, Volume 334 (2002) no. 9, pp. 649-663. doi : 10.1016/S1631-0713(02)01803-5. https://comptes-rendus.academie-sciences.fr/geoscience/articles/10.1016/S1631-0713(02)01803-5/

Version originale du texte intégral

Version abrégée

La solubilisation est le mécanisme général qui permet d'obtenir une solution homogène contenant de faibles concentrations d'une molécule « peu ou pas soluble » dans un solvant donné. Ainsi, la solubilisation permet de mettre en solution aqueuse des molécules « hydrophobes », telles des principes actifs médicamenteux, ou de mettre en solution dans l'huile des additifs « hydrophiles ». Augmenter et contrôler la solubilisation est un problème quotidien posé au formulateur, aussi bien dans l'industrie pharmaceutique, cosmétique, agroalimentaire que pétrochimique ou minière. Dans la formulation des peintures, des gels photographiques, des revêtements routiers ou des détergents liquides, le problème est souvent d'augmenter les quantités de solutés sans risquer l'instabilité de la solution formulée, qui contient plusieurs solutés peu solubles en coexistence. Industriellement, il existe trois méthodes générales de solubilisation :

– recourir à une émulsion, en dispersant une phase « huile » ou « eau » minoritaire qui permet une bonne solubilisation des solutés ;
recourir à des molécules dites « hydrotropes » (ces familles de molécules ne forment pas de systèmes moléculaires auto-organisés et augmentent la solubilité observée d'une molécule donnée ; on parle alors de « synergie », car la théorie des solutions régulières ne s'applique pas – les mécanismes moléculaires correspondants sont mal connus –) ;
recourir à des tensioactifs, qui forment des systèmes moléculaires organisés (micelles – directes ou inverses – cristaux liquides ou microémulsions).

L'article présenté ici a pour but de faire le point sur les compréhensions modernes et quantitatives qui concernent la troisième méthode, c'est-à-dire sur le recours à des systèmes moléculaires organisés à base de tensioactifs, aussi appelés surfactants. Cependant, les principes d'auto-assemblage s'appliquent à toutes molécules actives de surface qui forment en elles-mêmes par association un film (monocouche) de surface et de volume déterminés. La même méthodologie pourrait être utilisée pour traiter les surfactants, les lipides naturels ou de synthèse, les protéines actives de surface, les petits polymères auto-associatifs.

À l'équilibre thermodynamique – en évitant les problèmes de sursaturation – une des manières de quantifier la solubilisation est de déterminer la solubilité maximale ; c'est-à-dire la concentration maximale atteinte dans un fluide complexe homogène lorsque celui-ci est en équilibre avec un soluté en excès, solide ou liquide. Considérons, pour fixer les idées, un fluide complexe qui contient de l'eau, de l'huile et un soluté peu soluble dans l'eau. Connaissant la solubilité maximale du soluté dans l'huile et la fraction de volume d'huile dans le système moléculaire organisé final, on peut calculer de manière triviale, par simple proportionnalité, la solubilité maximale attendue. Or, expérimentalement, une solubilité supplémentaire – très importante pour les applications industrielles – est observée. On parle alors « d'excès de solubilisation ». Cet excès de solubilisation est exprimé sous forme de rapport molaire (λ) entre le soluté solubilisé en excès par rapport aux phases continues et la concentration molaire de tensioactif utilisé dans la formulation. Les molécules de cet « excès de solubilisation » peuvent être considérées comme adsorbées sur le film de tensioactif. Il y a ici des analogies profondes entre la solubilisation dans des microémulsions et l'adsorption de tensioactifs sur des particules minérales : on traitera d'adsorption progressive de solutés sur des films de tensioactifs, comme d'adsorption de tensioactifs sur des surfaces de particules d'argile. Le problème revient à déterminer des « isothermes » d'adsorption d'un soluté sur une surface d'accueil, qui, dans le cas des tensioactifs, est flexible.

Les surfaces de tensioactifs sont classiquement divisées en deux catégories :

– les tensioactifs ioniques, dont les têtes polaires sont dissociables ;
– les tensioactifs non ioniques, dont les têtes polaires ne portent pas de charges électriques, mais un grand nombre de molécules d'eau fortement liées aux têtes polaires.

Il est important de considérer la déformabilité du film pour les études de solubilisation. Les films flexibles, caractérisés par des constantes élastiques de l'ordre de $k T$ , peuvent être facilement déformés sous l'effet des fluctuations thermiques. Les films rigides ne peuvent être déformés par les fluctuations thermiques : la contrainte dominante est la contrainte de courbure. Dans les deux cas, la notion importante est la notion de courbure spontanée du film. Mathématiquement, la courbure est facilement exprimable sous forme de courbure moyenne et gaussienne. Physiquement, pour un film non déchirable de tensioactifs, il existe une relation générale et importante, dite « de couverture » entre courbure gaussienne K₀ et courbure moyenne H₀ :

P_{0} = 1 - H_{0} ℓ + \frac{1}{3} K_{0} ℓ^{2}

où ℓ est l'épaisseur du film. Le paramètre d'empilement P₀, ou paramètre de courbure spontanée, est un scalaire qui caractérise très généralement un film de tensioactif. Ce paramètre unifie les notions de courbure spontanée et est à la base moléculaire des échelles empiriques de type « HLB » ou dérivées. La différence entre le paramètre d'empilement spontané P₀ et le paramètre P imposé, lorsque le système moléculaire organisé est formé, est l'énergie libre de formation de micelles ou de microémulsions. Cette démarche permet d'unifier la compréhension des systèmes à base de tensioactifs, aussi bien dans les systèmes binaires tensioactif–eau que ternaires huile–eau–tensioactif.

Pour une composition donnée, tout système moléculaire organisé à base tensioactif est donc caractérisé par trois quantités :

– la surface spécifique Σ, qui est la somme des surfaces par tête et par unité de volume ; sa valeur est imposée par la concentration, car les films de tensioactifs ne sont pas étirables dans le sens latéral ; la surface par tête peut aussi être mesurée par diffusion de rayonnement (X ou neutrons), en considérant le comportement asymptotique des petits angles vers les grands angles de diffusion (limite dite de « Porod ») ;
– les fractions de volumes « hydrophiles » et « hydrophobes » présents, ces volumes étant imposés par les volumes molaires ;
– le paramètre d'empilement spontané P₀ et le paramètre d'empilement effectif P, qui est simplement déduit des structures présentes en solution.

Nous montrons dans cette revue que des approches modernes de la solubilisation partent d'une constatation de base : il existe une relation linéaire entre la courbure spontanée P₀ et l'excès de solubilisation λ. Dans tous les cas étudiés, cette relation est linéaire. Par exemple, dans le cas simple de tensioactifs non ioniques et de solutés non ioniques, en supposant que le soluté apporte son volume moléculaire dans le film de tensioactif, sans modifier au premier ordre, ni l'épaisseur du film, ni la surface par tête, la relation entre le paramètre d'empilement intrinsèque H₀ et l'excès λ de solubilisation mesuré est bien approchée. Nous donnons les références des travaux originaux qui ont été établis sur des systèmes modèles ainsi que des cas importants dans les applications industrielles.

1 Introduction

In a ‘surfactant’ molecule, a hydrophobic part is linked to a hydrophilic part. This duality is responsible for the self-organisation capacity of those molecules and induces reduction of surface tension, i.e., positive adsorption at the air–water interface. Lipids as well as detergents, most ‘complexing molecules’ as well as associative polymers belong to the ‘surfactant’ class of molecules according to this general definition.

The phase diagrams of surfactant in water (binary system) or in both water and oil (ternary system) experimentally obtained can be rationalised by the general principles of surfactant self-assembly. We will see in the following these general principles by the use of phase diagrams. In this short review, the phase diagrams are not included but they can be found in original references in the form of useful ‘Atlas’ of phase diagrams, a book [8] as useful to physical chemists than a good map for a geographer.

Surfactant molecule could be used to enhance the solubility of an insoluble substance in water. Until now, most uses of solubilisation properties for formulation have to be derived from tabulated values obtained from systematic titration [45]. We will present in the following how models for solubilisation can be generalised and unified by linking molar ratio of solutes to geometrical constraints, using the general principles of surfactant self-assembly.

2 Binary phase diagrams

Binary phase diagrams are determined when only surfactant and solvent are present in the sample. When the surfactant molecule is mixed with water, a transition from monomers to multi-molecular aggregates is observed as soon as the chemical potential is high enough to induce the transition from a molecular solution to organised molecular systems. This transition is called the critical micellar concentration (cmc). Even if it is numerically most of the time equivalent, the cmc should not be systematically identified to the concentration of monomers in dynamic equilibrium with micelles.

At atmospheric pressure, two thermodynamic variables define the system, i.e., the concentration of the surfactant and the temperature, which are the axis of the commonly found phase diagrams: an exhaustive ‘Atlas’ of binary systems, in the form of behaviour versus temperature and concentration of one surfactant has been recently critically compiled [29].

2.1 Generalities

Depending on concentration and temperature range, the aggregates formed by the surfactant present very different shapes. Assuming a complete segregation between hydrophobic and hydrophilic domains, the geometry of the aggregates can be described by the interface between the domains. The local geometry of the aggregates is characterised by the interfacial curvature of the surfactant film. The curvature of an interface is defined by using two circles tangent at each point to a general surface covered by surfactant monolayer. On each point, there is a maximal value (r₁) and a minimal value (r₂) for radii of circles tangent to the surface. The curvature (dimension: length⁻¹) is the inverse of the radius of the tangent circle. The average curvature H is the average of the inverse of the two radii of curvature. The gaussian curvature K is the geometrical mean of the inverse of the two radii of curvature.

Three cases frequently described in local packing topologies are: globular (K>0), cylindrical (K=0) and cubic (K<0). Curvature and Gaussian curvature are quantitatively lower in the case of lamellar phase, or locally lamellar structures.

Israelachvili et al. [22] postulated a preferred molecular shape for the molecule embedded in the surfactant film. This shape is described by the surfactant parameter:

P = V / σ ℓ

(1)

Thus reducing the solubility in water and increasing the solubility of the surfactant in oil, where, at the microscopic scale, the volume V is the volume of apolar part of the surfactant molecule, σ the area per molecule at the interface and ℓ the average chain length. This surfactant parameter characterises and determines the local shape of the interface.

For non-ionic systems, the surfactant parameter P is primarily varied by using temperature: high temperature dehydrates the ethoxy polar head-group, thus reducing the solubility in water and increasing the solubility in oil of the surfactant. For ionic surfactants, the situation is more complex, since the counter-ion density function near the oil/water interface sets the area per head-group and also the elastic bending constant of the interface, i.e., the energetic cost to deviate locally from the spontaneous curvature.

The coverage relation [21] links this local packing parameter P of neighbouring surfactant molecules to macroscopic curvatures imposed by topology:

P = 1 - 〈 H 〉 ℓ + \frac{1}{3} 〈 K 〉 ℓ^{2}

(2)

If 〈H〉 is positive, then the film is curved towards the hydrophobic region.

On a macroscopic scale, 〈H〉 is the average curvature averaged over the whole sample, and 〈K〉 is the gaussian curvature, averaged over the whole sample.

In the most simple case possible, i.e., the case of spherical micelles with a radius R, the average curvature is given by 1/R and the gaussian curvature is equal to 1/R².

Relations (1) and (2) are too crude to be used directly, but are the basis of any model evaluating the difference between two samples: they can be used differentially, considering temperature, concentration or salinity variations as well as solubilisation of a host molecule.

The spontaneous curvatures H₀ and K₀ are the curvatures [21,44] adopted by the surfactant film in the absence of non-local constraints. It corresponds to the minimisation of the total bending energy of the film. When the microstructure is not known a priori, the self-organisation of surfactant molecules can be rationalised in terms of chemical potential, primarily depending on the concept of spontaneous curvature of any surfactant monolayer.

The competition between the spontaneous curvatures, which depends on molecular shape, temperature, salinity and the curvatures imposed by sterical constraints such as micellar volume and surface, is the most general principle of surfactant self-assembly [21]. The spontaneous curvatures reflect the local packing constraints at the microscopic scale, while the curvature characterises the composition. The cost in the bending energy per unit area due to the difference between these two quantities is given by the following expression [17]:

F = 2 k_{c} {(〈 H 〉 - H_{0})}^{2} + \bar{k_{c}} (〈 K 〉 - K_{0})

(3)

On a macroscopic scale, 〈H〉 is the average curvature averaged over the whole sample, and 〈K〉 is the gaussian curvature, averaged over the whole sample.

The expression (3) presents serious self-consistency problems, as shown by Fogden et al. [14] in the case of non-zero spontaneous curvature. An alternative microscopic model of the membrane could be used to express the free bending energy of the surfactant film. With this model, the energy [20] of deformation of surfactant film is related to the deviation of the packing parameter from its preferred value P₀:

F = k^{*} {(P - P_{0})}^{2}

(4)

where

k^{*}

is a generalised bending constant, and P₀ is obtained by relation (2) with H₀ and K₀.

This energy F is an estimation of the cost in energy needed by the molecule to go from the preferred shape to the actual shape in the film. This expression using one variable only gives a simple expression of chemical potential versus one molecular quantity allowing schematic predictions [21] of phase sequence in binary phase diagram (surfactant–water).

2.2 Spherical micelles

The simplest case of aggregates for surfactant in water is obtained for spherical micelles. The maximum of surfactant per globular micelle, the so-called Tanford limit [49] for spherical micelle is obtained with simple geometrical arguments, using the surface to volume ratio of a sphere:

N_{agg}^{\max} = \frac{3 \times (apolar molecular volume)}{[(area per molecule at core / water interface) \times R]}

where R is the radius of the apolar core of the micelle; it must not exceed the chain length of the apolar part of the surfactant; the number N_agg^max generally lies between 20 and 200.

For ionic micelles, the aggregation of amphiphile is limited by head-group electrostatic repulsion, which is balanced by the adsorption of counter-ions at the micellar surface. The dissociation of the counter ions of the head group can be predicted within the frame of the ‘Dressed Micelle Model’ [16] from first principles and an approximate analytical solution of the Poisson–Boltzmann equation in spherical geometry. This model reduces the micellisation of an ionic surfactant to a single parameter only: the aggregation number. Therefore, for a given micelle, the effective charge, i.e., the net electrical charge taking into account adsorbed counter-ions and non-linear effects, can be explicitly calculated from molecular volumes, ion size and water–oil interfacial tension.

Hayter [16] gives a numerical calculation to obtain the effective charge, once volume and surface are known. This relation holds for all micelles and predicts effective charge in all cases where there is no ‘chemical’, i.e., non-electrostatic interaction between the oil–water interface and the counter-ion. The micelles that have a lower charge than calculated involve highly polarisable counter-ions, such as bromide and iodide, or specific receptors, such as cage molecule, implying ion head-group specific interaction [3]. A general sequence called the Hofmeister series seems to describe some ion-binding effect in a large number of systems. Recently, a general theory for the origin of this Hofmeister effect has been proposed and the consequences for the surfactant aggregation are described by Underwood and Anacker [54]. This ion effect is very sensitive, since the phase diagram of a surfactant–water binary system could be completely modified by the exchange of the counter-ions (bromide instead of chloride for example [5]).

2.3 Intermolecular interactions

In binary phase diagrams, the phase limits are set by intermolecular interactions. Therefore, the use of the phase boundaries that provide lines of known osmotic pressure is a powerful tool for determining molecular forces. When two phases coexist in a region of a binodal line, there is a competition for water. For example, in the case of a lamellar in equilibrium with pure water, the total balance of attractive and repulsive interactions between surfactant aggregates is zero, since the osmotic pressure of the water phase in excess is zero. Thus, a determination of the maximum observed periodicity versus any thermodynamical parameter such as temperature, ionic strength or composition of solvent is equivalent to a very sensitive molecular force balance [40]. Parsegian and co-workers [30] have shown that if the attractive and repulsive interactions are algebraically combined as an approximation, quantitative information about magnitude of interaction between membranes can be obtained.

3 Ternary phase diagrams

3.1 Pseudo-binary systems

The simplest case is the historic case of sodium octanoate/water/octanoic acid which is a quasi-binary system studied by Ekwall and co-workers [6,7], where the ‘oil’ and ‘surfactant’ are the acidic and sodium forms of the same molecule. In this system, the connected lamellar phase (sponge phase), i.e., the first non-globular micellar aggregates, as well as highly swollen lamellar phases have been discovered.

3.2 Two surfactants in water

The catanionic surfactant–water systems – in which an anionic surfactant is associated to a cationic surfactant in water – belong to the class of ternary self-assembling organised molecular systems. Strong ion pairing and low critical micellar concentrations characterise these types of solutions [24]. Catanionic mixtures provide a general way of producing long range correlation in microstructures since ion pairing produces robust lateral packing in mixed films: P₀ is close to one, bilayers are preferred and the resulting bilayer is stiff (k_c>1).

3.3 Surfactant/water/oil

The most general ternary phase system is obtained for a mixture of surfactant, water and oil. The ternary phase diagrams of ionic and non-ionic species demonstrate the interplay between curvature imposed by volume and surface constraints and spontaneous curvature, a basic property of a surfactant film. The phase diagrams are profoundly different for flexible and rigid surfactant films [4]. The flexible films are films for which the cost in bending energy of local curvature variations is smaller than thermal energy. The microstructure of flexible films is dominated by entropy and therefore the fluctuations. The rigid films can be modelled as molten liquid crystals or a glass of small crystallites of liquid crystals and therefore form more homogeneous microstructures. Basically, flexible films correspond to $k_{c} ⪡ k_{B} T$ and rigid films to $k_{c} ⪢ k_{B} T$ . The intermediate case where $k_{c} \approx k_{B} T$ and associated microstructure has only be examined recently [3].

3.3.1 Microemulsion

In general, the mixture of three components (water/oil/surfactant) results in a non-homogeneous solution of different phases. However, over a certain composition range the mixture spontaneously self assembles into a transparent stable liquid phase: a ‘microemulsion’. The properties and structure of this microemulsion and the observation of the phase limits depend on the nature of the film (rigid or flexible case). The microemulsion is a good medium to solubilise solute, as we will see in the next paragraph.

The structure of the microemulsion changes continuously as a function of the composition. Some microemulsions are like ‘micellar’ or ‘reversed micellar’ phase; however, in some cases, a ‘random bicontinuous dispersion’ is present. Experimentally, one always observes a broad scattering peak at:

q_{\max} = 2 π / D^{*} = (2 π / 5.8) [σ C_{s} / ϕ (1 - ϕ)]

(5)

with

q = 4 π / λ \sin θ

and θ, half the scattering angle with incident wavelength λ. The Bragg distance

D^{*}

is obtained from the maximum of the scattered intensity; it corresponds to the typical size of dispersion size in real space. φ is the polar part volume fraction of the sample,

Σ = σ C_{s}

is the oil–water specific interface at the interfacial film, which can be directly measured by the Porod asymptotic law of scattering at large angles:

{Lim}_{q \to \infty} I (q) q^{4} = 2 π σ C_{s} Δ ρ^{2}

(6)

where the scattered intensity is expressed in absolute units (cm⁻¹) and Δρ is the inside–outside contrast in scattering length density (cm⁻²).

Early microemulsion models developed in the literature are due to Talmon and Prager [48], who predict monotonic decrease without the presence of a scattering peak, as well as to de Gennes and Taupin [15] or to Cates, Roux, Andelman and Safran [2], who give a peak at twice the observed value, without any shift versus spontaneous curvature.

For ionic systems in the low salt case, the major component towards surfactant film rigidity is brought by distribution of counter-ions, universal expressions having been given for the case of monovalent counter-ions [13].

3.3.2 Rigid case (k_c>k_BT)

In this case, fluctuations in curvature are not dominant: this corresponds to double chain ionic surfactants, or ionic surfactants with co-surfactants and in the absence of salt in the solvent. Rigid ternary system is usually made with charged surfactants, the archetype being the easily hydrolysed and hard to purify AOT, for which no accepted complete ternary phase diagram exists yet.

In the case of a rigid interface, an analytic predictive model allowing explicit calculation of the location in phase diagrams of conductivity variation, associated to transition of microstructures between droplets, cylinders and locally flat connected bi-layers is available [55]. This Disordered, Open and Connected model [39] only considers conservation of volume, surface and curvature and predicts possible microstructures versus composition, as shown in Fig. 1, adapted from reference [56].

Figure 1
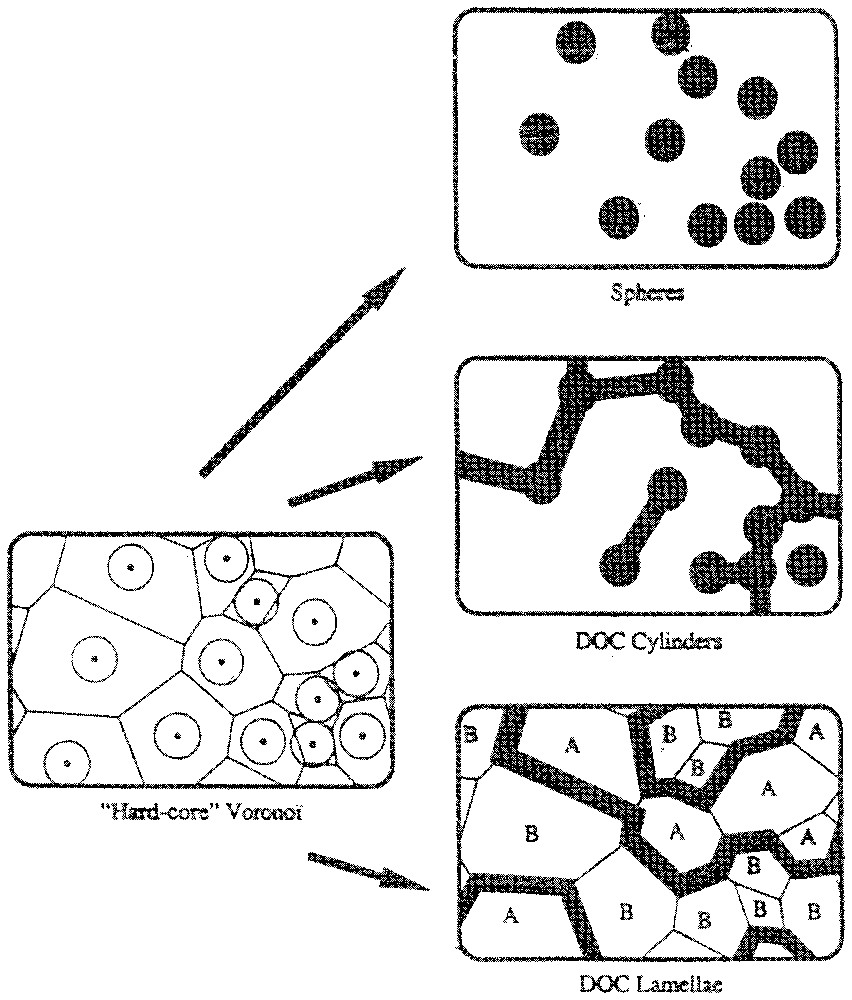
Three classes of structure obtained from the Disordered, Open and Connected model. This model is based on a generalised connected structure that locally satisfies three constraints: the volume fraction, the specific surface and the curvature. The microstructure is assimilated to a pure geometric question, neglecting entropy and curvature fluctuations effect. The structure is built from a Voronoi cell tessellation.
Trois classes de structure obtenues par le modèle Désordonné, Ouvert et Connecté (DOC). Ce modèle est construit à partir d'un réseau de cellule de Voronoı̈ et d'une structure connectée, qui satisfait localement trois contraintes : la fraction volumique, la surface spécifique et la courbure. La microstructure est obtenue par des considérations purement géométriques, en négligeant les effets de fluctuation dus à l'entropie ou à la courbure.

Particularly, this model predicts the antipercolation threshold in reversed microemulsion of the most widely studied stiff interface of ternary systems: the water/oil/DDAB system. The easiest way to obtain stiff interfaces is to combine electrostatic interaction, i.e., an ionic surfactant, with more than one chain per head-group. Electric antipercolation is the observation of a decreasing conductivity by orders of magnitude upon the addition of water for a given composition. The occurrence of antipercolation boundaries is general in microemulsions with stiff interfaces, This has been first discover by Kaler and co-workers [42] and illustrated in Fig. 2. The decrease of conductivity of the microemulsion with increasing water content is due to a microstructural change in the microemulsion. An abrupt change from interconnected cylinders towards water in oil separated spherical droplets, quantitatively described by the DOC model, is induced by the coverage relationship without excess bending energy. Conductivity measurement detects this antipercolation threshold, as the microemulsion will conduct at low water content and will not conduct at high water content. Hence, when the bending constant is higher than $k_{B} T$ , solubilisation of a solute in a microemulsion induces sterical constraints that modify the microstructure with easily measurable effects. The most spectacular effect is the variation of the antipercolation threshold [51].

Figure 2
a. Pseudo-ternary phase diagram of SDS/NBA-water-toluene at 25 °C. SDS: sodium dodecyl sulphate and NBA: butan-1-ol. b. Variation of conductivity K/K₀ versus toluene volume fraction along paths I through V in the microemulsion domain (reproduced with permission from reference [42]; copyright 1986, The American Chemical Society).
a. Diagramme de phase pseudo-ternaire SDS/NBA–eau–toluène à 25 °C. SDS : sodium de dodécyl sulfate et NBA : butan-1-ol. b. Variation de la conductivité K/K₀ en fonction de la fraction volumique de toluène le long des lignes I à V dans le domaine microémulsion (reproduit avec permission à partir de la référence [42] ; copyright 1986, The American Chemical Society).

3.3.3 Fluid case (bending constant k_c<k_BT)

The fluid interface archetype is the non-ionic surfactant/water/oil ternary system, as studied by Strey and co-workers [47] for which a temperature cut through the phase diagram is a convenient experimental method to establish surfactant efficiency and temperature of zero spontaneous curvature.

4 Solubilisation of solutes

We have illustrated in the previous paragraph how spontaneous curvature and surfactant layer bending constants are at the origin of the general layout of binary or ternary phase diagram. We will see in this part how those quantities allow us to distinguish between the different types of solubilisation observed experimentally.

We use the first definition of solubilisation given by Mc Bain [36]: solubilisation is the way to increase the solubility of an insoluble or slightly soluble substance in a given medium. This phenomenon involves the presence of surfactant molecules or colloidal particles in a single phase that incorporates totally the insoluble substance. We focus in this part on the solubilisation of a solute by the use of surfactant.

In binary as well as ternary systems, the amount of added solute dispersed in an organised molecular system can be analysed as the additive conjunction of homogenous solubilisation (the solute is soluble in ‘bulk’ solvents or in one of the ‘bulk’ solvents) and surfactant film solubilisation (the solute is located in the surfactant film). Homogenous solubilisation of a solute is identical to molecular dispersion in homogenous bulk solvent. In the case of surfactant film solubilisation, adsorption isotherms of solutes in a surfactant film can be derived from scattering experiment and phase diagram determination. The basic variable describing surfactant film part of the solubilisation in surfactant solutions is therefore the solute excess, expressed as a molar ratio λ:

λ = [excess solute in the film] / [surfactant in film]

(7)

When the solution is in equilibrium with excess solid solute λ=λ_max. Before this saturation point, adsorption isotherms of a solute on the surfactant interface have to be considered. The situation is the same than adsorption on a dispersed solid, if one considers that the presence of surfactant produces a specific area of oil–water contact of value σ per molecule.

The maximum amount λ_max of solute solubilised in a given medium and its localisation depend on the nature of the surfactant and therefore on the spontaneous curvature and bending energy of the film. To study solubilisation, three different approaches can be used:

(a) determining what is the maximum amount of solute that can be solubilised; the particular case of maximum of water solubilisation in a given amount of surfactant in oil demonstrates the relative importance of the different effects, which induces a limit of solubilisation and therefore a phase separation; the reverse case of solute in a given amount of surfactant in water is a difficult case, since it cannot be treated independently of the localisation of the solute in the spontaneously formed aggregate;
(b) the second case is the determination of the localisation of a solute; by topological demonstration, the localisation of a solute can be determined in reverse micelle of water in oil microemulsions; in direct ionic micelles, topological arguments alone are not sufficient to determine the localisation of the solute, since electrostatic interactions between surfactant have to be evaluated precisely;
(c) the determination of the amount of solute adsorbed in the interfacial film at the water–oil interface versus composition in microemulsions systems is the most complete approach, since it includes the determination of a full adsorption isotherm of the solute on the surfactant interface.

For the case (a), Shah and co-workers [19,34,35] propose a theory based on a phenomenological and qualitative approach to predict the maximum of water solubilisation in water in oil microemulsions. Zana and co-workers have confirmed the useful of considering two separate causes of instability in water in oil-reversed systems:

– the emulsification failure [43], where the ‘inside’ water part is expelled by the oil phase; upon titration with water, a final state of microemulsion coexists with excess pure water; the driving force for phase separation is then the violation of curvature constraint and
$〈 H 〉 = Σ / (3 ϕ) ⪡ H_{0}$
where 〈H〉 is the average curvature imposed by the molecular volumes and sample composition, Σ is the area of interface per unit volume and φ is the inside per volume fraction, and H₀ is the spontaneous curvature controlled by counter-ions in the case of ionic surfactant;
– the liquid–liquid phase separation, which can be driven by attractive interactions between droplets; the final state after phase separation is a thermodynamic coexistence of a droplet-rich and of a droplet-poor water in oil solution, like after a liquid–gas transition. The driving force is solvent-hydrocarbon chain wetting (penetration) additive with general Van der Waals attraction between droplets.

Shah and co-workers [34,35] minimise the total free energy with the radius or with the volume fraction of dispersed phase to obtain the maximum capacity for solubilisation of water. They demonstrate that solubilisation depends on the two following parameters:

– the spontaneous curvature H₀ related to the packing parameter;
– the elasticity constant of the surfactant film related to the bending energy required to bend the film.

The water capacity depends on both the size and the stability of the dispersed droplets. Maximum solubilisation is obtained with the optimal value of the interfacial curvature and of the elasticity where the bending stress and the attractive forces between droplets are minimised.

For rigid interfaces, phase separation occurs at R=R₀ (spontaneous radius) and the solubilisation capacity depends on the spontaneous curvature. For fluid interfaces, the phase separation will depends on the interdroplets free energy.

For small attractive interactions, the microemulsion demixes with an excess of water because of large difference between spontaneous and average curvature (emulsification failure: case A). For a sufficiently strong attractive droplets interaction, the droplets are stabilised leading to a phase separation of a microemulsion with smaller droplet, it is a liquid/gas transition (case B). Therefore, the maximum water capacity results from a compromise between these two opposite effects: curvature effect or attractive Van der Waals-type attraction between droplets.

Fig. 3 illustrates this theory by presenting the effect of the molecular volume of oil on the solubilisation capacity of water in a water–oil–AOT microemulsion [35]. Oils with small molecular volume or strong polarity interact strongly with the surfactant chain, leading to a high interfacial rigidity and a high spontaneous curvature (small natural radius). The solubilisation capacity is dominated by the curvature effect and at the phase separation microemulsions are in equilibrium with water in excess. From benzene to heptane, increasing the volume of oil induces an increase of the maximum of water solubilisation observed for a given surfactant in oil. But as the molecular volume increases further, the attractive interactions among droplets begin to play a major role. With larger oil molecules, the solubilisation capacity is decreasing from heptane to hexadecane, as the attractive interaction is increasing.

Figure 3
Effect of the molecular volume of oil on the capacity of a w/o microemulsion obtained with AOT at room temperature (reprinted with permission from [19]; copyright 1987, The American Chemical Society).
Effet du volume moléculaire de l'huile sur la capacité de solubilisation maximale de l'eau par une microémulsion inverse eau dans huile, obtenue avec de l'AOT à température ambiante (reproduit avec permission à partir de la référence [19] ; copyright 1987, The American Chemical Society).

In the case (b), the localisation of a solute could be determined by topological argument in the case of a solute in reverse micelles. Zemb and co-workers [41] studied the localisation of a solute in the case of soft charged interface in AOT–water in oil microemulsions. The topology of the microemulsion is dominated by geometrical constraints, as the area σ per head group is independent of the composition. The radius R is imposed by the composition of the microemulsion: $R = 3 ϕ / Σ$ if φ is the internal polar volume and Σ the interfacial area per volume unit of the monodisperse water in oil droplets. In the general case, we have to consider that film solubilisation of a solute induces itself modifications of the interfacial area or of the polar volume, resulting from a modification of the rigidity of the interface as well as of the spontaneous curvature. The solute localisation could be obtained from the induced perturbations in a given water in oil microemulsion:

(a) for a given water volume, the solute may increase the total interfacial area (it behaves as a surfactant); in this case the radius of the droplet will decrease and the density of droplets increase;
(b) the solute may also be localised in the core of the droplet, i.e., behave as added water; in this case, the solute increases the polar volume at a constant specific area; the radius of droplets increases and the number of droplets decreases;
(c) the solute, especially if it is a large insoluble molecule, may nucleate the formation of a second type of aggregate, one of them being a surfactant-covered solute; it is not possible to derive directly any information as the solution becomes polydisperse; in this case, determination of the adsorption isotherm of the surfactant by the solute in the absence of water is needed before further processing;
(d) if the solute is apolar and solubilised in the continuous phase, no variation of the radius or of the number and density of the droplets will be observed.

Variation of average water droplet size can be deduced from small angle X-ray or neutron scattering, as well as classical light scattering. Maximum water content can be obtained by titrations and gives the evolution of maximum water content at a given temperature. These elementary geometrical considerations always provide a first approximation about the localisation of a solute in a reverse microemulsion. In intermediate cases, when the solute increases both the interfacial area and the inside volume of droplets, it is also important to quantify the amount of the solute at the interface or in the core of the droplets.

Topological arguments are not enough to determine the localisation of a solute when there are lateral electrostatic interactions between ionic surfactant molecules in direct micelles. Jönsson and co-workers [1,28] have introduced an explicit model using numerical evaluation of the free energy variation associated with solubilisation, in order to predict the behaviour of uncharged molecules of different polarity in ionic surfactant aggregate. This model evaluates the thermodynamic properties of the solution from the knowledge of the molecular properties of both surfactant and solute. This model can predict the localisation of a solute in the micelle (core or palisade layer), but also the extension of different phases in the three-component phase diagram: ionic surfactant–water–solute. Self-consistent unambiguous definition of ‘palisade layer’ as the full thickness of a pure surfactant layer is considered. This definition allows calculation, but is slightly different from a more widely used definition as the layer where permittivity is different from what it is in oil and in water.

For micelles, the localisation of a solute depends on both the charge density of the micelle and the polarity of the solute. When a solute is solubilised in ionic micelles, there is a competition between the gain in surface charge density and the reduction in interfacial energy. The localisation results from the relative magnitude of these two opposite effects. The model proposed by Jönsson thus predicts and quantifies the average curvature change induced by the presence of solute.

Apolar solutes such as hydrocarbons are solubilised in the interior of micelles with a low charge density, because geometrical packing produces a large reduction in the interfacial energy in these cases. Such solutes are solubilised in the Palisade layer of micelles with a high charge density, because of the favourable mixing with amphiphiles and of the reduction of the surface charge density.

Polar solutes are also solubilised in the Palisade layer of highly charged micelles, whereas in the case of micelles with a low charged density, most of the polar solute is located in the interior of the micelles.

In the case (c), solubilisation of solutes in binary and ternary system can be understood as the sum of homogenous solubilisation in oil or water domain and surfactant film solubilisation. Since different environments are available, the interface can be considered as a pseudo-phase or a surfactant monolayer. In this last case, the water/oil interface is supposed to be covered by a monolayer surfactant film into which the solute can be adsorbed. In this case, we have to refer back to the basic variable, i.e., the interfacial composition, expressed in molar ratio λ =[excess solute in the film]/[surfactant in the film].

When the solution is in equilibrium, with excess solid solute, the saturation of the solution is obtained and λ=λ_max. At this point, there is an excess of solubilisation, since the amount of dispersed solute can be larger than the maximum value of solubility in the same volume of pure oil or/and pure water. Before this saturation point, there is an equilibrium of the solute between the bulk and the surfactant film; the adsorption curve (isotherms) of a solute on the surfactant interface can be determined [52].

The interplay between solubilisation expressed by λ and by the spontaneous curvature of the interface has been discovered independently and rationalised by Jönsson [1,28] for polar and apolar solute in ionic surfactant–water system and by Leodidis [31–33] for amino-acid solubilisation in reverse water in oil microemulsions.

Fletcher [10] and then Leodidis [31,32] indicate a general method to determine the amount of solute solubilised in reverse microemulsions, its localisation and the radius variation of the droplets induced by this solute. The phase transfer method is first used to determine the affinity of the solute towards the interfacial film. A reverse micellar phase in oil is in contact with a solution of amino-acids in water. After equilibrium is obtained, reverse micelles containing some amino-acid and water are in equilibrium with the remaining amino-acid in water. The rate transfer of one species (water or amino acid) is obtained by $t = N^{mwp} / N^{aq . in}$ , where N^mwp is the number of moles of the species in the reverse microemulsion and $N^{aq . in .}$ is the number of moles in the initial aqueous phase. Assuming that the water phase in excess is identical to the water phase composition within dispersed droplets, the rate transfer of amino-acid and of water are determined by titration of the two phases in equilibrium. The rate transfer of amino-acid is identical to the rate transfer of water when there is no adsorption of the solute at the interface. If there is an excess of solubilisation at the interface, the rate transfer of amino-acid is higher that the one of water. An excess of solubilisation can be evidenced by this method and quantified by the molar fraction–base partition coefficient:

K_{x} = \frac{X_{a}^{int}}{X_{a}^{mwp}}

where X_a^int is the molar fraction of amino acid at the interface (int) or in the water droplet of the microemulsion (mwp).

For example, it is demonstrated that there is an excess of solubilisation for phenylalanine, which is dispersed in the bulk water and in the interfacial film. Excess of solubilisation are measured as a function of the nature of the oil, the salinity and the surfactant concentration. Since all these factors affect the bending of the interface, the partition coefficient can therefore be related to the variation of the curvature of the interface.

Leodidis et al. [32] have demonstrated that a local equilibrium of solute adsorption at the interface can be related to the mean curvature of the surfactant film. The variation of K_x with curvature can be obtained from the equality of chemical potential of amino-acid in excess water and in the interface:

\ln K_{x} = \ln K_{x}^{0} - \frac{2}{k_{B} T} 〈 \bar{f_{a}} C ξ 〉 \frac{1}{R_{w}}

(8)

where K_x⁰ represents the coefficient transfer from water to interfacial film with a zero curvature, C is the elastic constant,

\bar{f_{i}}

is the partial molar area of the amino-acid (a) and ξ is a dimensionless quantity directly related to the variation of the elastic constant with the amount of solute located at the interface.

This thermodynamic model describes the ‘squeezing out’ phenomenon experimentally observed: curving the film squeezes out a part of the adsorbed solute (or increasing the curvature induces a decrease of K_x). This model gives also an explanation for the linear dependence of K_x with mean curvature, even if the predictive slope is not exactly equal to the experimental value. This work is one of the first predictive general models for solubilisation.

Using the same general approach, we have investigated [52] the case of the solubilisation of a hydrophobic solute (lindane: gamma-hexachlorocyclohexane) in oil in water microemulsions using non-ionic surfactants of the family of polyoxyethyleneglycol. By varying the temperature, the hydrophilic/hydrophobic balance (expressed as spontaneous curvature or surfactant packing parameter or equivalently the HLB balance [46]) of the non-ionic surfactant used in this study can be modified. Therefore, the spontaneous curvature turns from oil to water as the temperature is increased. We measure separately the amount of solute adsorbed in the interfacial film and the average curvature of the sample in order to establish a link between these too quantities.

The solute effect on spontaneous [52] curvature is determined from the phase diagram determination. A cut at equal water-to-oil ratio in the ‘temperature–water–oil–C_iE_j′ phase diagram gives a pseudo-binary phase diagram: the ‘temperature–C_iE_j mass fraction’. This way of establishing a partial phase diagram is a direct experimental method to obtain the temperature of zero spontaneous curvature of any given ternary system [47]. The influence of an added solute on the curvature of the surfactant film can be obtained by determining the modification of the pseudo-phase diagram when pure oil is replaced by an oil + solute pseudo-component. We find that increasing the amount of lindane in the oil induces a decrease of the zero spontaneous curvature, as it is shown in Fig. 4. Temperature of zero spontaneous curvature is decreasing when the surfactant is replaced by a less hydrophilic surfactant or when the oil is replaced by a less hydrophobic oil (more penetrating). Therefore, we conclude that solubilisation of lindane turns the curvature towards water at constant temperature.

Figure 4
Pseudo-binary phase diagram of water–oil (cyclohexane + lindane)–C₆E₅ for different initial weight compositions β of lindane in the oil: (□) 0%, (×) 4%, (•) 10% and (▴) 15%. The arrow indicates the variation of the fish tail with the increasing content of lindane in the oil. The temperature $\tilde{T}$ of the zero spontaneous curvature is given by the ordinate of the fish tail.
Diagramme de phase pseudo-binaire : eau–huile (cyclohexane + lindane)–C₆E₅ pour différentes compositions massiques initiales β de lindane dans l'huile : (□) 0%, (×) 4%, (•) 10% et (▴) 15%. Les domaines d'existence de la phase microémulsion seule (1) ou en coexistence avec de l'eau ( $\bar{2}$ ), de l'huile ( $\underline{2}$ ), ou les deux (3) sont représentés. Ces diagrammes prennent habituellement la forme schématique d'un poisson. La température $\tilde{T}$ de la courbure spontanée nulle est donnée par l'ordonnée du point d'intersection des deux courbes. La flèche indique le sens de variation de $\tilde{T}$ avec l'augmentation de la composition β de lindane dans l'huile.

By determining the maximum amount of lindane that can be solubilised in water–oil–C_iE_j microemulsion, we find explicitly the value of the excess of solubilisation. Stable microemulsions exist with a larger amount of lindane relative to the oil than the saturation value in the same oil alone at the same temperature. By titration of both microemulsions and oil in excess, we determine the interfacial composition ratio (lindane over surfactant at interface) versus the weight ratio of lindane in the oil. We obtain here the adsorption of lindane at the interface of water–oil–C₆E₅ microemulsions with a constant mean curvature (equal to zero).

Then, we deduce from phase diagram determination and titration a linear relation [50] between the solute molar ratio λ of lindane adsorbed at the interface and the curvature variation Δ〈H〉 induced by the solute:

Δ 〈 H 〉 \times ℓ = - 0.7 λ

(9)

To rationalise the experimental results, we use a geometric interpretation of the observed curvature variations. We find by SANS experiments that the solute has no effect on the area σ per polar head of the surfactant in the microemulsion. Therefore, the excess solute increases the effective volume only and hence the packing constraint

P = V / σ ℓ

at constant σ and ℓ. Considering the coverage relation (1) at the first order, we obtain the linear relation:

Δ 〈 H 〉 \times ℓ = - 0.4 λ

(10)

Comparison between curvature variation induced by solubilisation observed in several cases with the value expected from the sterical constraints as variation of P is illustrated in Fig. 5. We found in this case also that the saturation limit corresponding to the maximum amount of lindane that can be solubilised depends on the curvature.

Figure 5
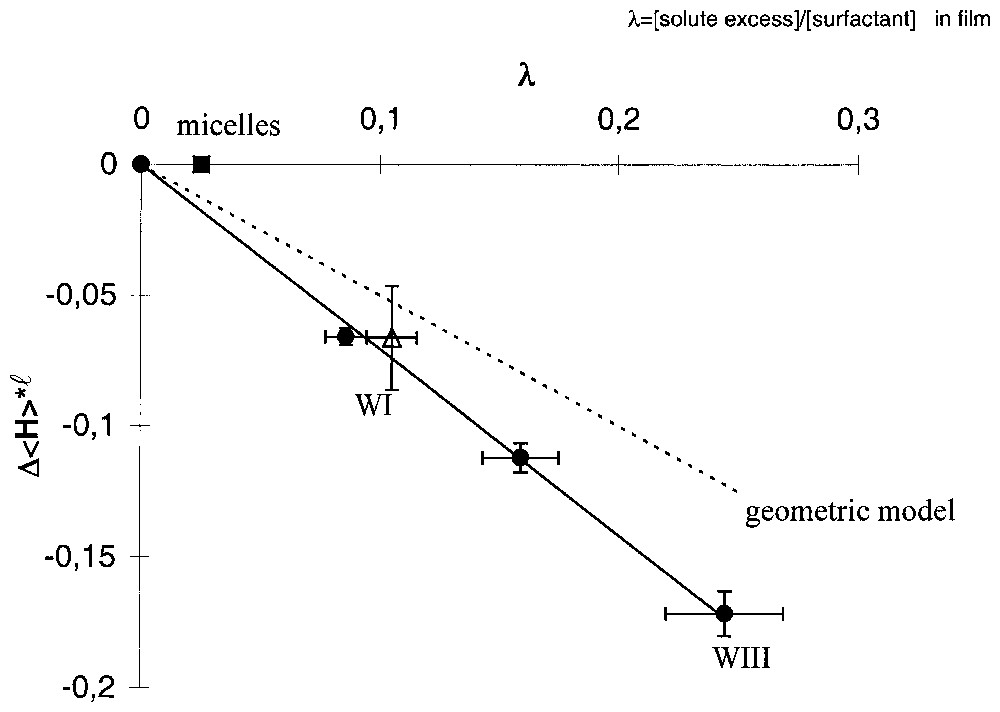
Variation of the reduced average curvature $〈 H 〉 ℓ$ versus interfacial molar composition λ, with ℓ representing the chain length of the surfactant. $Δ 〈 H 〉 ℓ = 〈 H (λ \neq 0) 〉 - 〈 H (λ = 0) 〉$ . The dashed line is calculated with the wedge model. (•) Experimental points obtained by phase diagram determination and titration in the Winsor III domain. (■) Maximum of solubilisation obtained in micellar systems. (▵) Obtained in a Winsor I microemulsion.
Variation de la courbure réduite moyenne $〈 H 〉 ℓ$ en fonction de la composition λ interfaciale molaire, avec ℓ la longueur de chaı̂ne du tensioactif. $Δ 〈 H 〉 ℓ = 〈 H (λ \neq 0) 〉 - 〈 H (λ = 0) 〉$ . La ligne en pointillés est calculée à partir du modèle de coin. (•) Points expérimentaux obtenus à partir de la détermination du diagramme de phase et des dosages dans le domaine Winsor III (microémulsion en coexistence avec de l'eau et de l'huile). (■) Maximum de solubilisation, obtenu expérimentalement dans le système micellaire. (▵) Point expérimental obtenu dans le domaine Winsor I (microémulsion en équilibre avec de l'huile en excès).

In all cases a–c, the link between curvature, area and volume perturbations induced by the presence of the solute in the film and the adsorption isotherm of the solute in the film allow to identify the instability inducing the presence of a phase boundary. Considering these general principles allows a quantitative approach to surfactant formulation in industrial applications.

5 Solubilisation in practice

A large number of industrial processes are dependent on self-organised molecular aggregates, such as micelles, reverse micelles, emulsions, microemulsions, and adsorbed monolayers. Even more complex architectures are single or multilayered vesicles, also called liposomes as well as cubosomes, the archetype of emulsion of a liquid crystal emulsification. At the molecular scale, the ‘solubilisation’ itself can occur in the ‘bulk’ medium, or in the surfactant film itself. The phenomenon of increasing solubility of apolar molecular in water can also be obtained by an ‘hydrotrope’, the generic name for small soluble molecules increasing observed solubility of a third component without forming self-assembled molecular structures by themselves. This subject has not been discussed in this article but is developed in references [11,38]. An overview of these three types of solubilisation in formulations including paints, detergents, lubricants, and food are critically examined in the Handbook of Surface and Colloid Chemistry [18].

In the case of the pharmaceutical industry, most drugs are not soluble in isotonic water solutions and thus, they must be delivered ‘solubilised’ in aqueous medium. In some cases, the drug is associated to a w/o or an o/w micellar solution. The effects of the drug itself on the structures and the stabilities of the vectoring system must be considered when optimising formulation. Therefore, knowing the general principle linking solubilisation to curvature could be very useful. For example in a micellar system, solubilisation can be limited by coalescence, i.e., a liquid–liquid phase separation, or by the emulsification failure, when spontaneous and effective curvatures are too different from each other. Recognising which type of phase separation occurs allows efficient formulation rules: an increase of the surfactant/apolar volume ratio in the first case, and a decrease in the second case. Several examples of phase transitions induced by the drug and stability studies of the carrier system are given in reference [37]. For example, the effect of an amphiphilic drug on the curvature of surfactant self-assemblies is given by Engström et al. [9]. These authors have determined a part of the phase diagram of monoolein–water–(lidocaine–base or lidocaine–HCl). The cubic phase formed by the monoolein–water system transforms into a lamellar liquid crystalline phase on addition of lidocaine–HCl, whereas it transforms into a reverse hexagonal or reversed micellar phase on addition of lidocaine–base. This is directly linked to the effect of the solute on the curvature of the surfactant film. Lidocaine–HCl is incorporated into the lipid layer and, because of the repulsive electrostatic interaction between the charges, the curvature towards water decreases, whereas addition of lidocaine–base causes the hydrophibic volume to increase and conducts to a transition in the other direction.

Another example of physical chemistry of solubilisation directly relevant to drug delivery is given by La et al. [27]. These authors have studied the solubilisation of indomethacin, a non steroid anti-inflammatory agent, in PEO-poly(β-benzyl L-aspartate) (PBLA) block copolymer micelles in order to reduce irritation of the gastrointestinal mucosa and central nervous system toxicity. The release of the lindomethacin at low pH – when the drug is uncharged – is slow, whereas the rate of the release is increasing with increasing pH above the pK_a of the drug. This is directly linked to the localisation of the drug within the micellar aggregate. There is a decrease of the preferential localisation in the hydrophobic core of the micelle, concomitant to an increase of the net electrostatic charge of the drug molecule.

Amphiphilic oil, such as triglycerides, middle or long chain alcohol or fatty acids, fatty acid ester and amino-acid-derived oil are very important for cosmetic, food and so on, because they are compatible with biological systems. Synthetic perfumes are often used in industrial products with other materials such as emulsifiers or solubilisers. Particularly, in cosmetic and food science, surfactants are used to solubilise oil synthetic perfumes in water. Hence understanding how the perfume or oils interact with the surfactant in an aqueous solution is essential for many industrials applications [53]. Kunieda et al. [23,25,26] studied the solubilisation of different synthetic perfumes in surfactant solutions. They have demonstrated that the hydrophilic properties of the perfume affect its solubilisation. The nature of the solute has a direct influence on its localisation in the aggregates and on the curvature layer of the aggregates; this is directly linked to the maximum of solubilisation in the surfactant media. They considered also the general case of added oil or perfume molecules on the structure of liquid crystals in poly(ethyleneglycol) monododecyl ether (C₁₂E_n)–water system by the means of phase diagrams and SAXS measurements. When decane is added to the C₁₂E₇–water system, a transition from normal hexagonal liquid crystal to water continuous cubic phase is observed, whereas a transition from lamellar to reverse hexagonal phase takes place when decane is added to the C₁₂E₃–water system. Adding oil has the opposite effects on the curvature of the surfactant layer, depending on the hydrophilic or lipophilic nature of the surfactant. This is the cause of the drastic effect on the curvature induced by oil on binary surfactant–water systems. These effects were explained by a simple model of localisation of the oil in the aggregates. The oil can penetrate into the chain layer and therefore tends to increase the effective area per surfactant molecule σ, without increasing the volume of the aggregate. This is the ‘penetration’ effect. On the other hand, the ‘swelling’ effect means that the oil increases the volume of the lipophilic part, without expanding σ. The relation between curvature and the ‘penetration’ or ‘swelling’ power of the oil in the aggregates allows modelling the phase transition when defining a formulation.

Detergency, food or cosmetic formulations are commonly made in the form of an emulsion. A two-phase emulsion system does not correspond to the case of solubilisation. However, a number of emulsions contain three phases and solubilisation could occur in the third phase. This is illustrated by Fiberg et al. [12] in the case of solubilisation of the vitamin E acetate in the lecithin–water system. The drug used is not solubilised in the lamellar liquid crystal and is very soluble in water. In this case, these authors show that vitamin E acetate droplets could be spontaneously solubilised in the liquid crystalline phase: the solubilisation is caused by the evaporation of the water from an emulsion made of vitamin E acetate droplets and liquid crystal particles dispersed in water. This is a common behaviour with usage of the lotion, since a fluid remaining on the skin transforms spontaneously from a liquid crystal layer including a small amount of vitamin E acetate droplets into a complex fluid thin layer, in which the vitamin compound is well distributed. This allows an evenly but still large distribution of the drug from a small quantity on a large area of skin.

The common point in all these examples is a direct impact of modern physical chemistry in formulation: knowledge of phase diagrams and determination of the influence of solute on the curvature effect allows to optimise the formulation as far as needed from equilibrium phase boundaries before and/or after ‘solubilisation’ of the active ‘insoluble’ component. However, in most uses, equilibrium phase diagram aspects have to be associated with a non-equilibrium aspect. Wetting phenomena in the case of detergency, molecular diffusion in controlled release of cosmetics and hydrodynamic interactions in the case of mineral flotation or lubricant fluids are classical examples of crucial industrial importance.

6 Conclusion

Any surfactant solution, whether binary or ternary, can be characterised by four primary quantities: apolar volume fraction φ, area $Σ = C_{s} σ$ (in cm⁻¹), spontaneous P₀ and effective packing parameter P. The addition of a solute induces a variation of all these quantities. Volume fraction φ may be increased or not depending on location of the solute. Solute may act as a surfactant or not depending whether Σ is varied by addition of the solute. Spontaneous and effective surfactant parameter, linked to curvature may also vary upon addition of a solute. Once these quantities are known, the adsorption isotherm can be established. In all fully documented cases so far, the phase diagram variation can be predicted by using the wedge model approximation when the molar fraction λ of the solute is present in the surfactant film:

P (λ) = (V + λ V_{s}) / (σ (λ) ℓ)

i.e., considering that the primary effect of solute is to modify the volume of the surfactant film and the area per molecule for which the curvature variation can be deduced assuming the robust approximation that ℓ is independent of λ. When values of volumes, surface and curvature after addition of solute are known, adsorption isotherms can be located in general phase diagrams.

Bibliographie

[1] M. Aamodt; M. Landgren; B. Jönsson Solubilization of uncharged molecules in ionic surfactant aggregates. 1. The micellar phase, J. Phys. Chem., Volume 96 (1992), pp. 945-950

[2] D. Andelman; M.E. Cates; D. Roux; S. Safran Structure and phase equilibria of microemulsions, J. Chem. Phys., Volume 87 (1987), pp. 7229-7241

[3] L. Arleth; M.S. Marcelja; T. Zemb Gaussian random fields with two level-cuts – model for assymetric microemulsions with non-zero spontaneous curvature?, J. Chem. Phys., Volume 115 (2001), pp. 3923-3936

[4] Y. Chevalier; T. Zemb The structure of micelles and microemulsions, Rep. Prog. Phys., Volume 53 (1990), pp. 279-371

[5] M. Dubois; T. Zemb; N. Fuller; R.P. Rand; V.A. Parsegian Equation of state of a charged bilayer system: measure of the entropy of the lamellar-lamellar transition in DDABr, J. Chem. Phys., Volume 108 (1998), pp. 7855-7859

[6] P. Ekwall; K. Fontell Solutions of alkali soaps and water in fatty acids. VII. X-ray scattering of the isotropic liquid L2-phase, Colloid. Polym. Sci., Volume 266 (1988), pp. 184-191

[7] P. Ekwall; L. Mandell Kolloid Z. Z. Polymere, 233 (1969), pp. 933-945

[8] P. Ekwall; L. Mandel; K. Fontell Solubilization in micelles and mesophases and the transition from normal to reversed structures, Mol. Cryst. Liq. Cryst., Volume 157 (1969) no. 8, pp. 157-252

[9] S. Engström; L. Engström Phase behaviour of the lidocaine–monoolein–water system, Int. J. Pharm., Volume 79 (1992), pp. 113-122

[10] P.D.I. Fletcher The partitioning of solutes between water-in-oil microemulsions and conjugate aqueous phases, J. Chem. Soc. Faraday Trans. I, Volume 82 (1986), pp. 2651-2664

[11] S.E. Fiberg Hydrotropes, Curr. Opin. Colloid Interface Sci., Volume 2 (1997), pp. 490-494

[12] S.E. Fiberg; J. Yang Solubilization in cosmetic systems, Surfactants in cosmetics, Surfactant Sci. Ser., Volume 68 (1997), pp. 225-238

[13] A. Fogden; B.W. Ninham Electrostatics of curved fluid membranes: the interplay of direct interactions and fluctuations in charged lamellar phases, Adv. Colloid Interface Sci., Volume 83 (1999), pp. 85-110

[14] A. Fogden; S.T. Hyde; G. Lundberg Bending energy of surfactant film, J. Chem. Soc. Faraday Trans. I, Volume 87 (1991), pp. 949-955

[15] P.-G. de Gennes; C. Taupin Microemulsions and the flexibility of oil/water interfaces, J. Phys. Chem., Volume 86 (1982), pp. 2294-2304

[16] J.B. Hayter A self-consistent theory of dressed micelles, Langmuir, Volume 8 (1992), pp. 2873-2876

[17] W. Helfrich Elastic properties of lipid layers theory and possible experiments, Z. Naturforsch., Volume 28 (1973), pp. 693-703

[18] K. Holmberg Handbook of Applied Surface and Colloid Chemistry, John Wiley, England, 2001

[19] M.-J. Hou; D.O. Shah Effects of the molecular structure of the interface and continuous phase on solubilization of water in water/oil microemulsions, Langmuir, Volume 3 (1987), pp. 1086-1096

[20] S.T. Hyde; I.S. Barnes; B.W. Ninham Curvature energy of surfactant interfaces confined to the plaquettes of a cubic lattice, Langmuir, Volume 6 (1990), pp. 1055-1062

[21] S. Hyde; S. Andersson; K. Larsson; Z. Blum; T. Landh; S. Lidin; B.W. Ninham The Language of Shape, Elsevier, 1997

[22] J.N. Israelachvili; D.J. Mitchell; B.W. Ninham Therory of self-assembly of hydrocarbon amphiphiles into micelles and bilayers, J. Chem. Soc. Faraday Trans. II, Volume 72 (1976), pp. 1525-1568

[23] N. Kanei; Y. Tamura; H. Kunieda Effect of types of perfume compounds on the hydrophile–lipophile balance temperature, J. Colloid Interface Sci., Volume 218 (1999), pp. 13-22

[24] A. Khan; E.F. Marquis Synergism and polymorphism in mixed surfactant systems, Curr. Opin. Colloid Interface Sci., Volume 4 (1999), pp. 402-410

[25] H. Kunieda; M. Horii; M. Koyama; K. Sakamoto Solubilization of polar oils in surfactant self-organized structures, J. Colloid Interface Sci., Volume 236 (2001), pp. 78-84

[26] H. Kunieda; K. Ozawa; K.L. Huang Effect of oil on the surfactant molecular curvatures in liquid crystals, J. Phys. Chem. B, Volume 102 (1998), pp. 831-838

[27] S.B. La; T. Okano; K. Katakoa Preparation and characterization of the micelle-forming polymeric drug indomethacin-incorporated poly(ethylene oxide)–poly(beta-benzyl L-aspartate) block copolymer micelles, J. Pharm. Sci., Volume 85 (1996), pp. 85-90

[28] M. Landgren; M. Aamodt; B. Jönsson Solubilization of uncharged molecules in ionic surfactant aggregates. 2. Phase equilibria, J. Phys. Chem., Volume 96 (1992), pp. 950-961

[29] R.G. Laughlin Aqueous Phase Behaviour of Surfactants, Academic Press, New York, 1994

[30] D.M. Le Neveu; R.P. Rand; V.A. Parsegian; D.L. Gingell Measurement and modification of forces between lecithin bilayers, Biophysical J., Volume 18 (1977), pp. 209-230

[31] E.B. Leodidis; A. Hatton Amino-acids in AOT reversed micelles. 1. Determination of interfacial partition coefficients using the phase-transfert method, and 2. The hydrophobic effect and hydrogen bonding as driving forces for interfacial, J. Phys. Chem., Volume 94 (1990), pp. 6400-6420

[32] E.B. Leodidis; A.S. Bommarius; T.A. Hatton Amino-acids in reversed micelles. 3. Dependence of the interfacial partition coeficient on excess phase salinity and interfacial curvature, J. Phys. Chem., Volume 95 (1991), pp. 5943-5956

[33] E.B. Leodidis; T.A. Hatton Amino-acids in reversed micelles. 4. Amino-acids as cosurfactants, J. Phys. Chem., Volume 95 (1991), pp. 5957-5965

[34] R. Leung; D.O. Shah Solubilization and phase equilibria of water in oil microemulsions I. Effects of spontaneous curvature and elasticity of interfacial films, J. Colloid Interface Sci., Volume 120 (1987), pp. 320-329

[35] R. Leung; D.O. Shah Solubilization and phase equilibria of water in oil microemulsions II, J. Colloid Interface Sci., Volume 120 (1987), pp. 330-344

[36] M.E.L. Mc Bain; E. Hutchinson Solubilization and Related Phenomena, Academic Press, New York, 1955

[37] M. Malmstem Surface chemistry in pharmacy (K. Holmberg, ed.), Handbook of Applied Surface and Colloid Chemistry, John Wiley & Son Press, England, 2001, pp. 3-38

[38] A. Matero Hydrotropes (K. Holmberg, ed.), Handbook of Applied Surface and Colloid Chemistry, John Wiley & Son Press, England, 2001, pp. 407-420

[39] B.W. Ninham; I.S. Barnes; S.T. Hyde; P.J. Derian; T. Zemb Random connected cylinders: a new structure in three-component microemulsions, Europhys. Lett., Volume 4 (1987), pp. 561-568

[40] V.A. Parsegian; R.P. Rand; N.L. Fuller; D.C. Rau Osmotic stress for the direct measurement of intermolecular forces, Methods Enzymol., Volume 127 (1986), pp. 400-416

[41] M.-P. Pileni; T. Zemb; C. Petit Solubilization by reverse micelles: solute localization and structure perturbation, Chem. Phys. Lett., Volume 118 (1985), pp. 414-420

[42] D.S. Rushforthy; M. Sanchez-Rubio; L.M. Santos-Vidal; K.R. Wormuth; E.W. Kaler; R. Cuevas; J.E. Puig Structural study of one-phase microemulsions, J. Phys. Chem., Volume 90 (1986), pp. 6668-6673

[43] S.A. Safran Fluctuations of spherical microemulsions, J. Chem. Phys., Volume 78 (1983), pp. 2073-2076

[44] S.A. Safran; L.A. Turkevich Phase diagrams for microemulsions, Phys. Rev. Lett., Volume 50 (1983) no. 24, pp. 1930-1933

[45] M.J. Schwuger Detergent in the Environment, Surfactant Science Series, 65, Marcel Dekker, New York, 1997

[46] K. Shinoda; S. Friberg Emulsion and Solubilizaton, Wiley, New York, 1986

[47] R. Strey Microemulsion microstructure and interfacial curvature, Colloid Polymer. Sci., Volume 272 (1994), pp. 1005-1019

[48] Y. Talmon; S. Prager The statistical thermodynamics of microemulsions. II. The interfacial region, J. Chem. Phys., Volume 76 (1982), pp. 1535-1538

[49] C. Tanford The Hydrophobic Effect: The Formation of Micelles and Biological Membranes, Wiley, New York, 1980

[50] F. Testard; T. Zemb Excess of solubilization and curvature in nonionic micromeulsions, J. Colloid Interface Sci., Volume 219 (1999), pp. 11-19

[51] F. Testard; T. Zemb Excess of solubilization of lindane in nonionic surfactant micelles and microemulsions, Langmuir, Volume 16 (2000), pp. 332-339

[52] F. Testard; T. Zemb; R. Strey Excess solubilization of lindane in bicontinuous microemulsions, Progr. Colloid Polym. Sci., Volume 105 (1997), pp. 332-339

[53] Y. Tokuoka; H. Uchiyama; M. Abe; S.D. Christian Solubilization of some synthetic perfumes by anionic–non-ionic mixed surfactant systems. 1, Langmuir, Volume 11 (1995), pp. 725-729

[54] A.L. Underwood; E.W. Anacker Counter-ion lyotropy and micelle formation, J. Colloid Interface Sci., Volume 117 (1987), pp. 242-250

[55] T. Zemb The DOC model of microemulsions: microstructure, scattering, conductivity and phase limits imposed by sterical constraints, Colloids Surfaces A, Volume 129–130 (1997), pp. 435-454

[56] T.N. Zemb; I.S. Barnes; P.J. Derian; B.W. Ninham Scattering as a critical test of microemulsion structural models, Progr. Colloid Polym. Sci., Volume 81 (1990), pp. 20-29

Commentaires - Politique