Abridged version
The atmosphere and the ocean are subject to many dynamical instabilities, which limit the time during which their behaviour can be deterministically forecasted [26]. For longer time-ranges, i.e., longer than 10 to 20 days, the atmosphere cannot be predicted only on a deterministic basis. Particular phenomena, like the Madden–Julian oscillation, exhibit predictability at the 40- to 50-day timescale. This, in turn, leads, for example, to the possibility to predict, using a mixed deterministic-statistical basis, the predominance of some weather regimes and the transitions between different regimes [36]. However, for the general case and for longer timescales, one has to turn to a statistical approach. Predictability at the seasonal and longer time-scales does indeed exist, and is related to the fact that the mean state of the atmosphere is influenced by variations in the other components of the climate system, and especially by variations in its slow components, like the ocean and the land-surface. Predictability is then said of either the first or the second kind [27], depending upon the fact that it originates from either anomalies in the initial forcing conditions, or from a slow evolution of the external forcing. Predictability of the first kind arises, among others, from the persistence of anomalies in the Sea Surface Temperature (SST) field, while predictability of the second kind originates, for example, from changes in radiative forcing associated with variations in the atmospheric chemical composition. Climate being defined at the mean over many different atmospheric states, it can then be predicted up to a few months in advance, which is the typical timescale for the ‘slow components’ of the climate system. This paper addresses the question of seasonal to inter-annual and decadal predictability, i.e., predicting the climate from a few months to a few seasons in advance.
Seasonal climate forecasting relies very often upon Monte-Carlo-type simulations, where the ensemble of realisations is made out of runs with slightly different initial conditions for either the atmosphere and/or the ocean. This allows for an increase in the forecast skill, as shown in Fig. 1, where it can be seen that the correlation coefficients between the observed and predicted anomalies of the 500-hPa geopotential height might reach values of the order of 0.25 for a three-month forecast. Assuming further that the atmospheric model is perfect and that the SST could be predicted with perfect accuracy, such studies show that correlation coefficients of 0.43 could be obtained (i.e., in the so-called ‘perfect-model approach’).
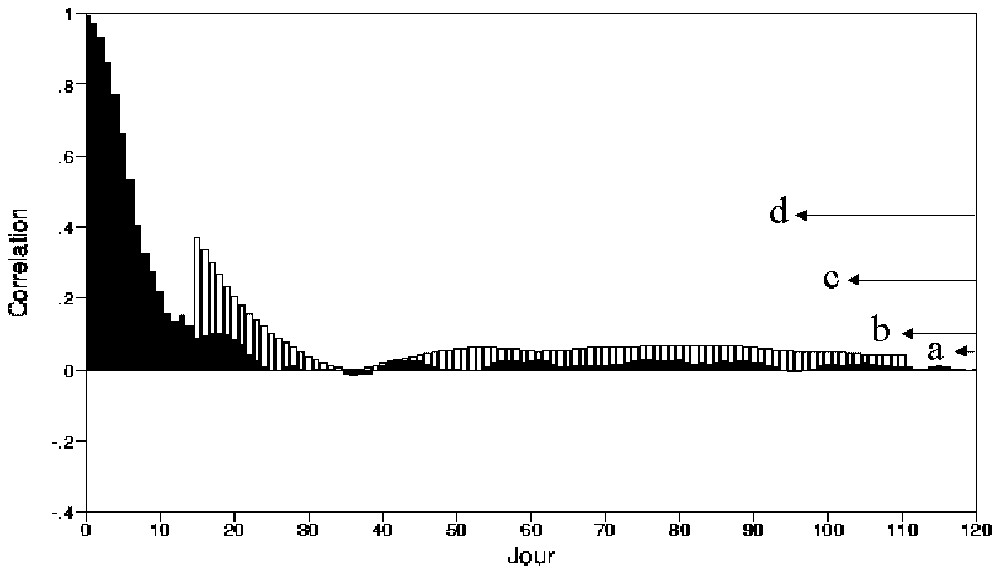
Coefficient de corrélation en fonction de l'échéance pour 15 prévisions quotidiennes (barres noires) et mensuelles (barres blanches) de la hauteur de géopotentiel à 500 hPa sur l'hémisphère nord. Le repère (a) indique le niveau moyen atteint par les présentes prévisions mensuelles ; le repère (b) indique celui atteint par une prévision avec des moyennes sur trois mois, tandis que le repère (c) indique celui atteint dans ce même cas d'une prévision à trois mois, mais réalisée dans le cadre d'une expérience d'ensemble ; le repère (d) indique, quant à lui, le niveau qui pourrait être atteint avec une connaissance parfaite de la TSO. Masquer
Coefficient de corrélation en fonction de l'échéance pour 15 prévisions quotidiennes (barres noires) et mensuelles (barres blanches) de la hauteur de géopotentiel à 500 hPa sur l'hémisphère nord. Le repère (a) indique le niveau moyen atteint par les présentes prévisions mensuelles ; ... Lire la suite
Correlation coefficient of the geopotential height at 500 hPa over the northern hemisphere, as a function of lead-time for 15 daily (black bars) and monthly (white bars) forecasts. Arrow (a) shows the mean skill reached by our actual monthly forecasts; arrow (b) shows the mean skill reached by a single forecast with a three-month average, while arrow (c) shows the mean skill reached by an ensemble-forecast with a three-month average; arrow (d) shows the skill which could be reached if one would know the SST with perfect accuracy. Masquer
Correlation coefficient of the geopotential height at 500 hPa over the northern hemisphere, as a function of lead-time for 15 daily (black bars) and monthly (white bars) forecasts. Arrow (a) shows the mean skill reached by our actual monthly forecasts; arrow (b) shows ... Lire la suite
Such operational seasonal forecasting is performed in a number of centres, among which two of the best known are the European Centre for Medium Range Weather Forecast (ECMWF, Reading, UK) in Europe and IRI in the United States. Both centres are able to provide up to six months in advance reasonably skillful forecasts for the appearance, maintenance, and decay of the El Niño Southern Oscillation (ENSO) phenomenon. ECMWF uses for this purpose a coupled ocean–atmosphere model with daily runs using assimilated SST, the seasonal forecast being the result of averaging over the ensemble of daily simulations. This and other European programmes (see, e.g., Fig. 2) involve ensemble simulations obtained with different atmospheric or coupled models, a technique which has been shown to increase the skill of the forecast [34].
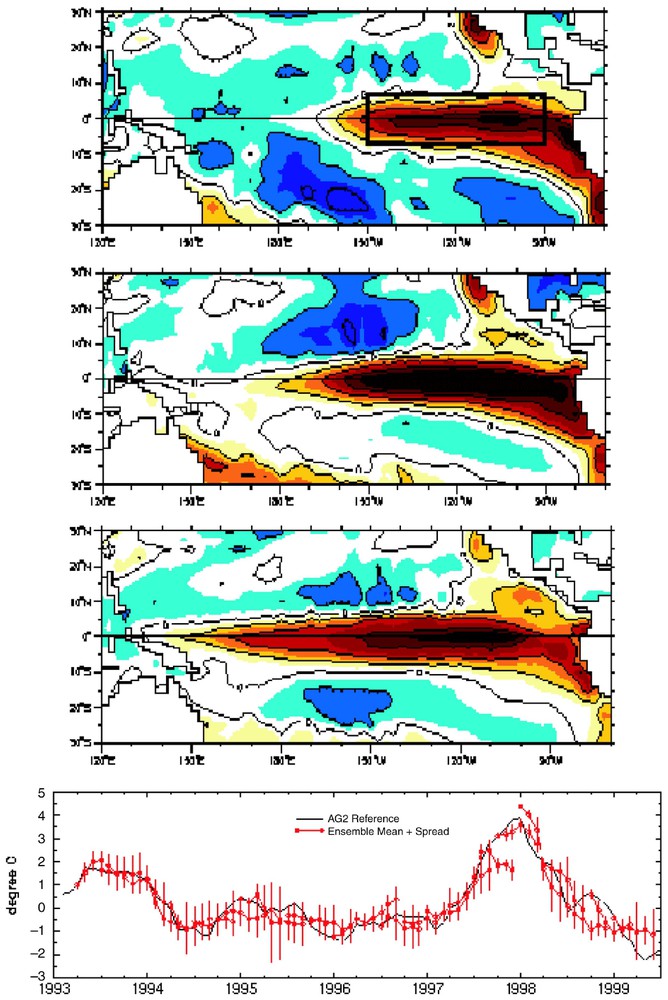
Exemples de prévisions climatiques saisonnières reconstituées réalisées au Centre européen de recherche et de formation avancée en calcul scientifique (CERFACS, Toulouse) [40] dans le cas du Pacifique tropical. De haut en bas : (a) anomalie de TSO observée lors du maximum de l'événement El Niño de fin 1997 ; le rectangle désigne la boı̂te dite « Niño3 » ; (b) prévision de la TSO réalisée trois mois à l'avance ; (c) prévision de la TSO réalisée six mois à l'avance ; (d) reconstitution des prévisions à six mois d'échéance (en rouge) pour la période 1993–1999, moyennées dans la boı̂te « Niño3 » (en noir, anomalie observée). Masquer
Exemples de prévisions climatiques saisonnières reconstituées réalisées au Centre européen de recherche et de formation avancée en calcul scientifique (CERFACS, Toulouse) [40] dans le cas du Pacifique tropical. De haut en bas : (a) anomalie de TSO observée lors du ... Lire la suite
CERFACS (‘Centre européen de recherche et de formation avancée en calcul scientifique, Toulouse’) examples of seasonal climate hindcasts [40] for the tropical Pacific. From top to bottom: (a) SST anomaly observed during the maximum of El Niño at the end of 1997; the rectangle shows the so-called ‘Niño3’ box; (b) 3-month-lead SST forecast; (c) 6-month-lead SST forecast; (d) 6-month-lead forecast (in red) averaged over the ‘Niño3’ box for the period 1993–1999 (the observed anomaly is shown in black).
The forecast can sometimes be extended to even longer time-scales, which is particularly true when the coupled ocean–atmosphere system is subject to relatively high frequency variability, as it is the case of the ENSO (here, high frequency corresponds to the small-end-side of climate variability periods, but is still larger than the periods of internal atmospheric instabilities). El Niño, or the warm phase of ENSO in the tropical Pacific, does indeed induce many climatic disturbances in other ‘teleconnected’ regions of the globe. These disturbances can be also forecasted due to the relatively large amplitude of El Niño-related disturbances. IRI is, for example, issuing seasonal forecasts based upon a consensus between different models, leading to qualify the forecast with a probabilistic rate of success (Fig. 3).
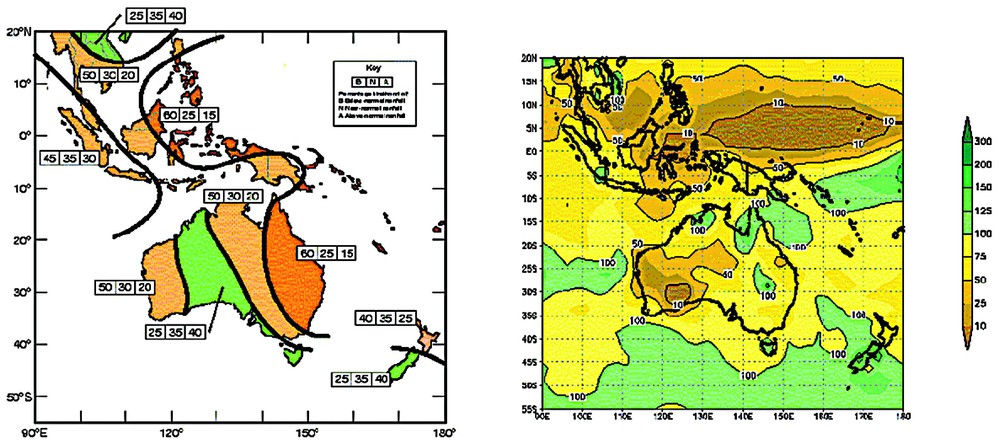
Exemple de prévision climatique saisonnière réalisée à l'IRI. À gauche : prévision probabiliste (exprimée en terciles) des précipitations en Indonésie–Australie, réalisée en octobre 1997 pour le trimestre janvier–février–mars 1998. À droite : pourcentage (par rapport à la climatologie) des quantités de pluies effectivement mesurées pendant la période.
Example of an IRI seasonal climate forecast. Left: probabilistic forecast (in terciles) of the Indonesian–Australian precipitation (the forecast was done in October 1997 for the January–March 1998 quarter). Right: percentage (wrt climatological values) of the precipitation amount that were measured during the period.
Forecasting for higher latitudes, and especially northern Atlantic and Europe, appears however less skillful. Increasing the skill of seasonal climate forecasting is intimately related to the possibility of predicting oceanic thermal structure and currents. It can only be achieved by developing more elaborated assimilation techniques of observational data into global oceanic models, both from in-situ and space-borne sensors [16,39].
Longer-term types of prediction also exist on inter-annual and decadal timescales, but only for certain climatic parameters and given locations. For example, numerical model results tend to indicate that:
- – tropical surface air temperature might be predictable a season or two in advance over the continents, and up to a few years over the oceans;
- – global annual mean temperature might be predictable one year in advance.
Alternative methods based upon variance analysis in the frequency domain [40] do confirm these indications (Fig. 4).
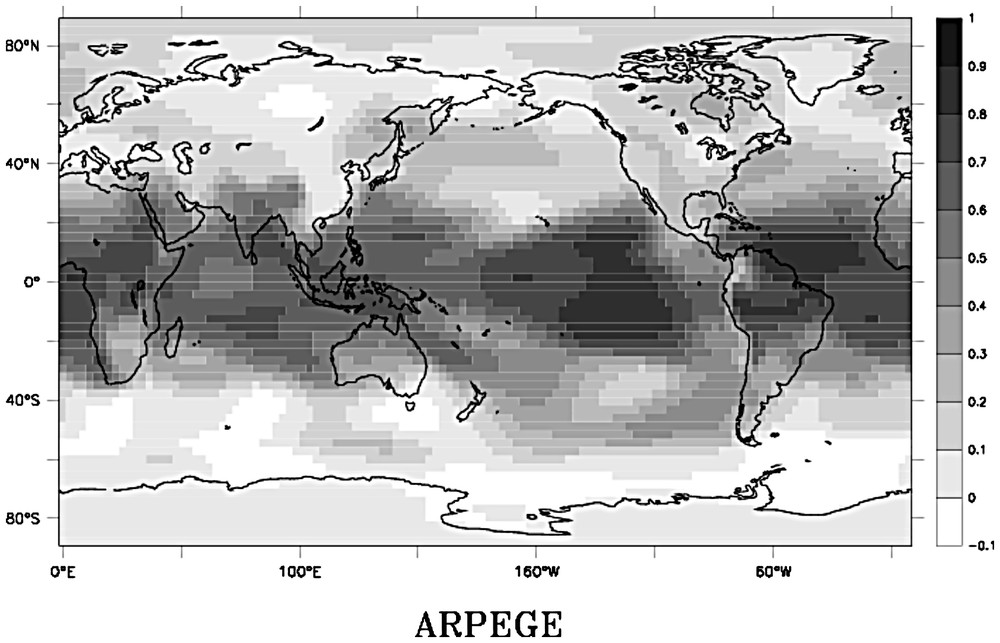
Fraction de variance des fluctuations décennales (supérieures à 6 ans) de la moyenne d'hiver (DJF) du champ de pression de surface due au forçage océanique. L'estimation est faite en appliquant la méthode ANOVA sur un ensemble de huit simulations atmosphériques réalisées avec le modèle ARPEGE forcé par la TSO observée sur la période 1948–1998.
Fraction of the variance of decadal fluctuations (longer than 6 years) of the mean winter (DJF) surface pressure due to oceanic au forcing. This estimation is made by applying the so-called ANOVA method to an ensemble of eight atmospheric simulations from the ARPEGE model forced by SSTs measured over the period 1948–1998.
As an application of seasonal climate forecast [37], electricity production is an example demonstrating the high economic added-value obtained from forecasting colder winter episodes with enough lead time (Fig. 5), although it is not clear yet why predictability is better for certain winters as compared to other ones [6]. Seasonal climate forecasting should anyway improve the management of power plants network, by making it possible to choose the most optimal economic equilibrium between various plants (nuclear, fuel, hydroelectric).
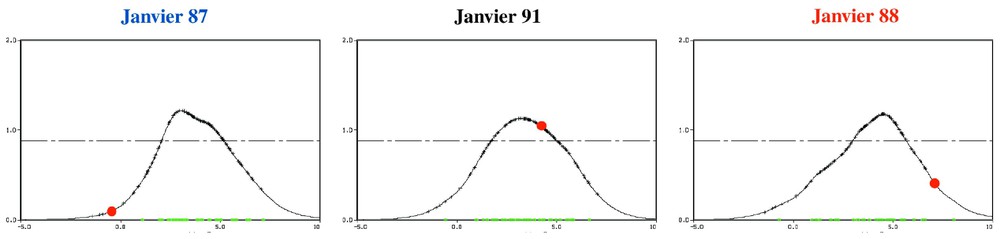
Fonctions de densité de probabilité pour la température moyenne de la France, pour les mois de janvier 1987 (froid), 1991 (modéré) et 1988 (chaud), construites à partir des réalisations fournies par les quatre modèles climatiques utilisés dans le projet PROVOST (36 réalisations). L'axe des abscisses représente les valeurs de la température moyenne pour la France ; le point rouge représente la valeur effectivement observée. Dans le cas médian (janvier 1991), il y a un bon accord entre le pic de la distribution et la valeur observée. Dans les deux autres cas, on constate un déplacement significatif latéral du pic de la distribution vers les valeurs observées, mais l'accord quantitatif est insuffisant, ce qui suggère que les modèles climatiques n'ont pas « capturé » correctement ces valeurs extrêmes. Masquer
Fonctions de densité de probabilité pour la température moyenne de la France, pour les mois de janvier 1987 (froid), 1991 (modéré) et 1988 (chaud), construites à partir des réalisations fournies par les quatre modèles climatiques utilisés dans le projet PROVOST ... Lire la suite
Probability density functions for the mean temperature over France, for the months of January 1987 (cold), 1991 (medium) and 1988 (warm), as derived from a series of simulations by the 4 climate models used in the PROVOST project (36-member ensemble). Abscissa shows the mean temperature for France, and the red dot shows the observed value. One can note a good agreement between the function maximum and the observation for the medium case of January 1991. One can however note a significant lateral displacement of the function maximum toward the observed values for the two other cases; such a relatively poor qualitative agreement suggests that the climate models have not been able to correctly capture these extreme values. Masquer
Probability density functions for the mean temperature over France, for the months of January 1987 (cold), 1991 (medium) and 1988 (warm), as derived from a series of simulations by the 4 climate models used in the PROVOST project (36-member ensemble). ... Lire la suite
1 Introduction
L'atmosphère et l'océan, les deux fluides qui régissent le temps météorologique et le climat, sont le siège de nombreuses instabilités, qui viennent limiter la possibilité d'en prévoir les évolutions temporelles ultérieures à partir de leurs états initiaux : Lorenz [26] a le premier montré que, pour de tels écoulements fluides turbulents, deux situations ne différant initialement l'une de l'autre que de façon infinitésimale aux plus petites échelles spatiales du mouvement, se décorrélaient progressivement, pour atteindre au bout de quelque temps des états totalement dissemblables.
La conséquence pratique la plus connue d'un tel comportement est l'impossibilité de parvenir à des prévisions météorologiques déterministes fiables au-delà d'une certaine durée de prévisibilité, déterminée de facto par le type et l'amplitude des erreurs affectant immanquablement la connaissance de la situation initiale. Dans l'état actuel des techniques météorologiques, cette limite de prévisibilité est estimée entre 10 et 20 jours [28,42].
Malgré cette limite de la prévisibilité météorologique déterministe, on peut légitimement se demander si d'autres types de comportements de l'atmosphère peuvent présenter une prévisibilité à plus longue échéance. Aux échelles intra-saisonnières, Madden et Julian [30] ont montré l'existence d'oscillations tropicales des vents et de la nébulosité, avec une période de 40–50 jours. Aux moyennes latitudes, la variabilité atmosphérique aux échelles 10–90 jours et sa prévisibilité ont fait l'objet de nombreuses études au cours des 20 dernières années. La méthodologie suivie s'est appuyée sur deux axes complémentaires : une approche dite épisodique, basée sur le concept de régimes de temps [24,38] et de transitions associées [50], et une approche cyclique, basée sur l'existence d'oscillations intra-saisonnière [29,36]. L'étude des liens entre les deux approches suggère que certaines phases des oscillations intra-saisonnières peuvent être utilisées comme prédicteurs de l'occurrence des régimes de temps [36].
Pour les échelles saisonnières, et au-delà, l'approche quasi-déterministe doit être abandonnée au profit de l'étude du comportement climatique, défini comme la distribution statistique des états atmosphériques sur un laps de temps donné. L'existence d'une prévisibilité à ces échelles repose alors sur la raison simple suivante : le comportement moyenné du fluide atmosphérique (c'est-à-dire ce qui correspond à la notion de climat) est lui-même très sensible à des modifications et à des variations de ses conditions et de ses forçages externes. Celles-ci concernent l'océan, via spécifiquement la température de surface océanique (TSO), avec lequel l'atmosphère échange masse et énergie, et qui évolue à une échelle de temps significativement moins rapide. Elles concernent aussi la surface des continents, qui peut exhiber, par exemple, des anomalies de longue durée (à l'échelle du temps de prévisibilité météorologique) de son humidité, affectant en retour l'alimentation énergétique de l'atmosphère. Selon Lorenz [27], la prévisibilité est alors dite « de première espèce » et repose sur la connaissance de l'état initial des composantes du système climatique à évolution lente (principalement océan et surfaces continentales) qui sont la « mémoire » du système climatique.
De récentes études ont essayé de quantifier la limite supérieure de prévisibilité, ou prévisibilité potentielle, en utilisant le concept de modèle parfait ou d'ensemble parfait [5,8,19–21]. Le principe consiste à utiliser un modèle couplé global océan–atmosphère (supposé parfait), et à effectuer un ensemble de simulations en perturbant très légèrement les conditions initiales atmosphériques (en supposant implicitement que l'état initial océanique peut être connu parfaitement et spécifié de manière identique pour toutes les simulations). La prévisibilité climatique potentielle peut alors être estimée en diagnostiquant la dispersion de l'ensemble des simulations en fonction de l'échéance. Des grandeurs statistiques classiques, telles que les coefficients de corrélation d'anomalies ou l'erreur quadratique moyenne, peuvent être utilisées pour mesurer la divergence des trajectoires.
Si l'on considère le fluide couplé océan–atmosphère comme un seul système, la variation du bilan radiatif représente dans ce cas une condition externe à celui-ci, dont les variations assurent une extension de prévisibilité. On parle alors, toujours selon Lorenz [27], de prévisibilité « de deuxième espèce ». On connaı̂t deux exemples, maintenant classiques, de ce phénomène : la possibilité d'expliquer les alternances entre climats glaciaires et périodes interglaciaires en réponse aux perturbations de l'orbite terrestre [3], et la prévision du réchauffement climatique anthropique aux échelles temporelles multi-décennales, résultant de l'augmentation de la quantité des gaz à effet de serre (cf., par exemple [15]). Cette prévisibilité de deuxième espèce, liée à la prévisibilité de l'évolution des conditions aux limites, peut également être estimée à partir du concept de modèle parfait.
Nous n'aborderons ici que la question de la prévision climatique dite « saisonnière » et son extension inter-annuelle et décennale : est-il possible de prévoir les anomalies climatiques quelques saisons à l'avance ? Et ceci, que la justification en soit l'existence de conditions de forçage variables, si l'on se restreint à la considération de l'atmosphère seulement, ou l'existence de modes temporels de relativement haute fréquence dans le système couplé océan–atmosphère, avant que celui-ci n'ait atteint lui-même sa propre limite de prévisibilité.
2 Le principe de la prévision climatique saisonnière
Pour illustrer plus spécifiquement ce propos, on considère un critère de prévisibilité parmi d'autres, mais qui a le mérite d'être largement employé en météorologie, le coefficient de corrélation sur l'hémisphère nord de la hauteur de géopotentiel à 500 hPa. Ce coefficient est calculé par corrélation entre les anomalies de géopotentiel prévues à l'échéance considérée et les anomalies observées ensuite à cette même date.
La Fig. 1 montre l'évolution en fonction de l'échéance (0 à 120 jours) pour une série de 15 prévisions d'hiver, réalisée avec une version récente du modèle ARPEGE–Climat [10]. Les barres noires montrent les scores des valeurs quotidiennes. Ceux-ci décroissent rapidement, pour atteindre quasiment zéro au-delà de 20 jours, qui est donc bien la limite de prévisibilité déterministe de l'atmosphère. « Quasiment » ne veut toutefois pas dire « exactement », car on constate des valeurs faiblement positives pour pratiquement toutes les échéances restantes. Il n'est pas aisé de prouver statistiquement que ces scores, de l'ordre de 0,01, sont significativement positifs. En revanche, si on calcule les scores sur les moyennes mensuelles glissantes du champ (barres blanches), c'est-à-dire si l'on commence à s'intéresser à l'aspect climatique, on trouve un palier au-delà de 40 jours, avec des corrélations de 0,05. Le minimum vers l'échéance 35 jours est un effet de l'échantillon et n'a pas été trouvé dans d'autres expériences : il n'y a pas de « retour de prévisibilité » (ou return of skill). Comme les prévisions ont été répétées 60 fois en perturbant les conditions aux limites, on peut calculer un intervalle de confiance qui montre que cette valeur de score est significativement positive.
L'explication de ce phénomène de prévisibilité résiduelle tient principalement à l'influence des conditions aux limites océaniques et, dans une moindre mesure, à celle des conditions initiales des variables évoluant lentement, comme l'humidité du sol profond ou la couverture de neige (mais ces dernières variables sont encore trop mal observées pour que leur influence sur la prévisibilité puisse être évaluée quantitativement [13]). La TSO imposée au modèle atmosphérique est prévue dans cet exemple par une méthode statistique, qui donne de bons résultats jusqu'à quatre mois d'échéance. Le modèle modifie son climat sous l'effet de ce forçage, mais y superpose ses « fantaisies », imprévisibles à plus de 10 jours d'échéance. L'opérateur de moyenne temporelle filtre une partie de ces fluctuations erratiques et permet de renforcer la partie de réponse du modèle au forçage océanique, qui a plus de chances de ressembler à la vraie réponse au forçage réel.
Le principe de la prévision climatique saisonnière est alors simple : jeter l'eau du bain et garder le bébé. En effectuant une moyenne sur trois mois au lieu d'un, le filtrage est plus efficace et on obtient une corrélation de 0,10 pour la moyenne des mois 2, 3 et 4 (ici janvier, février et mars). On pourrait augmenter la période de moyenne, mais la prévision perdrait en intérêt pour l'utilisateur, et la qualité se dégraderait, du fait que l'océan perd lui aussi progressivement sa prévisibilité. Pour augmenter l'efficacité du filtre, on répète la prévision, en perturbant aléatoirement les conditions initiales ou les conditions aux limites. Ici sont effectuées 60 prévisions, en introduisant un bruit aléatoire dans le schéma de prévision statistique de TSO [10]. La corrélation de la moyenne saisonnière atteint alors 0,25. Pour aller plus loin, il faut faire des progrès en modélisation et en prévision de la TSO. On peut aisément évaluer l'impact d'une excellente prévision de la TSO en remplaçant la TSO prévue par la TSO observée. Ce n'est plus une vraie prévision, mais le résultat est assez parlant : avec 60 nouvelles prévisions utilisant le forçage observé de la période 1979–1993, on obtient une corrélation de 0,43. Ceci fixe en quelque sorte le niveau maximal de qualité que pourront atteindre par cette méthode les prévisions climatiques saisonnières dans l'état actuel des capacités de modélisation de l'atmosphère.
3 État actuel de la prévision climatique saisonnière
L'effort actuellement consenti pour le développement de systèmes de prévision climatique saisonnière, en particulier en Europe, suit deux directions principales : d'une part, le développement de capacités de prévision en temps réel, principalement au sein des services météorologiques, et, d'autre part, des actions concertées entre les différents instituts de recherche dans le domaine du climat.
Le CEPMMT joue un rôle de premier plan pour ce qui concerne le premier aspect : la mise en place d'une équipe dédiée en 1995, puis, notamment, la prévision réussie de l'anomalie climatique majeure « El Niño » de 1997 et de son basculement vers la situation symétrique, appelée « La Niña » [16,17,33] l'ont placé à l'avant-garde. Le système de prévision utilise un modèle couplé, dont les composantes atmosphérique et océanique sont de résolution basse (respectivement 1,875 degrés et 2 degrés de latitude–longitude en moyenne), et sont initialisées par l'analyse météorologique du jour, et par l'assimilation des données océaniques de température in situ disponibles en temps réel, collectées par des bateaux et par des réseaux de bouées fixes. Chaque jour, une analyse océanique et une prévision à six mois d'échéance sont effectuées, les résultats étant ensuite regroupés pour chaque mois (les résultats des prévisions dans les tropiques sont consultables via Internet : http://www.ecmwf.int/services/seasonal/forecast/index.jsp). Ce type de système de prévision reste pourtant affecté d'erreurs systématiques, qui dépassent souvent l'amplitude des anomalies à prévoir [46]. La connaissance de ces erreurs nécessite de refaire un grand nombre de prévisions en temps passé et de les comparer à la réalité observée. Par conséquent, toute modification du système requiert la ré-analyse de sa capacité prédictive sur de grandes périodes. Ajouté à cela, la nature statistique de la prévision climatique saisonnière, qui impose des ensembles de prévisions de taille suffisante, fait que la capacité de calcul nécessaire à un tel système de prévision est très importante. C'est la raison pour laquelle les principaux services météorologiques, qui sont à même de disposer de cette puissance de calcul, ont entamé l'exploitation de systèmes plus ou moins proches, tels Météo France [10], qui utilise un modèle océanique simplifié de prévision statistique de la TSO (cf. ci-dessus), ou le Service météorologique du Royaume-Uni, qui utilise une composante océanique restreinte au Pacifique tropical.
Pour ce qui concerne le second aspect, les actions de recherche actuellement en cours entre les différents instituts, dans le cadre des programmes-cadres de recherche de l'Union européenne, préfigurent sans doute ce que les services météorologiques pourront mettre en œuvre de manière opérationnelle à moyen terme. Le projet PROVOST (PRediction Of climate Variations On Seasonal to interannual Timescales) [34] a permis de définir un protocole commun d'expériences de prévision d'ensemble (36 prévisions) pour comparer les capacités prédictives de quatre modèles climatiques atmosphériques (dont une version plus ancienne d'ARPEGE–Climat) dans des conditions où l'océan est supposé parfaitement connu via la TSO (coefficient de 0,38, cf. Fig. 1). Au-delà de cette comparaison, la mise en commun des résultats a permis la combinaison des résultats en un « multi-modèle », qui permet non seulement de prendre en compte l'incertitude liée à l'état initial de l'atmosphère, mais aussi celle liée à la connaissance de la physique du climat via la formulation des modèles. Les résultats montrent que, dans un cadre déterministe, le « multi-modèle » est meilleur que la moyenne des performances des modèles pris individuellement, mais pas meilleur que le meilleur des modèles [35]. On peut aussi considérer la prévision sous un angle probabiliste, c'est-à-dire en prédisant une probabilité d'occurrence pour certains événements climatiques choisis (tels que sécheresse, épisode froid...). En utilisant alors les mesures de performances appropriées [34], le « multi-modèle » est incontestablement supérieur, y compris au meilleur des autres modèles, et ce indépendamment du fait que l'ensemble de prévisions du « multi-modèle » est de plus grande taille.
Le projet DEMETER (Development of a European Multimodel Ensemble system for seasonal to inTERannual prediction ; voir http://www.ecmwf.int/research/demeter/) reprend les principes de PROVOST, en y ajoutant la prise en compte du couplage avec la composante océanique (cf. ci-dessous), ce qui est plus proche de véritables prévisions. L'échéance de prévision est de six mois et la période d'étude couvre environ trente ans (1970–2000). Outre ces expériences coordonnées d'étude de la prévisibilité, le projet entreprend de tester l'utilisation de ces prévisions dans différents domaines d'application (cf. ci-dessous). D'autres projets permettent d'étudier plus spécifiquement la prévisibilité liée à la mousson, d'étudier plus avant les erreurs systématiques des modèles ou de quantifier l'apport d'observations océaniques.
4 La prévision ENSO et les tropiques
Il est utile d'examiner plus spécialement les capacités de la prévision climatique saisonnière dans le cadre spécifique des tropiques, où la prévisibilité se révèle plus importante que pour les latitudes tempérées : le phénomène global « El Niño–Oscillation Australe » (ENSO en anglais) y a en effet une signature très forte. Le phénomène ENSO [4], signal inter-annuel couplé océan–atmosphère, a une période d'occurrence se situant entre deux et huit ans. El Niño et La Niña, qui représentent les phases plus chaudes ou plus froides que la normale dans le Pacifique équatorial, sont des signatures de l'ENSO dans ce même océan. Les phases ENSO du Pacifique commencent souvent d'avril à juillet et persistent pendant un an environ, affectant ainsi le climat de l'hiver et du printemps de l'hémisphère nord. Des évolutions semblables, avec des mécanismes physiques semblables à ceux du Pacifique, ont été récemment identifiées dans les océans Indien et Atlantique [31,49]. D'une manière générale, et malgré les efforts de surveillance du climat à partir de réseaux d'observation globaux, prévoir le démarrage d'une phase de l'ENSO présente aujourd'hui des difficultés plus grandes que celles relatives à la prévision de son évolution ultérieure (S. Zebiak, communication personnelle).
La prévision climatique saisonnière de l'ENSO (cf. par exemple [47]), se fait à partir de simulations de modèles couplés océan–atmosphère, initialisés avec les TSO du Pacifique tropical. Un des résultats immédiat en est la prévision de la TSO, à quelques mois d'échéance (six à neuf mois) dans cet océan. C'est ainsi qu'environ 60 % de la variance de la TSO Pacifique peut être prévue un an à l'avance (T. Barnston, communication personnelle). En s'appuyant sur cette prévision et sur des résultats statistiques, on peut ensuite estimer la pluviométrie dans des zones tropicales proches du Pacifique. Le problème se complique quand la prévision doit se faire sur des régions du globe plus éloignées, et quand les conditions thermiques « locales » des océans Indien et Atlantique deviennent importantes. Des modèles numériques imbriqués à échelle plus fine sont en cours de développement pour résoudre ces problèmes [45]. Quelquefois, ces modèles locaux sont forcés par la TSO prévue, paramètre utilisé alors comme une condition à la limite.
L'amélioration de la prévision de l'ENSO passant par le traitement statistique d'un ensemble de prévisions à partir d'un ou de plusieurs modèle(s), ceci permet de produire des prévisions dites objectives et consensuelles. La performance d'un modèle, et ce pour une saison donnée, doit d'abord être prise en compte. Ceci s'obtient en comparant statistiquement les modes propres des observations et des prévisions [32]. La matrice résultante des corrélations permet de savoir combien de modes observés seront reproduits effectivement par le modèle. Dans un centre de prévision climatique saisonnière, comme l'IRI aux États-Unis, cette technique de prévision d'ensemble multi-modèles (10 prévisions en général par modèle) comprend aujourd'hui en phase opérationnelle le modèle « ECHAM3 » [39] du Max-Planck-Institut für Meteorologie (MPI-Met, Hambourg, Allemagne), le modèle « MRF9 » [25] de la National Oceanic and Atmospheric Administration, National Centers for Environmental Prediction (NOAA/NCEP, Washington DC, USA) et le modèle « CCM3 » (http://www.cgd.ucar.edu/cms/ccm3) du National Center for Atmospheric Research (NCAR, Colorado, USA). D'autres modèles sont également évalués en parallèle, comme celui du CEPMMT (cf. ci-dessus). Les trois modèles cités sont d'abord forcés avec une TSO dite persistante, sur trois mois environ. En parallèle, une TSO, prévue de six à neuf mois à l'avance, est utilisée comme condition aux limites pour forcer les modèles atmosphériques de circulation générale. La Fig. 2 montre le degré de fiabilité atteint par ce type de prévision à six mois d'échéance dans le cas d'un modèle particulier [40].
Lorsque les prévisions d'ensemble sont établies (une trentaine de simulations), une information supplémentaire peut être obtenue sur la sensibilité des modèles à des conditions aux limites évolutives. Des modèles régionaux plus fins (méso-échelle), du type « RSM » [2] ou « MM5 » [18], peuvent être utilisés pour obtenir des scénarios climatiques sur les continents à partir de prévisions de champs de variables atmosphériques, tels que les géopotentiels, la pression en surface, les vents, l'humidité.
La présentation de la prévision climatique saisonnière de l'ENSO utilise à l'IRI la notion de terciles. Ce sont les trois intervalles à l'intérieur desquels les distributions probabilistes correspondant aux observations passées sont égales (en l'absence de prévision, les probabilités d'être dans l'un quelconque des terciles, et donc d'avoir une saison normale, plus sèche ou plus humide, sont respectivement égales à 33,3 %). La prévision climatique saisonnière de l'ENSO par les méthodes décrites ci-dessus permet de différencier ces probabilités, indiquant à la fois l'occurrence privilégiée d'un type de saison et l'incertitude de la prévision. Par exemple, une prévision de précipitation de 20 % pour le tercile le plus sec, de 35 % pour le tercile normal et de 45 % pour le tercile le plus humide, suggère qu'une saison plus humide a plus de chance de se produire, même si la prévision probabiliste demeure au-dessous de 50 %. Cela indique aussi qu'une fois sur cinq, il reste possible d'avoir une saison plus sèche. Des cartes globales et régionales de prévision climatique saisonnières six mois à l'avance sont disponibles (http://iri.columbia.edu/climate/forecast/) et prennent bien sûr en compte la phase de l'ENSO. Si la qualité de ces nouvelles prévisions reste toujours difficile à estimer au niveau régional, puisqu'elle ne repose que sur un nombre très limité de saisons, il n'en reste pas moins qu'elle peut atteindre des niveaux très satisfaisants (cf. Fig. 3). Cependant, si l'on moyenne pour toutes les saisons et pour des surfaces de la taille d'un continent, une évaluation peut être obtenue à partir de « scores de Heidke » [12] ou « ROC » (Relative Operating Characteristics). Dans les tropiques, les scores de Heidke sont en général positifs, mais tout en restant de valeur modeste. Les scores les plus élevés sont relatifs aux précipitations pendant les phases chaudes ou froides de l'ENSO. En dehors de la situation correspondant à une phase neutre de l'ENSO, les prévisions diffèrent en effet significativement de la répartition (1/3,1/3,1/3), avec pour certains terciles des valeurs atteignant, par exemple, 45 %. Il a aussi été noté des situations extrêmes prévues avec des valeurs de 60 % dans l'un des terciles, par exemple pour des précipitations au-dessus de la normale sur les côtes de l'Équateur et du Pérou au premier trimestre 1998, en bon accord avec la réalité.
5 La prévision océanique
Du fait de sa capacité de stockage de chaleur plusieurs milliers de fois supérieure à celle l'atmosphère et de sa très grande inertie par rapport à l'échelle de prévisibilité atmosphérique, l'océan, et en particulier l'océan tropical, joue donc un rôle crucial pour la prévisibilité du climat aux échelles saisonnières. Dans ce cadre, les données accumulées depuis les années 1980 lors de l'expérience internationale TOGA (Tropical Ocean, Global Atmosphere) [48], et plus encore les réseaux d'observation mis en place et perpétués depuis lors, sont une source d'information qui a permis l'amélioration des modèles océaniques. Par ailleurs, ces réseaux constituent une base de données unique pour tester l'impact de l'information océanique introduite dans un modèle couplé via des méthodes d'assimilation de données, analogues à ce qui se fait pour la prévision météorologique. La disponibilité, depuis le début des années 1990, d'observations altimétriques précises des variations de la hauteur de la mer a accru la quantité de données disponibles. Elle a aussi suscité le développement de méthodes d'assimilation capables de prendre en compte ces différents types de données. Il est maintenant acquis que l'observation océanique tropicale est indispensable à la prévision climatique saisonnière [16,22]. L'assimilation de l'altimétrie seule dans le cadre de méthodes d'assimilation de « première génération » (du type « interpolation optimale ») a un impact limité aux premiers mois de prévision [43] et pose toujours un certain nombre de problèmes scientifiques [40]. En revanche, son assimilation conjointe avec les données in situ est très prometteuse, mais encore peu abordée [44], et nécessite, soit une adaptation fine de ces méthodes, soit des méthodes plus évoluées. Enfin, l'impact des conditions océaniques, et plus précisément de leur incertitude dans les tropiques, peut être utilisé pour générer des ensembles de prévisions. Il s'agit d'introduire une perturbation dans les conditions initiales océaniques, de l'ordre de grandeur de l'incertitude, qui a en principe une persistance plus importante qu'une perturbation atmosphérique. Le projet DEMETER (cf. ci-dessus), ainsi que le deuxième système de prévision du CEPMMT en développement (D. Anderson, communication personnelle), utilisent entre autres ce procédé.
En dehors des tropiques, le rôle de l'océan à ces échelles de temps est moins bien connu. La variabilité océanique, plus complexe, n'est pas dominée par un mécanisme analogue aux ondes tropicales, et le couplage avec l'atmosphère y est moins intense aux échelles saisonnières. Par exemple, l'océan Atlantique nord est principalement forcé par les anomalies atmosphériques en hiver [11]. Néanmoins, l'étude attentive des ré-analyses atmosphériques récentes suggère une influence des anomalies océaniques dans l'Atlantique nord-ouest de fin d'été sur l'hiver suivant en Europe [14]. Il semble se confirmer, par des études faites avec l'hypothèse du modèle parfait, que la variabilité atmosphérique intrinsèque, dominante à ces latitudes, voit sa statistique perturbée par les conditions océaniques [7]. Dès lors, et puisque la prévision océanique à ces latitudes requiert la résolution des échelles moyennes (tourbillons), le développement de l'océanographie « opérationnelle » [9] ouvre des perspectives non encore explorées pour l'initialisation de modèles couplés de prévision. En particulier, un compromis devra être trouvé entre le coût de la résolution nécessaire pour modéliser correctement la dynamique et celui de méthodes d'assimilation complexes.
6 La prévisibilité aux échelles inter-annuelle à décennale
Pour des échelles de temps plus longues que celles considérées jusqu'ici, nombre des travaux déjà cités (qui, rappelons-le, utilisent des modèles différents) indiquent une convergence vers les résultats suivants.
- – La moyenne annuelle globale de la température de surface de l'air (TSA) est potentiellement prévisible une année à l'avance. Pour des échéances encore plus longues, la prévisibilité est très faible. En revanche, les moyennes globales de la TSA sur des périodes plus longues (quasi-décennale et plus) sont aussi potentiellement prévisibles [5,8].
- – La TSA au-dessus des régions océaniques semble sujette à une prévisibilité potentielle aux échelles inter-annuelles à décennales pour le Pacifique tropical, l'Atlantique tropical et l'Atlantique nord. Aux moyennes latitudes, il est aussi probable que le système a une mémoire supérieure à celle d'une simple couche de mélange océanique forcée par les fluctuations stochastiques de l'atmosphère. Le mécanisme de ré-émergence [1] et/ou l'existence d'éventuels modes couplés océan–atmosphère [23] pourrai(en)t être à l'origine de cette augmentation de variance aux basses fréquences. Enfin, le potentiel de prévisibilité sur l'Atlantique nord dépend de l'état initial océanique et en particulier de l'intensité de la circulation thermo-haline [19,20].
- – La TSA sur les surfaces continentales possède une prévisibilité potentielle aux échelles saisonnières à inter-annuelles dans la bande tropicale. En revanche, la prévisibilité potentielle est faible aux moyennes et hautes latitudes (ce qui est vrai aussi pour la pression de surface et les précipitations) et ce, quelle que soit l'échelle de temps [5,8].
Ces caractéristiques peuvent aussi être mises en évidence à partir d'une approche simplifiée du problème couplé complet, en utilisant l'analyse en variance (ANOVA) dans l'espace des fréquences [41] sur un ensemble de simulations atmosphériques multi-décennales forcées par les TSO observées (Fig. 4).
Cette figure montre que l'impact des TSO sur la variabilité décennale du champ de pression en hiver boréal est prédominant dans les régions tropicales, en particulier dans le Pacifique central, l'Atlantique tropical nord, l'Afrique équatoriale et l'Amérique du Sud. En revanche, l'influence des TSO est en général faible pour les latitudes extra-tropicales. Cependant, certaines régions, telles que le Pacifique nord, la côte est des États-Unis et l'Atlantique nord-ouest, ainsi que les mers nordiques et la Scandinavie, présentent des valeurs significatives de l'ordre de 20 à 30 %.
7 Applications économiques
Quelles que soient les performances actuelles et futures des prévisions saisonnières, il est légitime de se poser la question de leur utilité pour la société, et donc de leurs impacts économiques. Un certain nombre d'applications potentielles concernent l'agriculture, la sécurité alimentaire, les systèmes d'alerte précoce pour certaines maladies tropicales (malaria...), sans compter le très grand nombre des divers domaines marchands, dont la clientèle est sensible aux conditions climatiques [37]. Pour n'illustrer plus concrètement et complètement qu'un aspect, nous examinerons ici les utilisations possibles de la prévision climatique saisonnière dans le domaine de la production d'électricité.
L'électricité est un produit qu'il est difficile de stocker (autrement que dans une réserve hydraulique), et il est par conséquent nécessaire d'ajuster en temps réel le niveau de production à celui de la demande. Un producteur d'électricité doit planifier l'usage de ses réservoirs hydroélectriques, planifier la maintenance de ses centres de production thermique (fossiles ou nucléaires), et enfin prévoir sur le long terme des investissements dans de nouvelles capacités de production. Il est aisé de concevoir alors qu'à la fois la demande d'électricité (via l'éclairage, le chauffage, la climatisation) et la production d'électricité (régime des précipitations et son incidence sur le remplissage des retenues hydroélectriques, disponibilité des ouvrages de production d'électricité) soient étroitement liées à la météorologie et au climat, selon les différentes échelles de temps évoquées ci-dessus.
À titre d'exemple, 1 °C d'écart pendant l'hiver signifie, pour la France, la mise en service ou l'arrêt d'une unité de production de 1300 MW : l'hiver doux de 1989–1990 a ainsi entraı̂né une baisse de production de 10 TWh par rapport à une année normale (au sens climatique). Autre exemple, dans la partie ouest du Canada, la capacité de production peut varier dans un rapport 1,5 entre une année sèche et une année pluvieuse (de 35 à 55 TWh environ). Ainsi, anticiper une vague de froid hivernale plusieurs mois à l'avance pourrait s'avérer particulièrement stratégique et économiquement rentable, non seulement pour prévoir l'éventualité forte d'un pic de consommation, mais également pour savoir si les capacités de production seront disponibles au moment où il sera nécessaire de les employer et pour anticiper des stratégies de couverture du risque (en particulier en ce qui concerne la ressource hydraulique).
L'échelle de temps annuelle correspond à un horizon naturel de gestion pour un producteur et distributeur d'électricité. Ce besoin de représenter l'aléa climatique et hydrologique de une à plusieurs saisons en avance est actuellement intégré dans les outils de gestion de la production et dans les outils d'aide à la décision en matière de négoce d'électricité. Jusqu'à présent, ces aléas ont été représentés via des chroniques observées de données climatiques et hydrologiques passées. La prochaine étape sera de considérer l'utilisation des produits de la prévision climatique saisonnière : il faut préparer les méthodes, et apprendre à interpréter au mieux les résultats de ces prévisions. Il s'agira de mettre en liaison des mondes aussi divers que ceux de la météorologie, de l'hydrologie, de la gestion opérationnelle de systèmes électriques, et de la finance, en cherchant à répondre aux questions suivantes :
- – quelles sont les informations climatiques qui sont utiles à l'exploitant lorsqu'il doit arbitrer entre utilisation immédiate et utilisation différée de ses réserves hydrauliques, et quel est le niveau d'incertitude acceptable pour de telles informations ?
- – est-on (ou sera-t-on) capable d'obtenir ces informations avec le niveau de confiance requis ?
- – comment formuler au mieux une information saisonnière prévisionnelle (formulation probabiliste, pondération de scénarios-types) et l'incertitude associée pour faciliter son intégration dans les outils d'aide à la décision ?
Actuellement, plus d'une centaine de scénarios de température du passé sont utilisés pour représenter l'aléa climatique, mais ils sont considérés comme équiprobables. Le travail de recherche entrepris, en particulier dans le cadre du programme PROVOST (cf. ci-dessus), a permis d'étudier comment de telles prévisions saisonnières pourraient être utilisées dans le contexte de la gestion annuelle du parc de production français. Il s'agit de tirer parti d'ensembles de prévisions (sur le passé) assez riches (36 membres pour les hivers et 27 pour les autres saisons) pour fournir des probabilités différentes aux scénarios de base. Les premiers résultats montrent que, dans 70 % des cas environ, cette approche est pertinente [6], mais il reste à les confirmer en utilisant les résultats d'autres projets de recherche en cours. Il faut toutefois noter que certaines saisons particulières de la période considérée n'ont pas été correctement reproduites, et que, pour ces cas, l'emploi de la méthode proposée ci-dessus aurait conduit à des erreurs importantes (cf. Fig. 5).
La perspective de disposer à terme de prévisions saisonnières du climat sur une base régulière reste néanmoins très attrayante, même si des difficultés persistent : ces dernières sont moins de nature méthodologique que liées à la forte variabilité interne du climat aux latitudes tempérées. C'est pourquoi il reste nécessaire de procéder à des phases d'évaluation poussées dans les secteurs de l'économie qui sont susceptibles d'utiliser de tels produits prévisionnels.
8 Conclusion
Deux points particuliers méritent d'être soulignés en conclusion, touchant aux données et aux outils nécessaires à la prévision climatique à courte échéance.
La détermination du rôle respectif des conditions initiales et aux limites pour une échéance donnée est essentielle, si l'on veut concevoir un système opérationnel de prévision climatique. Par exemple, pour un système de prévision à l'échelle décennale, si la prévisibilité est un problème de première espèce (conditions initiales), il est alors crucial de mettre en place un système pérenne d'observations routinières de l'océan permettant de produire une analyse détaillée de l'état océanique servant à initialiser la prévision. Si, en revanche, des erreurs minimes sur les conditions initiales océaniques conduisent à une saturation de l'erreur pour des échelles de temps « rapides », c'est-à-dire ici inférieures à 10 ans, il est alors nécessaire de mieux comprendre la réponse du système climatique à des changements (relativement prévisibles) du forçage radiatif aux échelles pluriannuelles à décennales. La recherche dans ce domaine est actuellement très active, avec entre autres un nouveau projet européen, comme PREDICATE (http://ugamp.nerc.ac.uk/predicate), se donnant pour objectif d'étudier ces questions sur la région Nord-Atlantique et Europe.
Il n'est pas inutile enfin de souligner la très grande parenté des outils numériques qui sont utilisés pour les différents types de prévision, météorologique, saisonnière et climatique à longue échéance. Selon l'échéance visée, il s'avère certes nécessaire de représenter un plus grand nombre de milieux et de prendre en compte une gamme plus large de phénomènes physiques : la météorologie opérationnelle à l'échéance de quelques jours n'a pas besoin d'une prise en compte détaillée de l'océan, et la prévision climatique saisonnière peut considérer la composition chimique de l'atmosphère comme constante. Il n'en reste pas moins que tous ces modèles prévisionnels doivent inclure une description numérique performante pour l'atmosphère s'ils veulent représenter le climat, à quelque échelle de temps que ce soit. Le fait que nombre de modèles prévisionnels utilisent des variantes d'une même modélisation numérique de l'atmosphère représente de ce point de vue une caractéristique très bénéfique : la confrontation quotidienne du modèle d'atmosphère avec la réalité météorologique permet alors en effet d'en améliorer les performances et, peut-être plus encore, d'accroı̂tre la confiance que l'on peut mettre en sa qualité.


