Abridged version
1 Introduction
The analysis of river profiles may bring evidence for tectonic deformation. We analyse 12 parallel river profiles in southwestern Taiwan, at the front of the collision belt (Fig. 1). The region under consideration belongs to the fold-and-thrust belt of the Taiwan Foothills, where active shortening deformation occurs.
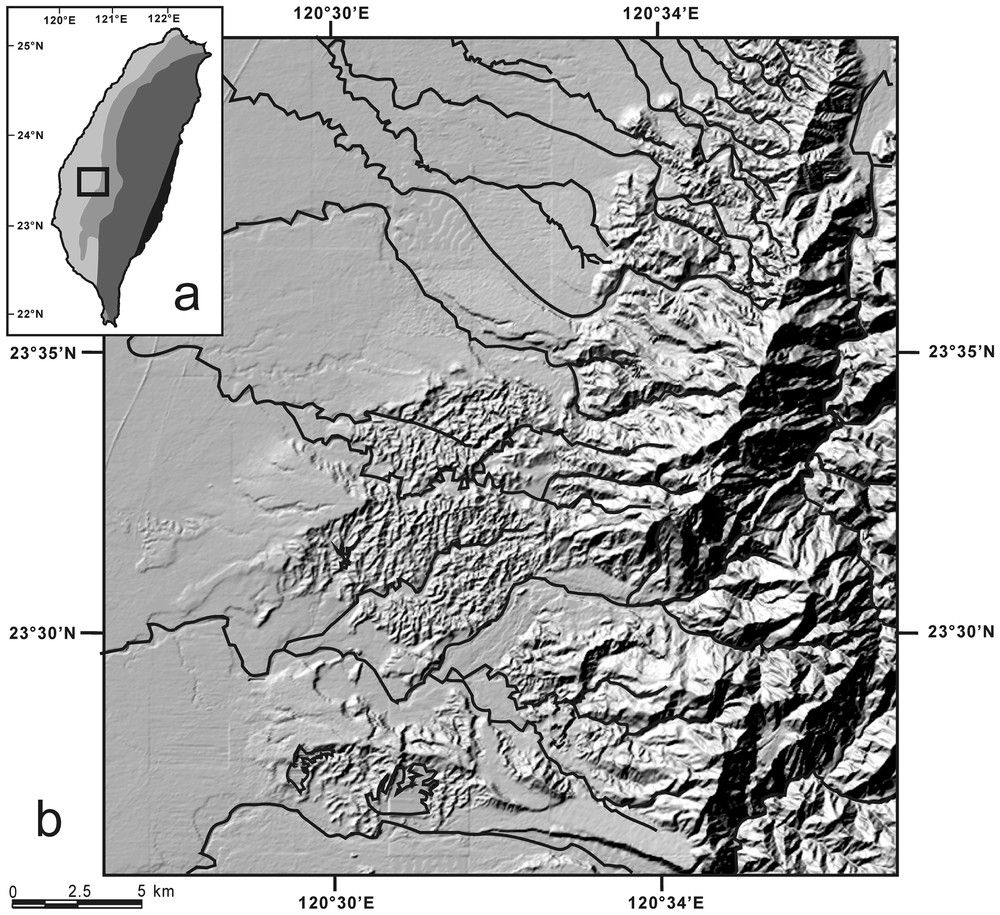
a. Localisation de la région étudiée (petit cadre carré). Unités principales de la chaı̂ne : plaine côtière en gris clair, piedmonts occidentaux en gris moyen, Hsüeshan Range et chaı̂ne centrale en gris sombre, chaı̂ne côtière en noir. b. Morphologie de la région de Chiayi (éclairage provenant du nord-ouest). Rivières en trait noir.
a. Location of the studied area (small square frame). Main units of the Taiwan belt: coastal plain in light grey, western foothills in medium grey, Hsüeshan Range and central range in dark grey, coastal range in black. b. Morphology of the Chiayi area (illuminated from northwest). Rivers highlighted as black lines.
2 Principle of mathematical analysis of river profiles
Considering the relationships between morphometric features and dynamic parameters, numerous physical models have been proposed. They are not referred to herein because, as will be shown, we had to adopt a different, empirical approach. In the absence of perturbation, most natural streams develop a smooth, upward-concave profile controlled by variables related to morphology, dynamics, and lithology. The profile of a major river is composed of segments, depending on the existence of tributaries. Anomalies may result from erosion–deposition phenomena, or active deformation. The anomaly may propagate far downstream. In Taiwan, the stage of maturity was almost never reached, because of active uplift and deformation. The neotectonic characteristics of the area studied suggest that it is reasonable to assume that the tectonic-erosional relationships are close to dynamic equilibrium.
A comprehensive physical analysis of the river behaviour in the studied area is not yet feasible, because it would require uncontrolled assumptions about major parameters (discharge, sediment transport, etc.). Where these parameters are not constrained by data, modelling uncertainties are too large. Our attempts at modelling in the Hsiaomei area revealed that no satisfactory modelling could be done with the presently available data. An additional difficulty resulted from the location of major anomalies near the junction between the hilly-mountainous domain and the coastal plain, where both the data and the physical laws differ. We consequently launched a 2002–2004 campaign of data acquisition in order to feed our future physical modelling, and adopted the empirical mathematical analysis described herein for the preliminary study of river profiles. Provided that drainage properties are taken into qualitative account, we claim that such an empirical analysis gives more robust results than a theoretical physical approach in cases where data cannot constrain river model parameters.
The principle of our study is simple. First, in the very first approximation, we consider the entire river profile and we adjust a smoothed profile. Second, we identify the altimetric anomalies of the riverbed with respect to this profile. We refine the numerical analysis through exclusion of the anomalous river portion, thus obtaining the theoretical profile that best fits the other portions; this profile is implicitly considered close to dynamic equilibrium. Third, we examine the anomaly zone in terms of spatial correlation between different streams, and we determine its origin through consideration of independent geological information.
3 Search for a best-fitting theoretical river profile
One should first define a theoretical profile, i.e. an equation giving z (riverbed elevation) as a function of x (downstream distance). Although our approach is purely empirical, the choice of the adopted functions is not arbitrary: based on theoretical considerations, Morris and Williams [8] recommended the use of exponential functions rather than power or logarithmic ones. The simplest exponential function results from differential equation (1), which means that for a small variation of x, the change in elevation is proportional to elevation. Integrating (1), one obtains Eq. (2), giving z as a function of x.
However, the comparison with actual profiles showed that Eq. (2) is too simple to provide acceptable fits. More degrees of freedom, and hence a larger number of parameters, are necessary. A number of experiments highlighted the capacity of the exponential function to yield realistic fits, provided that the exponent is a polynomial with a degree large enough. We finally adopted the general form of Eq. (3), with a degree n of the polynomial exponent function. This equation keeps major properties of Eq. (2). We carried out a regression analysis to find the theoretical profile as close as possible to the actual profile. We thus obtained the values of the n+1 parameters, ai (i=1,n) and λ, for the best-fitting theoretical curve. Weighting gave identical importance to all portions of river course.
To find the curve that best simulates the actual river profile, one should determine the appropriate value of the degree, n, of the polynomial exponent function. A low-degree function results in smoothing, a high-degree function tends to follow irregularities of the actual profile. For each river profile, we used several functions with increasing values of n. Values of n smaller than 4 generally provided unacceptable misfits. Fits with values larger than 6 were not significantly better than for degree 6, given the data uncertainties. With the profiles of Fig. 2, realistic fits were obtained with n from 4 to 6 (5–7 parameters).
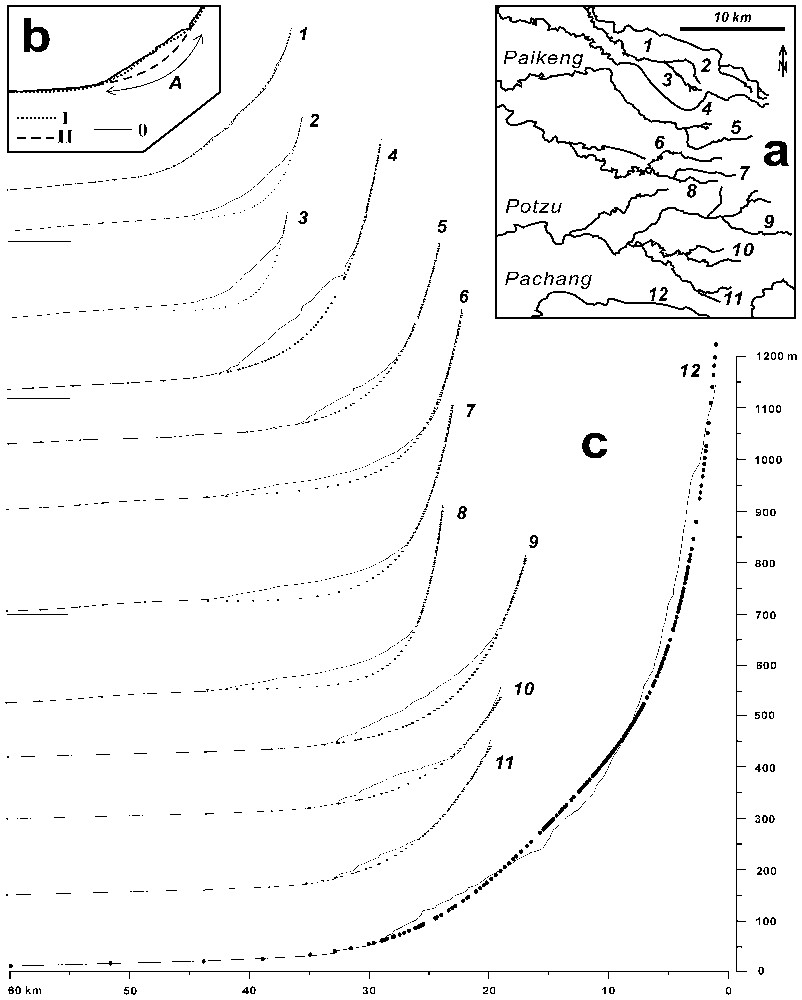
a. Localisation des 12 rivières étudiées (1, Shihniu ; 2, Luntzu ; 3, Kanting ; 4, Tahukou ; 5, Huahsing ; 6, Chiuchungkeng ; 7, Nanching ; 8, Kankou ; 9, Niuchou ; 10, Choushiu ; 11, Chingshui ; 12, Pachang). b. Principe de la recherche du meilleur ajustement. Profil observé en trait continu (0), premier profil théorique en pointillé (I), profil théorique final en tireté (II). La zone d'anomalie (A) influence la courbe I, non la courbe II. c. Les 12 profils longitudinaux de rivières. Ouest à gauche, numéros 1 à 12 comme précédemment. Profil réel en trait fin continu, profil théorique final avec des petits points noirs. Distance suivant le cours d'eau en abscisse, altitude du lit de rivière en ordonnée (zéro indiqué par un trait horizontal fin sous l'extrémité aval des profils).
a. Location of the 12 rivers studied (1, Shihniu; 2, Luntzu; 3, Kanting; 4, Tahukou; 5, Huahsing; 6, Chiuchungkeng; 7, Nanching; 8, Kankou; 9, Niuchou; 10, Choushiu; 11, Chingshui; 12, Pachang). b. Principle of search for the best fit. Observed profile as solid line (0), first theoretical profile as dotted line (I), final theoretical profile as dashed line (II). The anomaly zone (A) influences curve I, not curve II. c. The 12 longitudinal river profiles. West side on left, same numbers 1–12 as before. Actual profile as thin solid line, final calculated profile shown with small black dots. Along-stream distance as abscissa, riverbed elevation as ordinate (zero indicated by the thin horizontal line below the downstream tip of each profile).
4 Numerical search of the best-fitting river profiles
We constructed 12 longitudinal river profiles from 1:5000 topographic maps (Fig. 2c). The rivers, 1–12 in Figs. 2 and 3, are tributaries of the Peikang, Potzu and Pachang Rivers, 25–60 km long, flowing out of the mountain belt towards the Taiwan Strait (Fig. 1b).
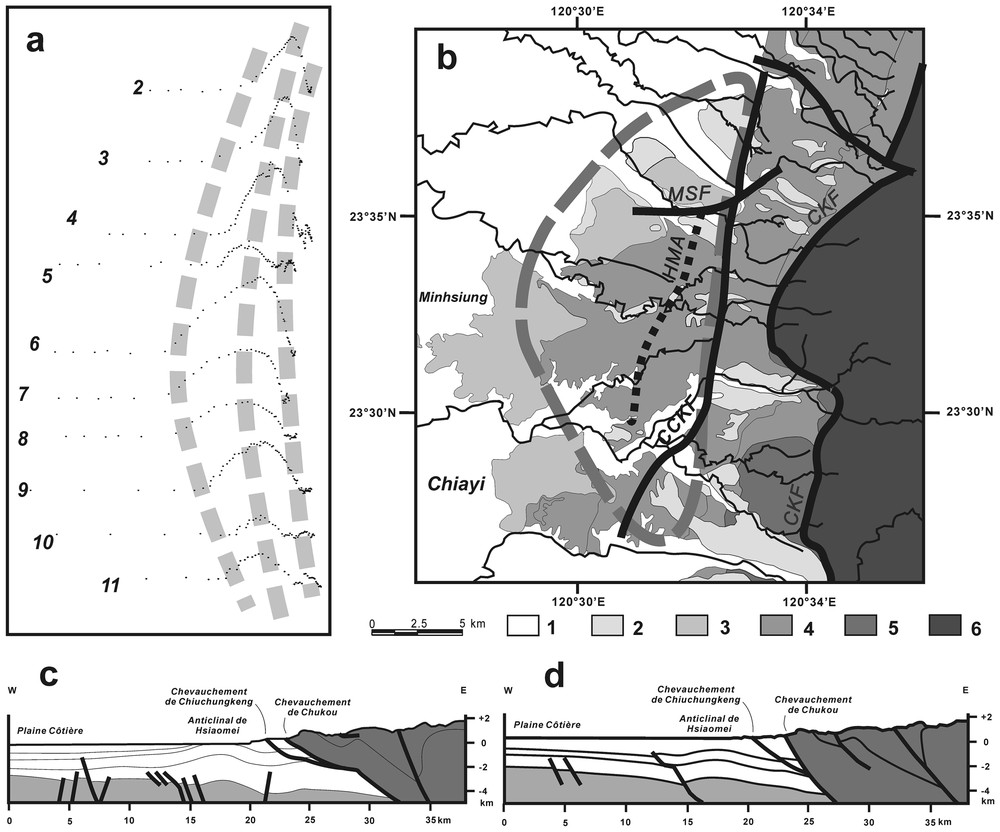
a. Corrélation spatiale entre les zones d'anomalie des profils de rivières 2 à 11. Écart illustré en tant que différence altimétrique entre le profil observé et le profil théorique de seconde étape, pour chaque point de mesure. Mêmes numéros de rivières que sur la Fig. 2. Les lignes grises en tireté épais indiquent le bord ouest, l'apex et le bord est de la zone de soulèvement. b. Contexte géologique de la zone de soulèvement (contour indiqué par la ligne grise en tireté épais). 1, Alluvions récentes, plaine côtière ; 2, terrasses du Quaternaire récent ; 3, terrasse latéritique pléistocène ; 4, formation Toukoshan du Pléistocène (avec deux termes, sableux et conglomératique) ; 5, Pliocène ; 6, unité chevauchante à l'est (indifférenciée). Principales failles en trait noir épais : chevauchement de Chukou (CKF), chevauchement de Chiuchungkeng (CCKF), faille de Meishan (MSF). Axe de l'anticlinal de Hsiaomei en trait noir épais pointillé (HMA). Carte géologique modifiée d'après [4]. c–d. Relation entre la zone de soulèvement de l'anticlinal de Hsiaomei et la structure de subsurface, d'après des coupes schématiques illustrant deux interprétations différentes. Bassin d'avant-pays en blanc, avec soubassement en gris clair, unités chevauchantes à l'est en gris foncé, failles normales importantes et principaux chevauchements en trait noir épais.
a. Spatial correlation between the anomaly zones in the ten river profiles 2–11. Misfit shown as the altimetric difference between the observed profile and the second-step theoretical profile, at each datum point. Same reference numbers as in Fig. 2. The thick dashed lines in grey indicate the western edge, the apex and the eastern edge of the uplift zone. b. Geological context of the uplift zone (contour shown as thick dashed line in grey). 1, Recent alluvium, coastal plain; 2, Late Quaternary terraces; 3, Pleistocene lateritic terrace; 4, Pleistocene Toukoshan Formation (with two members, sandy and conglomeratic); 5, Pliocene; 6, eastern thrust unit (undifferentiated). Major faults as thick black lines: Chukou thrust (CKF), Chiuchungkeng thrust (CCKF), Meishan fault (MSF). Axis of Hsiaomei anticline as thick dotted black line (HMA). Geological map modified from [4]. c–d. Relation between the uplift zone of the Hsiaomei anticline and the subsurface structure, based on schematic cross-sections, showing two contrasting interpretations. Foreland basin left white with basement in light grey, eastern thrust units in dark grey, major normal faults and thrusts as thick black lines.
For each river, we carried out two series of numerical adjustments. First, we determined the best-fitting curve (I in Fig. 2b) for the whole profile (0 in Fig. 2b). Whereas anomalies are minor in profiles 1 and 12, profiles 2–11 showed a major positive anomaly. As a second step, we ignored the data points inside the anomalous portion (A in Fig. 2b) and we performed a new regression with the remaining points. We thus obtained the curve (II in Fig. 2b) that best fits the profile, except the anomaly. The comparison between the original profile and this new theoretical profile (Fig. 2c) reveals the shape and along-stream location of the anomaly.
To characterise the anomaly regardless of the slope of the river, we simply calculated the difference in elevation between the observed and calculated profiles (Fig. 3a). This misfit is negligible along the downstream portion, in the Coastal Plain, and minor along the upstream portion. Between these portions, a major positive anomaly is evidenced in profiles 2–11. This anomaly zone is delineated in Figs. 3a and 3b, which reveal high levels of spatial correlation between independently reconstructed anomalies.
5 Tectonic significance of the riverbed elevation anomaly
The anomaly does not result from local sediment accumulation, because several rivers cut through the sedimentary formations of the Pleistocene (Fig. 3b). The differential erosion that results from variations in lithology cannot be invoked to explain the anomaly, because the formations cut by the rivers are variable in lithology (Fig. 3b). The positive anomaly thus reveals tectonic uplift. This conclusion is supported by the good correspondence between the elongated anomaly zone and the structural pattern of the area. Over a distance of about 20 km, the eastern edge of the anomaly zone coincides with the Chiuchungkeng Fault, a west-verging thrust fault west of the major Chukou thrust (Fig. 3b). The contour of the anomaly zone reflects the shape of a 30 km long uplift domain, the Hsiaomei anticline in the broad sense. We conclude that the anomaly zone indicates the ongoing uplift of this broad anticline.
The asymmetrical shape of the anomaly deserves consideration in light of the deep structure at the front of the fold-and-thrust belt (Fig. 3c and 3d). According to the classical interpretation [4], the Hsiaomei anticline is a simple fold of Quaternary age in the foreland previously affected by normal faulting during the Miocene. Recent studies [2,7] suggest that reverse offsets affect the western side of the Hsiaomei anticline. A west-verging Hsiaomei thrust ramp is probably inherited from a normal fault [7]. The structure is interpreted as a foreland anticline (Fig. 3c) or an incipient in-sequence thrust unit (Fig. 3d), possibly resulting from blind thrust activation [3]. The tectonic activity of the Chukou and Chiuchungkeng thrusts influenced the pattern of Late Pleistocene alluvial terraces to the west [5,6].
Serious earthquake damage occurred in the Chiayi region during the last hundred years, probably triggering motion on the Chukou fault zone [1]. We estimate the shortening across the Hsiaomei area by considering the results of the GPS surveys [9]. With respect to the Taiwan Strait, three stations near Chiayi, just west of the Hsiaomei anticline, consistently indicated displacement of towards azimuth 284. Two stations between the Chukou and Chiuchungkeng thrusts, and two other stations in the hangingwall of the Chukou thrust, consistently revealed displacement of towards azimuth 280, which shows that the shortening was absorbed across the Chiuchungkeng thrust and the Hsiaomei anticline. A velocity triangle shows that this shortening reached in the N85°W direction.
The peak amplitude of the altimetric anomaly falls in the range 20–50 m (Fig. 2c), based on adjustments that depend little on n-values. Based on the width of the deforming zone, this amplitude implies tilt angles shallower than one degree, except for the northern three profiles.
6 Conclusion
A mathematical analysis of 12 longitudinal profiles of rivers near Chiayi enabled us to characterise a domain of positive altimetric anomaly, with a length of about 30 km parallel to the belt front, and a width of up to 10 km. In this domain, the riverbeds are higher than reference profiles suggest. This anomaly does not coincide with homogeneous morphological or lithological domains, and cannot be explained by alluvium accumulation or erosion-resistant substratum. It coincides with the Hsiaomei anticline and Chiuchungkeng thrust, which accommodate active shortening at the front of the Taiwan belt. These results show that despite approximations a simple mathematical analysis of longitudinal river profiles enables one to characterise active deformation. As for future studies, it will be interesting to observe how far the dynamic modelling in progress in the same area will improve this result.
1 Introduction
L'analyse des profils de rivières donne accès, sous certaines conditions, à l'évaluation de mouvements verticaux. Nous illustrons cet aspect en analysant douze rivières parallèles situées au sud-ouest de Taiwan, au front de la chaı̂ne de collision (Fig. 1). La région considérée (Fig. 1a) appartient au système plissé et chevauchant des Piedmonts occidentaux de Taiwan, soumis à une déformation active majeure en raccourcissement.
2 Principe de l'analyse mathématique des profils de rivières
À partir des relations entre traits morphologiques (dont la pente du cours d'eau) et paramètres dynamiques (charge sédimentaire, écoulement, etc.), de nombreux modèles physiques du comportement des rivières ont été proposés. Ils ne sont pas énumérés ici car, comme il va être montré, nous avons dû adopter une approche différente, empirique. En l'absence de perturbation, la plupart des cours d'eau naturels atteignent, avec le temps, un profil d'équilibre longitudinal régulier, concave vers le haut. La concavité est fonction de variables liées à la morphologie, à la dynamique et à la lithologie. Le profil d'une rivière importante est formé de segments, en fonction de la présence d'affluents. Des anomalies peuvent être induites par des phénomènes d'érosion fluviatile et de dépôt alluvial, ou par une déformation active. L'anomalie peut se propager loin vers l'aval. À Taiwan, le soulèvement et l'existence de failles actives permettent rarement au profil d'atteindre un stade de maturité. Considérant les caractéristiques néotectoniques du domaine étudié, il est raisonnable de supposer que les relations tectonique–érosion sont proches de l'équilibre dynamique.
Une analyse physique exhaustive du comportement des rivières dans le secteur étudié n'est pas encore possible, car elle exigerait des suppositions incontrôlées relatives à des paramètres importants (débits, transport sédimentaire, etc.). Lorsque ces paramètres ne sont pas contraints par des données, les incertitudes des modèles sont trop grandes. Nos tentatives de modélisation dans la région de Hsiaomei ont montré que le nombre de données disponibles ne permettait pas encore d'atteindre un modèle physique satisfaisant. Une difficulté supplémentaire a résulté de la localisation des principales anomalies à proximité du raccord entre le domaine des montagnes–collines et le domaine de la plaine côtière, car les données disponibles et les lois physiques appropriées y sont différentes. Nous avons donc lancé une campagne d'acquisition de données pour nourrir un futur modèle physique. Parallèlement, nous avons élaboré l'approche mathématique empirique présentée ici pour effectuer l'analyse préliminaire des profils de ces rivières. À condition que les propriétés du drainage soient soigneusement prises en compte, nous prétendons qu'une telle analyse empirique peut donner des résultats plus fiables qu'une modélisation physique rigoureuse, dans les cas où les données ne permettent pas de contrôler les paramètres d'un modèle physique.
La présente étude obéit à un principe simple. Premièrement, nous considérons un profil de rivière dans son ensemble et nous nous efforçons de caractériser, en toute première approximation, un profil régulier. Deuxièmement, nous identifions les anomalies altimétriques le long du cours de la rivière, par comparaison avec ce profil. En refaisant l'analyse numérique après exclusion du tronçon de rivière où se trouve l'anomalie, nous obtenons un profil théorique ajusté aux autres tronçons du profil de rivière ; ce profil est implicitement considéré comme proche de l'équilibre dynamique. Troisièmement, nous examinons l'éventuelle corrélation spatiale entre les anomalies des différents cours d'eau, et nous reconstituons l'origine de l'anomalie en faisant appel à des données géologiques indépendantes.
3 Méthode d'ajustement d'un profil théorique de rivière
Il faut tout d'abord définir un profil théorique, c'est-à-dire une équation permettant de calculer z (altitude de la rivière) en fonction of x (distance vers l'aval). Bien que notre approche soit purement empirique, le choix des fonctions adoptées n'est pas arbitraire. À partir de considérations théoriques, Morris et Williams [8] ont en effet préconisé l'utilisation de fonctions exponentielles, plutôt que de lois de puissances ou logarithmiques. Dans sa forme la plus simple, la fonction exponentielle est le résultat de l'équation différentielle suivante :
| (1) |
| (2) |
Toutefois, la comparaison avec des profils réels a montré que l'équation (2) était trop simple pour conduire à des ajustements acceptables en pratique. Il faut adopter plus de degrés de liberté, donc un nombre accru de paramètres. Divers essais ont prouvé que la fonction de type exponentiel conduit à des ajustements réalistes, à condition d'adopter comme exposant une fonction de x de degré suffisant. Nous avons finalement adopté la forme suivante :
| (3) |
| (4) |
Respectant la contrainte d'une pente vers l'aval et choisissant un degré n, nous avons réalisé un processus de régression afin de définir un profil théorique aussi proche que possible du profil réel. Nous avons ainsi trouvé les valeurs des n+1 paramètres de l'équation (4), soit ai (i=1,n) et λ, décrivant le profil le mieux ajusté. Les points de mesure sont régulièrement espacés en altitude. Pour ne pas fausser le processus d'ajustement, nous avons ajouté une pondération qui confère la même importance à des tronçons de rivière de même longueur.
Il faut déterminer le degré n du polynôme exposant de l'équation (3), qui conditionne la flexibilité de la fonction simulant le profil de la rivière. Si une irrégularité est présente, un degré bas tend à la lisser, un degré élevé à en épouser la forme. Le meilleur degré dépend des données et de leurs incertitudes. Pour chaque profil, nous avons utilisé plusieurs fonctions, avec des valeurs croissantes de n. Les valeurs inférieures à 4 ont généralement fourni des écarts inacceptables. Au-delà de 6, les ajustements ne sont pas significativement meilleurs que pour le degré 6, compte tenu des incertitudes des données. Avec les profils de la Fig. 2, des ajustements réalistes ont été obtenus pour des valeurs de n de 4 à 6 (soit 5 à 7 paramètres).
4 Ajustements numériques des profils de rivières
Nous avons construit douze profils longitudinaux de rivières à partir des cartes topographiques à l'échelle 1 :5000 (Fig. 2c). Les rivières, numérotées de 1 à 12 sur les Figs. 2 et 3, sont les affluents des trois grandes rivières Peikang, Potzu et Pachang, longues de 25 à 60 km, qui s'écoulent de la chaı̂ne de montagnes vers le détroit de Taiwan (Fig. 1b).
Pour chaque rivière, nous avons réalisé deux séries d'ajustements. Premièrement, nous avons utilisé tous les points de mesure afin de trouver la courbe (I sur la Fig. 2b) qui rende au mieux compte du profil observé (0 sur la Fig. 2b). Le profil 1, au nord, ne révèle aucune anomalie significative. Les anomalies mineures du profil 12, au sud, reflètent des variations locales de lithologie–érosion du cours amont et un alluvionnement excédentaire à l'aval immédiat de la sortie des gorges. Les profils de rivières 1–11 montrent tous une anomalie positive, qui ne peut être expliquée aussi simplement. Lors d'une seconde étape d'ajustement, nous avons exclu les points de mesure localisés à l'intérieur de l'anomalie (A sur la Fig. 2b), avant d'effectuer une nouvelle régression numérique. Nous avons ainsi obtenu la courbe (II sur la Fig. 2b) qui s'ajuste le mieux au profil observé hors anomalie. La comparaison entre le profil original et ce second profil théorique (Fig. 2c) révèle la forme de l'anomalie et sa localisation le long de la rivière. Les courbes de la Fig. 2c ont été calculées avec un exposant polynomial de degré 6 pour l'équation (3), soit sept paramètres indépendants.
La zone d'anomalie altimétrique positive des profils de rivières est localisée sur la Fig. 3. Pour caractériser l'anomalie indépendamment de la pente générale de la rivière, nous calculons, pour chaque point de mesure, la différence d'altitude entre le profil observé et le profil calculé final (Fig. 3a). L'écart est négligeable pour le cours aval des rivières, mineur pour le cours amont. Entre ces tronçons amont et aval, une forte anomalie positive apparaı̂t sur les profils 2 à 11. Bien que les analyses des profils aient été conduites indépendamment, la distribution des anomalies témoigne d'une remarquable corrélation géographique (Fig. 3a).
5 Signification tectonique de l'anomalie altimétrique des lits de rivières
L'anomalie mise en évidence ne résulte pas d'accumulations alluviales locales, car plusieurs rivières incisent le substratum pléistocène, au lieu de s'écouler sur leurs propres alluvions (Fig. 3b). Une plus forte résistance du substratum à l'érosion ne rend pas davantage compte de l'anomalie, car les rivières entaillent des formations aux lithologies contrastées : terrasses d'alluvions à graviers et cailloutis, terrasses latéritiques plus anciennes, termes sableux et conglomératique de la formation pléistocène Toukoshan (Fig. 3b). L'anomalie positive révèle donc un soulèvement tectonique. Cette constatation est renforcée par le rapprochement entre son contour allongé et l'organisation structurale de la région. Le bord oriental de l'anomalie suit, sur environ 20 km, la faille de Chiuchungkeng, un chevauchement à vergence occidentale situé à l'ouest du chevauchement majeur de Chukou et à peu près parallèle (Fig. 3b). Le contour de la zone d'anomalie épouse la forme d'une zone de soulèvement longue de 30 km, l'anticlinal de Hsiaomei au sens large. La zone de soulèvement est limitée à l'ouest par des terrasses latéritiques basculées vers la plaine côtière, dessinant un arc de cercle convexe vers l'ouest (Fig. 3b). Nous concluons que la zone d'anomalie altimétrique des rivières est l'expression récente du soulèvement de ce large anticlinal.
Ce dispositif mérite examen dans le cadre de la structure profonde au front de la chaı̂ne plissée et chevauchante (Fig. 3c et 3d). Suivant l'interprétation classique [4], l'anticlinal de Hsiaomei est un simple pli d'âge Quaternaire dans un avant-pays auparavant découpé par des failles normales durant le Miocène. De récentes investigations [2,7] suggèrent qu'en profondeur, des jeux inverses affectent le flanc occidental de la structure anticlinale de Hsiaomei, tendant à développer une rampe chevauchante à vergence occidentale, vraisemblablement héritée d'une faille normale [7]. L'ensemble de la structure peut être interprété, soit comme un simple anticlinal d'avant-pays (Fig. 3c), soit comme une unité plissée et chevauchante au stade embryonnaire (Fig. 3d), résultant peut-être de l'activation d'un chevauchement aveugle [3]. L'analyse stratigraphique du chevauchement majeur de Chukou révèle une grande différence d'épaisseur sédimentaire entre les deux compartiments, différence liée au décalage normal qui prévalait avant la collision et l'inversion structurale. Le chevauchement majeur de Chukou tranche la formation Tokoushan d'âge Pléistocène, et son activité tectonique, comme celle de la faille voisine de Chiuchungkeng, a influencé la disposition des terrasses alluviales du Pléistocène récent, situées plus à l'ouest [5,6].
La région de Chiayi a subi de graves dommages lors de séismes durant les cent dernières années, séismes qui ont vraisemblablement fait rejouer la zone de chevauchement [1]. Nous évaluons le raccourcissement à travers la région de Hsiaomei en considérant les résultats des relevés GPS (par exemple, [9]). Par rapport au détroit de Taiwan, trois stations en bordure occidentale de l'anticlinal de Hsiaomei ont révélé un mouvement homogène de vers l'azimut 284. Deux stations situées entre les chevauchements de Chiuchungkeng et de Chukou, ainsi que deux autres stations sur le chevauchement de Chukou, se sont déplacées de vers l'azimut 280. Aucun déplacement horizontal important ne s'est donc produit sur le chevauchement de Chukou pendant la période de mesure. Le raccourcissement a été absorbé par la zone chevauchante de Chiuchungkeng et l'anticlinal de Hsiaomei. Un triangle des vitesses y indique un raccourcissement de dans la direction N85°W.
L'amplitude de l'anomalie va de 20 à 50 m environ (Fig. 2c). Les déterminations les plus fiables (20–50 m également) sont celles qui dépendent le moins du choix du degré n (rivières 4, 5 et 9). Pour ces profils, la longueur relative du tronçon anormal est moindre, ce qui explique pourquoi la courbe est mieux contrainte. Considérant la largeur de la zone de déformation, ces valeurs impliquent des angles de basculement inférieurs au degré, exception faite des trois profils septentrionaux, qui traversent une zone de soulèvement étroite.
6 Conclusion
L'analyse mathématique de 12 profils longitudinaux de rivières dans la région de Chiayi nous a permis de caractériser une zone d'anomalie altimétrique positive, longue d'environ 30 km et large de 10 km au plus, allongée parallèlement au front de la chaı̂ne. Les rivières y sont systématiquement à des altitudes supérieures à celles que laissent prévoir les profils de référence. Cette anomalie ne correspond pas à des domaines morphologiques ou lithologiques homogènes, et ne peut être expliquée par des particularités alluvionnaires ou de résistance du substratum à l'érosion. Elle coı̈ncide avec l'anticlinal de Hsiaomei et le chevauchement de Chiuchungkeng, qui absorbent un raccourcissement actif notable. Ces résultats montrent qu'en dépit des approximations, une analyse mathématique simple des profils de rivières permet de déceler une déformation active. Pour le futur, il sera intéressant de voir si la modélisation dynamique actuellement entreprise conduit à de meilleurs résultats.
Remerciements
Ce travail a été rendu possible par l'Institut français à Taipei, le National Science Council de Taiwan, le CNRS, l'Institut universitaire de France et le Crous. Nous remercions Q.-C. Sung, M.-L. Hsieh et H. Tsai pour des données ou des suggestions.


