Composition et volume molaire apparent des gels CaSi, une approche expérimentale

Alain Perruchot; Pierre Massard; Jérôme Lombardi

doi:10.1016/j.crte.2003.07.005

Résumés

Français
Anglais

Des gels silico-calciques (CaSi) de synthèse de différentes compositions ont été préparés à partir de solutions mères de métasilicate de sodium et de chlorure de calcium. Ces gels synthétiques CaSi sont de bons analogues des gels naturels frais trouvés au sein des bétons affectés par la réaction Alcalis–Silice (RAS). Les résultats obtenus montrent que ces gels synthétiques, en équilibre avec leurs solutions de formation respectives, présentent un optimum de composition correspondant à un rapport molaire CaO/SiO₂=(C/S)_g≅0,48. Corrélativement, pour cette valeur caractéristique de (C/S)_g, la variation du volume molaire apparent V_g de ces gels avec (C/S)_g semble indiquer un réarrangement dans la structure de ces derniers.

Synthetic CaSi gels of various compositions were prepared from sodium metasilicate and calcium chloride solutions. These synthetic CaSi gels are good analogues of fresh natural gels found within concrete affected by Alkalis–Silica Reaction (ASR). Results show that these synthetic gels in equilibrium with their formation solutions present an optimum of composition for a molar ratio CaO/SiO₂=(C/S)_g≅0.48. Correspondingly, this characteristic value of (C/S)_g denotes a rearrangement in the structure of gels accounted for the variation with (C/S)_g of the apparent molar volume V_g.

Abridged English version

1 Introduction

The silicated gels found in nature may be reasonably regarded as the precursors of well-crystallized minerals [11,12]. The CaSi gels are mainly found within concrete affected by Alkali–Silica Reaction (ASR). ASR consists of chemical attack of reactive silica of aggregate by the interstitial alkaline solution in the presence of portlandite Ca(OH)₂. The disorders of ASR within concrete are attributable to the expansive growth in the limited porous space of concrete of CaSi gels produced by ASR, hereafter called natural gels. The chemical composition of these natural gels was studied by Scanning Electron Microscopy–Energy Dispersive Spectroscopy (SEM–EDS) analysis by several authors [1–4,7].

On the other hand, synthetic CaSi gels are readily prepared by precipitation from mother-solutions of calcium chloride CaCl₂ and sodium metasilicate (SiO₂, Na₂O) [10]. These synthetic gels are good analogues of fresh natural gels products of ASR within concrete [7]. The conditions of growth of natural gels within concrete (hyperalkaline medium, porous limited space) and these previous works suggest a correlative evolution of composition and molar volume of gels. This experimental study is a first approach of that by means of synthetic gels.

2 Composition of gels

We studied eight synthetic gels of various compositions. The stoichiometric composition of gels is deduced from the composition of the residual formation solutions in equilibrium with these gels. According to the cement industry usage, the stoichiometric parameter used is the molar ratio C/S=CaO/SiO₂, respectively written (C/S)_g for the formed gels, and (C/S)₀ for the corresponding theoretical values given by initial solutions. The range of studied composition nearly corresponds to an order of magnitude:

0.3 ⩽ {(C / S)}_{0} ⩽ 2

The following expression permits a plain analysis of the relative difference of C/S between theoretical value and effective value of the gel over all studied range of composition:

\frac{Δ (C / S)}{{(C / S)}_{0}} = \frac{{| (C / S)}_{0} - {(C / S)}_{g} |}{{(C / S)}_{0}} = f [{(C / S)}_{0}]

2.1 Method

For any C/S ratio, the overall balanced reaction of a gel formation writes:

c {CaCl}_{2} + s ({SiO}_{2}, {Na}_{2} O) + x HCl + y NaOH \to {[{(CaO)}_{c}, {({SiO}_{2})}_{s}]}_{gel} + (2 c + x) NaCl + \frac{x + y}{2} H_{2} O

(1)

where c,s,x and y are stoichiometric coefficients. This overall balanced reaction takes into consideration that the formation of any gel does not seem to consume water [5,6]. Then, the following equation denotes the conservation of Na and Cl:

2 c + x = 2 s + y

and, by introducing the stoichiometric parameter C/S of the gel:

2 s (C / S - 1) = y - x

Moreover, all the mother-solution concentrations are 0.1 M in each species. Thus, the volumes of used solutions represent the proportions of reacting species according to c,s,x and y in the balanced reaction (1). Lastly, we put conventionally s=1 for 20 ml of 0.1 M (SiO₂, Na₂O) solution. Then, the previous equation can be written:

2 (C / S - 1) = y - x

According to the C/S value, three cases must be discussed:

• C/S>1⇔y>x; for x=0, it comes y_min such as y_min=2(C/S−1).
• C/S=1⇔y=x; x_min=y_min=0.
• C/S<1⇔y<x; for y=0, it comes x_min such as x_min=2(1−C/S).

So, for each theoretical (C/S)₀ value, the required volume of 0.1 M HCl or NaOH solution in overall balanced reaction (1) is respectively 20x_min ml or 20y_min ml.

Experiments were performed without stirring at 20 °C, 1 bar. Each experiment is independent of the others, and at least in duplicate. After 21 days, each equilibrium is fully reached [9,10] and chemical analyses of Ca and Si are performed by Inductive Current Plasma (ICP) on each residual formation solution in equilibrium with the corresponding gel. Na was not determined, the more that the CaSi structures of gels do not seem to incorporate alkalis cations [5,6].

2.2 Results

The data and the results of experiments are given in Table 1. The curve Δ(C/S)/(C/S)₀=f[(C/S)₀] drawn from these results (Fig. 1) shows a distinct minimum centred on (C/S)₀=0.5 for (C/S)_g≅0.48.

(C/S)₀	Si sol	Ca sol	Si gel	Ca gel	(C/S)_g	Δ(C/S)/(C/S)₀
	(mg l⁻¹)	(mg l⁻¹)	(10⁻³ mol)	(10⁻³ mol)
2	0,38	473,60	1,999	2,816	1,409	0,296
2	0,39	487,80	1,999	2,781	1,391	0,304
1,2	2,14	190,10	1,996	2,153	1,079	0,101
1,2	1,91	208,70	1,996	2,129	1,066	0,111
1	3,99	104,10	1,994	1,896	0,951	0,049
1	4,88	115,90	1,993	1,884	0,945	0,055
0,8	35,86	119,40	1,944	1,469	0,756	0,055
0,8	54,41	133,30	1,914	1,453	0,759	0,051
0,6	101,60	121,00	1,826	1,055	0,578	0,037
0,6	83,00	113,20	1,858	1,064	0,573	0,045
0,5	105,90	106,30	1,811	0,867	0,479	0,042
0,5	112,30	109,70	1,799	0,863	0,480	0,041
0,5	110,60	106,40	1,803	0,867	0,481	0,038
0,5	112,40	110,10	1,799	0,862	0,479	0,041
0,4	118,30	106,40	1,780	0,662	0,372	0,071
0,4	122,10	102,00	1,773	0,667	0,376	0,059
0,3	137,30	103,60	1,735	0,460	0,265	0,116
0,3	137,40	103,70	1,735	0,460	0,265	0,116

Fig. 1
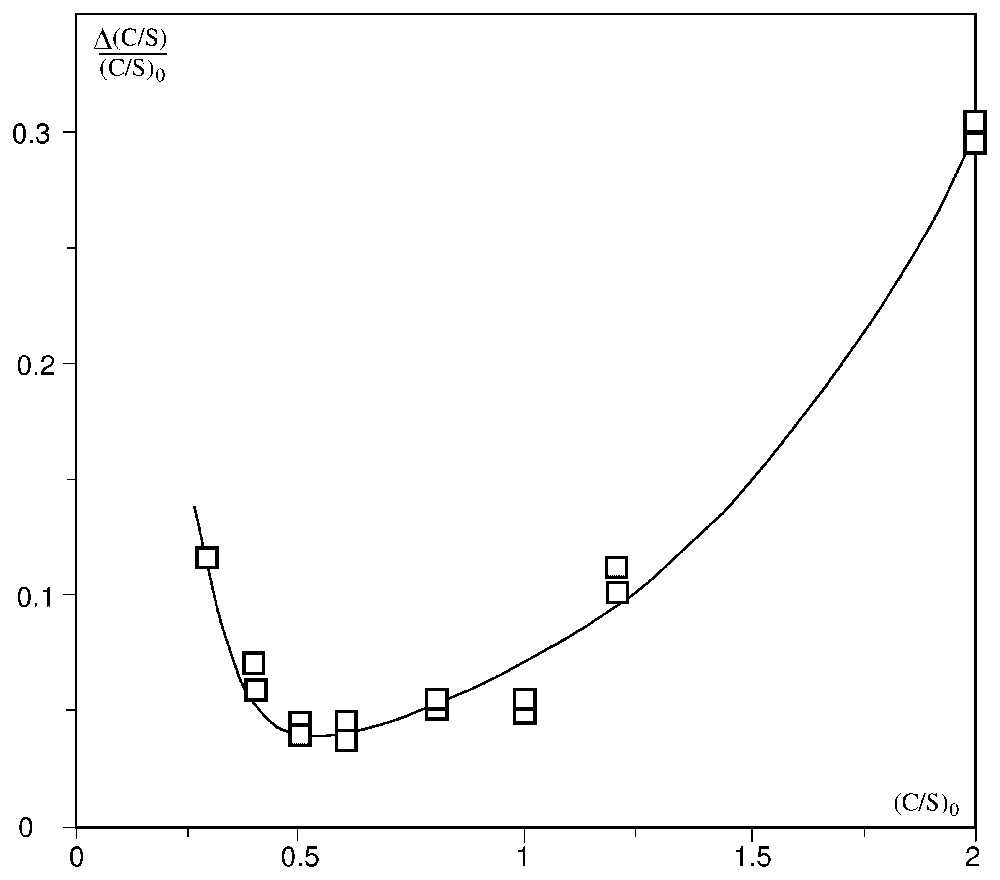
Variation relative de la valeur effective (C/S)_g en fonction de la valeur théorique (C/S)₀ pour huit gels synthétiques d'après les valeurs du Tableau 1. Ordonnées: Δ(C/S)/(C/S)₀; abscisses: (C/S)₀.
Relative variation of the effective value (C/S)_g as a function of the theoretical value (C/S)₀ for eight synthetic gels from the values of Table 1. Ordinate: Δ(C/S)/(C/S)₀; abscissa: (C/S)₀.

Then, this characteristic value indicates an optimum of composition of synthetic gels in equilibrium with their residual formation solutions.

3 Apparent molar volume of gels

As before, we formed eight gels over the range of composition 0.3⩽(C/S)₀⩽2. Nevertheless, the following experiments were conducted using 0.5 M mother-solution concentrations in each species. In these conditions, the amounts of synthetic precipitated gels are more important than with 0.1 M mother-solution concentrations.

3.1 Method

The different values of (C/S)₀ are obtained from 0.5 M mother solutions of each species by changing proportions. The sum of initial volumes of reactants in the overall balanced reaction (1) is always exactly 250 ml. For that, we used the same set of calibrated vessels (jars, pipettes) for all experiments. For each experiment, the positive measured variation of overall volume of the system after formation of gel is δV_m. As a first approximation, the partial molar volumes of reacting species in solution were not taken into account. Likewise, the correction for the volume of formed water given by the overall balanced reaction (1) for each (C/S)₀ value is approximated to be 18 cm³ mol⁻¹ as pure water. This volume of formed water is subtracted from δV_m. Thus, within the accuracy of experiments, the remaining variation of volume δV_g is attributable to the number of moles of gel formed. According to the definition of the compositional effective parameter (C/S)_g and the number s of moles of silica consumed, the apparent molar volume of gel V_g is given by:

V_{g} = \frac{1}{s} \frac{δ V_{g}}{[1 + {(C / S)}_{g}]}

Experiments are performed without stirring at 20 °C and 1 bar as previously. Each experiment is independent of the others, and repeated at least three times. Taking into account the accuracy of the measures, each result is the average of the values which display a dispersion lower than 10%.

3.2 Results

The data and the results of experiments are given in Table 2.

Tableau 2

Variation du volume global δV_m du système en fonction de C/S $=$ CaO/SiO₂ et évaluation du volume molaire apparent V_g du gel en équilibre avec la solution de formation résiduelle correspondante. (C/S)₀: valeur théorique initiale ; (C/S)_g: valeur effective dans le gel

Variation of the overall volume δV_m of the system as a function of C/S $=$ CaO/SiO₂ and evaluation of the apparent molar volume V_g of gel in equilibrium with the corresponding residual formation solution. (C/S)₀: theoretical initial value; (C/S)_g: effective value in gel

(C/S)₀	(C/S)_g	SiO_2 gel	H₂O	δV _m	δV _g	V _g
		(10⁻³ mol)	(10⁻³ mol)	(cm³)	(cm³)	(cm³ mol⁻¹)
2	1,400	25	25	1,750	1,300	21,22
1,2	1,072	25	5	1,227	1,137	21,95
1	0,948	50	0	2,000	2,000	20,51
0,8	0,757	50	10	1,900	1,720	19,57
0,6	0,575	25	10	1,000	0,820	20,82
0,5	0,480	50	25	2,200	1,750	23,65
0,4	0,375	25	15	1,045	0,775	22,56
0,3	0,265	25	17,5	0,864	0,549	17,35

Fig. 2 shows the curve V_g=f[(C/S)_g] drawn from these results. Within the limits of these experiments, the apparent molar volume V_g is noticeably constant from (C/S)_g≅0.5 upwards and decreases clearly from (C/S)_g≅0.5 downwards. Then, the apparent molar volume of gels V_g appears close to 21.5 cm³ mol⁻¹ for (C/S)_g⩾0.5.

Fig. 2
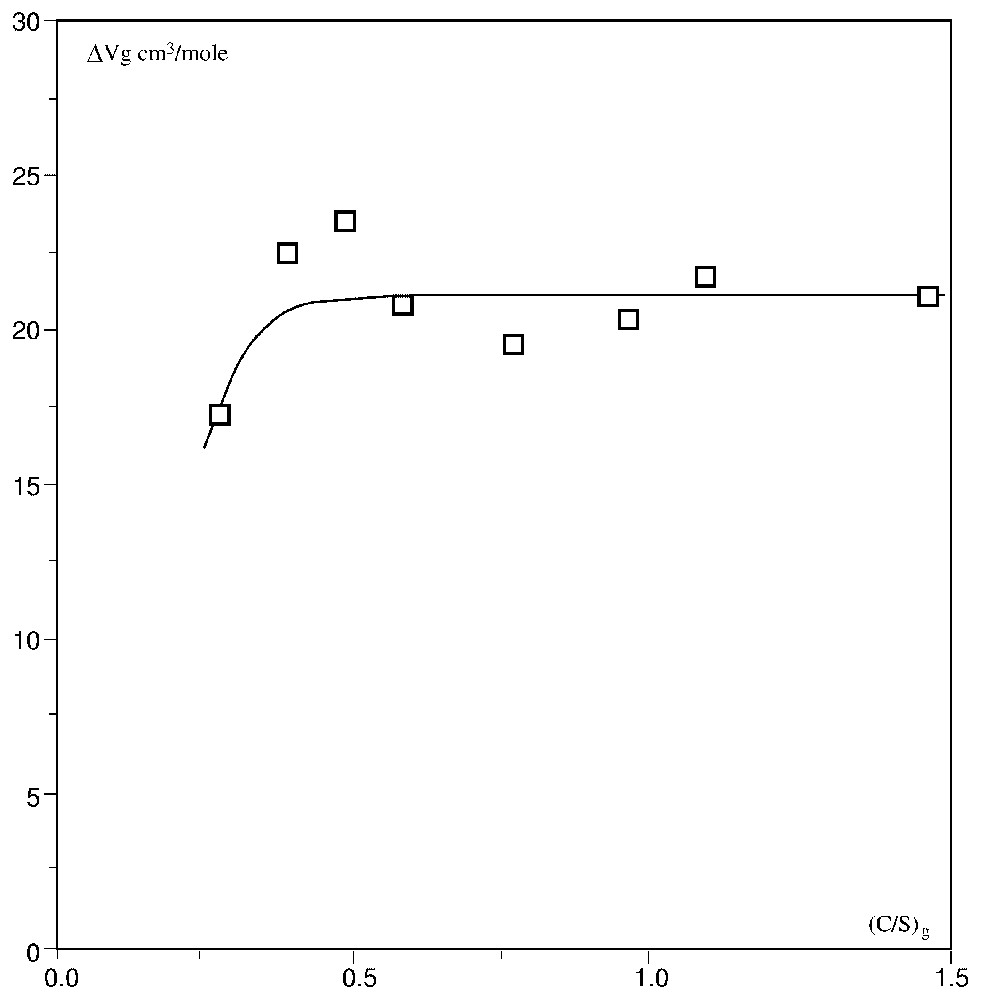
Variation du volume molaire apparent V_g des gels en fonction de la valeur effective (C/S)_g pour huit gels synthétiques d'après les valeurs du Tableau 2.
Variation of the apparent molar volume V_g of gels as a function of the effective value (C/S)_g for eight synthetic gels from the values of Table 2.

4 Conclusions

The characteristic molar ratio (C/S)_g≅0.48 denotes clearly a natural optimum of composition of synthetic gels in equilibrium with their residual formation solutions. These results corroborate the one settled by SEM–EDS analysis of synthetic gels and are also consistent with those which characterize the fresh natural gels products of ASR within their formation medium: reactive silica, portlandite and interstitial alkaline solution [7,8].

The apparent molar volume V_g increases with (C/S)_g, but from (C/S)_g≅0.5 upward, V_g becomes noticeably constant: the characteristic molar ratio corresponds probably to a rearrangement in the structure of gels. The explanation of this phenomenon needs further experiments to determine the real molar volume of these gels, taking into account the partial molar volumes of all reacting species for the same conditions.

1 Introduction

Les gels silicatés rencontrés dans la nature peuvent être considérés comme les précurseurs de minéraux néoformés [11,12]. Les gels silico-calciques (CaSi) se développent principalement au sein des bétons affectés par la réaction Alcalis–Silice (RAS). La RAS est une attaque chimique de la silice réactive du granulat par la solution hyperalcaline interstitielle, en présence de portlandite Ca(OH)₂. Les désordres engendrés par la RAS au sein des bétons sont imputés à la croissance expansive, dans un espace poreux limité, des gels CaSi résultant de ce processus délétère. La composition chimique de ces gels, dénommés par la suite gels naturels, a été largement étudiée par spectrométrie à dispersion d'énergie (MEB–EDS) [1–4,7].

Par ailleurs, des gels de synthèse CaSi de différentes compositions sont aisément préparés par précipitation à partir de solutions connues de chlorure de calcium CaCl₂ et de métasilicate de sodium (SiO₂, Na₂O) [10]. Placés dans des conditions identiques à celles favorisant le développement accéléré des gels naturels frais produits par la RAS au sein d'un béton, les gels de synthèse présentent des caractéristiques morphologiques et stœchiométriques quasi identiques à celles des gels naturels frais [7]. Ces constatations et les contraintes de milieu dans lesquelles les gels naturels se développent au sein d'un béton (milieu hétérogène hyperalcalin, espace poreux limité) suggèrent l'existence possible d'une corrélation entre la composition et le volume molaire de ces gels. Le présent travail constitue une première étude expérimentale de cette possible corrélation, à partir des analogues de synthèse.

2 Composition des gels

Nous avons synthétisé huit gels de diverses compositions. Les compositions de ces gels sont déduites de l'analyse des compositions de leurs solutions de formation résiduelles respectives à l'équilibre avec ceux-ci. Conformément à la notation cimentière habituelle, le paramètre stœchiométrique utilisé est le rapport molaire C/S $=$ CaO/SiO₂, respectivement noté (C/S)_g pour les gels formés et (C/S)₀ pour les valeurs théoriques imposées initialement par les proportions des solutions de formation. Compte tenu des contraintes inhérentes à la technique expérimentale employée, le domaine de composition étudié correspond pratiquement à un ordre de grandeur :

0, 3 ⩽ {(C / S)}_{0} ⩽ 2

Pour suivre la variation de la composition effective (C/S)_g des gels formés en fonction de la composition initiale théorique imposée (C/S)₀, nous introduisons l'expression suivante, qui permet de représenter simplement l'écart relatif entre ces deux valeurs sur tout le domaine de composition étudié :

\frac{Δ (C / S)}{{(C / S)}_{0}} = \frac{{| (C / S)}_{0} - {(C / S)}_{g} |}{{(C / S)}_{0}} = f [{(C / S)}_{0}]

2.1 Méthode

Pour un gel de rapport C/S donné, et compte tenu de la conservation de chaque élément, le bilan réactionnel global de la formation de ce gel s'écrit :

c {CaCl}_{2} + s ({SiO}_{2}, {Na}_{2} O) + x HCl + y NaOH \to {[{(CaO)}_{c}, {({SiO}_{2})}_{s}]}_{gel} + (2 c + x) NaCl + \frac{x + y}{2} H_{2} O

(1)

où c,s,x et y sont les coefficients stœchiométriques. Ce bilan réactionnel tient compte du fait que la formation d'un gel ne semble pas consommer d'eau [5,6]. Dans ce bilan, la conservation de Na et Cl s'exprime alors par l'équation complémentaire suivante :

2 c + x = 2 s + y

soit, en introduisant le paramètre stœchiométrique C/S du gel, et après réarrangement :

2 s (C / S - 1) = y - x

Par ailleurs, toutes les concentrations des solutions mères utilisées dans ces expériences sont 0,1 M en chaque espèce. Ainsi, les volumes de solutions utilisés sont dans les proportions des espèces réagissantes suivant les coefficients stœchiométriques c,s,x et y du bilan réactionnel (1). Enfin, ces volumes sont déterminés en posant conventionnellement s=1 pour 20 ml de solution (SiO₂, Na₂O) 0,1 M. L'équation précédente s'écrit alors :

2 (C / S - 1) = y - x

Compte tenu de la valeur de C/S, trois cas sont donc à envisager :

• C/S>1⇔y>x ; à x=0 correspond y_min tel que y_min=2(C/S−1).
• C/S=1⇔y=x ; alors x_min=y_min=0.
• C/S<1⇔y<x ; à y=0 correspond x_min tel que x_min=2(1−C/S).

Ainsi, pour chaque valeur imposée de (C/S)₀, le volume de solution 0,1 M HCl ou 0,1 M NaOH nécessaire pour satisfaire au bilan réactionnel (1) est respectivement 20x_min ml ou 20y_min ml.

Toutes les expériences ont été réalisées à 20 °C, 1 bar, et sans agitation mécanique du milieu réactionnel. Elles sont indépendantes les unes des autres, et chacune d'elles est répétée au moins deux fois. Après 21 jours, chaque équilibre est totalement établi [9,10]. Pour chaque solution de formation résiduelle à l'équilibre avec le gel correspondant, les analyses chimiques du calcium et du silicium sont effectuées par ICP. Le sodium n'a pas été analysé, étant donné que les structures des gels CaSi ne semblent pas incorporer les alcalins [5,6]. En raison de l'addition de HCl, ou de NaOH, suivant la valeur de (C/S)₀, le pH mesuré à l'équilibre varie entre 11,6 et 13,6.

2.2 Résultats

Les données et les résultats de ces expériences sont rassemblés dans le Tableau 1.

La courbe Δ(C/S)/(C/S)₀=f[(C/S)₀] tracée à partir de ces résultats (Fig. 1) montre un minimum très net, centré sur (C/S)₀=0,5 et correspondant à (C/S)_g≅0,48. Cette valeur caractéristique correspond donc à l'optimum de composition des gels de synthèse à l'équilibre avec leurs solutions de formation résiduelles respectives. Ces résultats confirment ceux obtenus par MEB–EDS, pour des gels synthétiques de diverses compositions, placés dans des conditions favorables au développement de la RAS au sein des bétons [7,8].

3 Volume molaire apparent des gels

En procédant comme précédemment, nous avons repris la synthèse de huit gels sur le même domaine de composition 0,3⩽(C/S)₀⩽2 et pour les mêmes valeurs de (C/S)₀. Cependant, afin d'obtenir des variations de volume plus aisément mesurables, nous avons utilisé des solutions mères 0,5 M en chaque espèce. Dans ces conditions, les quantités de gels formées sont nettement plus importantes qu'avec des solutions mères 0,1 M, et l'équilibre s'établit en une dizaine de jours seulement.

3.1 Méthode

Les différentes valeurs de (C/S)₀ sont donc ici encore obtenues en modifiant les proportions entre les volumes initiaux des solutions mères, suivant les coefficients stœchiométriques c,s,x, et y du bilan réactionnel (1). De plus, compte tenu du but recherché, la somme de ces volumes initiaux est toujours exactement calibrée à 250 ml. Pour cela, toutes les expériences sont réalisées avec un seul et même jeu de verrerie jaugée (classe A), dont les caractéristiques ont été au préalable vérifiées par pesée avec de l'eau distillée. Pour chaque expérience, la variation toujours positive du volume total du système, mesurée après la formation du gel, est notée δV_m. En première approximation, les volumes molaires partiels des espèces réagissantes dans les solutions mères n'ont pas été pris en compte. De même, la correction du volume d'eau formée, conformément au bilan réactionnel (1) et suivant la valeur de (C/S)₀, est déterminée en prenant, comme pour l'eau pure, 18 cm³ mol⁻¹. Ce volume d'eau formée est soustrait de δV_m. Ainsi, dans les limites de ces approximations et de la précision des mesures, la variation finale du volume δV_g est imputable au nombre de moles de gel formé. Compte tenu de la valeur du paramètre stœchiométrique effectif (C/S)_g et du nombre s de moles de silice consommée, le volume molaire apparent V_g du gel est donné par :

V_{g} = \frac{1}{s} \frac{δ V_{g}}{[1 + {(C / S)}_{g}]}

Comme précédemment, toutes les expériences ont été réalisées à 20 °C, 1 bar, et sans agitation mécanique du milieu réactionnel. Elles sont indépendantes les unes des autres, et chacune d'elles est répétée au moins trois fois. Compte tenu de la précision des mesures, chaque résultat est la moyenne des valeurs dont la dispersion n'excède pas 10 %.

3.2 Résultats

Les données et les résultats de ces expériences sont rassemblés dans le Tableau 2. La Fig. 2 montre l'allure de la courbe V_g=f[(C/S)_g] construite à partir de ces résultats. Dans la limite de ces expériences, le volume molaire apparent V_g est sensiblement constant pour (C/S)_g⩾0,5, et il décroı̂t nettement, lorsque (C/S)_g se situe en dessous de cette valeur. Ainsi, le volume molaire apparent V_g des gels semble voisin de 21,5 cm³ mol⁻¹ pour (C/S)_g⩾0,5.

4 Conclusions

Le rapport molaire caractéristique (C/S)_g $≅$ 0,48 indique clairement l'existence d'un optimum de composition des gels synthétiques CaSi à l'équilibre avec leurs solutions de formation résiduelles respectives. Ce résultat confirme ceux obtenus par MEB–EDS pour ces mêmes gels synthétiques, ainsi que ceux caractérisant les gels naturels frais extraits de leur milieu de formation : silice réactive, portlandite et solution interstitielle alcaline [7,8].

Le volume molaire apparent V_g est fonction croissante de (C/S)_g jusqu'à (C/S)_g≅0,5, valeur assimilable à 0,48 à la précision de nos mesures, et demeure sensiblement constant au-dessus de cette valeur remarquable. Cette valeur correspond donc très probablement à un réarrangement de la structure de ces gels. L'explication de ce phénomène nécessite davantage d'expérimentations pour déterminer le volume molaire réel de ces gels, notamment en prenant en considération les volumes molaires partiels de toutes les espèces réagissantes dans les mêmes conditions.