Version française abrégée
1 Introduction
L'érosion chimique ou l'altération des silicates est un des éléments clefs de la régulation du cycle long du carbone qui détermine les variations climatiques de premier ordre (par exemple, [2,3]). L'érosion chimique est soumise à un contrôle complexe comprenant les conditions climatiques, la végétation, l'érosion physique ou encore la lithologie. Parmi ces paramètres, l'érosion physique a été au centre des débats, car elle pourrait jouer un rôle fondamental pour le forçage tectonique du climat [21]. Ce type d'hypothèse reste largement débattu, car le contrôle de l'altération des silicates est complexe à déterminer [10,19,23]. L'érosion physique est très intense sur les bassins himalayens et l'on estime à seulement 3 % le flux d'érosion chimique transporté sous forme dissoute par les rivières. La plupart de ce flux dissous est cependant lié à la dissolution de carbonates [12] et résulte d'une grande variabilité des bassins sur le plan de leur climat, de leur végétation ou de leur topographie. Toute étude de l'érosion chimique en Himalaya est complexe en raison de très forts contrastes saisonniers des précipitations entre la période aride de l'hiver et la mousson qui se caractérise par des précipitations pouvant atteindre deux mètres par mois. Les rivières transportent ainsi près de 80 % de leur charge dissoute durant les seuls mois de mousson, de juin à septembre. Malgré cela, très peu de données sur les rivières himalayennes existent pour les périodes de mousson [12,22] en raison des difficultés d'échantillonnage.
2 Résultats
Nous présentons ici la première estimation complète pour les rivières du Népal central (Fig. 1) bâtie sur les données de plusieurs campagnes d'échantillonnage comprenant en particulier un échantillonnage complet en juillet 1998 (Tableau 1) et sur des données de flux hydrologiques détaillées [24]. Celles-ci permettent de calculer des compositions chimiques annuelles moyennes pour la plupart des grandes rivières du Népal central et quelques petits bassins caractéristiques (Tableau 2). Leur analyse suivant l'approche de Galy et France-Lanord [12] aboutit à l'estimation des parts respectives d'altération des carbonates et des silicates. Celles-ci varient respectivement entre 10 et 300 t km−2 an−1 et 6 et 52 t km−2 an−1 (Fig. 2). L'érosion chimique des carbonates est limitée par l'abondance des carbonates dans les bassins. Pour les grands bassins riches en carbonates, on distingue une relation positive entre le taux d'érosion chimique des carbonates et l'écoulement spécifique. Pour l'érosion chimique des silicates, cette relation est beaucoup plus claire et le facteur précipitation apparaı̂t comme le principal contrôle de l'altération des silicates. Pour un même écoulement spécifique, les rivières Andi, Chepe et Darondi montrent cependant des taux d'altération de silicate variant du simple au double (Fig. 2a). Cette différence pourrait être attribuée à la différence d'érosion physique entre les trois bassins. Les rivières des Siwaliks montrent des valeurs extrêmement élevées (exemple de la Surai), qui sont probablement liées à la dissolution de carbonates sodiques pédogéniques accumulés durant la formation des séries Siwaliks dans la paléo-plaine du Gange. Dans le détail, les facteurs de température, végétation ou érosion physique peuvent expliquer des variations plus discrètes, telles que celles observées entre les rivières Chepe et Darondi.

Map of central Nepal, showing the location of sampling sites on the river network. Geological contours after Colchen et al. [5]. TSS=Tethyan sedimentary series. HHC=High Himalayas crystalline. LH=Lesser Himalayas. HHL=High Himalayas leucogranite. LHN=Lesser Himalayas nappe.
Carte du Népal central, avec la position des sites d'échantillonnage du système de rivières. Les contours géologiques sont tirés de Colchen et coll. [5]. TSS=Séries sédimentaires téthysiennes. HHC=Haut Himalaya cristallin ou dalle du Tibet. LH=Moyen-pays ou bas Himalaya. HHL=Leucogranite du haut Himalaya. LHN=Nappes du bas Himalaya.
Unpublished chemical composition of Himalayan river water
Nouvelles données de concentrations en éléments dissous sur les rivières du Népal central
| Sample | Date | Location | pH | TDS | HCO3 | F− | Cl− | SO4−− | Na+ | K+ | Mg++ | Ca++ | H2SiO4 |
| MO 2 | 01/05/1997 | Marsyandi | 8.0 | 182 | 1746 | 341 | 317 | 381 | 60 | 329 | 812 | 150 | |
| MO 332 | 10/07/1998 | Marsyandi | 8.4 | 116 | 1113 | 3.9 | 59 | 140 | 103 | 62 | 153 | 492 | 135 |
| MO 84 | 09/05/1997 | Chepe | 32 | 252 | 6 | 78 | 67 | 41 | 25 | 130 | 134 | ||
| MO 364 | 16/07/1998 | Chepe | 6.5 | 19 | 117 | 0 | 4 | 32 | 39 | 23 | 17 | 44 | 144 |
| MO 91 | 10/05/1997 | Darondi | 118 | 1356 | 27 | 102 | 113 | 86 | 248 | 447 | 126 | ||
| MO 335 | 11/07/1998 | Darondi | 8.2 | 60 | 616 | 2.3 | 10 | 30 | 78 | 44 | 102 | 181 | 180 |
| MO 375 | 17/07/1998 | Darondi | 56 | 576 | 2.1 | 10 | 28 | 81 | 41 | 92 | 169 | 176 | |
| MO 377 | 18/07/1998 | Darondi | 52 | 548 | 2.1 | 11 | 22 | 70 | 46 | 78 | 167 | 154 | |
| MO 137 | 14/05/1994 | Trisuli 2 | 114 | 1252 | 36 | 112 | 159 | 50 | 146 | 503 | 116 | ||
| MO 300 | 07/07/1998 | Trisuli 2 | 74 | 797 | 2.2 | 10 | 43 | 50 | 41 | 51 | 350 | 86 | |
| MO 200 | 18/05/1997 | Seti | 225 | 3540 | 86 | 257 | 168 | 108 | 584 | 1349 | 100 | ||
| MO 304 | 07/07/1998 | Seti | 129 | 1424 | 0 | 15 | 80 | 46 | 57 | 205 | 543 | 109 | |
| MO 205 | 18/05/1997 | Andi | 132 | 1837 | 52 | 19 | 73 | 34 | 424 | 488 | 100 | ||
| MO 311 | 08/07/1998 | Andi | 8.2 | 68 | 796 | 0 | 21 | 7 | 31 | 16 | 171 | 221 | 91 |
| MO 308 | 07/07/1998 | Kali 4 | 8.6 | 120 | 1194 | 3.7 | 28 | 141 | 61 | 66 | 171 | 520 | 81 |
| MO 314 | 08/07/1998 | Kali 5 | 8.7 | 140 | 1537 | 4.6 | 23 | 97 | 53 | 48 | 308 | 521 | 118 |
| MO 500 | 26/07/1998 | Kali 1 | 8.0 | 180 | 1514 | 8.7 | 208 | 832 | 305 | 49 | 505 | 1015 | 54 |
| MO 515 | 27/07/1998 | Kali 2 | 147 | 1549 | 8.6 | 133 | 594 | 212 | 69 | 391 | 908 | 59 | |
| MO 517 | 27/07/1998 | Kali 3 | 8.6 | 157 | 1614 | 5.8 | 153 | 413 | 200 | 72 | 317 | 846 | 60 |
| MO 215 | 20/05/1997 | Narayani | 8.3 | 2387 | 108 | 218 | 236 | 73 | 421 | 896 | |||
| MO 330 | 10/07/1998 | Narayani | 8.4 | 139 | 1444 | 3.9 | 53 | 112 | 97 | 61 | 244 | 538 | 140 |
| MO 325 | 09/07/1998 | Surai | 8.4 | 306 | 3647 | 9.3 | 23 | 67 | 546 | 75 | 626 | 970 | 209 |
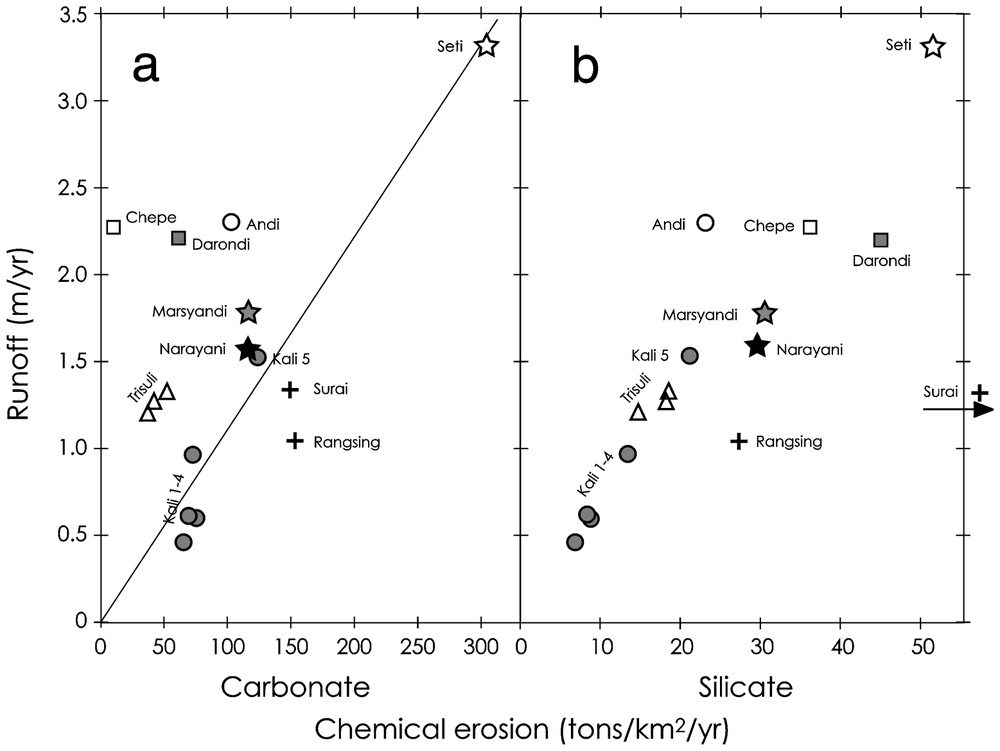
Relationship between river runoff and chemical erosion rates for carbonate (a) and silicate (b) derived from dissolved annual fluxes (Table 2). Chemical erosion rates are calculated from the mass flux of dissolved element divided by the total area of the watershed. Each cation is accounted for its oxide mass for silicate erosion (Na2O, K2O, MgO, CaO and SiO2) or carbonate mass (CaCO3 and MgCO3) for carbonate erosion.
Relations entre écoulement spécifique et érosion chimique des carbonates (a) et des silicates (b) dérivés des flux annuels dissous des rivières (Tableau 2). Chaque cation dissous est pris en compte pour son poids d'oxyde (Na2O, K2O, MgO, CaO et SiO2) pour les silicates ou son poids de carbonate (CaCO3 et MgCO3) pour les carbonates.
3 Conclusion
L'ensemble de ces données montre que l'érosion chimique est déterminée au premier ordre par les précipitations, sauf pour les carbonates, lorsque leur présence dans le bassin est mineure. L'érosion physique apparaı̂t aussi comme un paramètre critique, comme le montre le contraste entre les rivières Andi, Chepe et Darondi. Toutefois, seule une rivière documente les zones à faible vitesse de dénudation ce qui limite la valeur du test à ce niveau. Millot et al. [18] ont mis en évidence une relation entre vitesse d'érosion physique et chimique sur des bassins granitiques et volcaniques et ont proposé une loi puissance liant les deux processus. Appliquant cette relation aux bassins Marsyandi, Trisuli et Narayani, pour lesquels il existe des données de flux de matière en suspension [17], on détermine des flux d'érosion chimiques de silicates qui sont un ordre de grandeur au-dessus de ceux qui sont dérivés des flux dissous des rivières. La relation de Millot et al. est établie à partir d'une rivière à relativement faible vitesse d'érosion. Ceci implique qu'il existe peut-être un effet de saturation lorsque les vitesses d'érosion deviennent très importantes, comme en Himalaya. Si l'on compare maintenant la consommation de CO2 par altération de silicates des rivières himalayennes (0,2 à 0,3×106 mol km−2 an−1) à celles de bassins granitiques et volcaniques présentés par Dessert et coll. [8], les rivières himalayennes apparaissent comparables aux rivières granitiques en climat tempéré et ont une consommation de CO2 clairement inférieure à celle des rivières des bassins volcaniques. Ces deux comparaisons suggèrent que l'érosion physique, très importante, des bassins himalayens n'entraı̂ne pas un flux d'altération des silicates disproportionné. C'est plutôt l'intensité des précipitations liées à la mousson indienne qui détermine l'importance de ce flux.
1 Introduction
Chemical weathering, especially that of silicate rocks and minerals, is a vital component of the long-term regulation of the carbon cycle, which determines first-order climatic variations (e.g., [2,3]). Understanding how chemical weathering is controlled by different parameters, like temperature, lithology, or vegetation is therefore crucial for testing models of climatic regulation. Among those parameters, physical erosion has been highlighted as it may play a key role in tectonic forcing of climate [21]. Such hypotheses are still largely debated and the controlling factors on silicate weathering is a complex issue [10,19,23]. The Himalayas are dominated by physical erosion with only 3% of the total mass loss transported in the dissolved phase. Most of this dissolved flux, however, is related to carbonate dissolution [12] and is a function of complex basin physiography, which combines highly variable climate, lithology, vegetation, and relief. Any study of chemical weathering fluxes from the Himalayas is complicated by the wide disparity in precipitation from monsoon to dry season. Rivers swelled by the significant rains received from June to September carry up to 80% of the annual dissolved flux. Despite this observation, few data exist for Himalayan rivers during the wet season [12,22]. In this work, we present the first comprehensive estimate of annual dissolved fluxes from the rivers of Central Nepal using waters from several sampling campaigns including one during July 1998 and detailed data on hydrological fluxes [9]. These samples allow for a more inclusive analysis of the distribution of chemical erosion and its controlling factors over the Himalayan Basin.
2 The Himalayan basin
The Central Nepal basin covers 31 800 km2 and includes four trans-Himalayan rivers (from west to east: Kali Gandaki, Marsyandi, Bhuri Gandaki, and Trisuli). These north–south rivers incise the high Himalayan range in deep gorges and then join in an east–west drainage guided by the uplift of the Siwalik foothills (Fig. 1). Only the Narayani River crosscuts the Siwalik range and joins the Ganga floodplain, where it takes the name Gandak.
Four physiographic domains can be defined in the basin: the floodplain, the lesser Himalayas, the high-range and southern Tibet. A sharp climatic contrast exists between Tibet and the rest of the basin. The southern flank of the range and the plain are exposed to monsoon precipitation (2 to 4 m yr−1) whereas Tibet, in the rain shadow of the high Himalayas, is cold and receives only 0.2–0.5 m yr−1 of precipitations [1]. Following the major geographical bounds, the geology of the Himalayas can be divided into four units, separated by major thrust systems [5,6]. The rocks of the southern part of the Tibetan plateau mostly belong to the Tethyan Sedimentary Series (TSS), composed of Palaeozoic–Mesozoic carbonates and clastic sediments (North Indian shelf sediments). Underlying the TSS, the High Himalayas Crystalline (HHC) is the principal formation of the high range. It consists of ortho- and paragneisses, migmatites and highly metamorphosed marbles. The Lesser Himalayas (LH) is composed of variably metamorphosed Precambrian sediments. The lithologies are quartzo-pelitic schists, quartzites, and dolomitic carbonates. The southernmost part of the range consists of the recently uplifted Siwaliks, formed from Mio-Pliocene detrital sediments accumulated in the former Ganga plain.
3 Sampling and analyses
The monsoon sampling presented in this work was collected in July from the main tributaries of the Narayani watershed, including a profile along the Kali Gandaki River and some high-range southern-flank basins (Fig. 1). Additional samples, collected during earlier campaigns (February 1992 to July 2001 [12]), are used to calculate annual compositions.
All samples were filtered at 0.2 μm on nylon Millipore filters and stored in HNO3 acidified and non-acidified vials. Temperature, salinity and pH values were measured in the field. Major element concentrations were measured by ion chromatography at the CRPG. Separation of F−, Cl−, and SO42− was carried out on a AS12A column using non-acidified water. Acidified water was passed through a CS10 column in order to analyse Na+, K+, Mg2+ and Ca2+. Each ion was calibrated in a range from 0 to 2 mg l−1 and the water samples were diluted to fit this range. The detection limit for F− is 2 ppb, and for all other ions, the measured amounts are well above their detection limits. Reproducibility is around 10% (relative) for all ions. HCO3− was determined by charge balance from the other ions. Silica was measured by spectrophotometric measurement of the Mo blue complex.
4 Results
Unpublished data for major element concentrations including monsoon samples are listed in Table 1. Compared to dry season samples, they are more dilute but they have similar relative compositions. Overall, the river salinity during the monsoon drops by ca. 50%, while the river flux increases by a factor of 10. This implies that chemical erosion increases strongly during the wet period. The relative abundance of major cations is essentially stable over the year except in the Trisuli, which shows a clear increase in the Ca2+ fraction. This has been interpreted to reflect a change in the precipitation distribution for this basin [12]. Seasonal changes in anion concentrations are systematic however Cl− is more strongly diluted than any other element. This is particularly clear for the Kali Gandaki, for which the [Cl−] drops by a factor 5 to 10. Cl− is mainly supplied to Nepali rivers by thermal hot springs [9]. This likely reflects the fact that the flux of these hot springs does not increase in the same proportion than the rest of the hydrological system during the monsoon.
Calculated annual river compositions are listed in Table 2. For each month, one composition has been assigned using the best available data (Table 1 [4,9,12]). Depending on station, 2 to 14 samples were available (column N in Table 2). Annual compositions were then calculated using the monthly average discharge recorded over 5 to 20 years near sampling locations [24]. When no hydrological data were available, we used model fluxes computed from combined DEM and meteorological data over the watershed. For most locations, our estimates are potentially limited by the small sample size (2 to 4 samples). To test the accuracy of our approach, we calculated the annual river composition of the Trisuli River at Betrawati with two samples sets. The first consisted of only two dry season samples and one monsoon sample and average discharge over 28 years. The second calculation used a more detailed average based on a 14 sample time-series from 1994–1995 [12] and the corresponding discharge values. The detailed average is more dilute; however, both averages agree within 10%.
Mean annual chemical compositions calculated for central Nepal rivers and chemical erosion fluxes
Compositions chimiques annuelles moyennes calculées des rivières du Népal central et flux d'érosion chimiques spécifiques
| Site | Location | Position | Area | Elevation (m) | Discharge | Runoff | N | TDS | HCO3 | Cl | SO4 | Na | K | Mg | Ca | Sr | Si | Erosion | ||
| (km2) | Site | Average | (106 m3 yr−1) | (m yr−1) | (mg l−1) | (μmol l−1) | (t yr−1 km−2) | |||||||||||||
| carbonate | silicate | |||||||||||||||||||
| Chepe | Labsibot | 28°N 11′20″ | 125 | 1092 | 2791 | 283 | 2.27 | 2 | 23 | 160 | 4.8 | 46 | 48 | 28 | 19 | 72 | 0.13 | 141 | 10 | 36 |
| 84°E 30′10″ | ||||||||||||||||||||
| Darondi | 28°N 04′42″ | 370 | 700 | 1963 | 814 | 2.20 | 4 | 74 | 808 | 15.4 | 49 | 87 | 56 | 137 | 253 | 0.13 | 158 | 62 | 45 | |
| 84°E 39′32″ | ||||||||||||||||||||
| Andi kohla | Waling | 28°N 05′10″ | 249 | 820 | 1297 | 1091 | 2.29 | 3 | 94 | 1172 | 29.4 | 12 | 43 | 21 | 264 | 318 | 0.16 | 99 | 104 | 23 |
| 83°E 50′50″ | ||||||||||||||||||||
| Surai | 27°N 46′08″ | <80 | 300 | 3 | 377 | 4379 | 33.2 | 139 | 1276 | 92 | 726 | 940 | 2.45 | 226 | 148 | 105 | ||||
| 82°E 50′52″ | ||||||||||||||||||||
| Rangsing | Bhaluban | 27°N 48′20″ | <50 | 385 | 3 | 296 | 2594 | 30.5 | 58 | 241 | 60 | 386 | 1304 | 1.12 | 148 | 153 | 27 | |||
| 82°E 47′00″ | ||||||||||||||||||||
| Trisuli 1 | Betrawati | 27°N 58′08″ | 4634 | 619 | 4340 | 5580 | 1.20 | 14 | 73 | 758 | 23.2 | 58 | 79 | 39 | 66 | 327 | 0.45 | 81 | 39 | 14 |
| 85°E 11′00″ | ||||||||||||||||||||
| Trisuli 1 | Betrawati | 27°N 58′08″ | 4634 | 619 | 4340 | 5853 | 1.26 | 3 | 80 | 819 | 25.8 | 67 | 97 | 47 | 75 | 346 | 0.47 | 94 | 43 | 18 |
| 85°E 11′00″ | ||||||||||||||||||||
| Trisuli 2 | Benighat | 27°N 48′49″ | 6131 | 465 | 3616 | 8082 | 1.32 | 2 | 88 | 955 | 19.4 | 67 | 88 | 44 | 84 | 403 | 0.29 | 96 | 53 | 18 |
| 84°E 47′27″ | ||||||||||||||||||||
| Kali 1 | Tukuche | 28°N 42′30″ | 3471 | 2530 | 4739 | 1573 | 0.45 | 3 | 238 | 1825 | 323.1 | 913 | 439 | 56 | 618 | 1126 | 5.59 | 64 | 66 | 6 |
| 83°E 38′30″ | ||||||||||||||||||||
| Kali 2 | Dana | 28°N 32′00″ | 3988 | 1450 | 4639 | 2349 | 0.59 | 2 | 202 | 1826 | 234.8 | 674 | 312 | 74 | 489 | 1027 | 4.20 | 69 | 75 | 8 |
| 83°E 38′30″ | ||||||||||||||||||||
| Kali 3 | Tatopani | 28°N 28′00″ | 4026 | 1180 | 4622 | 2428 | 0.60 | 3 | 200 | 1845 | 226.8 | 501 | 279 | 73 | 416 | 947 | 3.36 | 69 | 70 | 8 |
| 83°E 38′30″ | ||||||||||||||||||||
| Kali 4 | Baglung | 28°N 16′00″ | 5983 | 740 | 4077 | 5724 | 0.96 | 3 | 157 | 1465 | 85.5 | 239 | 130 | 67 | 265 | 653 | 1.38 | 87 | 73 | 13 |
| 83°E 36′30″ | ||||||||||||||||||||
| Kali 5 | Ramdi | 27°N 54′04″ | 10557 | 460 | 3073 | 15991 | 1.51 | 3 | 165 | 1752 | 54.7 | 156 | 90 | 49 | 373 | 619 | 1.33 | 104 | 123 | 21 |
| 83°E 38′02″ | ||||||||||||||||||||
| Seti | Damauli | 28°N 04′20″ | 994 | 585 | 2058 | 3286 | 3.31 | 3 | 158 | 2013 | 36.1 | 134 | 81 | 70 | 315 | 769 | 0.77 | 107 | 303 | 52 |
| 84°E 04′15″ | ||||||||||||||||||||
| Marsyandi | Dumre | 27°N 57′00″ | 4119 | 435 | 3661 | 7347 | 1.78 | 3 | 134 | 1275 | 136.7 | 187 | 177 | 60 | 198 | 578 | 1.30 | 132 | 117 | 30 |
| 84°E 25′00″ | ||||||||||||||||||||
| Narayani | Narayanghat | 27°N 42′30″ | 31795 | 180 | 3028 | 50481 | 1.59 | 4 | 156 | 1607 | 66.0 | 144 | 123 | 61 | 291 | 600 | 0.93 | 140 | 116 | 29 |
| 84°E 25′50″ |
From these average compositions, we calculated rates of chemical erosion for the different watersheds. We distinguished the erosion of carbonate and silicate following the approach developed in [12]. This approach corrects for atmospheric input and allows for the determination of the relative contribution of carbonate vs. silicate dissolution based on the lithology of the Himalayan formations. Rate of erosion corresponds to the annual flux of dissolved elements derived from a given lithology, corrected from the amount of atmospheric CO2, and divided by the total area of the basin. Each cation is accounted for it's oxide mass. On plots of carbonate erosion rate versus runoff (Fig. 2a), there is no straightforward correlation, which suggests that multiple factors control weathering. On the contrary, silicate erosion appears more directly related to runoff (Fig. 2b).
5 Discussion
Chemical erosion of carbonates in the Narayani basin (Fig. 2a) is highly variable between 10 and 300 t km−2 yr−1. The primary control is the lithology or the presence of carbonates in the basin. The lowest rates of erosion are observed for the Chepe, Darondi and Trisuli Rivers. The Chepe and Darondi are small High Himalayan basins and have respectively no or very minor carbonates in their drainages. The Trisuli River is a very large basin that includes carbonate-bearing formations of the Tethyan Sedimentary Series. Compared to other large basins, the Trisuli drains significantly less carbonates and these are restricted to the northern part of the basin, where precipitations are low. In addition, the Chepe, Darondi, and Trisuli have river sediments free of calcite. In contrast, the other central Nepal rivers carry calcite in their sediments [11] and are oversaturated with respect to carbonate [12,15]. This holds true during the monsoon and suspended sediments sampled during the monsoon for these rivers contain between 5 and 40% carbonates (unpublished data). Chemical erosion of carbonates is therefore limited by saturation and it should be linearly correlated with runoff. This relationship appears roughly if we consider only the large watersheds (Marsyandi, Kali 5, Seti, Narayani). Such correlation cannot be perfect, since the rate of chemical erosion of carbonate is normalised to the total basin area and not to the carbonate area. The Seti River shows very high carbonate erosion rates (>300 t km−2 yr−1), which fit well with the very high runoff of the river. The Chepe, Darondi and the Trisuli plot above the correlation, due to the lack of carbonates in their basins. The Andi also appears to have low carbonate erosion, despite the presence of carbonated rocks in the basin and even in the river sediments. The low carbonate erosion could then derive from low physical erosion in this southern basin. On the other side, rivers draining the Siwaliks and the northern Kali Gandaki show higher carbonate erosion. Higher efficiency of carbonate dissolution can be related to several factors. In the northern Kali, this can be related to: (1) the low temperature as carbonate solubility increases with low temperature and (2) the effect of sulphide oxidation, which is particularly important in this basin. In the Siwaliks, the temperature is not a factor as average temperatures are 20 to 30 °C higher than in the upper Kali. More likely, the Siwaliks are porous formations rich in carbonate [7] that host aquifers favouring carbonate dissolution compared to higher Himalayan basin.
Silicate chemical erosion rates in the central Nepal rivers vary between 5 and 42 t km−2 yr−1 and one river from the Siwaliks shows an extreme rate of 105 t·km−2 yr−1 (Fig. 2b). To this exception, the other rivers display a clear correlation with runoff, the Seti River showing the highest erosion rate at 52 t km−2 yr−1, associated with the highest runoff. This suggests that precipitation plays the key role for the control of silicate weathering, despite the large contrasts in temperature and vegetation conditions that are observed here. In detail, rivers having similar runoff like the Andi, Chepe and Darondi can show quite variable silicate chemical erosion rate (23, 36, 45 t km−2 yr−1, respectively). These basins have quite contrasted characters that can qualitatively explain their differences. The Chepe and the Darondi are High Himalayan basins, with very steep relief. The headwater of the Darondi is a large glacier above 6000 m, whereas that of the Chepe is a deglaciated basin around 5000 m. Basins of the high Himalayas are characterized by high denudation rates (4 to 6 mm yr−1), whereas the Andi is a Lesser Himalayan basin, with smoother relief and lower denudation rates, around 2 mm yr−1 [16]. Vegetation and temperature is higher for the Andi and the Darondi Basins than for the Chepe Basin, as a consequence of their respective mean elevations: 1300, 1960 and 2790 m. The Darondi, which combines high denudation and rich vegetation in the lower part of the basin appears with the highest rate of chemical erosion of silicates. In contrast, the Andi, which has likely the lowest rate of physical erosion, shows comparatively low chemical erosion of silicate, despite its higher temperature and vegetation cover.
In the Siwaliks, very high silicate erosion rates are observed for the Surai (105 t km−2 yr−1), whereas the other river, the Rangsing, shows only a slightly higher rate compared to the general tendency. In the Surai, this is related to remarkably high concentrations of Na, and to a lesser extent of Mg, which are higher than those of Ca during the dry season. This likely derives from aquifer circulation as spring water sampled in the Surai River shows similar chemical characteristics [14]. Such high Na concentrations may reflect high plagioclase alteration in the Siwaliks [14] or, more likely, the dissolution of sodium carbonates that are frequently observed in the soils of the semi-arid Gangetic plain [20]. Those carbonates would have accumulated in the palaeosoils of the Siwaliks and would be rapidly dissolved during the erosion of these series. High Na concentrations in these rivers would then reflect indirect silicate weathering in the Gangetic plain. Nevertheless, the Rangsing River is draining the same Siwaliks formations and does not show such extreme compositions. In comparing Siwalik rivers during the dry season [12], we observe two groups: (1) high Na and Mg rivers that drain the Siwaliks front where rates of uplift are very high (up to 10 mm yr−1) and (2) ‘normal’ Ca-dominated rivers that drain the northern Siwaliks, where rates of uplift are much lower (e.g., [13,16]). The very high flux of sodium could therefore be related to the rapid exhumation of the Siwaliks series, which supports our sodium carbonate hypothesis, as rapid dissolution would be favoured by rapid exhumation. The Siwaliks Na flux would therefore reflect past silicate erosion in the Gangetic plain rather than modern and extremely rapid silicate weathering.
6 Conclusion
This set of data shows that chemical erosion is controlled on the first order by the runoff except for carbonates when their abundance is limited. Physical erosion is also a critical parameter, as shown by the contrast between the Andi, Chepe and Darondi Rivers. To the exception of the Andi River, all others belong to high Himalayan range or to the Siwaliks, characterized by very high denudation rates. Hence the database is limited to really test the dependence of chemical erosion to the physical erosion. Millot et al. [18] have shown a relationship between physical and chemical erosion of granitoid and basaltic watersheds and they proposed a power law: Chem=0.39×(Phy)0.66, which we can apply to Himalayan rivers. Few data exist for these rivers and they certainly underestimate the real physical erosion flux as the transport of bed-load sand and pebble was not monitored. The suspended load flux for the Marsyandi, Trisuli, and Narayani Rivers, physical erosion is between 1000 and 4500 t km−2 yr−1 [17]. Following the relationship of Millot, these sediment fluxes would imply chemical erosion rates between 40 and 100 t km−2 yr−1. These rates are only based on the sum of silicate cations (Na, K, Mg, and Ca) excluding Si and using the cation mass instead of the oxide mass [18]. The corresponding chemical erosion rates derived from the dissolved load of the Marsyandi, Trisuli, and Narayani are between 6 and 7 t km−2 yr−1, which is well below the values predicted from physical erosion. Millot's relationship is based on rivers having much lower physical erosion rates. It is quite possible that for very high rate of erosion the system becomes ‘saturated’ and that the relationship cannot be applied, as already suggested by Millot et al. Himalayan rates of silicate chemical erosion can also be compared to those of granitic and basaltic lithologies following Dessert et al. [8]. The calculated CO2 uptake by silicate weathering for Himalayan rivers is between 0.2 and 0.3×106 mol km. This is very similar to those of other granitic basin under temperate climate and high runoff and clearly lower than for volcanic lithologies. Both comparisons suggest that the rates of chemical erosion in the Himalayas are not exceptional, in spite of the very high physical erosion. Rather, it is the high runoff due to the Indian monsoon that controls the intensity of the silicate weathering.
Acknowledgements
This work was supported by the French INSU ‘Programme national sol–érosion’ (PNSE). We are grateful to Prof. B.N. Upreti, Dr A. Gajurel and Sarki Man for precious help and support during field work in Nepal. We thank Jérôme Gaillardet and François Chabaux for constructive comments. CRPG contribution No. 1653.


