Predicting landscape-scale erosion rates using digital elevation models

David R. Montgomery

doi:10.1016/j.crte.2003.10.005

Surface Geosciences

Predicting landscape-scale erosion rates using digital elevation models

David R. Montgomery ¹

¹ Department of Earth & Space Sciences, University of Washington, Seattle, WA 98195-1310, USA

Comptes Rendus. Géoscience, Volume 335 (2003) no. 16, pp. 1121-1130.

Abstracts

English
French

Functional relationships between erosion rates and topography are central to understanding controls on global sediment flux and interactions among tectonics, climate, and erosion in shaping topography. Based on such relations digital elevation models (DEMs) allow predicting landscape-scale erosion rates to the degree that process models can be calibrated and to the extent that such processes reflect elevation, drainage area, and aspect, or their derivatives such as slope and curvature. Digital elevation models allow investigating the influence of erosional processes on landscape form and evolution through generalized quantitative expressions often referred to as ‘erosion laws’. The analytical forms of such expressions are derived from physical principles, but only limited data are available to guide calibration to particular landscapes. In addition, few studies have addressed how different transport laws interact to set landscape-scale erosion rates in different environments. Conventionally, landscape-scale sediment flux is considered to be linearly related to slope or relief, but recent analyses point toward non-linear relations for steep terrain in which changes in the frequency of landsliding accommodate increased rates of rock uplift. In such situations, landscape-scale erosion rates are more closely tied to erosion potential predicted by models of bedrock river incision. Consequently, I propose that using DEMs to predict absolute or relative erosion rates at the landscape-scale counter-intuitively involves the rate of fluvial processes as governing the sediment flux from steep landscapes, and rates of hillslope processes as governing sediment flux from low-gradient landscapes.

Les relations fonctionnelles entre taux d'érosion et topographie sont au centre des contrôles de compréhension des flux globaux de sédiments et des interactions entre tectonique, climat et érosion dans la topographie du modelé. Fondés sur ces relations, des modèles numériques d'altitude (DEMs) permettent de prévoir les taux d'érosion à l'échelle du paysage au degré où les modèles des mécanismes peuvent être calibrés et à l'extension à laquelle de tels mécanismes reflètent l'altitude, la zone de drainage et l'aspect, ou leurs dérivés, tels que pente ou inflexion. Les modèles numériques d'altitude permettent aussi de rechercher l'influence des processus d'érosion sur les formes du paysage et leur évolution par le biais d'expressions quantitatives généralisées, souvent rapportées à des « lois d'érosion ». Les formes analytiques de telles expressions dérivent de principes physiques, mais on ne dispose que de données limitées pour guider la calibration de paysages particuliers. En outre, peu d'études se sont attachées à chercher comment différentes lois de transport interagissent pour établir des taux d'érosion à l'échelle du paysage dans différents environnements. Par convention, le flux de sédiments à l'échelle du paysage est considéré comme relié linéairement à la pente ou au relief. Mais les analyses récentes font apparaı̂tre des relations non linéaires dans le cas des terrains escarpés, pour lesquels des changements de fréquence des glissements de terrain accommodent des taux accrus de surrection. Dans de telles situations, les taux d'érosion à l'échelle du paysage sont plus fortement liés au potentiel d'érosion prédit par les modèles d'incision du soubassement rocheux par les rivières. En conséquence, il est ici proposé que les modèles DEMs utilisés pour prévoir les taux d'érosion relative et absolue à l'échelle du paysage désignent la vitesse des processus fluviaux comme agent responsable des flux de sédiments à partir des paysages escarpés et la vitesse des processus de pente comme agent responsable des flux de sédiments à partir de paysages à faible dénivelée.

Metadata

Received: 2003-01-20
Accepted: 2003-10-10
Published online: 2003-12-01

DOI: 10.1016/j.crte.2003.10.005

Keywords: digital elevation models (DEMs), erosion rates, global sediment flux, tectonics–climate–erosion interactions, shaping topography
Mot clés : modèles numérique d'altitude (DEMs), taux d'érosion, flux global de sédiments, interactions tectonique–climat–érosion, modèle de paysage

Author's affiliations:

David R. Montgomery ¹

¹ Department of Earth & Space Sciences, University of Washington, Seattle, WA 98195-1310, USA

@article{CRGEOS_2003__335_16_1121_0,
     author = {David R. Montgomery},
     title = {Predicting landscape-scale erosion rates using digital elevation models},
     journal = {Comptes Rendus. G\'eoscience},
     pages = {1121--1130},
     publisher = {Elsevier},
     volume = {335},
     number = {16},
     year = {2003},
     doi = {10.1016/j.crte.2003.10.005},
     language = {en},
}

TY  - JOUR
AU  - David R. Montgomery
TI  - Predicting landscape-scale erosion rates using digital elevation models
JO  - Comptes Rendus. Géoscience
PY  - 2003
SP  - 1121
EP  - 1130
VL  - 335
IS  - 16
PB  - Elsevier
DO  - 10.1016/j.crte.2003.10.005
LA  - en
ID  - CRGEOS_2003__335_16_1121_0
ER  -

%0 Journal Article
%A David R. Montgomery
%T Predicting landscape-scale erosion rates using digital elevation models
%J Comptes Rendus. Géoscience
%D 2003
%P 1121-1130
%V 335
%N 16
%I Elsevier
%R 10.1016/j.crte.2003.10.005
%G en
%F CRGEOS_2003__335_16_1121_0

David R. Montgomery. Predicting landscape-scale erosion rates using digital elevation models. Comptes Rendus. Géoscience, Volume 335 (2003) no. 16, pp. 1121-1130. doi : 10.1016/j.crte.2003.10.005. https://comptes-rendus.academie-sciences.fr/geoscience/articles/10.1016/j.crte.2003.10.005/

Version originale du texte intégral

1 Introduction

Classic conceptual models of landscape evolution incorporate the implicit assumption of a simple linear functional relation between faster erosion and greater relief or steeper slopes [24,45]. Such intuitive relations between process and form reflect fundamental notions about the role of topography in setting rates of geomorphological processes, and therefore controls on landscape-scale sediment flux. Although many models of interactions between tectonics and erosion adopt linear functional relations among erosion rates and elevation, slope, or relief, there are various styles of interaction among hillslope and fluvial processes in shaping topography. As landscape-scale erosion rates are controlled by a number of interacting processes, it is reasonable to hypothesize that different functional controls dominate landscape-scale erosion rates in different environments and geological settings.

In the early 1960s, Schumm [52] reported a linear relation between erosion rate and drainage basin relief (the difference in height between the highest and lowest points) for basins in the continental United States. Based on a compilation of data for mid-latitude drainage basins, Ahnert [2] reported a linear relation between erosion rate and mean local relief (the difference in elevation measured over a specified length scale). Pazzaglia and Brandon [43] bolstered Ahnert's relation with additional data drawn primarily from the central and eastern United States. In a similar analysis for major world drainage basins, Summerfield and Hulton [57] reported that local relief and runoff are the dominant controls on erosion rate. Pinet and Souriau [44] reported that erosion rates are correlated with mean elevation and further suggested that different relations characterize tectonically active and inactive mountain ranges. Milliman and Syvitski [36] also emphasized the importance of small rivers in tectonically active regions on global sediment yields.

The influence of climate in setting landscape-scale erosion rates occupies a key place in both current and classical geomorphological thinking [8]. Langbein and Schumm [31], for example, argued that erosion rates were greatest in semi-arid landscapes due to the dearth of runoff in drier environments and the protective effects of dense vegetation cover in humid and tropical environments. Willett et al. [61] showed that differences in rainfall on windward and leeward sides of a mountain range lead to topographic asymmetry due to differences in long-term erosion rates. Brozovic et al. [7] argued that greater erosion by glacial processes limited the height of mountain ranges. Providing support for this hypothesis, Montgomery et al. [42] showed that spatial variability in the maximum height of the Andes tracked the regional snowline and Pleistocene glacial limit and that landscape hypsometry differed in glaciated and fluvially dominated terrain. Comparison of sediment yields [27] and valley morphology [6,38] indicate that erosion by glacial processes results in greater sediment flux than fluvial processes. Montgomery et al. [42] also showed that latitudinal variations in precipitation controlled long-term differences in erosion rates that contribute to along-range variation in the width of the Andes. While variability in climate (runoff and temperature), vegetation, geology (soil and rock strength and erodibility) and tectonics all are generally acknowledged to influence erosion rates, Riebe et al. [46,47] recently argued for minimal climate influence on long-term differences in erosion rates within the Sierra Nevada, and a weak climate influence on chemical erosion rates worldwide. Considered broadly, however, climate certainly influences landscape-scale erosion rates through the amount and style of precipitation, as well as the associated patterns of vegetation.

Recent work documenting strongly coupled feedback between erosional processes and tectonic forcing motivates revisiting traditional assumptions regarding linkages between slope morphology and long-term erosion rates. Studies reporting evidence for an apparent decoupling of erosion rate and slope morphology in steep, landslide-prone terrain [11,41] support the relevance of landscape evolution models that represent hillslope erosion rates with either critical-slope thresholds or non-linear expressions, some of which asymptotically approach a limiting hillslope angle [3,15]. Montgomery and Brandon [41] recently compiled erosion rates from tectonically active regions and showed that while a linear relation between slope and erosion rate provided a reasonable fit to data in low-gradient landscapes, non-linear relations provided a better fit to data from steep tectonically active mountain ranges. Aalto et al. [1] further showed that when normalized for differences in basin lithology, erosion rates in the Bolivian Andes increased non-linearly with mean slope. Evidence for the development of threshold, or near-threshold slopes implies that landsliding allows hillslope lowering to keep pace with river incision [11,37,51], in which case erosion rates in steep terrain increase greatly with only minor increases in slope or topographic relief. Such extreme sensitivity of erosion rates to increases in slope complicates efforts to predict erosion rates from digital topography in steep terrain because of the wide range of erosion rates that could be reasonably inferred from a narrow range of slopes.

Derived from the application of soil mechanics to analysis of hillslope processes, the concept of threshold hillslopes originally held that material properties of the soil impose a limiting upper bound to hillslope angles in soil-mantled landscapes [12,13]. Extension of this concept to larger scales showed that bedrock strength could limit local relief in a mountain range, and implied that once hillslopes approached a mechanically limiting steepness, landsliding would lower ridgelines at the pace set by the rate of river incision [11,51]. A lack of variation in mean hillslope angles across areas with significant variability in river incision rates provides compelling evidence for the development of strength-limited, threshold hillslopes both along the gorge of the Indus River [11] and across the core of the Olympic Mountains where mean local slope varies by only a few degrees despite strong gradients in long-term erosion rates [37]. Roering et al.'s [49,50] studies of hillslopes in the Oregon Coast Range point to non-linear diffusion as governing hillslope development in steep terrain, and further imply that steeper hillslopes become relatively insensitive to changes in erosion rates as slopes approach an upper limiting angle. Most recently, Montgomery and Brandon [41] reported that landscape-scale erosion rates vary non-linearly with mean slope, confirming that topographically mediated feedback limits the local relief that can be created by rapid rock uplift in the steep topography of tectonically active mountain ranges. Taken together, these studies imply that linear relationships between slope (or local relief) and erosion rate may have only limited relevance to long-term, landscape-scale erosion rates in the steep topography of tectonically active mountain ranges.

Nonetheless, the functional form of relations between erosion rates and topographic attributes, such as hillslope gradients or local relief, is central to the prediction of erosion rates from DEM analyses. In reviewing the prediction of landscape scale erosion rates from DEMs, I examine limitations due to scale and generalization of process, issues arising from erosion laws cast at scales larger than the fundamental physics underlying them, and problems involved in the integration of different processes over long time-scales.

2 Digital elevation models

Digital elevation models consist of a spatially registered set of elevation points that collectively describe a topographic surface. Data are organized as either a matrix of points that form a regular grid, or as the coordinates and elevation of points that define a triangulated irregular network (TIN). Analyses of DEMs allow predicting styles and rates of geomorphological processes and their relation to landscape evolution and sediment flux only to the extent that such processes reflect elevation, drainage area, and aspect, or their derivatives such as slope and curvature. When combined with additional spatially explicit information, DEM-based analyses can incorporate spatial variability in material properties or climate forcing through accounting for spatial variability in precipitation [22,23]. The scale of topographic representation imposes intrinsic limitations on using DEMs for simulating geomorphological processes due to an inherent abstraction of process when using coarse-resolution DEMs.

Both the grid scale and the original density of independent elevation points influence DEM resolution and the nature of artifacts incorporated into a DEM. A fine-scale grid superimposed on a coarse original elevation data set results in different artifacts than a coarse-scale grid superimposed on an original high-resolution data source. A key aspect of using DEMs to model erosional processes is that average slopes decrease with increasing grid size [63]. Consequently, parameter values for use in DEM-driven erosion models are inherently scale-dependent. In addition to the technical issues associated with DEM production, the use of DEMs in geomorphological analyses involves rate law parameterizations that attempt to generalize the essential physics controlling erosional processes over spatial and temporal scales across which they can't be measured directly and will not be constant anyway. Consequently, rate constants and parameterizations appropriate for large-scale erosional simulations need not be identical to those directly related to processes governing the finer-scale mechanics actually controlling erosional processes. Ideally, however, such parameterizations should be based on a physical principle or mechanism, and it should be possible to calibrate such relations against field measurements [20]. Although the basic functional forms of so-called ‘erosion laws’ – quantitative statements of the relations among the basic processes controlling erosion rates – are being actively debated, tested, and evaluated, a general consensus appears to be emerging as to the nature of a basic set of relations.

3 Erosion laws

Models of landscape-scale erosional processes involve either (i) statistical relations of river sediment yield to drainage basin attributes based on empirical correlation, or (ii) physically based models of processes thought to control erosion rates. Statistical models based on slope, climate and so on can be applied simultaneously to large portions of Earth's surface [32,58] but the particular functional relationship between driving factors and erosional response is empirical and context dependent (i.e., both scale and place matter). Extrapolation to new environments therefore can prove questionable. Physically based models attempt to represent the key processes by specifying a priori the expected form of relationships. Although founded on theoretical grounds, such models generally rely on calibration through rate constants because the explicit physics of erosional systems are difficult to grapple with under the most controlled circumstances and become virtually unmanageable in a reductionist manner for problems of landscape evolution and sediment yield that extend beyond the time and spatial scales for data that are typically available. In short, both statistical and physics-based approaches to modeling landscape-scale sediment flux using DEMs involve some form of calibration.

Models for a wide range of erosional processes can be cast in terms of drainage area and slope [18,29] and field studies have shown that the spatial distribution of a number of erosional processes can be discriminated based on models cast in these terms [19,39,40]. Landscape evolution models tend to be based on different combinations of mathematical statements for either the volumetric sediment transport rate (volume per time) or for the local lowering rate (length per time). Landscape evolution models for non-glaciated terrain incorporate two distinct zones of processes – hillslopes and channels – with the governing relationships typically cast in terms of drainage area and/or slope. Models of glacial erosion based on the hypothesis that glacial erosion rates scale with the basal sliding velocity, such as those by Braun et al. [5] and MacGregor et al. [33], remain difficult to either test empirically or cast as an erosion law expressed in terms of drainage area and slope.

3.1 Hillslope processes

Models of hillslope erosion or sediment transport rates are typically cast as:

Q_{s} = KS

(1)

where Q_s is the sediment transport rate, K is a rate constant often referred to as the hillslope diffusivity, and S is the local slope. This formulation follows from Gilbert's [25] conceptualization of hillslope evolution and the controls on the evolution of ridge top convexities. Recent studies using cosmogenic radionuclides [35,55] report direct evidence in support of a simple linearly slope-dependent model of hillslope erosion on relatively gentle slopes, and reported estimates of field determined hillslope diffusivities span a range from about 10 to over 300 cm² yr⁻¹ [17].

Dietrich and Montgomery [17] argued that in steep terrain where landsliding is an important process, Eq. (1) only applies on gentle slopes near ridge crests. Roering et al. [49] proposed a non-linear transport law to describe hillslope erosion in steep terrain where slopes approach a critical gradient (S_c) that defines a maximum stable slope angle:

Q_{s} = KS / [1 - {(S / S_{c})}^{2}]

(2)

They [49] presented evidence that Eq. (2) explained hillslope form in small basins in landslide-dominated terrain of the Oregon Coast Range.

A generic landscape scale erosion law can be cast by modifying Eq. (2) to include a background erosion rate (E₀) attributable to dissolution and chemical weathering [41]:

E = E_{0} + KS / [1 - {(S / S_{c})}^{2}]

(3)

This formulation implies that weathering processes control erosion rates where slopes are low and chemical erosion strong, that Eq. (1) will describe landscape-scale erosion rates in gentle terrain, and that erosion rates will increase non-linearly as slopes approach the critical slope in steep terrain. Montgomery and Brandon [41] applied this model to a high-resolution (10-m grid) DEM of the Olympic Mountains, Washington, and showed that the relation predicted the form of the functional relation between mean local slope and long-term denudation rate using S_c=40° and E₀=0.05 mm yr⁻¹, the latter based on the average of reported measurements for drainage basins in the area [16]. They also reported that Eq. (3), substituting mean local relief instead of mean local slope due to the coarse resolution of current global DEMs, provided a reasonable prediction of landscape-scale denudation rates for a compilation of global data.

3.2 Fluvial processes

The fundamental driving force behind sediment transport and river incision into bedrock is generally considered to be the shear stress acting on the riverbed

τ_{b} = ρ gDS

(4)

where τ_b is the basal shear stress (kPa), ρ is the density of water (kg m⁻³), g is the gravitational acceleration (m s⁻²), D is the flow depth (m), and S is the channel slope. Momentum losses caused by hydraulic roughness reduce the portion of the shear stress available for sediment transport or bed incision such that the effective basal shear stress (τ′) is given by:

τ' = τ_{b} - τ ″ - τ ‴ - \dots τ^{n}

(5)

where τ″−τ‴−⋯τⁿ accounts for the roughness attributable to bedforms, woody debris, boulder obstructions, and so on [9]. While it is possible to predict flow depth from drainage area using empirical relations of hydraulic geometry, and thereby in combination with channel slope estimate τ_b from DEM analysis, the information required to evaluate τ′ cannot be derived from DEMs.

Sediment transport begins when τ′ exceeds the critical shear stress required to initiate grain motion (τ_c) and is generally considered to follow

q_{b} = β {(τ' - τ_{c})}^{λ}

(6)

where q_b is the river's transport capacity (kg m⁻² s⁻¹), and β and λ are empirical constants. The problem of erosion into cohesive bedrock is even more complex, and the effects of corrosion, corrasion, and cavitation further complicate the prediction of the critical shear stress necessary to initiate bedrock erosion. Hence, predicting long-term rates of sediment transport or river incision inherently involves scaling up and calibrating physically based models of river incision.

A number of closely related models consider the rate of river incision to drainage area and slope through either basal shear stress or stream power [28,56,59]. The case of detachment limited bedrock incision is typically cast as

E = {kA}^{m} S^{n}

(7)

where E is the rate of river incision (m yr⁻¹), k is a coefficient that incorporates bedrock erodibility, A is drainage area (m²), S is slope, and the exponents on m and n have different values for incision driven by shear stress (m=1/3, n=2/3) and unit stream power formulations (m=0.5, n=1). For the case of transport-limited incision where the sediment flux from upstream reduces the ability to incise rock, the governing relation is typically expressed as

E = {kA}^{m} S^{1 - n}

(8)

While a number of studies have addressed the implications of Eqs. (7) and (8) for landscape evolution, tests of bedrock river incision models have shown that k varies by at least five orders of magnitude between different lithologies and that no single model adequately describes the evolution of all bedrock rivers [56].

Increasing evidence points to rates of bedload transport and storage of bedload on the riverbed as key controls on bedrock river incision [53,54]. A necessary condition to expose the bedrock beneath riverbeds to erosive action is entrainment of the sediment cover. Hence, a simple way to account for this effect is to modify the form of a fluvial incision ‘law’ to account for the critical shear stress necessary to mobilize the bed covering sediment by incorporating a threshold below which erosion does not occur, such as in:

E = k [A^{m} S^{n} - {(A^{m} S^{n})}_{c}]

(9)

where the subscript ‘c’ denotes a threshold value associated with the onset of sediment transport or erosion of the channel bed. For simplicity, many models, implicitly set the (A^mSⁿ)_c term, or its equivalent, equal to zero thereby ignoring the critical shear stress. However, this likely over represents the erosional work done by small events and therefore under represents the importance of rare large discharges. Sklar and Dietrich [53] proposed a more complicated, and more realistic, incision law for abrasion based on incorporating both the availability of tools (i.e., sediment) in the flow and the effect of sediment cover on shielding bedrock from erosion.

No single mechanism of bedrock incision is likely to explain river incision rates in all landscapes. Instead, a family of mechanisms, implying a family of erosion laws, can be related to the dominant process, rock type, and the geological and tectonic setting (Fig. 1). Bedrock erosion by plucking and quarrying would be expected to dominate bedrock incision in strong, highly fractured heterogeneous rocks, whereas abrasion should be a major mechanism in strong, massive, homogenous rocks. Weathering-limited erosion, such as by spalling, likely characterizes erosion of weak, friable rocks. While all three styles of incision may occur in a river, the relative importance of each mechanism should vary with lithology and geotectonic setting. Nonetheless, landscape-scale erosion rates could be predicted in principle based on Eqs. (1) through (9), and a number of workers have used landscape evolution models to investigate the evolution of specific mountain ranges [3,21,26].

Fig. 1
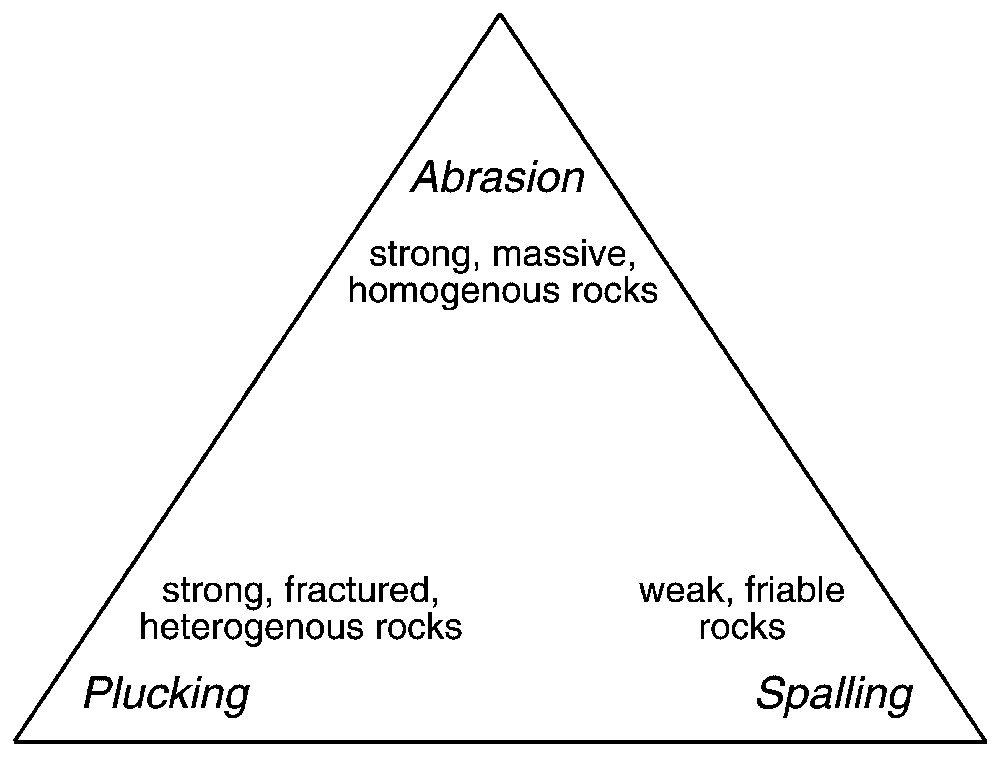
Ternary diagram illustrating relations between rock characteristics and styles of bedrock river incision.
Diagramme ternaire illustrant les relations entre les caractéristiques de la roche et les styles d'incision du soubassement rocheux par la rivière.

3.3 Scale issues

Another key issue for macro-scale geomorphology is how to parameterize landscape evolution models given their generally coarse grid scales. Koons' [30] groundbreaking model of the topographic evolution of the Southern Alps of New Zealand highlighted the problem of how to parameterize hillslope processes, as the rate constant K in Eq. (1) needed to generate appropriately scaled relief was orders of magnitude greater than values measured from field studies on actual hillslopes. Dietrich and Montgomery [17] derived an expression for the effective diffusivity that would be apparent from subsuming the effects of channel processes in headwater portions of the drainage network into the hillslope diffusivity in models with coarse-scale grid resolution:

E = K^{*} S

(10)

K^{*} = KS + {kA}^{m} S^{n - 1}

(11)

where

K^{*}

is the effective diffusivity that incorporates the influence of sub-grid scale channels. Hence, the hillslope diffusivity (K) in landscape evolution models is inherently scale dependent. In addition, channel slopes derived from DEMs are grid-scale dependent, and therefore the fluvial erosivity constant (k) is also scale-dependent.

4 Erosion index

While drainage area and slope are readily determined from digital topography, values for the constants (k,K,E₀, and S_c) cannot be evaluated from physiography alone. Consequently, in some applications it is advantageous to predict spatial patterns of relative erosion potential by subsuming into an erosion index the rate constants that incorporate erodibility. A generic erosion index for predicting spatial patterns in erosion potential due to spatial patterns of precipitation, drainage area, and slope may be cast as

EI = [\sum_{i} {(AP)}_{i}^{m}] S^{n}

(12)

in which the spatially weighted precipitation upslope of a grid cell is summed and multiplied by the slope of the cell of interest [22,42]. This approach has the advantage that it folds unknown (and potentially unknowable) parameters into a single index. Among its key disadvantages is that it does not represent or discriminate among different processes. Moreover, since the erosion index incorporates factors controlling erodibility (like lithology) into the index, the approach can only predict relative erosion potential rather than variations in actual erosion rates. Subject to its inherent limitations, the erosion index provides a convenient way to characterize erosion potential across large areas, particularly for applications where coarse-scale grid elements necessitate abstraction of multiple, interacting sub-grid-scale processes or where it is necessary to account for spatial variability in precipitation.

5 River incision, hillslope erosion, and landscape evolution

A new view of the coupling and feedback among climate, erosion, and tectonic processes is emerging from recent studies focused on their interactions. Numerical simulations of material flow pathways through evolving and steady-state orogens show that metamorphic gradients exposed at the surface reflect both the influence of spatial variability in erosion rates and tectonic processes [60–62]. Geologists now recognize that spatial gradients in the climate forcing that drives erosion can influence the development and evolution of mountain ranges. Development of mountain ranges strongly influences patterns of precipitation [4], which in turn influence the form of topography [48] and can also increase weathering rates through greater mechanical breakdown of rocks by glacial and periglacial processes. Gradients in climate and tectonic forcing strongly influence erosional intensity, which governs the development and evolution of topography. Consequently, it is clear that climate, erosion, and tectonics are coupled through large-scale feedback systems that operate over a range of scales.

First-order controls on feedback between these systems are set by global-scale variations in climate and tectonic setting. Rates of tectonic forcing are governed largely by plate tectonics. Ancient cratons and passive margins have low rock uplift rates, flexure and lateral escarpment retreat characterize rifted margins, and active convergent margins can support very rapid erosion [10], depending upon the rate of convergence and rock uplift across the margin. Whereas the geographical distribution of plate tectonic environments has changed over geologic time, the global climate exhibits robust latitudinal patterns with high rainfall zones in the equatorial tropical convergence zone, a mid-latitude belt of deserts, and stronger glacial influences toward the poles. The strong feedback between climate, erosion, and tectonics suggests that fundamental large-scale controls constrain the global character of topography, with high plateaus likely to form astride the desert latitudes and high mountains unlikely to form in the equatorial or polar regions [7,42]. Together such controls suggest a global view of mountain range formation and evolution that rests on feedback among systems in different geological settings.

Three fundamentally different types of landscapes exhibit distinct geomorphological controls on landscape-scale erosion rates (Fig. 2). Chemical weathering dominates landscape-scale erosion rates in the low-gradient terrain of ancient cratons where chemical denudation exceeds mechanical denudation. In low-relief and post-orogenic landscapes with low rock uplift rates, hillslope processes set the pace of landscape lowering and landscape-scale erosion rates would be expected to reflect mean slope or local relief. In contrast, in the steep terrain of tectonically active landscapes where hillslope lowering keeps pace with river incision, the landscape-scale erosion rate will be controlled by the rate of river incision. However, if erosion cannot keep pace with rock uplift, then mass will accumulate until the relief of the range becomes limited by the thermal-mechanical properties of the crust, at which point the range can grow laterally but will rise no further, leading to a high plateau. These distinct styles of landscape evolution imply that changes in climate or tectonic forcing can influence landscape-scale erosion rates in low-relief landscapes through changes in hillslope steepness, whereas in high-relief landscapes, changes in rock uplift rate influence erosion rates primarily through adjustments in the frequency of slope failure.

Fig. 2
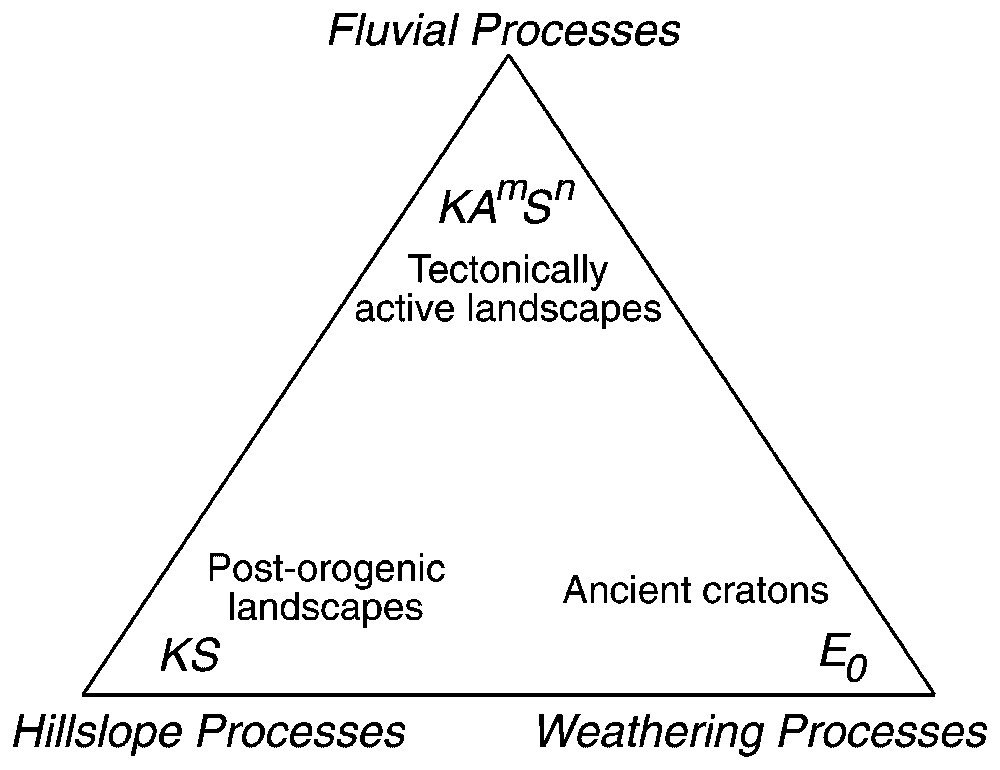
Ternary diagram illustrating relations between geological setting and dominant controls on landscape-scale erosion rates.
Diagramme ternaire illustrant les relations entre le contexte géologique et les contrôles dominants sur les taux d'érosion à l'échelle du paysage.

Considered broadly, these distinct styles of landscape behavior correspond to active orogens, post-orogenic landscapes, and ancient cratons. The former case generally corresponds to classical concepts of Davis' [14] mature topography and Mackin's [34] graded river, both of which held that the erosion rates of rivers and hillslopes were adjusted to each other. In contrast, degrading post-orogenic landscapes lose relief over time as rates of hillslope erosion exceed rates of river incision. The converse is true in landscapes where relief is being created, akin to Davis' [14] immature topography. In applying current understanding to these classical models, it is apparent that controls on landscape-scale erosion rates involve the counter-intuitive phenomenon that in steep landscapes the rate of river incision governs landscape-scale sediment flux, whereas rates of hillslope processes govern sediment flux in low-gradient landscapes. In post-orogenic landscapes, low-energy rivers are slaved to the hillslope flux leading to a long slow tail of landscape response. In steep landscapes where river incision controls landscape-scale erosion rates, the rate of tectonic forcing ultimately controls the sediment flux, as the frequency of landslide initiation would presumably adjust to match rock uplift. In the coming years, the increasing availability and resolution of digital elevation models should allow greater exploration of the coupling of climate, tectonics, and erosion in shaping topography and influencing sediment fluxes on the surface of the Earth.

References

[1] R. Aalto, T. Dunne, J.-L. Guyot, Geomorphic controls on Andean denudation rates, J. Geol. (in press)

[2] F. Ahnert Functional relationship between denudation, relief, and uplift in large mid-latitude drainage basins, Am. J. Sci., Volume 268 (1970), pp. 243-263

[3] R.S. Anderson Evolution of the Santa Cruz Mountains, California, through tectonic growth and geomorphic decay, J. Geophys. Res., Volume 99 (1994), pp. 20161-20179

[4] A.P. Barros; D.P. Lettenmaier Dynamic modeling of orographically produced precipitation, Rev. Geophys., Volume 32 (1994), pp. 265-284

[5] J. Braun; D. Zwartz; J. Tomkin A new surface processes model combining glacial and fluvial erosion, Ann. Glaciol., Volume 28 (1999), pp. 282-290

[6] S.H. Brocklehurst; K.X. Whipple Glacial erosion and relief production in the Eastern Sierra Nevada, California, Geomorphology, Volume 42 (2002), pp. 1-14

[7] N. Brozovic; D.W. Burbank; A.J. Meigs Climatic limits on landscape development in the Northwestern Himalayas, Science, Volume 276 (1997), pp. 571-574

[8] J. Büdel Climatic Geomorphology, Translated by L. Fischer and D. Busche, Princeton University Press, Princeton, NJ, 1982 (443 p)

[9] J.M. Buffington; D.R. Montgomery Effects of hydraulic roughness on surface textures of gravel-bed rivers, Water Resour. Res., Volume 35 (1999), pp. 3507-3521

[10] D.W. Burbank Rates of erosion and their implications for exhumation, Mineral. Mag., Volume 66 (2002), pp. 25-52

[11] D.W. Burbank et al. Bedrock incision, rock uplift and threshold hillslopes in the northwestern Himalayas, Nature, Volume 379 (1996), pp. 505-510

[12] M.A. Carson An application of the concept of threshold slopes to the Laramie Mountains, Wyoming, Slopes: Form and Process, Inst. Br. Geogr. Spec. Publ., 3, 1971, pp. 31-47

[13] M.A. Carson; D.J. Petley The existence of threshold hillslopes in the denudation of the landscape, Inst. Br. Geogr. Trans., Volume 49 (1970), pp. 71-95

[14] W.M. Davis The geographical cycle, Geogr. J., Volume 14 (1899), pp. 481-504

[15] A.L. Densmore; M.A. Ellis; R.S. Anderson Landsliding and the evolution of normal-fault-bounded mountains, J. Geophys. Res., Volume 103 (1998), pp. 15203-15219

[16] D.P. Dethier Weathering rates and the chemical flux from catchments in the Pacific Northwest, USA (S.M. Colman; D.P. Dethier, eds.), Rates of Chemical Weathering of Rocks and Minerals, Orlando, Florida, Academic Press, 1986, pp. 503-530

[17] W.E. Dietrich; D.R. Montgomery Hillslopes, channels, and landscape scale (G. Sposito, ed.), Scale Dependence and Scale Invariance in Hydrology, Cambridge University Press, Cambridge, UK, 1998, pp. 30-60

[18] W.E. Dietrich; C.J. Wilson; D.R. Montgomery; J. McKean; R. Bauer Channelization thresholds and land surface morphology, Geology, Volume 20 (1992), pp. 675-679

[19] W.E. Dietrich; C.J. Wilson; D.R. Montgomery; J. McKean Analysis of erosion thresholds, channel networks and landscape morphology using a digital terrain model, J. Geol., Volume 101 (1993), pp. 259-278

[20] W.E. Dietrich; D.G. Bellugi; L.S. Sklar; J.D. Stock; A.M. Heimsath; J.J. Roering Geomorphic transport laws for predicting landscape form and dynamics (R.M. Iverson; P. Wilcock, eds.), Prediction in Geomorphology, Geophys. Monogr., 135, Am. Geophys. Union, Washington DC, 2003, pp. 103-132

[21] M.A. Ellis; A.L. Densmore; R.S. Anderson Development of mountainous topography in the Basin Ranges, USA, Basin Res., Volume 11 (1999), pp. 21-41

[22] D.P. Finlayson; D.R. Montgomery; B.H. Hallet Spatial coincidence of rapid inferred erosion with young metamorphic massifs in the Himalayas, Geology, Volume 30 (2002), pp. 219-222

[23] D.P. Finlayson; D.R. Montgomery Modeling large-scale fluvial erosion in geographical information systems, Geomorphology, Volume 53 (2003), pp. 147-164

[24] G.K. Gilbert Geology of the Henry Mountains, US Geol. Geogr. Surv. of the Rocky Mountain Region, Government Printing Office, Washington DC, 1877

[25] G.K. Gilbert The convexity of hill tops, J. Geol., Volume 17 (1909), pp. 344-350

[26] K.M. Gregory; C.G. Chase Tectonic and climatic significance of a late Eocene low-relief, high-level geomorphic surface, Colorado, J. Geophys. Res., Volume 99 (1994), pp. 20141-20160

[27] B. Hallet; L. Hunter; J. Bogen Rates of erosion and sediment yield by glaciers: a review of field data and their implications, Global Planet. Change, Volume 12 (1996), pp. 213-235

[28] A.D. Howard Long profile development of bedrock channels: interaction of weathering, mass wasting, bed erosion, and sediment transport (K.J. Tinkler; E.E. Wohl, eds.), Rivers Over Rocks: Fluvial Processes in Bedrock Channels, Am. Geophys. Union, Washington, DC, 1998, pp. 297-319

[29] M.J. Kirkby Hillslope process-response models based on the continuity equation, Inst. Br. Geogr. Spec. Publ., Volume 3 (1971), pp. 15-30

[30] P.O. Koons The topographic evolution of collisional mountain belts: a numerical look at the Southern Alps, New Zealand, Am. J. Sci., Volume 289 (1989), pp. 1041-1069

[31] W.B. Langbein; S.A. Schumm Yield of sediment in relation to mean annual precipitation, Trans. Am. Geophys. Union, Volume 39 (1958), pp. 1076-1084

[32] W. Ludwig; J.-L. Probst River sediment discharges to the oceans: present-day controls and global budgets, Am. J. Sci., Volume 298 (1998), pp. 265-295

[33] K.R. MacGregor; R.S. Anderson; S.P. Anderson; E.D. Waddington Numerical simulations of glacial-valley longitudinal profile evolution, Geology, Volume 28 (2000), pp. 1-21

[34] J.H. Mackin Concept of the graded river, Bull. Geol. Soc. Am., Volume 59 (1948), pp. 463-511

[35] J.A. McKean; W.E. Dietrich; R.C. Finkel; J.R. Southon; M.W. Caffee Quantification of soil production and downslope creep rates from cosmogenic ¹⁰Be accumulations on a hillslope profile, Geology (1993), pp. 343-346

[36] J.D. Milliman; J.P.M. Syvitski Geomorphic/tectonic control of sediment discharge to the ocean: the importance of small mountainous rivers, J. Geol., Volume 100 (1992), pp. 525-544

[37] D.R. Montgomery Slope distributions, threshold hillslopes, and steady-state topography, Am. J. Sci., Volume 301 (2001), pp. 432-454

[38] D.R. Montgomery Valley formation by fluvial and glacial erosion, Geology, Volume 30 (2002), pp. 1047-1050

[39] D.R. Montgomery; W.E. Dietrich Channel initiation and the problem of landscape scale, Science, Volume 255 (1992), pp. 826-830

[40] D.R. Montgomery; W.E. Dietrich Landscape dissection and drainage area-slope thresholds (M.J. Kirkby, ed.), Process Models and Theoretical Geomorphology, John Wiley & Sons, Chichester, UK, 1994, pp. 221-246

[41] D.R. Montgomery; M.T. Brandon Non-linear controls on erosion rates in tectonically active mountain ranges, Earth Planet. Sci. Lett., Volume 201 (2002), pp. 481-489

[42] D.R. Montgomery; G. Balco; S.D. Willett Climate, tectonics, and the morphology of the Andes, Geology, Volume 29 (2001), pp. 579-582

[43] F.J. Pazzaglia; M.T. Brandon Macrogeomorphic evolution of the post-Triassic Appalachian mountains determined by deconvolution of the offshore basin sedimentary record, Basin Res., Volume 8 (1996), pp. 255-278

[44] P. Pinet; M. Souriau Continental erosion and large-scale relief, Tectonics, Volume 7 (1988), pp. 563-582

[45] J.W. Powell Report on the Geology of the Eastern Portion of the Uinta Mountains and a Region of Country Adjacent Thereto, US Geol. Geogr. Surv. Territ., Government Printing Office, Washington DC, 1876

[46] C.S. Riebe; J.W. Kirchner; D.E. Granger; R.C. Finkel Minimal climatic control on erosion rates in the Sierra Nevada, California, Geology, Volume 29 (1991), pp. 447-450

[47] C.S. Riebe; J.W. Kirchner; D.E. Granger; R.C. Finkel Strong tectonic and weak climatic control of long-term chemical weathering rates, Geology, Volume 29 (1991), pp. 511-514

[48] G. Roe; D.R. Montgomery; B. Hallet Effects of orographic precipitation variations on the concavity of steady-state river profiles, Geology, Volume 30 (2002), pp. 143-146

[49] J.J. Roering; J.W. Kirchner; W.E. Dietrich Evidence for nonlinear, diffusive sediment transport on hillslopes and implications for landscape morphology, Water Resour. Res., Volume 35 (1999), pp. 853-870

[50] J.J. Roering; J.W. Kirchner; L.S. Sklar; W.E. Dietrich Hillslope evolution by nonlinear creep and landsliding: an experimental study, Geology, Volume 29 (2001), pp. 143-146

[51] K.M. Schmidt; D.R. Montgomery Limits to relief, Science, Volume 270 (1995), pp. 617-620

[52] S.A. Schumm, The disparity between present-day denudation and orogeny, US Geol. Surv. Prof. Pap. 454-H, Washington DC, 1963, 13 p

[53] L. Sklar; W.E. Dietrich River longitudinal profiles and bedrock incision models stream power and the influence of sediment supply (K.J. Tinkler; E.E. Wohl, eds.), Rivers Over Rocks: Fluvial Processes in Bedrock Channels, Am. Geophys. Union, Washington DC, 1998, pp. 237-260

[54] L. Sklar; W.E. Dietrich Sediment supply, grain size, and rock strength controls on rates of river incision into bedrock, Geology, Volume 29 (2001), pp. 1087-1090

[55] E.E. Small; R.S. Anderson; G.S. Hancock Estimates of the rate of regolith production using Be-10 and Al-26 from an alpine hillslope, Geomorphology, Volume 27 (1999), pp. 131-150

[56] J.D. Stock; D.R. Montgomery Geologic constraints on bedrock river incision using the stream power law, J. Geophys. Res., Volume 104 (1999), pp. 4983-4993

[57] M.A. Summerfield; N.J. Hulton Natural controls of fluvial denudation rates in major world drainage basins, J. Geophys. Res., Volume 99 (1994), pp. 13871-13883

[58] D.E. Walling; B.W. Webb Erosion and sediment yield: a global overview (D.E. Walling; B.W. Webb, eds.), Proc. Int. Symp. on Erosion and Sediment Yield: Global and Regional Perspectives, Int. Assoc. Hydrol. Sci., No. 239, IAHS-Publications, 1996, pp. 2-19

[59] K.X. Whipple; G.E. Tucker Dynamics of the stream-power river incision model: implications for height limits of mountain ranges, landscape response timescales, and research needs, J. Geophys. Res., Volume 104 (1999), pp. 17661-17674

[60] S.D. Willett Orogeny and orography: the effects of erosion on the structure of mountain belts, J. Geophys. Res., Volume 104 (1999), pp. 28957-28981

[61] S.D. Willett; C. Beaumont; P. Fullsack Mechanical model for the tectonics of doubly vergent compressional orogens, Geology, Volume 21 (1993), pp. 371-374

[62] S.D. Willett; R. Slingerland; N. Hovius Uplift, shortening, and steady state topography in active mountain belts, Am. J. Sci., Volume 301 (2001), pp. 455-485

[63] W. Zhang; D.R. Montgomery Digital elevation model grid size, landscape representation, and hydrologic simulations, Water Resour. Res., Volume 30 (1994), pp. 1019-1028

Comments - Politique