1 Introduction
Water is the most abundant liquid on the Earth's surface: the oceans contain 109 km3 of it. There is also a large amount of water (equivalent to one ocean) that is dissolved in the Earth's ‘mantle’. Water, in the form of ice, is present in large quantities in space, and in particular in the solar system. Europa, one of Jupiter's satellites, has been known for a long time to be covered by ice and it has been claimed that traces of water were found on Mars. Water is also one of the essential constituent of comets: it can be found in large quantities as small ice grains in the Oort's cloud, a huge cloud some 10 000–30 000 AU away from the sun, where long-period comets are formed.
Water is a liquid with extraordinary properties: it has unusually high melting and boiling temperatures, a huge heat capacity, one of the highest dielectric constants among non-metallic liquids, and a series of anomalies in its specific volume (ice floats on water, etc.). A minimal approach for understanding this liquid would include the following questions:
- – why is water a liquid at ambient temperature and pressure, rather than a gas, or a solid?
- – what type of a liquid is it, i.e. are its properties similar to those of other liquids?
- – can we understand how this liquid functions, i.e. how its behaviours derive from the properties of the molecule?
We would like to answer these questions using a small number of ingredients: start with a few molecular properties, and find out which ones are really required to reproduce the properties of the liquid.
2 The cohesion of liquid water (a liquid or a gas?)
Liquid water has an exceptionally high cohesion, which manifests itself through high melting and boiling temperatures, a high surface tension, and a large specific heat. Such characteristics are usually found in liquids that are made of large molecules, or in liquids that are either ionic or metallic: in those liquids, it takes a lot of energy to overcome the cohesive forces and separate a volume of liquid into smaller volumes, or stretch its surface, or extract some molecules from it. Yet the water molecule is quite small, and pure water is neither ionic nor metallic.
The homologous compounds H2S, H2Se, and H2Te are gases at ambient temperature. Their boiling temperatures rise with molar mass, because of stronger van der Waals forces that keep the molecules together. Extrapolating that trend, we would predict that liquid water at ambient pressure would boil at , i.e. 180 °C lower than the experimental boiling temperature (Fig. 1). This unusual cohesion has its origin in the strength of hydrogen bonds (H bonds) that bind the water molecules together. Other homologous molecules such as H2S, etc., do not form H bonds, because the heavier atoms S, Se, and Te are less electronegative than the oxygen atom [24].
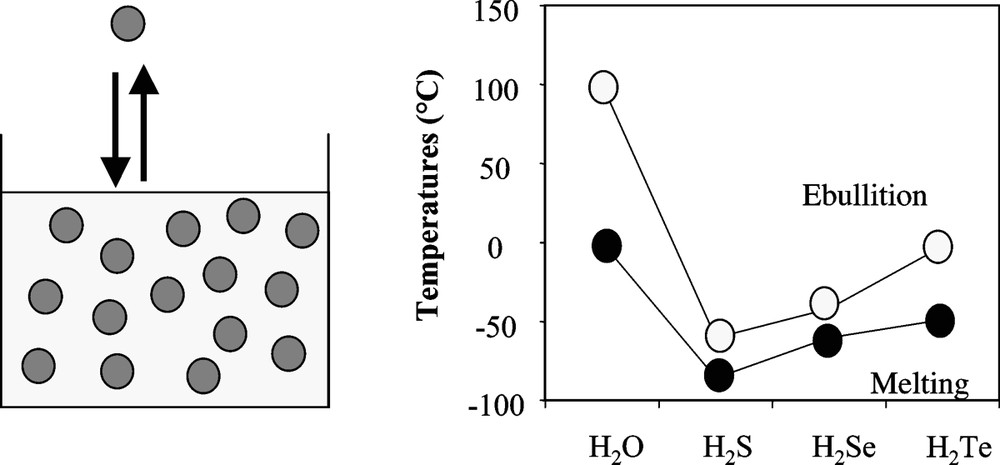
Melting and boiling temperatures of the homologous liquids H2O, H2S, H2Se, and H2Te. The higher temperatures for H2O result from cohesion through H-bonds.
Températures de fusion et d'ébullition des liquides homologues H2O, H2S, H2Se, and H2Te. Celles de l'eau sont anormalement élevées à cause de la cohésion due aux liaisons H.
The strength of an H-bond in liquid water at ambient temperature is eight times the energy of thermal agitation kT [8]. The number of bonds in liquid water, divided by the number of molecules, is 1.75 (but each bond connects two molecules, hence each molecule is connected to others through 3.5 bonds) [21,28–30]. Counting also weaker cohesive forces, such as the van der Waals attractions, we get a cohesive energy per molecule that is . Other liquids that are associated through H bonds also have cohesive energies per molecule that are in line with their boiling temperatures. Thus, the cohesive energy per molecule is in ammonia (), in hydrogen fluoride (), in methanol () and in hydrazine (). However, the cohesive energy density of water is superior to those for any of these other associated liquids, because the water molecule is quite small (Table 1). This raises the question of how a small molecule can produce such strong bonds.
Comparison of cohesive properties for liquid water and for a few other associated liquids (at 25 °C unless specified otherwise): molar volume v in , melting and boiling temperatures in °C, latent heat of vaporization ΔH in kJ mol−1, cohesive energy density ΔH/v in , dipole moment of the isolated molecule p in Debyes (1 D=3.33×10−30 C m), relative dielectric constant . Water is unusual in its cohesive energy density ΔH/v, and in the high value of the ratio
Comparaison des propriétés cohésives de l'eau liquide et de quelques autres liquides associés (à 25 °C, sauf spécification contraire) : volume molaire v en , températures de fusion et d'ébullition en °C, chaleur latente de vaporisation ΔH en kJ mol−1, densité d'énergie cohésive ΔH/v en , moment dipolaire de la molécule isolée p en debyes (1 D=3,33×10−30 C m), constante diélectrique relative . L'eau est exceptionnelle de par sa densité d'énergie cohésive ΔH/v et le rapport
| Δ H | |||||||
| Water | 18 | 0 | 100 | 44 | 2.4 | 1.85 | 78.4 |
| Hydrazine | 32 | 1.4 | 113.5 | 45 | 1.4 | 1.86 | 51.7 |
| Formamide | 40 | 2.5 | 220 | 60 | 1.5 | 3.73 | 109 |
| Methanol | 41 | −97 | 64.6 | 37 | 0.9 | 1.7 | 33 |
| Ethanol | 58 | −114 | 78.2 | 42 | 0.7 | 1.69 | 24 |
| Ethyleneglycol | 56 | −1.3 | 197.3 | 2.28 | 47 |
The cohesion of water is also the cause of an enormous specific heat: it takes three times as much energy to heat up water than for the same mass of pentane, and ten times more than for the same mass of iron. This specific heat is more than twice that of ice, whereas most liquids have specific heats that are close to those of the corresponding solids. This resistance to temperature changes has important climatic consequences, since the heat capacity of the oceans causes them to act as thermal regulators. It has its origin in the absorption of heat through the breaking of H-bonds: the heat that is used by this process is not available for increasing the kinetic energy of the water molecules, which reduces the rise in temperature. This brings us back to the very high cohesive energy density of liquid water: how can such a small molecule produce such strong bonds?
3 The isolated water molecule
The water molecule can be represented in different ways. For a chemist, the most useful choice is the Lewis representation [24], where the electron pairs are assigned to bonding and non-bonding orbitals. A refined version of this representation would show the localization of electrical charges, i.e. positive charges on the nuclei, and negative charges on electronic orbitals (Fig. 2). This is interesting because it shows that all positive charges are grouped on one side of the molecule, while the majority of negative charges are on the other side. Finally, physicists, particularly those involved in numerical simulations of water (see the original work of Bernal and Fowler [6]), tend to consider an equivalent electrostatic object (for instance two positive charges localized on the protons, at 0.0957 nm from the O atom in directions that make an angle of 104.5°, and two negative charges localized on the non-bonding orbitals, at 0.07 nm from the O atom in directions that make an angle of 109.5°). The separation of positive and negative charges gives rise to a dipole moment: for the isolated molecule, its magnitude is 1.85 D.
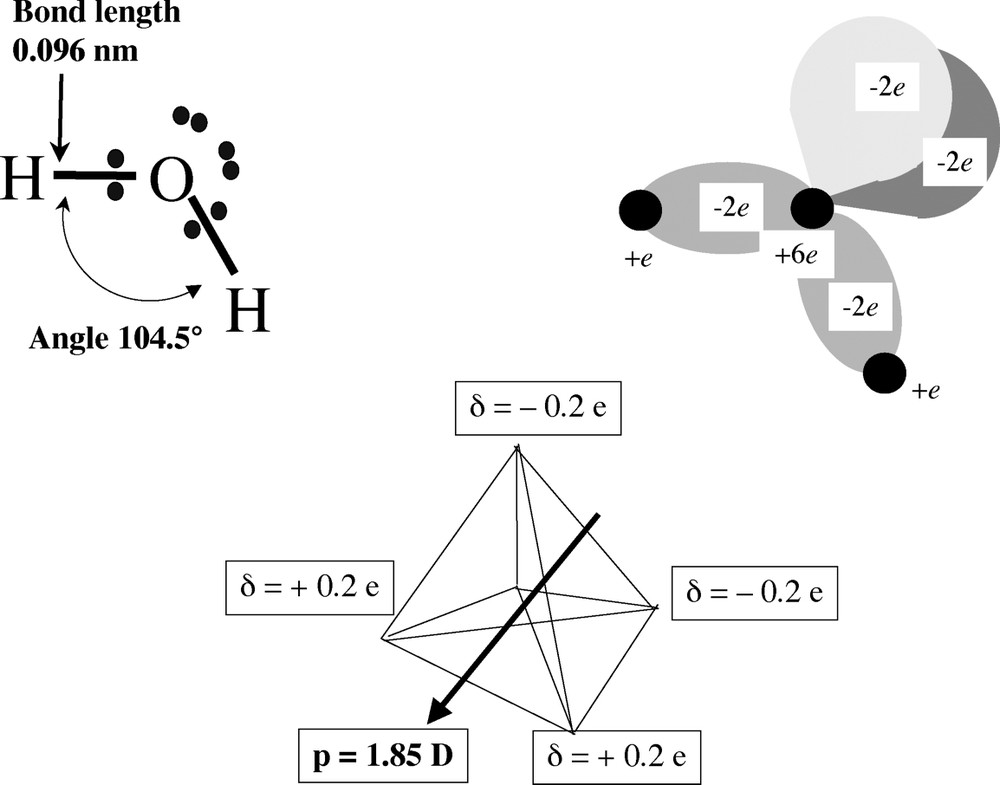
Geometrical and electrical characteristics of the water molecule. Top left: ‘Lewis’ representation; top right: location of nuclei and electronic orbitals; bottom; equivalent electrostatic object for use in numerical simulations.
Caractéristiques géométriques et électriques de la molécule d'eau. En haut à gauche : représentation selon Lewis ; en haut à droite : localisation des noyaux et des orbitales électroniques ; en bas : objet électrostatique équivalent utilisé dans les simulations numériques.
A proper quantum mechanical calculation of the electronic orbitals gives the electronic densities shown in Fig. 3. The orbitals shown here are ‘localized’ orbitals, which correspond to the chemical description of electrons in covalent bonds and in non-bonding pairs [17]. The bonding orbitals are indeed localized on the OH bonds, with a high electronic density near the O atoms, due to its electronegative character. The non-bonding orbitals are in the other side of the O atom, in tetrahedral directions with respect to the OH bonds. Again, considering both positive and negative charges, it appears that most of the positive charge is on one side of the molecule (near the protons) and most of the negative charge on the other side, thereby producing a strong dipole moment.
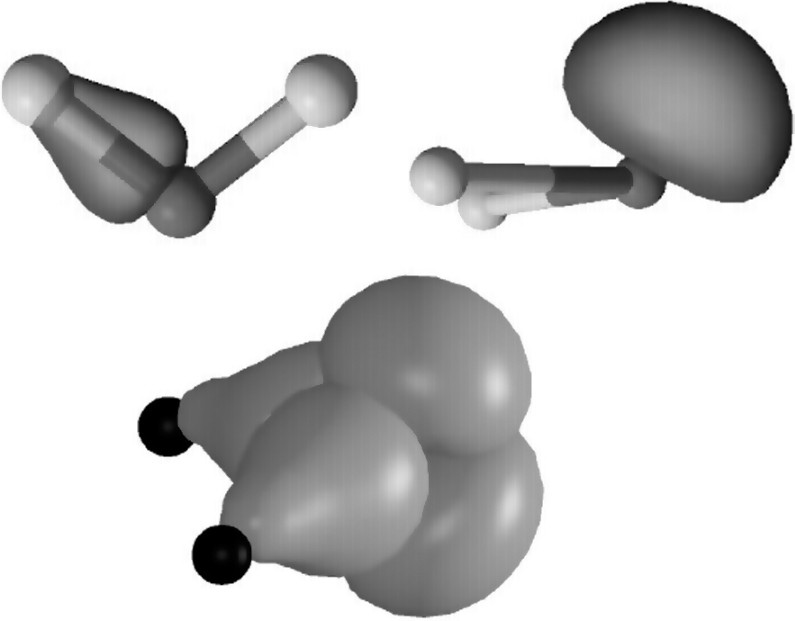
Electronic densities in the water molecule, obtained through quantum-mechanical calculations of localized orbitals. Left: bonding orbitals. Right: non-bonding orbitals. Bottom: bonding and non-bonding orbitals.
Densités électroniques de la molécule d'eau, obtenues par calcul des orbitales localisées via la mécanique quantique. À gauche : orbitales liantes. À droite : orbitales non liantes. En bas : orbitales liantes et non liantes.
4 The water dimer and the H-bond
In order to understand the properties of liquid water, we need to know how these molecules interact. The first step is to examine the dimer, formed of two water molecules connected by one H bond (Fig. 4). In this configuration, the water molecule that is on the left-hand side acts as a proton donor, because its H atom is involved in the H-bond, and the water molecule that is on the right-hand side acts as a proton acceptor, because its electronic orbitals interact with the H atom of the first molecule. The H-bond derives its strength mainly from the electrostatic attraction of the non-bonding electron pairs localized on the proton acceptor molecule (right) by the positive charges of the nuclei in the proton donor molecule (left). Since the molecules have very small dimensions, these attractions are quite strong and they cause the molecules to come so close to each other that they overlap (i.e. the donor molecule is pulled into the space occupied by the acceptor molecule).
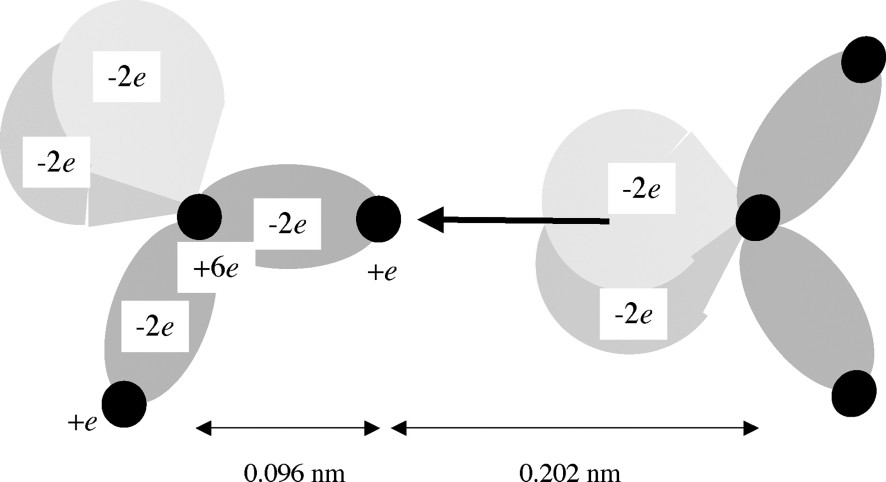
Interactions between two water molecules in a dimer. The molecule on the left-hand side acts as a ‘proton donor’; that on the right-hand one as a ‘proton acceptor’. The H-bond attraction results mainly from the attraction of the non-bonding electron pairs of the acceptor molecule by the positive charge of the proton (and also, to a lesser extent, by the positive charges carried by the other nuclei) of the donor molecule.
Interactions entre les deux molécules d'eau d'un dimère. La molécule de gauche agit comme « donneur de proton » et celle de droite comme « accepteur de proton ». La liaison H résulte principalement d'une attraction entre les doublets électroniques non liants de la molécule « accepteur » par la charge positive du proton (et aussi, dans une moindre mesure, par les charges positives portées par les autres noyaux) de la molécule « donneur ».
The total electronic density of the dimer, obtained through a proper quantum mechanical calculation of the electronic orbitals, is shown in Fig. 5. When the molecules are in the H-bonding configuration, the calculations show that the total electronic density has a ‘bridge’ joining the two molecules. This bridge results from the overlap caused by the attraction of the donor molecule by the acceptor molecule. It is the ‘signature’ of the H-bond.
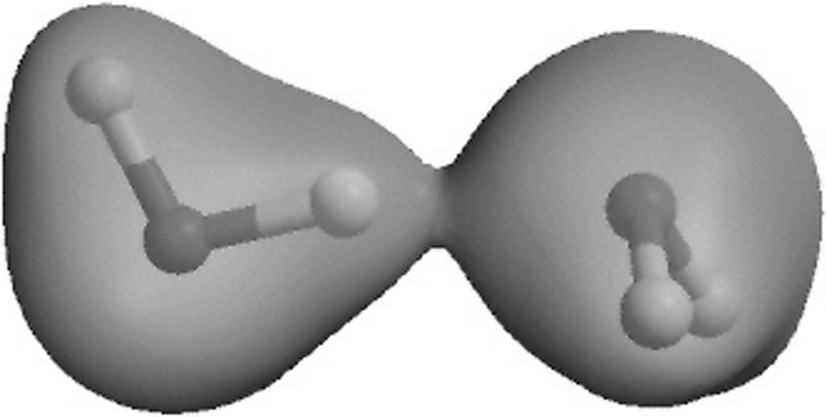
Electronic densities in the water dimer, obtained through quantum-mechanical calculations of localized orbitals. The ‘bridge’ of electronic density that joins the two molecules is the ‘signature’ of a H-bond.
Densités électroniques du dimère, obtenues par calcul des orbitales localisées via la mécanique quantique. Le « pont » de densité électronique qui joint les deux molécules est la « signature » de la liaison H.
The interaction of two water molecules in the configuration where they act as donor and acceptor is particularly strong because the two molecules polarize each other. Indeed, the electrons of the acceptor molecule (right) push away the electrons of the donor molecule (left). This displacement shows up in a map of the variations of electronic density (with respect to the electronic densities of the isolated molecules) (Fig. 6). Indeed, these variations show alternating excess and lack of electronic density, with a net polarization directed from the proton acceptor to the proton donor (at every location, the electrons are pushed from the right to the left of the figure).

Variations in electronic density caused by the interactions of the two molecules in a dimer, with respect to the electronic densities of isolated molecules. The regions of excess electronic density are shaded dark grey, and those with a loss of electronic density are shaded white. The alternating pattern of excess and loss of electronic density reveals a mutual polarization of the molecules, which increases the total dipole moment.
Variations de densité électronique causées par les interactions des deux molécules du dimère, par rapport aux densités électroniques de molécules isolées. Les régions où la densité électronique du dimère est excédentaire sont ombrées en gris, celles qui ont perdu de la densité électronique en blanc. L'alternance régulière de régions contenant un excès et un défaut de densité électronique crée une polarisation des molécules, qui augmente le moment dipolaire du dimère.
5 The dielectric cohesion of liquid water
Besides its contribution to the bond strength, this polarization has another important consequence: it makes the total dipole moment much stronger than the sum of dipole moments of isolated molecules. Indeed, the set of alternating displacements shown in Fig. 6 produces a polarization that reinforces the dipole moments of the molecule. In liquid water, this effect is even stronger, because the polarizations created by all bonds reinforce each other in a cooperative way. Consequently, the dipole moment per molecule in liquid water is much larger (3 D) than that of the isolated molecule (1.85 D) [14–16,18,25,26]. (Note, however, that the dipole moment per molecule is not an observable and thus is not well defined; it is, however, a powerful computational intermediate for modelling water.)
Because of these mutual polarizations of the molecules, liquid water has an extremely strong response to electric fields. For instance, when an ion is introduced in water, the dipoles of the neighbouring water molecules align themselves in the field of the ion and create a “reaction field” that nearly compensates the field of the ion (Fig. 7).
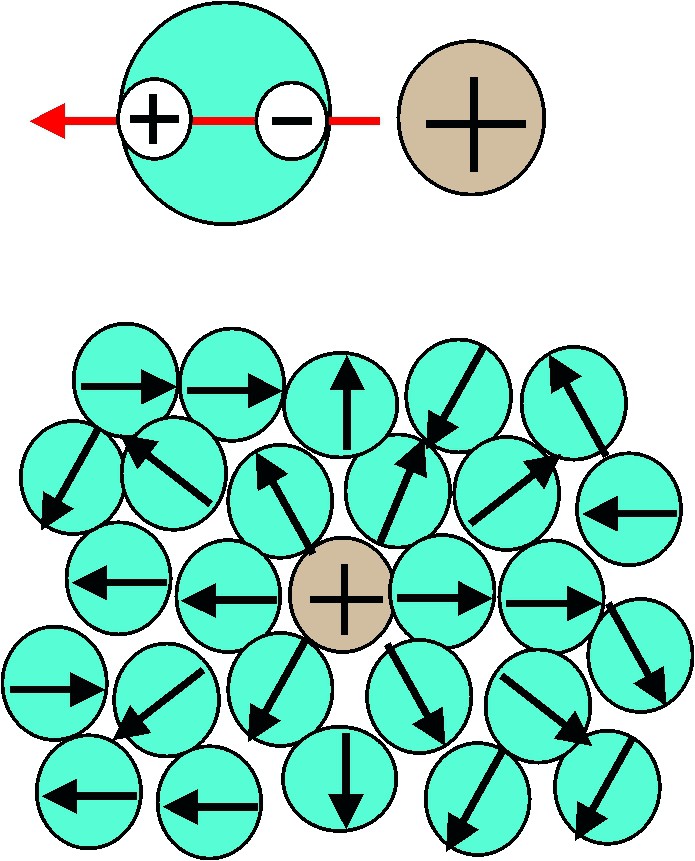
Orientations of water dipoles around an ion. The electric field created by the dipoles nearly compensates the field of the ion. This reduces the Born energy of the ion to a value that is much smaller than its Born energy in a vacuum [8].
Orientations de molécules d'eau autour d'un ion. Le champ électrique de leurs dipôles compense presque totalement le champ de l'ion. Cet effet réduit l'énergie de Born de l'ion à une valeur très inférieure à son énergie dans le vide [8].
This response to electric fields is measured by the dielectric constant of water. Fig. 8 presents the relative dielectric constants for polar liquids, plotted according to the magnitudes of the dipole moments of the isolated molecules. For ‘regular’ polar liquids, the dielectric constants vary as the square of this dipole moment, as expected for the response of a collection of independent dipoles. Some liquids, however, have dielectric constants that are much above the response expected for isolated molecules. In these liquids, the rotation of one molecule causes many others to follow, because these molecules are all connected through H-bonds. These liquids are called associated liquids. Among such liquids, water is exceptional, because its relative dielectric constant ( at 20 °C) is so much higher than the value expected for independent water molecules.
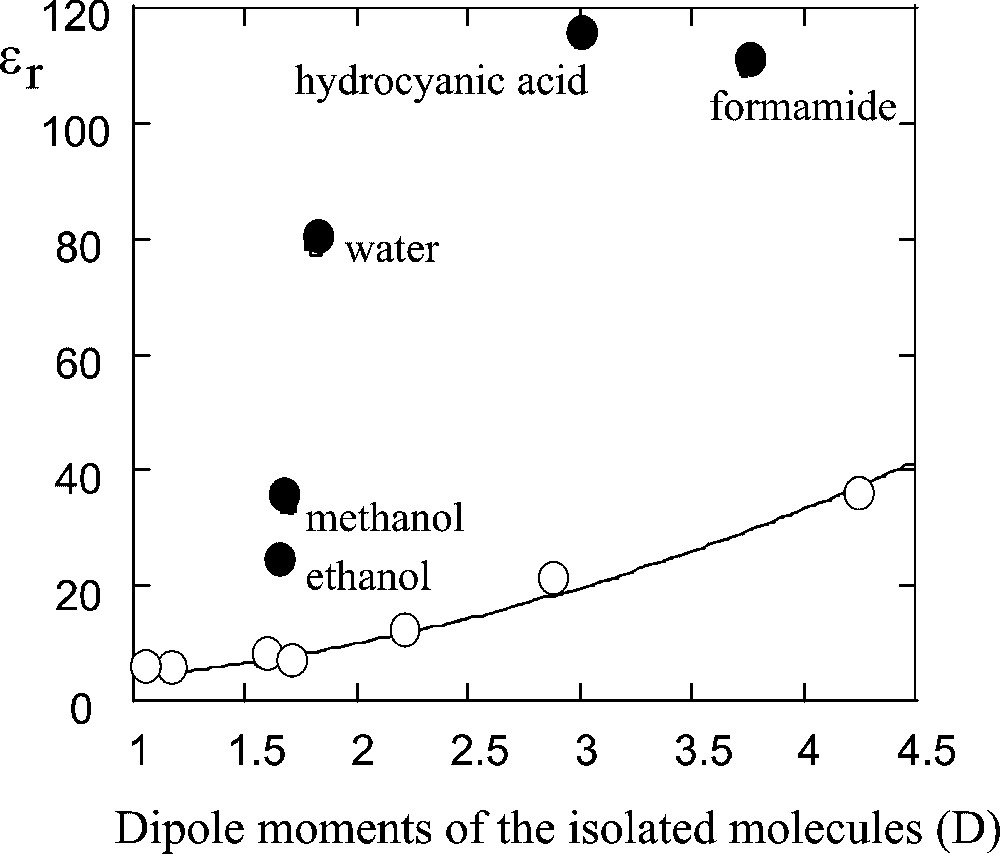
Relative dielectric constants of common polar liquids (circles: from left to right, chloroform, diethyl ether, aniline, chlorobenzene, pyridine, acetone, nitrobenzene) and of associated liquids (filled dots). The very high value for water is due to the mutual polarization of the molecules.
Constantes diélectriques relatives des liquides polaires usuels (cercles : de gauche à droite, chloroforme, diéthyl éther, aniline, chlorobenzène, pyridine, acétone, nitrobenzène), et de liquides associés (points noirs). La valeur anormalement élevée de la constante diélectrique de l'eau est due à la polarisation mutuelle des molécules dans le liquide.
It is thanks to this exceptionally high dielectric constant that life evolved in water and nowhere else. Indeed, the polarization of water dipoles around an ion makes it possible to dissociate ion pairs and therefore to dissolve ionic crystals (Fig. 9). The ionic concentrations that water can hold are enormous: for NaCl, up to six moles of salt can be dissolved into 55 moles of water. At this composition, the solution has only nine molecules of water per ion pair. This number is not much above the number of water molecules that are in the hydration shells of the ions, which means that very little free water is needed to turn a hydrated crystal into a liquid. Seawater is, of course, the most abundant ionic solution, but all biological fluids are, like seawater, concentrated ionic solutions. Moreover, most biochemical processes require the dissociation of ion pairs and the screening of electrical charges, which are possible only in water or in ionic solutions.
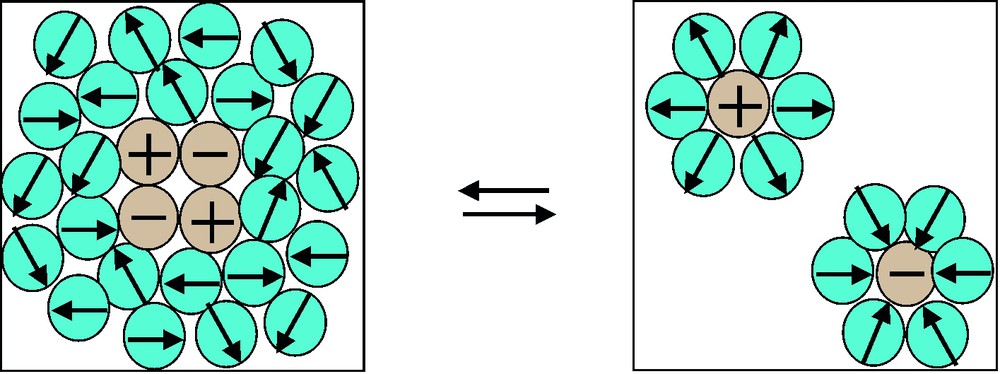
Dissolution of an ionic crystal into water. The polarization of the water dipoles by the ions nearly compensates the loss of electrostatic energy from the ion–ion interactions.
Dissolution d'un cristal ionique dans l'eau. La polarisation des dipôles des molécules d'eau par les ions compense presque totalement la perte de l'énergie électrostatique due aux interactions entre ions.
At this stage, we can identify three properties of the water molecule that are responsible for the exceptional cohesion of liquid water: (a) its ability to form H-bonds; (b) its very small size; (c) its ability to interpenetrate and polarize neighbouring molecules. However, with this unusually strong cohesion, we are now faced with a problem that is opposite to our initial question: how can water be a fluid rather than a solid?
6 The fluidity of water (a liquid or a solid?)
In liquid water, each molecule is connected to its neighbours by 3.5 H-bonds (on average). The resulting network has a high degree of connectivity. Moreover, these bonds are quite strong (eight times the energy of thermal agitation). At first sight, these features would seem to make it particularly difficult for water molecules to move and switch neighbours. Therefore, the fluidity of liquid water would appear to be some kind of a mystery.
Of course, strong bonds do not necessarily last forever, so we must examine the lifetimes of these H bonds. Spectroscopic experiments indicate that these lifetimes are quite short, in the order of 1 ps. This observation pushes the problem one step further: how can strong bonds have such short lifetimes?
One way to answer this question is to examine the distribution of bond energies [21]. Sure enough, this distribution has a peak at the average energy per bond, i.e. . However, there are large numbers of bent or strained bonds with smaller energies (3 to ). Any given bond may frequently go through such strained configurations, where it is much more likely to be broken, giving way to a new bond with different partners. Thus, the energetic cost of switching bonds may not be nearly as high as the average bond energy.
Another way to see the same question is through a consideration of the numbers of bonds per molecule. Fig. 10 presents the distribution of molecules that have respectively zero, one, two, three, four or five bonds, according to numerical simulations of liquid water [18]. Most molecules have three or four bonds, as expected. However, there is a significant proportion of water molecules with only two bonds. These molecules are ‘caught in the act’ of switching their bonds from one set of partners to another. The resulting residence time, averaged over all molecules in the liquid, is about 3 ps. Thus, despite the high degree of connectivity of the H-bond network, diffusive motions and flow are made possible by the very short lifetime of these bonds.
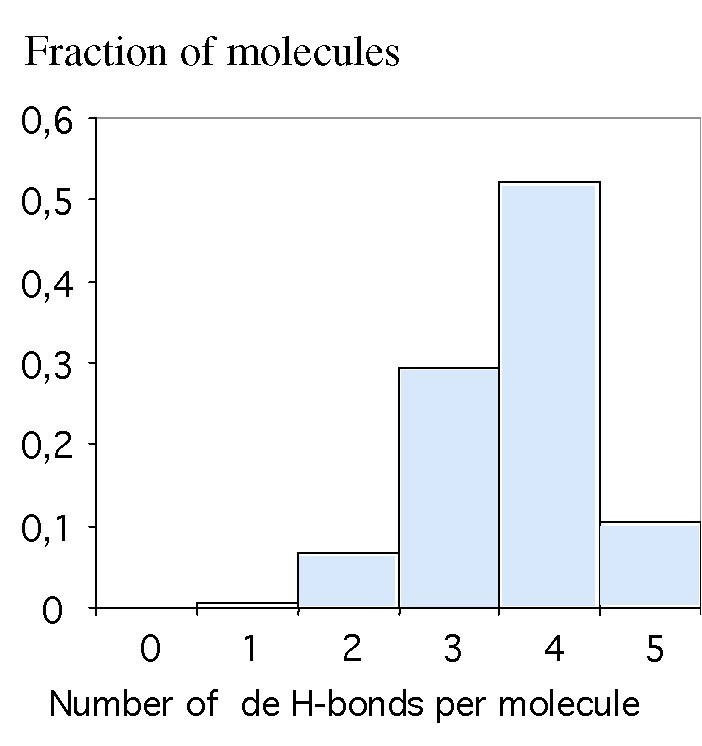
Numbers of water molecules (as fractions of the total number of water molecules in the liquid) that have respectively two, three, four or five bonds. From [6].
Nombres de molécules d'eau (exprimés en fractions du nombre total de molécules) qui ont respectivement deux, trois, quatre ou cinq liaisons H. D'après [6].
7 The density of liquid water (a liquid that is full of voids)
Now that we understand how water can be a liquid at ambient temperature and pressures, we may wonder what kind of a liquid it is: does it have properties that are in line with those of other liquids, or does it have unusual properties?
The simplest property of a liquid is its mass per unit volume. In most liquids, the cohesive forces pull the atoms together, and the mass per unit volume corresponds to a dense packing of the atoms or molecules, with a few vacancies that allow for the disorder that characterizes the liquid state. This dense packing is achieved in liquids that owe their cohesion to non-directional forces, such as van der Waals attractions – i.e. rare gases, and most molecular liquids. A useful comparison is with the rare gas neon, because its electronic configuration is the same as that of water. The mass per unit volume of liquid neon is 1200 kg m−3 at low temperature (near the triple point), whereas that of liquid water is 1000 kg m−3. Another comparison is with aliphatic oils: most oils have a mass per unit volume that is close to that of water, but their cohesive forces are much weaker. Thus, the mass per unit volume of water is low for a liquid that has such a strong cohesion.
The small mass per unit volume of water results from the fact that the atoms are not densely packed: the volume that is occupied by the atoms of the water molecule is 0.0146 nm3, whereas the volume per molecule in the liquid is 0.02992 nm3. The ratio of these volumes is only 0.49, whereas a dense packing of spherical molecules would yield 0.74. Thus, a large part of the volume of liquid water is actually made of voids.
The specific volume of water is also anomalous in the way it varies with temperature. For most liquids, this volume diminishes regularly when the temperature is lowered, because the number of thermal vacancies is reduced [11]. To the contrary, water expands when it is cooled below a temperature that is called ‘temperature of maximum density’ (TMD for H2O) [19,20]. Thus, low-temperature water has a much lower density compared with what would be expected according to its high-temperature behaviour (Fig. 11). Water also becomes more compressible at low temperature (the temperature of minimum compressibility is 46.5 °C), whereas the opposite is true for most other liquids, since they lose the thermal vacancies that make the compression easier.
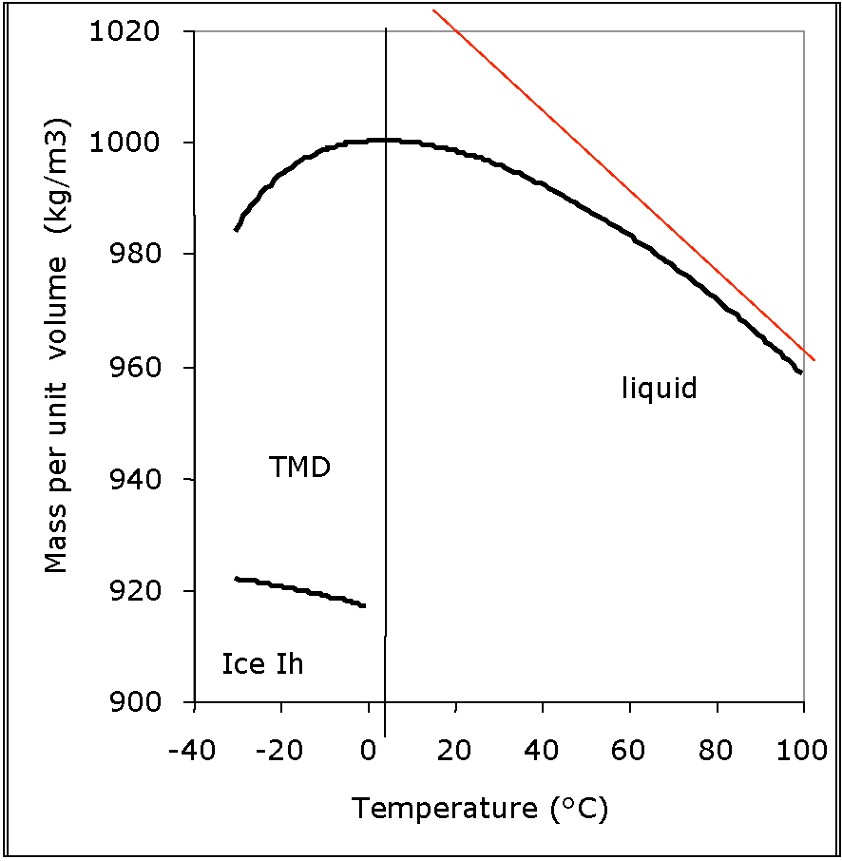
Variations with temperature of the mass per unit volume of liquid water, according to [19,20]. For most liquids, the variation is monotonically decreasing, as indicated by the straight line. The temperature of maximum density (TMD) is 4 °C in H2O, 11.2 °C in D2O and 13.4 °C in T2O. The decrease in density at low temperatures results from a change to a structure that has more bonds and voids.
Variation de la masse volumique de l'eau liquide avec la température, d'après [19,20]. Pour les liquides « normaux », la masse volumique décroît de manière monotone, comme indiqué sur la ligne droite. La température du maximum de densité de l'eau vaut 4 °C dans H2O, 11,2 °C dans D2O et 13,4 °C dans T2O. La décroissance de la densité à basse température résulte d'un changement de la structure du liquide, qui crée systématiquement des liaisons et des cavités.
For most other liquids, the specific volume decreases by about 10% upon crystallization, since the atoms or molecules are more efficiently packed in the crystal [11]. On the contrary, water expands by 9% when it crystallizes. Regular ice has a very large specific volume: the ratio of the volume that is actually occupied by the atoms to the total volume of the solid is only 0.45, against 0.49 for the liquid in the same conditions (0 °C, 1 atm). This increase in specific volume causes ice to float on top of water, which has important environmental consequences. Indeed, if ice was heavier than water, all the ice that is formed in the northern regions would sink to the bottom of the Arctic Ocean instead of forming an ice shelf that provides thermal insulation to the liquid below, and the production of ice would continue until the Arctic Ocean were completely frozen form the bottom up to the surface.
For most other liquids, an increase in pressure makes them less fluid (because it reduces the free volume that allows the molecules to move) and it favours the solid state (because the solid uses less volume than the liquid). On the contrary, for low-temperature water, the application of pressure increases its fluidity, and it favours the liquid state with respect to the solid: the melting temperature is lowered at high pressure. There is a common belief that this melting under pressure is what makes it possible for skiers and skaters to slide easily on ice crystals. In fact, the pressures exerted by the skates or skis on the supporting ice crystals are not high enough to change their melting points. However, the surface of ice always produces a film of liquid water, regardless of the applied pressure, and this film lubricates the contact.
None of the other associated liquids has similar anomalies in their specific volume. There are a few liquids that expand upon crystallization, and this appears to be related to a particularly open structure of the solid (for instance, silicon has a tetrahedral ordering in the crystal) [11]. Thus, in order to understand these anomalies, we need to examine the structures of water in its liquid and solid states.
8 The structure of liquid water (one or two liquids?)
A proper description of the liquid involves not only how molecules are connected, but also how they are arranged with respect to each other. Ideally, we would need some information on the structures of groups of three, four, five or six molecules. In the liquid, however, structural experiments provide us only with some information concerning pairs of molecules. Indeed, the X-ray or neutron scattering experiments determine the pair distribution function of the molecules, i.e. the distribution of probabilities for molecules in a given pair to be at a distance r. This function has peaks at preferred distances, particularly at the distance of molecules joined by one H-bond, or by two consecutive H-bonds. From the areas under these peaks, we may calculate the numbers of molecules that are at specific distances in the coordination shell of a given molecule. In this way, images of the structure can be constructed.
It is, of course, easier to start with well-known structures. From an energy point of view, the best ordering of water molecules is a tetrahedral ordering, where each molecule is connected to four others, located in directions that make angles of 109° between them. In this way, the angle between two consecutive bonds matches the geometry of the molecules (Fig. 2), and all four bonds are equally strong. This structure is found in ordinary ice, which is formed at ambient pressure and low temperatures (it is also called hexagonal ice, or ice Ih, because the tetrahedral coordination gives rise to a lattice with hexagonal patterns when viewed in the direction of a bond). The most remarkable feature of this structure is that it is full of voids. This is shown in Fig. 12, which presents two views of the same lattice. In one view, the hexagonal symmetry is apparent, and one cavity is figured as a shaded area enclosed by the lattice. In the other view, the water molecules are grouped in tetrahedra, and each one is enclosed in a small cube, but every other cube of this lattice is vacant. It is useful to give a number, which is the fraction of the volume that is actually occupied by the atoms: in hexagonal ice, this fraction is only 0.45!
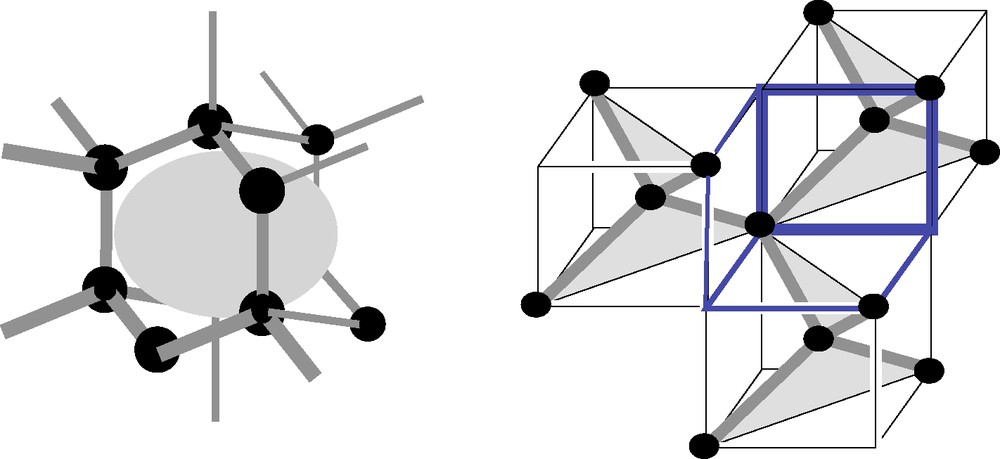
Two views of the crystal lattice of ice Ih. Left: the molecules (black disks) are placed on a ‘diamond’ lattice, with tetrahedral coordination (H-bonds are represented as grey sticks). The shaded area is a structural cavity; every cell in the lattice contains such a cavity. Right: each group of four molecules forms a tetrahedron, which is placed in a cube. These cubes are repeated as in a simple cubic lattice, but every other cube is vacant; in the figure, a vacant cube, located at the front of the array, is indicated with dark edges; it forms one of the structural cavities of the lattice.
Deux vues de la structure cristalline de la glace Ih. À gauche : les molécules (disques noirs) sont placées sur un réseau « diamant » caractérisé par une coordination tétraédrique (les liaisons H sont représentées par des tiges noires). Chaque cellule du réseau contient une cavité telle que la zone ombrée de la figure. À droite : chaque groupe de quatre molécules forme un tétraèdre, qui est placé dans un cube. Les cubes sont répétés comme dans un réseau cubique simple, mais un cube sur deux est vide. Sur la figure, un cube vide est signalé par des arêtes renforcées : c'est une des cavités structurales du réseau.
In liquid water at low temperature, the pair distribution function resembles that of ice Ih: each molecule is surrounded by a small number of nearest neighbours located at the H-bonding distance, in the H-bonding directions (Fig. 13).

Locations of the first neighbours of a water molecule in low-temperature liquid water, according to numerical simulations. The reference molecule is represented in the centre, with its O atom (in black) and H atoms (in white). Two neighbouring molecules act as proton acceptors to the reference molecule; they are located in the grey-shaded areas that are to the right and to the left. The other two neighbours act as proton donors; they are located in the grey-shaded areas that are to the back and above the reference molecule.
Localisations des premières voisines d'une molécule d'eau dans le liquide à basse température, d'après les simulations numériques. La molécule de référence est placée au centre, avec ses atomes O (en noir) et H (en blanc). Deux molécules voisines agissent comme accepteurs de protons vis-à-vis de la molécule de référence ; elles sont localisées dans les zones ombrées situées à gauche et à droite. Les deux autres voisines agissent comme donneurs de protons ; elles sont localisées dans les zones ombrées situées en dessous et en dessus de la molécule de référence.
The next shell of neighbours is at the distance that corresponds to coordination through two consecutive H-bonds, with the correct angle between them. Indeed, the ‘signature’ of this structure in the pair-correlation function is the location of the second neighbours at the position dictated by the propagation of tetrahedral coordination (Fig. 14). The disorder that characterizes the liquid state is minimal in the first shell (bond length is constant), moderate in the second shell (bond angle is also maintained) and almost complete beyond this second shell (the orientation of the third bond is nearly free) [7,12,13,22,23,27,31].

Locations of the first and second neighbours of a water molecule. Left: low temperature, low pressure. Each molecule has four nearest neighbours, connected through H-bonds, and located in tetrahedral directions. The second neighbours are connected through two successive bonds, with an angle between bonds equal to the tetrahedral angle, i.e. 109°. Right: high temperature or high pressure: the angle between bonds is no longer retained, and the shell of second neighbours collapses on the shell of first neighbours.
Localisations des premières et secondes voisines d'une molécule d'eau. À gauche : structure à basse température et basse pression. Chaque molécule a quatre voisines, connectées par des liaisons H, et localisées dans des directions tétraédriques. Les secondes voisines sont reliées à la molécule de référence par deux liaisons successives, qui forment entre elles un angle égal à l'angle du réseau tétraédrique, soit 109°. À droite : structure à haute température ou haute pression : l'angle entre liaisons successives n'est pas conservé, et la couche de secondes voisines s'effondre sur la première couche.
At higher temperature, however, this open structure is not retained: the shell of second-neighbours collapses onto the shell of first neighbours (Fig. 14). This high-temperature structure is denser than the low-temperature one, because the reference molecule is now surrounded by additional molecules that are not directly connected to it. From an energy point of view, this is less favourable, since the angle between consecutive bonds does not match the geometry of the molecule. This dense ordering resembles the structures of some varieties of ice that are formed at very high pressures, but of course it is more disordered, since the liquid explores all configurations that are accessible without changing bond lengths.
The change from an open structure at low temperature to a denser structure at high temperature is the cause of the density anomaly of water: the liquid has a density maximum at 4 °C. At lower temperature, it becomes less dense, because it takes an open structure, which is full of voids. At higher temperature, the ordering is denser, but vacancies are generated by thermal disorder, and normal thermal expansion sets in (Fig. 11).
At this point, it would be tempting to make a simple model in which water would be described as a mixture of two liquids: a liquid with a structure that resembles regular ice, having many structural cavities and a low overall density, and a liquid with a structure that resembles the high-pressure forms of ice, having a higher density. The anomalous variation of the density of water would then be caused by a change in the proportions of these two components. These two-state models have been quite popular for a long time, because they made it possible to reproduce many anomalous behaviours of water, including the density anomaly, and the variations in fluidity and compressibility with temperature [1,9,10,33,34]. However, structural experiments do not support this view: instead, they demonstrate that water is fully homogenous at all scales, without the density fluctuations that would be the signature of a two-component liquid [7,12,13,22,23,27,31]. Experiments performed at extremely low temperatures do produce, depending on the pressure, two distinct amorphous forms of ice; however, all experiments performed at more moderate temperatures, on supercooled water, indicate that the separation of two liquid phases would only occur at temperatures for which the liquid turns spontaneously into a solid [2–5].
At this stage, we can identify one property of the molecule that is responsible for the large specific volume of liquid water, and for all the anomalies that are associated with this volume. This property is the orientation of bonding and non-bonding orbitals (Fig. 2), which causes the molecule to form four bonds in a tetrahedral configuration, and leads to the open ice-like structures. Interestingly, it is not the tetrahedral symmetry per se that is the cause of the anomalies, but rather the fact that this symmetry is associated with an open structure. Indeed, models that ignore the tetrahedral ordering but introduce a systematic coupling between the formation of bonds and the presence of voids do reproduce the basic thermodynamic behaviours of liquid water [32].
9 Conclusions
At present, the most detailed descriptions of liquid water are provided by numerical simulations. However, despite great progress in reproducing the interactions of water molecules, none of these simulations can reproduce simultaneously the three most basic features of the liquid, i.e. the liquid gas coexistence curve up to the critical point, the temperature of maximum density, and the dielectric constant.
On the theoretical side, there have been countless attempts to explain the anomalies in the behaviour of liquid water using specific structures: ‘icebergs’, i.e. small domains of ice-like water immersed in a disordered liquid, ‘clathrates’, i.e. clusters with icosahedral symmetry, again immersed in a disordered phase, and the ‘two-state’ models referred to above. All these theories fail because they do not describe properly the disorder, and therefore the entropy of liquid water. In this sense, liquid water has been a fantastic ‘graveyard’ for theories that are clever but wrong.
The best liquid-state theories are the statistical theories that have as a basic ingredient the coupling between bond formation and the presence of voids in the structure [32]. These theories reproduce the basic thermodynamic behaviours of liquid water – but at the cost of seven adjustable parameters, which do not have an obvious interpretation at the molecular level.
It may appear as a paradox that we should be able to describe our universe at extremely large scales, and also at the scale of elementary particles, but yet unable to understand the liquid that we are made of. However, it is quite a tough problem. To some extent, the difficulties have their origin in the limitations of experimental techniques. It would seem that every property of liquid water has been measured. However, we do not know how to determine, in a liquid, the correlations of small groups of molecules (three or more): all available methods provide us only with measurements of the pair-correlation function. We also do not know how to describe, in a statistical way, a liquid in which the interactions have a strong directional character. We know how to describe each bond, we can simulate the motions of molecules that make such bonds and are submitted to thermal agitation, and we can thus reproduce some properties of the liquid – but we do not have a real theory of liquid water.


