1 The flood forecasting and warning problem
Of all natural disasters, floods impact on the greatest number of people across the world. In the UK, the Easter 1998 floods had an effect on flood defence investment, policy, and operations whilst floods in Autumn 2000 raised questions of climate change attribution from government. Recent flooding across Europe has had both large-scale (Rhine–Meuse: January 1995, Oder: 1997; Elbe: August 2002) and local impacts (Mediterranean flash-floods). The ‘Great Flood’ on the Mississippi in 1993 was the most severe on record in the USA. Catastrophic floods in China and Bangladesh are a way of life associated with much human suffering and death. Miller [22] provides an international perspective on flood risk and strategies for prevention as a United Nations contribution to the International Decade for Natural Disaster Reduction.
The science and technology of flood disaster mitigation addresses policy, planning, design, and operational aspects. Good policy and planning can reduce the exposure to flooding through control of land management and housing development whilst well-designed flood defence schemes will alleviate the impact of flooding. However, complete protection from flooding is rarely a viable goal. Provision of flood forecasting and warning systems can bring significant benefits through giving forewarning of imminent flooding, allowing timely evacuation, relocation of valuables, and management of affected infrastructure. Effective mechanisms of dissemination and human response are required to ensure that the potential benefits of forewarning are realised.
The warning problem is made particularly complicated by the uncertainty in the flood forecast used within the decision-making chain for issuing flood warnings. Imperfect estimates of rainfall (for both past and future times) and river flow are used with mathematical models of river systems that aim, in an approximate way, to represent the physical processes affecting water movement. The estimation of rainfall, the formulation of mathematical models of river systems and the construction of flood forecasts for use in warning are the main issues addressed in this paper. The scientific intent is to research methods that reduce the uncertainty in the flood forecast and to develop easy-to-use systems supporting rainfall estimation and flood forecasting across possibly complex river networks. Characterisation of forecast uncertainty, and embracing this within the flood warning decision-making process, is discussed briefly as an ongoing research challenge.
The framework underpinning the paper is provided by Fig. 1. This presents an integrated flood forecasting system ‘chain’ with rainfall measurement sources, rainfall displays providing first-alert and flood-preparedness information, rainfall processing providing inputs to flood forecasting and modelling systems, and decision-support facilities that trigger dissemination of flood warnings to communities informed on how to respond. The paper focuses on research progress in the UK that has led to operational improvements in flood forecasting and warning. It also identifies some future research challenges.
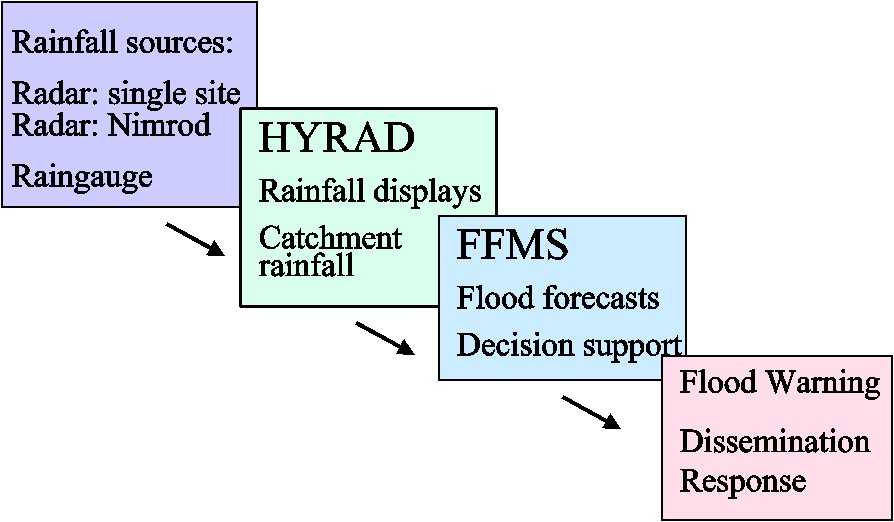
Framework for an integrated flood forecasting and warning system.
Cadre général d'un modèle intégré pour la prévision et l'annonce de crue.
2 The rainfall estimation problem
The importance of rainfall estimation to flood forecasting is highlighted by results obtained by Bell and Moore [6] as part of the HYREX (HYdrological Research EXperiment) research programme. Raingauge data from a special network of 49 tipping-bucket raingauges in the 132 km2 Brue catchment in southwest England was used with the PDM (Probability Distributed Model) rainfall–runoff model to explore the sensitivity of flow simulations to rainfall. A catchment of this size in the UK would typically only have one raingauge available for use in flood forecasting. Fig. 2 shows the spread of rainfalls measured by the raingauge network obtained over two-day periods for a stratiform and a convective storm. The cumulative hyetographs highlight the significant spatial variability of rainfall within the catchment during convective rainfall; a degree of variability is still apparent for the stratiform storm. Using the PDM rainfall–runoff model, calibrated using the catchment average rainfall, with each raingauge in turn produces the ensemble of simulated flow hydrographs shown in Fig. 3. The spread of hydrographs, particularly for the convective case, serve to highlight the importance of rainfall estimation when flood forecasts are to be based on use of a rainfall–runoff model. It is results of this kind that continue to stimulate research on improved spatial estimation of rainfall, including the use of weather radar.
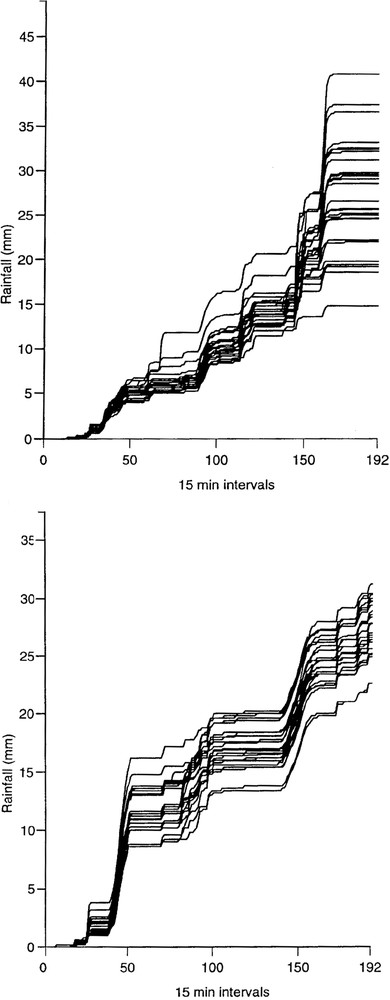
Cumulative raingauge hyetographs for stratiform (top) and convective (bottom) rainfall events in the Brue basin.
Hyétogramme cumulé des pluies pour un épisode pluvieux stratiforme (haut) ou convectif (bas) dans le bassin de Brue.
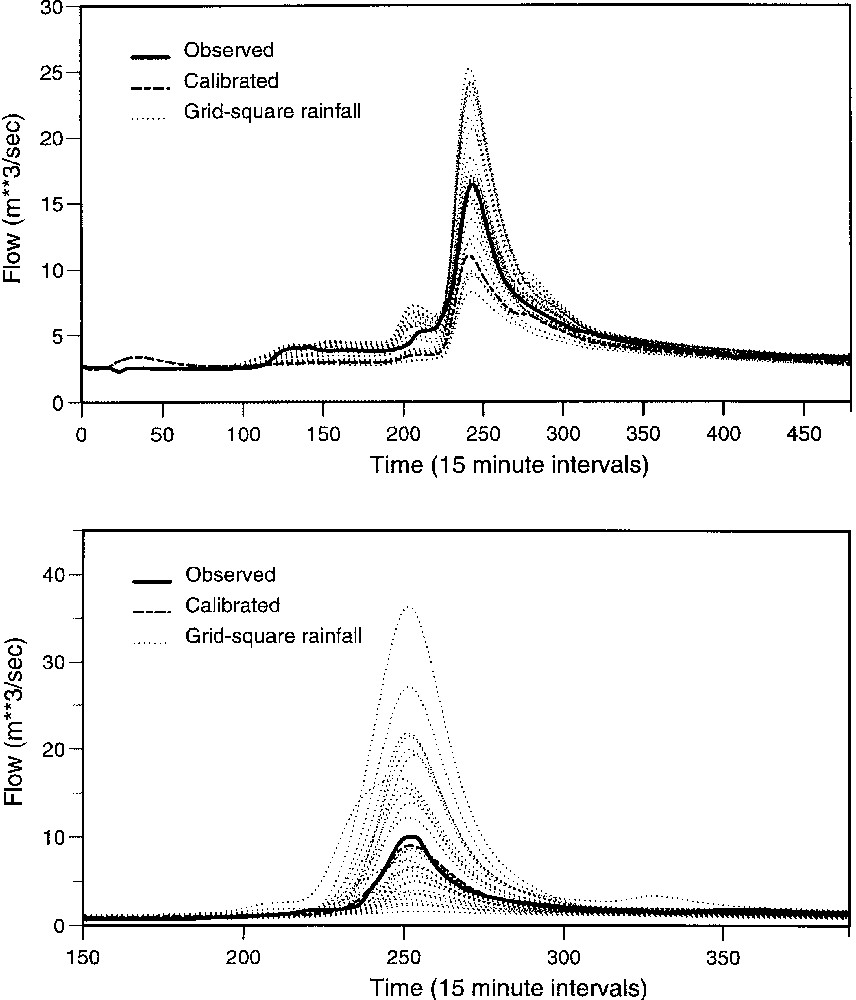
Ensemble hydrographs for stratiform (top) and convective (bottom) rainfall events in the Brue basin. Each ensemble member is obtained using a different raingauge in the basin. The calibrated hydrograph is obtained using an average of all raingauges.
Hydrogrammes des débits pour des épisodes pluvieux stratiformes (en haut) ou convectifs (en bas) dans le bassin de Brue. Chaque hydrogramme est obtenu en utilisant un seul des pluviomètres du bassin. L'hydrogramme calibré est obtenu avec une moyenne de tous les pluviomètres.
3 Rainfall estimation using weather radar
Whilst a raingauge provides a measurement of rainfall at a point, weather radar provides a volume-integrated estimate of rainfall aloft through its measurement of radar reflectivity and its relation to rain drops. The size and height of the sampled volume increases with range from the radar, reducing spatial resolution and making it a potentially poorer estimate of rainfall at ground level. Some of the problems associated with radar rainfall measurement are summarized in Fig. 4. Use of radar scans at different beam elevations allows the vertical profile of radar reflectivity to be characterized and used in inferring rain rate at the ground as a function of range. Corrections used in the UK network radars are reviewed by Harrison et al. [15] and Lynch et al. [21], whilst Borga et al. [8] provide a useful insight into the relative magnitude of different forms of correction for one radar in the UK network.
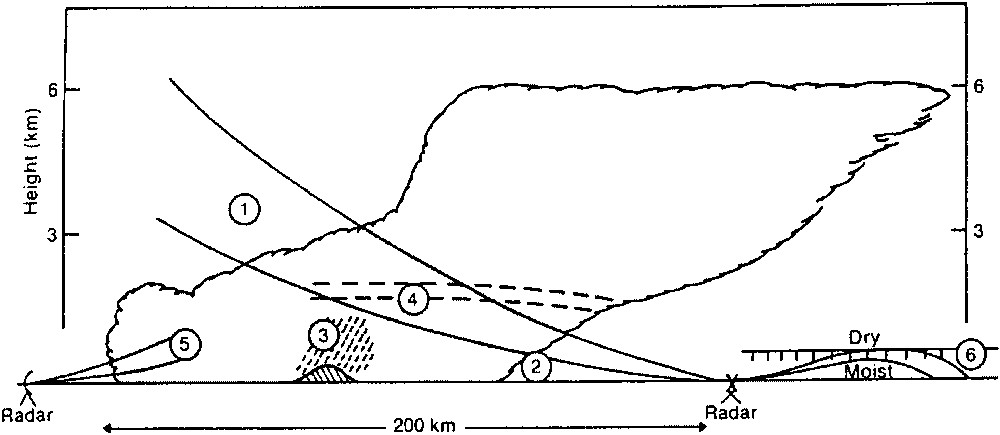
Problems with radar rainfall measurement. 1. Radar beam overshooting shallow precipitation at long range. 2. Low-level evaporation below radar beam. 3. Orographic enhancement over hills, which is undetected below beam. 4. Bright-band. 5. Underestimation of intensity of drizzle due to absence of large droplets. 6. Bending of radar beam in presence of strong hydrolapse down to ground or sea.
Problèmes rencontrés avec les radars pluie.
Whilst physics-based corrections to radar data normally take precedence, it is generally acknowledged that combination with point raingauge measurements can have real benefits to rainfall estimation accuracy. In some cases, this may take the form of a periodic adjustment to the radar bias with reference to a raingauge network. For operational purposes, the Hyrad system [25,35] employs a multiquadric surface fitting scheme to spatially interpolate radar adjustment factors (formed as a ratio of gauge to raingauge estimates) in merging rainfall estimates from radar and raingauge networks. The surface used for dynamic adjustment is recalculated every 15 min. Moore [26] reports on how the density of the raingauge network used for merging impacts on rainfall estimation accuracy. Wood et al. [40] have distinguished between a climatological, long-term adjustment for bias and a dynamic adjustment. The latter aims to make allowance for more short-term variations in the relation between reflectivity and rain-rate, for example corresponding to changes in drop size distributions during the passage of a storm. A combination of climatological and dynamic adjustment is proposed, where the efficacy of the latter depends on the raingauge density in relation to the spatial variability of the storm. This is being considered in a future upgrade to Hyrad.
4 Rainfall forecasting
The greatest uncertainty in rainfall relates to forecast estimates. The state-of-the-art indicates that simple advection forecasts based on inferring storm movement from time-displaced radar images work best, for lead times out to, say, 6 h. The forecasts are normally smoothed with increasing lead-time, towards the current field-average value in the case of Hyrad [25,34] and towards a numerical weather prediction (NWP) forecast on a 15-km grid in the case of the Nimrod UK product [14]. A probabilistic extension of Nimrod, called STEPS, is under development and capable of providing ensembles of rainfall forecasts [37]. Following workers in the USA [12,20] and France [1], Bell and Moore [5] have pursued a more conceptual water balance approach to storm rainfall forecasting. The basic premise is to use a simple representation of storm dynamics combined with frequent state correction of the water volume in an atmospheric column, as inferred from multi-scan radar measurements. Inferring storm development in this way has yet to be demonstrated to have convincing benefits; however, improvements to multi-scan strategies in the UK have yet to be explored in this context. The longer-term goal relating to rainfall forecasting in the UK is to pursue higher resolution (moving from circa 12 km to 4 and 1 km) NWP formulations capable of representing the initiation and development of convection. At present, NWP rainfalls out to 1.5 days on a 15 km grid are used in support of flood warning in England and Wales, via the Hyrad system, serving primarily as a first-alert flood indicator.
5 Improved hydro-meteorological systems for hydrological use
The basic sources of information for rainfall estimation are raingauge network data and weather radar products. Without further reception, processing, and support tools, these sources cannot easily be used to provide an initial warning of impending flooding or as direct input to flood forecasting models. Hyrad has transformed the use of weather radar for hydrological use in the UK by providing a software system that is easy to use for the visualization of a variety of radar, and weather-related, products and that interfaces to flood forecasting systems.
Fig. 5 shows the main components of Hyrad: data reception, spatial image database (SIDB), hydrology kernel (anomaly removal, radar-raingauge merging, rainfall forecasting, catchment average rainfall estimation), client visualization, and system monitoring/scheduling/control. Mosaics of windows can be configured to visualize rainfall fields at different scales (European, regional and catchment) and in different ways (animated images highlighting motion, cumulative fields revealing anomalies, catchment average time-series portraying storm profiles): an example display is shown in Fig. 6.
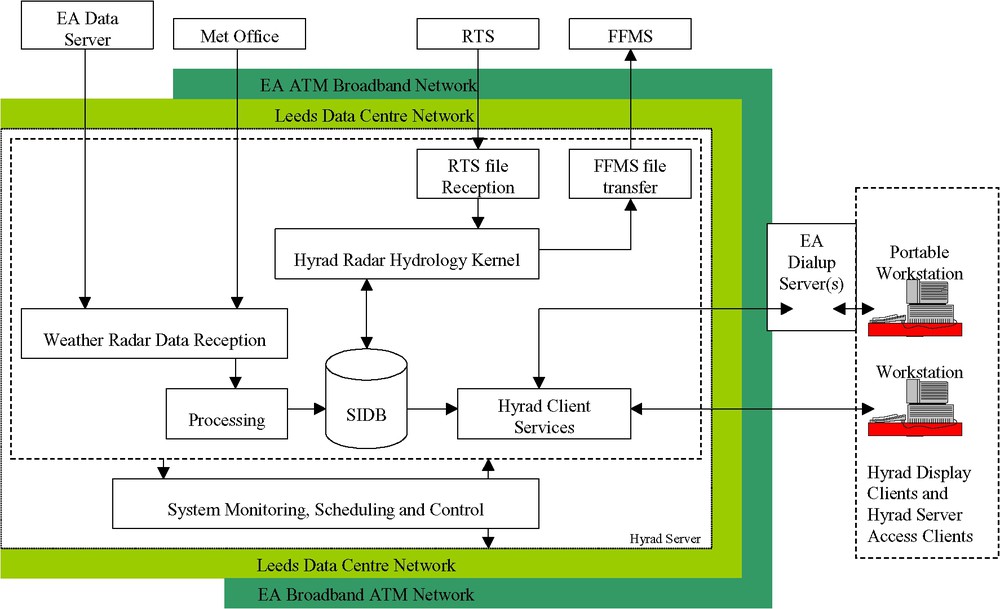
Conceptual design of the Hyrad Client-Server system (EA: Environment Agency, RTS: Regional Telemetry Scheme, FFMS: Flood Forecasting and Modelling System, SIDB: Spatial Image Database).
Schéma conceptuel du système Hyrad liant clients et fournisseurs (EA : Agence de l'environnement ; RTS : schéma régional de télémétrie ; FFMS : système de prévision et de modélisation des crues ; SIDB : base de données des images spatiales).
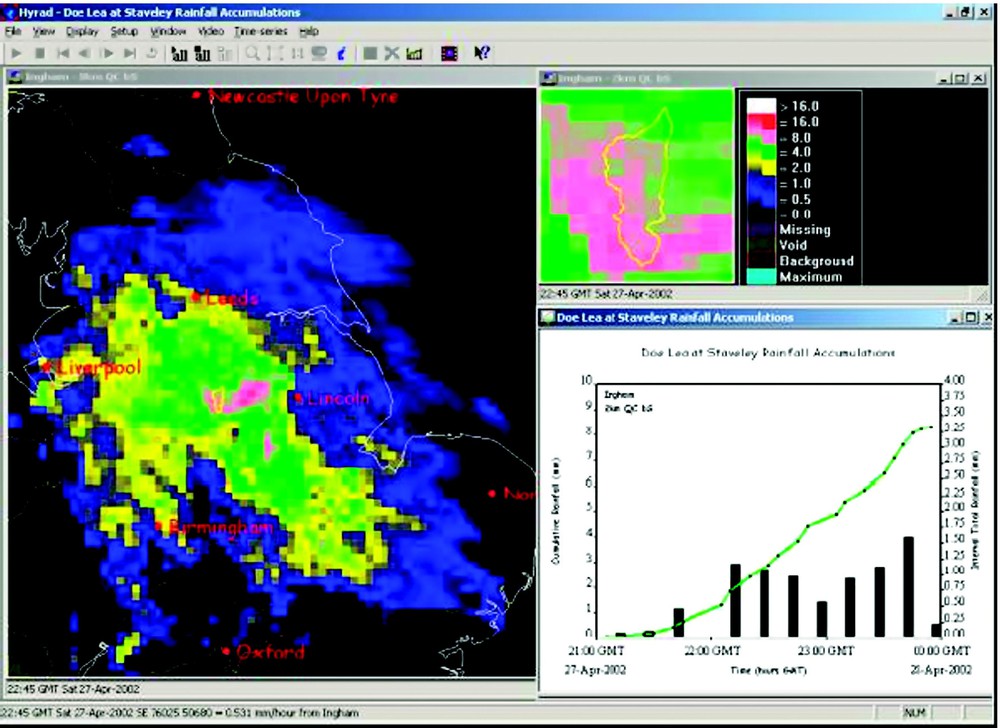
Hyrad regional, catchment and time-series radar rainfall display mosaic.
Mosaïque d'affichage des pluies radar du système Hyrad régional, du basin versant et des historiques.
The hydrology kernel removes static and transient anomalies in fields of different resolution and combines them to form a composite image. Rainfall fields can be estimated by radar-raingauge merging and raingauge-only interpolation and rainfall forecasts derived from these fields. These local Hyrad products, along with any external source products, can be processed to derive catchment average estimates for feeding forward to flood forecasting and modelling systems. The activities within the kernel are summarized in Fig. 7.
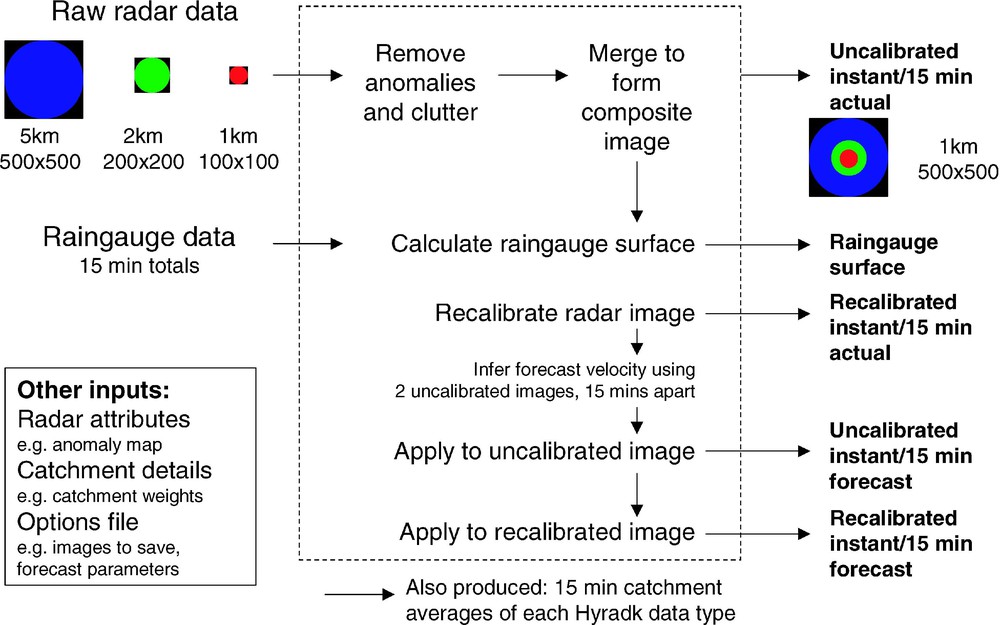
Hyrad hydrology processing kernel.
Noyau du calcul hydrologique dans Hyrad.
The generic, configurable form of Hyrad allows other spatial products to be received, visualized, and processed: examples are NWP rainfall and temperature and MOSES (Met Office Surface Exchange Scheme) soil moisture, evaporation, and runoff products.
6 Rainfall forecasts, first-alert and performance monitoring
In England and Wales, rainfall forecasts are used as a form of first-alert for flood warning and as a basic ingredient of a ‘Flood Watch’ service for areas not served by flood forecasting systems. The Daily Weather Forecast provides 6-h-interval forecasts for areas out to 1.5 days (and less frequent ones to 5 days), as typical amounts and most likely maximum along with a 3-category measure of confidence. Heavy rainfall warnings are triggered to be sent when certain conditions apply: these are presented in probability form for some regions. Monitoring of the performance of this service is done routinely and feeds into the post-event assessment of flood warning provision.
Jones et al. [17] report on a detailed consideration of methodologies for assessment aligned to operational requirements for monitoring. A set of performance statistics are identified for assessing different forms of forecast, which includes a form of continuous Brier Score for use with probabilistic forecasts. A PC tool has been developed to help assess the Heavy Rainfall Forecast [18]. The study included a methodology to compare the relative performance of different forecast sources. This indicated there is skill in the forecasts, in relation to naïve forecasts such as persistence, but this is weak reflecting the difficulty of rainfall prediction. Whilst not conclusive, due to the limited extent of the comparison dataset, using radar rainfall out to 6 hours and NWP rainfall out to two days could prove as good on average as the ‘added-value’ daily weather forecast product. NWP rainfall forecasts are now routinely made available to the flood warning process via Hyrad.
7 Systems for flood modelling and forecasting
Flood modelling and forecasting involves far more than the traditional crafts of rainfall–runoff modelling, channel flow routing and forecast updating. Commenting on progress in these traditional crafts will be deferred to subsequent sections. The theme of systems will be continued here to highlight the connectivity of the rainfall and flood forecasting system chain. Fig. 8 presents a schematic design of an advanced flood forecasting and modelling system based on the river flow forecasting system or RFFS [25,28]. A shell-kernel architecture is presented, in which the shell is receptive to incoming data from hydrometeorogical systems such as Hyrad and from hydrometric telemetry networks. These external data sources feed a modelling database, which is also receptive to locally generated forecasts produced by the modelling kernel. Observation and forecast data can be visualised on user PCs and flood warning reports generated and disseminated via linked applications.
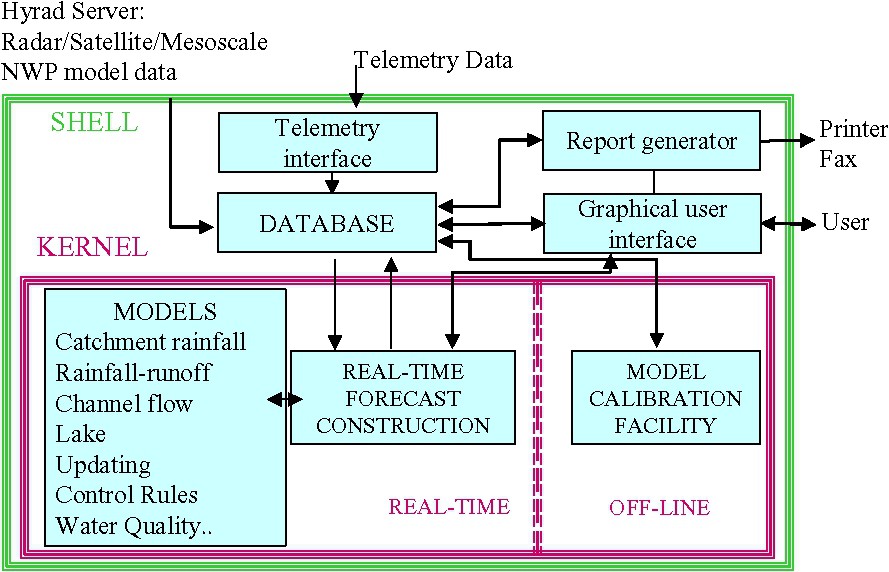
Flow Forecast and Modelling System (FFMS) configuration.
Configuration du système FFMS (prévision des débits et modélisation).
At the heart of the modelling kernel is the information control algorithm or RFFS-ICA [28], which serves as a generic, configurable forecast construction environment. This allows forecasts to be constructed using any set of models in any river network configuration, using data files to define the arrangement independent of the coding of the models (which are plug-in-and-play) and construction of the forecasts. The concept of a two-layer configuration of models is used in which a model component layer allows a model algorithm layer to be embedded within it. This provides a level of modularity that can be exploited to considerably simplify commonly occurring assemblages of model elements to form larger building blocks with internal structures that frequently repeat. For example, a headwater model component structure may typically combine precipitation merging and snowmelt codes with rainfall–runoff models and updating procedures and possibly local stage-discharge relations; the elements are configured as model algorithms.
A forecast requirement layer allows forecasts at the same location to be constructed using different models, as defined in the model component layer. It also defines the inputs and connectivity of the model network. Fig. 9 presents an example of a complex Model Network schematic, in this case as used for flood forecasting throughout northeastern England. The ICA can be scheduled to run in harmony with telemetry polling. The use of a model state set ensures that the results can be equivalent to a seamless continuous running of the system. The state set may be improved at times of late receipt of telemetry data by manually starting a run from a previously saved state set.
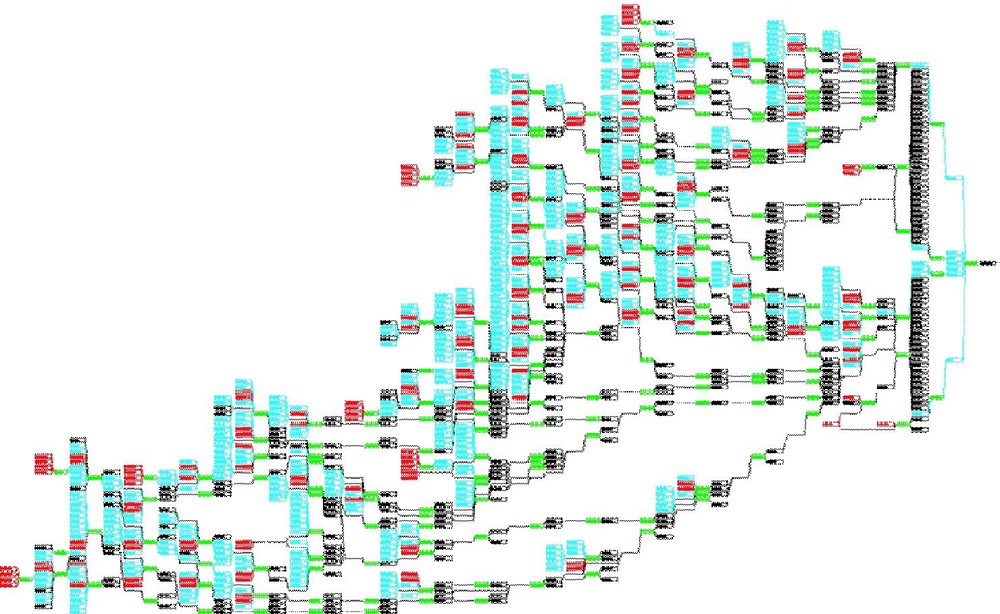
RFFS Model Network schematic for Northeast England encompassing the Yorkshire Ouse, Tees and Northumbria rivers. The linked boxes relate to Model Components and the Forecast Requirements they meet.
Schéma du réseau de modèles RFFS pour l'Angleterre du Nord, comprenant les rivières Yorkshire Ouse, Tees et Northumbria. Les liens entre boîtes représentent les composantes du modèle et les contraintes de prévision qu'elles doivent respecter.
An example flood forecast from a Flood Forecasting and Modelling System is shown in Fig. 10. This illustrates a forecast obtained from the PDM rainfall–runoff model for a river basin in northeastern England. State correction is used to initialise the model to produce a flow at the forecast time-origin close to the observation of flow. Two forecasts are presented, one based on perfect foreknowledge of rainfall and the other based on a negligible rainfall forecast. The importance of a good rainfall forecast becomes clearly evident for higher forecast lead-times. The modelling and forecast updating methods used to produce this forecast are discussed in the next section.
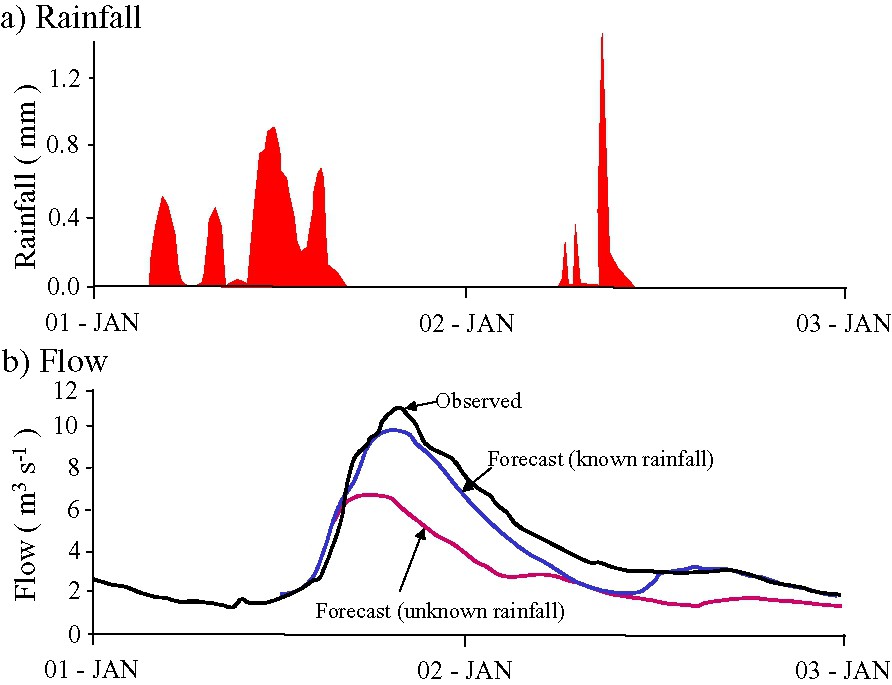
Flood forecasts from a flood forecast and modelling system showing the effect of different rainfall forecast assumptions – perfect foreknowledge of rain and no-rain – on flood-forecasting performance.
Prévision de crues par le système FFMS montrant l'effet de différentes hypothèses sur la prévision des pluies (connaissance parfaite ou pas de pluies) sur la performance de la prévision.
8 Flood modelling for forecasting
To some researchers, flood forecasting is synonymous with rainfall–runoff modelling and a major preoccupation. The previous section has highlighted that forecasting systems can involve complex networks of interconnected models of different kinds, representing processes as diverse as snowmelt and the hydrodynamics of rivers under the influence of tide and barrier control. This diversity is added to by the need to develop procedures to assimilate up-to-the-minute observations of river flow or level so as to improve model forecast performance, via so-called updating methods. Selected issues concerning these modelling and updating requirements will be considered here.
8.1 Rainfall–runoff modelling toolkits
Beginning with the traditional preoccupation with rainfall–runoff modelling, there is a growing recognition that the plethora of brand-name models shares common elements that disguises a degree of homogeneity in approach. The most popular approaches are conceptual in nature, formulated to preserve mass balance, and sometimes referred to as explicit moisture accounting procedures. The basic building blocks commonly relate to three main processes: runoff production, fast response routing and slow response routing. Runoff production can involve water storage (and possibly the interplay with infiltration if this is a limiting factor) and soil drainage processes. Fast response routing concerns translation of runoff to the basin outlet via pathways that are fast, such as surface channels and subsurface macropores. Slow response routing concerns water translation via subsurface pathways, and is normally associated directly with groundwater storage and the baseflow component of basin runoff.
With the recognition that rainfall–runoff models share a limited set of common elements, there is a trend towards building ‘model toolkits’ that encompass these basic elements and can be configured to represent different forms of catchment behaviour. This was one motivation behind building the PDM (Probability Distributed Model) as one of the more popular rainfall–runoff models used in practise in the UK [23–25]. The PDM is presented in Fig. 11 in the structural form most commonly used in practise. Both fast and slow response routing components, here more loosely referred to as surface and subsurface storages, can be represented by the Horton–Izzard equation [10]. This equation results from continuity and the simple nonlinear storage form of momentum equation, , where q is flow rate per unit area, S is water storage per unit area and (the storage time constant) and n are parameters of the relation. Solutions for different values of n are provided that cater for behaviours characteristic of channel and groundwater translation systems (see Appendix A of [31]). As an alternative to the Horton–Izzard formulation, either routing storage can be represented by a cascade of two linear reservoirs. Solution of this system takes the form of a transfer function (TF) model with dependence on two past outputs and the present and past input [9,36]. Whilst the TF model has four parameters, this is linked directly to the two physical time constants of its equivalent reservoir storage model and its continuity constraint; imposing equality of time-constants reduces the parameters to one.
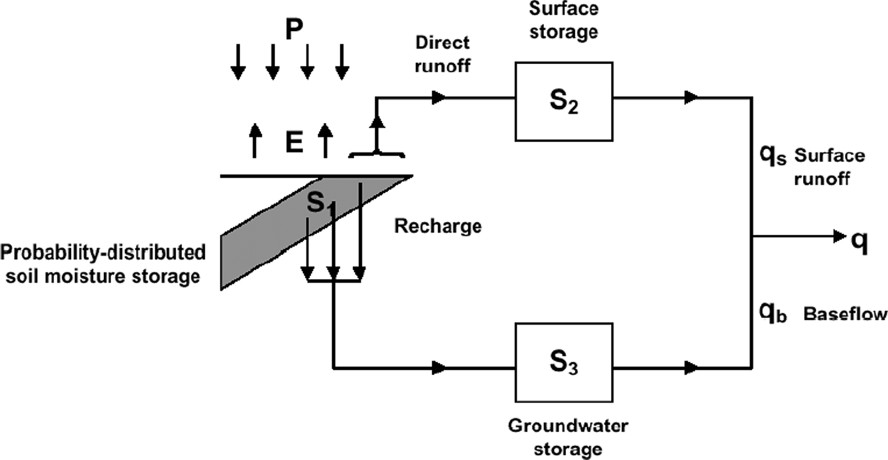
The PDM rainfall–runoff model.
Le modèle pluie–débit PDM.
A relevant digression is that this theory demonstrates the conceptual interpretation of TF models as storage routing functions representing the translation phase of the rainfall–runoff process. Relaxing the constraint of continuity allows runoff production to be represented by a TF model equivalent in form to a simple loss factor on the rainfall input. However, introducing dependence of losses on soil moisture into TF models naturally leads down a development path that can result in just another brand-name conceptual model! The relevance of this digression to flood forecasting is the continuing debate on the relative merits of simple TF models versus conceptual water accounting models: a debate which, in many ways, is delusory.
In practice, the PDM is usually applied in a form that invokes a cubic storage representation of the subsurface (groundwater) store and a cascade of two linear reservoirs (the TF model) for the surface (channel) storage.
The runoff production component of the PDM assumes that runoff is generated via a saturation excess mechanism controlled by the combined absorption capacity of the soil, canopy, and surface depressions. Infiltration capacity control on water entry into the soil is assumed not to be a dominant process (although a variant has been developed for this). It is recognised that absorption capacity will vary from point to point within a river basin and, whilst the geometric (location specific) form of this variation may be difficult to establish, the frequency of occurrence of capacities of different size can be readily parameterised. Thus by invoking a probability density distribution, , of absorption capacity, c, across the basin, then the proportion of the basin with point capacities less than or equal to is given by the distribution function . With A denoting the area of the basin, then is the contributing area of direct runoff. If the initial state of the basin is such that all stores of capacity less than are full and net rainfall occurs at a rate π over an interval Δt, then the initial rate of runoff production per unit area is and the volume of runoff production per unit area over the interval is . At the end of the interval, all stores with capacities not greater than are full and primed to generate runoff from more rain. The storage of water in the basin (expressed as a depth over the basin) at the start of the interval is and at the end is given by continuity as . Some refinement of these expressions is required if the maximum storage capacity of the basin, , is reached within the time interval. It becomes a simple algebraic task to obtain solutions for the integral expressions, for chosen forms of density function, so as to calculate the volume of runoff generated at each time step and maintain the basin storage water balance. A Pareto or truncated Pareto distribution is normally invoked for practical applications although the PDM toolkit offers a range of options. The probability-distributed theory and solutions to the integrals are developed further in [23,25,31]. Paper [31] is also of relevance in showing how the Horton–Izzard equation for a nonlinear storage element can be extended to accommodate representation of an aquifer subject to pumped abstractions and ephemeral streamflow behaviour. This has been developed within the PDM modelling toolkit.
Rainfall–runoff models can also encompass snowmelt routines that differentiate between rainfall and snowfall based on a temperature threshold, represent the melt process by a simple temperature-excess formula or energy balance methods of varying complexity, and make allowance for partial snow-cover effects. Moore et al. [32] and Bell and Moore [4] report on a trial in the UK of a variety of snowmelt methods used in conjunction with two rainfall–runoff models: the PDM and the distributed Grid Model [2,3]. The PACK model that features in this trial is used operationally across Northeast England and an elevation-zone extension of it has been proposed for future use.
8.2 Channel flow routing models
It is a common occurrence in a river basin to encounter reaches of rivers that are gauged at their upstream and downstream ends. Whilst there is normally information from maps available, the extent of information usually does not extend to detailed cross-sectional surveys. Backwater influences from control gates, tributary junctions and tides may also not dominate propagation of flow through the reach. It is in such typical situations that simple channel flow routing models can be usefully employed in preference to more complex hydrodynamic river models.
The extended KW model [19,25,27] was developed in a basic form from the kinematic wave equation with the kinematic wave speed as its only parameter. This allowed simple empirical functions with a conceptual base to be introduced as the complexity of flow propagation warranted. Initially, the wave speed parameter was allowed to vary as a function of discharge using parametric forms motivated by the shape of curves inferred by more complex models and observational data. Simple piecewise-linear approximations to these curves sometimes proved even more useful along with some knowledge of bankfull discharge. Losses of water to floodplains could be accommodated using ‘computational nodes’ positioned with reference to map information and model response. Piecewise-linear segments were again used to represent the transfer of water through a node, with a relation up to bankfull, decreasing amounts above, and with the option to lose or return stored flow to the river downstream. Estimation of ungauged tributaries to a reach could be the greater source of error relative to errors of model simplification, and this argued against more complex and complete modelling for a poorly observed system. Typically, ungauged tributaries were estimated by scaling nearby or similar gauged tributaries, initially using physical weightings based on relative areas and standard average annual rainfalls and later refining these weights through calibration. Practical situations have arisen in which a stage-discharge relation did not exist for the gauge at one end of the reach. Provided ungauged lateral inflows did not dominate the response, it was found that embedding a stage-discharge relation within the KW model framework, and controlling the model calibration carefully provided a way of deriving an approximate relation from river level measurements. In the above way, the KW model has evolved to deal with a variety of practical forecasting problems affecting the modelling of river reaches.
It is beyond the scope of the present perspective to deal in any detail with hydrodynamic models based on computational solutions to the Saint-Venant equations. In many ways there is a greater convergence of model approach relative to the rainfall–runoff models and simpler channel flow routing models discussed above. The river flow forecasting system (and its extension to FloodWorks form) currently supports two hydrodynamic models in operational use: the RFFS-Hydro model developed for real-time use from the National Weather Service DWOPER code [11] and the RFFS–ISIS code developed from the Halcrow/HR Wallingford ISIS–Flow code. Some of the issues relating to preparing hydrodynamic model codes for real-time use are discussed by Moore and Jones [29].
9 Updating methods for flood forecasting
A unique feature of real-time flood forecasting is the ability to use observations of the state of the basin up to the current time to improve model performance. Most commonly, the observations relate to river level or flow but other relevant observations on the state of the basin, such as groundwater well levels and soil moisture content might be used. The most natural method of forecast updating is state correction in which a direct or related measurement of a model state is used to adjust its value so as to improve forecast performance. River flow, as the most commonly used observation for updating, can be used to calculate a model error which, when factored and added to the state value to be corrected, provides a basis for updating the state. If the model states chosen for correction are the fast and slow response flows from the PDM model and the factors are chosen to be the proportion of each flow to the total model flow, then the corrected flows will sum to the observed flow. Introducing relaxation coefficients into the factors allows more conservative adjustments to be made; these coefficients may be arrived at through optimisation using historical records. Note that by adjusting the two model flows, the water contents of the stores that they derive from are also state corrected indirectly. The equations for correction are set down in [25].
The above outline of ‘empirical state correction’ has its origins in the more formal theory of Kalman filtering [13,16], which employs the same basic form of adjustment, but defines the factors as gains which are estimated according to the relative uncertainties associated with the model and observation estimate of each state to be corrected. The theory is optimal for linear models and observation systems and if the uncertainties are correctly characterised. Approximate solutions exist relevant to the nonlinear systems and forms of error encountered in hydrology. Computations based on such solutions can be highly complex and there is no guarantee that they will provide better forecasts than ones based on the simple empirical scheme described above. This is the basis for recommending the latter for practical application.
The same underlying form of correction can be used to adjust model parameters in real-time, treating these essentially as extended state variables. This approach is still used when models take very simple forms, such as those based on pure TF model concepts, where the inadequate model dynamics are compensated for by shifting the parameter values to keep the forecasts on track. The approach is not generally recommended as the need for time-varying parameters is a diagnostic of an imperfect model structure and highlights the need to account for the variation within the model to predict future variations. It might for example diagnose the need for an explicit moisture accounting model component to remove the need to track a time-varying gain within a TF model.
Errors in the model inputs can be treated with similar state correction schemes. If flow observations are used as the basis of correction, then the inputs are related only very indirectly and with time delays, making robust adjustment difficult. For this reason, input correction of this form is generally not practised. Note that a major reason for employing state correction of the normal form is that errors in the rainfall input propagate through a rainfall–runoff model as errors in the store water contents, which are more reliably corrected at this stage.
A very different approach to updating focuses on the predictability of the model errors themselves. It is a common feature of models that transform one or more inputs to an output that errors in the model output series – the so-called simulation-mode errors – exhibit runs of over-estimation and under-estimation. This serial dependence can be used as the basis of predicting future errors which, when added to the modelled output for the same time, provides the updated forecast required. A simple structure for an error model is obtained as a weighted linear combination of a certain number of past simulation-mode errors. This structure is referred to as autoregressive, or AR, and the number of past errors included referred to as the model order p indicating that there is this number of weights or AR parameters. An extension of this idea is to also include a weighted combination of q past one-step ahead forecast errors in the predictive equation for the model error. This is referred to as the moving average or MA component and, when used in combination with the AR part, is referred to as an ARMA error predictor. It can be the case that a high order AR error model may be better represented by a low order ARMA error model. If the ARMA model structure is well identified and appropriate, the one-step-ahead prediction errors should approximate white noise with an absence of serial correlation. Unlike state correction, the methodology is applied externally to the ‘process’ model and can be applied to any model including rainfall–runoff, channel flow, and hydrodynamic forms. The level of success achieved is a function of the strength of the serial dependence in the simulation-mode errors. Unfortunately this can be weakest in the vicinity of the rising limb and the peak of the flood hydrograph and strongest on the recession limb where correction is least important. It is normally used in preference to state correction when time-delay effects are judged to make such correction unreliable: for example, for multi-reach channel flow routing. Variants can be developed based on the use of proportional, rather than the normal additive, errors [25].
10 Next-generation flood models?
10.1 Lessons from model intercomparisons
A recent review and comparison of rainfall–runoff models for use for flood forecasting in the UK found that no one model consistently out-performed all others across all catchments [30,33]. The assessment encompassed eight models across nine basins of varying character. Often there was little to choose between models when judged using the -efficiency statistic. Somewhat greater separation was apparent using a threshold critical success index (CSI), which placed emphasis on the crossing of flow thresholds, of particular relevance to triggering flood warnings.
Only one of the models in the intercomparison was of distributed form, the Grid Model [2,3], and this was applied on only the three basins for which grid-square radar data were available. It consistently ranked second best in terms of , but less well according to the threshold CSI. A potential advantage of such distributed models is the ability to fully exploit the gridded nature of radar data. Their structure and parameterisation can also be supported through the use of digital datasets relating to elevation, soil, land cover, and geology. It is tempting to conjecture that a new generation of distributed models, tailored to exploit such datasets and radar rainfall data, may emerge that consistently outperforms the lumped conceptual and TF models used in practice. At the present time this is not the case in the UK; the recently published ‘Distributed Model Intercomparison Project’ (DMIP) in the USA does not contradict this finding [38]. However, there is a shared belief that distributed modelling for flood forecasting is strongly deserving of further research and will prove of real benefit in certain situations. In particular, it is seen as an important way forward for forecasting at locations that are ungauged.
10.2 Flood warning for ungauged locations and area-wide forecasting
Popular methods of forecasting for ungauged basins include scaling of rainfall–runoff model forecasts from neighbouring or similar basins and model transfer based on a belief of similarity. Basin area and standard average annual rainfall are commonly used as the basis of scaling. In the model transfer approach, model parameters are retained, whilst using the actual ungauged basin area and rainfall estimate, allowing for any factoring differences in the latter (due, for example, to raingauge representativeness or radar bias). As an extension of this approach, estimates of model parameters from several sites may be combined taking account of basin similarity measures. The empirical approach of model simplification and regression on catchment properties, developed in the 1960s, is still used for model transfer, although more so for design applications where the need to forecast an actual flood assumes less prominence. A stronger, more physically based approach is clearly called for.
New approaches are emerging that seek more direct conceptual-physical linkages between the structures and properties of a model and spatial digital datasets on terrain, soil, land cover and geology. These models may be either lumped or distributed in form. Whilst the former are invariably catchment-based, the latter can be formulated for an arbitrary area containing any number of gauged and ungauged basins. An intrinsic feature is the ability to infer a model structure across the whole area and obtain a small subset of area-wide parameters calibrated using observations for the gauged basins. These map though to a distributed model structure and properties, facilitating forecasting at any location across the area. Such approaches are appealing in providing a natural conceptual-physical framework for modelling and forecasting at ungauged sites.
A major challenge in model formulation is to seek process representations relevant to scales beyond the point. The model conceptualisations used by land surface exchange schemes in weather and climate models commonly focus on point-wise process representations emphasising vertical water movement. As the scale of modelling moves outwards to a hillslope, a radar grid-square, a catchment, and a region, runoff production may become increasingly dominated by horizontal water transfers controlled by topography and soil properties. Todini [39] proposes one possible representation for this. Grid-to-grid routing of surface and sub-surface flows at an appropriate space and time scale, with return flows linking the two pathways, also becomes a natural model construct to employ [7]. There are exciting opportunities for model development here.
Whilst the potential for forecast updating at ungauged sites may appear limited, the possibility to transfer model errors from a gauged site to improve forecast performance deserves serious consideration. Research is needed to develop and assess these methods of updating alongside the emerging new generation of models outlined above. Delivery of this next generation of forecasting approaches presents an exciting challenge, bringing real benefits to flood warning coverage.
11 Future challenges for flood forecasting
Developing a new generation of flood model on a distributed grid has great appeal, not only as a solution to forecasting for the ungauged location. Such area-wide models can also provide the basis of a first-alert flood warning system when fed by hydro-meteorological information from weather radar and numerical weather prediction model forecasts out to one or two days ahead. They can be configured to provide national, European and even global coverage. Offering an indicative level of warning, they serve to complement more detailed flood forecasting systems operating at a regional level and with higher levels of data assimilation. Such systems offer the potential to map flow dynamically down a river network and to delineate areas of inundation, at least at an indicative level, enhancing the present flood watch service.
Arguably the greatest challenge confronting flood forecasting and warning is to develop methodologies capable of embracing forecast uncertainty into the decision-making process. This will demand close cooperation between meteorological and hydrological communities to make real scientific progress. Providing probability estimates of rainfall fields for past and future times that are credible is a difficult challenge, and may need to encompass consideration of varying measurement and modelling methods at different times. Propagating probability estimates of rainfall through networks of hydrological models – with errors in their structure, parameters, and states – to obtain probabilistic flow forecasts that are plausible is not straightforward.
Pierce et al. [37] present a first-step approach to probabilistic forecasting by generating an ensemble of radar-rainfall forecasts from a stochastic advection-based scheme and using these in the PDM rainfall–runoff model; it is assumed that errors in rainfall forecasting dominate those associated with the hydrological model. The difficulties of a decomposition approach to characterising uncertainty may lead to more pragmatic methods being explored, such as empirical analysis and characterisation of the forecast errors themselves.
Given a plausible probability forecast of river flow and a loss function for the location to be warned, then a probability forecast of damage costs can be derived based on standard decision theory. This probabilistic damage cost forecast can be used as the scientific basis for deciding if, and how early, to warn. Developing this methodology into a practical decision-support system for flood warning across a region has the potential to be of great benefit to flood defence operations.


