Tenseurs de perméabilité équivalente d'un domaine hétérogène fini

Ahmad Pouya

doi:10.1016/j.crte.2005.02.002

Géosciences de surface (Hydrologie–Hydrogéologie)

Tenseurs de perméabilité équivalente d'un domaine hétérogène fini
[Equivalent permeability tensors of a finite heterogeneous block]

Presented by: Ghislain de Marsily

Ahmad Pouya ¹

¹ Laboratoire central des Ponts et Chaussées, 58, bd Lefebvre, 75732 Paris cedex 15, France

Comptes Rendus. Géoscience, Volume 337 (2005) no. 6, pp. 581-588.

Abstracts

French
English

Dans un précédent article, nous avons défini, pour un domaine de taille finie de perméabilité hétérogène, un tenseur de perméabilité équivalente reliant le flux moyen au gradient moyen de pression dans le domaine sous les conditions de pression linéaire au contour. Nous avons montré que ce tenseur, noté ici $K^{p}$ , est symétrique et défini positif. Nous définissons, dans cet article, les conditions de flux constant au contour. Nous montrons que, sous ces conditions, il existe également un tenseur symétrique et défini positif, noté $K^{q}$ , qui permet de relier le flux moyen au gradient moyen de pression. Nous montrons, par ailleurs, que $K^{q}$ et $K^{p}$ donnent respectivement les perméabilités équivalentes dans les directions du gradient moyen et du flux moyen pour le domaine considéré. Nous montrons enfin que $K^{q}$ fournit des valeurs de perméabilités directionnelles inférieures à $K^{p}$ .

In an earlier paper, it has been shown that for a heterogeneous block of finite size, under linear boundary pressure conditions, a symmetric and positive definite tensor, denoted here by $K^{p}$ , exists, which relates the mean flux to the mean gradient of pressure in the block. In this paper, the conditions of constant boundary flux are first defined. Then it is shown that, under these conditions also, a symmetric and positive definite tensor, denoted $K^{q}$ , exists, which relates the mean flux to the mean pressure gradient. It is then shown that $K^{q}$ and $K^{p}$ respectively give the equivalent permeability in the direction of mean gradient and of mean flux. The directional permeability values given by $K^{q}$ are shown to be smaller than $K^{p}$ .

Metadata

Received: 2004-06-30
Accepted: 2005-01-04
Published online: 2005-03-08

DOI: 10.1016/j.crte.2005.02.002

Mots-clés : Perméabilité, Hétérogénéité, Perméabilité équivalente, Homogénéisation, Réseau de fractures
Keywords: Permeability, Heterogeneity, Equivalent permeability, Upscaling, Fracture networks

Author's affiliations:

Ahmad Pouya ¹

¹ Laboratoire central des Ponts et Chaussées, 58, bd Lefebvre, 75732 Paris cedex 15, France

@article{CRGEOS_2005__337_6_581_0,
     author = {Ahmad Pouya},
     title = {Tenseurs de perm\'eabilit\'e \'equivalente d'un domaine h\'et\'erog\`ene fini},
     journal = {Comptes Rendus. G\'eoscience},
     pages = {581--588},
     publisher = {Elsevier},
     volume = {337},
     number = {6},
     year = {2005},
     doi = {10.1016/j.crte.2005.02.002},
     language = {fr},
}

TY  - JOUR
AU  - Ahmad Pouya
TI  - Tenseurs de perméabilité équivalente d'un domaine hétérogène fini
JO  - Comptes Rendus. Géoscience
PY  - 2005
SP  - 581
EP  - 588
VL  - 337
IS  - 6
PB  - Elsevier
DO  - 10.1016/j.crte.2005.02.002
LA  - fr
ID  - CRGEOS_2005__337_6_581_0
ER  -

%0 Journal Article
%A Ahmad Pouya
%T Tenseurs de perméabilité équivalente d'un domaine hétérogène fini
%J Comptes Rendus. Géoscience
%D 2005
%P 581-588
%V 337
%N 6
%I Elsevier
%R 10.1016/j.crte.2005.02.002
%G fr
%F CRGEOS_2005__337_6_581_0

Ahmad Pouya. Tenseurs de perméabilité équivalente d'un domaine hétérogène fini. Comptes Rendus. Géoscience, Volume 337 (2005) no. 6, pp. 581-588. doi : 10.1016/j.crte.2005.02.002. https://comptes-rendus.academie-sciences.fr/geoscience/articles/10.1016/j.crte.2005.02.002/

Original version of the full text

The full text below may contain a few conversion errors compared to the version of record of the published article.

Abridged English version

Among the methods used for the determination of the effective permeability of a heterogeneous medium [1,7,9,10,12,16,17], the methods called ‘direct’ by [2] or ‘non-local’ by [3,13,15] are based on flow simulations in a finite-size block. A stationary flow regime is simulated in a block Ω under pressure and flux conditions prescribed at the boundary ∂Ω, and the mean flux $\vec{Q}$ and the mean pressure gradient $\vec{G}$ , defined by (3), are calculated. One then tries to determine the relation between these two quantities [3,14]. Nevertheless, it is well known that different boundary conditions can lead to the same value of $\vec{Q}$ , but to different values of $\vec{G}$ , or vice versa. This creates a difficulty to define an equivalent permeability tensor which has to relate these two quantities. It was shown in [11] that under linear boundary pressure conditions, defined by (8), a unique tensor, denoted here by $K^{p}$ , exists, which relates $\vec{Q}$ to $\vec{G}$ by (10). This tensor was shown to be symmetric and positive definite. The properties (9) and (12) were also demonstrated in this case. The relations (6) and (7) were also demonstrated in the general case by using mass conservation (2) and the equalities (5) which are a consequence of the Green formula (4).

In this paper, a new family of boundary conditions, called constant boundary flux, defined by (13), is introduced. In addition to these conditions, the pressure value must be fixed at one point of Ω for the pressure field $p (\vec{x})$ to be completely determined. The solution ${p (\vec{x}), \vec{q} (\vec{x})}$ of the flow problem for an incompressible fluid must satisfy (13), Darcy's law (1) and mass conservation (2).

Let us denote by ${\vec{B}}^{1}$ and ${\vec{B}}^{2}$ two values of $\vec{B}$ and by ${p_{1} (\vec{x}), {\vec{q}}_{1} (\vec{x})}$ and ${p_{2} (\vec{x}), {\vec{q}}_{2} (\vec{x})}$ the solutions of flow problems with constant boundary flux (13), corresponding to these two values of $\vec{B}$ . Let $λ_{1}$ and $λ_{2}$ be two scalars and define ${\vec{B}}_{3} = λ_{1} {\vec{B}}_{1} + λ_{2} {\vec{B}}_{2}$ . The linearity of Eqs. (1), (2) and (13) implies that ${p_{3} (\vec{x}), {\vec{q}}_{3} (\vec{x})}$ where $p_{3} (\vec{x}) = λ_{1} p_{1} (\vec{x}) + λ_{2} p_{2} (\vec{x}) + p_{0}$ , $p_{0}$ being a general scalar, and ${\vec{q}}_{3} (\vec{x}) = λ_{1} {\vec{q}}_{1} (\vec{x}) + λ_{2} {\vec{q}}_{2} (\vec{x})$ , is solution of the flow problem with constant boundary flux ${\vec{B}}_{3}$ . The relation $p_{3} (\vec{x}) = λ_{1} p_{1} (\vec{x}) + λ_{2} p_{2} (\vec{x}) + p_{0}$ implies then that the mean pressure gradients of the three flow regimes verify ${\vec{G}}_{3} = λ_{1} {\vec{G}}_{1} + λ_{2} {\vec{G}}_{2}$ . This shows that $\vec{G}$ is a linear function of $\vec{B}$ . This result can be written as (14), where the tensor $H_{Ω}$ only depends on the geometry of Ω and the distribution $k (\vec{x})$ . With the methods used in [11], $H_{Ω}$ can be shown to be symmetric and positive definite. Therefore, its reverse, denoted $K^{q}$ , is also symmetric and positive definite. Replacing $\vec{q} \cdot \vec{n}$ by $\vec{B} \cdot \vec{n}$ in the expression of $\vec{Q}$ given by (6), and using the second relation of (5), one finds (15). Then, taking account of (14), one can write (16). $K^{q}$ is called the equivalent permeability tensor of Ω under constant boundary flux conditions.

By using (7), the mean real dissipation [6,8] in Ω can be written as the last member of (17). For constant boundary flux conditions, replacing $\vec{q} \cdot \vec{n}$ by $\vec{B} \cdot \vec{n}$ in this integral, and using the first relation of (6), one finds that this integral is equal to $\vec{B} \cdot \vec{G}$ . Then, using (15) and (16), one finds (18). The equality of the mean real dissipation with the macroscopic dissipation calculated by $K^{q}$ , is, in this way, demonstrated for this family of flow regimes.

Let us now compare linear boundary pressure and constant boundary flux flow regimes to stationary flow regimes of a general type in Ω. Let ${p (\vec{x}), \vec{q} (\vec{x})}$ be the pressure and flux fields obtained under general conditions prescribed on ∂Ω, and $\vec{Q}$ and $\vec{G}$ be the corresponding mean flux and pressure gradient. An auxiliary flow ${p_{1} (\vec{x}), {\vec{q}}_{1} (\vec{x})}$ in Ω can be defined, which has the same mean pressure gradient $\vec{G}$ , but corresponds to constant boundary flux. The boundary condition is given by (19) with ${\vec{Q}}_{1} = - K^{q} \cdot \vec{G}$ . According to (16), ${\vec{G}}_{1}$ verifies ${\vec{Q}}_{1} = - K^{q} \cdot {\vec{G}}_{1}$ , and hence ${\vec{G}}_{1} = \vec{G}$ . The integral $I_{1}$ defined by (20) is positive, since $k (\vec{x})$ is positive. Using Darcy's law, and the symmetry of $k (\vec{x})$ , $I_{1}$ can be written as (21). The second integral of (21) can be transformed by using (7). Substituting then in the transformed expression ${\vec{q}}_{1} \cdot \vec{n}$ by ${\vec{Q}}_{1} \cdot \vec{n}$ , and using the first relation of (6), this integral can be shown to be equal to ${\vec{Q}}_{1} \cdot ({\vec{G}}_{1} - 2 \vec{G})$ , and since ${\vec{G}}_{1} = \vec{G}$ and ${\vec{Q}}_{1} = - K^{q} \cdot \vec{G}$ , it will be equal to $\vec{G} \cdot K^{q} \cdot \vec{G}$ . Introducing this equality in (21) and writing $I_{1} ⩾ 0$ , one finds (22). In the case of homogeneous domains with a permeability K, the lower bound of $D / (\vec{G} \cdot \vec{G})$ , taken over all possible flow fields, is equal to the permeability in the gradient direction, ( $\vec{G} \cdot K \cdot \vec{G}) / (\vec{G} \cdot \vec{G})$ . By extension to heterogeneous domains, the equivalent permeability in the gradient direction can be defined as the lower bound of $D / (\vec{G} \cdot \vec{G})$ . Then, according to (22), this permeability is given by $K^{q}$ .

One can also define an auxiliary flow regime ${p_{2} (\vec{x}), {\vec{q}}_{2} (\vec{x})}$ that has the same mean flux $\vec{Q}$ , but is obtained under linear boundary pressure conditions (23) where ${\vec{G}}_{2} = - {(K^{p})}^{−1} \cdot \vec{Q}$ . Using the positivity of the integral (24), which can be written as (25), one can establish the inequality (26). The equivalent permeability in the flux direction can be defined, as in the previous case, as the upper bound of $(\vec{Q} \cdot \vec{Q}) / D$ taken over all possible flow fields in Ω. According to (26), this permeability is given by $K^{p}$ .

Now, assume that ${p (\vec{x}), \vec{q} (\vec{x})}$ corresponds itself to linear boundary pressure conditions, $p (\vec{x}) = \vec{N} \cdot \vec{x}$ on ∂Ω, where $\vec{N}$ is a unit vector. According to (9), $\vec{G} = \vec{N}$ , and using (12), the inequality (22) will lead to (27). This inequality means that $K^{q}$ gives smaller values for directional permeability than $K^{p}$ .

Analogous results have been established by Huet [4,5] for linear elastic and viscoelastic behaviour of heterogeneous materials.

These results are illustrated in the case of 2D fracture networks (Fig. 1). Linear boundary pressure $p^{(κ)} = \vec{A} \cdot {\vec{x}}^{(κ)}$ , or constant boundary flux $q^{(κ)} = S^{(κ)} \vec{B} \cdot {\vec{n}}^{(κ)}$ conditions are prescribed on the fracture network, and, after resolution of the flow equations in the fracture network, $\vec{G}$ and $\vec{Q}$ are obtained from (28). Two different values of $\vec{A}$ (or $\vec{B}$ ) allow us to determine $K^{p}$ (or $K^{q}$ ). These tensors, determined for three increasing size blocks (Fig. 2a) are represented by ellipses (Fig. 2b). The small and large half-diameters of the ellipses represent the principal directions and eigenvalues of the tensor. It can be noticed that the $K^{q}$ ellipse is, for each block, interior to the $K^{p}$ ellipse.

Fig. 1
Discrétisation de la frontière du domaine fracturé.
Discretisation of the boundary of the fractured block.

Fig. 2
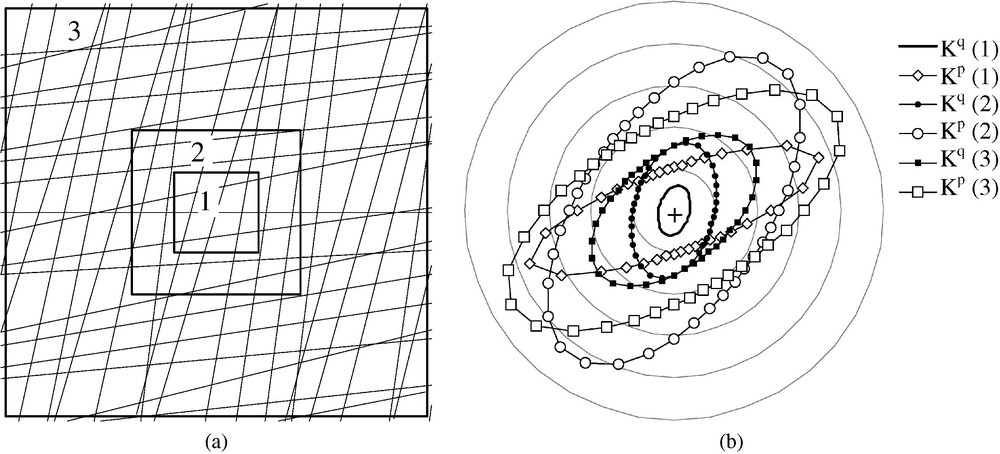
Domaines fracturés de tailles croissantes (a), et ellipses représentatives des tenseurs $K^{q}$ et $K^{p}$ de ces domaines (b).
Increasing size fractured blocks (a) and representative ellipses for the corresponding $K^{q}$ and $K^{p}$ tensors (b).

If an effective permeability exists for the medium, then $K^{q}$ and $K^{p}$ must tend, with increasing block sizes, to this same limit. If, for solving engineering problems, a lower or upper estimate of the effective permeability is desired, it seems more appropriate to use respectively $K^{q}$ or $K^{p}$ .

1 Introduction

Parmi les différentes méthodes de détermination de la perméabilité effective ou équivalente des milieux hétérogènes [1,7,9,10,12,16,17], les méthodes appelées « directes » par [2] ou « non locales » par [3,13,15], passent par la simulation d'écoulements dans un domaine de taille finie. Dans ces méthodes, on impose des conditions de pression ou de flux au contour du domaine et on détermine les champs de pression et de flux s'établissant en régime stationnaire dans le domaine. On calcule ensuite la moyenne spatiale du flux, notée $\vec{Q}$ , et du gradient de pression, notée $\vec{G}$ , et on essaie de déterminer le tenseur reliant ces deux grandeurs entre elles [3,14]. Ce tenseur représenterait la perméabilité équivalente du domaine. L'idée serait ensuite de faire croître la taille du domaine, et de voir si ce tenseur tend vers une limite pour les grandes tailles de domaine. Cette limite représenterait la perméabilité à grande échelle, ou la perméabilité effective du milieu considéré.

Mais il est bien connu que différents écoulements s'établissant dans le domaine, sous des conditions aux limites différentes, peuvent correspondre à une même valeur de $\vec{Q}$ , mais à des valeurs différentes de $\vec{G}$ , ou vice versa. De ce fait, ces deux grandeurs ne sont pas reliées entre elles par un tenseur unique [13]. Ceci pose une vraie difficulté pour la définition d'un tenseur de perméabilité équivalente pour un domaine fini.

Pouya et Courtois [11] ont étudié les écoulements obtenus sous des conditions de pression variant linéairement sur le contour du domaine (la formule (8) ci-après). Ils ont montré que pour ces écoulements, il existe un tenseur unique reliant $\vec{Q}$ à $\vec{G}$ , qui, de plus, est symétrique et défini positif. Ce tenseur, appelé perméabilité équivalente sous conditions de pressions linéaires au contour, permet une estimation bien définie des propriétés hydrauliques moyennes du domaine. Dans le présent travail, nous allons compléter les travaux précédents en introduisant une nouvelle famille d'écoulements s'établissant dans le domaine, sous des conditions aux limites dites de flux constant au contour. Nous étudierons quelques propriétés de ces écoulements et nous les comparerons au cas général d'écoulements stationnaires.

2 Position du problème

Un corps de perméabilité hétérogène et occupant un domaine Ω est le siège d'un écoulement de fluide incompressible sous l'effet de pressions et de flux imposés sur son contour ∂Ω. En tout point de Ω, de vecteur position $\vec{x}$ , l'écoulement obéit à la loi de Darcy :

\forall \vec{x} \in Ω; \vec{q} (\vec{x}) = - k (\vec{x}) \cdot \vec{\nabla} p (\vec{x})

(1)

où

\vec{q} (\vec{x})

est le flux,

\vec{\nabla} p (\vec{x})

, le gradient de pression et

k (\vec{x})

, le tenseur de perméabilité au point

\vec{x}

. On suppose que le tenseur k est en tout point symétrique et défini positif. L'équation de conservation de la masse s'écrit :

\forall \vec{x} \in Ω; div \vec{q} (\vec{x}) = 0

(2)

Les champs p et $\vec{q}$ , solutions du problème d'écoulement, doivent vérifier ces deux équations et les conditions aux limites de flux ou de pression imposées sur ∂Ω. On définit le gradient moyen de pression et flux moyen dans le domaine Ω par les relations suivantes, dans lesquelles V représente le volume de Ω :

\vec{G} = \frac{1}{V} \int_{Ω} \vec{\nabla} p (\vec{x}) d v, \vec{Q} = \frac{1}{V} \int_{Ω} \vec{q} (\vec{x}) d v

(3)

L'objectif est d'étudier les relations entre $\vec{Q}$ et $\vec{G}$ pour un domaine donné.

Nous rappelons quelques résultats mathématiques utiles pour la suite. En utilisant la formule de Green :

\int_{Ω} \partial_{i} f (\vec{x}) d v = \int_{\partial Ω} f (\vec{x}) n_{i} (\vec{x}) d S

(4)

dans laquelle f est une fonction quelconque, et

\vec{n}

, le vecteur unitaire sortant sur ∂Ω, les identités mathématiques suivantes peuvent être démontrées :

\int_{\partial Ω} \vec{n} d S = 0, \int_{\partial Ω} x_{i} n_{j} d S = V δ_{i j}

(5)

À partir de ces relations et de (2), il a été démontré que $\vec{Q}$ et $\vec{G}$ , définis par (3), peuvent se calculer à partir des valeurs au contour par les relations suivantes [9,11,12,15] :

\vec{G} = \frac{1}{V} \int_{\partial Ω} p (\vec{x}) \vec{n} (\vec{x}) d S, \vec{Q} = \frac{1}{V} \int_{\partial Ω} (\vec{q} \cdot \vec{n}) \vec{x} d S

(6)

Par ailleurs, la conservation de la masse permet d'écrire,

(\partial_{i} p) q_{i} = \partial_{i} (p q_{i})

. En intégrant ces égalités dans le volume Ω et en appliquant (4) au second membre, on montre que :

\int_{Ω} \vec{\nabla} p \vec{q} d v = \int_{\partial Ω} p \vec{q} \cdot \vec{n} d S

(7)

Les conditions aux limites de pression linéaire au contour sont définies par :

\forall \vec{x} \in \partial Ω p (\vec{x}) = \vec{A} \cdot \vec{x} + P

(8)

où

\vec{A}

est un vecteur constant et P un scalaire constant. Il a été démontré [11] que, sous ces conditions, on a :

\vec{G} = \vec{A}

(9)

et qu'il existe un tenseur symétrique et défini positif, noté ici

K^{p}

, ne dépendant que de la géométrie de Ω et de la distribution de

k (\vec{x})

dans Ω, tel que pour les écoulements vérifiant (8), on ait :

\vec{Q} = - K^{p} \cdot \vec{G}

(10)

Si on note D la dissipation moyenne réelle [6,8] :

D = \frac{1}{V} \int_{Ω} \vec{\nabla} p \cdot k \cdot \vec{\nabla} p d v

(11)

Il a été démontré [11,12] que, sous les conditions aux limites (8), il y a égalité entre cette dissipation et la dissipation macroscopique calculée par $K^{p}$ :

\frac{1}{V} \int_{Ω} \vec{\nabla} p \cdot k \cdot \vec{\nabla} p d v = \vec{G} \cdot K^{p} \cdot \vec{G}

(12)

3 Conditions de flux constant au contour

Les conditions de flux constant au contour correspondent à un flux $\vec{q} (\vec{x})$ imposé au contour ∂Ω vérifiant :

\forall \vec{x} \in \partial Ω; \vec{q} (\vec{x}) \cdot \vec{n} (\vec{x}) = \vec{B} \cdot \vec{n} (\vec{x})

(13)

où

\vec{B}

est un vecteur constant. Cette condition respecte bien la conservation de la masse. En effet, si

\vec{q} (\vec{x})

vérifie (13), on a, en vertu de la première identité (5) :

\int_{\partial Ω} \vec{q} \cdot \vec{n} d S = \int_{\partial Ω} \vec{B} \cdot \vec{n} d S = \vec{B} \cdot \int_{\partial Ω} \vec{n} d S = 0

Le champ de pression correspondant à cet écoulement est défini à une constante près. Cette constante est déterminée en fixant la valeur de la pression en un point de Ω. Mais le champ de gradient $\vec{\nabla} p (\vec{x})$ , et donc sa moyenne $\vec{G}$ , sont indépendants de cette constante, et ne dépendent que de $\vec{B}$ (pour un domaine Ω et une distribution $k (\vec{x})$ fixés).

Considérons maintenant deux vecteurs ${\vec{B}}^{1}$ et ${\vec{B}}^{2}$ et les deux écoulements s'établissant dans Ω sous les conditions de flux ${\vec{B}}^{1}$ et ${\vec{B}}^{2}$ imposés au contour – formule (13) – et la valeur de la pression fixée en un point. Notons respectivement ${p_{1} (\vec{x}), {\vec{q}}_{1} (\vec{x})}$ et ${p_{2} (\vec{x}), {\vec{q}}_{2} (\vec{x})}$ les champs de pression et de flux de ces écoulements. Chacun de ces champs vérifie la loi de Darcy (1), la conservation de la masse (2), et la condition aux limites (13) avec le $\vec{B}$ correspondant. Notons ${\vec{B}}_{3} = λ_{1} {\vec{B}}_{1} + λ_{2} {\vec{B}}_{2}$ où $λ_{1}$ et $λ_{2}$ sont deux constantes quelconques, et étudions le problème d'écoulement dans Ω sous les conditions aux limites (13) où on prendrait $\vec{B} = {\vec{B}}_{3}$ , et en fixant la valeur de la pression en un point. Du fait de la linéarité des équations (1), (2) et (13), on vérifie aisément que le champ ${p_{3} (\vec{x}), {\vec{q}}_{3} (\vec{x})}$ avec $p_{3} (\vec{x}) = λ_{1} p_{1} (\vec{x}) + λ_{2} p_{2} (\vec{x}) + p_{0}$ et ${\vec{q}}_{3} (\vec{x}) = λ_{1} {\vec{q}}_{1} (\vec{x}) + λ_{2} {\vec{q}}_{2} (\vec{x})$ , $p_{0}$ étant une constante quelconque, est bien solution de ce problème. La constante $p_{0}$ permet de fixer la valeur de la pression au point donné de Ω. Notons maintenant ${\vec{G}}_{1}$ , ${\vec{G}}_{2}$ et ${\vec{G}}_{3}$ les gradients moyens de pression des trois écoulements. La relation $p_{3} (\vec{x}) = λ_{1} p_{1} (\vec{x}) + λ_{2} p_{2} (\vec{x}) + p_{0}$ implique ${\vec{G}}_{3} = λ_{1} {\vec{G}}_{1} + λ_{2} {\vec{G}}_{2}$ . Comme en partant de ${\vec{B}}_{3} = λ_{1} {\vec{B}}_{1} + λ_{2} {\vec{B}}_{2}$ , on aboutit à ${\vec{G}}_{3} = λ_{1} {\vec{G}}_{1} + λ_{2} {\vec{G}}_{2}$ , on déduit que $\vec{G}$ est une fonction linéaire de $\vec{B}$ , ce qui s'écrit sous la forme :

\vec{G} = - H_{Ω} \cdot \vec{B}

(14)

Le tenseur $H_{Ω}$ ne dépend que de la géométrie de Ω et de la distribution $k (\vec{x})$ dans Ω.

Par ailleurs, pour les écoulements vérifiant les conditions aux limites (13), en partant de l'expression de $\vec{Q}$ donnée par (6), en remplaçant $\vec{q} \cdot \vec{n}$ par $\vec{B} \cdot \vec{n}$ , et en utilisant la seconde relation de (5), on trouve :

\vec{Q} = \vec{B}

(15)

En notant $K^{q}$ l'inverse de $H_{Ω}$ , les relations (14) et (15) conduisent à :

\vec{Q} = - K^{q} \cdot \vec{G}

(16)

Nous appelons

K^{q}

le tenseur de perméabilité équivalente de Ω sous les conditions de flux constant au contour.

On peut montrer, par les mêmes méthodes utilisées dans [11] pour $K_{Ω}$ (ici noté $K^{p}$ ), que $H_{Ω}$ est symétrique et défini positif. Donc son inverse $K^{q}$ l'est aussi.

Par ailleurs, (7) permet d'écrire la dissipation moyenne réelle (11) sous la forme :

D = \frac{1}{V} \int_{Ω} \vec{\nabla} p \cdot k \cdot \vec{\nabla} p d v = - \frac{1}{V} \int_{Ω} \vec{\nabla} p \cdot \vec{q} d v = - \frac{1}{V} \int_{\partial Ω} p \vec{q} \cdot \vec{n} d S

(17)

Pour les écoulements à flux constant au contour, on peut remplacer dans l'intégrale du dernier membre

\vec{q} \cdot \vec{n}

par

\vec{B} \cdot \vec{n}

, et en utilisant la première relation de (6), montrer que le dernier membre est égal à

- \vec{B} \cdot \vec{G}

. En utilisant (15) et (16), on trouve alors :

\frac{1}{V} \int_{Ω} \vec{\nabla} p \cdot k \vec{\nabla} p d v = \vec{G} \cdot K^{q} \cdot \vec{G}

(18)

On trouve ainsi que, pour ces écoulements, il y a égalité entre la dissipation moyenne réelle et la dissipation macroscopique calculée par $K^{q}$ .

4 Comparaison des écoulements

Nous avons introduit deux types de conditions aux limites imposées au contour du domaine, permettant de calculer deux tenseurs différents de perméabilité équivalente, $K^{p}$ et $K^{q}$ . Nous allons maintenant les comparer aux grandeurs calculées pour un écoulement de type général.

Considérons le cas d'un écoulement général dans le domaine Ω sous l'effet de conditions aux limites quelconques imposées au contour. Notons ${p (\vec{x}), \vec{q} (\vec{x})}$ les champs de pression et de flux de cet écoulement, et $\vec{G}$ et $\vec{Q}$ les moyennes respectivement du gradient de pression et du flux de cet écoulement données par (3).

Considérons maintenant un écoulement ${p_{1} (\vec{x}), {\vec{q}}_{1} (\vec{x})}$ dans Ω ayant le même gradient de pression $\vec{G}$ , mais sous des conditions de flux constant au contour : le flux moyen sera ${\vec{Q}}_{1} = - K^{q} \cdot \vec{G}$ , a priori différent de $\vec{Q}$ . Les conditions aux limites de cet écoulement sont :

\forall x \in \partial Ω; {\vec{q}}_{1} (\vec{x}) \cdot \vec{n} (\vec{x}) = {\vec{Q}}_{1} \cdot \vec{n} (\vec{x})

(19)

et on a

{\vec{G}}_{1} = \vec{G}

. Définissons l'intégrale :

I_{1} = \frac{1}{V} \int_{Ω} (\vec{\nabla} p - \vec{\nabla} p_{1}) \cdot k \cdot (\vec{\nabla} p - \vec{\nabla} p_{1}) d v

(20)

Comme k est défini positif, on a

I_{1} ⩾ 0

. En développant l'intégrande, en remplaçant

k \cdot \vec{\nabla} p

par

- \vec{q} (\vec{x})

et

k \cdot \vec{\nabla} p_{1}

par

- {\vec{q}}_{1} (\vec{x})

et, en remarquant que, du fait de la symétrie de k, on a

\vec{\nabla} p_{1} \cdot \vec{q} = {\vec{q}}_{1} \cdot \vec{\nabla} p

, on trouve :

I_{1} = \frac{1}{V} \int_{Ω} \vec{\nabla} p \cdot k \cdot \vec{\nabla} p d v - \frac{1}{V} \int_{Ω} {\vec{q}}_{1} \cdot (\vec{\nabla} p_{1} - 2 \vec{\nabla} p) d v

(21)

En appliquant (7) à la seconde intégrale de (21), en remplaçant ${\vec{q}}_{1} \cdot \vec{n}$ sur la frontière par ${\vec{Q}}_{1} \cdot \vec{n}$ , et en utilisant la première relation de (6), on trouve que cette intégrale est égale à ${\vec{Q}}_{1} \cdot ({\vec{G}}_{1} - 2 \vec{G})$ , ou encore, puisque ${\vec{G}}_{1} = \vec{G}$ et ${\vec{Q}}_{1} = - K^{q} \cdot \vec{G}$ , qu'elle est égale à $\vec{G} \cdot K^{q} \cdot \vec{G}$ . En reportant dans (21) et écrivant $I_{1} ⩾ 0$ , on trouve :

\frac{1}{V} \int_{Ω} \vec{\nabla} p \cdot k \cdot \vec{\nabla} p d v ⩾ \vec{G} \cdot K^{q} \cdot \vec{G}

ou encore :

D ⩾ \vec{G} \cdot K^{q} \cdot \vec{G}

(22)

Pour un domaine homogène de perméabilité K, l'inégalité (22) s'écrit $D ⩾ \vec{G} \cdot K \cdot \vec{G}$ , l'égalité étant atteinte pour les écoulements uniformes ( $\vec{q}$ et $\vec{\nabla} p$ constants) dans Ω. Remarquons que ceci permet de définir, dans le cas de Ω homogène, la perméabilité dans la direction du gradient $(\vec{G} \cdot K^{q} \cdot \vec{G}) / (\vec{G} \cdot \vec{G})$ comme étant la borne inférieure de $D / (\vec{G} \cdot \vec{G})$ prise sur tous les écoulements possibles. On peut alors, par extension au cas des domaines Ω hétérogènes, définir la perméabilité équivalente dans la direction du gradient comme étant la borne inférieure de $D / (\vec{G} \cdot \vec{G})$ prise sur tous les écoulements possibles sur Ω. L'inégalité (22) indique alors que cette grandeur est donnée par le tenseur $K^{q}$ du domaine. Cette borne est atteinte par les écoulements à flux constant au contour – équation (18).

Considérons maintenant un autre écoulement ${p_{2} (\vec{x}), {\vec{q}}_{2} (\vec{x})}$ dans Ω ayant le même gradient de pression $\vec{Q}$ , mais sous des conditions de pression linéaire au contour : le gradient moyen de pression sera ${\vec{G}}_{2} = - {(K^{p})}^{−1} \cdot \vec{Q}$ , a priori différent de $\vec{G}$ . Les conditions aux limites de cet écoulement s'écrivent :

\forall \vec{x} \in \partial Ω; p_{2} (\vec{x}) = {\vec{G}}_{2} \cdot \vec{x}

(23)

et on a

{\vec{Q}}_{2} = \vec{Q}

.

Définissons l'intégrale suivante :

I_{2} = \frac{1}{V} \int_{Ω} (\vec{\nabla} p - \vec{\nabla} p_{2}) \cdot k \cdot (\vec{\nabla} p - \vec{\nabla} p_{2}) d v

(24)

Comme ci-dessus, on a

I_{2} ⩾ 0

, et on peut mettre

I_{2}

sous la forme :

I_{2} = \frac{1}{V} \int_{Ω} \vec{\nabla} p \cdot k \cdot \vec{\nabla} p d v - \frac{1}{V} \int_{Ω} \vec{\nabla} p_{2} \cdot ({\vec{q}}_{2} - 2 \vec{q}) d v

(25)

On peut alors appliquer (7) à la seconde intégrale de (25), remplacer

p_{2}

sur la frontière par

{\vec{G}}_{2} \cdot \vec{x}

, et utiliser la seconde égalité de (6) pour trouver que cette intégrale est égale à

{\vec{G}}_{2} \cdot ({\vec{Q}}_{2} - 2 \vec{Q})

, ou encore, compte tenu de

{\vec{Q}}_{2} = \vec{Q}

, et

{\vec{G}}_{2} = - {(K^{p})}^{−1} \cdot \vec{Q}

, égale à

\vec{Q} {(K^{p})}^{−1} \vec{Q}

. En reportant alors dans (25), en écrivant

I_{2} ⩾ 0

et en utilisant (11), on trouve :

D ⩾ \vec{Q} \cdot {(K^{p})}^{−1} \cdot \vec{Q}

(26)

Dans le même esprit que ci-dessus, on peut définir, pour un domaine hétérogène Ω, la perméabilité équivalente dans la direction du flux comme étant la borne supérieure des valeurs de $(\vec{Q} \cdot \vec{Q}) / D$ prise sur tous les écoulements possibles dans Ω. Dans ce cas, l'inégalité (26) indiquerait que cette perméabilité peut être calculée par le tenseur $K^{p}$ . Cette borne est atteinte par les écoulements à pression linéaire au contour.

Supposons maintenant que l'écoulement ${p (\vec{x}), \vec{q} (\vec{x})}$ dont nous sommes partis soit lui-même à pression linéaire au contour, avec $p (\vec{x}) = \vec{N} \cdot \vec{x}$ sur ∂Ω. On trouve alors $\vec{G} = \vec{N}$ (relation (9)), et d'après (12) on a $D = \vec{G} \cdot K^{p} \cdot \vec{G}$ . L'inégalité (22) s'écrit dans ce cas :

\vec{N} \cdot K^{p} \cdot \vec{N} - \vec{N} \cdot K^{q} \cdot \vec{N} ⩾ 0

(27)

Si on suppose $\vec{N}$ unitaire, $\vec{N} \cdot K \cdot \vec{N}$ est la perméabilité dans la direction $\vec{N}$ . D'après l'inégalité (27), $K^{p}$ conduit à des valeurs de perméabilité directionnelle plus grandes que $K^{q}$ .

Des résultats analogues à (9), (10), (12), (15), (16), (18), (22), (26) et (27), et sur certains points plus larges, ont été démontrés par Huet [4,5] pour les comportements élastique et viscoélastique des matériaux hétérogènes.

5 Illustration sur des milieux fracturés bidimensionnels

Pour un point numéroté κ d'intersection des fractures avec le contour du domaine, on note ${\vec{x}}^{(κ)}, {\vec{n}}^{(κ)}$ et $S^{(κ)}$ respectivement le vecteur position, la normale unitaire sortante et l'élément de longueur associé à ce point sur le contour (Fig. 1). On note $p^{(κ)}$ la pression et $q^{(κ)}$ le flux sortant de la fracture. Le débit $\vec{q} \cdot \vec{n} \cdot S^{(κ)}$ sortant du domaine à travers le segment $S^{(κ)}$ , équivalent de $\vec{q} \cdot \vec{n} d S$ dans la configuration continue, se confond ici avec le débit $q^{(κ)}$ sortant de la fracture au point κ. Les relations (6) deviennent :

\begin{matrix} \vec{G} = \frac{1}{V} \sum_{κ} p^{(κ)} {\vec{n}}^{(κ)} S^{(κ)}, \\ \vec{Q} = \frac{1}{V} \sum_{κ} q^{(κ)} {\vec{x}}^{(κ)} \end{matrix}

(28)

Pour simuler un écoulement à pression linéaire au contour, on impose $p^{(κ)} = \vec{A} \cdot {\vec{x}}^{(κ)}$ , on résout le système d'équations d'écoulements dans le réseau de fractures pour calculer les $q^{(κ)}$ , et on en déduit $\vec{Q}$ par (28).

Pour simuler un écoulement à flux constant au contour, on impose $q^{(κ)} = \vec{B} \cdot {\vec{n}}^{(κ)} S^{(κ)}$ au réseau de fractures. Cette condition ne peut être appliquée que si le réseau de fractures est entièrement connecté ; sinon, elle peut être incompatible avec la conservation de la masse dans certaines parties du réseau. On fixe aussi la pression en un point κ, et on résout le système d'équations d'écoulement dans les fractures pour en déduire les $p^{(κ)}$ . On calcule alors $\vec{G}$ par (28). Il peut paraître numériquement plus simple de partir d'une distribution de valeurs de $p^{(κ)}$ et de calculer les $q^{(κ)}$ en résolvant le système d'équations d'écoulement dans les fractures. En comparant alors les $q^{(κ)}$ obtenus aux valeurs attendues de $\vec{B} \cdot {\vec{n}}^{(κ)} S^{(κ)}$ , on peut apporter de petites modifications $δ p^{(κ)}$ tendant à diminuer l'écart $q^{(κ)} - \vec{B} \cdot {\vec{n}}^{(κ)} S^{(κ)}$ . On peut, de cette façon, par itérations successives, tendre vers une distribution de valeurs de $p^{(κ)}$ produisant un écoulement à flux constant au contour, c'est-à-dire vérifiant $q^{(κ)} = \vec{B} \cdot {\vec{n}}^{(κ)} S^{(κ)}$ sur le contour. Nous avons suivi cette méthode.

En prenant deux directions différentes de $\vec{A}$ (ou $\vec{B}$ ), on construit $K^{p}$ (ou $K^{q}$ ).

Nous avons calculé ces tenseurs pour trois domaines carrés de tailles croissantes (Fig. 2a). On représente graphiquement chacun des tenseurs $K^{p}$ ou $K^{q}$ de ces domaines par une ellipse dont les diamètres principaux représentent les directions propres du tenseur et ses demi-diamètres, les valeurs propres correspondantes (Fig. 2b). On remarque que, comme prévu, l'ellipse $K^{q}$ est toujours intérieure à $K^{p}$ .

6 Discussions

La différence entre les deux ellipses diminue dans l'exemple ci-dessus quand la taille du domaine croît, mais ceci n'est pas une propriété générale. Si une perméabilité à grande échelle existe pour le milieu fracturé, les deux tenseurs $K^{q}$ et $K^{p}$ doivent tendre, pour des tailles croissantes de domaine, vers une limite commune représentant cette perméabilité. La différence entre ces deux tenseurs permet d'estimer si le domaine considéré est suffisamment grand pour constituer un volume élémentaire représentatif. Elle donne aussi une idée de la variabilité des valeurs de perméabilité directionnelle que l'on peut calculer sur un domaine de taille finie. Dans certains cas d'application aux problèmes de l'ingénieur (par exemple le calcul du débit d'exhaure maximum susceptible d'arriver dans un tunnel), on cherche à estimer des perméabilités maximums du massif fracturé. L'utilisation de $K^{p}$ paraît plus adaptée à ces cas, sans toutefois garantir de donner des majorants absolus de la perméabilité effective. Dans d'autres cas (pétroliers, géothermie), on cherche à estimer une perméabilité minimum ; l'utilisation de $K^{q}$ paraîtrait alors plus adaptée.

References

[1] M.C. Cacas; E. Ledoux; G. de Marsily; B. Tillie Modeling fracture flow with a stochastic discrete fracture network: calibration and validation. 1. The flow model, Water Resour. Res., Volume 26 (1990) no. 3, pp. 479-489

[2] C. Fidelibus; G. Barla; M. Cravero Alternative schemes for the assessment of the equivalent continuum hydraulic properties of rock masses (G. Barla, ed.), Eurock'96, Balkema, Rotterdam, 1996, pp. 1243-1252

[3] J.J. Goméz-Hernández; X.H. Wen Upscaling hydraulic conductivities in heterogeneous media: an overview, J. Hydrol., Volume 183 (1996), p. ix-xxxii

[4] C. Huet Application of variational concepts to size effects in elastic heterogeneous bodies, J. Mech. Phys. Solids, Volume 38 (1990) no. 6, pp. 813-841

[5] C. Huet Coupled size and boundary-condition effects in viscoelastic heterogeneous and composite bodies, Mech. Mater., Volume 31 (1999) no. 12, pp. 787-829

[6] P. Indelman; G. Dagan Upscaling of permeability of anisotropic heterogeneous formations. 1. The general framework, Water Resour. Res., Volume 29 (1993) no. 4, pp. 917-923

[7] J.C.S. Long; J.S. Remer; C.R. Wilson; P.A. Witherspoon Porous media equivalents for networks of discontinuous fractures, Water Resour. Res., Volume 18 (1982) no. 3, pp. 645-658

[8] G. Matheron Éléments pour une théorie des milieux poreux, Masson, Paris, 1967

[9] A. Njifenjou Expression en termes d'énergie pour la perméabilité absolue effective, Rev. IFP, Volume 49 (1994) no. 4, pp. 345-358

[10] B. Nœtinger Computing the effective permeability of log-normal permeability fields using renormalization methods, C. R. Acad. Sci. Paris, Ser. IIa, Volume 331 (2000), pp. 353-357

[11] A. Pouya; A. Courtois Définition de la perméabilité équivalente des massifs fracturés par des méthodes d'homogénéisation, C. R. Geoscience, Volume 334 (2002), pp. 975-979

[12] P. Renard, Modélisation des écoulements en milieu poreux hétérogène. Calcul des perméabilités équivalentes, thèse, École des mines de Paris, Mém. Sci. Terre n° 37, 1996

[13] P. Renard; G. de Marsily Calculating equivalent permeability: a review, Adv. Water Resour., Volume 20 (1997) no. 5–6, pp. 253-278

[14] Y. Rubin; J.J. Goméz-Hernández A stochastic approach to the problem of upscaling of conductivity in disordered media: theory and unconditional numerical simulations, Water Resour. Res., Volume 26 (1990) no. 4, pp. 691-701

[15] X. Sánchez-Vila; G.P. Girardi; J. Carrera A synthesis of approaches to upscaling of hydraulic conductivities, Water Resour. Res., Volume 31 (1995) no. 4, pp. 867-882

[16] X. Zhang; D.J. Sanderson Numerical Modelling and Analysis of Fluid Flow and Deformation of Fractured Rock Masses, Pergamon Press, Amsterdam, 2002

[17] R.W. Zimmerman; G.S. Bodvarsson Effective transmissivity of two-dimensional fracture networks, Int. J. Rock Mech. Min. Sci. Geomech. Abstr., Volume 33 (1996) no. 4, pp. 433-438

Comments - Policy