Version française abrégée
Les modèles numériques de terrain (MNT) sont nécessaires et parfois indispensables à diverses applications thématiques (environnement, cartographie géologique, aménagement...). Cependant, certaines parties du globe manquent de données topographiques, comme c'est le cas d'une grande partie des zones tropicales et équatoriales. Ces zones sont peu couvertes par les capteurs satellitaires optiques, en raison d'une forte couverture nuageuse quasi constante. Seuls les capteurs radars sont donc disponibles pour la fabrication de modèles numériques de terrain à l'échelle régionale, indépendamment de la présence nuageuse. Les deux méthodes les plus utilisées pour fabriquer des MNT à partir d'images radar sont : (1) la radargrammétrie, dérivée de la photogrammétrie et opérant sur la base d'une méthode stéréoscopique et (2) l'interférométrie, basée sur la différence de phase entre deux images [1,11,13]. Différentes études ont montré que les MNT interférométriques sont de meilleure précision que les MNT radargrammétriques, et que la précision altimétrique dépend du type de terrain [1,3,12].
Réalisée en février 2000, la mission SRTM (Shuttle Radar Topography Mission) de la navette spatiale américaine a permis de cartographier près de 80 % de la surface terrestre entre 60°N et 56°S [5]. Basée sur l'interférométrie, elle a utilisé deux radars à ouverture synthétique, SIR-C (bande C) et X-SAR (bande X). Pour l'Amérique du Sud, seul un MNT à maille de 90 m × 90 m est disponible pour l'instant. Ce MNT SRTM correspond au sommet de la canopée, avec une légère pénétration dans le couvert végétal.
Ce papier a pour objectif d'analyser la précision du MNT SRTM bande C sur un site d'étude situé au sud de Cayenne en Guyane Française, composé de marécages, de savanes, et de zones de forêt dense. Le site d'étude est majoritairement plat ou légèrement ondulé, avec des altitudes comprises entre 0 et 400 m (montagne de Kaw). Pour la validation du MNT SRTM, nous disposons de trois types d'informations (Fig. 1) :
- – des données laser aéroportées définies le long de lignes de vol orientées N30°, avec un espacement de 500 m, et de lignes orientées N120°, avec un espacement de 5 km. Ces données laser correspondent au premier obstacle rencontré par le faisceau laser (fréquemment, le sommet de la canopée). La fréquence d'échantillonnage est d'environ 7 m le long des lignes de vol et la précision altimétrique d'environ ±2 m ;
- – des données laser héliportées acquises sur la partie sud de notre site d'étude, entièrement couverte par la forêt dense. Les données altimétriques, mesurées au pas de 50 m × 15 m, avec une précision de quelques dizaines de centimètres, correspondent au sol. Un MNT héliporté a été dérivé de ces données en calculant l'altitude moyenne sur des pixels de 90 m × 90 m. L'erreur introduite par le krigeage est d'environ 1 m ;
- – 398 points cotés digitalisés sur des cartes IGN au . Les points cotés, dont l'altitude varie de 0 à 391 m, ont une précision d'environ 1 m.
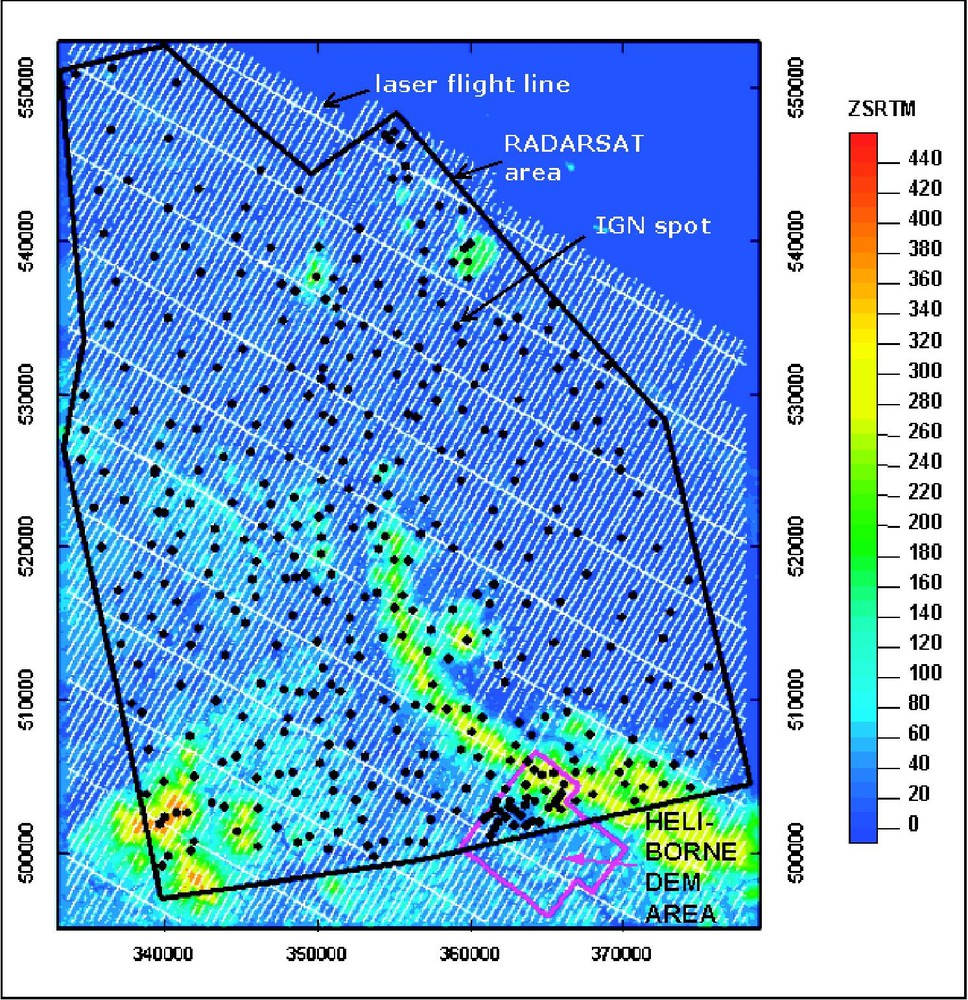
The SRTM DEM and available data (airborne laser flight lines, heliborne DEM, IGN spots). Universal Transverse Mercator projection, zone 22, international 1909 spheroid system C.S.G., 1967.
Le MNT SRTM et les données disponibles (lignes de vol laser airoporté, MNT héliporté, points cotés IGN). Projection Universal Transverse Mercator, zone 22, système sphéroïde international 1909 C.S.G., 1967.
De plus, un MNT radargrammétrique créé à partir de deux images RADARSAT a également été utilisé et comparé au MNT SRTM. Il correspond au sommet de la canopée, avec des pixels de 50 m × 50 m (avec une légère pénétration du couvert). La précision altimétrique de ce MNT RADARSAT est de l'ordre de la vingtaine de mètres [1].
Pour comparer le MNT SRTM aux altitudes laser aéroportées, les points laser correspondant au sommet de la canopée ont été extraits des données laser aéroportées [1]. Les points « sommets de canopée » sont définis comme le maximum local à l'intérieur d'une fenêtre glissante optimale de 56 m (neuf points laser). Sur l'ensemble de la zone d'étude, la différence moyenne entre les points laser « sommets de canopée » et le MNT SRTM est d'environ 4,3 m. Ce biais correspond à la variation verticale du couvert végétal dans un pixel SRTM de 90 m × 90 m, et à une faible pénétration du signal radar en bande C dans le couvert forestier (Fig. 2). Ce biais peut atteindre 8,5 m dans les zones de forêt dense (en particulier, les altitudes les plus élevées de la zone).
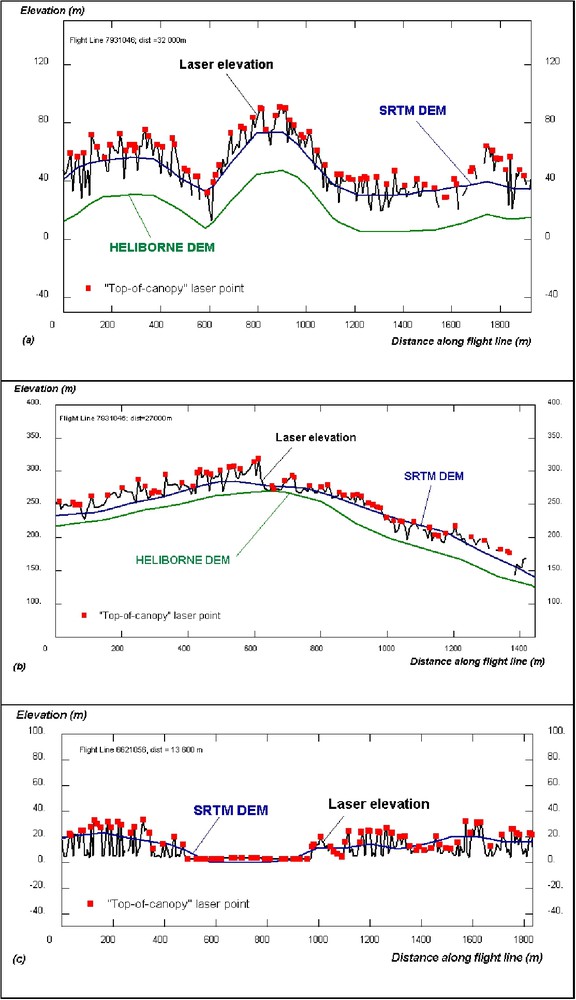
Comparison of the DEMs along airborne vertical laser profiles: (a) area of localized low-lying hills, (b) area of higher elevation, (c) profile intersecting a river.
Comparaison des MNT le long des profils laser aéroportés : (a) zone de petites collines, (b) altitudes plus élevées, (c) profil recoupant une rivière.
La comparaison entre le MNT SRTM et le MNT héliporté montre que la différence moyenne entre les deux MNT est d'environ 26,5 m (Tableau 1). Si on rajoute le biais observé entre le MNT SRTM et les points laser « sommets », de canopée, qui est de 7 m dans la zone du MNT héliporté, nous obtenons une estimation de la hauteur moyenne du « sommet » de la canopée d'environ 33,5 m dans cette zone. Sur l'ensemble de la zone d'étude, la différence entre le MNT SRTM et les points cotés IGN est de 13,3 m, ce qui, ajouté à la différence moyenne de 4,3 m, correspond à une hauteur moyenne de la canopée de 17,6 m. Cette hauteur est inférieure aux 33,5 m de la zone du MNT héliporté, car la plupart des points cotés IGN sont situés en zones plates et de marécage, où les arbres sont plus petits et parfois inexistants, tandis que le MNT héliporté correspond à une zone de forêt dense.
Differences between the satellite DEMs and validation data. elevation; elevation; DEM elevation; spot-height elevation. LE90 = Linear error at the 90% confidence level
Différences entre les MNT satellitaires et les données de validation. SRTM ; RADARSAT ; du MNT héliporté ; des points cotés IGN. LE90 = erreur linéaire avec un intervalle de confiance de 90%
| Difference computed | No. of comparison points | Mean error (m) | Standard deviation (m) | Minimum error (m) | Maximum error (m) | LE90 (m) |
| 7125 pixels of 90 m × 90 m | 26.5 | 8.2 | −10.8 | +59.6 | ±13.5 | |
| 8610 pixels of 50 m × 50 m | 36.7 | 25.3 | −52 | +148 | ±44 | |
| 398 IGN spots (within 1920 km2) | 13.3 | 10.2 | −12.2 | +44.2 | ±15.5 | |
| 398 IGN spots (within 1920 km2) | 17.1 | 21.2 | −59 | +140 | ±33 |
La précision altimétrique du MNT SRTM, en terme d'écart type des différences d'altitude, est de 8,2 m en comparaison du MNT héliporté, et de 10,2 m en comparaison des points cotés IGN. Ce résultat montre que la précision du MNT SRTM est deux à trois fois meilleure que celle du MNT RADARSAT (Tableau 1) [1]. La qualité du MNT SRTM est très dépendante de la pente du terrain et de son exposition (Fig. 3) [8,9]. La différence entre l'altitude SRTM et l'altitude du MNT héliporté (le sol) augmente presque linéairement avec la pente. L'exposition de la pente joue un rôle majeur sur l'amplitude de l'erreur et sur son signe : les altitudes sont sous-estimées pour les pentes exposées au nord-ouest, c'est-à-dire face à la direction de visée du satellite, alors qu'à l'inverse, elles sont surestimées pour les pentes exposées au sud-est. Ce sont également ces deux orientations de pente qui donnent les erreurs maximales (Fig. 3). Pour les zones de faible relief, le variogramme des données SRTM est plus élevé que celui des données laser aéroportées, ce qui montre que les données laser dans ces zones sont de meilleure qualité que les données SRTM (Fig. 4a). Pour les autres zones, les variogrammes des données SRTM deviennent plus faibles que ceux des données laser ou du même ordre de grandeur (Fig. 4b–d). On observe également la meilleure qualité du MNT SRTM en comparaison au MNT RADARSAT, surtout dans les zones de faibles altitudes.
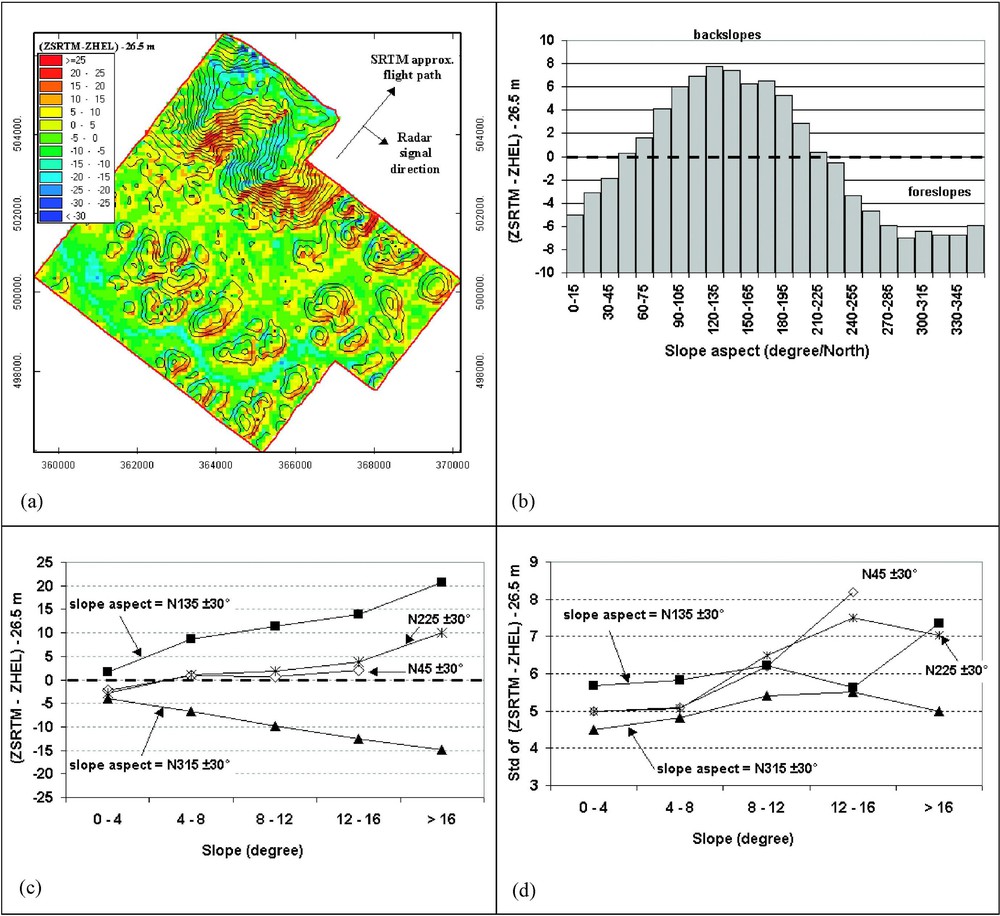
Elevation errors of the SRTM DEM as a function of slope and slope aspect. (a) Map of the difference between SRTM DEM elevation and heliborne DEM elevation . The subtracted value 26.5 m is the overall bias between these two DEMs, and is mainly due to the canopy thickness. (b) Elevation error versus slope aspect (in degrees). (c) Elevation error versus terrain slope, for four slope aspects. (d) Standard deviation of elevation error versus terrain slope, for four slope aspects.
Erreurs d'altitude du MNT SRTM en fonction de la pente du terrain et de son exposition. (a) Carte de la différence entre le MNT SRTM (ZSRTM) et le MNT héliporté (ZHEL). La valeur de 26,5 m retranchée correspond au biais global entre les deux MNT et est liée principalement à l'épaisseur de la canopée. (b) Erreur d'altitude en fonction de l'exposition de la pente (en degrés). (c) Erreur d'altitude en fonction de la valeur de la pente, pour différentes valeurs d'exposition ; (d) Écart type de l'erreur d'altitude en fonction de la valeur de la pente, pour différentes valeurs d'exposition.

Variograms of elevation for each relief zone ( elevation in 2 km × 2 km areas). elevation; elevation; ‘top-of-canopy’ laser elevation.
Variogramme des altitudes pour chaque zone d'altitude ( médiane dans une fenêtre de 2 km × 2 km). SRTM ; RADARSAT ; laser « sommet de la canopée ».
1 Introduction
Digital elevation models (DEM) are necessary, even vital tools in a variety of thematic applications in the environmental sector or in geological mapping. Some parts of the world are clearly lacking for topographic data, as is the case in a large part of the tropical and equatorial zones. These zones are covered with dense equatorial forests, where optical satellite methods cannot be used due to constant cloud cover. Only SAR (Synthetic Aperture Radar) data are available for developing regional-scale DEMs regardless of the presence of cloud cover. The two most common methods for extracting DEMs from SAR images are: (1) radargrammetry, derived from photogrammetry and operating on the basis of a stereoscopic method and (2) interferometry, based on the phase difference between two images. These methods are described in greater detail in [1,11,13], which show that elevation accuracy varies considerably depending on the method used and the type of environment. However, interferometric DEMs have a better accuracy than radargrammetric DEMs. In forest areas, the two methods provide an image of the topography of the top of the vegetation cover (modulo a slight penetration).
Baghdadi et al., and Bourgine et al., showed, in a dense equatorial forest context located in French Guiana, that it was possible to merge a radargrammetric SAR DEM with low spatial resolution laser airborne data, in order (1) to improve the accuracy of the SAR DEM, and (2) to derive a ground-level DEM [1,2]. The originality of this work lies in the aim of putting to good use two complementary data sources: (1) a radargrammetric top-of-canopy DEM with an elevation accuracy of about 25 m, dense and regularly spaced (grid of 50 m × 50 m), and (2) a low-spatial-resolution airborne laser altimeter, more accurate than the radargrammetric DEM (elevation accuracy of about 2 m), but irregular and sparse (flight lines spacing of 500 m). Accuracy was improved from 25 to 11 m and a ground-level DEM was computed. Geostatistical techniques were used for the processing.
In this new study, an interferometric C-band DEM of the Shuttle Radar Topography Mission (SRTM) is used instead of the radargrammetric DEM with a two-fold objective: (1) to assess the accuracy of the SRTM DEM at the same study site in French Guiana, and (2) to merge the SRTM DEM with airborne laser data, using a similar method as the one mentioned above, in order to derive a ground-level DEM and evaluate the gain in accuracy compared to the results obtained in previous works.
After presenting the available data, the paper considers the validation of the SRTM DEM in three ways: qualitative, statistical and geostatistical analysis.
2 Data description
2.1 Study area
A study area measuring 45 km × 55 km was selected in an equatorial environment to the south of Cayenne in French Guiana (long. to and lat. to ) (Fig. 1). French Guiana is entirely covered by Amazonian forest. The study area, located along the coast, is characterized by virgin forest, marsh zones and savannah. Most of the area is flat or slightly undulating, with elevation ranging from 0 m to about 400 m a.s.l. (e.g., Kaw mountain).
2.2 Airborne data
The airborne data comprise laser elevation data acquired during an airborne geophysical survey over French Guiana in 1996. As these laser data were acquired for the purpose of checking the quality of the geophysical survey, particularly the flight ground clearance, a low sampling frequency was chosen and only the first pulse considered (i.e. the first obstacle encountered).
Flight lines were oriented N30° with a 500-m spacing, complemented by transverse flight lines oriented N120° with a 5-km spacing (Fig. 1b). Laser sampling density was approximately 7 m along flight lines (sampling frequency = 10 Hz). Laser wavelength is 905 nm and footprint size is 35 cm. The laser measurements are therefore considered as point data. The quality of the airborne data was assessed and the elevation accuracy estimated at around ±2 m.
2.3 Heliborne data
For checking purposes, heliborne laser data are available in an 8 km × 8.5 km zone in the southern part of our study area (Fig. 1). The heliborne data are located in an area covered entirely by thick forest. Ground elevation was provided over an almost-regular 50 m × 15 m measurement grid. The accuracy announced by the provider of this data set (ALTOA Company) was some tens of centimetres. To be consistent with the SRTM DEM pixel size, a 90-m heliborne DEM was derived from this dataset. The average elevation over each 90 m × 90 m block was calculated by kriging, with a kriging standard deviation of around 1 m. Elevation in the heliborne DEM area varies from 1.5 to 315 m, with an average of 120 m, and corresponds to ground-level elevations. This heliborne DEM was used to validate the various DEMs.
2.4 IGN spot heights
Most of the study area is covered by 1:25 000-scale IGN maps providing the elevation of many spot heights (accuracy around 1 m) and contour lines every 10 m. Three hundred and ninety-eight IGN spot heights ranging from 0 m to 391 m, with an average of 50 m, were digitized (Fig. 1). These spots were only used to assess the accuracy of the method.
2.5 SRTM DEM
The Shuttle Radar Topography Mission (SRTM) of February 2000 has totally revolutionized the concept of global topographic mapping. A global DEM was acquired using C-band (SIR-C) and X-band (X-SAR) Interferometric Synthetic Aperture Radars (INSAR) for almost 80% of the Earth's land surface between 60°N and 56°S [5,7]. NASA's Jet Propulsion Laboratory (JPL) performed preliminary processing of the raw C-band SRTM data. A 1-arc-second DEM and a downgraded 3-arc-second DEM where then derived from this data by the National Geospatial-Intelligence Agency (NGA) and its contractors [6]. The 30-m DEM, available for North America, and the 90-m DEM can be downloaded from the NASA ftp server. The vertical accuracy of the C-band SRTM DEMs is stated as ±16 m at the 90% confidence interval [6,8]. On another hand, the X-band SRTM data was processed by the DLR (Deutches Zentrum fur Luft und Raumfahrt, Germany) and the ASI (Agenzia Spatiale Italiana). The resulting DEM is known to have a better accuracy than the C-Band DEM: about 4 m in open landscape and 10 m in forested areas [3,9]. In the present study, we use the only SRTM DEM available for South America, i.e. the 90 m C-band SRTM DEM. The available 90-m DEM of our study area is displayed in Fig. 1.
One great limitation of the SRTM DEM is the presence of voids, due to the nature of the used INSAR technology, combined with the interaction of radar energy with the atmosphere and ground targets. Such voids appear within water bodies or in areas of steep reliefs. A lot of research teams are currently working on void-filling algorithms and interesting results have already been published [6,8]. In our case, we did not encounter problems with voids: our DEM had only 0.003% of voids or anomalous values, and those voids, being of a very small size, could be easily filled by interpolation from surrounding pixels (using a Delaunay triangulation algorithm).
At last, note that the SRTM C-band antenna was right-looking with respect to the flight direction, which was southwest to northeast (ascending orbit).
2.6 RADARSAT DEM
A radargrammetric top-of-canopy DEM created from two RADARSAT images acquired in S2 Standard and F5 Fine modes with a pixel size of 50 m × 50 m was also used [1]. The accuracy of this DEM was found to be about 21.2 m compared with the IGN spot heights, with a maximum error of 140 m and a minimum error of (Table 1). Elevation accuracy compared to the heliborne DEM was estimated at about 25.3 m. This RADARSAT DEM proved inconsistent in flat areas , where non-existent relief is generated by satellite imagery. This is due to a poor correlation between the SAR images in such a homogeneous environment. We also noted a smoothing effect on topography.
3 Assessment of SRTM DEM accuracy
3.1 Qualitative analysis
A qualitative analysis of SRTM DEM was carried out by comparing SRTM elevations with vertical laser profiles along airborne flight lines on the one hand, and with the heliborne DEM on the other (Fig. 2). The heliborne DEM, considered as the ‘true’ ground-level DEM, is reported in Fig. 2a and b. Fig. 2c shows a profile crossing a river at a distance of 500 m to 1000 m, in an area were the heliborne DEM is not available.
As the SRTM DEM represents an elevation over 90 m × 90 m pixels, local variations in vegetation height are smoothed within the pixels. Conversely, airborne laser elevations show local-scale fluctuations according to whether in reality the point corresponds to a treetop or a branch at intermediate level. It can be seen in Fig. 2 that the laser points are almost systematically located well above the heliborne DEM, i.e. the ground, with only a few seeming to reach or near the ground. The SRTM DEM appears to be well correlated with the laser profiles and follows them relatively well.
In order to estimate the SRTM bias with respect to the highest laser points, we tried to define a ‘canopy surface’ (or top of canopy) from the laser points. This was defined arbitrarily by discarding points corresponding to intermediate elevations between the top of canopy and the ground, in order to eliminate short-scale fluctuations [1]. Basically, this algorithm selects laser points that are local maxima within a moving window along the laser profile. The optimal size of the window was found to be 56 m, i.e. nine laser points with 7-m spacing between them: it actually corresponds to the smallest size from which the laser elevation variogram no longer shows a nugget effect, and from which the ‘rapid’ local fluctuations are eliminated. After processing, we are left with a ‘top-of-canopy’ laser point every 25 m on average. Top-of-canopy laser points are displayed in Fig. 2. SRTM elevation was then compared to the elevation derived from the ‘top-of-canopy’ laser points. We found an average difference of 2.3 m for low elevations comprising for a large part marsh areas with a much lower tree density, and 8.5 m for higher elevations mainly corresponding to dense forest zones, giving an average of 4.3 m for the whole study area (SRTM elevation being lower than ‘top-of-canopy’ laser-point elevation). This bias corresponds to the vertical variation in vegetation cover within a radar pixel measuring 90 m × 90 m; penetration of the cover by the radar signal (low in C-band) must also be taken into account. Breit et al. found a bias between validation data and X-band SRTM DEM (X-band has a lower penetration than C-band) that varied from 2 m to 6.2 m in forested areas of western Germany, depending on ground relief (moderate relief and flat terrain, respectively) [3].
3.2 Statistical analysis
From a statistical point of view, it is a difficult task to compare the SRTM DEM with available validation data (IGN spot height and heliborne DEM). The SRTM DEM gives the average elevation, within 90 m × 90 m pixels, of the top of the vegetation cover (modulo a slight penetration), whereas the validation data gives a ground elevation. A quasi-systematic bias is thus observed between the SRTM data and the validation data, due to the forest cover. To quantify the accuracy of the DEM, we therefore prefer to use the standard deviation of the ‘elevation errors’, i.e. the difference between the SRTM elevation and the validation-data elevation.
Table 1 shows a comparison between SRTM and validation-data elevations. The overall difference between SRTM and heliborne elevations is about 26.5 m. If we add the bias between SRTM and top-of-canopy laser points, which is 7 m in the heliborne DEM zone, we obtain an estimated average top-of-canopy height of 33.5 m in this area. This is consistent with the average difference observed between the elevations of the top-of-canopy laser points and those of the heliborne DEM (33.2 m). The difference with the IGN spot heights is less (13.3 m), which gives an average canopy height of 17.6 m over the whole study area. This height is lower than the previous 33.5 m value because compared to the heliborne DEM that is located in a dense forest area; here many of the IGN spots are situated in areas – mainly flat and marshy – where the trees are lower or non-existent.
Standard deviation (accuracy) is 8.2 m when compared to the heliborne DEM, and 10.2 m when compared to IGN spot heights. The elevation error is found to be independent of the elevation value. We also notice that elevation errors range between and . These results are much better than those that where obtained with the RADARSAT DEM [1]: in fact, the standard deviation and the difference between maximum and minimum errors are divided by a factor greater than 2 (Table 1).
In conclusion, the accuracy of the SRTM is found to be about 10 m, and it has a bias between 2.3 m and 8.5 m with the ‘top-of-canopy’ surface. If we compute the linear error at the 90 confidence level (‘LE90’ in Table 1), we obtain 13.5 m when compared to the heliborne DEM, and 15.5 m when compared to IGN spot heights. This is in accordance with the announced accuracy for C-band SRTM DEM.
To check the dependency of the error with the terrain slope, we compared SRTM DEM to the local heliborne DEM, where a ‘true’ terrain slope can be calculated. The heliborne DEM area only represents 58 km2, but includes a part of the highest relief of the study zone (the Kaw mountain), as well as low elevations. It also includes small hills (Fig. 3a). The elevation difference between the SRTM DEM and the heliborne DEM was calculated for each SRTM pixel. To make the results easier to understand in terms of over- or under-estimation, we subtracted from this difference the overall bias of SRTM DEM compared to heliborne DEM, i.e. 26.5 m. Assuming that this overall bias corresponds to a quasi-constant canopy thickness, the difference corresponds to the ground level. The difference is then positive when the SRTM DEM (corrected from vegetation) is above ground level, and negative in the opposite case. Of course canopy thickness is not constant. In order to evaluate the possible bias introduced by this simplification, we estimated the canopy thickness in the heliborne area, by comparing top-of-canopy laser points to ground-level laser points (both derived from airborne laser data). Ground-level laser points were defined as laser points reaching (or nearly reaching) the ground level, and were calculated using a moving window algorithm described in [2]. We found that 82% of canopy heights in the heliborne area were ranging in the interval around the average canopy thickness. Taking into account the fact that these punctual variations are smoothed when considering average canopy thickness over 90-m pixels, the possible bias introduced by the quasi-constant thickness assumption is probably lower than 5 m. Consequently, a difference lower than 5 m can be partly or totally due to a variation of canopy thickness and not necessarily to a SRTM DEM error. This verification being done, terrain slope and slope aspect were calculated using a -pixel window around each initial pixel. The difference was found to be heavily influenced by the terrain slope and by the slope aspect (Fig. 3). Fig. 3a and b show that elevations are underestimated for slopes facing radar sensor (foreslopes, northwest) and are overestimated in the opposite direction (backslopes, southeast). For intermediate directions, the difference is generally close to zero. For a given slope aspect, the absolute value of the error and the standard deviation of the error tend to increase almost linearly with the terrain slope (Fig. 3c and d). These results are in accordance with previous papers [8,9,12].
We also note that SRTM seems to smooth the steepest slopes: the maximum slope in the SRTM DEM is 20.6° instead of 33.8° in the heliborne DEM (Table 2). The standard deviation of slope is also lower. The curvature (calculated here as the sum of the second derivative along the X axis and of the second derivative along the Y axis) is also smoothed for the SRTM DEM. In fact, the correlation factor between SRTM and heliborne DEMs drops from 0.99 for the elevation, to 0.85 for the slope and 0.51 for the curvature, showing that, as expected, minor errors on elevations can generate greater errors on derivatives (slope and curvature). Other types of comparisons have been attempted by other authors to evaluate SRTM DEM accuracy, including spectral analysis [10], but have not been tested here.
Statistics on slope and curvature for the Heliborne DEM and the SRTM DEM
Statistiques sur les pentes et les courbures du MNT hélicoptère et du MNT SRTM
| Variable | No. of comparison points | Mean | Standard deviation | Minimum | Maximum |
| HELIBORNE DEM Slope (deg) | 7125 pixels of 90 m × 90 m | 5.7 | 4.4 | 0 | 33.8 |
| SRTM DEM Slope (deg) | 7125 pixels of 90 m × 90 m | 6.3 | 4.1 | 0 | 20.6 |
| HELIBORNE DEM Curvature | 7125 pixels of 90 m × 90 m | 0 | 0.19 | −1.13 | 1.12 |
| SRTM DEM Curvature | 7125 pixels of 90 m × 90 m | 0 | 0.17 | −0.75 | 0.61 |
3.3 Geostatistical analysis
Another way to assess the quality of SRTM data is to compare the variogram of SRTM elevation with that of airborne laser elevation. Relief zones were identified over the study area using the median airborne laser elevation in ‘blocks’, and selected as appropriate for zoning the relief in our study area [1]. Variograms [4] of the elevation were computed for each relief zone and for each data source: ‘top-of-canopy’ laser elevation (punctual), SRTM DEM (90 m ×90 m pixels), RADARSAT DEM (50 m × 50 m pixels). Fig. 4 shows that the SRTM variogram is always much closer to the airborne laser variogram than the RADARSAT variogram, thus showing a marked improvement. The SRTM variogram's behaviour is very similar to that of the laser data, whatever the relief zone. As the SRTM DEM represents an average elevation within 90 m × 90 m pixels, its variogram should be lower than that of the ‘top-of-canopy’ laser points. This is not the case for very low elevations (, Fig. 4a), corresponding mainly to rivers and marshy areas, because the satellite response is of a lower quality than the laser in low-relief areas. A similar phenomenon is observed for the RADARSAT data with, in addition, a more marked difference. In the case, the SRTM variogram becomes lower than the laser variogram, but not the RADARSAT variogram (Fig. 4b). In the other cases (, Fig. 4c, and , Fig. 4), the smoothing effect of the satellite (RADARSAT and SRTM) elevations is reflected by a constant difference between variograms where great distances are concerned (some 60 m2, for example, between the and the variograms). This effect is proportionally greater in the case where , because the value of the variogram is in the order of 150 m2 towards 1000 m (Fig. 4c), whereas it is 1500 m2 in the case where (Fig. 4d). It is thus the actual elevation that above all influences the value of the variogram.
4 Conclusions
We have evaluated the accuracy of a 90 m × 90 m C-band SRTM DEM on a study area in French Guiana. The SRTM DEM appears visually to be of good quality. Its accuracy (standard deviation of elevation errors) is found to be about 10 m, when compared to spot heights and a local accurate heliborne DEM. The elevation error at the 90% confidence level is about ±16 m. The SRTM bias, compared to that of ‘top-of-canopy’ laser points, is in the range 2.3 m to 8.5 m, the highest bias corresponding to dense forest areas. This bias incorporates the vertical variation in tree height within a radar cell, as well as a slight penetration of the radar signal in C-band. Elevations are underestimated for slopes facing radar sensor (foreslopes) and are overestimated in the opposite direction (backslopes). For a given slope aspect, elevation errors increase almost linearly with terrain slope. At last, the slopes tend to be smoothed, especially the highest ones.
Acknowledgements
The present study was funded by BRGM (French Geological Survey). The RADARSAT data were provided free of charge as part of the ADRO2 program of the Canadian Space Agency. The heliborne DEM used was built by the company ALTOA on behalf of the mining company ASARCO. We would also like to thank Catherine Truffert, José Perrin and Philippe Daniels for their support, as well as the two anonymous reviewers for their comments.


