Expériences de drainage et estimation de paramètres en milieu poreux non saturé

Hussein Beydoun; François Lehmann

doi:10.1016/j.crte.2005.12.004

Géosciences de surface (Hydrologie–Hydrogéologie)

Expériences de drainage et estimation de paramètres en milieu poreux non saturé

Présenté par : Ghislain de Marsily

Hussein Beydoun ¹ ; François Lehmann ¹

¹ Institut de mécanique des fluides et des solides, UMR ULP–CNRS 7507, 2, rue Boussingault, 67000 Strasbourg, France

Comptes Rendus. Géoscience, Volume 338 (2006) no. 3, pp. 180-187.

Résumés

Français
Anglais

Les paramètres hydrodynamiques d'un sable sont estimés par approche inverse, en utilisant les observations de deux expériences de drainage en milieu homogène. Nos résultats, fondés sur l'analyse des sensibilités et des incertitudes sur les paramètres, montrent que (i) les données de teneur en eau sont indispensables pour estimer tous les paramètres de la courbe de rétention du modèle de van Genuchten–Mualem, (ii) la conductivité hydraulique à saturation ( $K_{s}$ ) est peu sensible aux données de pression et insensible aux autres mesures (teneur en eau et quantité d'eau drainée), (iii) l'approche inverse utilisée peut être vérifiée en comparant la quantité d'eau drainée simulée à celle mesurée.

Two drainage experiments were carried out to identify the hydraulic parameters of a quartz sand by using inverse modelling. Our results, based on sensitivity and error analyses, show that (i) water content measurements are essential to estimate the parameters of the van Genuchten–Mualem retention curve, (ii) the saturated conductivity ( $K_{s}$ ) has a low sensitivity to pressure data and is not sensitive to other measures (water content and measured outflow), (iii) the inverse approach can be verified by comparing the simulated outflow to the measured one.

Métadonnées

Reçu le : 2005-04-01
Accepté le : 2005-12-11
Publié le : 2006-02-01

DOI : 10.1016/j.crte.2005.12.004

Mot clés : Paramètres hydrodynamiques, Expériences de drainage, Approche inverse
Keywords: Hydraulic properties, Drainage experiment, Inverse

Affiliations des auteurs :

Hussein Beydoun ¹ ; François Lehmann ¹

¹ Institut de mécanique des fluides et des solides, UMR ULP–CNRS 7507, 2, rue Boussingault, 67000 Strasbourg, France

@article{CRGEOS_2006__338_3_180_0,
     author = {Hussein Beydoun and Fran\c{c}ois Lehmann},
     title = {Exp\'eriences de drainage et estimation de param\`etres en milieu poreux non satur\'e},
     journal = {Comptes Rendus. G\'eoscience},
     pages = {180--187},
     publisher = {Elsevier},
     volume = {338},
     number = {3},
     year = {2006},
     doi = {10.1016/j.crte.2005.12.004},
     language = {fr},
}

TY  - JOUR
AU  - Hussein Beydoun
AU  - François Lehmann
TI  - Expériences de drainage et estimation de paramètres en milieu poreux non saturé
JO  - Comptes Rendus. Géoscience
PY  - 2006
SP  - 180
EP  - 187
VL  - 338
IS  - 3
PB  - Elsevier
DO  - 10.1016/j.crte.2005.12.004
LA  - fr
ID  - CRGEOS_2006__338_3_180_0
ER  -

%0 Journal Article
%A Hussein Beydoun
%A François Lehmann
%T Expériences de drainage et estimation de paramètres en milieu poreux non saturé
%J Comptes Rendus. Géoscience
%D 2006
%P 180-187
%V 338
%N 3
%I Elsevier
%R 10.1016/j.crte.2005.12.004
%G fr
%F CRGEOS_2006__338_3_180_0

Hussein Beydoun; François Lehmann. Expériences de drainage et estimation de paramètres en milieu poreux non saturé. Comptes Rendus. Géoscience, Volume 338 (2006) no. 3, pp. 180-187. doi : 10.1016/j.crte.2005.12.004. https://comptes-rendus.academie-sciences.fr/geoscience/articles/10.1016/j.crte.2005.12.004/

Version originale du texte intégral

Abridged English version

1 Introduction

Unsaturated water flow in porous media is classically modelled by Richards' equation. The capillary pressure h, the water content θ, and the hydraulic conductivity K of the porous media appear in this equation. Richards' equation becoming strongly nonlinear in unsaturated zone, its resolution requires the knowledge of the two relations $θ (h)$ and $K (h)$ . These expressions depend on the intrinsic hydraulic parameters of the porous medium. Some of these parameters are physically measurable, whereas some others need indirect evaluation. Conventional methods to determine the relations $θ (h)$ and $K (h)$ exist and are often applied under steady-state conditions that are difficult to realize [4]. Moreover, it is not possible to obtain these two relations with the same experimental device under a steady state [2]. The disadvantages of these methods were discussed by Salehzadeh and Demond [11]. During the last years, inverse parameter identification under transient conditions became increasingly employed. It allows us to determine simultaneously both relations $θ (h)$ and $K (h)$ by finding the minimum of an objective function expressing the quadratic differences between measured and predicted values using an optimization procedure.

At the laboratory scale, the most popular identification methods are one-step [5] or multistep outflow experiments [12]. They are generally applied to soil samples of very small volumes. Few experiments are carried out on large columns [9]. In many cases, the physically measurable parameters, like saturated hydraulic conductivity, residual and saturated water content, are not estimated by the inverse procedure, but are fixed at values determined from conventional measurement techniques. Therefore, these measured values are not given at the same scale as the others.

The objective of this study is to identify all the necessary hydraulic parameters of a sand (Table 1), needed to simulate the flow in unsaturated porous media. The aim is also to evaluate the parameters uncertainty and the model sensitivity to the measurements.

Sable	Diamètre des grains (mm)	$θ_{s}$ (–)	Densité apparente sèche (–)
K30	$d_{10} = 0, 339$ ; $d_{50} = 0, 493$ ; $d_{60} = 0, 541$	0,38	1,63

2 Experimental device

An experimental system enabling the simulation of the water flow in a vertical column of 10-cm diameter and 1-m height is placed in a conditioning chamber in order to reduce the temperature fluctuations. The column is placed over a 7-mm-thick porous ceramic plate and then filled with sand up to a height of 1.10 m. Pressure sensors and capacitive probes are installed at ten equidistant levels. The outflow Q is weighted with a numerical balance. The data acquisition of the state variables ( $θ, h$ , and Q) is performed by a computer with a time step in accordance with the evolution of the recording signal (from 10 s to every hour). Two drainage experiments (Exp1 and Exp2) were carried out in an identical way by applying pressure steps at the bottom of the column.

3 Numerical model

The governing equation for vertically flow in an unsaturated porous medium is given by the mixed form of the Richards' equation (Eq. (1)). Its solution is obtained with the Galerkin finite element method using an implicit finite difference scheme in time. The resulting non-linear problem is solved using a Newton–Raphson iterative technique [7]. The water retention curve and the unsaturated hydraulic conductivity function are given by the commonly used van Genuchten–Mualem model [8,13].

The optimization procedure minimize the sum of weighted squared residuals between observed and simulated state variables in order to obtain an estimate of the hydraulic parameters using the objective functions given by Eq. (4). Kool and Parker [5] determined weighting coefficients by using the mean measured values of pressure head, water content and/or the outflow volume. Therefore, the mean measured values of pressure head may be zero when the considered medium is variably saturated. For that, we developed a new formulation allowing us to normalize the different sets of measurements by dividing by the maximal squared differences between the measured values (Eq. (5)).

Minimization of the objective function is based on the Levenberg–Marquardt nonlinear minimization technique [5]. Once the acceptable minimum has been found, it is interesting to analyze the value of the objective function for each type of observation – pressure head $ϕ (h)$ , water content $ϕ (θ)$ and weighted outflow $ϕ (Q) -$ , even for those that were not used in the optimization procedure.

A detailed error analysis of the final residuals and estimated parameters has been conducted by calculating the covariance matrix of the standard errors in the estimated parameter (Eq. (6)) and the correlation coefficients (Eq. (7)). The conditions of parameter identifiability [3,5] were investigated by evaluating the composite sensitivity ratios γ (Eq. (9)).

4 Results, discussions and conclusion

Measured data are introduced in inverse procedure to estimate the sand hydraulic properties described by five parameters { $K_{s}, θ_{r}, θ_{s}, α, n}$ in the van Genuchten–Mualem model.

Several scenarios were studied in order to evaluate the role of the porous plate, the importance and the influence of the type of observations introduced into the objective function. For the inverse modelling problem (nine simulations on the whole, Table 2), we took as initial parameters those of a sand following the classification of the U.S. Department of Agriculture [1]. The first eight simulations (Sim1 to Sim8) are carried out with the data obtained in the first experiment. The ninth simulation, Sim9( $θ - h$ ), is carried out with measurements obtained in the second experiment (Exp2) and by using measurements of pressure head (h) and water content (θ). For Sim1, the large values of $ϕ (h)$ and $ϕ (θ)$ show the need for identifying the saturated hydraulic conductivity of the porous plate (Table 2). This is related to the fact that the flow in the column is conditioned by the saturated hydraulic conductivity of the porous plate.

Paramètres	$K_{s}$ (cm h⁻¹)	$K_{s} (P)$ (cm h⁻¹)	$θ_{r}$ (–)	$θ_{s}$ (–)	α (cm⁻¹)	n (–)	$ϕ (y; p)$ (–)	$ϕ (h)$ (–)	$ϕ (θ)$ (–)	$ϕ (Q)$ (–)
Initiaux	29,7	0,03096	0,045	0,43	0,145	2,68	321,19	5,91	131,31	183,97
Sim1(θ−h−Q)	0,57 ± 0,70	0,03096 (fixé)	0,028 ± 0,158	0,377 ± 0,053	0,040 ± 0,023	10,06 ± 23,61	16,31	7,79	8,31	0,21
Sim2(θ−h)	39,53 ± 262,92	0,00312 ± 0,00151	0,086 ± 0,041	0,376 ± 0,022	0,052 ± 0,023	7,47 ± 6,61	2,58	0,79	1,79	0,04
Sim3(θ−h−Q)	43,37 ± 252,48	0,003 ± 0,0013	0,087 ± 0,039	0,375 ± 0,021	0,053 ± 0,022	7,45 ± 6,60	2,61	0,79	1,79	0,03
Sim4(h−Q)	30,78 ± 294,45	0,0031 ± 0,0008	0,078 ± 320889	0,346 ± 320888	0,064 ± 0,036	5,33 ± 12,49	0,63	0,56	17,34	0,07
Sim5(θ−Q)	106,73 ± 4506	0,00301 ± 0,0023	0,088 ± 0,017	0,375 ± 0,017	0,054 ± 0,044	7,45 ± 7,84	2,69	0,90	1,78	0,01
Sim6(θ)	98,77 ± 3938	0,00302 ± 0,003	0,088 ± 0,077	0,376 ± 0,018	0,054 ± 0,069	7,37 ± 9,95	3,70	0,88	3,70	0,02
Sim7(h)	507,58 ± 134748	0,0069 ± 1837	0,031 ± 351871	0,562 ± 413731	0,07433 ± 0,088	6,07 ± 21,13	0,52	0,52	209,3	52,8
Sim8(Q)	1500 ± 86421	0,0030 ± 0,0002	0,055 ± 134318	0,369 ± 134318	0,056 ± 0,021	2,93 ± 4,27	0,002	20,90	6,94	0,002

Sim9(θ−h) Exp2	13,55 ± 58,38	0,0029 ± 0,0013	0,076 ± 0,047	0,372 ± 0,020	0,052 ± 0,021	7,39 ± 4,71	2,09	0,56	1,53	0,31

Simulations Sim4( $θ - h$ ), Sim7(h) and Sim8(Q) (Table 2) give large uncertainties on the parameters $θ_{r}$ and $θ_{s}$ and strong correlations between the parameters as well as a large variation $ϕ (θ)$ for the water contents (Table 2). This shows the need for introducing into the objective function the measurements of water content or for fixing the parameters $θ_{s}$ and $θ_{r}$ [6]. All simulations Sim2( $θ - h$ ), Sim3( $θ - h - Q$ ), Sim5( $θ - Q$ ), Sim6(θ) and Sim9( $θ - h$ ; Exp2) use measurements of water contents and provide very satisfactory results (Table 2).

For Sim5( $θ - h$ ) and Sim6(θ), the coefficients γ calculated for the parameter $K_{s}$ (Table 3) are much lower than 0.01. Therefore, this parameter is not identifiable with water contents and weighted outflow measurements only. Other calculated coefficients γ show that the other estimated parameters are more easily identifiable. For Sim2( $θ - h$ ), Sim3( $θ - h - Q$ ) and Sim9( $θ - h$ ; Exp2), the use of the measured pressure head compared to Sim5( $θ - Q$ ) and Sim6(θ) make it possible to estimate the parameter $K_{s}$ with a value of the coefficient γ close to 0.01. Uncertainty on $K_{s}$ is very significant, which shows that a reliable estimate of this parameter is difficult. Other coefficients γ are significantly larger than 0.01 (Table 3). For Sim2( $θ - h$ ), Sim3( $θ - h - Q$ ), Sim5( $θ - Q$ ), Sim6(θ) and Sim9( $θ - h$ ; Exp2), all the correlation coefficients are lower than the breaking value of 0.95 data given by Hill [3]. Parameters estimated for Sim2( $θ - h$ ) and Sim9( $θ - h$ ; Exp2) indicate weak correlations between them and are not very different from one experiment to another. These results make it possible to appreciate the reproducibility of the experiments. For Sim6(θ), the measured water contents, introduced only into the inverse approach, are sufficient to estimate reasonably the parameters $θ_{s}$ , $θ_{r}$ , α, and n. The simulated outflow, close to the measured one, is used to check the inverse approach.

γ	$K_{s}$	$K_{s} (P)$	$θ_{r}$	$θ_{s}$	α	n
Sim2(θ−h)	0,013	0,298	0,161	1	0,341	0,099
Sim3(θ−h−Q)	0,013	0,306	0,165	1	0,336	0,098
Sim5(θ−Q)	0,003	0,304	0,169	1	0,304	0,065
Sim6(θ)	0,003	0,298	0,165	1	0,303	0,066
Sim9(θ−h) Exp2	0,018	0,306	0,136	1	0,336	0,107

The results obtained by the inverse approach show that it is possible to estimate the hydraulic parameters of an unsaturated homogeneous porous medium starting from only one experimental device. However, saturated hydraulic conductivity of sand is less identifiable and cannot be estimated with a high degree of accuracy by this type of experiment. The use of measurements of water content is essential to estimate the sand hydraulic parameters and sufficient to determine the parameters of the water retention curve $θ (h)$ .

1 Introduction

L'essentiel des transferts assurant le renouvellement et/ou la dégradation des ressources en eaux souterraines se fait à travers les sols et la zone non saturée de l'aquifère [10]. L'écoulement d'eau en milieu poreux saturé/non saturé est modélisé d'une manière classique par l'équation de Richards. Cette équation fait intervenir la pression de la phase eau h, la teneur en eau θ et la conductivité hydraulique K du milieu. L'équation de Richards devenant fortement non linéaire en milieu non saturé ; sa résolution nécessite la connaissance des deux relations $θ (h)$ et $K (h)$ . Dans ces relations interviennent des paramètres hydrodynamiques caractérisant le milieu poreux. Des méthodes conventionnelles pour construire les relations $θ (h)$ et $K (h)$ existent et sont souvent appliquées sous des conditions d'équilibre hydrostatique difficiles à réaliser [4]. En plus, elles ne permettent pas de représenter ces deux fonctionnelles à partir d'un même dispositif expérimental [2]. Les inconvénients de ces méthodes ont été discutés par Salehzadeh et Demond [11]. Au cours des dernières années, l'identification des paramètres par approche inverse, en conditions d'écoulement transitoire, est devenue de plus en plus employée. Cette approche permet une estimation simultanée des fonctionnelles $θ (h)$ et $K (h)$ , en minimisant une fonction objectif représentant les écarts quadratiques entre les observations et les simulations à l'aide d'un algorithme d'optimisation.

Les méthodes d'identification les plus utilisées en laboratoire sont les dispositifs expérimentaux de drainage à paliers de pression unique [5] ou multiples [12]. Elles sont généralement appliquées à des échantillons de sol de très petit volume. Peu d'expériences sont réalisées sur des colonnes de plus grande dimension [9]. Dans de nombreux cas, les paramètres physiquement mesurables, comme la conductivité hydraulique à saturation, la teneur en eau résiduelle et la teneur en eau à saturation ne sont pas estimés par approche inverse, mais fixés aux valeurs déterminées par des techniques de mesure classiques. Par conséquent, ces valeurs mesurées ne sont pas déterminées à la même échelle que les autres. Dans cette étude, nous utilisons deux expériences de drainage sur une colonne en laboratoire, en milieu homogène, pour identifier tous les paramètres nécessaires à la modélisation d'écoulements en milieu poreux non saturé en eau. Il s'agit également d'estimer les incertitudes sur ces paramètres et d'analyser leurs sensibilités par rapport aux quantités mesurées.

2 Description du dispositif expérimental

Un dispositif expérimental permettant de simuler les transferts d'eau dans une colonne verticale de dix centimètres de diamètre et de 110 cm de hauteur a été mis en place dans une enceinte climatisée, afin de limiter les fluctuations de température. La colonne, posée sur une plaque céramique poreuse, est remplie de sable sur une hauteur de 1 m. Des capteurs de pression et des sondes capacitives mesurant la teneur en eau sont installés à différentes hauteurs par rapport à la surface du sable (neufs points de mesure $z_{1} = 90 cm$ , $z_{2} = 80 cm$ , $z_{3} = 70 cm$ , $z_{4} = 60 cm$ , $z_{5} = 50 cm$ , $z_{6} = 40 cm$ , $z_{7} = 30 cm$ , $z_{8} = 20 cm$ et $z_{9} = 10 cm$ ). La mesure de pression est réalisée en couplant, par l'intermédiaire d'un tube en plexiglas, un capteur de pression à une bougie en céramique poreuse de la société SoilMoisture (réf. 0652X03-B01M3). La masse d'eau cumulée en sortie de colonne est déterminée par pesée continue à l'aide d'une balance. La colonne est initialement saturée en eau par imbibition. La température de l'enceinte est maintenue constante à 13 °C pendant toute la durée de l'expérience, pour éviter tout dégazage. Une lame d'eau de quelques centimètres submerge le milieu poreux avant de commencer l'expérience de drainage. À partir d'un même sable de quartz monodisperse de coefficient d'uniformité de 1,6, dénommé K30 (Tableau 1), deux expériences de drainage (Exp1, Exp2) ont été réalisées, de façon identique, en appliquant des paliers de dépression à la base de la colonne (de 60, 30, 0 et $- 30 cm$ en termes de hauteur de colonne d'eau) à l'aide d'un déversoir. L'acquisition des données est assurée par un ordinateur et fixée selon l'évolution du signal d'enregistrement (de 10 s à toutes les heures). Elle permet de suivre les variations temporelles de la pression $h (t)$ et de la teneur en eau $θ (t)$ aux différentes hauteurs fixées, ainsi que la masse d'eau drainée cumulée à la sortie du déversoir. L'incertitude type composée sur la mesure donnée par le constructeur est de l'ordre de 2 cm pour les capteurs de pression et de 1 g pour la balance. La teneur en eau à saturation $θ_{s}$ est déterminée par pesée sur un échantillon de diamètre 10 cm, identique à celui de la colonne et de hauteur 20 cm. L'étalonnage des sondes capacitives est établi par comparaison directe avec des mesures de teneur en eau pondérale et de masse volumique apparente sèche. L'incertitude type composée sur la mesure de teneur en eau est estimée à 1% après étalonnage. La teneur en eau à saturation de la plaque poreuse $θ_{s} (P)$ est également déterminée par pesée et correspond à celle fournie par le constructeur (0,45 cm cm⁻³). La conductivité hydraulique à saturation de la plaque poreuse $K_{s} (P)$ donnée par le constructeur est de $8, 6 \times 10^{−8} m s^{−1}$ (0,03096 cm h⁻¹). Une fois saturée en eau, cette plaque reste en permanence saturée, sa pression d'entrée d'air étant de 1 bar.

3 Le modèle mathématique

L'écoulement en milieu poreux non saturé est décrit par l'équation de Richards sous sa forme mixte :

\frac{\partial θ}{\partial t} = div [K (h) (\frac{\partial h}{\partial z} - 1)]

(1)

où θ est la teneur en eau [L L⁻³], h la pression de l'eau [L⁻¹], K la conductivité hydraulique [L T⁻¹], z la profondeur orientée vers le bas [L]. Les conditions initiales et aux limites appropriées au système combiné sable–plaque poreuse sont utilisées en fonction de la lame d'eau initiale et de la dépression appliquée à la base de la colonne.

La discrétisation spatiale de l'équation de Richards est réalisée en utilisant la méthode des éléments finis de type Galerkin, avec un schéma en différences finies totalement implicite en temps. L'équation est ensuite linéarisée par la méthode de Newton–Raphson [7]. Les relations $θ (h)$ et $K (h)$ nécessitent la connaissance des paramètres de van Genuchten–Mualem [8,13] :

{\begin{matrix} S_{e} = \frac{θ - θ_{r}}{θ_{s} - θ_{r}} = \frac{1}{{[1 + {(α | h |)}^{n}]}^{m}} & pour h < 0 et m = 1 - \frac{1}{n} \\ S_{e} = 1 & pour h ⩾ 0 \end{matrix}

(2)

K (h) = K_{s} S_{e}^{0, 5} {[1 - {(1 - S_{e}^{1 / m})}^{(m)}]}^{2}

(3)

θ_{r}

la teneur en eau résiduelle [L L⁻³],

θ_{s}

la teneur en eau à saturation, n un paramètre du modèle lié à la distribution des tailles de pores [–], α un paramètre du modèle dont l'inverse correspond à la pression d'entrée d'air [L⁻¹] et

K_{s}

la perméabilité à saturation.

4 Procédure d'optimisation

La procédure d'optimisation consiste à minimiser les écarts quadratiques entre les variables d'état mesurées et celles simulées, en utilisant la fonction objectif suivante :

ϕ (y; p) = \sum_{n = 0}^{n_{ty}} \sum_{j = 1}^{n_{y}} W_{y} {[{\hat{y}}_{j}^{n + 1} - y_{j}^{n + 1} (p)]}^{2}

(4)

où

n_{ty}

est le nombre de pas de temps de mesure,

n_{y}

le nombre de mesures à un temps donné (nombre de points × nature des mesures),

y_{j}^{n + 1} (p) = {h_{j}^{n + 1} (p); θ_{j}^{n + 1} (p)

;

Q_{j}^{n + 1} (p)}

les valeurs calculées et

{\hat{y}}_{j}^{n + 1}

mesurées au pas de temps

n + 1

et au

j^{e}

point de mesure.

p = {p_{k}} = {K_{s}, θ_{r}, θ_{s}, α, n}

est le vecteur des paramètres à identifier et

W_{y}

est le poids associé aux valeurs mesurées. Dans ce travail, nous utilisons une nouvelle formulation de ce poids :

W_{y} = {[\frac{1}{\max ({\hat{y}}_{j}^{n + 1}) - \min ({\hat{y}}_{j}^{n + 1})}]}^{2}

(5)

Cette formulation permet de normaliser les différents types de mesures (lame d'eau cumulée, teneur en eau et pression) en divisant par l'écart quadratique maximal des valeurs mesurées. Cette formulation est préférable à celle de Kool et Parker [5], qui fait intervenir la moyenne des valeurs mesurées en termes de pression ou de masse d'eau cumulée ou de teneur en eau. En effet, la moyenne des pressions en eau mesurées peut être nulle dans le cas d'une expérience en milieu saturé/non saturé.

La minimisation de la fonction objectif est résolue de façon itérative, un jeu initial de paramètres est donné par l'utilisateur. Il faut rechercher les corrections à apporter au jeu de paramètres courant, telles que la fonction objectif diminue. Le calcul se poursuit de façon itérative jusqu'à ce que la fonction objectif soit inférieure à un seuil de tolérance et/ou que les corrections à apporter au jeu de paramètres soient inférieures à un seuil de tolérance donné. Les corrections à apporter au jeu de paramètres courant sont calculées en utilisant l'algorithme de Levenberg–Marquardt [5]. La méthode des sensibilités exactes est utilisée pour le calcul de la matrice jacobienne, ainsi que pour le gradient de la fonction objectif [6]. À la fin du processus d'optimisation, il est intéressant de comparer les écarts quadratiques pour chaque type d'observation (pressions $ϕ (h)$ , teneurs en eau $ϕ (θ)$ et lame d'eau cumulée $ϕ (Q))$ , même celles qui n'ont pas été utilisées dans l'approche inverse.

Nous calculons également la matrice de covariance des paramètres (Cov) au voisinage du minimum donnée par la relation [3,5] :

Cov = {Cov}_{i j} = σ_{F}^{2} {(J^{T} W_{y} J)}^{−1}

(6)

avec

σ_{F}^{2} = ϕ (p_{f}) / (n_{t} - n_{p})

l'estimation de la variance des erreurs de mesure,

ϕ (p_{f})

la valeur de la fonction objectif pour le jeu final de paramètres

p_{f}

au voisinage du minimum.

n_{t} = n_{ty} \times n_{y}

est le nombre total d'observations et

n_{p} = 5

est le nombre de paramètres estimés. Le jacobien

J = \frac{\partial y_{j}^{n + 1}}{\partial p_{k}}

du système est calculé à partir des dérivées des variables d'état par rapport aux paramètres. Les racines carrées des éléments diagonaux de la matrice de covariance représentent une estimation des incertitudes sur les paramètres. Cette matrice de covariance permet de calculer la matrice de corrélation entre les paramètres :

Cor = {Cor}_{i j} = \frac{{Cov}_{i j}}{\sqrt{{Cov}_{i i} {Cov}_{j j}}}

(7)

Pour l'analyse des sensibilités [3], comme les paramètres ont des unités différentes, nous utilisons le coefficient de sensibilité adimensionnel

\frac{\partial y_{j}^{n + 1}}{\partial p_{k}} \cdot p_{k} W^{1 / 2}

. À partir de ce coefficient, nous définissons la sensibilité totale (ST) du paramètre

p_{k}

par :

{ST}_{k} = {[\frac{1}{n_{t}} \sum_{n = 0}^{n_{ty}} \sum_{j = 1}^{n_{y}} {(\frac{\partial y_{j}^{n + 1}}{\partial p_{k}} p_{k} W_{y}^{1 / 2})}^{2}]}^{1 / 2}

(8)

Pour une comparaison simplifiée des valeurs associées aux différents paramètres, un rapport ( $γ_{k}$ ) est défini par :

γ_{k} = \frac{{ST}_{k}}{\max (ST)}

(9)

Par conséquent, la valeur maximale de γ est l'unité. Un paramètre avec un γ très réduit ( $< 0, 01$ ) n'est probablement pas identifiable en utilisant les observations correspondantes [3].

5 Résultats et discussions

L'approche inverse est appliquée aux deux expériences pour estimer les cinq paramètres hydrodynamiques ( $K_{s}$ , $θ_{r}$ , $θ_{s}$ , α et n) du sable. Plusieurs scénarios sont élaborés pour évaluer le rôle de la plaque poreuse, ou l'importance et l'influence du type d'observations introduites dans la fonction objectif. Pour le calcul du problème inverse (neuf simulations au total – Tableau 2), nous avons pris comme paramètres initiaux ceux d'un sable suivant la classification de l'U.S. Department of Agriculture [1]. Les huit premières simulations (Sim1 à Sim8) sont réalisées à partir des données de la première expérience. La neuvième simulation, Sim9( $θ - h$ ), est réalisée avec les mesures de la deuxième expérience (Exp2) et en utilisant les mesures de pression en eau (h) et de teneur en eau (θ).

Pour la Sim1, la conductivité hydraulique à saturation de la plaque poreuse $K_{s} (P)$ est fixée à la valeur donnée par le constructeur et les observations de pression (h), de teneur en eau (θ) et de la lame d'eau cumulée (Q) sont introduites dans l'approche inverse (type $θ - h - Q$ ). Cette simulation donne des écarts importants de $ϕ (h)$ et $ϕ (θ)$ (Tableau 2). Ceci est lié au fait que l'écoulement dans le système en série sable–plaque poreuse est conditionné par la plaque poreuse. Par la suite, toutes les autres simulations sont réalisées en identifiant également $K_{s} (P)$ . La perméabilité de la plaque poreuse estimée (Tableau 2) est dix fois plus faible que celle donnée par le constructeur : cela provient du colmatage de la plaque poreuse par des particules d'argile. Ce colmatage a été observé après avoir vidé la colonne.

La Sim2 est réalisée avec les observations de type ( $θ - h$ ), la Sim3( $θ - h - Q$ ), la Sim4( $h - Q$ ), la Sim5( $θ - Q$ ), la Sim6(θ), la Sim7(h) et la Sim8(Q). Le nombre de mesures pour les pressions et les teneurs en eau est de 1071 chacune, correspondant à neuf points d'observation pour 119 pas de temps. Le nombre de mesures de la lame d'eau drainée cumulée est de 119.

Les simulations Sim4( $h - Q$ ), Sim7(h) et Sim8(Q) (Tableau 2) donnent de grandes incertitudes sur les paramètres $θ_{r}$ et $θ_{s}$ et de fortes corrélations entre les paramètres, ainsi qu'un grand écart $ϕ (θ)$ pour les teneurs en eau (Tableau 2). Ceci montre la nécessité d'introduire dans la fonction objectif les mesures de teneur en eau ou de fixer les paramètres $θ_{r}$ et $θ_{s}$ [6]. Il faut aussi remarquer que les mesures de la lame d'eau drainée cumulée permettent de diminuer sensiblement l'incertitude sur le paramètre n. Les simulations Sim2( $θ - h$ ), Sim3( $θ - h - Q$ ), Sim5( $θ - Q$ ), Sim6(θ) et Sim9( $θ - h$ ; Exp2) utilisent toutes les mesures de teneur en eau et donnent, dans l'ensemble, des résultats très satisfaisants. Les paramètres $θ_{s}$ , $θ_{r}$ , α et n obtenus sont du même ordre de grandeur (Tableau 2). Les incertitudes sur ces paramètres sont acceptables, elles varient entre 20 et 60% pour $θ_{r}$ , entre 40 et 130% pour α et n et elles sont de l'ordre de 5% pour $θ_{s}$ . Pour ces simulations, nous avons obtenu des écarts très faibles entre les valeurs simulées et celles observées (Figs. 1–3).

Fig. 1
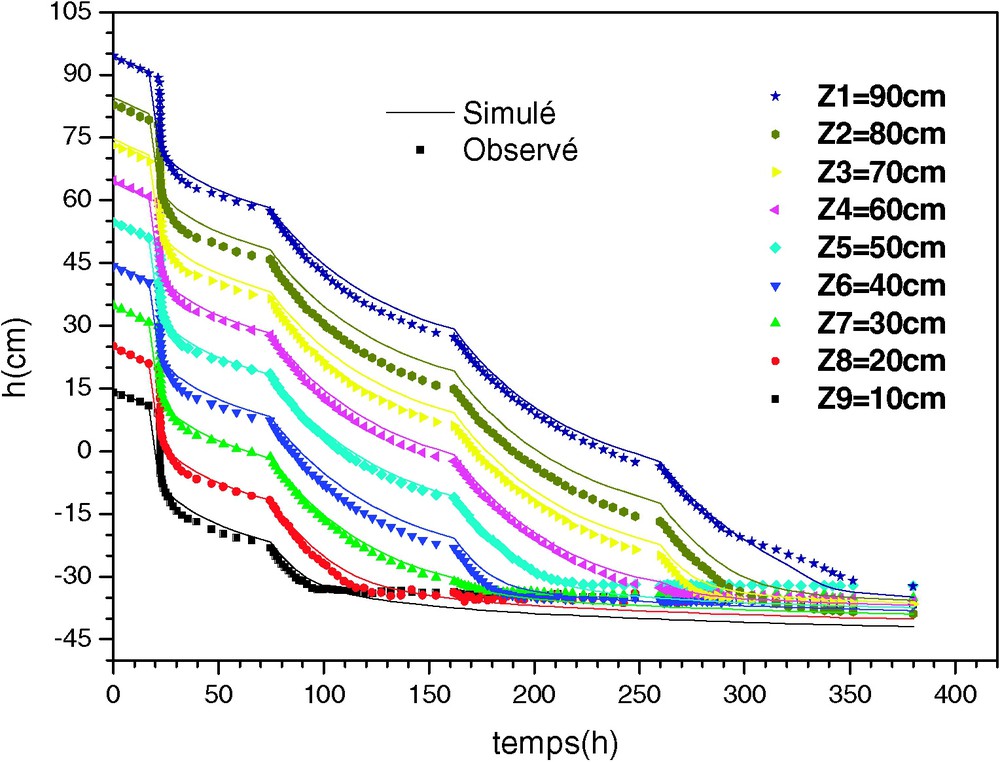
Évolution de la pression d'eau aux différentes profondeurs : Sim2(θ−h).
Time variation of water pressure at different levels: Sim2(θ−h).

Fig. 2
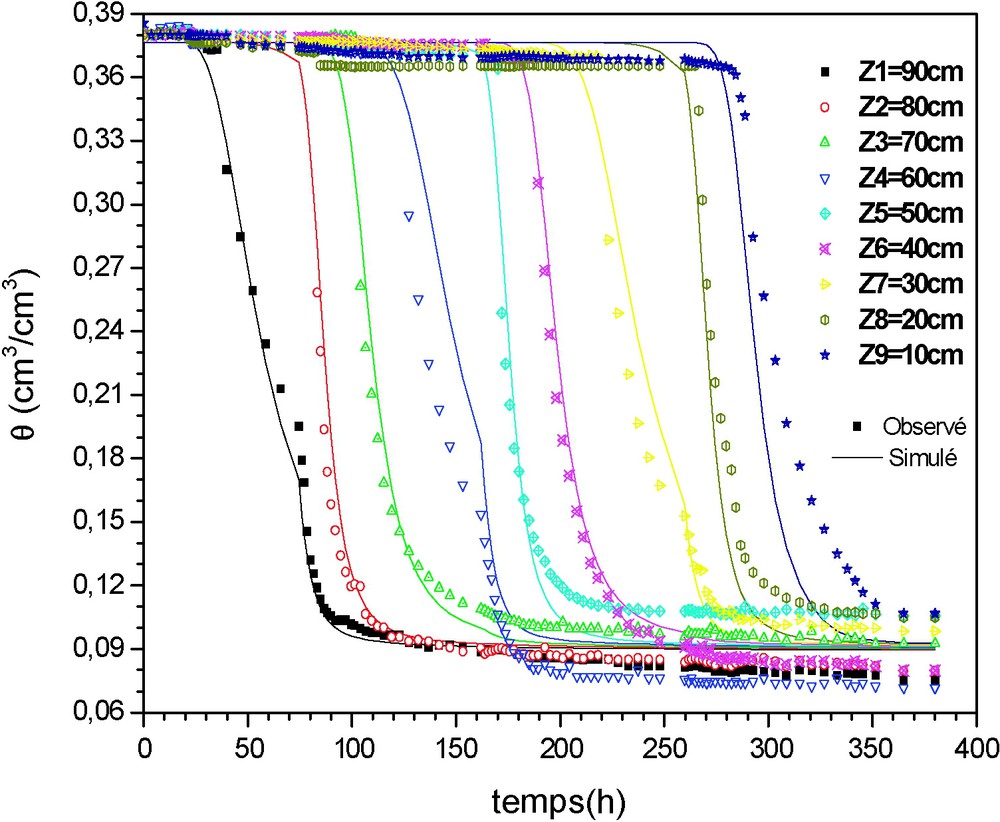
Évolution de la teneur en eau aux différentes profondeurs : Sim2(θ−h).
Time variation of water content at different levels: Sim2(θ−h).

Fig. 3
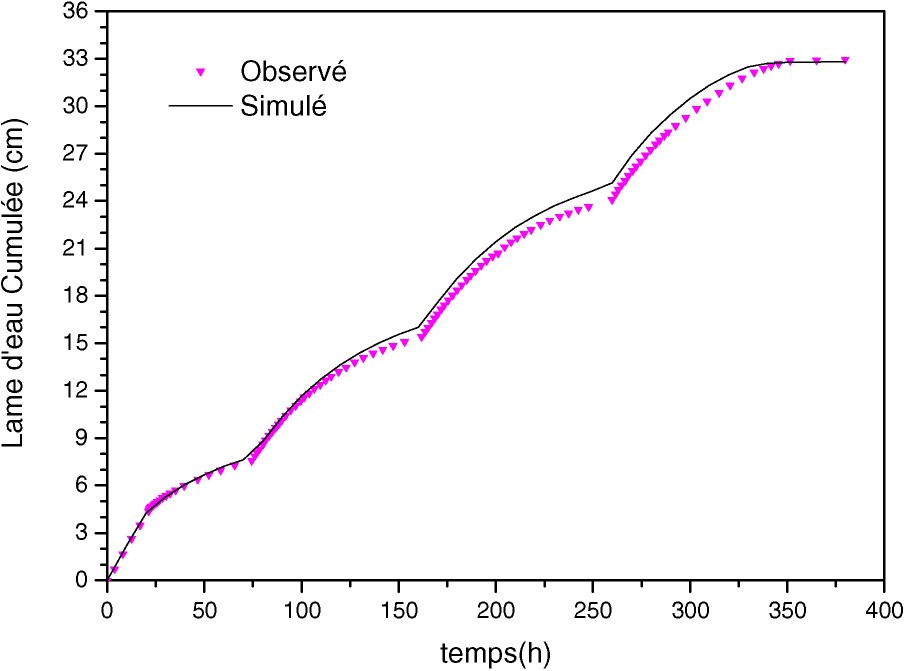
Évolution de la quantité d'eau drainée cumulée à la base de la colonne : Sim2(θ−h).
Time variation of the cumulated water outflow at the bottom of the column: Sim2(θ−h).

Pour les Sim5( $θ - Q$ ) et Sim6(θ), les coefficients γ calculés pour le paramètre $K_{s}$ (Tableau 3) sont largement inférieurs à 0,01. Par conséquent, ce paramètre n'est pas identifiable à partir des seules données de teneur en eau et de lame d'eau drainée cumulée. Les autres coefficients γ calculés montrent que les autres paramètres sont plus facilement identifiables.

Pour les Sim2( $θ - h$ ), Sim3( $θ - h - Q$ ) et Sim9( $θ - h$ ; Exp2), la présence des données de pression par rapport aux Sim5( $θ - Q$ ) et Sim6(θ) permet d'estimer le paramètre $K_{s}$ avec un coefficient γ calculé proche de 0,01. L'incertitude sur $K_{s}$ est très importante : elle montre qu'il est difficile d'estimer ce paramètre de façon fiable. Les autres coefficients γ calculés sont largement plus grands que 0,01 (Tableau 3).

Pour les simulations Sim2( $θ - h$ ), Sim3( $θ - h - Q$ ), Sim5( $θ - Q$ ), Sim6(θ) et Sim9( $θ - h$ ; Exp2), tous les coefficients de corrélation calculés sont inférieurs à la valeur critique de 0,95 donnée par Hill [3]. Les paramètres estimés pour les Sim2( $θ - h$ ) et Sim9( $θ - h$ ; Exp2) indiquent de faibles corrélations entre eux et sont peu différents d'une expérience à l'autre. Ces résultats permettent d'apprécier la reproductibilité des expériences.

Pour la Sim6(θ), les données de teneurs en eau introduites seules dans l'approche inverse sont suffisantes pour estimer de façon raisonnable les paramètres $θ_{s}$ , $θ_{r}$ , α et n. La lame d'eau drainée cumulée simulée, proche de celle mesurée, permet de vérifier l'approche inverse utilisée.

6 Conclusion

Les résultats obtenus par approche inverse montrent qu'il est possible d'estimer les paramètres hydrodynamiques d'un milieu poreux homogène non saturé à partir d'un seul dispositif expérimental. Cependant, la conductivité hydraulique à saturation du sable est peu identifiable et ne peut être estimée avec une grande précision par ce type d'expérience. L'estimation de la conductivité hydraulique à saturation de la plaque poreuse est indispensable pour une bonne estimation des paramètres hydrodynamiques du milieu. La nouvelle formulation des pondérations à associer aux observations permet de bien minimiser la fonction objectif et d'estimer les paramètres. L'utilisation des mesures de teneur en eau est indispensable pour estimer les paramètres hydrodynamiques et suffisante pour déterminer les paramètres de la courbe de rétention $θ (h)$ . La comparaison de la masse d'eau drainée cumulée simulée avec celle mesurée à la sortie de la colonne permet de vérifier l'approche inverse. Notons que, dans le cas d'un sable très fin, les informations sur les mesures de pression peuvent devenir plus importantes. Pour ce type de matériau, les dépressions seront plus grandes et les sensibilités vis-à-vis des pressions d'eau seront de l'ordre de celles obtenues en fin de drainage. D'autres expériences avec des sables plus fins et avec des milieux hétérogènes stratifiés sont envisagées et permettront de valider le dispositif expérimental et l'approche inverse utilisés.

Remerciements

Ce travail a bénéficié d'une aide financière recueillie dans le cadre du Programme national de recherche en hydrologie de l'Insu–CNRS. Une première version du manuscrit a été nettement enrichie et améliorée à la suite d'une expertise par Ghislain de Marsily et un autre rapporteur anonyme.

Bibliographie

[1] R.F. Carsel; R.S. Parrish Developing joint probability distributions of soil water retention characteristics, Water Resour. Res., Volume 24 (1988), pp. 755-769

[2] S. Finsterle; B. Faybishenko Inverse modelling of a radial multistep outflow experiment for determining unsaturated hydraulic properties, Adv. Water Resour., Volume 22 (1998), pp. 431-444

[3] M.C. Hill, Methods and guidelines for effective model calibration, U.S. Geological Survey Water-Resources Investigations Rep. 98-4005, U.S. Geol. Survey, Reston, VA, USA, 1998

[4] A. Klute; C. Dirksen Conductivities and diffusivities of unsaturated soils (A. Klute, ed.), Methods of Soil Analysis, Part 1, Physical and Mineralogical Methods, Agronomy Monograph, vol. 9, ASA and SSSA, Madison, WI, USA, 1986, pp. 687-734

[5] J.B. Kool; J.C. Parker Analysis of the inverse problem for transient unsaturated flow, Water Resour. Res., Volume 24 (1988), pp. 817-830

[6] F. Lehmann; Ph. Ackerer Determining soil hydraulic properties by inverse method in one-dimensional unsaturated flow, J. Environ. Qual., Volume 26 (1997), pp. 76-81

[7] F. Lehmann; P. Ackerer Comparison of iterative methods for improved solutions of the fluid flow equation in partially saturated porous media, Transp. Porous Media, Volume 31 (1998), pp. 275-292

[8] Y. Mualem A new model for predicting hydraulic conductivity of unsaturated porous media, Water Resour. Res., Volume 12 (1976), pp. 513-522

[9] G. Nützmann; M. Thiele; S. Maciejewski; K. Joswig Inverse modelling techniques for determining hydraulic properties of coarse-textured porous media by transient outflow methods, Adv. Water Resour., Volume 22 (1998), pp. 273-284

[10] P.-A. Roche; G. Billen; J.-P. Bravard; H. Décamps; D. Pennequin; E. Vindimian; J.-G. Wasson Les enjeux de recherche liés à la directive-cadre européenne sur l'eau, C. R. Geoscience, Volume 337 (2005), pp. 243-267

[11] A. Salehzadeh; A.H. Demond Apparatus for the rapid automated measurement of unsaturated soil transport properties, Water Resour. Res., Volume 30 (1994), pp. 2679-2690

[12] J.C. van Dam; J.N.M. Stricker; P. Droogers Inverse method for determining soil hydraulic functions from multi-step outflow experiments, Soil Sci. Soc. Am. J., Volume 58 (1994), pp. 647-652

[13] M. van Genuchten A closed-form equation for predicting the hydraulic conductivity of unsaturated soils, Soil Sci. Soc. Am. J., Volume 44 (1980), pp. 892-898

Commentaires - Politique