Analyse multi-échelle par ondelettes des contacts géologiques : application à la carte gravimétrique du Maroc nord-oriental

Driss Khattach; Hamid Mraoui; Driss Sbibih; Touria Chennouf

doi:10.1016/j.crte.2006.03.002

Résumés

Français
Anglais

L'application de l'analyse multi-échelle par ondelettes à la carte gravimétrique du Maroc nord-oriental a permis de cartographier les principaux contacts géologiques, en mettant en évidence le tracé, le sens du pendage et le degré d'importance des failles qui affectent la zone d'étude. Les résultats obtenus sont confirmés par les données sismiques ; ce qui atteste l'efficacité de la méthode, en particulier au niveau des plaines, où les méthodes structurales classiques sont inadaptées. La carte structurale établie permettra de mieux rationaliser les recherches hydrogéologiques ou minières à entreprendre dans le secteur d'étude.

The multiscale wavelet analysis has been applied to the gravity data from northeastern Morocco to map the major geological contacts, such us faults. Hence, the faults affecting the survey area were outlined with their importance level and dip direction. Seismic data confirm these results and testify the efficiency of this method, particularly in studying structure of plains. The structural map established is a very useful document in the planning of natural resources investigations (i.e. water, mines) to be undertaken in the area of study.

Abridged English version

In the last decade wavelet analysis has been proposed in various fields, including image processing such as geophysical potential-field images, mainly as an alternative to Fourier analysis. Potential field theory is suitable for multiscale wavelet analysis [1,4,6]. In this work we present an application of the wavelet analysis in mapping and multiscale analysis of geological contacts using gravity data.

The gravity field above the vertical contact between rocks of different densities shows a low on the side of the low-density rocks and a high on the side of the high-density rocks. The inflection point is located just above the contact, which is defined as a local extrema in horizontal derivative. In the case of a steeply dipping contact, the extrema stays close to the contact, but moves in the down dip direction.

Maxima from the magnitude of horizontal derivative of the Bouguer anomaly and its upward continuation at several heights show alignments outlining the contacts [5]. In the case of a dipping contact the maxima move down dip with increasing continuation height. By applying this approach to potential field theory, Moreau et al. [6] and Hornby et al. [4] have shown that, with the choice of an appropriate wavelet, derived from Green's function of gravitational acceleration, the measured potential field or its spatial derivatives can be treated as a wavelet transform of the source distribution.

Many traditional potential field operations have an elegant and compact expression in wavelet domain, the most obvious being the equivalence between the concept of change of scale and upward continuation. The reader is referred to Hornby et al. [4] for a formal presentation of the underlying theory, to Archibald et al. [1] for the application of multiscale edges to the enhanced visual interpretation of potential field data.

The particular wavelet transform of the gravitational acceleration at zero height can be calculated at scales $s > 1$ from measurements at height $z = z_{0}$ as follows:

(1) upward continue the measured field to a level $z = s z_{0}$ ;
(2) take the 2-D gradient in the $(x, y)$ plane;
(3) and multiply the resulting vector by the factor $s = z / z_{0}$ .

A code in the MATLAB system was made to perform the wavelet transform WT and to extract the multiscale contacts as local extrema of the WT, using Blakely and Simpson (1986) technique [2] for locating maxima of the magnitude of WT.

This method was applied to gravity data of the northeastern Morocco (Fig. 1). Inspection of the Bouguer anomaly map of the study area (Fig. 2) [5] shows that there are three major zones of anomalies extending in an ENE-direction: two gravity highs associated with an uplift of the Palaeozoic basement in the Beni-Snassen and Kebdana belts and a gravity low over the Triffa depression. These zones are bounded by strong gravity gradients.

Fig. 1
Schéma structural du Maroc nord-oriental.
Structural map of northeastern Morocco.

Fig. 2
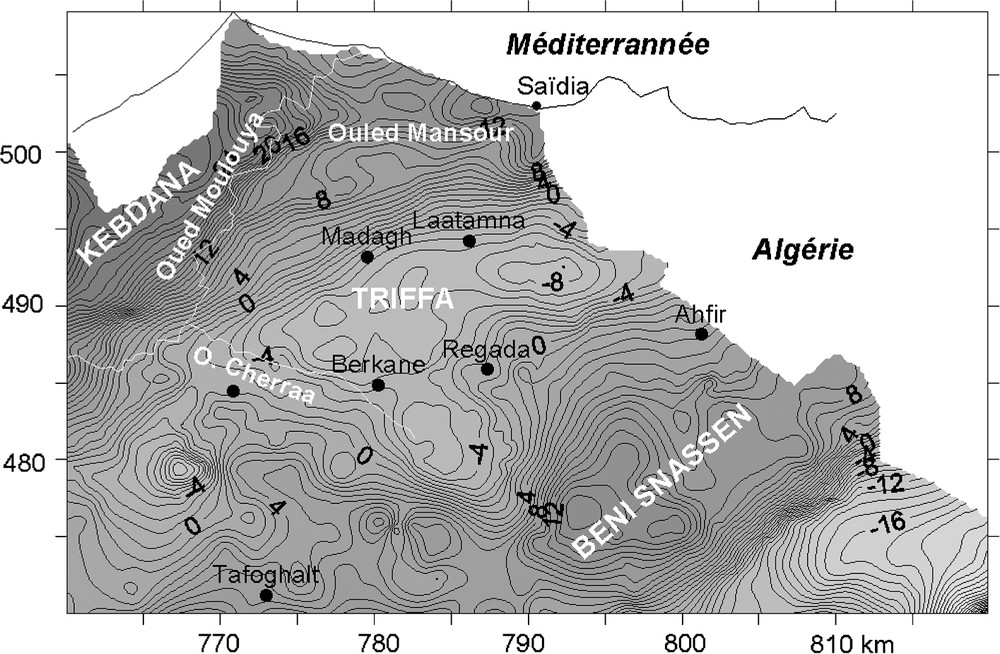
Carte gravimétrique de la zone d'étude (anomalies de Bouguer, densité de correction $d = 2, 2 g / {cm}^{3}$ , intervalle = 1 mGal).
Bouguer anomaly map (reduction density: 2.2 g/cm³). Minimum contouring interval is 1 mGal.

Maxima from the horizontal derivative of the Bouguer anomaly and its wavelet transform at several scales, up to $s = 12$ , are displayed in Fig. 3. They show alignments outlining the contacts. In the case of a dipping contact the maxima move down dip with increasing scales. The contacts, interpreted as faults, are plotted on Fig. 4 with three-importance level ( $s = 1$ , $s = 5$ and $s = 10$ ). The directions of the main faults (no 1 to 9) are NE–SW, ENE–WSW and NW–SE.

Fig. 3
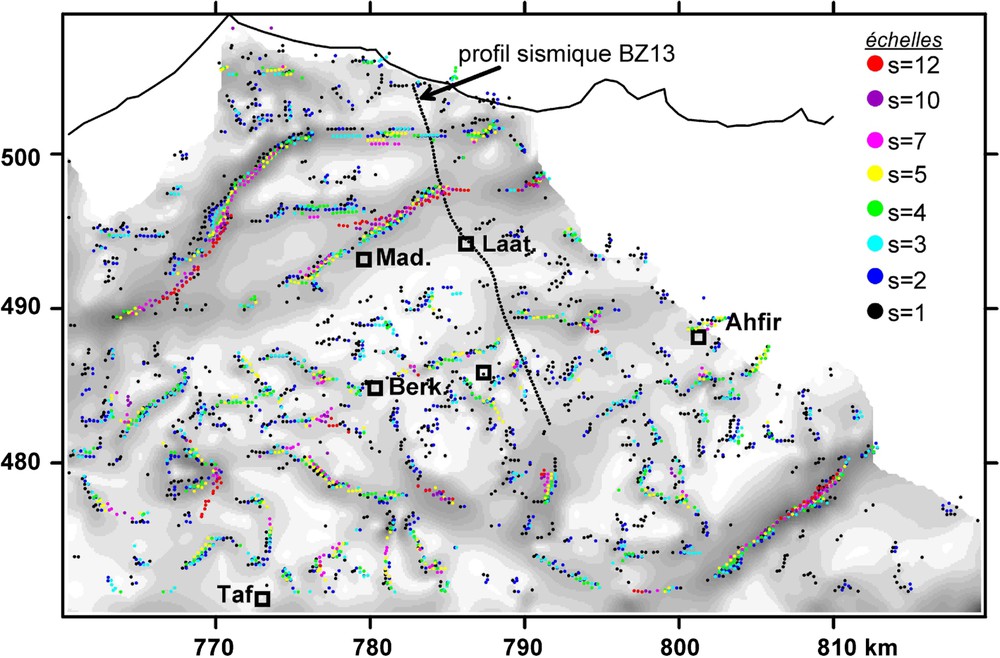
Représentation multi-échelle des contacts déterminés sur la carte gravimétrique (s : échelle ; en pointillés le profil sismique BZ13).
Multiscale edges calculated from the Bouguer anomaly (s: scale; in dots seismic line BZ13).

Fig. 4
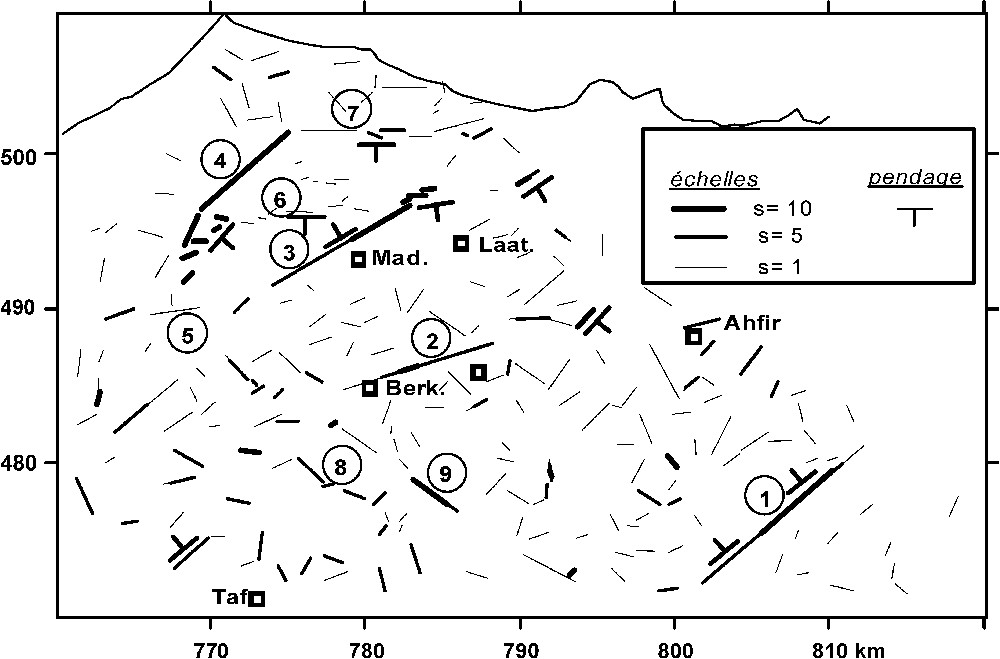
Tracé des failles interprétées sur la Fig. 3 ; l'épaisseur du trait est fonction du degré d'importance de ces failles.
Faults interpreted from Fig. 3; the line thickness is dependent on the importance level of these faults.

The BZ13 seismic section (Fig. 5) confirms these results; it shows structures in horsts and grabens broadsides by normal faults that affect the cover as well as the Palaeozoic basement with an apparent vertical throw which can reach the 300 milliseconds in double time.

Fig. 5
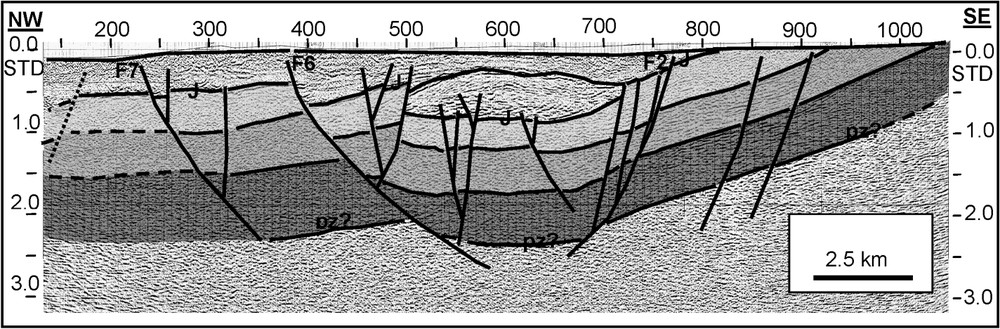
Section sismique montrant les principales failles interprétées (Pz : Paléozoïque, J : Jurassique, F : faille, voir Fig. 4).
Seismic section showing main faults interpreted (Pz: Paleozoic, J: Jurassic, F: fault, see Fig. 4).

The morphology of different structures raised seems to be guided by two fault directions families east–west and NE–SW. Results from this work show the importance of using wavelet transform of gravity data for mapping the geological contacts and their multiscale analysis.

They also provide new insights into the structure of the study area, particularly in the plain (northern part). The structural map is a very useful document in the planning of hydrogeological or mining research to be undertaken in the area of study.

1 Introduction

Durant la dernière décennie, l'analyse par ondelettes a été appliquée dans différents domaines, tels que dans le traitement d'images et en géosciences, comme une alternative à l'analyse de Fourier. En géophysique, ce traitement constitue l'analyse la plus moderne des champs de potentiel (gravimétrie et magnétisme) [1,4,6]. Nous présentons, dans cette note, une application des ondelettes à la cartographie et l'analyse multi-échelle des contacts géologiques, tels que les failles, à partir de données gravimétriques, en se fondant sur la méthode du gradient horizontal couplée à un changement d'échelle. La zone d'étude correspond au Maroc nord-oriental (Fig. 1) où nous disposons de données sismiques qui vont servir à valider les résultats obtenus par l'analyse de la carte gravimétrique.

2 Méthodologie

Les forts contrastes que montrent les données gravimétriques sont supposés résulter de discontinuités ou interfaces telles que les failles, les flexures, les contrastes des roches intrusives... Pour l'analyse des contacts entre les structures géologiques, on utilise classiquement les méthodes fondées sur la localisation des maxima locaux du module du gradient horizontal [2] ou total (signal analytique) [7], ou bien la méthode de la déconvolution d'Euler [8]. Cette dernière technique permet, en plus de la localisation dans le plan horizontal des contacts, une estimation de leur profondeur.

Le champ gravimétrique, au-dessus d'un contact vertical, mettant en présence des roches de densité différente est matérialisé par un bas du côté des roches de faible densité et un haut du côté des roches de haute densité. Le point d'inflexion se trouvera à l'aplomb de ce contact vertical. On peut se servir de cette caractéristique des anomalies gravimétriques pour localiser les changements abrupts de densité. Si le contact a un pendage, les maxima des gradients horizontaux se déplacent du côté du pendage, mais ceux-ci resteront cependant près de ce contact pour des valeurs de pendage élevées.

Pour déterminer le sens du pendage des différents contacts, on prolonge la carte de Bouguer vers le haut à différentes altitudes. À chaque niveau, les maxima du gradient horizontal sont localisés. En principe, les niveaux de prolongement les plus élevés correspondent aux contacts les plus profonds et vice versa. Si les structures sont verticales, tous les maxima se superposent. En revanche, le déplacement des maxima avec le prolongement vers le haut indique le sens du pendage.

La théorie du potentiel se prête parfaitement à une analyse multi-échelle par les ondelettes. Par le choix d'une ondelette appropriée [4,6], dérivant de la fonction de Green de l'accélération gravitationnelle, les mesures du champ de potentiel ou de ses dérivées spatiales peuvent être traitées comme une transformée en ondelettes. En effet, cette analyse unifie différentes techniques classiques : elle traite des gradients qui ont été prolongés vers le haut à une série d'altitudes. Les expressions des différentes opérations classiques sur le champ de potentiel prennent une forme compacte et élégante dans le domaine des ondelettes ; la plus importante est l'équivalence entre le concept de changement d'échelle et le prolongement vers le haut. En effet, la transformée en ondelettes de l'accélération gravitationnelle $g_{0} (x, y)$ à une certaine échelle $s = z / z_{0}$ , peut être obtenue à partir des mesures faites sur le niveau $z_{0}$ par [2] :

(1) prolongement vers le haut à $z = s z_{0}$ ;
(2) calcul du gradient horizontal ;
(3) multiplication par s.

Pour une analyse multi-échelle des contacts, il suffit donc de chercher les maxima locaux du module des coefficients de l'ondelette pour différentes échelles s. La méthode de Blakely et Simpson [2] a été adoptée pour la localisation de ces maxima. Pour réaliser ces différentes opérations, un programme informatique sous MATLAB a été développé.

Pour les développements théoriques et les applications de l'analyse multi-échelle des contacts, le lecteur est invité à consulter, par exemple, les travaux de Archibald et al. [1] et Hornby et al. [4].

3 Application

Nous avons appliqué cette méthode à la carte gravimétrique de la région de Berkane (Maroc nord-oriental) établie par le ministère de l'Énergie et des Mines du Maroc (Fig. 1). Cette carte a été tracée à partir de 1160 stations qui ont permis de calculer une grille régulière ayant un pas de 250 m. Cette carte a été interprétée par Khattach et al. [5] en appliquant différentes techniques, à savoir le gradient vertical, le gradient horizontal, prolongement vers le haut et la déconvolution d'Euler. Elle montre la présence (1) d'anomalies positives au niveau des chaînes des Béni-Snassen et des Kébdana où des terrains primaires affleurent ; (2) d'anomalies négatives telles que l'anomalie allongée dans la direction ENE–WSW et générée par la cuvette des Triffa remplie de terrains plioquaternaires ; (3) de forts gradients qui matérialisent des changements brutaux de densité dans le sous-sol.

La superposition des maxima locaux déterminés à différentes échelles ( $s = 1$ à 12) met en évidence les différents contacts présents sur la carte (Fig. 2). Les contacts linéaires correspondent à des failles, alors que ceux de forme circulaire sont les limites de diapirs ou de corps intrusifs. Le déplacement des maxima induit par l'accroissement de la valeur d'échelle ( $s = 1$ à 12) indique le sens du pendage des contacts.

La carte de la Fig. 4 représente les failles interprétées pour trois échelles différentes, $s = 1$ , $s = 5$ (altitude de prolongement 500 m) et $s = 10$ (altitude de prolongement 1000 m). Elle montre les différentes failles avec leur degré d'importance (épaisseur du trait) et leur pendage. Les principaux accidents sont ceux qui subsistent sur les échelles élevées (en trait épais) ; ils sont, en principe, les plus profonds. Ainsi, on peut signaler la présence : (1) de quatre accidents de direction NE–SW à ENE–WSW et qui délimitent, du sud vers le nord, le massif des Béni-Snassen (n^os 1 et 2), la cuvette de Madagh (n° 3) et la partie nord située entre Madagh et oued Moulouya (n° 4) ; (2) d'accidents est–ouest (n^os 5, 6 et 7) et (3) d'accidents de direction NW–SE au niveau du massif des Béni-Snassen (n^os 8 et 9).

Pour valider localement les résultats obtenus par l'analyse de la carte gravimétrique et apprécier la composante verticale des structures mises en évidence, nous avons étudié un profil de sismique réflexion (Figs. 3 et 5), issu de l'exploration lancée dans la région des Béni-Snassen par l'Office national de recherche et d'exploitation pétrolière (Onarep) en 1985. Cette section sismique confirme les résultats obtenus par le traitement des anomalies gravimétriques : la structure en graben du bassin des Triffa et les différentes failles qui l'affectent. Elle montre clairement que la faille F2 est subverticale, alors que les failles F6 et F7 présentent un pendage vers le sud. La faille F6, au nord de Laâtamna, est une faille normale à rejet vertical apparent très important, d'environ 300 ms en temps double. La morphologie des différentes structures mises en évidence semble être guidée par le jeu de deux familles de failles de directions respectives est–ouest (F5, F6, F7) et NE–SW (F2, F3, F4). Ces accidents affectent aussi bien la couverture que le socle paléozoïque, on les attribuerait à des failles majeures du socle qui auraient rejoué lors des orogenèses atlasique et alpine ; en effet, leur structure en « fleur négative » (Fig. 5) décrite par Harding et al. [3] caractérise des décrochements de socle à composantes normales.

4 Conclusion

Les résultats de cette étude montrent que l'analyse multi-échelle fondée sur les ondelettes est un outil très efficace pour l'étude des contacts géologiques, tels que les failles, à partir des cartes d'anomalies gravimétriques. En effet, il permet non seulement de cartographier les failles, mais aussi de déterminer le degré de leur importance et le sens du pendage. Ce type d'analyse des cartes gravimétriques ou magnétiques, appuyé par les données sismiques, permet de compléter les études structurales classiques, en particulier au niveau des plaines. Les failles sont des structures géologiques qui présentent souvent un grand intérêt dans la prospection hydrogéologique ou minière, mais aussi dans les études des risques naturels (tremblements de terre ou glissement de terrain).

Remerciements

Cette étude a été réalisée dans le cadre du PROTARSIII N° D11/18.