Détection des transitions lithologiques par l'analyse de la composante fractale des diagraphies par transformée continue en ondelettes

Naima Zaourar; Mohamed Hamoudi; Louis Briqueu

doi:10.1016/j.crte.2006.03.008

Géophysique interne

Détection des transitions lithologiques par l'analyse de la composante fractale des diagraphies par transformée continue en ondelettes

Présenté par : Jean-Louis Le Mouël

Naima Zaourar ¹ ; Mohamed Hamoudi ¹ ; Louis Briqueu ²

¹ Department of Geophysics, FSTGAT, USTHB, BP 32 USTHB, 16123 Bab-Ezzouar, Alger, Algérie
² Laboratoire « Dynamique de la lithosphère », UMR 5573, UM2/CNRS, case 060, université Montpellier-2, 34095 Montpellier cedex 5, France

Comptes Rendus. Géoscience, Volume 338 (2006) no. 8, pp. 514-520.

Résumés

Français
Anglais

L'analyse fréquentielle des diagraphies montre que leurs composantes stochastiques sont régies par des lois de puissance, caractéristiques des bruits, en $1 / f$ . Elles peuvent être modélisées par des mouvements browniens fractionnaires. Leur transformée continue en ondelettes permet de déterminer les exposants spectraux locaux de ces lois d'échelle. Ils mesurent la rugosité fractale de milieu géologique en chaque point de profondeur dans le forage. La méthode est justifiée par quelques rappels théoriques et appliquée à un signal synthétique, puis à des données provenant du forage MAR203, dont les résultats sont comparés à la description des carottes.

The frequency analysis of many log data permits to verify that their stochastic component show ‘power-law-type’ spectral densities, characteristic of $1 / f$ noise. They can be modelled by fractional Brownian motions. Continuous Wavelet Transformation (CWT) provides us with very efficient methods to determine the local spectral exponents of these scaling laws. These new attributes are related to the local fractality of these signals. We first present some theoretical results and an application to a fractional Brownian motion. The second application concerns a dataset recorded in the MAR203 borehole. We show that clustering of these new pseudo-logs leads to a good resolution between different lithofacies.

Métadonnées

Reçu le : 2005-08-03
Accepté le : 2006-03-20
Publié le : 2006-05-02

DOI : 10.1016/j.crte.2006.03.008

Mot clés : Stochastique, Fractal, Exposant spectral, Ondelette, Diagraphie, Lithologie
Keywords: Stochastic, Fractal, Spectral exponent, Wavelet, Well log, Lithology

Affiliations des auteurs :

Naima Zaourar ¹ ; Mohamed Hamoudi ¹ ; Louis Briqueu ²

¹ Department of Geophysics, FSTGAT, USTHB, BP 32 USTHB, 16123 Bab-Ezzouar, Alger, Algérie
² Laboratoire « Dynamique de la lithosphère », UMR 5573, UM2/CNRS, case 060, université Montpellier-2, 34095 Montpellier cedex 5, France

@article{CRGEOS_2006__338_8_514_0,
     author = {Naima Zaourar and Mohamed Hamoudi and Louis Briqueu},
     title = {D\'etection des transitions lithologiques par l'analyse de la composante fractale des diagraphies par transform\'ee continue en ondelettes},
     journal = {Comptes Rendus. G\'eoscience},
     pages = {514--520},
     publisher = {Elsevier},
     volume = {338},
     number = {8},
     year = {2006},
     doi = {10.1016/j.crte.2006.03.008},
     language = {fr},
}

TY  - JOUR
AU  - Naima Zaourar
AU  - Mohamed Hamoudi
AU  - Louis Briqueu
TI  - Détection des transitions lithologiques par l'analyse de la composante fractale des diagraphies par transformée continue en ondelettes
JO  - Comptes Rendus. Géoscience
PY  - 2006
SP  - 514
EP  - 520
VL  - 338
IS  - 8
PB  - Elsevier
DO  - 10.1016/j.crte.2006.03.008
LA  - fr
ID  - CRGEOS_2006__338_8_514_0
ER  -

%0 Journal Article
%A Naima Zaourar
%A Mohamed Hamoudi
%A Louis Briqueu
%T Détection des transitions lithologiques par l'analyse de la composante fractale des diagraphies par transformée continue en ondelettes
%J Comptes Rendus. Géoscience
%D 2006
%P 514-520
%V 338
%N 8
%I Elsevier
%R 10.1016/j.crte.2006.03.008
%G fr
%F CRGEOS_2006__338_8_514_0

Naima Zaourar; Mohamed Hamoudi; Louis Briqueu. Détection des transitions lithologiques par l'analyse de la composante fractale des diagraphies par transformée continue en ondelettes. Comptes Rendus. Géoscience, Volume 338 (2006) no. 8, pp. 514-520. doi : 10.1016/j.crte.2006.03.008. https://comptes-rendus.academie-sciences.fr/geoscience/articles/10.1016/j.crte.2006.03.008/

Version originale du texte intégral

Abridged English version

1 Introduction

The well logs offer the opportunity to directly access some petrophysical parameters linked to the characteristics of a reservoir. Some preliminary studies have shown that the stochastic component of these measurements is a self-similar fractal signal [21]. It can be modelled as a fractional Brownian motion (fBm) and is governed by a scale law. The information about the power spectrum obtained by Fourier Transform (Fig. 1) is adequate to describe such statistical processes [21], but is not adapted to locate their spatial heterogeneities. To determine the distribution of local regularities of such signals, we use a Continuous Wavelet Transform (CWT) [1,3,6,7,11,16]. This numerical tool is applied to synthetic and actual datasets.

Fig. 1
Densité spectrale de quatre diagraphies différentes mesurées dans un même puits. Toutes présentent une décroissance algébrique caractéristique des bruits en 1/f. L'intervalle fréquentiel exploré est contraint par les lois de Nyquist.
Periodogram of four well logs recorded in the same borehole. All show a power-law-type behaviour like the 1/f noise signals.

2 Signal processing

Because well-log data may be described by scale laws [4,9,10,14,15,19,21], their power spectra are approximately inversely proportional to the wave number in log–log plots:

S (k) \sim k^{- β}

(1)

The spectral exponent is related to the number of Hurst according to: $β = 2 H + 1$ , which shows the degree of correlation between successive points. For $1 < β < 3$ , the Gaussian scale noise corresponds to a fractional Brownian function. The wavelet transform is a particularly well-adapted tool for analysing such scaling processes. Indeed, the scale invariance can be reflected by CWT as long as the analysing wavelet decreases quickly enough to zero [6,11]:

C_{s} (λ k, z_{0} + λ z) \approx λ^{h (z_{0}) + \frac{1}{2}} C_{f} (k, z_{0} + z)

(2)

The time/scale map (or scalogram) is defined by the square of the wavelet coefficients:

P (k, z) = {| C_{s} (k, z) |}^{2}

For sufficiently large wavenumbers, this relation can be rewritten as [3,6]:

P (k, z) \approx k^{- β (z)}

(3)

where

β (z)

describes the local changes of the power law. Computed in every point of the signal, it defines a new statistical attribute that we call ‘pseudo-log’.

3 Datasets and discussion

3.1 Synthetic dataset

Let us now illustrate, with an fBm process of a synthetic log, how the wavelet-based estimation of the spectral exponent can be used to detect the spatial variations of the signal. The quality of a given analysing method is assessed by the difference between the spectral exponent, more precisely the Hurst number H chosen for the model and the value estimated from the analysis. The synthetic stochastic fluctuations of well data are modelled here by filtering a normally distributed random number sequence by the square root of the power spectrum of a von Karman self-correlation function [15] in the wavenumber domain.

We have tested our algorithm on an academic model with eight layers (Table 1 and Fig. 2a). Its scalogram (Fig. 2b) reflects the energy distribution into the time/frequency space. It also shows local changes of the spectral exponent $β (z)$ estimated from the slope of the local power-law spectrum. Comparing the result (Fig. 2c) to the initial signal, we note that spatial variations of the spectral exponent reflect all the modelled sub-units. The resolution decreases with the number of samples. If the sampling step of this academic example was 0.1524 m as for the many current log data, then our CWT method would permit to detect a layer about 5 m thick, as illustrated by unit C4.

Couches	C1	C2	C3	C4	C5	C6	C7	C8
N	512	32	512	32	128	64	256	512

Profondeur cumulée (m)	77,87	82,75	160,78	165,66	185,17	194,92	233,93	311,96
β	1,0	1,4	1,6	2,0	2,3	2,6	2,9	3,0

Fig. 2
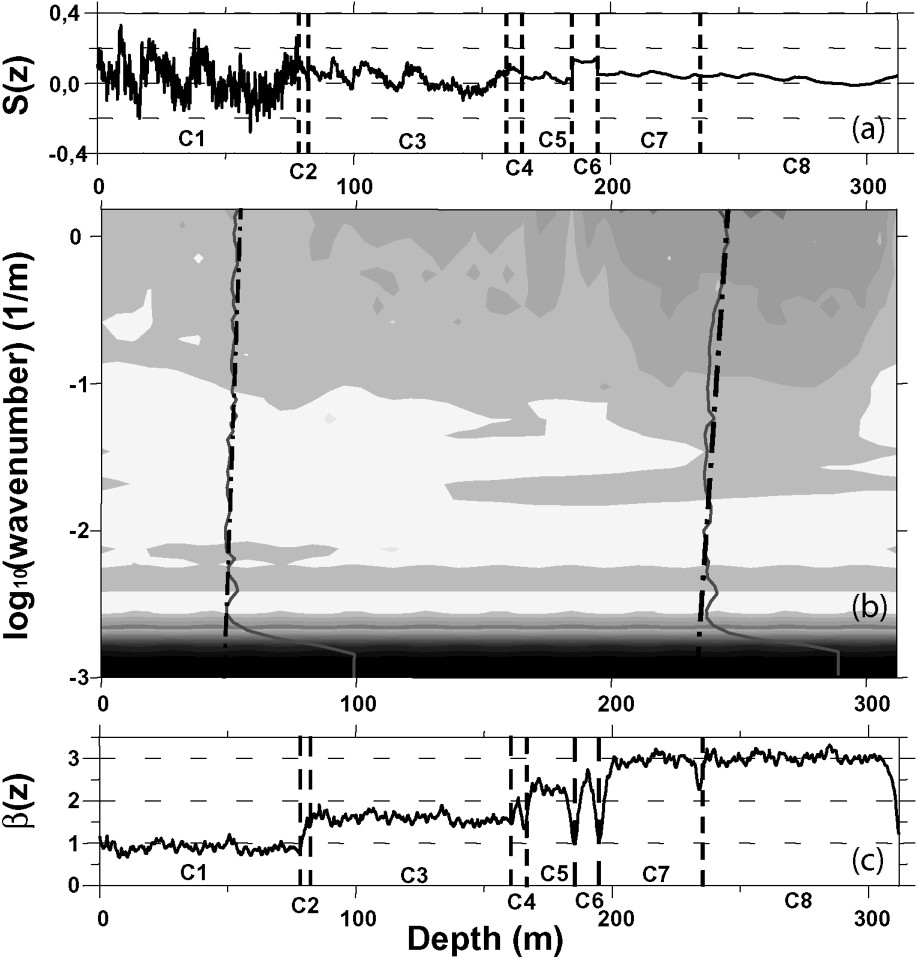
Analyse spectrale d'un signal synthétique de type mBf (a) ; son scalogramme obtenu par transformée continue en ondelettes (b) ; trace des exposants spectraux locaux (c).
CWT spectral analysis of a fBm synthetic signal (a); its scalogram, showing two local cross-sections (b); plot of the local spectral exponent (c).

3.2 Actual datasets

To better assess the potential of the CWT transform, we have extended its application to actual data coming from the MAR203 borehole located in the Rhone valley, near Marcoule (France). This well samples continuously the Cretaceous sedimentary deposits stacked on the western part of the Tethys passive margin. The Urgonian marine deposits are associated with a deformation of the carbonate platform. The Gargasian marl series, well known in the region, is absent below MAR203, where the margin does not sink before Albian time. Then, the platform gets immerse and is stacked with a tick silty layer (called CSM). Because the basin remains shallow, the upper part of the CSM is strongly bioturbated. During the Lower Cenomanian, a regression follows up at the top of the CSM, with an alternation of playa and lacustrine units [5,18].

Using the CWT method, we have determined the spectral exponent of the following well logs: SFLU, NPHI, v-DT and GR of this borehole. The plots of one of them, its stochastic component and its derived $β (z)$ using CWT are shown in Fig. 3b–d. Using the previously exposed neural statistical method [2,8], we have inferred the lithology sampled by the drill in two different ways: firstly from direct measurements and secondly using their corresponding spectral exponents. The results of these two determinations are compared in Fig. 3f and e. The $β (z)$ -derived logs are more efficient than the direct downhole measurements to determine the alternation of thin sandy and silty beds of the Albian and Cenomanian units.

Fig. 3
Traitement des diagraphies du puits MAR203 : (a) log sédimentologique résultant de l'observation des carottes (document Andra) ; (b) trace de la diagraphie sonique ; (c) trace de sa composante stochastique ; (d) trace de son exposant spectral ; (e) détermination des propriétés réservoir à partir des quatre diagraphies SFLU, NPHI, DT et GR ; (f) détermination des propriétés réservoir à partir des quatre β(z) correspondants (voir le texte pour une discussion).
Interpretation of the MAR203 well logs: (a) reference log resulting from core observations; (b) plot of the sonic log; (c) plot of the stochastic component of the sonic log; (d) plot of the spectral exponent of the sonic log; (e) reconstitution of the reservoir properties from SFLU, NPHI, DT and GR; (f) reconstitution of the reservoir properties from their respective β(z) (see text for discussion).

1 Introduction

Comme tout signal, une diagraphie est composée d'une partie déterministe (par exemple, une formation sédimentaire est d'autant plus radioactive qu'elle est argileuse...) et d'une partie aléatoire, souvent implicitement assimilée au bruit instrumental.

De nombreuses lois phénoménologiques, telle la loi d'Archie, permettent de déterminer la lithologie traversée par le forage et de caractériser ses propriétés pétrophysiques à partir de la composante déterministe. Quoique peu nombreux, quelques travaux sont consacrés au traitement de la partie stochastique des données de puits [4,7,9,10,14,15,19,21]. Ils montrent l'importance de l'information spécifique portée par cette composante aléatoire, qui ne se réduit pas à un simple bruit blanc. En effet, dans l'espace des fréquences, leur densité spectrale suit une loi de décroissance caractéristique des « bruits en $1 / f$ ». L'exposant de la loi de puissance, appelé « exposant spectral » est proportionnel au nombre de Hurst, donc aussi à la dimension fractale du signal, dont il mesure, globalement ou localement, la rugosité.

Dans ce travail, au travers de l'étude d'un cas, nous montrons que nombre de propriétés pétrophysiques mesurées en forage présentent de telles caractéristiques d'autosimilarité, et comment il est possible d'extraire ces nouveaux attributs statistiques, caractéristiques du milieu géologique, à l'aide de la méthode de la transformée continue en ondelettes (TOC) dont nous rappelons qu'elle consiste en un produit de convolution du signal $s (z)$ par une fonction oscillante, l'ondelette mère, $ψ (\frac{(z - b)}{a})$ , à décroissance rapide et de moyenne nulle :

C_{s} (a, b) = \frac{1}{\sqrt{a}} \int_{- \infty}^{+ \infty} s (z) \bar{ψ} (\frac{z - b}{a}) d z

(1)

a étant le paramètre de modulation en fréquence de l'ondelette analysante. Il décrit l'intervalle fréquentiel permis par les lois relatives aux signaux échantillonnés ; b est le paramètre de translation de l'ondelette le long du signal analysé. De par ces propriétés de bonne localisation en temps et en fréquences, la TOC est souvent comparée à un microscope mathématique permettant d'explorer un signal à toutes ses échelles [3,16].

2 Méthodologie

Le périodogramme résultant de la transformée de Fourier (TF), même si sa mise en œuvre n'est pas toujours justifiée [6,17], permet d'explorer facilement la nature d'un bruit analytique. Si, dans une représentation bi-logarithmique, la densité spectrale est constante, le bruit est blanc ; si elle décroît en fonction de la fréquence, alors elle porte une partie de l'information qu'il serait dommage de négliger [1,3]. C'est le cas des diagraphies. Dans la Fig. 1, nous avons représenté les périodogrammes de la vitesse acoustique (vDT), d'une résistivité électrique, (SFLU), d'une radioactivité naturelle (GR) et d'une mesure nucléaire induite : la porosité « neutron » NPHI. Ces quatre signaux mesurés dans le même forage MAR203, mais choisis parce que mesurant des propriétés pétrophysiques très différentes, présentent tous le même type de comportement fréquentiel, caractéristique des bruits dits en $1 / f$ . Lorsque l'exposant de la loi de puissance est compris entre 1 et 3 (en valeur absolue), comme c'est le cas pour ces quatre diagraphies, les signaux sont autosimilaires : ils ne sont pas stationnaires, mais leurs accroissements le sont.

Le mouvement brownien fractionnaire (mBf), parce qu'il est gaussien, est le processus le plus couramment mis en œuvre pour modéliser de tels bruits. La TOC d'un mBf permet donc d'illustrer les potentialités de cette méthode appliquée aux bruits en $1 / f$ . Le mBf est un processus autosimilaire d'exposant H (nombre de Hurst compris entre 0 et 1), c'est-à-dire que, pour tout $k > 0$ , il satisfait une loi de la forme :

S (k z) \overset{d}{=} k^{H} S (z)

(2)

l'égalité étant prise au sens des distributions.

L'analyse temps/fréquence – dans le cas des mesures en forage, on lira « profondeur » en lieu et place de « temps » – permise par la TOC est particulièrement bien adaptée à l'étude de tels processus. En effet, d'après [6], la stationnarité des accroissements du mBf, jointe au fait qu'une ondelette $Ψ (t)$ soit à moyenne nulle, assure que la TOC « stationnarise » le mBf. Il est donc possible de définir, à chaque échelle ou fréquence, une fonction de corrélation stationnaire. La densité spectrale qui en résulte s'exprime par :

Γ_{B_{H}} (ν, a) = C \frac{σ^{2}}{{| ν |}^{2 H + 1}} a | Ψ {(a ν)}^{2} |

(3)

Ce résultat justifie le comportement en

1 / f

du mBf, l'exposant spectral de la loi puissance étant égal à

2 H + 1

. Qui plus est, par la TOC, l'autosimilarité du mBf est contenue dans la loi de progression constante de la moyenne du scalogramme (représentation temps–échelle ou temps–fréquence du carré du module des coefficients d'ondelettes) à travers les échelles, en effet [3] :

E {{| {TOC}_{{mBf}_{H}} (t, k a) |}^{2}} = k^{2 H + 1} E {{| {TOC}_{{mBf}_{H}} (t, a) |}^{2}}

(4)

Les exposants spectraux moyens ainsi déterminés sont équivalents et directement comparables à ceux estimés globalement par TF.

Dans l'algorithme spécifique mis en œuvre pour le calcul de la TOC, nous avons adopté l'approche proposée par [15]. Fort du théorème de Parceval, elle consiste en un produit des TF du signal et de l'ondelette dans l'espace des fréquences, moyennant certaines adaptations, telles que $b = z$ , qui signifie que la translation b de l'ondelette est effectuée pour chaque point en profondeur z et $k = \frac{2 \sqrt{α}}{a}$ correspond au nombre d'onde [7,12,13]. Nous avons choisi comme ondelette analysante, l'ondelette de Morlet pour sa propriété de décroissance rapide et son nombre important de moments nuls, ces deux propriétés étant indispensables à une bonne « décorrélation » entre deux segments adjacents du scalogramme et donc à une bonne résolution temporelle (ou spatiale) de la méthode [6].

Parce que le mBf possède la propriété d'avoir des accroissements stationnaires, les processus qu'il modélise présentent des effets de corrélation à long terme. Autrement dit, leurs fluctuations sont d'autant plus régulières que H est proche de 1 et d'autant plus irrégulières que H est proche de 0. Ce comportement se traduit par l'existence d'une dimension fractale, dont on montre qu'elle vaut $D = 2 - H$ [20]. L'existence d'une telle dimension fractale a une autre conséquence particulièrement intéressante dans le cas des signaux considérés. Dans le scalogramme, la loi de variation des coefficients d'ondelettes à travers les fréquences permet d'accéder à une mesure locale de la régularité du signal. En effet, en supposant qu'il soit de régularité uniforme H, au sens holdérien du terme, ne serait-ce que localement sur un intervalle donné, c'est-à-dire si, en un point $z_{0}$ , le signal satisfait à :

| s (z_{0} + τ) - s (z_{0}) | ⩽ C {| τ |}^{H (z_{0})} avec 0 < H < 1

(5)

Alors, d'après [6,11], sa TOC, exprimée sous la forme du carré du module des coefficients temps/fréquence, conduit à la relation :

P (λ k, z_{0} + λ z) \approx λ^{2 h (z_{0}) + 1} P (k, z_{0} + z)

(6)

Aux grands nombres d'onde k, (6) peut être approximée par une loi de puissance, expression de la régularité du signal au voisinage du point d'échantillonnage

z_{0}

[3] :

p (k, z) \approx k^{- β (Z)}

(7)

Autrement dit, pour chaque coupe en profondeur du scalogramme d'une diagraphie, la régression linéaire (en échelle bi-logarithmique) réalisée sur la décroissance régulière des coefficients d'ondelettes permet d'estimer la dimension fractale locale du signal. Calculés ainsi en chaque point du signal, les exposants spectraux définissent un signal dérivé qui constitue un attribut statistique, caractéristique de la « rugosité » – au sens physico-mathématique du terme – du milieu géologique.

3 Applications

3.1 Modélisation de la composante stochastique d'une diagraphie

Afin de vérifier le pouvoir de résolution de la méthode mise en œuvre, nous l'appliquons à un signal synthétique présentant, par construction même, les propriétés d'autosimilarité requises. Le signal que nous avons généré (Fig. 2a) est construit en concaténant huit régimes mBf différents, dont les paramètres sont rassemblés dans le Tableau 1. Pour calculer chacune des parties, nous générons une séquence de $N_{i}$ nombres aléatoires distribués normalement ${x_{i}}_{i = 1, N_{i}}$ . Sa TF $X (k)$ est filtrée par la fonction d'autocorrélation de von Karman, qui permet d'introduire variance et longueur de corrélation [20]. Le signal mBf correspond alors à la partie réelle de la TF inverse de ce produit.

Le scalogramme (Fig. 2b) représente la distribution d'énergie dans le plan profondeur/nombre d'onde. Le signal dérivé obtenu par le calcul des exposants spectraux locaux en chaque point du signal est représenté dans la Fig. 2c. Deux exemples de spectres locaux sont superposés au scalogramme. L'écart de leurs traces à la verticalité permet d'illustrer le calcul des exposants spectraux locaux.

La comparaison du signal dérivé et du signal originel montre que les couches C1 et C3 sont identifiées sans aucune ambiguïté, à cause d'un échantillonnage suffisant. La couche C2 est noyée dans la transition entre C1 et C3, en raison de son faible nombre d'échantillons et d'un contraste insuffisant entre son exposant spectral et celui des couches adjacentes. La couche C4, quoique aussi mince que C2, est repérée par un pic identifiable, du fait d'un contraste suffisant de son $β (z)$ avec celui des couches voisines. Les limites des couches C5 et C6 sont marquées par des changements brusques de l'exposant spectral. La transition entre C7 et C8, dont les exposants spectraux sont proches, est néanmoins bien identifiée par une discontinuité de $β (z)$ . Si le pas d'échantillonnage de ce signal était comparable à celui des diagraphies (0,1524 m), la méthode permettrait de détecter une couche de l'ordre de 5 m d'épaisseur, pour peu que son exposant spectral présente un écart de l'ordre de 0,4 (en valeur absolue) avec celui d'une des deux couches adjacentes.

3.2 Application à un cas réel

Afin d'illustrer cette approche de traitement numérique des diagraphies, nous l'avons appliquée aux mesures enregistrées dans le forage MAR203 implanté dans le Gard rhodanien par l'Andra, lors de ses études préliminaires à la réalisation d'un laboratoire souterrain destiné à l'étude de faisabilité du stockage à long terme des déchets nucléaires en formation géologique profonde. Outre les diagraphies enregistrées, ce forage a fait l'objet d'un carottage en continu, ce qui a permis une description précise de la lithologie (Fig. 3a). Il a été arrêté à la cote −892 m dans la formation sommitale de la plate-forme carbonatée urgonienne. Les unités crétacées postérieures sont caractérisées par la présence d'une épaisse couche de silt, laminée à la base, bioturbée au sommet, la couche silteuse de Marcoule (CSM). Elle repose sur la dalle récifale urgonienne par un niveau de marnes calcaires, surmonté par un banc de grès glauconieux à gravier. Le cycle Vraconnien–Cénomanien, au cours duquel elle s'est déposée, se termine par l'alternance de faciès de plage et de faciès lagunaires [5].

Les densités spectrales des quatre diagraphies traitées sont représentées dans la Fig. 1. Elles satisfont toutes les quatre les critères de décroissance caractéristiques de signaux autosimilaires. Elles peuvent donc faire l'objet d'un traitement en ondelettes pour l'extraction des exposants spectraux des lois d'échelle sous-jacentes. À titre d'illustration, la trace de la diagraphie vDT, de sa composante stochastique et de son exposant spectral sont représentés dans les Fig. 3b–d. Si l'épaisse couche silteuse présente des propriétés pétrophysiques homogènes entre les cotes −482 et −774 m [18], tout juste marquées par un gradient vertical résultant de la compaction de la série, il n'en est pas de même pour les exposants spectraux, qui montrent des variations significatives, révélant la structure sous-jacente des milieux géologiques.

Afin de tirer parti de ces informations, nous avons déterminé la structure interne de la séquence crétacée, en traitant séparément, d'une part, les diagraphies elles-mêmes et, d'autre part, leurs signaux dérivés par TOC. Dans l'un et l'autre cas, nous avons mis en œuvre la même méthode de partitionnement des données que celle développée dans des travaux antérieurs [2,8] sur cette même série de données. Les résultats des deux traitements sont représentés dans les Fig. 3e et f. La transformation des données par le calcul des exposants spectraux apporte un gain substantiel d'information pour la partie sommitale gréseuse de la formation silico-clastique, faite d'une alternance de grès propres et de grès argileux, interlités avec des bancs minces de lignites ou de calcaires lacustres. Ces sous-unités sont bien différenciées, alors qu'elles ne le sont pas par le traitement direct des diagraphies. La structure de la CSM est également mieux résolue par le traitement des exposants spectraux. Sa partie supérieure, comprise entre les cotes −367 et −484 m, est une alternance de bancs décimétriques de grès glauconieux assez grossiers bioturbés et de marnes silteuses ou sableuses glauconieuses, plus ou moins bioturbées. Cette succession de bancs minces est mal rendue par le traitement direct des diagraphies, alors qu'elle l'est par le traitement des exposants spectraux. Entre les cotes −484 et −781 m, la CSM est également mieux résolue par le traitement des exposants spectraux que par celui des diagraphies. Ils permettent de mettre en évidence l'homogénéité de la couche silteuse jusqu'à la cote −700 m, puis le passage à l'unité basale, plus marneuse et surtout plus laminée. Dans l'un et l'autre cas, la semelle calcaire est bien identifiée et localisée en profondeur. La méthode des exposants spectraux semble être moins performante pour résoudre la partie basale de l'unité silteuse. Le découpage obtenu par le traitement direct des diagraphies semble être mieux en adéquation avec le log sédimentologique résultant de la description des carottes. Dans ce cas, la méthode des exposants spectraux surligne les discontinuités sédimentaires plutôt que les variations lithologiques.

4 Conclusion

Les composantes stochastiques des diagraphies sont des « bruits en $1 / f$ ». Dans l'espace des fréquences, leurs densités spectrales suivent des lois de décroissance algébrique caractéristiques des signaux autosimilaires. D'après [9,20], la multifractalité de ces enregistrements reflète la multifractalité des processus qui régissent les dépôts sédimentaires qui sont aussi, de fait, des séries chronologiques. Toutefois, c'est sans doute dans la physique même de la dispersion des impulsions instrumentales mises en œuvre pour ces mesures en forage par un milieu granulaire nécessairement anisotrope, que réside la cause des variations de « rugosité » des signaux enregistrés. Leur transformée en ondelettes permet de déterminer leur dimension fractale en chaque point de profondeur. Il est alors possible de tirer partie de ces bruits pour caractériser le milieu géologique.

Remerciements

Nous tenons à remercier l'Andra pour avoir mis à notre disposition les données du forage MAR203, ainsi queles experts auxquels a été confié le manuscrit pour leurs remarques utiles à l'amélioration de sa structuration.

Bibliographie

[1] P. Abry; P. Gonçalvès; P. Flandrin Wavelet spectrum analysis and $1 / f$ processes, Wavelets and Statistics, Lecture Notes in Statistics, vol. 103, Springer, 1995, pp. 15-39

[2] L. Briqueu; S. Gottlib-Zeh; M. Ramadan; J. Brulhet Traitement des diagraphies à l'aide d'un réseau de neurones du type « carte auto-organisatrice » : application à l'étude lithologique de la couche silteuse de Marcoule (Gard, France), C. R. Geoscience, Volume 334 (2002), pp. 331-337

[3] R. Carmona; W.L. Hwang; B. Torrésani Practical Time–Frequency Analysis. Gabor and Wavelet Transforms with an Implementation in S, Academic Press, 1998

[4] S.S. Dolan; C. Bean; B. Riollet The broad-band fractal nature of heterogeneity in the upper crust from petrophysical logs, Geophys. J. Int., Volume 132 (1998), pp. 489-507

[5] S. Ferry Apport des forages Andra de Marcoule à la connaissance de la marge crétacée rhodanienne. Étude du Gard rhodanien, Actes des journées scientifiques, CNRS–Andra, EDP Sciences, 1999, pp. 63-91

[6] P. Flandrin Temps–Fréquence, Hermès, Paris, 1998

[7] P. Gaillot, Ondelettes continues en sciences de la Terre, méthodes et applications, thèse, université Toulouse-3, 2000, http://www.isteem.univ-montp2.fr/LGHF/equip/gaillot/PDF_these/TM.html

[8] S. Gottlib-Zeb, L. Briqueu, A. Veillerette, Indexed self-organizing map: a new calibrating system for geochemical interpretation of logs, in: S.J. Lippard, A. Naess, R. Sinding-Larsen, (Eds.), Proc. IAMG'99, Fifth Annual Conference of the International Association for Mathematical Geology, Trondheim, Norvège, 1999, pp. 183–189

[9] F. Herrmann; J.R. William; C. Stark Seismic facies characterization by monoscale analysis, Geophys. Res. Lett., Volume 28 (2001), pp. 3781-3784

[10] K. Holliger Upper crustal seismic velocity heterogeneity as derived from a variety of P-wave sonic log, Geophys. J. Int., Volume 125 (1996), pp. 813-829

[11] M. Hölschneider Wavelet an Analysis Tool, Clarendon Press, Oxford, UK, 1995

[12] M. Holschneider; M.S. Diallo; M. Kulesh; M. Ohrnberger; E. Lück; F. Scherbaum Characterization of dispersive surface waves using continuous wavelet transforms, Geophys. J. Int., Volume 163 (2005), pp. 463-478

[13] C. Lauer-Leredde; L. Briqueu; T. Williams A wavelet analysis of physical properties measured downhole and on core from Holes 1095B and 1096C (Antarctic Peninsula), Init. Repts., Volume 178 (1999), pp. 1-174 http://www-odp.tamu.edu/pub-lications/178SR/chap32/chap32.html (available from World Wide Web:)

[14] C.-F. Li Rescaled-range and power spectrum analyses on well-logging data, Geophys. J. Int., Volume 153 (2003), pp. 201-212

[15] X.P. Li Wavelet power spectrum analysis of heterogeneities from sonic velocity logs, Geophys. Prospect., Volume 46 (1998), pp. 455-475

[16] Y. Meyer Wavelets: Algorithms and Applications, SIAM Press, Philadelphia, PA, 1993

[17] V. Perrier; T. Philipovitch; C. Basdevant Wavelet spectral compared to Fourier spectra, J. Math. Phys., Volume 36 (1995), pp. 1506-1519

[18] C. Robelin; Y.-M. Le Nindre La Couche silteuse de Marcoule : analyse des caractéristiques pétrographiques et de leurs variations, Actes des journées scientifiques, CNRS–Andra, EDP Sciences, CG8, 1999, p. 17

[19] K. Shiomi; H. Sato; M. Ohtake Broad-band power-law spectra of well-log data in Japan, Geophys. J. Int., Volume 130 (1997), pp. 57-64

[20] D.L. Turcotte Fractal and Chaos in Geology and Geophysics, Cambridge University Press, Cambridge, 1997

[21] R.S. Wu; X. Zhengyu; X.P. Li Heterogeneity spectrum and scale-anisotropy in the upper crust revealed by the German Continental Deep-Drilling (KTB) Holes, Geophys. Res. Lett., Volume 21 (1994), pp. 911-914

Commentaires - Politique