Plan
Comptes Rendus
no. 8

Internal Geophysics
Further details on the applicability of Thellier paleointensity method: The effect of magnitude of laboratory field
[Nouveaux détails sur l'applicabilité de la méthode de paléointensité de Thellier : l'effet de l'intensité du champ en laboratoire]

Présenté par : Jean-Louis Le Mouël

Juan Morales1  ; Avto Goguitchaichvili1  ; Luis M. Alva-Valdivia1  ; Jaime Urrutia-Fucugauchi1
1 Laboratorio de Paleomagnetismo y Geofisica Nuclear, Instituto de Geofisica, UNAM, Ciudad Universitaria S/N, 04510 México DF, Mexico
Comptes Rendus. Géoscience, Volume 338 (2006) no. 8, pp. 507-513.

Résumés

Twenty years after Tanaka and Kono's pioneering contribution (Tanaka and Kono, 1984), we give some new details on the effect of applied field strength during Thellier paleointensity experiments. Special attention is paid to the relation of magnitude of laboratory field and Coe's quality factors (Coe et al., 1978). Full thermoremanent magnetizations were imparted on natural samples containing low-Ti titanomagnetites of pseudo-single domain structure in a 40-μT magnetic field from 600 °C to room temperature. The samples were subjected to the routine Thellier procedure using a wide range of applied laboratory fields. Results indicate that values of laboratory fields may be accurately reproduced within 2% of standard error. The quality factors, however, decrease when the magnitude of ‘ancient’ field does not match to applied laboratory fields.

Vingt ans après la contribution pionnière de Tanaka et Kono (Tanaka et Kono, 1984), nous donnons de nouveaux détails sur l'effet de l'intensité du champ appliqué au cours d'expériences de paléointensité de Thellier. Une attention particulière est apportée à la relation de l'intensité de champ en laboratoire et des facteurs de qualité de Coe et al. (Coe et al., 1978). L'ensemble des l'aimantation thermorémanentes ont été imparties aux échantillons naturels contenant des titanomagnétite pauvres en titane et de structure en pseudo-mono-domaine, dans un champ magnétique de 40 μT, depuis 600 °C jusqu'à la température ambiante. Les échantillons ont été soumis à la procédure de routine de Thellier, utilisant une vaste gamme de champs appliqués en laboratoire. Les résultats indiquent que les valeurs de champ en laboratoire peuvent être reproduites avec précision, avec une marge d'erreur de 2%. Cependant, les facteurs de qualité diminuent lorsque la magnitude de champ « ancien » n'est pas similaire aux champs appliqués en laboratoire.

Métadonnées
Reçu le :
Accepté le :
Publié le :
DOI : 10.1016/j.crte.2006.02.007
Keywords: Paleointensity, Thellier method, Rock magnetism
Mot clés : Paléo-intensité, Méthode de Thellier, Magnétisme des roches
Juan Morales 1 ; Avto Goguitchaichvili 1 ; Luis M. Alva-Valdivia 1 ; Jaime Urrutia-Fucugauchi 1

1 Laboratorio de Paleomagnetismo y Geofisica Nuclear, Instituto de Geofisica, UNAM, Ciudad Universitaria S/N, 04510 México DF, Mexico 
@article{CRGEOS_2006__338_8_507_0,
     author = {Juan Morales and Avto Goguitchaichvili and Luis M. Alva-Valdivia and Jaime Urrutia-Fucugauchi},
     title = {Further details on the applicability of {Thellier} paleointensity method: {The} effect of magnitude of laboratory field},
     journal = {Comptes Rendus. G\'eoscience},
     pages = {507--513},
     publisher = {Elsevier},
     volume = {338},
     number = {8},
     year = {2006},
     doi = {10.1016/j.crte.2006.02.007},
     language = {en},
}
TY  - JOUR
AU  - Juan Morales
AU  - Avto Goguitchaichvili
AU  - Luis M. Alva-Valdivia
AU  - Jaime Urrutia-Fucugauchi
TI  - Further details on the applicability of Thellier paleointensity method: The effect of magnitude of laboratory field
JO  - Comptes Rendus. Géoscience
PY  - 2006
SP  - 507
EP  - 513
VL  - 338
IS  - 8
PB  - Elsevier
DO  - 10.1016/j.crte.2006.02.007
LA  - en
ID  - CRGEOS_2006__338_8_507_0
ER  - 
%0 Journal Article
%A Juan Morales
%A Avto Goguitchaichvili
%A Luis M. Alva-Valdivia
%A Jaime Urrutia-Fucugauchi
%T Further details on the applicability of Thellier paleointensity method: The effect of magnitude of laboratory field
%J Comptes Rendus. Géoscience
%D 2006
%P 507-513
%V 338
%N 8
%I Elsevier
%R 10.1016/j.crte.2006.02.007
%G en
%F CRGEOS_2006__338_8_507_0
Juan Morales; Avto Goguitchaichvili; Luis M. Alva-Valdivia; Jaime Urrutia-Fucugauchi. Further details on the applicability of Thellier paleointensity method: The effect of magnitude of laboratory field. Comptes Rendus. Géoscience, Volume 338 (2006) no. 8, pp. 507-513. doi : 10.1016/j.crte.2006.02.007. https://comptes-rendus.academie-sciences.fr/geoscience/articles/10.1016/j.crte.2006.02.007/

Version originale du texte intégral

1 Introduction

Absolute paleointensity data provide an important source of information on the physics of the Earth's deep interior. Despite more than forty years of research, paleointensity data are scarce [9,17,19,22] and they cannot be yet used to document a long-term variation in the intensity of the Earth's magnetic field through geological time. The major reason for this small number of determinations is that paleointensity is the most difficult component of the magnetic field to determine and that the failure rate is often large, in general of the order of 80% [2,12].

The Thellier method [23] is currently considered as the most reliable technique to retrieve the absolute intensity of geomagnetic field [8,15] from volcanic rocks and archaeological material. Although numerous methodological studies (e.g., [2,4,5,10–13,20,21]) were devoted to investigate the causes of failure and its prevention, the problem is still not fully understood.

Recent critical analyses of paleointensity variation trough time [1,9] indicate that all reported data might differ by a factor of 2 or 3 from present-day strength. During geomagnetic reversals or excursions, however, the paleointensity may decrease by a factor of 5 to 8 [3,8,18]. The laboratory field used during Thellier experiments may frequently differ from true geomagnetic paleointensity. In this note, we report new high-quality experimental data to evaluate the effect of applied field on the quality of paleointensity determination.

2 Samples and laboratory procedures

Samples used in this study belong to three independent, Late Quaternary lava flows from Chichinautzin volcanic field in Central Mexico [14]. The main magnetic carriers are low-Ti titanomagnetites as evidenced by reasonably reversible susceptibility versus temperature curves. On the other hand, the ratios of hysteresis parameters point out that all samples fall in the pseudo-single domain grain size region, probably indicating a mixture of multidomain and a significant amount of single-domain grains (more detailed description of samples are reported in Morales et al. [14,15]). The natural remanence of these samples is characterized by stable univectorial magnetization, observed upon both alternating field and thermal treatments. The median destructive fields (MDF) range mostly from 50 to 70 mT, suggesting ‘small’ pseudo-single domain grains as remanent magnetization carriers [7].

The full TRM's (thermoremanent magnetizations) were imparted to previously AF (alternating field)-treated samples from 600 °C to room temperature in a 40-μT magnetic field. Thellier experiments in their modified form [6] were carried out on each set of samples using 10-, 20-, 40-, 60- and 80-μT laboratory fields, respectively. Finally, the extreme case was also investigated: a full TRM was imparted on 16 samples in a 10-μT magnetic field while the laboratory field was set to 80 μT. Ten to 16 double-heating steps were distributed between room temperature and 600 °C, according to the sample's blocking temperature spectra [14]. Several control heating steps (commonly referred as partial TRM checks (pTRM checks)) were performed throughout the experiment. Remanence measurements were made using both AGICO Ltd. JR5 and JR6 spinner magnetometers.

3 Results

Paleointensity data are reported on Arai-Nagata [16] plots in Fig. 1 and in Tables 1 and 2. The accepted determinations fulfill the following conditions: (1) at least 8 NRM–TRM points, corresponding to a NRM fraction larger than 0.4 (Tables 1 and 2); (2) a quality factor q [6] of about 8 (a minimum value obtained in this study, excepting two cases) or more. The q factor is related to f(remanence fraction used to determine paleointensity) and g(the gap factor) by following expression: q=fgm/δm, where m is slope of the best fit line adjusted to the ‘NRM’–TRM points and δm is the standard deviation of the slope; and (3) positive ‘pTRM’ checks (i.e. pTRM checks must agree with the original pTRM data within 15%).

Fig. 1

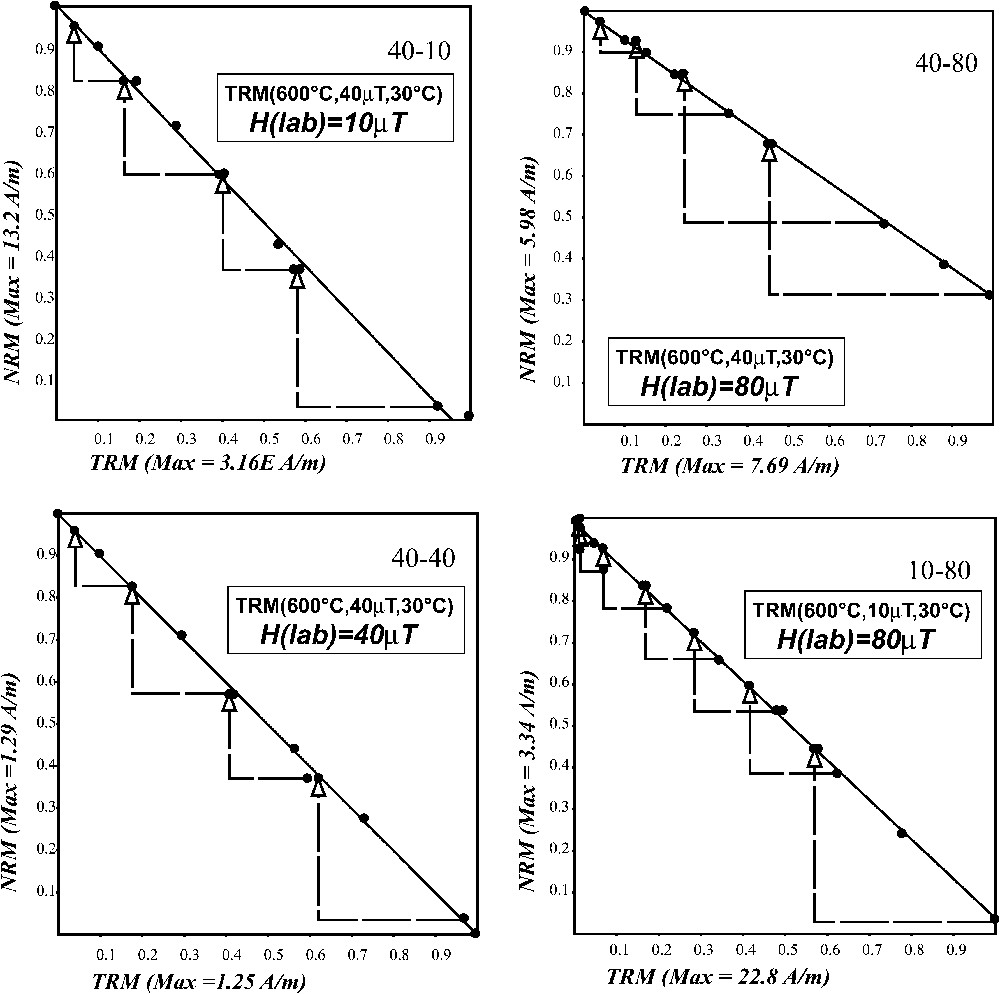
Representative NRM–TRM plots for different set of samples (see also text).

Diagrammes représentatifs NRM–TRM pour les différentes séries d'échantillons (voir aussi le texte).

Table 1

Experimental results. n, Number of ‘NRM’–TRM points used for determination; m, slope of the best fit line adjusted to the ‘NRM’–TRM points; δm, standard deviation of the slope; Hlabest, estimated strength of the laboratory field intensity used to create the full TRM; δHlabest, associated error of Hlabest; f, g and q fraction of extrapolated NRM used for intensity determination, gap and quality factor [6], respectively; and Hlab, laboratory field intensity employed in each experiment (10, 20, 40, 60, and 80 μT)

Résultats expérimentaux. n, Nombre de points « NRM » –TRM utilisés pour la détermination ; m, pente de la droite la mieux ajustée aux points « NRM »–TRM ; δm, déviation standard de la pente ; Hlabest, intensité au champ estimée, utilisée pour créer TRM total ; δHlabest, erreur associée à Hlabest ; f, g et q ; fraction de NRM extrapolé utilisée pour la détermination de l'intensité, de groupement et de qualité facteurs [6], respectivement et Hlab, intensité de champ en laboratoire, utilisée dans chaque expérience (10, 20, 40, 60 et 80 μT)

TRM (600 °C, 40 μT, T0)
Sample n m δm Hlabest [μT] δHlabest [μT] f g q
H lab = 10 μT
JJ2Y 10 −3.8130 0.2220 38.130 2.220 0.8550 0.8200 12.030
JJ8 10 −3.8944 0.7475 38.944 7.475 0.9307 0.4916 2.384
JJ10 10 −4.1000 0.9020 41.000 9.020 0.9320 0.5990 2.537
JJ11V 11 −4.1325 0.4000 41.325 4.000 1.0052 0.8049 8.360
JJ11X 11 −4.1295 0.0630 41.295 0.630 0.9841 0.8544 55.105
JJ11Y 11 −4.1648 0.1586 41.648 1.586 0.9779 0.8519 21.873
JJ11Z 11 −4.1669 0.1367 41.669 1.367 1.0010 0.8515 25.976
JJ12 12 −4.4834 0.1495 44.834 1.495 1.0013 0.8702 26.446
Mean −4.111 0.347 41.11 0.961 0.768 19.34
S.E. = 0.71 0.018 0.050 6.16
H lab = 20 μT
JH10Y 8 −1.8400 0.1000 36.800 2.000 0.8084 0.7890 11.736
JH10Z 9 −1.9500 0.1000 39.000 2.000 0.9487 0.8014 14.825
JH11U 8 −2.1400 0.0840 42.800 1.680 0.8822 0.7218 16.223
JH11Y 9 −1.9200 0.0700 38.400 1.400 0.9140 0.8477 21.252
JH12Y 9 −1.9100 0.1400 38.200 2.800 0.9095 0.8657 10.742
JH14Y 9 −1.9900 0.0980 39.800 1.960 0.9010 0.8434 15.431
JH15 9 −2.1500 0.1500 43.000 3.000 0.5972 0.8451 7.233
JH17Z 8 −2.0300 0.1200 40.600 2.400 0.8738 0.8424 12.452
Mean −1.991 0.108 39.83 0.854 0.820 13.74
S.E. = 0.78 0.039 0.017 1.49
H lab = 40 μT
JJ2Y 11 −1.0169 0.0188 40.676 0.752 1.0010 0.8770 47.500
JJ8 11 −1.0229 0.0271 40.916 1.082 0.9970 0.8250 31.000
JJ10 10 −1.0600 0.0120 42.408 0.480 0.7210 0.8700 54.040
JJ11V 11 −0.9689 0.0097 38.756 0.388 0.9690 0.8750 84.590
JJ11X 11 −1.0850 0.0126 43.400 0.502 0.9710 0.8520 71.500
JJ11Y 11 −1.0121 0.0143 40.486 0.573 0.9900 0.8760 61.250
JJ11Z 11 −1.0204 0.0109 40.814 0.436 0.9910 0.8680 80.580
JJ12 11 −1.0386 0.0115 41.543 0.460 0.9990 0.8640 78.040
Mean −1.028 0.015 41.12 0.955 0.863 63.56
S.E. = 0.49 0.034 0.006 6.57
H lab = 60 μT
JM5A 9 −0.6606 0.0216 39.636 1.296 0.9244 0.7909 22.401
JM6A 9 −0.6779 0.0250 40.674 1.500 0.7742 0.7843 16.453
JM7A 9 −0.7043 0.0196 42.258 1.176 0.7653 0.7826 21.533
JM9A 10 −0.6889 0.0136 41.334 0.816 0.9764 0.7537 37.197
JM10A 9 −0.7073 0.0165 42.438 0.990 0.8383 0.7858 28.174
JM11A 9 −0.6957 0.0168 41.742 1.008 0.8629 0.7720 27.634
JM12A 9 −0.6571 0.0251 39.426 1.506 0.9198 0.7657 18.454
JM12B 9 −0.6434 0.0197 38.604 1.182 0.9750 0.7095 22.549
Mean −0.679 0.020 40.76 0.880 0.768 24.30
S.E. = 0.50 0.029 0.009 2.32
H lab = 80 μT
JH10Y 8 −0.5043 0.0106 40.344 0.848 0.5554 0.7995 21.130
JH10Z 8 −0.4856 0.0170 38.852 1.359 0.4179 0.7332 8.760
JH11U 11 −0.4826 0.0045 38.608 0.363 0.9843 0.7264 76.010
JH11Y 9 −0.4930 0.0072 39.441 0.576 0.9897 0.8113 55.120
JH12Y 11 −0.4966 0.0096 39.732 0.764 0.9938 0.8551 44.200
JH14Y 11 −0.5070 0.0066 40.558 0.532 0.9979 0.8253 62.810
JH15 11 −0.5364 0.0040 42.912 0.319 0.6893 0.8426 78.030
JH17Z 11 −0.4965 0.0106 39.722 0.845 1.0015 0.8312 39.290
Mean −0.500 0.009 40.02 0.829 0.803 48.17
S.E. = 0.47 0.084 0.017 8.77
Table 2

Same notations as in Table 1. The full TRM is produced under a 10-μT magnetic field from 600 °C to room temperature and the laboratory field is set to 80 μT

Mêmes notations que dans le Tableau 1. TRM total est produit sous un champ magnétique de 10 μT depuis 600 °C jusqu'à la température ambiante, et le champ imposé en laboratoire est de 80 μT

Sample n m δm Hlabest [μT] δHlabest [μT] f g q
TRM tot = 10 μT H lab = 80 μT
92H010A 15 −0.1257 0.0038 10.058 0.300 0.9844 0.8153 26.886
92H010B 15 −0.1189 0.0052 9.509 0.418 1.0090 0.7990 18.324
92H011A 15 −0.1264 0.0036 10.109 0.292 0.9714 0.7562 25.451
92H011B 13 −0.1440 0.0070 11.519 0.560 0.7185 0.8116 12.002
92H012A 15 −0.1391 0.0054 11.128 0.433 0.9993 0.8511 21.874
92H014A 15 −0.1328 0.0043 10.626 0.342 1.0015 0.8286 25.905
92H015A 15 −0.1373 0.0036 10.982 0.292 0.7399 0.8596 23.960
92H017A 15 −0.1360 0.0057 10.880 0.453 1.0017 0.8251 20.172
92J02A 16 −0.1177 0.0060 9.418 0.480 0.9729 0.8693 16.590
92J08A 16 −0.1309 0.0024 10.474 0.189 0.9815 0.7716 41.921
92J10A 16 −0.1377 0.0039 11.018 0.310 0.9858 0.8897 31.140
92J11A 16 −0.1293 0.0062 10.343 0.493 0.9933 0.8746 18.224
92J11B 16 −0.1393 0.0027 11.148 0.213 0.9613 0.8738 44.007
92J11C 16 −0.1320 0.0057 10.558 0.453 0.9816 0.8702 19.907
92J11D 16 −0.1362 0.0052 10.894 0.420 0.9735 0.8443 21.298
92J12A 16 −0.1389 0.0022 11.110 0.180 0.9690 0.8835 52.750
Mean (Hlabest)=10.61
S.E. = 0.15

The magnetic field of 40 μT used to impart most of TRM's was very accurately reproduced by paleointensity determination in each case. Standard error of the mean (S.E.) does not exceed 2% of the expected value in any of the cases. For these samples, the ‘NRM’ fraction f used for determination ranges between 0.774 to ∼1.0, except for two cases; and the quality factor q varies from 8.4 to 84.6, except for two cases (Table 1). It should be noted that when the strength of applied laboratory field matches to ‘ancient’ field intensity, the mean q value is at least 30% higher. The same is true for f and g factors, respectively. Moreover, the combination of these latter factors yields the same pattern as the q factor alone (Fig. 2).

Fig. 2

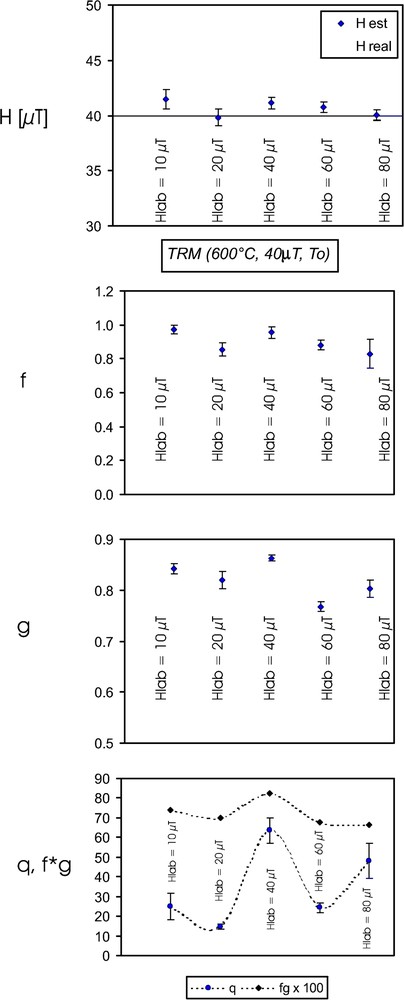
Paleointensity and Coe's [6] quality factors versus applied laboratory field. The full TRM is produced under a 40-μT magnetic field from 600 °C to room temperature (see text for details).

Paléointensité et facteurs de qualité de Coe et al. [6] en fonction du champ appliqué en laboratoire. TRM total est produit sous un champ magnétique de 40 μT, depuis 600 °C jusqu'à la température ambiante (voir le texte pour les détails).

In the specific case in which TRM's were imparted in 10 μT and the laboratory field was set to 80 μT, the intensity was also precisely reproduced (S.E. < 0.2%, Table 2, Fig. 3). It is quite evident that the intensity of the magnetic field may be reproduced even if the magnitudes of ‘ancient’ and laboratory fields differ too much.

Fig. 3

Paleointensity and Coe's [6] quality factors for each one of the 16 samples. The full TRM is produced under a 10-μT magnetic field from 600 °C to room temperature and the laboratory field is set to 80 μT (see text for details).

Paléointensité et facteurs de qualité de Coe et al. [6] pour chacun des 16 échantillons. TRM total est produit sous un champ magnétique de 10 μT, depuis 600 °C jusqu'à la température ambiante (voir le texte pour les détails).

4 Conclusion

Results obtained in this study reinforce the general conclusion reached by Tanaka and Kono [21]. On the other hand, the quality of determination, expressed here as Coe's quality factors (Figs. 2 and 3), are significantly higher when the strength of the applied laboratory field matches the ‘ancient’ field intensity.

Acknowledgements

This study was supported by UNAM–DGAPA IN 100403 and CONACYT grant n° 42661. We thank A. Gonzalez-Rangel for assistance with the paleointensity measurements.

Bibliographie

[1] A.J. Biggin; D.N. Thomas Analysis of long-term variations in the geomagnetic poloidal field intensity and evaluation of their relationship with global geodynamics, Geophys. J. Int., Volume 152 (2003), pp. 392-415

[2] M. Calvo; M. Prévot; M. Perrin; J. Rissager Investigating the reasons for the failure of paleointensity experiments: A study on historical lava flows from Mt. Etna (Italy), Geophys. J. Int., Volume 149 (2002), pp. 44-63

[3] A. Chauvin; P. Roperch; R.A. Duncan Records of geomagnetic reversals from volcanic islands of French Polynesia. 2. Paleomagnetic study of a flow sequence (1.2–0.6 Ma) from the Island of Tahiti and discussion of reversal models, J. Geophys. Res., Volume 95 (1990), pp. 2727-2752

[4] R.S. Coe Paleo-intensities of the Earth's magnetic field determined from Tertiary and Quaternary rocks, J. Geophys. Res., Volume 72 (1967) no. 12, pp. 3247-3262

[5] R.S. Coe; C.S. Grommé A comparison of three methods of determining paleointensities, J. Geomagn. Geoelectr., Volume 25 (1973), pp. 415-435

[6] R.S. Coe; C.S. Grommé; E.A. Mankinen Geomagnetic paleointensity from radiocarbon-dated flows on Hawaii and the question of the Pacific nondipole low, J. Geophys. Res., Volume 83 (1978), pp. 1740-1756

[7] D. Dunlop; Ö. Özdemir Rock-Magnetism, Fundamentals and Frontiers, Cambridge University Press, 1997 (573 p.)

[8] A. Goguitchaichvili; M. Prévot; P. Camps No evidence for strong fields during the R3–N3 Iceland geomagnetic reversals, Earth Planet. Sci. Lett., Volume 167 (1999), pp. 15-34

[9] A. Goguitchaichvili; J.L. Urrutia-Fucugauchi; M. Alva-Valdivia; J. Morales; J. Rissager; P. Rissager Long-term variation of geomagnetic field strength: A cautionary note, EOS Trans., Volume 85 (2004) no. 21

[10] A.A. Khodair; R.S. Coe Determination of geomagnetic paleointensities in vacuum, Geophys. J.R. Astron. Soc., Volume 42 (1975), pp. 107-115

[11] M. Kono; H. Tanaka Influence of partial pressure of oxygen on thermoremanent magnetization of basalts, Phys. Earth Planet. Inter., Volume 13 (1977), pp. 276-288

[12] A. Kosterov; M. Prévot Possible mechanisms causing failure of Thellier paleointensity experiments: results of rock-magnetic study of the Lesotho basalt, Southern Africa, Geophys. J. Int., Volume 134 (1998), pp. 554-572

[13] S. Levi The effect of magnetite particle size on paleointensity determination of the geomagnetic field, Phys. Earth Planet. Inter., Volume 13 (1977), pp. 245-259

[14] J. Morales; A. Goguitchaichvili; J. Urrutia-Fucugauchi A rock-magnetic and paleointensity study of some Mexican volcanic lava flows during the Latest Pleistocene to Holocene, Earth Planets Space, Volume 53 (2001), pp. 893-902

[15] J. Morales; A. Goguitchaichvili; J. Urrutia-Fucugauchi An experimental evaluation of Shaw's paleointensity method and its modifications using Late Quaternary basalts, Phys. Earth Planet. Inter., Volume 138 (2003), pp. 1-10

[16] T. Nagata; Y. Arai; K. Momose Secular variation of the geomagnetic total force during the last 5000 years, J. Geophys. Res., Volume 68 (1963), pp. 5277-5281

[17] M. Perrin; V.P. Shcherbakov Paleointensity of the Earth magnetic field for the past 400 My: evidence for a dipole structure during the Mesozoic low, J. Geomagn. Geoelectr., Volume 49 (1997), pp. 601-614

[18] M. Prévot; R.S. Mainkinen; R.S. Coe; S. Grommé The Steens Mountain (Oregon) geomagnetic polarity transition. 2. Field intensity variations and discussion of reversal models, J. Geophys. Res., Volume 90 (1985), pp. 10417-10448

[19] P. Riisager; J. Rissager; N. Abrahamsen; R. Waagstein Thellier paleointensity experiments on Faroes Flood Basalts: Technical aspects and Geomagnetic Implications, Phys. Earth Planet. Inter., Volume 131 (2002), pp. 91-184

[20] H. Tanaka Paleointensities of the geomagnetic field determined from recent four lava flows of Sakurajima Volcano, J. Geomagn. Geoelectr., Volume 32 (1980), pp. 171-179

[21] H. Tanaka; M. Kono Analysis of the Thelliers' Method of Paleointensity Determination. 2: Applicability to high and low magnetic fields, J. Geomagn. Geoelectr., Volume 36 (1984), pp. 285-297

[22] H. Tanaka; M. Kono; H. Ushimura Some global features of paleointensity in geological time, Geophys. J. Int., Volume 120 (1995), pp. 97-102

[23] E. Thellier; O. Thellier Sur l'intensité du champ magnétique terrestre dans le passé historique et géologique, Ann. Géophys., Volume 15 (1959), pp. 285-376

Commentaires - Politique

Ces articles pourraient vous intéresser

Further absolute geomagnetic paleointensities from Baja California: evaluation of Pliocene and Early/Middle Pleistocene data

Juan Morales; Avto Goguitchaichvili; Edgardo Cañon-Tapia; ...

C. R. Géos (2003)

Absolute paleointensity of the Earth's magnetic field during Jurassic: case study of La Negra Formation (northern Chile)

Juan Morales; Avto Goguitchaichvili; Luis M. Alva-Valdivia; ...

C. R. Géos (2003)

Mineralogical changes upon heating in the Millbillillie meteorite: Implications for paleointensity determination in Apollo samples

Cécile Cournède; Ian Garrick-Bethell; Robert S. Coe; ...

C. R. Géos (2016)