Abridged English version
The contamination of groundwaters by nitrates in the M'nasra aquifer has raised special interest in the last few years [10,17] because of the worries generated by the increasing level of degradation of water quality and the related toxicological consequences of nitrates for human health [4]. With the intensification and modernization of agriculture, the amounts of nitrogen fertilizers are constantly increasing. The potential impact of contamination by fertilizers and pesticides on water supply led to the development of models to simulate the soil and plant system. Saadi and Maslouhi [10] developed for instance a mechanist model to predict the water run-off, and the transport and transformations of nitrogen in the unsaturated soil in the agricultural area of M'nasra.
Our research work deals with a sandy soil contained in two PVC columns of 1-m height and 0.52-m diameter. A TDR probe was inserted into the centre of each column to measure the moisture of the soil in each profile. In this study, different irrigation intensities into the column were applied as a function of time. The total simulated intensities for a period starting 4 May (0 h) to 10 June 2002 (888 h) corresponds to a total irrigation of 325 mm. 200 kg N/ha as ammonium nitrate NH4NO3 were applied at the top of the first column 24 h after the first irrigation, and none to the second. The mathematical model used for water flow and transport is one-dimensional. In this study, we used subroutines that simulate the soil water regime based on the numerical solution of Richard's equation and the transport of chemicals in the soil by the general convection–dispersion equation.
Results shown in Fig. 2 indicate that the losses of nitrogen by leaching were very high at the exit of the soil column having received an application rate of 200 kg N/ha. This indicates that the ions are not retained by the soil, which leads to a linear response between fertilization rate and the concentration of the leached water. The quantities of nitrate nitrogen drained are of 4044 mg N–NO3, i.e. 191 kg N/ha.
Teneurs volumiques en eau, mesurées et calculées dans les différents niveaux du profil du sol.
Measured and calculated volumetric water content at different soil profile depths.
The column with a 0 kg N/ha application gives an output exceeding of 320 mg N–NO3, equivalent to 15 kg N/ha that ends up in drainage water and which is the result of the mineralization of soil organic matter.
Fig. 3 represents the observed and simulated time variation of the quantity of nitrate nitrogen leached (kg/ha) above the bottom of the soil column. One can see that experimental measurements and simulations by the model are close. Furthermore, the simulated nitrate leaching dynamic is satisfactory. During the simulation period, the quantity of drained nitrate nitrogen calculated by the model was 233 kg N/ha and exceeded the measured quantity (191 kg N/ha). The observed differences may be explained per measurement errors, by the difference between the real content of soil organic matter and that taken into consideration by the model, or by the values assigned to potential parameters of mineralization and nitrification kinetics, which depend on water content and temperature, factors not taken into consideration in our study.
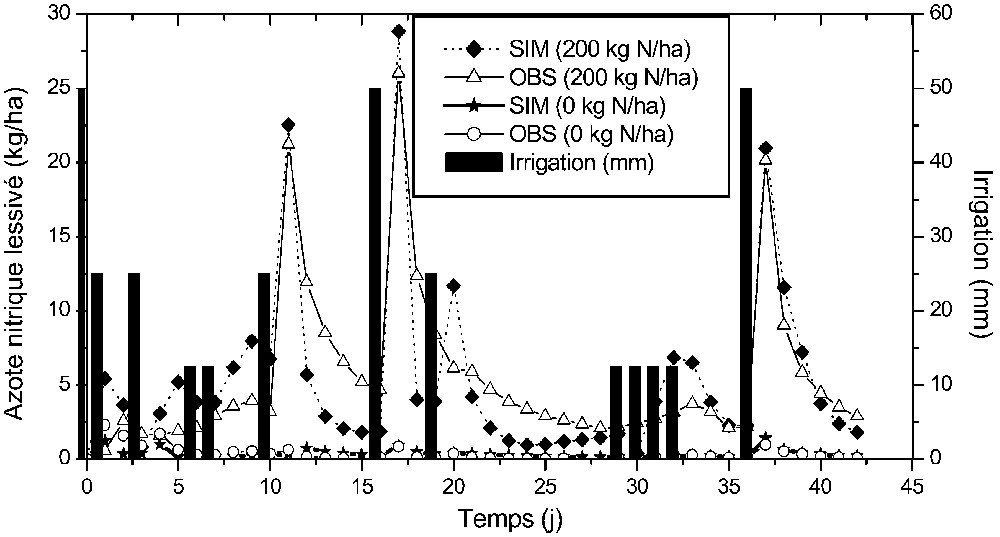
Quantités d'azote nitrique lessivé mesurée et calculée à l'aide du modèle pour les deux colonnes.
Leached quantities of nitric nitrogen measured and calculated by the model for both columns.
In conclusion, the present study showed the impact of organic matter on the increase of nitrate nitrogen leaching in soils, which translated into an appreciable loss of nitrates from the soil columns and their accumulation in the drainage water. The dynamic of nitrate nitrogen in a soil column was well represented by the model with a slight overestimation of the leached amount.
1 Introduction
La contamination des eaux souterraines au Maroc [6,11,17] a suscité, ces dernières années, une attention particulière, en raison des problèmes causés par la dégradation de plus en plus importante de la qualité de l'eau des nappes par les nitrates, avec des conséquences toxicologiques sur la santé des individus [4]. Les mauvaises pratiques agricoles, notamment les apports abusifs d'engrais azotés, conjugués à un mode d'irrigation inadapté, en demeurent les principales causes. Ces dernières années, un certain nombre de modèles ont été développés pour étudier le transport de solutés réactifs dans les milieux poreux [3,16]. L'impact potentiel de la contamination par les engrais azotés sur la nappe de M'nasra a incité Saadi et Maslouhi [10] à développer un modèle mécaniste capable de prédire l'écoulement de l'eau, le transport et les transformations de l'azote dans la zone non saturée des sols agricoles de la région de M'nasra.
Dans le cadre de cette étude, nous avons utilisé un sol sablonneux similaire à celui de la zone de M'nasra, disposé dans deux colonnes de laboratoire, dont le but était d'étudier l'impact des irrigations successives sur la lixiviation de l'azote appliqué à deux doses de 200 kg N/ha et 0 kg N/ha de nitrate d'ammonium NH4NO3, respectivement. Sur la première colonne, l'application d'engrais a été suivie de plusieurs irrigations. Sur la deuxième colonne, les mêmes irrigations ont été faites, mais sans apport initial d'azote. L'objectif de ce travail est l'étude de l'impact des effets de l'irrigation sur la lixiviation de l'azote nitrique et, d'autre part, la comparaison des données expérimentales d'azote nitrique lixivié avec les simulations numériques, à l'échelle d'une colonne de laboratoire contenant un sol sableux, plus ou moins stratifié. Le modèle numérique utilisé est un modèle mécaniste développé au LMFTT de la faculté des sciences de Kénitra [10]. Cette étude sera exploitée à grande échelle dans les sols agricoles de la région de M'nasra.
2 Matériels et méthodes
2.1 Déroulement expérimental
Le présent travail de recherche a porté sur un sol sablonneux dont les caractéristiques physico-chimiques sont reportées dans le Tableau 1. Ce sol est disposé dans deux colonnes identiques en PVC de 1 m de hauteur et 0,52 m de diamètre (Fig. 1). Une sonde TDR à profil a été insérée verticalement dans chacune des deux colonnes, et permet la mesure instantanée de l'humidité pour différentes profondeurs [7]. Les deux sondes ont été reliées à un multiplexeur. Chaque profil d'humidité en 5 segments est mesuré toutes les 10 min. Différentes intensités d'irrigation simulées en fonction du temps ont été appliquées aux deux colonnes, dont la somme pour la période allant du 4 mai (0 h) au 10 juin 2002 (888 h) correspond à un total d'irrigation de 325 mm. D'autre part, 200 kg N/ha de nitrate d'ammonium NH4NO3 ont été appliqués à la surface de la première colonne, 24 h après la première irrigation, et rien sur la seconde. L'application d'engrais a été suivie d'une première irrigation d'intensité simulée de 50 mm/h (30 min), puis respectivement de 50, 25, 25, 50, 100, 50, 25, 25, 25, 25 et 100 mm/h (Fig. 3). L'échantillonnage des eaux de drainage en bas de la colonne a été effectué manuellement. Les nitrates ont été analysés par la méthode de réduction des nitrates par le cadmium.
Caractéristiques physico-chimiques initiales du sol étudié
Initial physicochemical characteristics of the studied soil
| Profondeur (cm) | pH | Ntotal en g/kg | Ctotal en g/kg | Sable en % | Argile en % |
| 15 | 7,24 | 0,005 | 0,24 | 98,4 | 1,6 |
| 30 | 7,29 | 0,003 | 0,17 | 97,8 | 2,2 |
| 45 | 7,07 | 0,059 | 1,8 | 97,2 | 2,8 |
| 60 | 7,09 | 0,140 | 1,2 | 96,60 | 3,1 |
Montage expérimental.
Experimental setup.
2.2 Description du modèle
Le modèle mathématique utilisé est un modèle mécaniste, dont les paramètres peuvent être déterminés à partir des propriétés physicochimiques du sol ou trouvés dans la littérature. L'écoulement non saturé de l'eau est décrit par l'équation monodimensionnelle de Richard sous sa forme capacitive.
| (1) |
Les courbes caractéristiques du milieu poreux non saturé, i.e. sa courbe de rétention et sa conductivité hydraulique non saturée , sont décrites par les équations de Van Genuchten [14] et de Brooks et Corey [2], respectivement :
| (2) |
| (3) |
La granulométrie du sol étudié est très proche du sol sableux de la zone de M'nasra. Les cinq paramètres () ont été déterminés (Tableau 2), en combinant les modèles de Van Genuchten et de Brooks et Corey avec la technique de mesure in situ de l'infiltrométrie à disque à charge négative [12].
Paramètres hydrodynamiques et dispersifs du sol étudié
Hydraulic and dispersive parameters of the studied soil
| Paramètres | Littérature | Calés |
| 5,6 (m j−1) | ||
| 0,34 (m3 m−3) | ||
| 0,012 (m3 m−3) | ||
| −0,275 (m) | ||
| m | 0,173 | |
| η | 6,2 | |
| 4,2×10−4 (j−1) | ||
| 0,15 (j−1) | ||
| 6,24×10−5 (m2 j−1) | ||
| λ | 0,06 (m) |
Le transport de l'azote dans le sol est décrit par l'équation générale de convection–dispersion [15] :
| (4) |
Par la suite, on ne présentera que les processus dominants dans la colonne du sol, la minéralisation et la nitrification.
La minéralisation est l'un des processus qui conduit à un gain d'azote minéral. C'est la phase de minéralisation qui conduit à une décomposition de la matière organique pour donner, entre autres, l'azote ammoniacal (). Elle est décrite dans ce travail par le modèle simplifié de Hénin [5] :
| (5) |
Le processus de la nitrification traduit l'oxydation biologique de l'ammonium en nitrates () par des microorganismes adaptés. Il est modélisé par une cinétique du premier ordre, selon le modèle de Misra et al. [8] :
| (6) |
Le Tableau 2 fournit les valeurs des paramètres cinétiques retenus.
2.3 Effets hydriques et thermiques sur les cinétiques biochimiques
Les constantes réelles (K) des lois cinétiques (5) et (6) sont déduites des valeurs potentielles () ( ou ) en utilisant les facteurs de pondération thermique () et hydrique () :
| (7) |
Pour tenir compte de l'effet thermique sur les processus de minéralisation et de nitrification, le modèle utilisé se base sur une loi en qui permet de déterminer le facteur pour des écarts de température de l'ordre de 10 °C [1] :
| (8) |
2.4 Conditions initiales et conditions aux limites
2.4.1 Conditions initiales
La teneur en eau et la concentration en azote nitrique initiales, relatives à chaque couche de chaque colonne, sont reportées dans le Tableau 3.
Valeurs initiales de la teneur volumique en eau et de l'azote nitrique
Initial values of volumetric water-content and nitric nitrogen
| Couche (cm) | Teneur volumique en eau initiale (cm3 cm−3) | Concentration initiale en azote nitrique (mg kg−1) |
| 0–15 | 0,052 | 0,21 |
| 15–30 | 0,067 | 0,32 |
| 30–45 | 0,122 | 0,6 |
| 45–60 | 0,10 | 0,70 |
| 60–75 | 0,097 | 0,5 |
| 75–90 | 0,098 | 0,5 |
2.4.2 Condition à la limite supérieure
La dissolution, dans l'eau de l'irrigation, de la masse d'azote apportée à la surface de la colonne entraîne un flux massique résultant d'un terme convectif et d'un terme dispersif.
Ceci se traduit mathématiquement par l'expression suivante :
2.4.3 Condition à la limite inférieure
La condition de drainage gravitaire traduit un gradient de concentration nul à la sortie de la colonne, exprimé par :
3 Résultats et discussion
3.1 Analyse de la teneur volumique en eau
La Fig. 2 montre les profils hydriques simulés et mesurés après une durée de 30 min d'infiltration pour différentes profondeurs de sol : (0–15, 30–45, 45–60 et 60–75 cm). On constate que les écarts entre la teneur volumique en eau initiale et maximale Δθ sont presque identiques pour les différentes couches, cette constatation confirmant le respect du bilan de masse hydrique que l'on a calculé et qui était toujours égal à 100%. Ceci prouve que le modèle numérique est stable et qu'il peut être utilisé pour des temps d'infiltration très importants. Par ailleurs, on constate que les simulations reproduisent d'une manière satisfaisante les mesures expérimentales.
3.2 Analyse de l'azote nitrique dans les eaux de drainage
La quantité d'azote nitrique lessivée en fonction du temps, au niveau des deux colonnes de sol, est illustrée sur la Fig. 3 (résultats observés). La production de lixiviat est directement reliée aux épisodes d'irrigation. Ces résultats montrent que, durant les quatre premiers jours, la quantité d'azote nitrique drainée provient surtout de la matière organique que contient le sol et non pas des engrais azotés apportés au sol sous forme minérale. En effet, le temps nécessaire à l'engrais azoté pour arriver à la base de la colonne est directement lié à la très lente dissolution de l'engrais appliqué au sol.
Par ailleurs, les tests effectués sur la première colonne montrent que l'effet de la quantité d'eau sur le transport de l'azote nitrique en profondeur se traduit par une perte appréciable des nitrates au niveau des couches supérieures et leur accumulation dans les couches profondes pour se retrouver finalement dans les eaux de drainage, avec un cumul de 4044 mg (soit 191 kg N/ha) pour un taux d'épandage de 200 kg N/ha (correspondant à 4240 mg d'azote nitrique épandu). Ce phénomène de lixiviation a été décrit, entre autres, par Poss et Saragoni [9]. De plus, les tests effectués sur la deuxième colonne (apport de 0 kg N/ha) indiquent qu'une quantité de 320 mg de N–NO3, équivalant à 15 kg/ha, est retrouvée dans les eaux de drainage. Ce résultat montre bien que la quantité d'azote nitrique drainée pour cette colonne est due uniquement à la minéralisation de la matière organique contenue dans le sol.
Enfin, en tenant compte de la quantité d'azote libérée par minéralisation obtenue pour la deuxième colonne (sans apport d'engrais) et supposée égale à celle libérée par la première colonne, on peut calculer par différence la quantité d'azote lixiviée provenant directement de l'engrais appliqué au niveau de cette première colonne, qui est de 176 kg/ha. De ce fait, on peut affirmer, à partir des résultats obtenus, qu'une quantité résiduelle d'azote nitrique équivalant à 24 kg N/ha reste stockée dans l'humidité résiduelle du sol. Ceci est montré par les résultats d'analyse, à la fin de l'essai, de l'azote nitrique contenu dans les différentes couches du sol de la première colonne (Tableau 4), où l'on retrouve une quantité résiduelle d'azote nitrique, de l'ordre de 8 mg/kg, équivalant à 18 kg/ha, dans le profil du sol 0–75 cm. À cette quantité devrait s'ajouter la quantité de l'azote nitrique qui reste stockée dans la couche 75–90 cm et qui n'a pas été analysée.
Valeurs finales des quantités résiduelles de l'azote nitrique observé stocké dans le sol
Final values of observed nitric nitrogen stored in the soil
| Profondeur (cm) | 0–15 | 15–30 | 30–45 | 45–60 | 60–75 | Total (kg/ha) |
| observé (mg kg−1) | 0,62 | 0,81 | 1,95 | 2,26 | 2,3 | 18,04 |
Il ressort de cette étude que les aquifères de sol sablonneux à faible teneur en argile et en matière organique, tel que celui de la région de M'nasra au Maroc, sont particulièrement sensibles à la contamination par l'azote nitrique. Toute sur-fertilisation se retrouvera rapidement lessivée vers la nappe phréatique à la suite de périodes d'irrigation ou de pluie. Ces sols retiennent très peu l'azote, qui pourrait être subséquemment utilisé par les plantes.
3.3 Simulation de la lixiviation de l'azote nitrique
La Fig. 3 représente les variations temporelles, simulées et observées, des quantités d'azote nitrique lessivé (kg N/ha) à la base des deux colonnes de sol utilisées. Pour la première colonne (apport de 200 kg N/ha), on constate l'apparition des pics des concentrations d'azote nitrique lessivé pendant les périodes d'irrigation. Ceci est expliqué par l'évolution de l'ion () qui se comporte comme un traceur et peut donc facilement être entraîné par l'eau dans ce type de sol. Par ailleurs, les mesures expérimentales et les simulations du modèle sont très proches. En effet, la dynamique de lessivage du nitrate simulée est satisfaisante. Durant la période de simulation, la quantité calculée d'azote nitrique drainée a été de 233 kg/ha, et dépasse un peu celle mesurée pour le sol sablonneux, qui est de 191 kg/ha, soit une surestimation de 20%. Par ailleurs, on constate que, pour la deuxième colonne (0 kg N/ha), le modèle numérique (Fig. 3) reproduit d'une manière satisfaisante les faibles quantités d'azote nitrique lessivé observées par l'expérience.
Les écarts observés peuvent être dus aux erreurs de mesure et d'analyse chimique, à la différence entre la quantité de la matière organique réellement existante dans le sol étudié et celle prise en compte par le modèle, ou bien à l'influence d'autres phénomènes physiques mal connus, qu'il faudrait probablement introduire dans la modélisation.
4 Application du modèle : effet de la quantité d'azote appliquée
La Fig. 4 montre les résultats des simulations pour quatre doses d'azote (NH4NO3) de 0 à 300 kg N/ha. Cette figure montre la quasi-linéarité entre le taux d'épandage d'azote et la lixiviation de l'azote nitrique au niveau des sols sablonneux. Par ailleurs, on remarque que la lixiviation nitrique est importante quand la dose d'azote est élevée et que les quantités d'azote épandues à la surface du sol nu se retrouvent totalement dans les eaux de drainage. Ceci est évidemment lié à la nature sableuse du sol et à la fréquence d'irrigation durant la période de l'essai. En général, les agriculteurs de la zone de M'nasra ont tendance à exagérer les apports d'azote (Tableau 2) pendant les périodes d'épandage (enquête faite par la SCET–Maroc [11] auprès des agriculteurs de la zone de M'nasra). La nature sableuse des sols de M'nasra (similaire à celle du sol des colonnes étudiées) font que les excès d'azote vont être disponibles pour un entraînement vers les couches plus profondes des sols et éventuellement s'accumuler dans les nappes superficielles de la zone. Saadi et Maslouhi [10] ont montré que, lorsque la dose d'engrais est au moins de 120 kg N/ha, la concentration annuelle en nitrates , qui peut être observée dans l'eau de la nappe de la zone de M'nasra, est toujours supérieure à 50 mg/l (11 mg/l ).
Variation de l'azote nitrique lessivé en fonction de la dose d'engrais azoté.
Leached nitric nitrogen variation as a function of the amount of nitrate fertilizer applied.
5 Conclusion
L'étude expérimentale a montré que l'accumulation de quantités importantes d'azote nitrique dans les eaux de drainage est reliée, d'une part, à la nature du sol (sablonneux) et, d'autre part, à l'effet d'irrigations successives. Ceci montre que les aquifères de sol sablonneux à faible teneur en argile et en matière organique, tel que celui de la région de M'nasra (Maroc), sont particulièrement sensibles à la contamination par l'azote nitrique. D'où la nécessité de contrôler les pratiques d'irrigation et l'augmentation de la teneur en matière organique des sols, tout en réduisant l'apport d'engrais minéral aux sols sablonneux.
Par ailleurs, le modèle numérique utilisé a permis de simuler la dynamique de l'azote nitrique dans les deux colonnes de sol étudiées. Il a, en effet, pu reproduire d'une manière satisfaisante les quantités d'azote nitrique lessivées à la sortie de la colonne, avec cependant une légère surestimation. De plus, pour les conditions d'expérimentation, le modèle montre une quasi-linéarité entre le taux d'épandage d'engrais et la lixiviation de l'azote nitrique au niveau des sols sablonneux, et a mis en évidence le fait que toute fertilisation excessive se retrouvera rapidement lessivée vers la nappe phréatique à la suite d'un épisode d'irrigation ou de pluie.
Remerciements
Les auteurs tiennent à remercier le projet PROTARS III n○ D45/06 pour l'aide fournie lors de la réalisation de la présente étude.