Abridged English version
Introduction
Inclinometry is the discipline that studies variations of ground tilt under the action of geophysical phenomena in relation to an initial state. It is used in various fields, for example, vulcanology [2], tectonics [3] or the study of Earth tides. Recent technical improvements of these instruments [6,10] make it possible to imagine an extension of their use. This paper proposes to study the capacity of inclinometry and hydrostatic tiltmeters to monitor aspects of the evolution of an aquifer. Measurements of the loading effects associated with water oscillations in the Gulf of Corinth (Fig. 1) indicate that this capacity exists.
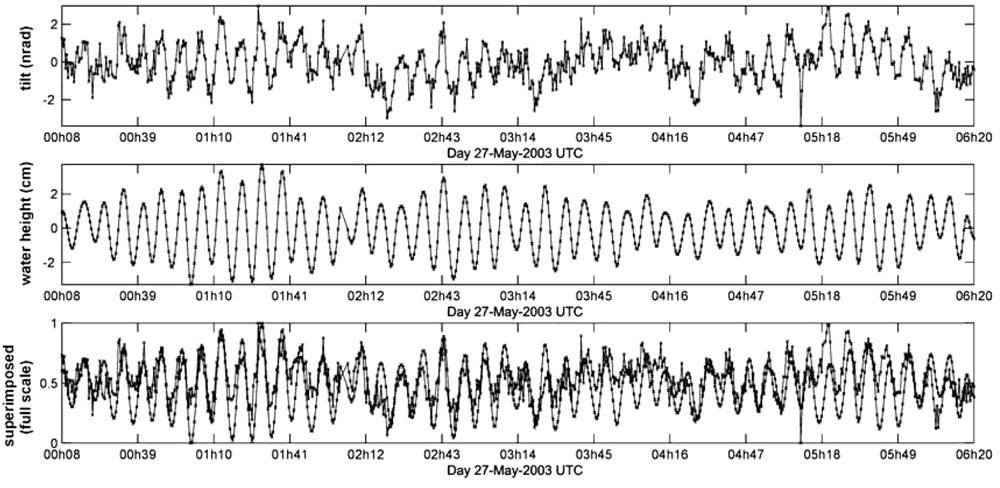
Signal inclinométrique associé à une seiche de quelques centimètres dans le golfe de Corinthe. Il montre que l'on a une réponse flexurale de l'ordre de 10−9 rad par centimètre de colonne d'eau, augurant le potentiel de l'inclinométrie pour l'étude des aquifères.
Inclinometer signal associated with a cuttlefish of a few centimetres in the Gulf of Corinth. It shows that the response is flexural and in the order of 10−9 rad per centimetre of water column, indicating that tilt measurements may be useful in aquifer studies.
Theoretical formulation of the incline produced by a load
The tilt measures the angular time variation between the normal to the geoid (plumb line or vertical) and the direction of a reference linked to the ground, with respect to an arbitrary initial state. The theoretical work by Farell [11] and Pagiatakis [16] explains the relation linking a spatial surface load distribution to the induced tilt signal. Assuming a spherical Earth and a linearity of the Earth's response to the applied forcing, Green's function, providing the tilt response, is simply a convolution with the load. The same applies to gravity, variations of the potential and radial displacements. Imagining a sufficiently dense hypothetical network of inclinometers, it should be possible to know the variations in load by deconvolution. As the Green function of tilt behaves in (Fig. 3), one can expect a more or less identical sensitivity of the incline to the different spatial scales of load variation. Moreover, the convolution properties are such that one can show the signal to be dependent on the sole load gradient, which is hydrogeologically significant.
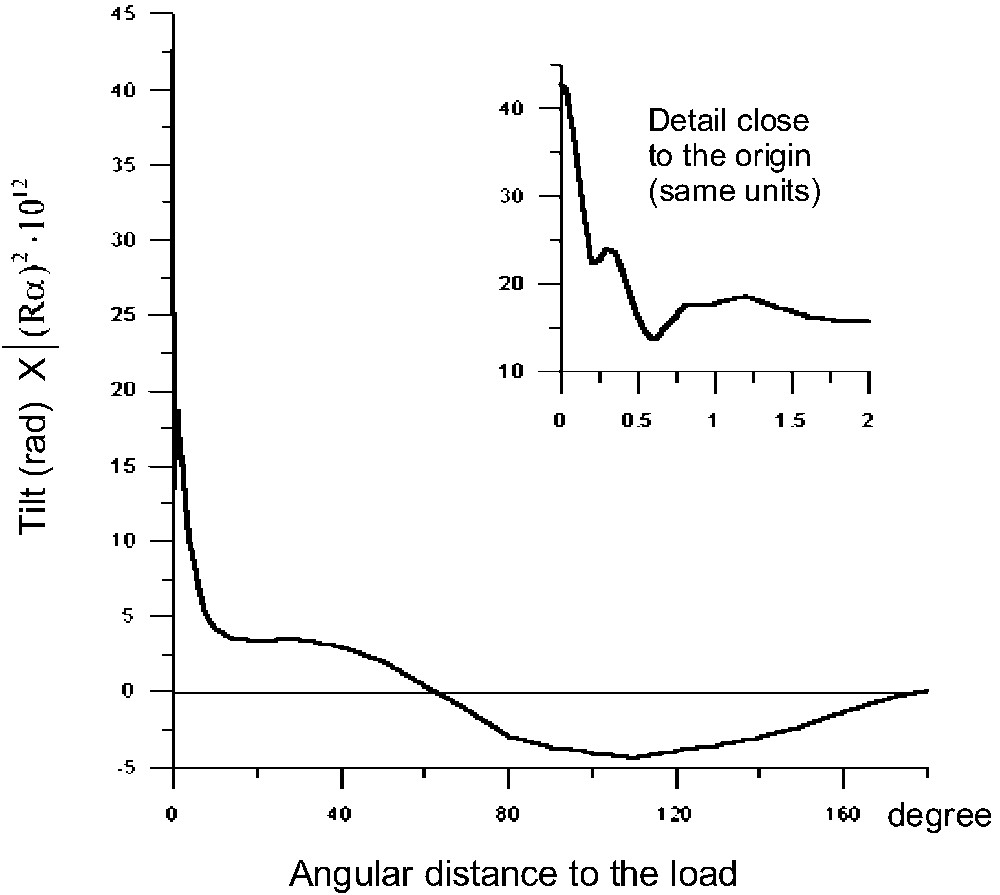
Fonction de Green pour l'inclinaison créée par une charge unitaire et ponctuelle placée à la distance angulaire α du point de calcul. Résultats d'après le tableau de Pagiatakis [16]. Une normalisation par 1012 a été appliquée à la fonction (où R est le rayon terrestre moyen).
Green's function for the inclination created by a unit point load placed at the angular distance α from the calculation point. Results according to the table by Pagiatakis [16]. The function was normalised by 1012 (R is the mean Earth radius).
Inclinometric modelling of simple hydrogeological systems
In order to quantify the tilt signal in basic configurations, two computing grid schemes were used: one with a rectangular grid, with finer meshes around the point where the convolution is estimated (this is necessary because of the singularity at the origin of the Green function); the second one with a circular symmetry, whose annular meshes increase in size in . These two models were validated by the comparison of their results on simple hydrogeological cases. We chose the second one which produced similar results with a minimum number of cells. Thus, we obtained information on the relationship between inclinometry and hydrogeology. The order of magnitude of the tilt caused by a realistic aquifer (10 cm of water recharge on a 50-km square) is thus in the order of 10−9 to , which lies within the sensitivity range of modern tiltmeters (Fig. 4). Moreover, as expected, the tilt is particularly sensitive to a discontinuity in the aquifer. Finally, the simulation of the incline for a sinusoidal aquifer of variable wavelength (Fig. 5) confirmed our assumption of an equal sensitivity to all scales of load variation.
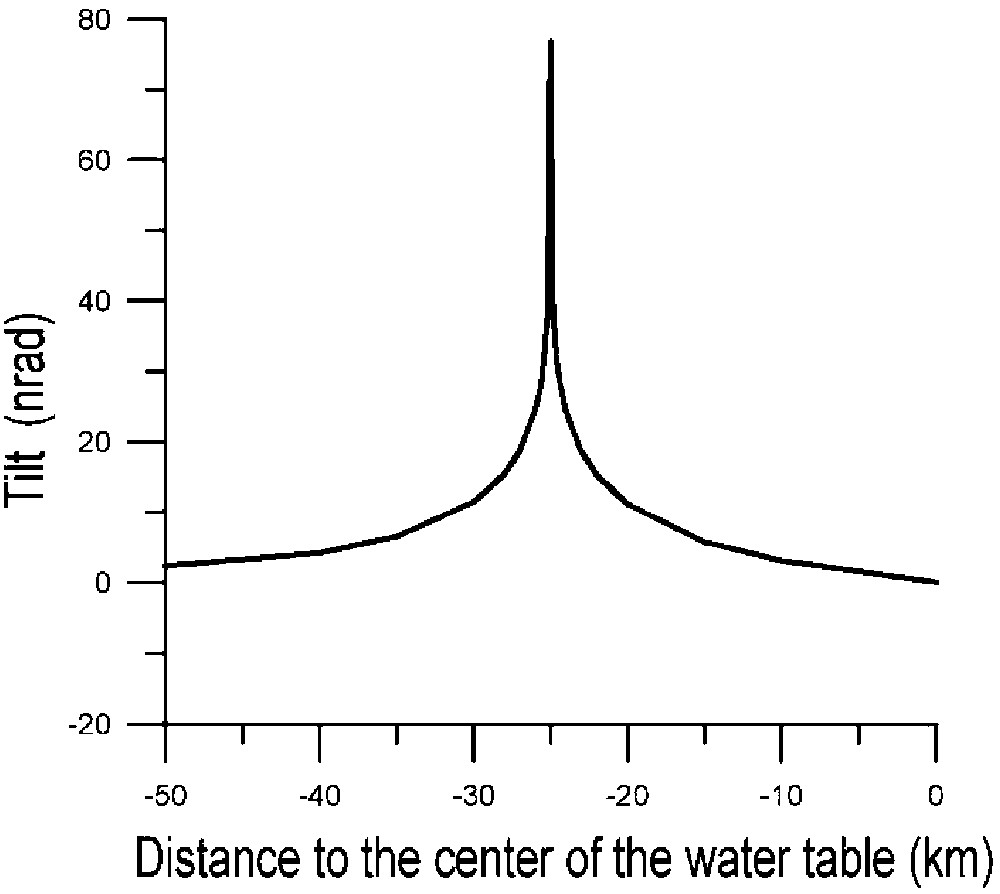
Inclinaison due à une variation de 1m du niveau d'eau dans un aquifère carré (50 km de côté) de porosité 10%. Les points sont répartis le long d'un profil partant du centre (distance = 0 km) et passant par le côté d'un carré (distance = −25 km). L'inclinaison selon la direction du centre de l'aquifère a été calculée par la méthode décrite dans le texte, pour un maillage « cible de fléchettes », en chacun des points du profil.
Inclination due to a 1-m water level variation in a square aquifer (50-km side) with a 10% porosity. The points are distributed along a profile starting from the centre (distance = 0 km) and passing through the side of a square (distance = −25 km). The inclination in the direction of the aquifer centre was calculated at every point of the profile by the method described in the text using a ‘dart-board’ grid.
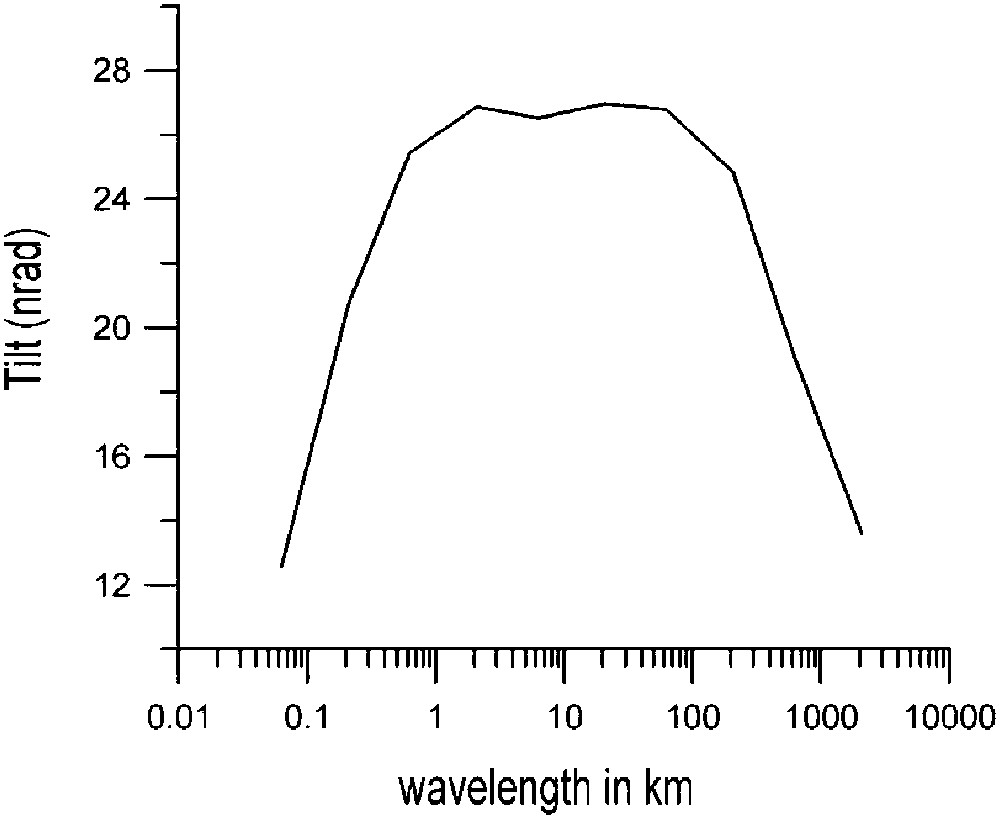
Inclinaison calculée au centre d'une nappe dont le niveau varie sinusoïdalement (amplitude : 1 m). La longueur d'onde des variations est donnée en abscisse.
Calculated inclination at the centre of an aquifer whose level varies sinusoidally (amplitude: 1 m). The wavelengths of the variations are shown on the horizontal axis.
Study of the Seine basin (France)
This model was applied to data resembling reality, taken from the hydrogeological modelling done by Eric Gomez [12] on the Seine basin aquifer. The circular symmetry model was used to estimate the inclinometer signal along a transverse cross-section of the Seine basin during a hydrological year from August 1990 to July 1991.
The magnitude of the calculated incline was found to be about , which agrees with the magnitude of the fluctuations generally observed in inclinometer recordings [6]. Furthermore, the results can be interpreted in hydrogeological terms. The transverse projection of the tilt with respect to the mean Seine direction (Fig. 7) is noticeably amplified at the margins of the chalk plateaus north and south of the basin. This is a real-case illustration of the sensitivity of the tilt to hydrogeological discontinuities. The projection of the tilt along the axis of the basin in the Paris region (Fig. 8) shows a general load gradient that increases in the course of the hydrologic year, which is also in agreement with the hydrogeological reality.
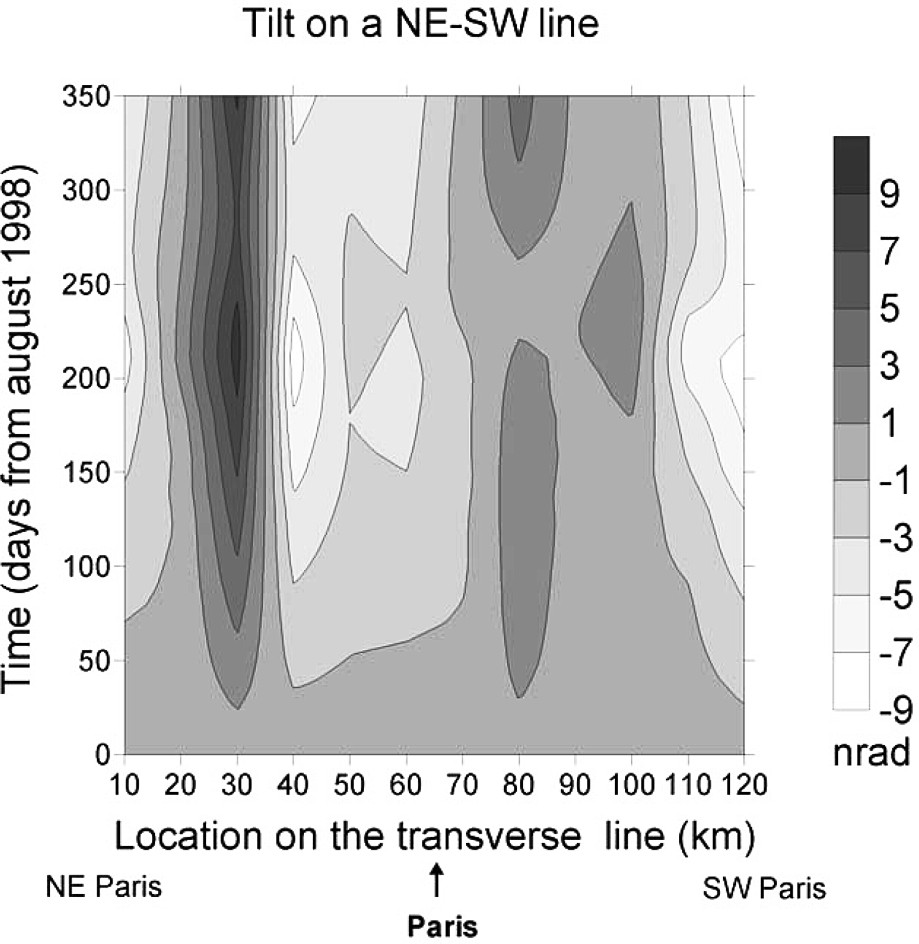
Variations temporelles entre août 1990 et juillet 1991 de l'inclinaison calculée d'après les données Modcou. L'effet de charge est estimé en 12 points distants de 10 km, répartis le long d'un profil passant par Paris, dans la direction normale à l'axe de la Seine. Le pas d'échantillonnage temporel est de 10 jours.
Variations in time between August 1990 and July 1991 of the inclination calculated with the Modcou data. The load effect is estimated at 12 points, separated by 10 km and distributed along a profile crossing Paris and running in a direction perpendicular to the Seine axis. The sampling time step is 10 days.
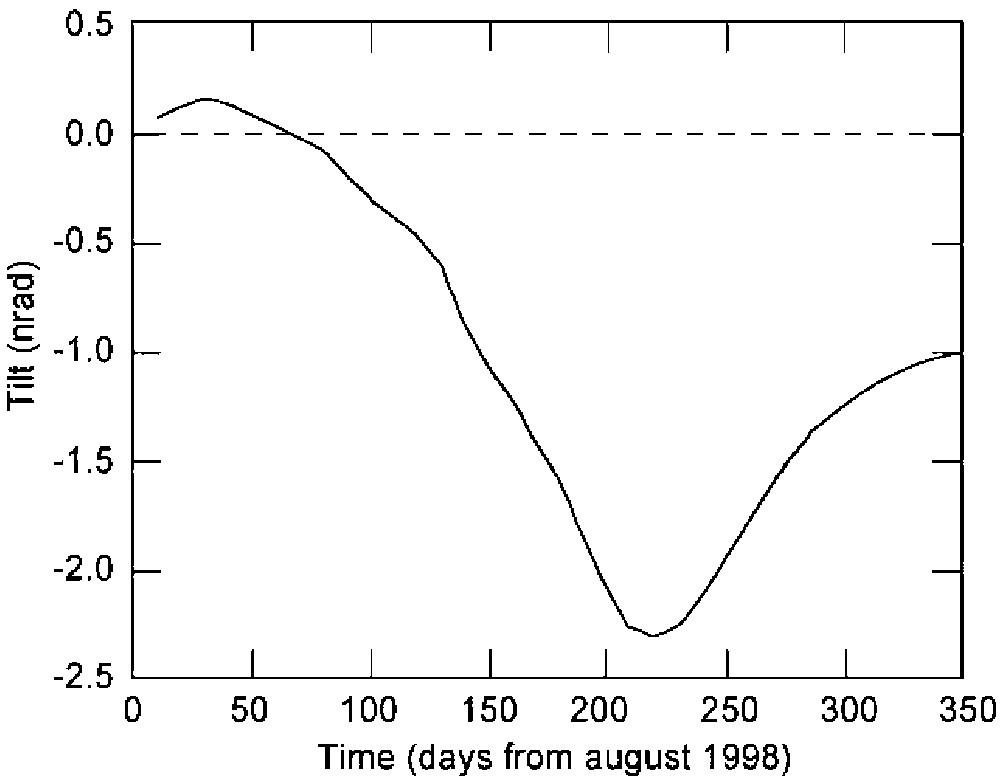
Effet inclinométrique calculé à Paris (selon l'axe moyen de la Seine) à partir des données hydrologiques fournies par le modèle Modcou, d'août 1990 à juillet 1991.
Inclinometer effect calculated in Paris (following the mean Seine direction) from hydrologic data provided by the Modcou model from August 1990 to July 1991.
Experiments in the Vosges
Two tiltmeters have been implemented in an ancient mine, in the Vosges. Observed tilt variation and predicted groundwater water induced tilts seems to be correlated and reach about 20 nrad (Fig. 9).
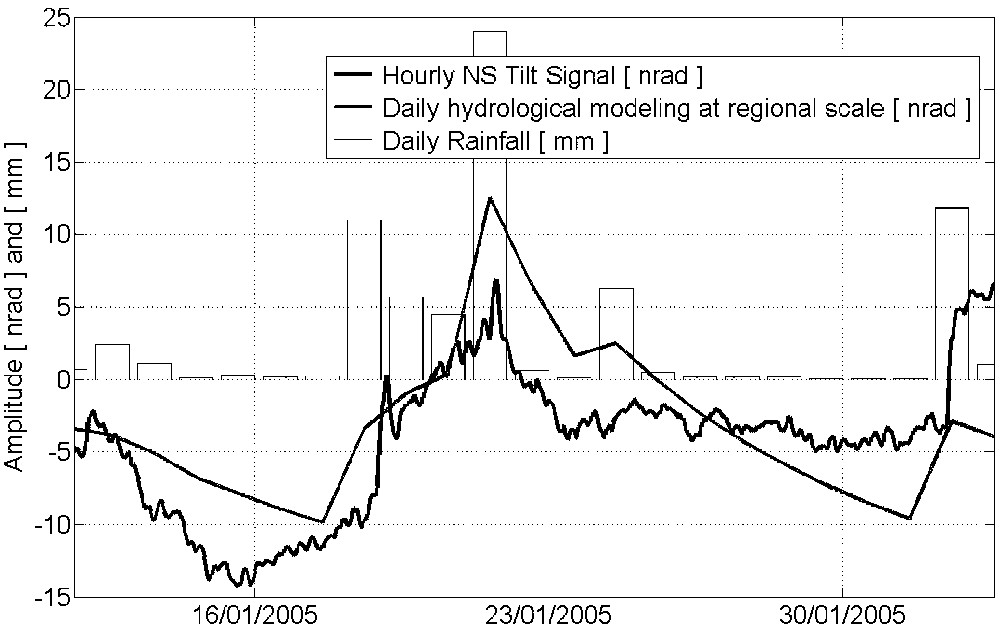
Premiers résultats expérimentaux, comparés aux effets prédits à partir d'un modèle hydrologique élémentaire, obtenus sur le site de Sainte-Croix-aux-Mines, où deux inclinomètres viennent d'êtres installés dans une ancienne galerie de mine.
First experimental results and predicted hydrological effects at the Sainte-Croix-aux-Mines site, where tiltmeters have been settled in and old mine gallery.
Conclusion
The initial estimates show that inclinometry could become a tool for monitoring groundwater reserves, provided that contributions by Earth tides and atmospheric pressure are removed from the signal (atmospheric pressure effects can be eliminated by formalisms similar to those used for groundwater reserves, while Earth tide contributions are well known). Tests are underway in the Sainte-Marie-aux-Mines valley (Vosges, France) and will soon begin on the karstic plateau of Calern (Alpes-Maritimes, France) in order to evaluate the potential of these new approaches.
1 Introduction
L'inclinométrie est la discipline qui étudie l'inclinaison prise par le sol sous l'action de phénomènes géophysiques variés : mouvements tectoniques, tassements de terrains, effets de surcharge (remplissage de lacs ou effets de la charge variable des océans, poids de l'atmosphère), marées terrestres... Le phénomène est souvent extrêmement ténu – du pico-radian à quelques microradians –, si bien qu'il est pratiquement impossible de référencer les mesures par rapport à un repère inertiel à caractère absolu (tel que celui fourni par exemple par l'International Terrestrial Reference Frame [5]). L'utilisation de pendules horizontaux (de type Zöllner) ou de systèmes de vases communicants (inclinomètres hydrostatiques) permet, cependant, une mesure directe de l'inclinaison prise par le sol par rapport à l'horizontale (qui est la surface équipotentielle représentée par le géoïde lorsque l'on est au niveau de la mer). Étant donné que cette horizontale n'est pas stable dans le temps (elle est également affectée par les phénomènes qui déforment la croûte terrestre), ces inclinomètres mesurent, de fait, la variation temporelle de l'écart angulaire entre la surface matérialisée du sol et l'équipotentielle locale, elle-même variable dans le temps.
Les développements de l'inclinométrie datent du XIXe siècle : ils ont notamment permis les premières mises en évidence expérimentales des marées terrestres [15 (chap. 8)]. Revivifiées en France, notamment grâce au travail de Pierre-Antoine Blum [4,17], ils bénéficient aujourd'hui de progrès technologiques et théoriques [6,10].
Ainsi, l'inclinométrie est-elle utilisée dans le cadre d'études en volcanologie (voir, par exemple, [2]), en tectonique (mouvements du sol liés aux séismes [3]), ou pour l'observation de la marée terrestre. Son application à d'autres phénomènes a longtemps été limitée par certains effets environnementaux parasites ou générant des artefacts (effets de cavité, variations thermiques, pression atmosphérique, etc.), que l'on ne savait pas modéliser par le passé, ou qui n'étaient pas contrôlés instrumentalement. Par exemple, les marées océaniques contribuent à des variations inclinométriques essentiellement semi-diurnes et diurnes, que l'on ne sait modéliser que depuis l'avènement de modèles océaniques ad hoc [8,18]. Ces signaux restent encore difficiles à séparer des marées terrestres proprement dites. L'inclinométrie commence toutefois à être utilisée, avec la gravimétrie et les techniques GPS, pour la validation des modèles de marées océaniques [14].
Comme la plupart des principaux phénomènes affectant l'inclinaison du sol peuvent être modélisés, il est possible de les séparer les uns des autres dans le cadre d'études spécifiques.
Dans cet article, nous étudions les possibilités de l'inclinométrie et d'inclinomètres hydrostatiques pour le suivi temporel des aquifères, par l'intermédiaire de la flexure crustale induite par la surcharge correspondante (terme associé au poids de l'eau – et non à la charge des hydrogéologues, qui est liée à une pression). Un objectif est de viser la quantification, à l'aide de cet outil, des variations de stocks d'eau, sur une échelle de temps allant de quelques minutes à quelques années, grâce à l'observation et à la modélisation de l'inclinaison de la croûte terrestre générée par les variations de surcharge associées à ceux-ci.
Pour l'étude de ces phénomènes, les inclinomètres dits hydrostatiques sont les mieux adaptés (particulièrement en termes de dérive instrumentale). Ils fonctionnent suivant le principe des vases communicants. La sensibilité de ces appareils dépend de la distance entre les deux vases. Des études récentes [3,6,10] montrent qu'elle peut atteindre pour un instrument de 100 m de long, avec une stabilité dans le temps supérieure à (pour illustration, une inclinaison de correspond à une élévation de 1 μm sur une distance de 1 km ou de 1 mm sur 1000 km). Bien que de nombreux arguments convergent pour conduire à l'affirmation que la surcharge hydrologique est mesurable avec de tels instruments, la démonstration instrumentale de la mise en évidence de ce phénomène reste à faire. De fait, plusieurs expériences nous convainquent du potentiel de cette approche. Un exemple en est donné par la mesure, tout à fait effective, de l'effet de surcharge associé à des seiches dans le golfe de Corinthe, illustré par la Fig. 1. Du point de vue de la dynamique de la croûte, les fréquences mises en jeu dans cette surcharge impliquent un fonctionnement quasi-statique : on peut ainsi faire l'analogie entre l'effet de surcharge observé (induit par cette houle) et ce que produirait un aquifère dont les variations temporelles reproduiraient la colonne d'eau équivalente. Dans le cas présent, le caractère périodique de la fonction d'excitation facilite l'identification de la cause du signal observé. Mais, pour des inclinomètres situés en plein domaine continental, cette identification doit encore être faite, et ne sera pas facilitée par le caractère stochastique du chargement (qui résulte lui-même du caractère aléatoire de la recharge des nappes). La validation passera obligatoirement par une concordance attendue entre l'observation et les effets de surcharge modélisés.
Notons que l'on n'aborde pas ici les effets de déformation des réservoirs pouvant résulter des variations de pression porale. On suppose que les inclinomètres destinés à la mise en évidence des effets de flexure sont installés à distance de tels milieux (par exemple sur un socle peu perméable, dans une galerie souterraine, etc.).
2 Formulation théorique de l'inclinaison induite par une surcharge
2.1 Généralités
Sous l'action d'une variation temporelle de force, par exemple due au poids des eaux souterraines, la Terre va réagir de façon élastique. La surface du sol se déforme, et le champ de pesanteur local est affecté, tant en amplitude qu'en direction, ce qui implique une modification de son équipotentielle origine (cette dernière définissant, comme le niveau moyen des mers, le géoïde instantané). L'inclinaison mesurée par les instruments est alors la différence entre l'inclinaison de la surface physique où se trouve mécaniquement attaché l'instrument (par rapport à son état initial, dans un référentiel assimilé inertiel) et l'inclinaison de la surface équipotentielle – qui est l'horizontale locale à laquelle se rapporte un niveau quasi-hydrostatique [15]. La Fig. 2 illustre ce phénomène dans le cas d'un inclinomètre hydrostatique, avec des échelles grandement exagérées.
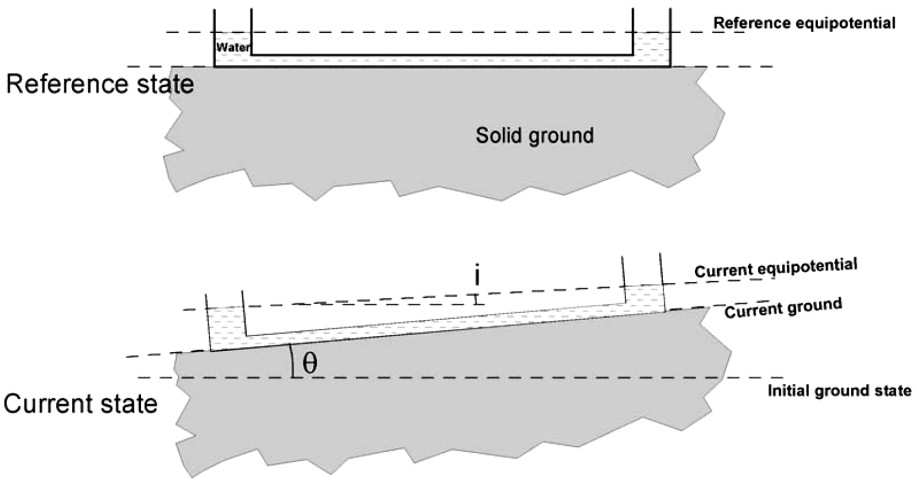
L'inclinomètre mesure la différence d entre l'inclinaison i du sol et l'inclinaison θ du géoïde, angles qui apparaissent lors de la déformation du support de l'instrument sous l'action d'une force – ici, une charge placée en surface : d=i−θ.
The tiltmeter measures the difference between the inclination i of the ground and the inclination θ of the geoid, which are angles that appear when the support of the instrument is deformed due to a forcing – here, a load placed on the surface: d=i−θ.
La théorie de la déformation quasi-statique de la planète sous l'action d'un champ de force de surcharge est synthétisée dans un article de Farrell [11]. Mais c'est dans Pagiatakis [16] que l'on trouve une réalisation numérique de la fonction de Green, qui permet de calculer, en n'importe quel point, l'angle d'inclinaison résultant de la présence d'une surcharge en surface.
Dans le cas qui nous intéresse ici, celui d'une surcharge hydrologique, on reprend d'assez près le formalisme utilisé habituellement pour le calcul de la surcharge océanique, familier dans les communautés géodésiques ; la principale différence résulte de ce que, sur le continent, on se trouve, pour le calcul des effets de la surcharge océanique, en dehors du domaine où s'exerce la surcharge, ce qui n'est pas le cas pour les aquifères. Dans tous les cas, on ne considère que les variations temporelles des masses excitatrices ou de leurs effets, par rapport à un état initial qui sert de référence (par exemple, pour la surcharge océanique, on ne tient pas compte du poids moyen des océans).
Notons que les équations ont été développées pour une Terre sphérique, constituée de couches homogènes concentriques, avec des paramètres variables du centre vers la surface. Les développements déjà cité de Farell [11] et Pagiatakis [16] adaptent, pour les effets de charge, les développements donnés par Alterman, Jarosch et Pekeris [1]. Dehant et al. [9] ont estimé les incidences de l'ellipticité, de la rotation et même de la convection mantellique, mais leur approche raffinée n'est pas requise pour une première approximation. Enfin, il a été vérifié, tant théoriquement qu'expérimentalement, que, s'agissant de très petites déformations, la réponse de la Terre est extrêmement proche de la linéarité.
Pour des raisons de symétrie, la fonction de Green ne dépend que de la distance angulaire entre la charge et le point du calcul, si bien que le formalisme avec noyau d'opérateur général dégénère en opérateur de convolution. Il est représenté sur la Fig. 3 (et numériquement donné par Pagiatakis [16]). Il peut être noté que, dans le cas d'un demi-espace homogène et isotrope, la fonction de Green se comporte à peu près en en (on parle alors du « problème de Boussinesq » [7]). Ce comportement asymptotique (aussi bien près de l'origine que pour les grandes distances) est grossièrement conservé pour la fonction de Green d'une Terre sphérique, l'écart multiplicatif à ce comportement ne s'écartant pas d'un facteur supérieur à 3, dans la limite des 180° de distance à la charge.
Une propriété notable de ce comportement est sa divergence près de l'origine. Cette divergence disparaît lors de la convolution, puisque l'intégration sur un disque de rayon r et de surface en compense cette divergence. De fait, cette intégration sur un disque de rayon r par la fonction de Green en démontre une forme d'invariance d'échelle : l'inclinaison au voisinage d'un disque uniforme ne dépend pas du rayon de ce disque. Il n'en est pas de même avec les fonctions de Green du déplacement horizontal, vertical ou de la pesanteur, qui, après intégration, sont des fonctions croissantes du rayon pris en considération. Dans le signal inclinométrique, c'est le rapport du déplacement vertical au déplacement horizontal qui est homogène à l'inclinaison. Cette propriété confère une sensibilité de la méthode sensiblement égale pour les charges locales et étendues, ce qui peut être un atout ou un inconvénient, selon que l'une ou l'autre de ces échelles est ou n'est pas modélisable (notamment pour ce qui nous concerne, selon les qualités de la description hydrogéologique à ces différentes échelles).
Cette invariance d'échelle confère un caractère apparemment absurde à la limite inférieure : une particule quasi microscopique de masse surfacique donnée produit, par effet de surcharge, en son voisinage, la même inclinaison qu'un objet étendu (de même masse surfacique). Ce paradoxe physique est levé si l'on considère la dimension intrinsèque d'un inclinomètre : quelques décimètres, pour le support d'un inclinomètre pendulaire, jusqu'à plusieurs centaines de mètres, pour un inclinomètre hydrostatique. L'instrument est intégratif selon sa dimension. De plus, les stations inclinométriques seront avantageusement installées à une certaine distance des causes induisant l'inclinaison, ou bien enfin le phénomène physique lui-même sera de dimension caractéristique bien supérieure à l'instrument.
La modélisation de la réponse à une surcharge surfacique, s'appuie la sur discrétisation de la charge en mailles élémentaires. On peut ainsi écrire que l'inclinaison en un lieu est égale à la somme des inclinaisons créées par chaque point de charge élémentaire. Une telle somme est bien l'intégrale de convolution calculée sur la totalité du domaine. On l'écrit avec des coordonnées géographiques (sphériques) :
2.2 Quelques propriétés de cette intégrale de convolution
Sous une forme condensée, l'intégrale de convolution entre la fonction T et la fonction de charge H donnant l'inclinaison peut s'écrire :
Il existe une fonction T (obtenue en résolvant le système d'équations de la déformation) pour chaque grandeur d'intérêt géodésique : déplacement vertical ou horizontal, variations de l'accélération de la pesanteur, inclinaison. Notons U et W les fonctions qui décrivent respectivement le déplacement vertical U et l'effet sur le potentiel W. L'inclinaison β est alors la différence entre le gradient (la pente) affectant le sol et le gradient (la pente) acquise par le géoïde (toujours par rapport aux surfaces initiales qui constituent la référence). Nous pouvons écrire :
D'après les propriétés de la dérivation d'une convolution, nous pouvons alors écrire :
3 Modélisation inclinométrique dans des situations hydrogéologiques simples
Nous allons tout d'abord modéliser un aquifère très simple, afin d'obtenir un ordre de grandeur des inclinaisons et avoir une première simulation de la répartition spatiale du phénomène. Cela donnera aussi une idée sur la manière d'installer des inclinomètres sur le terrain, en identifiant au préalable les zones où le signal est le plus fort. Ce premier modèle est à l'échelle d'un bassin versant régional, échelle à laquelle le problème peut être supposé plan.
3.1 Maillage de la zone de calcul
Pour l'intégration spatiale, il est nécessaire d'adapter les dimensions des mailles à la résolution du modèle d'aquifère et d'être attentif à la gestion de la fonction de Green au voisinage de la masse. En effet, les variations de cette fonction deviennent considérables près de l'origine, nécessitant un raffinement du maillage. De fait, il y a avantage, en tenant compte de l'invariance d'échelle évoquée plus haut, à ce que le rapport de la dimension d'une maille à la distance au point de charge demeure grossièrement constant.
Deux types de maillages ont été testés.
Le premier concerne une zone de , découpée selon une maille carrée de 1 km, l'endroit où est calculée l'inclinaison se trouvant au centre du maillage. Les quatre carrés (de 1 km × 1 km) touchant le point où l'on fait l'estimation sont découpés en mailles de 1 m, afin de raffiner la convolution lorsque la charge hydrologique est à proximité.
Le second est un maillage en cercles concentriques, de rayon égal à , où et C un coefficient fixé à 0,1. Chaque anneau ainsi défini est découpé en secteurs de largeur environ 10% du rayon, pour un total de 63 mailles par anneau. On obtient une distribution de l'espace semblable à une cible de jeu de fléchettes sur une zone qui s'étend d'un peu plus de 12 m à un peu plus de 500 km du point de calcul. L'influence des mailles diminue comme le carré de leur distance au centre, mais elle est compensée par l'augmentation de la surface, afin que chacune contribue à part à peu près égale dans la convolution (toujours par le jeu de l'invariance d'échelle, au facteur 3 (cité plus haut) près).
3.2 Simulation pour un aquifère simple
Un exemple de modèle de surcharge hydrogéologique élémentaire consiste en une couche d'eau d'épaisseur uniforme, répartie sur une surface carrée. Il peut représenter une variation d'un mètre du niveau d'une nappe, contenue dans un aquifère d'une porosité typique de 10% et d'une largeur de 50 km (la charge fait alors 10 cm d'épaisseur équivalente en eau).
Nous calculons le signal inclinométrique associé à cette surcharge le long de profils partant du centre de l'aquifère et passant par le centre d'un côté, sur 50 km de distance (débordant ainsi la limite de la nappe de 25 km). Les deux adaptations de grilles précédemment proposées sont testées.
La comparaison des valeurs calculées fait apparaître des différences inférieures à 1% entre les deux modèles, montrant une bonne indépendance au choix du maillage. Nous choisissons donc de ne plus utiliser que le maillage à symétrie cylindrique, pour lequel le temps de calcul est inférieur et qui s'adapte mieux au caractère cylindrique de la fonction de Green. La Fig. 4 montre le résultat obtenu après convolution. L'inclinaison reste très faible à l'intérieur de l'aquifère (par symétrie, elle doit être nulle au centre), sauf lorsqu'on s'approche de ses bords – il faut être à moins de 5 km d'une bordure pour que l'inclinaison dépasse . Le maximum est atteint sur la limite de l'aquifère, où l'on a une valeur de . De façon quasi symétrique, l'inclinaison diminue très rapidement lorsqu'on s'éloigne de l'aquifère, pour passer en dessous de à 30 km du centre de la nappe. À 50 km, elle ne sera plus que de , à la limite de la détection par les inclinomètres.
Il ressort de ce premier cas de figure que les fluctuations naturelles du niveau des nappes, généralement supérieures au mètre et dans des milieux de porosité parfois plus forte que 10%, sont théoriquement observables à l'aide d'inclinomètres. La sensibilité est meilleure dans les zones de fort gradient de la surcharge (plus exactement de ses variations temporelles), ce qui semble naturel et est bien appuyé par la considération que le signal inclinométrique peut s'obtenir directement par convolution d'une fonction de Green appropriée avec, directement, ce gradient de surcharge. Cela doit guider l'implantation des capteurs lors d'études expérimentales du phénomène, et il serait inopportun d'installer un instrument clinométrique au centre d'un aquifère.
Dans le cadre d'une étude autre qu'hydrogéologique – tectonique par exemple –, on pourra prendre soin de ne pas implanter de capteur en limite d'aquifère (et même, si possible, complètement en dehors).
3.3 Simulation pour un modèle de variations piézométriques sinusoïdales
On propose maintenant d'étudier le phénomène sur des nappes dont le niveau varierait de 1 m pour une porosité de 10% de façon monodirectionnelle sinusoïdale dans l'espace, ce qui constitue une modalité de variation qui certes n'est pas réaliste, mais permet d'étudier le phénomène de chargement en fonction du nombre d'onde « topographique » de la nappe. La nappe est limitée par un carré, de 500 km de côté. Les résultats sont donnés sur la Fig. 5, pour des longueurs d'onde allant de 2 m à 500 km. Notons que, pour les longueurs d'ondes les plus petites, la signification des résultats est limitée par la non-prise en compte d'une profondeur de toit d'aquifère qui interviendrait pour un modèle plus réaliste. Le modèle de surcharge utilisé consiste toujours en un effet « plaqué ». Cependant, dès lors que la longueur d'onde mise en jeu est notablement plus grande que la profondeur, les amplitudes observées sont assurément représentatives.
Ce que l'on remarque de façon évidente sur la Fig. 5 est la stabilité du résultat. L'inclinaison a, pour toutes les échelles, une valeur proche de . Cette invariance est à relier à la propriété d'invariance d'échelle mentionnée plus haut (pour une Terre homogène), mais n'est pas valable dans le détail – le modèle de Terre pris en compte n'étant pas homogène. La valeur atteinte se situe largement dans la gamme de sensibilité des inclinomètres modernes.
Ce résultat illustre combien il est nécessaire de prendre en compte toutes les échelles pour bien modéliser l'inclinaison. La décroissance observée du côté des grandes et petites longueurs d'ondes est le reflet des bornes choisies pour les longueurs d'onde et de l'extension latérale (500 km) mises en œuvre dans cette simulation.
4 Étude pour le bassin de la Seine (France)
4.1 Modèle et approche de la modélisation
Pour l'étude de l'inclinaison engendrée par les systèmes aquifères du bassin de Paris, nous avons utilisé les sorties du modèle Modcou appliqué au bassin de la Seine [13]. Il fournit, interpolées, les charges hydrauliques des différents aquifères, calées sur des piézomètres choisis, au pas journalier, pendant 20 ans [12]. Le modèle Modcou tient compte du caractère libre ou captif des différents aquifères et prend en compte les transferts d'eau entre eux.
L'intérêt d'utiliser des sorties de modèles hydrogéologiques comme descriptif des variations du niveau des nappes est de disposer de données continues dans le temps, distribuées sur l'ensemble du domaine. Elles sont bien sûr plus réalistes que les modèles simplistes utilisés dans les exemples précédents, même si elles ne font que reproduire de façon approchée les observations réelles.
Le bassin se compose précisément de trois aquifères superposés. Le plus profond se trouve dans des craies du Crétacé supérieur ; c'est aussi le plus étendu, nécessitant un découpage en 14 812 mailles. Les deux autres sont de taille nettement plus petite, ils sont dans des terrains Éocène et Oligocène et il a fallu respectivement 5082 et 2422 mailles pour les décrire. La grille utilisée a une base carrée de 8 km de côté, redivisée en mailles plus petites – 4, 2 ou 1 km – près des rivières (Fig. 6).
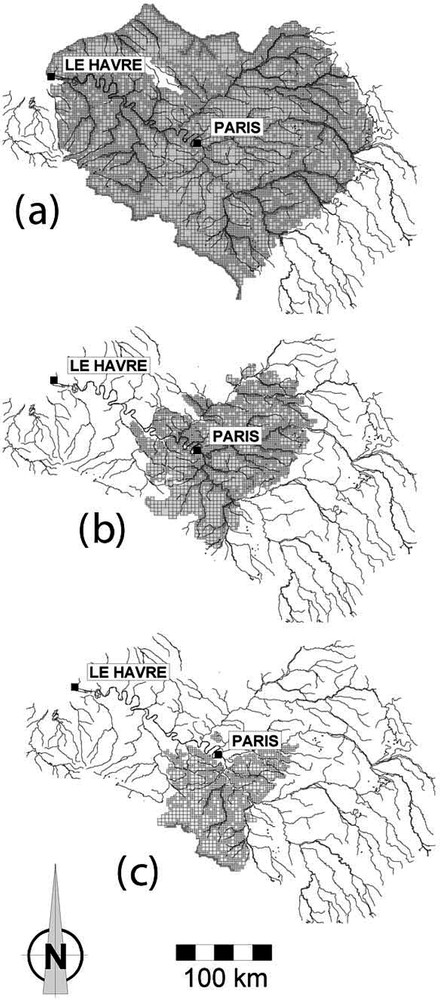
Maillage des différents aquifères superposés dans le bassin de la Seine. Le plus étendu se trouve dans des craies du Crétacé supérieur (a). Il est surmonté d'un aquifère dans les terrains éocènes (b) et d'un autre, plus superficiel, dans les terrains oligocènes (c). Le modèle Modcou utilisé dans notre étude prend en compte les échanges d'eau entre les trois aquifères.
Grid of the different stacked aquifers in the Seine basin. The largest one lies in the chalk of the Upper Cretaceous (a). It is overlaid by an aquifer in the Eocene layers (b) and by another, more superficial, in the Oligocene formations (c). The Modcou model used in this study takes into account the exchanges of water between the three aquifers.
La simulation inclinométrique d'un bassin comme celui de la Seine doit permettre d'explorer les deux volets du sujet qui nous intéresse :
- (1) l'hydrologie doit-elle être prise en compte pour la séparation des phénomènes physiques qui contribuent au signal inclinométrique (par exemple, constitue-t-elle un parasite lors d'études néotectoniques) ?
- (2) l'inclinométrie peut-elle constituer un outil pour caractériser un système hydrogéologique ?
Dans l'application que nous faisons du modèle, nous choisissons Paris comme origine géométrique. À partir de ce point, nous traçons une droite dans l'axe normal à la direction moyenne d'écoulement de la Seine. Sur cet axe, nous choisissons 12 points espacés de 10 km. Ils rejoignent les plateaux crayeux situés de part et d'autre du bassin, du nord vers le sud. En chacun de ces points, nous calculons l'inclinaison tous les dix jours, de début août 1990 à fin juillet 1991. Nous projetons ensuite ce tilt dans la direction de l'axe des points, simulant des inclinomètres qui auraient la même direction de sensibilité.
L'inclinométrie n'ayant de sens que par ses variations temporelles, nous avons choisi comme état de référence le niveau piézométrique des nappes à un instant donné, fixé à la fin août 1990. Tous nos calculs d'effet de surcharge hydrologique sont comptés par rapport à cet état de référence. Notre mode de convolution est basé sur le second type de maillage – à symétrie cylindrique autour du point de calcul. Les données piézométriques de Modcou n'offrent pas de résolution spatiale meilleure que celle du kilomètre. Nous n'effectuons pas de découpage en dessous de 500 m, les données kilométriques ne pouvant plus nous renseigner sur les variations à cette échelle (en réalité, il doit en exister, particulièrement à proximité des captages).
On peut, certes, se poser la question, compte tenu de ce qui a été dit sur l'invariance d'échelle, des limites qu'une résolution spatiale limitée implique. Toutefois, le fait que d'éventuels capteurs inclinométriques opéreraient bien au-dessus du toit de la nappe constitue en soi un filtrage passe-bas de la déformation induite. En première approche, la longueur d'onde de coupure du filtre mécanique que constitue le terrain est proche de l'épaisseur des terrains non saturés (en prenant pour négligeables les masses d'eau de la zone non saturée).
Nous prolongeons le maillage jusqu'à 400 km du point de convolution, ce qui permet le calcul jusqu'à l'extérieur de la surface couverte par l'aquifère sans rogner aucune partie des nappes (avec cette distance prise en compte, tout l'aquifère reste pris en compte pour un calcul de l'inclinaison fait à l'extérieur de celui-ci).
Il faut ensuite redistribuer les hauteurs piézométriques en fonction de la grille centrée sur le point de calcul. L'interpolation de ces données pose des problèmes différents pour les mailles proches et pour les mailles lointaines. À proximité, nous effectuons une interpolation linéaire qui doit rendre compte du gradient de surcharge locale, dont nous avons vu l'importance. À grande distance, où nous disposons de plusieurs points de mesure sur une maille, nous nous contentons de moyenner ces données.
4.2 Résultats de la modélisation
La Fig. 7 montre le signal obtenu de part et d'autre de l'axe de la Seine. On peut noter d'emblée que l'inclinaison calculée est comprise entre –10−8 et . Ceci correspond encore à un ordre de grandeur accessible à la mesure, et est effectivement représentatif des fluctuations observées sur des inclinomètres [6]. Nous voyons que, globalement, le signal s'amplifie au cours de l'année. Au bout de 12 mois, il n'y a pas, comme on aurait pu s'y attendre, retour à une situation proche de celle de départ, mais cela reflète bien la variabilité interannuelle des stocks d'eau.
Au voisinage de , le profil calculé présente un fort pic. Ce point correspond à peu près sur la carte à une limite de plateau. Nous sommes ici en présence d'une discontinuité hydrogéologique, avec le passage d'une zone de plaine aux faibles variations piézométriques, à une zone de plateau aux variations plus fortes. L'inclinaison a bien lieu dans le sens prévu, c'est-à-dire vers le nord, où se situe le plateau.
Regardons à présent le signal inclinométrique temporel projeté selon l'axe (moyen) du fleuve, à Paris. La Fig. 8 trace les variations au cours de l'année étudiée en un point fixe pris au centre de la capitale. Une inclinaison positive correspond au cas où la zone aval du fleuve se soulèverait. Nous voyons nettement se dessiner un pic négatif pour l'inclinaison au plus fort de l'année hydrologique (février), où le domaine aval est plus fortement chargé. Sur ce cycle annuel, la variation crête à crête de l'inclinaison atteint .
Avec cette modélisation de l'effet hydrologique, nous avons voulu nous rapprocher de conditions réelles en regardant les effets calculés à partir de données issues du modèle Modcou. Pour compléter ces premiers résultats, il serait utile d'approfondir la connaissance des approximations internes de ce modèle (élaboré par Éric Gomez [12]) ; mais, considérant qu'il assimile des données réelles, les ordres de grandeur obtenus sont vraisemblablement corrects. On peut toutefois se poser la question de savoir ce que l'erreur du modèle hydrogéologique engendrerait comme variation indéterminable de l'inclinaison, compte tenu de l'invariance d'échelle qui donne un poids équivalent aux hauteurs d'eau voisines du point d'observation et à celles qui sont plus lointaines, dont on peut espérer que l'intégrale soit plus représentative de la réalité.
5 Premiers résultats sur une expérimentation en grandeur réelle
Afin de commencer à tester et valider cette étude théorique, une expérience a débuté durant l'hiver 2004–2005. Deux inclinomètres hydrostatiques sont installés en croix sur la commune de Sainte-Croix-aux-Mines, dans une mine de la vallée de Sainte-Marie-aux-Mines (massif des Vosges). Le premier est opérationnel depuis la fin décembre 2004, et les premiers résultats montrent une résolution de l'ordre de . La Fig. 9 montre, d'une part, le signal inclinométrique prédit à partir de la pluviométrie journalière, en supposant l'eau rassemblée dans le vallon attenant), dont les variations atteignent plus de 20 nrad, et, d'autre part, le signal mesuré (données horaires, corrigées des effets inclinométriques de la pression atmosphérique donnée par l'ECMWF). Prédiction–modélisation et signal mesuré apparaissent bien corrélés, tant en phase qu'en amplitude. Cela constitue un ensemble de premiers résultats encourageants, qui nous ont incités à poursuivre cette entreprise.
6 Conclusion
Nous avons présenté, dans cet article, une étude de simulation des effets inclinométriques provoqués par les surcharges associées aux variations temporelles des stocks d'eaux souterraines. Ces simulations ont mis en œuvre plusieurs types d'aquifères simplifiés ou réalistes, ce afin d'estimer les variations d'amplitude du signal inclinométrique auxquelles on peut s'attendre et, in fine, dans l'intention d'évaluer la capacité des instruments inclinométriques à observer ce type de forçage.
En utilisant un modèle réaliste du bassin de la Seine, nous avons pu estimer l'ordre de grandeur des effets d'inclinaison dus aux variations des niveaux d'eau dans ce bassin, sur une année. Le signal théorique a été calculé grâce à un formalisme convolutif, faisant intervenir une fonction de Green à symétrie radiale et les variations du niveau piézométrique fournies par le modèle. Les résultats fluctuent entre et au cours de l'année.
Ces premières estimations montrent que l'inclinométrie pourrait devenir un outil de suivi des stocks d'eau, à condition de prendre en compte les autres phénomènes temporels qui viennent se superposer : il s'agit notamment des effets atmosphériques, ou encore des effets de marée terrestre. D'un même ordre de grandeur (10−9 à ), les premiers peuvent être calculés grâce aux modèles météorologiques disponibles (comme ceux de l'ECMWF), tandis que les seconds peuvent être estimés, de longue date, avec une bonne précision. À l'intérieur des terres, les variations de charge dues aux marées océaniques sont également estimées, grâce aux modèles océaniques, avec une précision correcte. Nettoyé de ces diverses contributions, le signal inclinométrique est alors représentatif des variations de charge hydrologiques, et ce qui est encore, aujourd'hui, qualifié de « bruit » sur certains instruments (de l'ordre de ) devrait pouvoir être reproduit par l'estimation du forçage correspondant.
Afin de commencer à tester et à valider cette étude encore théorique, une expérience a débuté durant l'hiver 2004–2005. Les premiers résultats montrent la compatibilité en phase en en amplitude des signaux prédits et observés. D'autres instruments sont planifiés aujourd'hui sur divers sites de lithologie variés. Ces expériences, avec la prise en compte des forçages météoritiques et de modèles de stocks d'eaux souterraines, devraient permettre une validation des possibilités de ces nouvelles approches, que ce soit pour des applications hydrogéologiques ou pour caractériser la surcharge hydrologique venant « parasiter » d'autres applications de l'inclinométrie.
Remerciements
Ce travail de recherche (intitulé Hydrologie et inclinométrie) a est été soutenu par le Programme national/ACI de l'Insu (CNRS) et du ministère de la Recherche, dans le cadre de l'action thématique ECCO-PNRH (Programme national de recherche en hydrologie) ; il se poursuit dans le cadre du projet Hydrologie et géodésie, labellisé pour la période 2005–2007, grâce au financement de l'Agence nationale pour la recherche (ANR) dans le cadre du programme ECCO, que nous tenons à remercier.


