1 Introduction
The Neoproterozoic is marked by severe changes in continental mass distribution, climate, and biological evolutionary trends (see [24] and references therein). In approximately 500 million years, continents have drifted from a Rodinia configuration, with most landmasses near the Equator by 1000 Ma, towards a Gondwana configuration at Cambrian times, assembling several continental blocks in the southern hemisphere (e.g., [37] and references therein). Between Rodinia dispersal and Gondwana assembly, the Earth's climate seems to have experienced strong oscillations. Glacial deposition occurred in most of the cratonic units during that time [22], some of them bearing low-inclination magnetizations, indicating that they were deposited near the Equator (e.g., [14,48]). These deposits are often covered by carbonate layers (cap carbonates) with negative carbon isotope signatures, which are interpreted as an effect of the rapid thaw of glaciers [26]. Whether the diamictite–carbonate successions were formed due to hard (Snowball Earth) or mild (Slushball Earth) global glacial events, or yet in Phanerozoic-like ice ages, is still a matter of debate.
The interest of palaeomagnetic data in constraining the Late Neoproterozoic environment is two-fold. On the one hand, it allows us to infer the latitude of deposition of the sedimentary deposits at a time when other proxies such as carbonates and evaporites may depart from their Phanerozoic distribution, and the fossil record does not provide palaeoclimatic information. On the other hand, it permits the reconstruction of the palaeogeography at the time of glacial episodes, which is of key importance to palaeoclimate models (e.g., [13,28]). In order to infer the palaeolatitude of sedimentary deposition, one needs either a direct palaeomagnetic result related to the sedimentary unit of interest or a good age constraint on the sedimentary deposits and a contemporaneous pole from the same continental block. Palaeomagnetic reconstruction, by its turn, demands good-quality poles from all the continents addressed in the reconstructions. Pole ages should match within a confidence limit so that plate movements are negligible. Additional geological and isotopic information helps to overcome longitude and polarity ambiguities.
Two thorough reviews of the palaeomagnetic database for the Neoproterozoic glacial units were performed by Meert and Van der Voo [36] and Evans [15]. Interestingly enough, these compilations have depicted opposing scenarios, respectively contra and pro Neoproterozoic low-latitude glacial deposition (see commentaries in [15 (pp. 405–406)]. Since then, new palaeomagnetic poles were obtained on key cratonic units, such as Amazonia, southern and northwestern China, and Arabia, and some of the previous results were refined through new radiometric ages. In this contribution, we aim to provide the reader of this thematic issue with a concise and up-to-date review of the current palaeomagnetic evidence on the Neoproterozoic ice ages. We first present a selection of geochronological data in order to access the synchronicity of glacial events, and to delimit the time interval of our analysis. The ages on the glacial deposits will also be used to derive indirect palaeolatitude estimates based on coeval reference poles. Then, we present the latitudinal distribution of glacial deposits based on the most reliable palaeomagnetic data presently available for these units and the cap carbonates. Finally, these poles and other reference poles for the end of the Neoproterozoic are used to draw palaeogeographic scenarios into which the Neoproterozoic ice ages may have been produced.
2 Age of glacial events
The chronology of Neoproterozoic glacial deposits and the carbon isotope record of cap carbonates were recently reviewed by Halverson et al. [21]. Based on these data, these authors have proposed a triad of glacial events, named ‘Sturtian’, ‘Marinoan’, and ‘Gaskiers’. In Table 1, we report the most reliable data listed by Halverson et al. [21], as well as new entries to this rapidly growing geochronological database. They comprise 25 U–Pb ages (ID-TIMS, SHRIMP and LA-ICPMS methods), most of them obtained from zircon crystals extracted from tuffs, ash beds or volcanic rocks, or yet from detrital grains separated from the glacial rocks. Eight results give direct constraints on the age of glacial sedimentation for the following units: Baiyisi (or Beiyixi) (Tarim) [27], Ghubrah (Arabia) [1,4], Gaskiers (Avalonia) [39], Edwardsburg (western Laurentia) [34], Scout Mountain (western Laurentia) [18], Ghaub (Kaoko belt) [23] and the Grand Conglomérat (eastern Congo craton) [30]. Data from tuffs 2.3 m and 9.5 m above the Nantuo glacial deposits constrain the end of glacial deposition in southern China [9,61]. Other results correspond to maximum ages (e.g., detrital zircons) or minimum ages (e.g., ages of intrusive rocks) for the deposition of glacial units.
Reference geochronological data for Neoproterozoic glacial events
Tableau 1 Données géochronologiques de référence pour les événements glaciaires néoprotérozoïques
| Age (Ma) | Method | Location | Unit (dated rock/mineral) | Significance | Reference |
| Tasmania/Australia | |||||
| 575 ± 3 | U–Pb SHIRMP | King Island | Grassy Gr. (zircon from intermediate sill) | Minimumageofglacialdeposition (Cottons Breccia) | Calver et al. (2004) [6] |
| 582 ± 4 | U–Pb SHRIMP | Tasmania | Togari Gr. (zircon from riodacites within diamictites) | Maximum age of glacial deposition (Crolles Hill diamictite) | Calver et al. (2004) [6] |
| 657 ± 17 | U–Pb SHRIMP | Adelaide | Marino Arkose (detrital zircons) | Maximum age of glacial deposition (Marinoan) | Ireland et al. (1998) [29] |
| 760 ± 12 | U–Pb SHIRMP | Tasmania | Basement (zircons from granites) | Maximum age of glacial deposition (Julius River diamictite) | Turner et al. (1998) [55] |
| 777 ± 7 | U–Pb SHIRMP | Adelaide | Burra Gr. (zircons from volcanics) | Maximum age of glacial deposition (Sturtian) | Preiss (2000) [45] |
| Southern China | |||||
| a621 ± 7 | U–Pb SHRIMP | Yangtze Gorges | Doushantuo cap carbonate (zircon from tuff) | Minimumageofglacialdeposition (2.3 m above Nantuo) | Zhang et al. (2005) [60] |
| a635.2 ± 0.6 | U–Pb TIMS | Yangtze Gorges | Doushantuo cap carbonate (zircon from tuff) | Minimumageofglacialdeposition (2.3 m above Nantuo) | Condon et al. (2005) [9] |
| 632.5 ± 0.5 | U–Pb TIMS | Yangtze Gorges | Doushantuo cap carbonate (zircon from tuff) | Minimumageofglacialdeposition (9.5 m above Nantuo) | Condon et al. (2005) [9] |
| 663.3 ± 4.5 | U–Pb TIMS | Eastern Guizhou | Datangpo Fm. (zircon from tuff) | Maximum age of glacial deposition (tuff ∼150 m below Nantuo) | Zhou et al. (2004) [61] |
| Northwestern China | |||||
| 727 ± 10 | U–Pb SHRIMP | Tarim Block | Baiyisi Fm. (zircon from volcanics interbeded w/diamic.) | Age of glacial deposition (Baiyisi) | Huang et al. (2005) [27] |
| 755 ± 15 | U–Pb SHRIMP | Tarim Block | Baiyisi Fm. (zircon from volcanics, base of Baiyisi) | Maximum age of glacial deposition (Baiyisi) | Xu et al. (2005) [59] |
| Baltica | |||||
| 620 ± 14 | U–Pb LA-ICPMS | SE Norway | Rendalen Fm. (detrital zircon) | Maximum age of glacial deposition (Moelv) | Bingen et al. (2005) [2] |
| Arabia | |||||
| b723+16−10 | U–Pb TIMS | Jebel Akhdar, Oman | Ghubrah Fm. (zircon from volcanics) | Age of glacial deposition (Ghubrah) | Brasier and Shield (2000) [4] |
| b711.8 ± 1.6 | U–Pb TIMS | Jebel Akhdar, Oman | Ghubrah Fm. (zircon from volcanics) | Age of glacial deposition (Ghubrah) | Allen et al. (2002) [1] |
| Avalonia/Laurentia | |||||
| 580 ± 1 | U–Pb TIMS | Newfoundland | Gaskiers Fm. (zircon from tuff) | Age of glacial deposition (Gaskiers) | Bowring et al. (2003) [3] |
| 595 ± 2 | U–Pb TIMS | Boston Basin | Squantum tillite (zircon from tuff's fragment) | Maximum age of glacial deposition (Squantum tillite) | Thompson & Bowring (2000) [51] |
| 601 ± 4 | U–Pb TIMS | Dalradian, Scotland | Tayvallich Fm. (zircon from tuff) | Minimumageofglacialdeposition (Port Askaig) | Dempster et al. (2002) [12] |
| 685 ± 1 | U–Pb SHRIMP | Idaho | Edwardsburg Fm. (zircon from volcanics) | Age of glacial deposition (Edwardsburg) | Lund et al. (2003) [34] |
| 709 ± 5 | U–Pb SHRIMP | Idaho | Pocatelo Fm. (zircon from tuff, base of Pocatelo) | Age of glacial deposition (Scout Mountain) | Fanning & Link (2004) [18] |
| 755 ± 18 | U–Pb TIMS | NW Canada | Granite pebble in Rapitan Gr. diamictite | Maximum age of glacial deposition (Rapitan) | Ross & Villeneuve (1997) [46] |
| Kalahari | |||||
| 741 ± 6 | Pb–Pb evarpor. | South Namibia | Rosh Pinah Fm. (zircon from acid volcanic) | Minimumageofglacialdeposition (Kaigas) | Frimmel et al. (1996) [20] |
| Congo/São Francisco | |||||
| 635.5 ± 1.2 | U–Pb TIMS | North Namíbia | Ghaub Fm. (zircon from volcanic ash) | Age of glacial deposition (Ghaub) | Hoffman et al. (2004) [23] |
| 746 ± 2 | U–Pb TIMS | North Namíbia | Naauwpoort Fm. (zircon from acid volcanics) | Maximum age of glacial deposition (Chuos) | Hoffman et al. (1996) [25] |
| 735 ± 5 | U–Pb SHRIMP | Zambia | Kundelungu Gr. (zircon from mafic volcanics) | Age of glacial deposition (Grand Conglomerat) | Key et al. (2001) [30] |
a indicates ages obtained in different studies performed on equivalent samples (collected at the same stratigraphic level and same location).
b indicates ages obtained in different studies performed on equivalent samples (collected at the same stratigraphic level and same location).
Age distribution is shown in Fig. 1. The older glacial units, usually embodied into the ‘Sturtian’ glaciation, present the largest number of ages. They show a large spread between 750 and 670 Ma, including a set of glacial successions with ages around 750 Ma (Kaigas, Grand Conglomérat), the Baiyisi glacials with ages between 755 and 727 Ma (volcanics interbedded with diamictites), and younger units with ages ranging from 710 to 670 Ma (Ghubrah, Edwardsburg, Pocatelo). Either they represent different discrete glacial events, or the Sturtian glaciation is a protracted event encompassing almost 80 Ma. The younger events have a more limited number of ages. In spite of that, it is worth noting the coincident end of glacial events in Namibia and China constrained by high-precision ID-TIMS dating [9,23]. These data, obtained on different cratons, point to an age of around 635 Ma for the ‘Marinoan’ event. However, the actual age of the Marinoan glacial deposits in Australia is poorly defined. A maximum age of 657 ± 1 7 Ma is given by detrital zircons in the underlying Marino Arkose [29], but much younger ages have been suggested based on purportedly correlative deposits recently dated at ∼580 Ma in Tasmania [6]. Ages within 580 ± 1 Ma were also obtained for tuffs collected below, within and above the Gaskiers Formation (not fully published yet: see abstract by [3]). The Squantum tillite (Boston basin), the Loch na Cille Boulder Bed (Dalradian) and the Moelv tillite (Norway) are usually correlated with the Gaskiers Formation. The age of the Squantum tillite is bracketed between 595 and 570 Ma [51]. Maximum ages of 601 and 620 Ma were obtained, respectively, for Loch na Cille and the Moelv tillite [2,12]. Although these data do not rule out correlation, the deposits of Gaskiers, Squantum, Loch na Cille and Moelv could equally represent distinct, short-lived glacial incursions.
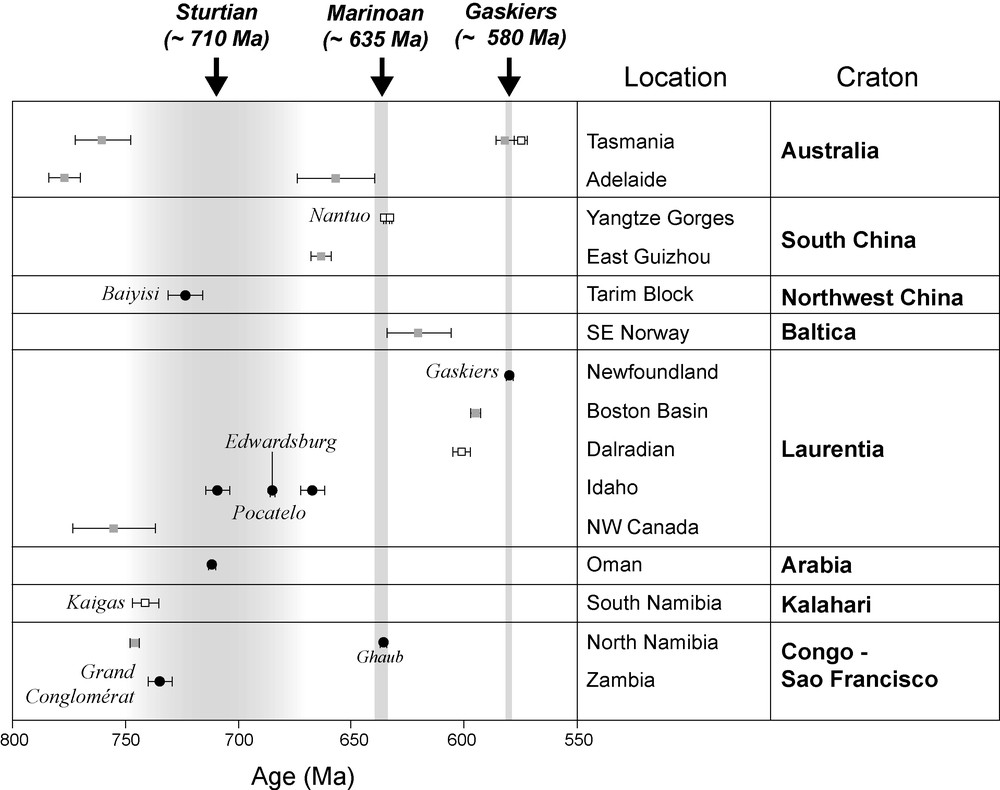
Age of Neoproterozoic glacial deposits. Filled black circles are data obtained directly on the (quoted) glacial unit. Empty and full (grey) squares are minimum and maximum age constraints. Grey, vertical bars indicate the three glacial intervals usually referred to in the literature.
Fig. 1. Âge des dépôts glaciaires néoprotérozoïques. Les cercles noirs pleins correspondent aux données obtenues directement sur l’unité glaciaire (citée). Les carrés (gris) vides et pleins représentent les contraintes d’âge minimum et maximum. Les barres verticales grises indiquent les trois intervalles glaciaires couramment répertoriés dans la littérature.
3 Palaeolatitude of glacial deposits
In Table 2, we list ten poles obtained directly from the glacial units, or alternatively from the cap carbonates, for which the magnetization is considered to be primary in origin. In selecting these poles, we have picked only those for which stability tests ascertain the primary (depositional or early-diagenetic) nature of the magnetization. They are: Elatina Formation (Central Australia) [47,48], Walsh cap carbonate (NW Australia) [33], Doushantuo Formation (South China) [35], Nyborg Formation (Baltica) [52], Huqf Supergroup (Arabia) [31], Rapitan Group (western Laurentia) [42], Squantum Member (Avalonia) [17], Puga cap carbonates (Amazonia) [54], and La Tinta Formation (Rio de la Plata) [56]. The pole for Baiyisi (Tarim) [27], obtained on volcanic rocks interbedded within the glacial deposits of that unit, is regionally consistent after tilt correction, and was thus included into the list, despite the lack of a robust stability test. Good age constraints are available for three of these poles: Baiyisi, Doushantuo, and Squantum.
Palaeomagnetic poles for glacial units or cap carbonates, and reference poles for the Neoproterozoic
Tableau 2 Pôles paléomagnétiques pour les unités glaciaires et les cap carbonates et pôles de référence pour le Néoprotérozoïque
| Craton/Unit | Age(Ma) | Direction | Palaeomagnetic pole | Precision | Quality index | |||||||||||||||||
| Dec | Inc | Lat | Lon | N | n | dp | dm | K | A95 | Plat | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Q | Reference | |||
| Tasmania/Australia | Max | |||||||||||||||||||||
| 1 | Elatina Fm. (1) | 657 (max) | 197 | −5 | −52 | 347 | 10 | 79 | 3.7 | 7.4 | 5.7 | 7.4 | 2.5 ± 3.7 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 4 | Schmidt & Williams (1995) [47] |
| 1 | Elatina Fm. (2) | 657 (max) | 212 | −17 | −40 | 2 | 58 | 126 | 3.3 | 6.4 | 9.9 | 6.2 | 8.7 ± 3.1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 6 | Sohl et al. (1999) [48] |
| Yaltipena Fm. | 657 (max) | 204 | −16 | −44 | 353 | 16 | 36 | 5.9 | 11.4 | 12.2 | 11.0 | 8.2 ± 5.5 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 5 | Sohl et al. (1999) [48] | |
| 2 | Walsh tillite ‘cap dolostone’ | ? | 149 | −63 | −21 | 282 | 5 | 27 | 12.2 | 15.4 | 62.3 | 9.8 | 44.5 ± 4.9 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 5 | Li (2000) [33] |
| Mundine Well dikes | 755 ± 3 | 15 | 31 | 45 | 135 | 14 | 116 | 4.1 | 4.1 | – | 5.0 | 16.7 ± 2.5 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 5 | Wingate & Giddings (2000) [58] | |
| Southern China | ||||||||||||||||||||||
| 3 | Doushantuo Fm. | 632.5 ± 0.5 | 271 | −7 | 1 | 197 | 7 | 80 | 4.5 | 9.0 | 45.0 | 9.1 | 3.5 ± 4.6 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 6 | Macouin et al. (2003) [35] |
| Liantuo Fm. (pole CIT) | 748 ± 12 | 288 | −53 | 3 | 164 | – | 106 | 2.1 | 2.7 | 59.0 | 1.8 | 33.6 ± 0.9 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 6 | Evans et al. (2000) [15] | |
| Liantuo Fm. (pole UWA) | 748 ± 13 | 276 | −57 | 14 | 165 | – | 13 | 7.0 | 9.6 | 40.0 | 6.6 | 37.6 ± 3.3 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 4 | Evans et al. (2000) [15] | |
| Northwestern China | ||||||||||||||||||||||
| 4 | Baiyisi volcanics | 727 ± 10 | 245 | 2 | −18 | 14.2 | 6 | 43 | 3.0 | 6.0 | 124.7 | 6.0 | 1.0 ± 3.0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 4 | Huang et al. (2005) [27] |
| Baltica | ||||||||||||||||||||||
| 5 | Nyborg Fm. | 620 (max) | 110 | 52 | 24.3 | 88.5 | 6 | 55 | 17.1 | 24.9 | 14.6 | 18.0 | 32.6 ± 9.0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 3 | Torsvik et al. (1995) [52] |
| Egersund dolerites | 616 ± 3 | 119 | 61 | 22 | 50 | 4 | 35 | 16.4 | 21.4 | 44.0 | 14.0 | 42.1 ± 7.0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 4 | Poorter (1972) [44] | |
| Arabia | ||||||||||||||||||||||
| 6 | Huqf Supergorup | ? | 169 | 28 | −52 | 74 | 25 | 86 | 4.4 | 8 | 16.7 | 7.3 | 14.9 ± 3.7 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 6 | Kilner et al. (2005) [31] |
| Dokhan Volcanic Fm. | 593 ± 15 | 178 | 37 | −43 | 36 | 10 | 49 | 7.0 | 11.0 | 33.0 | 10.0 | 20.6 ± 5.0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 4 | Davies et al. (1980) [11] | |
| Avalonia/Laurentia | ||||||||||||||||||||||
| 7 | Rapitan Gr. | 755 (max) | 261 | 12 | −1 | 334 | 10 | 25 | 4.0 | 9.0 | 34.0 | 8.0 | 6.1 ± 4.0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 4 | Park (1997) [42] |
| 8 | Squantum Mb. | 595 (max) | 219 | 71 | 13 | 267 | 4 | 13 | 7.9 | 9.0 | 311.2 | 5.2 | 55.4 ± 2.6 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 3 | Fang et al. (1986) [17] |
| Catoctin A | 564 ± 8 | 68 | 84 | −42 | 117 | 6 | 28 | 17.4 | 17.7 | 59.0 | 9.0 | 78.1 ± 3.0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 5 | Meert et al. (1994) [38] | |
| Catoctin B | 564 ± 9 | 92 | 17 | −4 | 184 | 9 | 50 | 6.9 | 13.4 | 16.0 | 13.0 | 8.7 ± 7.0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 4 | Meert et al. (1994) [38] | |
| Sept-Îles Complex B | 565 ± 3 | 105 | 82 | −44 | 135 | 16 | 76 | 9.7 | 9.9 | 53.2 | 5.1 | 74.3 ± 9.6 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 5 | Tanczyk et al. (1987) [50] | |
| Sept-Îles Complex A | 565 ± 4 | 333 | −29 | 20 | 141 | 10 | 51 | 5.0 | 9.0 | 34.0 | 8.0 | 15.5 ± 4.9 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 5 | Tanczyk et al. (1987) [50] | |
| Callander Complex | 575 ± 5 | 82 | 83 | −46 | 121 | 26 | 205 | 5.9 | 6.1 | 83.0 | 3.1 | 76.2 ± 5.9 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 6 | Symons & Chiasson (1990) [49] | |
| Long Range dykes | 614 ± 6/−4 | 125 | 56 | 12 | 346 | 12 | 69 | 18.3 | 25.7 | 48.0 | 18.0 | 36.5 ± 19.4 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 4 | Murthy et al. (1992) [41] | |
| Franklin dykes | 723 ± 4/−2 | 124 | 1 | 9 | 153 | 13 | 82 | 2.6 | 5.3 | 63.0 | 5.0 | 0.5 ± 2.5 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 6 | Christie & Fahrig (1983) [7] See also Buchan et al. (2000) [5] | |
| Congo/Sao Francisco | ||||||||||||||||||||||
| Mbozi Complex | 755 ± 25 | 320 | 16 | 46 | 325 | 10 | 64 | 5 | 9 | 32 | 9 | 8.2 ± 4.8 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 5 | Meert et al. (1995) [39] | |
| West Africa | ||||||||||||||||||||||
| Adma Diorite | 616 ± 11 | 317 | 79 | 34 | 344 | 13 | 62 | 16.1 | 17.1 | 22.0 | 9.0 | 68.8 ± 16.0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 3 | Morel (1981) [40] | |
| Amazonia | ||||||||||||||||||||||
| 9 | Puga cap carbonates A | 623 ± 15? | 181 | 39 | 51 | 249 | 13 | 51 | 6.0 | 9.0 | – | 8.0 | 22.0 ± 5.7 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 5 | Trindade et al. (2003) [54] |
| Rio de la Plata/Luis Alves | ||||||||||||||||||||||
| 10 | La Tinta Fm. | ? | 360 | −66 | 79 | 121 | 5 | 53 | 4.8 | 4.8 | 17.0 | 5.0 | 48.3 ± 6.7 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 5 | Valencio et al. (1980) [56] |
| Campo Alegre Gp. | 598 ± 29 | 36 | −40 | 57 | 43 | 6 | 46 | 9.0 | 9.0 | 56.0 | 10.0 | 22.8 ± 7.3 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 6 | D’Agrella–Filho & Pacca (1988) [10] | |
| India | ||||||||||||||||||||||
| Malani Igneous suite | 760 ± 12 | 9 | 65 | 68 | 88 | 9 | 85 | 12.7 | 15.7 | 29.4 | 9.7 | 47.0 ± 12.7 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 6 | Torsvik et al. (2001) [53] |
In addition to the ten poles listed above, palaeolatitudinal information could also be gathered from reference poles contemporaneous to the remaining well-dated glacial deposits from Arabia, Laurentia, and Congo–São Francisco. Unfortunately, there is no strict coincidence in age between available reference poles and these glacial deposits, but palaeolatitudes can be tentatively attributed to the Grand Conglomérat (735 ± 5 Ma) and the base of Pocatelo (709 ± 5 Ma), based on the Mbozi complex (755 ± 25 Ma) [39] and the Franklin dykes (723 ± 25 Ma) [5,7] poles, respectively. Laurentia lacks reference poles between 720 and 620, thus hindering any palaeolatitudinal control on the Edwardsburg Formation, and the end of Pocatelo deposition (∼670 Ma). There are also no poles for Arabia at the time of the Ghubrah glacial deposition (711.8 ± 1.6 Ma).
Palaeolatitudes vary from near the palaeo-Equator to moderate and high latitudes (Fig. 2). It is worth noting that even after the inclusion of recent poles and applying restrictive screening to the database, we still observe the low-latitude cluster previously recognized by Chumakov and Elston [8] and Evans [15]. Indeed, several high-rank palaeomagnetic data (Q-index 5 or higher: see Table 2) give low latitudes for the glacial deposition (Fig. 2a). These results include, not only palaeomagnetic poles obtained on sedimentary units, for which post-depositional inclination–shallowing could introduce a low-latitude bias, but also poles obtained in interbedded volcanics (Baiyisi). Estimates transferred from reference poles to well-dated glacial deposits also give palaeolatitudes below 15° (Fig. 2b). Palaeolatitudes higher than 30° are recorded in four units, even reaching 55° for the Squantum tillite. The large age uncertainty for most palaeomagnetic entries (denoted by the long empty rectangles in Fig. 2b) frustrates any attempt to recover the latitudinal distribution of glacial deposits through time. Nevertheless, results from Baiyisi (λ = 1 ± 3°) and Doushantuo (λ = 3.5 ± 4.6°) indicate that ice caps did reach the Equator ∼740 and ∼635 Ma ago.
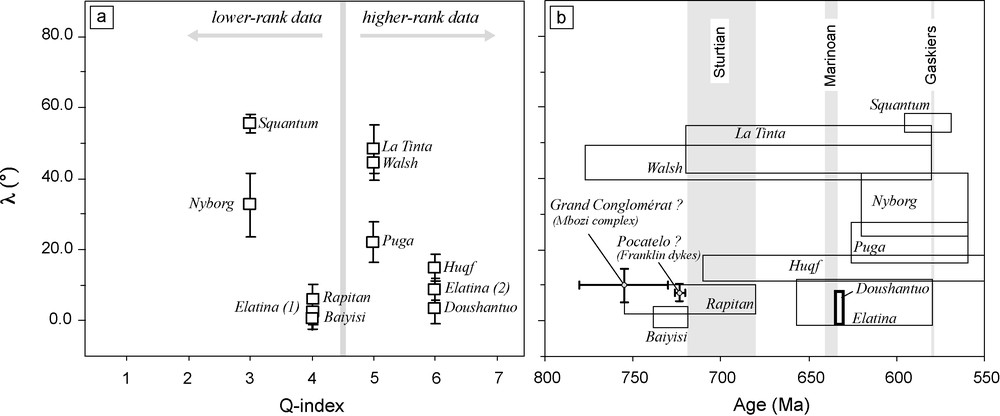
Palaeolatitude estimates on the Neoproterozoic glacial deposits and cap carbonates. (a) Palaeolatitude (λ) with error bars against Q–index [57]. (b) Palaeolatitude against age. Height and length of rectangles indicate error estimates in palaeolatitude and age, respectively. Palaeolatitude estimates obtained from reference poles (Mbozi complex and Franklin dykes) are shown in (b), with error bars for latitude and age.
Fig. 2. Estimations de paléolatitudes obtenues pour les dépôts glaciaires et les cap carbonates néoprotérozoïques. (a) Paléolatitude (λ) avec barres d’erreur, en fonction de l’index-Q [57]. (b) Paléolatitude en fonction de l’âge. La hauteur et la longueur des rectangles indiquent, respectivement, les estimations d’erreur en paléolatitude et en âge. Les estimations de paléolatitudes obtenues à partir des pôles de référence (complexe de Mbozi et dykes de Franklin) sont indiquées en (b), avec les barres d’erreur pour la latitude et l’âge.
4 Palaeogeographic reconstructions
The Neoproterozoic glacial episodes occurred between the demise of the supercontinent Rodinia and the assembly of Gondwana. Several Rodinia configurations were proposed in the last decade, implying different connections of cratonic units with Laurentia, which is the central piece in all reconstructions (see review in [37]). In Fig. 3, we propose four palaeogeographic configurations for three periods: ∼750, 620, and 580 Ma, respectively. We note, however, that these reconstructions are based on a rather limited number of poles (only cratons in dark colour have latitudinal constraints), most of them with slightly different ages within 30 Ma. Thus, these Neoproterozoic palaeomaps should be taken as very sketchy.
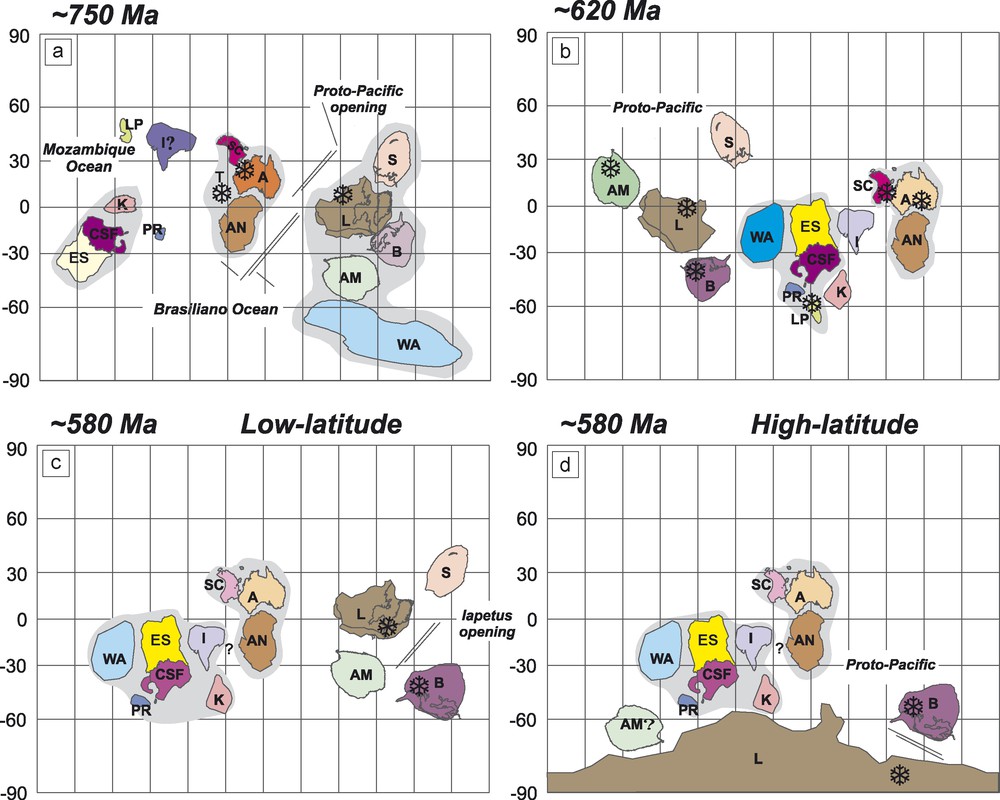
Palaeogeographic reconstructions between 750 and 580 Ma based on the palaeopoles given in Table 2. Shaded areas around some groups of blocks delineate the large palaeogeographic blocks. The position of glacial units is depicted by snowflakes. See text for details. I = India; M = Madagascar; AN = Antarctica; A = Australia; S = Siberia; L = Laurentia; B = Baltica; ES = East-Sahara block; T = Tarim block, CGM = Coats Land/Grunehogna/Maudheim; K = Kalahari; CSF = Congo-São Francisco; LP = Rio de la Plata; AM = Amazonia; RA = Rio Apa; PR = Paraná; WA = West Africa.
Fig. 3. Reconstitutions paléogéographiques entre 750 et 580 Ma basées sur les paléopôles présentés dans le Tableau 2. Les zones ombrées autour de certains groupes de blocs délimitent de larges blocs paléogéographiques. La position des unités glaciaires est indiquée par des flocons de neige. Voir le texte pour les détails.
The first interval of widespread glacial deposition occurs at around 750 Ma, some millions of years after the break-up of Rodinia along the western margin of Laurentia [58]. The corresponding reconstruction (Fig. 3a) is based on reference poles from Australia (Mundine Well dykes; 755 ± 3 Ma), southern China (Liantuo Formation; 748 ± 12 Ma) [16], northwestern China (Baiyisi volcanics; 755–727 Ma) [27], Congo–São Francisco (Mbozi Complex; 755 ± 25 Ma) [39] and India (Malani Igneous suite; 760 ± 12 Ma) [53]. Laurentia was positioned according to the slightly younger Franklin dykes pole (723+4/–2 Ma) [5,7]. Australia, Antarctica, and South China are represented separated from Laurentia as a consequence of the proto-Pacific rift. The Tarim block, northwestern China, is placed close to southern China and Australia, following Huang et al. [27]. The Congo–São Francisco craton and the adjoining cratonic fragments (East-Sahara, Luis Alves, and Parana) are also represented separated from the other cratons. A large oceanic domain is inferred along the (present-day) western margin of the Congo–São Francisco block based on protracted collisional events from 940 up to 630 Ma [43].
The next interval of interest corresponds to the ‘Marinoan’ event marked by the coincident dates of 635 Ma for Doushantuo (Nantuo cap carbonate) and Ghaub Formations. For this time, the Doushantuo pole [35] suggests a low-latitude deposition of the underlying Nantuo glacial deposit. However, no other poles are available for the same age. Thus, a reconstruction for ∼620 is presented in Fig. 3b, which may represent approximately the palaeogeography by the time of the Nantuo/Ghaub (‘Marinoan’) event. In such a reconstruction, Laurentia is positioned at low latitudes according to the long-range dykes pole (614+6/–4 Ma) [41], Baltica is placed according to the Egersund dolerites (616 ± 3 Ma) [44], and West Africa is placed according to the Adma diorite (616 ± 11 Ma) [40]. The approximate position of southern China is based on the Doushantuo pole (632.5 ± 0.5 Ma) [35]. In addition, we have used the poles of Puga and Huqf to position Amazonia and Arabia, assuming that their ages are closer to the ‘Marinoan’ event, as suggested by Trindade et al. [54] and Kilner et al. [31], respectively. The position of the Congo–São Francisco is tentatively placed on this reconstruction using the Dokhan volcanics pole [12]. This pole was obtained from Egypt, which has already joined the eastern Saharan craton at this time and, in spite of its younger age of 593 ± 15 Ma, it is the best available constraint to the position of central Gondwanan blocks. The position of other cratonic units is still more uncertain, due to the lack of reliable contemporaneous poles. Fig. 3a and b, although still poorly constrained, suggest that, by ∼620 Ma, most landmasses have preferentially occupied low latitudes. Interestingly enough, this palaeogeography has strong implications on global climate.
The last interval of interest at around 580 Ma comprehends the short-lived Gaskiers glaciation and its possible correlatives, Squantum, Loch na Cille, and Moelv. However, palaeogeographic models between 590 and 560 Ma are highly controversial, due to the ambiguous results presented by the Laurentian poles. Two studies [38,50] of well-dated igneous complexes (Catoctin and Sept-Îles) have isolated a pair of magnetic components, giving either high latitudes or low latitudes for Laurentia at ∼580 Ma (see Table 2). Here we show two alternative palaeogeographic models that account for low latitudes (Fig. 3c) and high latitudes (Fig. 3d). In the low-latitude model, we have used the Catoctin B (564 ± 8 Ma) and Sept-Îles A (565 ± 3 Ma) for Laurentia. In the high-latitude model, Laurentia was positioned according to the following poles: Callander Complex pole (575 ± 5 Ma) [49], Catoctin A (564 ± 8 Ma), and Sept-Îles B (565 ± 3 Ma). If the latter configuration is confirmed, then a rapid shift in distribution of landmasses has occurred between 620 and 580 Ma. The glacial units observed in eastern Laurentia, Baltica, Cadomia, and Avalonia occupy high latitudes, and could thus have been produced in Phanerozoic-like conditions.
The position of continental landmasses has a strong influence on the climate [19]. Several authors have claimed that the equatorward distribution of continents at the Neoproterozoic might have induced strong weathering, leading to the drawdown of CO2 necessary to trigger the glacial events (e.g., [24,32]). However, whether landmasses are grouped (supercontinents) or dispersed also plays a role in regulating the sink of CO2 through weathering. Applying a coupled climate-geochemical model, Donnadieu et al. [13] have shown that the dispersal of Rodinia engenders the enhancing of CO2 consumption, due to the larger runoff on the total length of continental margins. This mechanism could pave the way for events of severe (even global) glaciation. If low-latitude palaeogeographies with dispersed continental masses have prevailed between the demise of Rodinia and the final assembly of Gondwana (Fig. 3a–c), such mechanism could explain the dominantly cold climate of that time, sometimes falling into deep freeze (equatorial ice caps).
5 Conclusions
Geochronological and palaeomagnetic data for the Neoproterozoic glacial deposits and cap carbonates attest the widespread occurrence of glacial deposition at low latitudes (<30°) between 750 and 570 Ma. Well-dated poles constrain at least two advances of ice caps down to the Equator at 730 and 635 Ma. Palaeogeographic reconstructions based on reference poles suggest a dominantly equatorial position of several cratons throughout the Cryogenian with possible consequences on the dominantly ice-house climate of that time.
Acknowledgments
We warmly thank A. Nédélec for her thorough review and the editorial handling of this manuscript. L.C. Vieira has given invaluable help with final edition of figures and text. This work is financed by FAPESP (05/53231-1) through the Eclipse program (CNRS).