Version française abrégée
Le Néoprotérozoïque est une période marquée par des épisodes de glaciation majeurs [17,20,21,24]. Trois événements ont été jusqu’à présent identifiés : la glaciation sturtienne (vers 750–710 Ma) [10], la glaciation marinoenne (autour de 635 Ma) [21] et la glaciation varangienne ou Gaskiers (580 Ma) [4,45]. Parmi ces trois glaciations, les deux premières pourraient correspondre à des glaciations totales dites « boule de neige », consécutives, en particulier, à l’abondance de dépôts glaciaires à basse latitude [10,20,21,25]. Si l’existence de glaciations « boule de neige » durant le Néoprotérozoïque tend aujourd’hui à faire l’unanimité, les causes de ces événements restent largement inexplorées.
Dans le cadre du programme ECLIPSE du CNRS Comprendre et modéliser les glaciations du Néoprotérozoïque, nous avons développé un outil numérique nouveau (GEOCLIM [7]), couplant un modèle climatique de basse résolution (le modèle CLIMBER, 50°de longitude × 10° de latitude [39]), et un modèle géochimique décrivant, entres autres, les cycles globaux du carbone et de l’alcalinité (COMBINE [14]). GEOCLIM permet donc de calculer la teneur en CO2 atmosphérique à l’équilibre, avec une configuration paléogéographique donnée (Fig. 1), et pour un dégazage de la Terre solide fixé (Fig. 2). En effet, la résolution spatiale 2D de GEOCLIM autorise le calcul de la consommation de CO2 atmosphérique par altération des silicates à la surface des continents, avec une résolution spatiale non nulle. Cette résolution permet d’étudier, de manière explicite, l’impact de la configuration continentale sur le ruissellement continental, premier facteur contrôlant l’altération des silicates [6,37], ce qui était inaccessible aux modèles 0D existants [2]. GEOCLIM nous a permis d’explorer pour la première fois l’impact géochimique et climatique du fractionnement du supercontinent Rodinia, qui débute aux alentours de 800 Ma [32].
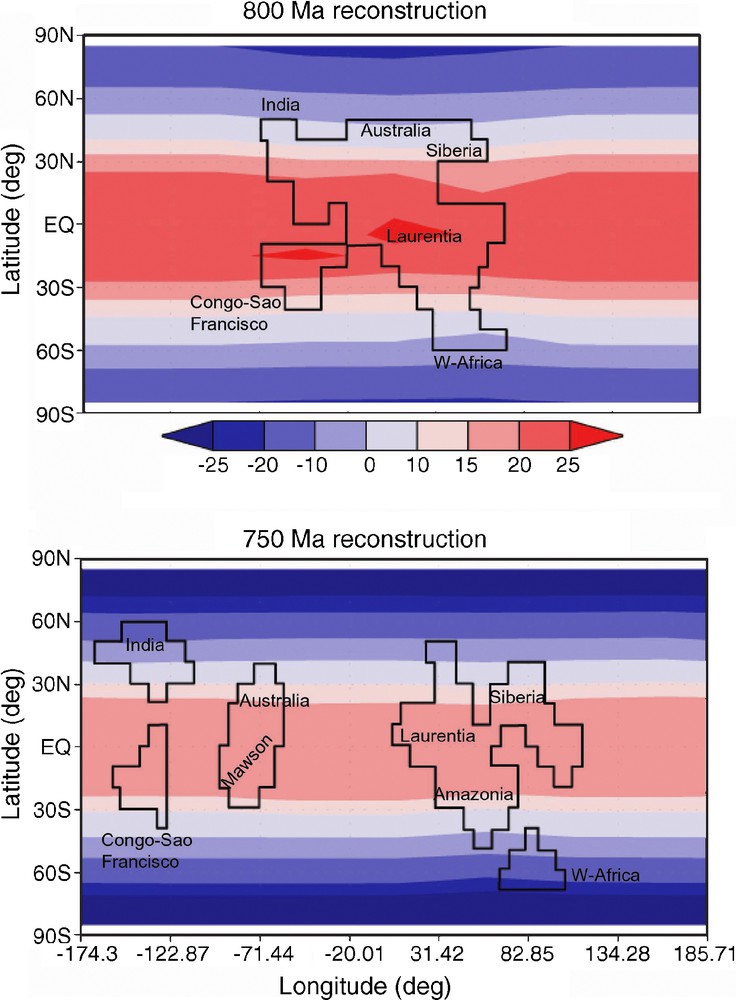
Continental reconstructions at 800, 750 and 580 Ma [33]. ANS: Arabian Nubian Shield; LIP: large igneous provinces with inferred continental basalt flows (traps); Mad: Madagascar; NC: Napier Complex.
Fig. 1. Paléogéographies à 800, 750 et 580 Ma [33]. ANS : Bouclier arabo-nubien ; LIP : grandes provinces magmatiques avec extension probable des coulées basaltiques (traps) ; Mad : Madagascar ; NC : complexe de Napier.
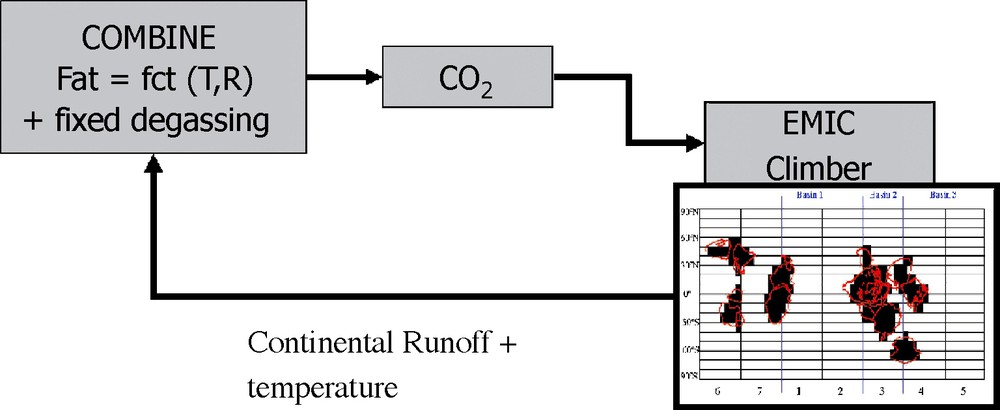
A schematic description of the GEOCLIM coupled model. The COMBINE model is forced with a given degassing rate, and calculates the sink of carbon through silicate continental weathering with a 2D resolution of 50°long. × 10°lat. Based on the carbon budget of the oceans and atmosphere boxes, COMBINE calculates the partial pressure of CO2 in the atmosphere. This pCO2 is then used by the CLIMBER climate model, which calculates continental air temperature and runoff on the same spatial grid. These new climatic parameters are then used by the COMBINE model that estimates a new coeval pCO2. GEOCLIM is then run until a steady state is reached for climate and pCO2 all together.
Fig. 2. Une vue schématique du modèle couplé GEOCLIM. Le modèle COMBINE est forcé avec un dégazage fixé, et calcule le puits de carbone par altération des silicates continentaux avec une résolution spatiale de 50° longitude × 10° latitude. Sur la base de la résolution du budget de carbone des océans et de l’atmosphère, COMBINE calcule la pression partielle du CO2 dans l’atmosphère. Ce pCO2 est alors utilisé par le modèle climatique CLIMBER, qui calcule le ruissellement et la température sur la même grille continentale. Ces nouveaux paramètres climatiques sont alors utilisés par COMBINE, qui estime un nouveau pCO2. Le modèle GEOCLIM tourne ainsi jusqu’à l’obtention d’un état stationnaire simultanément pour le climat et le pCO2.
Vers 800 Ma, la Rodinia se trouve localisée à l’équateur et sa dislocation disperse les blocs continentaux le long de celui-ci. Les paléolatitudes maximales atteintes par ces blocs continentaux aux alentours de 730 Ma restent comprises entre 40°N et 40°S [31,32]. Cette configuration continentale est particulière au Néoprotérozoïque, et ne se rencontre jamais au cours du Phanérozoïque (Fig. 1).
Une première simulation de GEOCLIM à 800 Ma calcule une pression partielle de CO2 de 1830 ppmv, correspondant à une situation où l’ensemble de la surface de la Rodinia est libre de glace (Fig. 3A). En revanche, une simulation réalisée à 730 Ma, dans une configuration paléogéographique disloquée le long de l’équateur (Fig. 1), fournit une teneur en CO2 de 510 ppmv seulement (température moyenne mondiale correspondante de 2 °C, Fig. 3B). Cette baisse de la teneur en CO2 correspond à un refroidissement global majeur de 8 °C. Ce refroidissement est lié à l’augmentation du ruissellement continental lié à l’accroissement de sources d’humidité à proximité des continents (Fig. 4), elle-même due à l’ouverture de nombreux bras de mer (dont le proto-Pacifique) [7]. Il se produit à dégazage de la Terre solide constant. C’est la première fois que l’effet climatique à long terme de la dislocation d’un supercontinent est estimé, en couplage avec les changements dans l’altération continentale (Fig. 5).
Annual mean air temperature (°C) calculated by the GEOCLIM model for (A) the 800 Ma paleogeographic setting, (B) 750 Ma.
Fig. 3. Température moyenne annuelle (°C) calculée par le modèle GEOCLIM pour (A) la configuration paléogéographique à 800 Ma, (B) à 750 Ma.
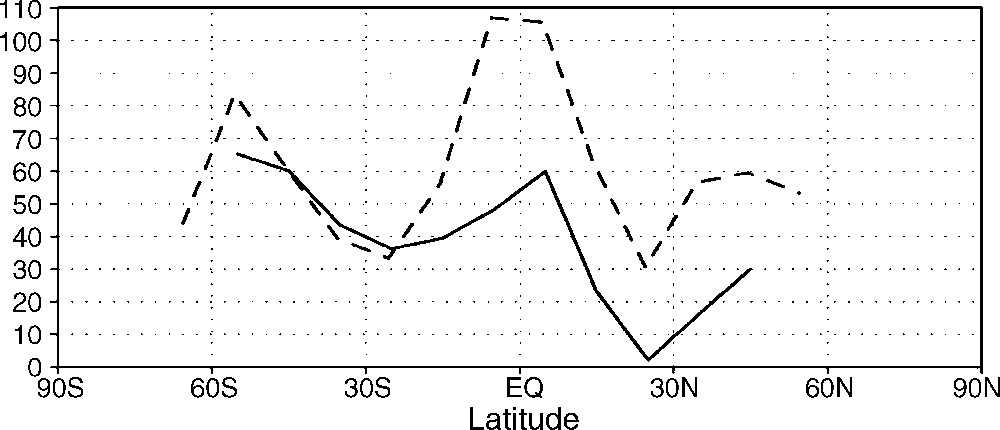
Continental runoff in cm yr−1 as a function of latitude as calculated by the GEOCLIM model at a pCO2 of 1830 ppmv. Solid line is for the 800-Ma paleogeographic setting, and dashed line for 750 Ma (adapted from [7]).
Fig. 4. Ruissellement continental (cm an–1) en fonction de la latitude, calculé par le modèle GEOCLIM à 1830 ppmv. La ligne continue représente la configuration paléogéographique à 800 Ma, et la ligne pointillée la configuration à 750 Ma (adapté de [7]).
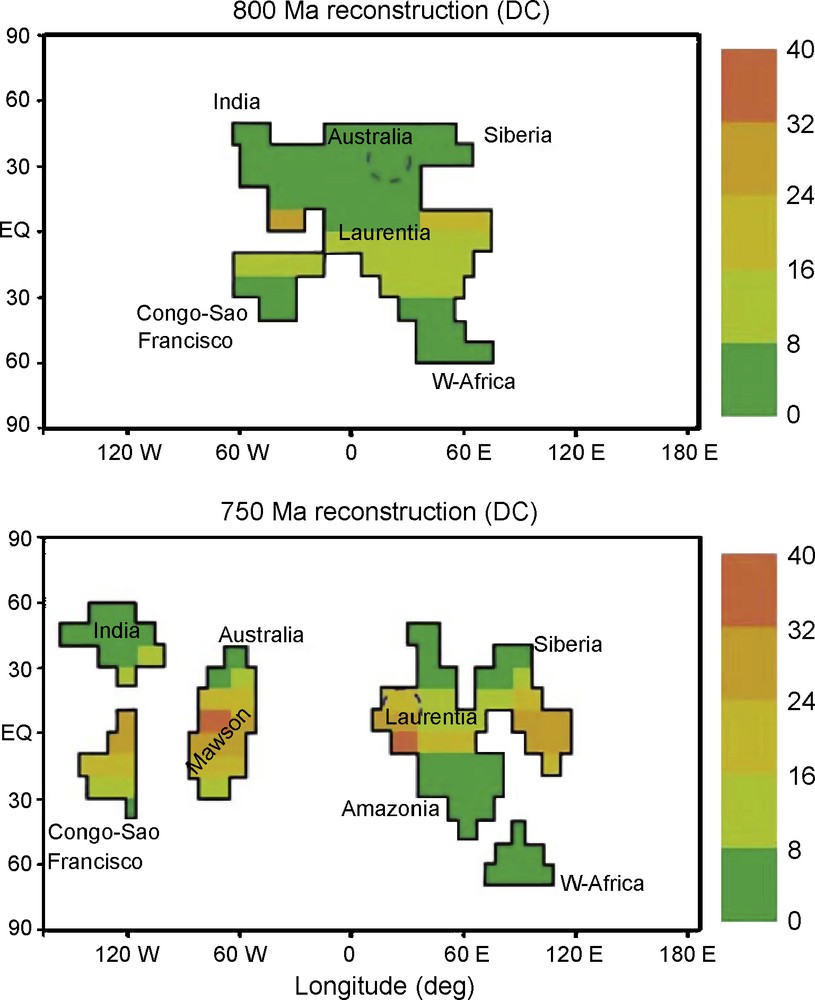
Continental silicate weathering (in 104 mol of Ca2+ or Mg2+ km−2 yr−1) calculated by GEOCLIM at (A) 800 Ma, and (B) 750 Ma. The dashed circle locates the Laurentian magmatic province. Adapted from [7].
Fig. 5. Altération des silicates continentaux (en 104 mol de Ca2+ ou Mg2+ km−2 an−1), calculée par le modèle GEOCLIM à (A) 800 Ma, (B) 750 Ma. Le cercle pointillé représente la position de la province magmatique Laurentienne. Adapté de [7].
De plus, la dislocation de la Rodinia est précédée et accompagnée de la mise en place de nombreuses provinces basaltiques entre 825 et 725 Ma [15,27,28]. L’altération chimique de ces provinces accroît la consommation de CO2 atmosphérique et aggrave le refroidissement climatique global [5,15]. Cet effet devient particulièrement efficace lorsque ces provinces sont amenées dans la zone équatoriale par la dérive des plaques continentales, où le ruissellement et la température élevés optimisent la consommation de CO2. C’est particulièrement le cas pour l’une des plus grandes d’entre elles, la province magmatique Laurentienne, d’âge 780 Ma, dont l’éruption se produit vers 30° de latitude, et qui atteint la zone équatoriale vers 730 Ma, ce qui accroît la consommation de CO2 atmosphérique (Fig. 5) [15]. La simulation GEOCLIM de l’effet d’augmentation de ruissellement due à la dislocation d’un supercontinent, combiné à la consommation accrue de CO2 par les provinces basaltiques, permet de franchir le seuil de CO2, sous lequel une glaciation de type « boule de neige » est initiée (250 ppmv) [7] (Fig. 6).
Schematic representation of the onset of the Sturtian snowball glaciation. Calculated pCO2 is on the Y axis. The blue/grey area represents the CO2 values at which the Earth is totally frozen (calculated by CLIMBER). The dashed line shows the upper and lower limits of the pCO2 required to settle a snowball glaciation calculated by a variety of other climate models. Time is running from left to right. Stage 1 corresponds to the calculated pCO2 for the Rodinia supercontinental configuration, stage 2 is the calculated pCO2 for the Rodinia supercontinent with the Laurentia magmatic province (first located in dry area, where only slow weathering and CO2 consumption occur), and stage 3 stands for the 750-Ma dislocated configuration where the Laurentia magmatic province has been driven to the equatorial humid area. Stage 3 corresponds to a snowball glaciation. The total decrease in the radiative forcing from 800 Ma to the snowball onset reaches more than 10 W m−2.
Fig. 6. Représentation schématique de la mise en place d’une glaciation « boule de neige » au Sturtien. La pCO2 calculée est représentée par l’axe des Y. La surface bleue (ou en grisé) représente les valeurs de CO2 pour lesquelles la Terre est totalement englacée (calculées par CLIMBER). Les lignes pointillées représentent les limites supérieure et inférieure pour lesquelles une glaciation « boule de neige » est produite, pour divers autres modèles climatiques. Le temps s’écoule de la droite vers la gauche. L’étape 1 correspond à la pCO2 calculée pour une configuration supercontinentale (Rodinia). L’étape 2 est la teneur en CO2 calculée pour la configuration Rodinia, avec en plus la présence de la province magmatique Laurentienne (d’abord localisée dans une zone à faible ruissellement, ce qui limite fortement l’altération et la consommation de CO2). L’étape 3 correspond à la configuration paléogéographique disloquée à 750 Ma, où la province magmatique Laurentienne a atteint la zone équatoriale humide. L’étape 3 correspond à une Terre « boule de neige ». La baisse totale du forçage radiatif de 800 Ma à la mise en place de la glaciation « boule de neige » dépasse 10 W m−2.
Concernant la glaciation Gaskiers, la configuration continentale est totalement différente de la configuration sturtienne, puisque l’ensemble des masses continentales se trouve localisé dans l’hémisphère sud, avec le Gondwana ouest (Afrique de l’Ouest et Amérique du Sud) et la Laurentia situés à proximité immédiate du pôle (Fig. 1) [46]. Une simulation GEOCLIM avec la configuration paléogéographique à 580 Ma calcule une teneur en CO2 atmosphérique à l’équilibre de 1037 ppmv, prenant en compte l’effet d’accroissement de l’altération chimique des continents par altération mécanique accrue dans la zone des orogènes panafricains. Néanmoins, quoiqu’une glaciation régionale soit initiée dans la simulation [9] (en grande partie liée à la perturbation de la circulation atmosphérique engendrée par la présence de l’orogène, Fig. 7), elle n’atteint pas l’ampleur d’une glaciation de type « boule de neige », le seuil de CO2 requis pour une telle glaciation étant de 77 ppmv.
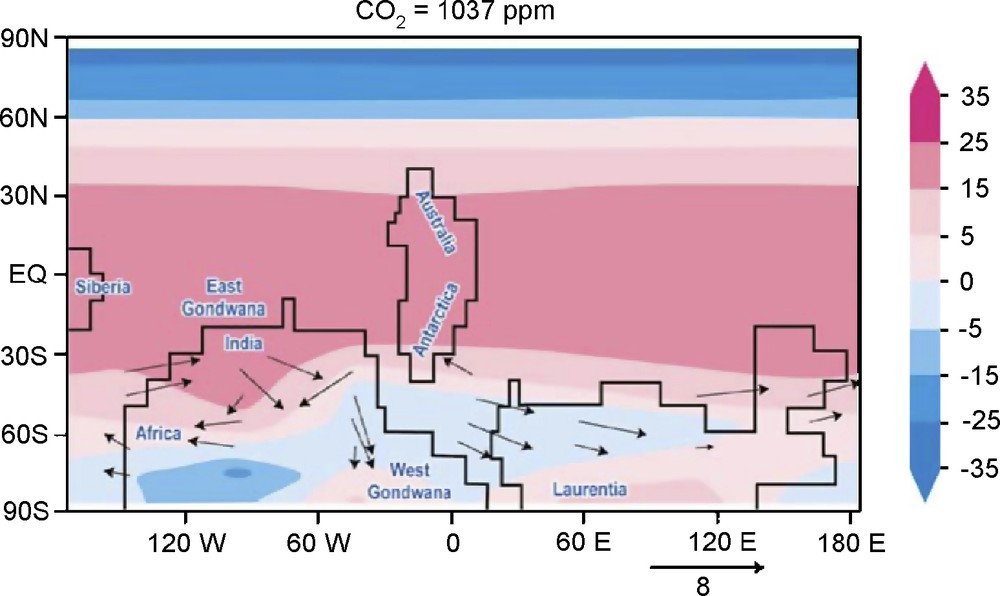
Mean annual air temperature calculated by the GEOCLIM model for the 580-Ma paleogeographic setting (pCO2 = 1037 ppmv). Pan-African orogen is located by a grey shaded contour. Perennial snow can accumulate above the West Gondwana (where the presence of the Pan-African orogen results in very low temperatures) and part of the Laurentia cratons. Surface winds are also shown for the latitudes 30°S–90°S, the size of the vector below the panel is for a wind of 8 m s−1. Adapted from [9].
Fig. 7. Température moyenne annuelle de l’air calculée par le modèle GEOCLIM pour la configuration paléogéographique à 580 Ma (pCO2 = 1037 ppmv). Les conditions climatiques sont requises pour l’accumulation de neige pérenne sur le Gondwana ouest (où la présence de l’orogène panafricain impose des températures très basses), et sur une partie de la Laurentia. Les vents en surface sont représentés par les flèches (la flèche sous le graphique représente un vent de 8 m s−1). Adapté de [9].
Enfin, l’épisode glaciaire du Marinoen n’a pu être simulé par manque de données paléogéographiques fiables et par manque de contraintes temporelles fiables. Néanmoins, des études récentes semblent indiquer, d’une part, un âge plus ancien qu’initialement estimé (635 Ma au lieu de 600 Ma [18]) et, d’autre part, une localisation toujours équatoriale de plusieurs blocs continentaux [30], deux arguments tendant à suggérer l’applicabilité de notre modèle paléogéographique des glaciations néoprotérozoïques.
En conclusion, nos résultats suggèrent que les glaciations « boule de neige » se sont produites dans une fenêtre temporelle où la distribution paléogéographique des continents était essentiellement équatoriale et dispersée. Lorsque la dérive des continents a modifié cette configuration (vers 580 Ma, la plupart des continents sont dans l’hémisphère sud), le temps des glaciations « boule de neige » était terminé.
1 Introduction
The climate of the Late Proterozoic has received much attention in the recent years, since the suggestion of the occurrence of global glaciations in the Sturtian (730 Ma) and Marinoan (635 Ma) time periods (the so-called ‘snowball’ glaciations) [17,18,21,24]. A third event (the Gaskiers or Varanger glaciation, 580 Ma) has also been recognized as a major glaciation although probably not a snowball event [25]. Apart from the intense debate regarding the exact amplitude of the glacial events themselves [11,21–23], there is little doubt that these glacial episodes were intense compared to the Pleistocene glaciations, with glaciers reaching sea level near the equator [10]. The snowball hypothesis is probably the most attractive model up to now [21], since it successfully explains most of the extraordinary geological observations regarding the glaciations [20]. However, one of the most critical questions remains the cause of the extreme climate deterioration, which has not been experienced since the Neoproterozoic era.
Among the plausible explanations invoked to explain snowball-like glaciations lies the fainter sun at this time period. However, as a direct and obvious consequence of the negative feedback existing between consumption of atmospheric CO2 through continental silicate weathering and climate [47], a fainter sun would be totally compensated for by a higher partial pressure of CO2 into the atmosphere [44,47]. High obliquity (>54°) has been also invoked as a plausible cause for unusual location of the glacial deposits, resulting in a colder climate at the equator compared to the Polar Regions [48]. Indeed this hypothesis does not require the onset of a complete snowball glaciation to explain the presence of low-latitude glacial deposits. However, this hypothesis has been tested through climate simulations [8] showing that high obliquity fails to trigger extensive ice-sheets on polar supercontinents. This is a crucial point, since it was the main requirement for the sole proposed mechanism to recover from high to low obliquity in the Williams model [48], invoking climate friction [19]. Furthermore, Levrard and Laskar [26] have dismissed the high-obliquity model by demonstrating that climate friction can only explain a 2–4° decrease of the Earth obliquity over a typical time span of 100 million years, while Williams’ model requires a value of 40° decrease.
Another explanation relies on changes in the partial pressure of greenhouse gases. Numerous numerical climate simulations were performed at various partial pressure of atmospheric CO2 in order to see whether a snowball-like glaciation might be initiated under Neoproterozoic conditions. Note that the answer to this question is still a matter of debate, particularly when coupled ocean-atmosphere models are used [40,41]. Nevertheless, threshold pCO2 below which runaway ice-albedo feedback drives the Earth into a snowball glaciation ranges from 130 to about 500 ppmv depending on the climate model used. However, all these studies used the partial pressure of atmospheric CO2 as a boundary condition. This is particularly critical for the ‘slushball’ model that simulates areas of open ocean along the equator, while all continents are covered by ice down to the equator [22]. This was obtained assuming 700 ppmv of CO2 in the atmosphere, but this value remains totally arbitrary. Atmospheric CO2 level is controlled at the million year timescale by the balance between volcanic degassing and silicate weathering consumption [47]. Any hypothesis arguing in favor of a change in pCO2 should deal with changes in CO2 degassing, or the strength of the silicate weathering feedback, which is heavily dependent on climatic conditions (temperature and runoff [6,37]).
Methane has been invoked as a possible trigger for snowball events. Pavlov and co-authors [38] suggested that the Neoproterozoic atmosphere might have been methane-rich because of sustained methane degassing from the oxygen-poor ocean. An oxidation event at the end of the Proterozoic might have drastically reduced the methane content of the atmosphere, leading to a rapid decrease in the greenhouse effect and to a snowball glaciation. However, this scenario may explain the occurrence of only one snowball glaciation. Similarly, an hypothetical release of methane into the atmosphere just prior to the snowball glaciation has been also suggested, that boosted the hydrological cycle on continents resulting in an increase in continental runoff, leading to a decrease in partial pressure of CO2 consumed by boosted silicate weathering. Once the source of methane is arbitrarily turned down, and if CO2 has fallen below the required threshold, a snowball Earth might be generated [43]. However, the ad-hoc release of methane, which is required to match the observed Marinoan pre-glacial decrease in marine δ13C, is difficult to constrain, mainly because the timing of the δ13C decrease is not easy to fix. Furthermore, the response of the hydrologic cycle to a sudden burst in the greenhouse effect heavily depends on the paleogeographic configuration (as will be shown below), and might not be assumed as a simple linear response to enhanced air temperature.
Apart from possible but yet to be demonstrated methane degassing prior to the snowball events, the most prominent feature of the global environmental changes is the fragmentation of the long-lived Rodinia supercontinent. This fragmentation started 800 Myr ago [32,33], about 70 million years prior to the first snowball Earth event, and was accompanied by an intense magmatic activity [29]. In this contribution, we summarize the main results obtained within the framework of the Eclipse program pertaining to the global climatic and geochemical impact of supercontinental breakup, and show that it could be the main cause of the triggering mechanism for extreme glaciations in the Neoproterozoic.
2 Testing the impact of Rodinia dislocation on the global carbon cycle and climate: need for new 2D climate-geochemical models
By 800 Ma, the Rodinia supercontinent was probably still assembled or was in the early stages of the breakup process [29,31–33] (Fig. 1). Its precise location ca 800 Ma still remains a matter of debate, and Rodinia might have been centered on the equator [32,33], or spread from the equator to the pole [29]. Nevertheless, even in the last configuration, Rodinia might have been driven down to the equator through true polar wander triggered by the initiation of a mantle superplume [29] prior to 750 Ma, followed by the fragmentation of the supercontinent with the spreading of the continental blocks between 40°S and 40°N [31]. In both cases, the fragmentation process can thus be assimilated to the breakup at low latitudes of a supercontinent initially centered on the equator (Fig. 1). The opening of many seaways increased the source of humidity along the borders of the newly formed continental blocks, and most probably precipitations above continents. The subsequent increase in runoff should increase continental weathering, particularly of silicates [5,37], and hence atmospheric CO2 consumption. Although already suggested in the early 1990s [24] to explain qualitatively snowball glaciations, this scenario has never been quantitatively tested, mainly because numerical models of the long-term carbon cycle and climate were not designed for such experiments. The WHAK [47], BLAG [3], and GEOCARB [2] models are all 0D models, where global air temperature is a simple logarithmic function of pCO2 and, despite various attempts towards better constraining of fluctuations in runoff as a function of paleogeography [2], runoff is assumed to be a simple linear function of global mean air temperature to the first order. As a result, such models assume that a warmer world is a wetter world. This basic assumption might be probably true for a given stable paleogeography with changing atmospheric partial CO2 pressure, but cannot be asserted when paleogeography is changing. Furthermore, the impact of the breakup of a supercontinent cannot be simulated with such models, since these geochemical–climate models have no explicit spatial resolution. Calculated partial pressure of atmospheric CO2 is not sensitive to paleogeography in 0D models. More sophisticated models, such as the François and Walker model [12] and derived models [13,14], account for the latitudinal dispersion of the continental masses. Furthermore, these global biogeochemical models are fully coupled to a 1D energy balance model, calculating air temperature as a function of latitude, solar constant, latitudinal dispersion of continents, and pCO2. Although the François–Walker type models introduce a spatial resolution into long-term geochemical models, they cannot be applied to the Rodinia breakup, for two main reasons:
- (1) the Rodinia breakup occurred at a roughly constant latitude, all continental blocks moving along the equator [34], which cannot be simulated by a 1D latitudinal model,
- (2) an energy balance climate model does not calculate explicitly the water cycle, and runoff (and hence continental weathering) cannot be realistically evaluated above continents.
Because of all these limitations, we developed a new numerical model of the global carbon–alkalinity cycles working at the million-year timescale, coupled to a 2D climate model: the GEOCLIM model (Fig. 2). A full description of this model has been previously published [7,9]. The geochemical module consists of a 6-box carbon-alkalinity cycle model (COMBINE, [14]), while the climate module is an Earth model of intermediate complexity (CLIMBER, [39], adapted for Neoproterozoic conditions [8]). Both models are coupled so that COMBINE calculates the partial pressure of atmospheric CO2 by solving the global carbon budget (including continental silicate weathering, while volcanic degassing is a forcing), and this pCO2 is used by CLIMBER to calculate continental air temperature and runoff with a resolution of 50°long. × 10°lat. (details about the coupling procedure can be found in Donnadieu et al. [7]). These climatic variables are used to calculate new continental weathering fluxes (including silicate weathering) with a 2D spatial resolution, and COMBINE calculates a new pCO2. GEOCLIM is then run until a steady-state solution for both pCO2 and climate is found. Steady state is reached when continental silicate weathering balances exactly volcanic CO2 degassing (requiring about 5 million years simulated).
3 Rodinia dislocation initiates a severe global cooling: the Sturtian glaciation
All simulations were performed assuming a reduction in solar luminosity by 6% relative to the present-day value. The solid Earth CO2 degassing rate is held constant at its present value (estimated at 6.8 × 1012 mol yr−1 in order to balance the present-day CO2 consumption through silicate weathering [6]), since no reliable constraint on this flux exists for Neoproterozoic times. Although not necessarily realistic in the context of supercontinental breakup, this assumption allows us to isolate the effect of paleogeographic change on climate. Furthermore, while there is no doubt that the Rodinia breakup was accompanied by flood basalt volcanism [15,27,28], there is no evidence for long-term (107 years) sustained increased degassing rate related to breakup.
Continental silicate weathering is assumed to be a linear function of continental runoff, and an exponential function of annual mean air temperature with activation energy of 48 700 J mol−1 [37] for each continental pixel. Since the spatial resolution of the GEOCLIM model is quite crude (50°long. × 10°lat.), we assume that under equivalent temperature and runoff conditions, the consumption of CO2 per square meter through silicate weathering is the same for all continental pixels. This assumption is equivalent to the assumption that the ratio between silicate outcrops versus total surface within each continental pixel is constant.
A first simulation was performed using the 800-Ma Rodinia reconstruction of [31] and [33], to calculate steady state pCO2 prior to continental breakup. GEOCLIM calculated a coeval steady-state pCO2 of 1830 ppmv [7], a positive annual mean air temperature for all continental surfaces (Fig. 3A), and global mean annual temperature of 10.8 °C. Continental surfaces are quite dry, with the northern part of Rodinia being the driest area (Fig. 4). This explains why the partial pressure of CO2 is so high, while degassing rate is fixed at its present-day value. Dry conditions reduce the efficiency of silicate weathering, hence leading to an increase in pCO2 and a warming of global climate.
A second GEOCLIM simulation was then performed using the 750 Ma post-breakup continental configuration of [31] and [33]. The steady-state partial pressure of CO2 declined to 510 ppmv in this model run, while mean annual air temperature fell below 0 °C over large areas of the continents (mainly above 40 to 45°lat.), as previously established by [7] (Fig. 3B). Global mean annual air temperature fell by more than 8°C from the 800-Ma configuration to the 750-Ma configuration (characterized by a mean global air temperature of 2°C), corresponding to a negative radiative forcing of 6.85 W m−2. The reason for this decrease lies in the increase of continental runoff through the opening of seaways in between continental masses, enhancing the supply of humidity to continents, finally resulting in an enhanced runoff and consumption of CO2 through silicate weathering (Fig. 5). It is noteworthy that solid Earth degassing rate is kept the same for both 800- and 750-Ma simulations, while climate changes radically, a conclusion that cannot be reached with 0D/1D models for this paleogeographic configuration.
We conclude that the breakup of a supercontinent exerts a strong cooling effect, especially when the breakup occurs at low latitude as it did in the Neoproterozoic. However, despite a strong cooling, this process alone cannot initiate a snowball glaciation, since the partial pressure of CO2 reached at 750 Ma is approaching, but still above the pCO2 threshold required to generate the climatic instability leading to a snowball glaciation [20] (here, the CLIMBER 2 model calculates this threshold at 250 ppmv [7], a value compatible with previous studies).
4 Initiating a Sturtian snowball Earth through basaltic surface weathering
As already mentioned above, the breakup of the Rodinia supercontinent is accompanied by the eruption of large magmatic provinces between 825 and 723 Ma [15,27,28]. As already demonstrated for the Deccan traps at the K–T boundary [5], the subsequent weathering of these fresh basaltic surfaces initiates a long term global climate cooling. Global cooling during the Rodinian breakup would be enhanced. As demonstrated in Goddéris et al. [15] and Donnadieu et al. [7], the weathering of the Laurentian magmatic province (erupted at 780 Ma, with a size arbitrarily fixed to 7 × 106 km2, a size comparable to the Siberian traps just after their eruption) might drive the Earth into a snowball, by enhancing the global cooling initiated by the increase in runoff triggered by the dislocation itself. This supplemental cooling forcing drove the icecap to reach 30° latitude, where the resulting climatic instability forced the Earth system into a snowball state. The cooling effect (additional negative radiative forcing of 3.8 W m−2) resulting from the weathering of basaltic surfaces is particularly efficient, since the Laurentia magmatic province, initially in the sub-tropic area (the driest simulated region), where chemical weathering is inefficient, is rapidly driven into low-latitude area through continental plate motions around 750–710 Ma, where runoff and temperature conditions optimize the weathering and subsequent consumption of atmospheric CO2 (Fig. 5).
As a result, we suggest that the breakup of the Rodinia supercontinent starting 800 Myr ago is the main culprit of the onset of the Sturtian snowball glaciation about 50 or more million years later, through enhanced weathering triggered by enhanced runoff, and weathering of fresh basaltic surfaces (Fig. 6).
5 Simulating the Gaskiers glaciation (580 Ma): no snowball
A second set of GEOCLIM simulations was performed using the 580-Ma paleogeographic reconstruction [9], which corresponds to the Gaskiers glacial deposit in Newfoundland [4]. This glaciation was first correlated with the Marinoan event, which is the strongest candidate for a snowball event. However, recent work indicates that the 580-Ma glaciation post-dates the Marinoan glaciation, and although likely severe, was not a snowball [1,10,25,42], and may have been short-lived [4].
The paleogeographic setting at 580 Ma is totally different compared to the setting at 750 Ma [46]. Most of the continental masses are located in the southern hemisphere, with West Gondwana and Laurentia located near the South Pole (Fig. 1). Furthermore, the continental topography is dominated by highlands related to the Pan-African orogeny. Under these paleogeographic conditions, the pCO2 threshold required to initiate a snowball glaciation was calculated by the CLIMBER climate model at 77 ppmv, while the steady-state pCO2 calculated by a GEOCLIM simulation stabilizes at 1477 ppmv (with present-day CO2 degassing), corresponding to a mean global air temperature of 10.8 °C [9], far above the threshold for snowball initiation (Fig. 7). This high steady-state pCO2 is mainly the result of the polar location of the continental masses, where low temperatures inhibit chemical weathering. Going below the 77 ppmv threshold through reduction of the degassing would require unrealistic lowering of solid Earth degassing rates, or unrecognized controls on silicate weathering. One such control might be the impact of high rates of mechanical erosion in the Pan-African mountain belts, which would increase chemical weathering rates by increasing the area available for these reactions to occur. We have tested this effect on our 580 Ma reconstruction by assuming that mechanical erosion in the Pan-African orogen is roughly three times higher than mechanical erosion in low lands, similar to observed rates in the Himalayan orogen [35]. Based on the work by Millot et al. [36], we multiply the spatialized weathering rates by a factor , with in flat lands, and 3 inside the Pan-African mountain belts. Despite this additional CO2 consumption, the steady-state pCO2 calculated by the GEOCLIM model falls to 1037 ppmv, still far from the snowball threshold.
However, a regional-scale glaciation is generated in any case, with possible development of ice sheets on the Gondwana and Laurentia cratons. In the GEOCLIM simulation, accumulation of perennial snow above these cratons is largely driven by the strong perturbation in the atmospheric circulation induced by the Pan-African mountain belts [9] (Fig. 7) (a GEOCLIM simulation performed assuming flat continents does not show any perennial snow accumulation).
Therefore, GEOCLIM simulations for the Gaskiers ice age suggest the development of a severe regional glaciation [42], but do not allow the initiation of a snowball Earth, which is consistent with geological evidence that does not indicate global glaciation at this time [25].
6 The Marinoan glaciation: a question of paleogeographic setting
The Marinoan event is probably the best documented Neoproterozoic glaciation, and a strong candidate for a snowball Earth event at 635 Ma [18]. However, the lack of well-defined paleomagnetic poles for this time precludes any precise paleogeographic reconstructions, and GEOCLIM simulations cannot be confidently performed. Recent studies suggest that an equatorial location of continental masses might still apply to the Marinoan ice age [30]. The question whether this configuration can be qualified as ‘dispersed’ is open. If continents were still in a dispersed configuration similar to the Sturtian one, then partial pressure of CO2 should have been kept at low levels, and the global climate prior to the snowball glaciation should be rather chilly, facilitating the onset of a snowball Earth. Nevertheless, the final trigger leading to complete glaciation was most probably different from the Sturtian to the Marinoan ice age, as recorded in the δ13C of marine carbonates just prior to the onset of the snowball: the Sturtian record shows a small increase of the δ13C, while a strong decrease reaching 10‰ is observed worldwide prior to the Marinoan glaciation [16].
7 Uncertainties and limitations
This study aims at understanding the coupled behavior of the global geochemical cycles and climate during the Neoproterozoic. It integrates numerous processes that are sometimes difficult to constrain, particularly for the distant past, and further investigations are strongly required to quantify and/or constrain each of these processes in order to validate our scenario. Among them lies:
- (a) the solid Earth CO2 degassing, that was held constant in this study mainly due to the lack of constraints, but is suspected to fluctuate during a supercontinent breakup;
- (b) the paleogeography, particularly for Marinoan times, and the timing of the glacial events;
- (c) the question of the precise extent and location of basaltic provinces that are almost totally eroded now;
- (d) the exact geometry of the Pan-African mountain belts, and clues of their mechanical erosion rate.
Constraining all these uncertainties is a challenge for future research aiming at understanding the catastrophic glaciations that occurred at the end of the Neoproterozoic.
8 Conclusions
The GEOCLIM model simulations suggest that the Sturtian glaciation was triggered by the Rodinia breakup at low latitudes. By the time of the Gaskiers glaciation (580 Ma), a dispersed continental configuration along the equator was no more topical, and continental drift towards the South Pole precluded the initiation of a snowball glaciation. We suggest that such extreme glaciations were greatly facilitated by the dispersal of an equatorial supercontinent that increased continental runoff, enhanced consumption of atmospheric CO2 through silicate weathering and created the conditions for the initiation of the snowball events. The final trigger might have been different for the Sturtian and Marinoan events. We suggest that weathering of large basaltic provinces erupted during the early stages of the Rodinia breakup was responsible for the Sturtian snowball glaciation, adding its cooling effect on global climate to the runoff enhancement effect of the Rodinia dislocation. Our results suggest that this control on atmospheric CO2 was for more than 60% of the global cooling leading to the snowball. As a result, the time window for snowball Earth events ranges from the fragmentation of the Rodinia supercontinent (ca 800 Ma) until the convergence of West Gondwana and Laurentia around the South Pole (ca 580 Ma). An exclusively equatorial paleogeographic configuration has not occurred since, explaining why the Phanerozoic glaciations were never as intense as the Neoproterozoic events.
Acknowledgements
This work was achieved thanks to the financial support of the CNRS through the Eclipse program “Comprendre et modéliser les glaciations du Néoprotérozoïque”.