Abridged English version
Different approaches can be used to estimate extreme rainfall quantiles. The first model described here is based on the statistical analysis of rainfall depth series measured at gauging stations, using for example the recent extreme value theory. However, this approach suffers from considerable sampling uncertainties when dealing with high return period quantiles, because the measurement series are often short compared to the return period of interest. The second approach is based on stochastic rainfall generators calibrated on observed rainfall events, which enables the simulation of long data series in agreement with observations. The long simulated series are then used to build the cumulative distribution function (cdf) of extreme rainfall depths. This reduces sampling uncertainties, but raises the question of validation of the cdf obtained, especially for the cdf tail, where few observations are available.
In this paper, we compare the three methods to estimate the cdfs of extreme daily rainfall:
- • M1: the cdfs of maximum annual daily rainfall are deduced from simulations of stochastic rainfall generators;
- • M2: a regional approach uses the French Weather Forecast rain gauge network for the construction of a cdf for regional maximum annual daily rainfall;
- • M3: an exponential cdf is fitted to the data series at a given gauge.
In M1, the French rainfall generator SHYPRE, developed by CEMAGREF [1,6] is used. SHYPRE uses a geometrical description of the temporal rain signal. The internal structure of the rainfall event at one-hour time steps is described by nine variables. Their cdfs are estimated from observed hourly rainfall events sampled at 217 rain gauges. Twenty parameters have to be calibrated if hourly data are available. In the regional version, a relation between the parameter and daily rainfall requires only three parameters; these are mapped for the whole of France using 2812 daily rainfall events and the Aurelhy methods [5]. Simulated rainfall events are constructed using Monte Carlo simulations. One property of SHYPRE is that the simulated cdfs usually deviate from the Gumbel cdfs and give higher quantiles.
In the M2 method, the regional cdf of maximum annual daily rainfall is built for an area of about 10,000 km2 in the French Mediterranean region using 165 daily rain gauges [11]. The maximal annual daily rainfalls are sampled at each gauge, and the independence and homogeneity of the regional sample are checked. All the data at a given site are then normalized using the average maximum annual daily rainfall of the gauge, PJMOY. A generalized extreme value distribution is then fitted to the 5120 values of the regional sample. From this regional cdf, the maximal annual daily rainfall quantiles at a given site can be deduced from the reduced quantiles obtained with the regional cdf and the PJMOY parameter. The latter can be estimated either from observed values or by regionalisation based on the spatial interpolation of PJMOY using a multiple regression of the relief characteristics and kriging.
The exponential cdf in method M3 is fitted to maximal annual daily rainfall values (or maximum annual daily rainfall) sampled at a given gauge using the classical method of moments.
In this paper, the three methods are compared using two procedures: their parameters are calibrated locally (i) using the information observed at a given gauge, and (ii) with a calibration using regionalised parameters. The results of methods M1 and M2 show good agreement. In procedure (i), both methods fit the cdf observed at the different gauges, and their extrapolation to the highest frequencies for which no observations are available is quite similar. Moreover, methods M1 and M2 show a cdf with a heavy tail that deviates from the exponential cdf. In procedure (ii) with regional parameterisation, the differences between the two quantiles are always less than 30%, which is less than the quantile confidence intervals. The differences between the 1000-year return period quantiles are less than 20%. The greatest differences are observed on the relief, and can be explained by the regionalisation of the parameters.
The SHYPRE model (M1) and the regional approach (M2) appear to be much more robust with respect to regionalisation than the classical mapping of local quantiles deduced from fitting the cdf to local series (M3).
1 Introduction
La prédétermination des pluies extrêmes consiste à calculer, en un point de l’espace, une hauteur ou une intensité de pluie, sur une durée de cumul fixée, correspondant à une fréquence de non-dépassement ou à une période de retour donnée. Ces méthodes peuvent être regroupées en deux catégories :
- • les méthodes directes : elles consistent à ajuster une série pluviométrique par un modèle probabiliste [12,15] ;
- • les méthodes indirectes : elles consistent à construire un modèle de génération de chroniques pluvieuses calé sur des chroniques observées et à déduire les différents quantiles des pluies générées par ces modèles sur de longues périodes de simulation [1,17,22].
Les plus employées restent de loin les méthodes directes, malgré les larges incertitudes associées aux quantiles extrêmes dues à des séries d’observations souvent courtes et au problème de représentativité des échantillons étudiés [4]. Les méthodes indirectes permettent de s’affranchir de cet inconvénient, car les quantiles sont déduits de chroniques simulées sur de longues périodes. On trouvera une bibliographie détaillée des différents modèles dans [13]. Un modèle a été développé en France par le Cemagref, à travers la méthode Shypre. Ce modèle permet de générer des événements pluvieux ponctuels au pas de temps horaire [1,6], qui sont transformés en événements de crues pour l’analyse du risque hydrologique. Un des problèmes soulevé par cette approche est la validation des distributions empiriques obtenues à partir des chroniques simulées. En effet, s’il est possible de valider ces distributions pour des fréquences courantes dans la plage des observations disponibles, on peut s’interroger sur la validité des quantiles extrêmes obtenus par simulation. En particulier, la méthode Shypre fournit des distributions de pluies à comportement généralement hyper exponentiel, c’est-à-dire dont les quantiles de pluies augmentent plus vite que le logarithme des périodes de retour associées. Ce comportement plus qu’exponentiel n’est pas lié à la paramétrisation des lois de probabilité utilisées pour décrire les variables du modèle, puisque la variable décrivant le volume des averses qui composent un événement est caractérisée par une loi strictement exponentielle. Ce comportement hyper-exponentiel est en particulier dû à la prise en compte du phénomène de persistance des averses qui caractérise les événements extrêmes, phénomène observé et modélisé [3]. Bien que le comportement hyper-exponentiel des pluies suggéré par Shypre soit dû à la modélisation d’un phénomène observé, la validation des résultats vers les fréquences rares reste difficile, puisque l’on est dans un domaine d’extrapolation au-delà des fréquences observées. Se pose alors le problème de la validation des modélisations vers les valeurs extrêmes. Cette question peut être abordée en comparant les distributions de pluie simulées de Shypre avec des distributions de pluie observées déduites, soit (a) de longues séries de mesures, soit (b) d’une approche régionale. Cette approche repose sur la construction d’une loi de distribution régionale à partir d’un échantillon composé d’observations à différentes stations, réduisant ainsi les incertitudes d’échantillonnages, en particulier sur la queue de distributions de fréquences [11,18].
Une comparaison des distributions de pluies journalières simulées par Shypre avec des distributions empiriques déduites de longues séries, supérieures à 100 ans, tend à confirmer le comportement hyper-exponentiel [19]. Cependant, cette comparaison n’a pu être réalisée que sur 22 stations dont la stationnarité a été vérifiée. L’objectif de cet article est de confronter les distributions de pluies journalières générées par Shypre aux distributions issues d’une approche régionale, développée en région méditerranéenne, afin de confirmer ou d’infirmer le comportement hyper exponentiel des distributions, et d’apprécier les écarts auxquels conduit l’application de ces deux approches. Les deux premières sections sont consacrées à la présentation des modèles : Shypre et la loi régionale des pluies journalières. Une troisième partie montre les résultats de la comparaison des deux approches et enfin, au regard de ces résultats, une discussion sur le comportement asymptotique des pluies extrêmes est présentée.
2 L’approche Shypre (méthode 1, notée M1)
La méthode Shypre (Simulation d’HYdrogrammes pour la PRÉdétermination des crues), est basée sur le développement d’un générateur stochastique de pluies horaires [1,6] permettant la simulation d’une multitude de scénarios pluvieux statistiquement équivalents aux événements pluvieux observés. Un simple classement des pluies simulées permet de tracer les distributions de fréquence « empiriques » des pluies de toutes durées et d’en déduire les quantiles pour une large gamme de périodes de retour, de 2 à 1000 ans, par exemple.
Le modèle de génération de pluie s’appuie sur une description géométrique du signal temporel de pluie. La génération du signal temporel de pluie est réalisée en deux étapes (Fig. 1). La première étape est l’étude descriptive du phénomène. Elle s’appuie sur l’analyse de la structure temporelle interne des événements pluvieux observés au pas de temps horaire, un événement pluvieux étant analysé s’il présente une hauteur journalière de pluie supérieure à 20 mm. Cette analyse conduit à la définition de variables descriptives et au choix des lois de probabilité qui les caractérisent. La seconde étape est la reconstitution de la chronique de pluie par les variables descriptives, générées de façon aléatoire par une méthode de Monte Carlo.
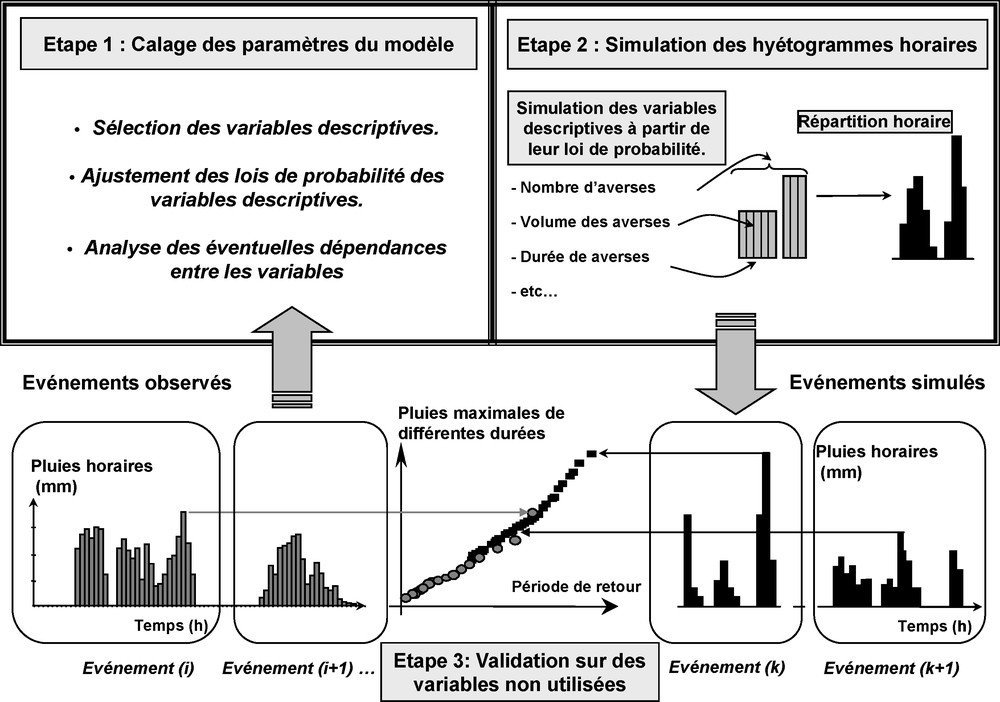
Principe de l’approche par simulation de chronique de pluies : SHYPRE (M1).
Fig. 1. Description of the SHYPRE simulation rainfall chronics.
L’étude de 217 postes pluviographiques, situés en France métropolitaine, a permis de déterminer les lois de probabilité théoriques qui reproduisent au mieux les distributions de fréquences empiriques des différentes variables. Le calage de ces différentes lois de probabilité à chacun des postes permet de définir un modèle local, noté « M1 loc ». Dans sa version locale (calage des paramètres sur une chronique de pluies horaires), le modèle de génération des pluies horaires est défini par neuf variables, nécessitant le calage de 20 paramètres.
La régionalisation des paramètres du modèle a été réalisée pour pouvoir générer des pluies horaires et en déduire les courbes intensité–durée–fréquence (IDF) en tout point de France métropolitaine.
Elle s’est faite en trois étapes :
- • la simplification du modèle ; différents tests de sensibilité ont permis de réduire le nombre de variables du modèle à cinq, sans altérer sensiblement les performances ;
- • la recherche de variables exogènes explicatives des paramètres du modèle de génération. L’information de la pluie journalière a pu être utilisée, à travers trois paramètres moyens, ce qui est particulièrement intéressant au regard de la bonne disponibilité de cette information dans l’espace ;
- • la régionalisation proprement dite des trois paramètres. Ce travail a été effectué par Météo France [23], grâce à l’information de 2812 postes journaliers (Fig. 2), sur l’ensemble de la France, à partir de la méthode Aurelhy [5].
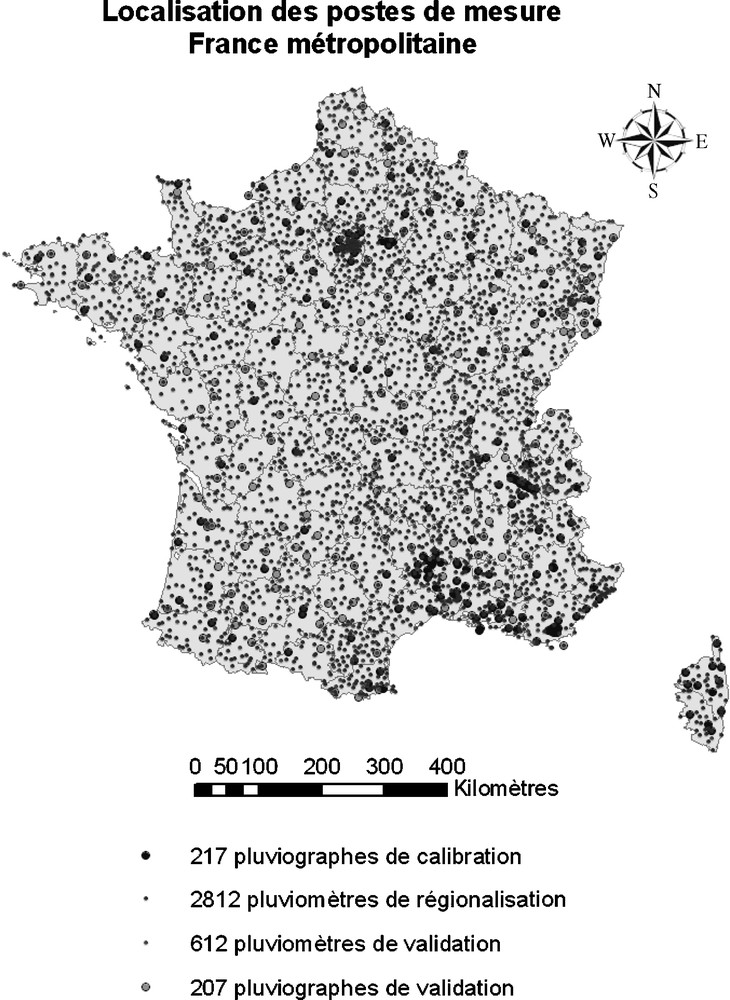
Localisation des stations de mesures utilisées pour régionaliser l’approche SHYPRE.
Fig. 2. Rain gage used for the regionalisation of the SHYPRE approach.
Le modèle de simulation de chroniques peut alors été appliqué dans sa version régionalisée, notée « M1 rég », en tout point du territoire français (y compris les DOM), sur une maille de 1 km2. On obtient ainsi, sur la totalité de la zone étudiée, des chroniques de pluies horaires qui sont utilisées pour tracer les distributions de fréquence des pluies de différentes durées et en déduire les quantiles de pluie de différentes périodes de retour [2].
3 Loi régionale des pluies journalières (méthode 2, notée M2)
L’approche régionale consiste à constituer un échantillon unique à partir des observations réalisées à différentes stations de mesures. Elle repose sur les hypothèses suivantes :
- • l’homogénéité spatiale de la variable étudiée ;
- • l’indépendance spatiale des observations ;
- • les distributions des variables en chaque station ne diffèrent que par un facteur d’échelle [9,20,21,24].
Cette approche a été appliquée en région méditerranéenne, sur la zone des Cévennes (Fig. 3). La période d’observation est 1958–2002 et seuls les postes d’au moins 15 années de mesures sont retenus. La pluie journalière maximale annuelle a été échantillonnée sur les 165 postes pluviométriques du Gard, de l’Hérault et de la Lozère, satisfaisant ce critère. L’homogénéité spatiale est vérifiée par la méthode présentée dans la référence [14]. Elle repose sur une mesure de discordance établie à partir des L-moments à l’aide des coefficients de variation, d’aplatissement et d’asymétrie. Elle conduit à rejeter six postes, jugés non homogènes. L’indépendance spatiale des stations est obtenue en ne retenant que les stations distantes de plus de 80 km, lorsque le maximum annuel correspond au même événement sur différents postes. Les maxima annuels à chaque station sont ensuite réduits par la moyenne des pluies journalières maximales annuelles de la station [11], paramètre noté PJMOY. Un échantillon régional des 5120 valeurs réduites est ensuite constitué. Une loi GEV dont la fonction de répartition est donnée par l’équation (1), y est ajustée par les L-moments.
| (1) |
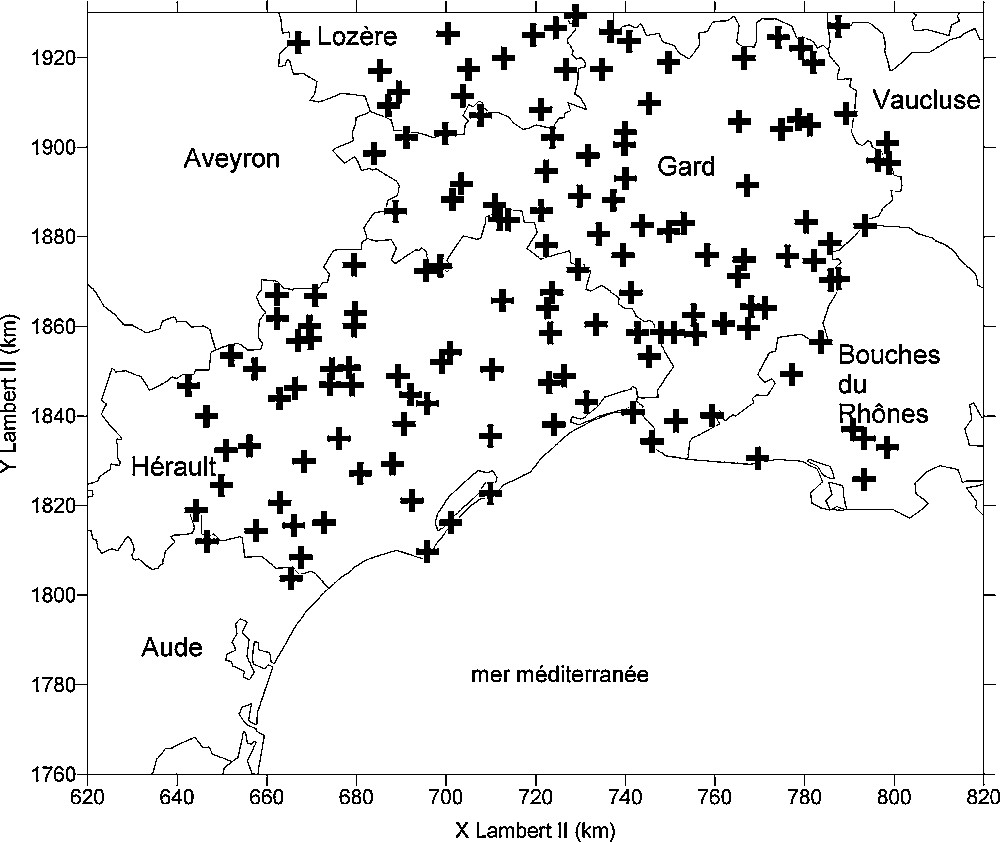
Localisation des 165 postes journaliers utilisés pour établir la loi régionale (M2).
Fig. 3. Daily rain gages used for the estimation of the regional cdfs.
De cette loi régionale, nous pouvons déduire les quantiles réduits pour des périodes de retour données, puis les quantiles correspondants pour tout site, en multipliant la valeur réduite par sa moyenne (paramètre PJMOY). Pour une application dite locale, notée « M2 loc », le paramètre PJMOY est calculé à un poste de mesures, à partir des observations. Pour une application dite régionale, notée « M2 rég », le paramètre PJMOY résulte d’une interpolation spatiale de ce paramètre réalisée à partir des valeurs de ce paramètre, calculées aux différents postes de mesures. On notera le coefficient de forme () négatif qui traduit un comportement hyper-exponentiel de la loi régionale (Fig. 4), concordant ainsi avec les résultats de Shypre mais aussi de nombreuses études récentes [7,8,16].
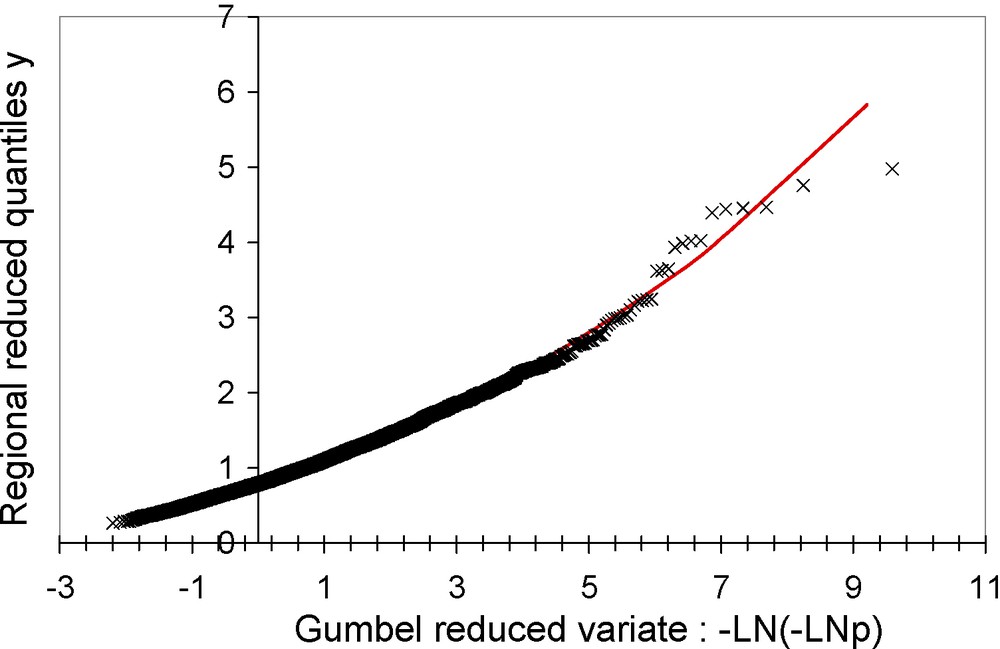
Loi régionale des quantiles réduits de pluie journalière maximale annuelle.
Fig. 4. Regional dfs of reduced maximal annual daily rainfall.
L’interpolation de PJMOY est réalisée en deux temps, suivant le principe de la méthode Aurelhy : une régression multiple faisant intervenir différents descripteurs géographiques est construite, et les résidus sont ensuite interpolés par krigeage. On utilise 109 postes disposant d’au moins 20 ans de mesures. Les caractéristiques géographiques du relief sont déterminées à partir d’une analyse en composantes principales (ACP) des altitudes, sur une fenêtre de 30 × 30 km2 [10]. Les caractéristiques du relief expliquant le plus la variabilité spatiale de PJMOY sont estimées par une régression stepwise. Les trois premières composantes principales de l’ACP, les distances à l’Aude, aux Cévennes et à la mer Méditerranée sont les variables retenues. Elles expliquent 90 % de la variance spatiale de PJMOY (Fig. 5). Les résidus de cette régression sont krigés. Ainsi, en un point quelconque de l’espace, le paramètre PJMOY est obtenu en sommant l’estimation de PJMOY par la régression multiple et la valeur du résidu interpolé en ce point. La
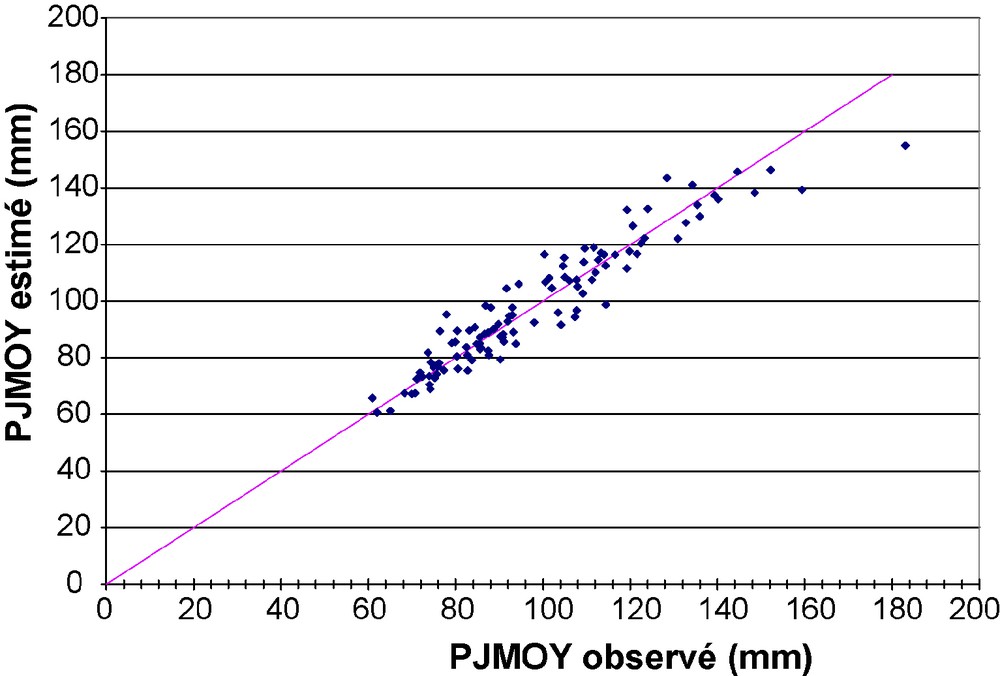
Pluie journalière maximale annuelle moyenne observée et estimée par la régression multiple avec des paramètres de relief sur 109 postes.
Fig. 5. Average of the maximum annual daily rainfall observed and estimated by a multiple regression for 109 rain gages.
Fig. 6 présente la carte du PJMOY interpolé et les postes utilisés pour la régionalisation.
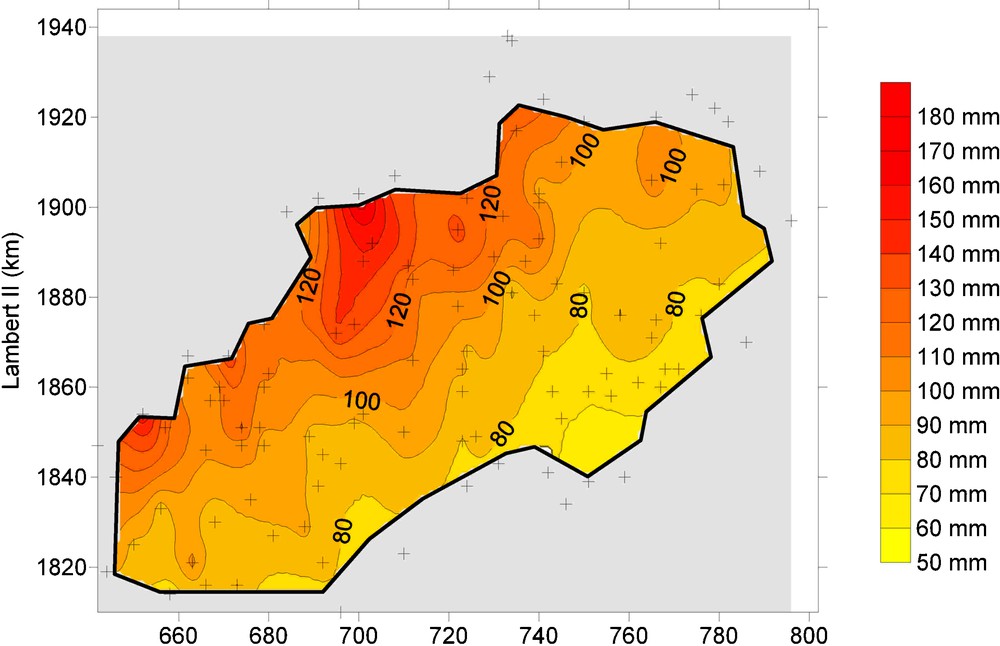
Cartographie du paramètre PJMOY sur le domaine retenu pour la comparaison des deux approches, à partir de l’équation de régression utilisant les variables descriptives du relief et un krigeage des résidus. Les croix représentent les postes utilisés pour l’interpolation.
Fig. 6. Mapping of the PJMOY parameter over the region used for the both approaches comparison, obtained with the regression based on the relief's description and with kriging of the residuals. The crosses are the rain gages used for interpolation.
4 Comparaison de la loi régionale des pluies journalières maximales annuelles et des distributions journalières du modèle Shypre
La comparaison des approches est réalisée avec les versions régionalisée et locale des deux modèles (M1 et M2), sur le domaine d’étude commun composé des départements de l’Hérault et du Gard (Fig. 3), zone particulièrement soumise à une forte variabilité spatiale du risque pluviométrique.
4.1 Modèles régionalisés
Sur le domaine de comparaison, on calcule, sur chaque maille de 1 km2, les quantiles décennaux, centennaux et millénaux avec le modèle Shypre régionalisé (M1 rég) et la loi régionale (M2 rég). Les écarts relatifs, notés ER et exprimés en %, sont définis par :
| (2) |
On constate que les écarts relatifs sont, en valeur absolue, toujours inférieurs à 30 % pour 95 % des 8523 pixels de la zone d’étude (Fig. 7 et Tableau 1). C’est sur la zone de l’Aigoual que les écarts relatifs sont les plus importants. Les écarts relatifs sont variables suivant la période de retour, mais tendent à se réduire pour les fortes périodes de retour : pour 80 % de la zone d’étude, les quantiles décennaux estimés par les deux méthodes diffèrent de moins de 20 %, 70 % pour les quantiles centennaux, et pour seulement 4 % de la zone d’étude, les quantiles de période de retour 1000 ans diffèrent de ± 20 %. Les écarts les plus importants concernent toujours des zones de relief, avec des quantiles du modèle « M1 rég » supérieurs à ceux du modèle « M2 rég ». On peut noter ici que les écarts relatifs les plus forts sont obtenus pour la période de retour 100 ans. Ce point s’explique par le phénomène de persistance, plus ou moins marqué sur la région étudiée, qui influence le comportement hyper-exponentiel de Shypre. Suivant l’importance de ce phénomène, le comportement hyper-exponentiel commence à se produire dans la gamme des périodes de retour comprises entre 10 et 100 ans [3], conduisant à des ratios quantile 100 ans sur quantile 10 ans variables, alors que la loi régionale implique un ratio constant.
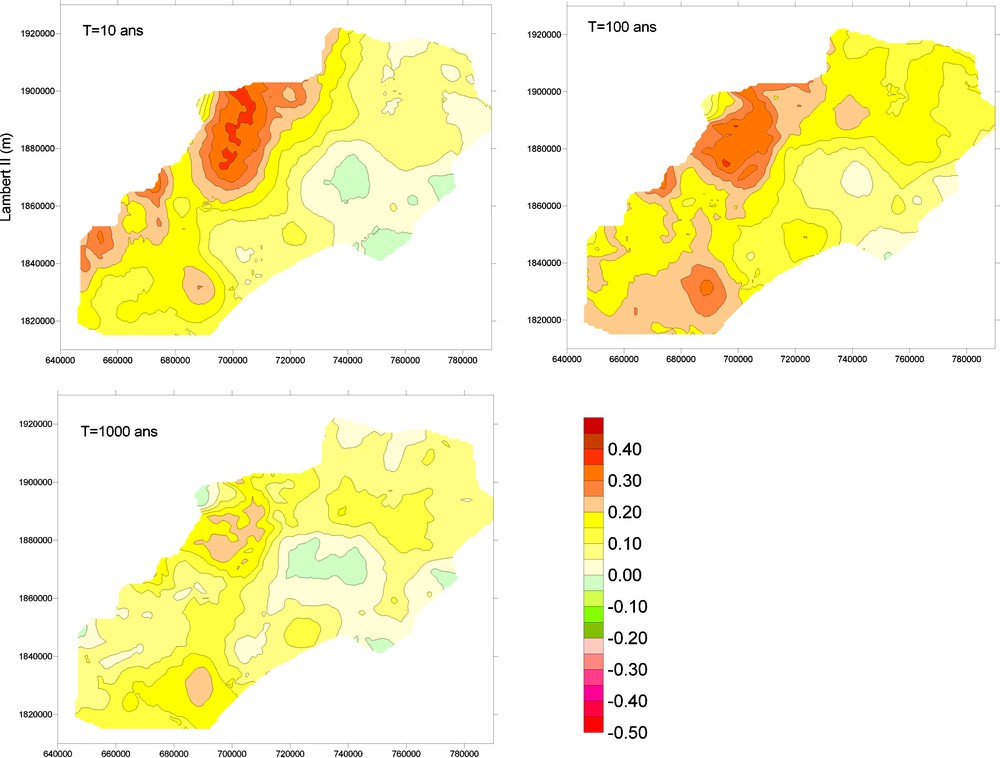
Cartographie des écarts relatifs (QuantilesM1, reg – Quantiles M2, reg)/QuantilesM2, reg, pour T = 10, 100 et 1000 ans.
Fig. 7. Mapping of the relative differences (QuantilesM1, reg – Quantiles M2, reg)/QuantilesM2, reg pdf, for the 10-, 100- and 1000-year return periods.
Pourcentage de pixels associés à une gamme d’écart relatif donnée
Table 1 Percentage of the area according to (quantilM1,reg – quantilM2, reg)/quantilM2, reg
| Erreur relative entre (%) | T = 10 ans (%) | T = 100 ans (%) | T = 1000 ans (%) |
| [−10 ; + 10] | 46,6 | 15,2 | 63,6 |
| [−20 ; + 20] | 78,7 | 69 | 96,5 |
| [−30 ; + 30] | 94,5 | 95,5 | 100 |
Un premier résultat intéressant est que les deux approches conduisent à des estimations très proches dans leur domaine d’extrapolation, alors que c’est dans le domaine des quantiles extrêmes que l’on observe généralement des divergences marquées entre les méthodes.
4.2 Modèles locaux
La comparaison des deux modèles a été effectuée sur 12 postes journaliers « tests » choisis aléatoirement sur la zone d’étude, sur lesquels le calage des méthodes a été réalisé avec l’information locale. Dans ce cas, la loi régionale est appliquée avec une valeur du paramètre PJMOY calculée à partir des mesures disponibles des pluies journalières. Pour l’approche Shypre, dont l’objectif premier est l’estimation de quantiles de pluies de courtes durées, le calage sur une station donnée nécessite normalement une information horaire. Dans le cas où l’on ne dispose que de l’information journalière, on utilise les relations déterminées pour la régionalisation, qui permettent d’estimer les paramètres horaires avec des variables journalières. Cependant, les résultats vont être altérés suivant la qualité des régressions entre les paramètres horaires et les variables journalières. C’est pourquoi, dans le cadre de cette étude, l’application « locale » de Shypre sur des postes journaliers a été réalisée par un calage des paramètres journaliers, de façon à respecter le quantile de période de retour 5 ans de la distribution des pluies journalières observées. Dans ce cas, l’interpolation spatiale des paramètres n’intervient plus, et les paramètres des modèles sont calés pour reproduire au mieux les distributions des pluies journalières dans la gamme des fréquences courantes.
Les résultats des deux approches ont aussi été comparés à un ajustement statistique classique d’une loi exponentielle calée localement, notée modèle « M3 loc ». Le graphique de gauche sur la Fig. 8 montre que les modèles M1 loc et M2 loc ont un comportement très proche. Calés sur les mêmes quantiles pour la période de retour 5 ans, ils conduisent pratiquement aux mêmes estimations des quantiles de 100 et 1000 ans. Le graphique de droite de la Fig. 8 compare les deux modèles M1 loc et M2 loc au modèle plus classique M3 loc. On observe alors un écart croissant des estimations des quantiles extrêmes obtenus par les méthodes M1 et M2 par rapport à ceux de la méthode M3. Cependant, bien que le comportement des modèles M1 et M2 soit qualifié d’hyper-exponentiel, l’ajustement local d’une loi d’exponentielle peut parfois conduire à des quantiles plus forts en présence d’une valeur extrême dans l’échantillon.

Comparaison des quantiles 5 ans, 100 ans et 1000 ans obtenus sur 12 postes pluviométriques « tests » de la zone d’étude, par les trois approches dans leur version locale.
Fig. 8. Quantiles corresponding to the 5-, 100- and 1000-year return periods for 12 rain gages, obtained with the both methods with their parameters estimated at each gage.
5 Discussion
Une première analyse des résultats montre que, dans leur version régionalisée, les deux méthodes sont très proches en termes d’extrapolation vers les fréquences rares (moins de 20 % d’écart). Ce point est particulièrement intéressant quand on sait que c’est généralement en extrapolation que des méthodes peuvent diverger. Les écarts obtenus pour les quantiles millénaux sont d’un ordre de grandeur nettement inférieur aux intervalles de confiance que l’on peut calculer pour cette période de retour. On peut alors raisonnablement penser que les extrapolations auxquelles conduisent les deux méthodes convergent vers les mêmes estimations.
Les écarts observés entre les deux approches sont essentiellement dus à la régionalisation de leurs paramètres respectifs. Les paramètres étant déterminés par des valeurs moyennes, les écarts entre les approches sont directement proportionnels aux écarts entre ces paramètres. Lorsque ces écarts sont faibles, les écarts entre les deux approches restent faibles.
Les résultats obtenus avec les versions locales des deux approches sont particulièrement intéressants. En partant d’approches totalement différentes dans leur principe, on obtient pratiquement les mêmes résultats. Si ce point paraît évident pour les fréquences courantes (on retrouve les quantiles « observés »), il n’était pas nécessairement attendu en extrapolation vers les valeurs extrêmes.
Le point commun de ces deux approches est la prise en compte de l’information régionale des pluies, réduisant ainsi leur sensibilité à l’échantillonnage. Elles conduisent à une estimation des quantiles rares plus robuste et plus cohérente spatialement.
Pour juger de la cohérence spatiale des approches M1 et M2, nous avons contrôlé les résultats sur 16 postes journaliers supplémentaires non utilisés lors de leur développement. Pour cela, les méthodes M1, M2 et M3 sont appliquées dans leur version « locale » et dans leur version « régionale ». Par ailleurs, la régionalisation des approches a été réalisée suivant deux méthodes d’interpolation : par l’inverse de la distance (notée « idw ») et par la méthode Aurelhy, prenant en compte les paramètres du relief (notée relief).
Dans le cas des méthodes M1 et M2, ce sont les paramètres estimés localement sur 115 postes qui sont interpolés sur la zone d’étude. Cela permet d’estimer les quantiles de pluies en tout point de la zone par les deux approches (M1 et M2), notamment sur les 16 postes de comparaison. Dans le cas de la méthode M3, ce sont les quantiles 10, 100 et 1000 ans, obtenus localement par la méthode M3 sur ces 115 postes, qui sont interpolés sur la zone d’étude.
Sur les 16 postes non utilisés dans la phase de régionalisation, on calcule un critère de Nash pour chaque méthode M et pour les trois quantiles de pluie journalière (10, 100 et 1000 ans), PJXAT, de façon à juger de la robustesse des méthodes utilisées dans leur version régionalisée :
| (3) |
Le Tableau 2 synthétise les résultats obtenus. On constate que les méthodes Shypre (M1) et loi régionale (M2) régionalisées restent robustes, quelle que soit la méthode d’interpolation des paramètres qui est utilisée : les critères de Nash varient peu avec la période de retour et sont au moins de l’ordre de 70 % avec une méthode « idw » et de plus de 80 % avec la méthode prenant en compte le relief. En revanche, une régionalisation directe des quantiles ne permet pas une estimation aussi bonne : le critère de Nash est au maximum de 57 %, et décroît nettement avec la période de retour (33 % pour les quantiles millénaux). Ceci traduit la sensibilité de la méthode M3 à l’échantillonnage, contrairement aux méthodes régionales M1 et M2, dont la régionalisation repose sur des paramètres qui sont des moyennes, moins sensibles à l’échantillonnage.
Critère de Nash pour chaque méthode, comparant une estimation des quantiles PJXAT avec la version régionale du modèle M à la version locale de ce même modèle, calculée sur les 16 postes de validation
Table 2 Nash criterion for a comparison of the regional and local estimation of the quantiles PJXAT for each model M
| Interpolation des paramètres : inverse de la distance | Interpolation des paramètres : régression multiple avec variables descriptives du relief | |||||
| T = 10 ans (%) | T = 100 ans (%) | T = 1000 ans (%) | T = 10 ans (%) | T = 100 ans (%) | T = 1000 ans (%) | |
| Shypre (M1) | 74 | 69 | 68 | 82 | 82 | 82 |
| Loi régionale (M2) | 75 | 75 | 75 | 86 | 86 | 86 |
| Ajustement loi exponentielle (M3) | 57 | 39 | 33 | 49 | 46 | 39 |
On illustre ainsi clairement la supériorité des méthodes basées sur des approches régionales selon deux critères :
- • une bien moins grande dispersion des estimations des quantiles extrêmes ;
- • une meilleure cohérence spatiale des quantiles estimés sur une région.
Remerciements
Les auteurs tiennent à remercier Météo France pour la mise à disposition des chroniques pluviométriques utilisées pour cette étude.


