1 Introduction
Two parameter classes may be used to characterize clay sediment properties. The first one concerns the geotechnical index properties linked to the particles’ mineralogical nature and can be represented, for example, by the Atterberg limits, or by their equivalent void ratios,
2 The Biarez & Favre (B&F) model
The soil – a granular and discontinuous medium (DM) – may be seen as a virtual continuous medium (CM), using, for statistical connections, the logical framework shown in Table 1. The ‘mechanical properties of soils’ thus appear as the integration of the grain properties (called ‘nature of grains’) in their spatial configuration (called ‘arrangement of grains’) and their mechanical boundary conditions (which can be represented by the consolidation stress tensor). In the case of remoulded clays, Favre [11,12] shows that the Atterberg limits (‘nature of grain’ parameters) allow us to explain the mechanical properties. In mineral clays, these properties are strongly linked by the following relation:
| (1) |
Logical framework for statistical connections
Tableau 1 Cadre logique pour les liaisons statistiques
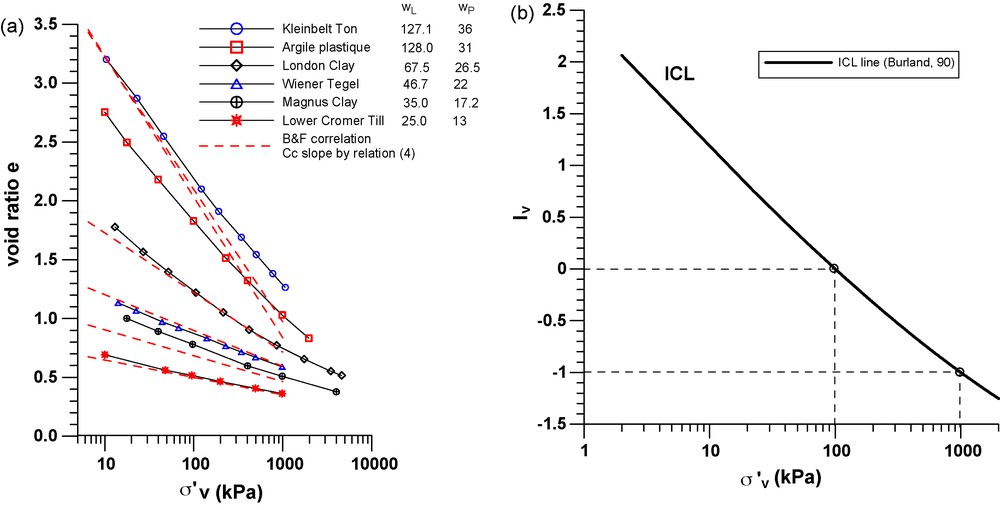
In this way, the model proposed in Fig. 1a, which, plotted with the Casagrande A line, defines the mineralogical nature of the clay.

Biarez and Favre correlations for the normally consolidated remoulded clays.
Fig. 1. Corrélations de Biarez et Favre pour les argiles reconstituées, normalement consolidées.
On the other hand, a large number of results collected by Favre [11,12] show that the 6.5- and 1000-kPa loadings on the oedometric path correspond, on average, to wL and wP, respectively (or eL and eP, considering
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
By comparison with relation (5), proposed by Skempton [16] for remoulded clays, we underestimate by 10% the compression index Cc for wL = 40% and by 5% for wL = 70%. Nevertheless, the simple model represented by relations (2) and (4) was retained for the oedometric test, and hence, by relation (1), it uses only one Atterberg limit, wL. It is a straight line in the
| (7) |
The ‘arrangement of grains’ therefore appears to be directly linked to the consolidation stress tensor, through the mineralogical properties. This connection corresponds in the
3 Burland's model
Burland [8] collected and analyzed the oedometric compressibility of several clay sediments remoulded and reconstituted in the laboratory and with liquid limit wL varying from 25% to 159%. The curves obtained in the (
| (8) |
| (9) |
The intrinsic compression line by Burland [8].
Fig. 2. Ligne de compression intrinsèque de Burland [8].
The ICL (Intrinsic Compression Line) curve, corresponding to equation (10) and represented by Fig. 2b, can then be deduced from a statistical model based on the experimental curves passing through the two specific points (
| (10) |
The two particular parameters
| (11) |
3.1 Comment
Although both approaches appear to be based on a similar method, there is a fundamental difference in the manner in which the intrinsic characteristics of the ‘arrangement of grains’ were defined on the oedometric path. Burland does this using two experimental values (

Variations of
Fig. 3. Variations des paramètres
4 Comparison of models and mixed model
4.1 B&F's model in Burland's space (
According to correlation (7), we have:
| (12) |
Using Eqs. (9) and (12), to express B&F's model as a function of Iv, we get the NCRS equation (13) in Burland's space.
| (13) |
| (14) |
| (15) |
| (16) |
Equation (16) is a straight line in the (

Comparison between the two statistical models for the one-dimensional loading in (
Fig. 4. Comparaison entre les deux modèles statistiques pour le chargement unidimensionnel dans les plans (
Characteristics of the models
Tableau 2 Caractéristiques des modèles
| Burland's model | B&F's model | B&F's mixed model | |
| Equation |
|
|
|
| Characteristic points |
|
|
|
| Compression index |
|
|
|
4.2 B&F's ‘mixed’ model represented in Burland's space (
In the linear relation (13) resulting from B&F,
| (17) |
Here ζ and χ are the parameters given by equation (18) as function of the eL and eP limits, defined by their experimental values:
| (18) |
The ‘mixed’ model described above is applied to the two kinds of clay and are represented in the (
The experimental path evolves first from one point located above the ICL curve (sensitive clays) towards a domain that exhibits a ‘fictitious consolidation stress’ and a supplementary cohesion on the oedometric curve. The latter is due to the beginning of the degradation of the cementation between particles developed in situ during the sedimentation and the consolidation processes. Afterwards, the cementation is gradually destroyed (destructuring according to Leroueil et al. [15], and the experimental curves tend to converge at high stresses (up to 1000 kPa) towards the ICL curve of the remoulded state of the material. Clays structuring has been quantified by Cotecchia and Chandler [9,10] using the sensitivity parameter St (Skempton and Northey [17]) as a normalizing parameter for the structure. Thus, the evolution of St may be used to describe the destructuration phenomenon (destructuration law of Baudet and Ho [1]).
4.2.1 Remark
Burland's relation (10) expressed in the (IL – log σ’v) plane using equation (11) becomes equation (19) as a function of the eL and eP limits, ζ and χ being defined by relation (18):
| (19) |
Since the ICL depends on eL (Fig. 4b), it is transformed in the (
B&F's assumption that
5 Conclusion
Two intrinsic compressibility concepts proposed for the remoulded reconstituted clays are discussed in this paper. The NCRS, resulting from the Biarez and Favre's correlation [2,3], is based on the liquid index parameter IL = (w–wP)/(wL/wP). The ICL, resulting from the Burland's correlation [8], is based on a normalized void index parameter
The ‘arrangement of grains’ in Biarez and Favre is defined through wL and wP (or eL and eP) – two ‘nature parameters’ – whereas in Burland, this is done by means of the two ‘arrangement parameters’
When the NCRS is represented in Burland's plane (Iv,
Acknowledgements
This work was conducted in the framework of the CLAROM Deepwater sediments project – on the site B Stacor core from the Gulf of Guinea. Project partners were: IFP, IFREMER, Fugro-France, Saipem-SA, Stolt Offshore, Technip, and Total.


