1 Introduction
Deep geothermal systems are not yet completely understood and the science about them is still an evolving process. Only few deep geothermal power plants exist and for further spreading, economics is the key of the technology. The economic evaluation of an Enhanced Geothermal System (EGS) is complex due to multiple physical and financial dependencies. The financial characteristics are determined by physical, geological and hydrogeological properties. Comprehensive economic calculations of geothermal Hot Dry Rock (HDR) power generation were firstly performed by Tester (1982), later by Smolka and Kappelmeyer (1991).
Prior to the Euronaut software here presented, an earlier software HDRec (Hot-Dry-Rock economic evaluation, Heidinger et al. (2006)) with similar features to the first configuration already existed. Changes in strategy and continuous enhancements on elements of the plant became more and more difficult to implement in the code due to growing number of dependencies and serial character of the programming language (Fortran77). Finally, the software was rewritten from scratch using the object-oriented Java language. The main focus of this new software was the ability to change and grow. Only the economic approach of discounted cash flows (DCF) was set as a kind of root to the software. All other calculations are performed in separate modules, which can be linked together by interfaces. The modules can be changed or re-arranged simply by mouse-clicks. The modularity of the software limits the implementation of changes, enhancements or the implementation of results from other programs to the affected modules only. All elements of the EGS system are implemented in modules and not in the Euronaut software itself. As a side effect, the Euronaut software is not limited to EGS calculations only but can handle any kind of economic evaluation. Payments evolving during the entire lifetime phases of the project: the investments, the operating costs, the revenues and the dismantling costs are applied to the evaluation. The EGS system is wrapped into modules resulting in a “tree-like” structure. Calculating the cash flows for all modules and for all the lifetime cycle, the financial characteristics of the project are determined. The main results are the net present value (NPV), the return on investment (ROI) and the prime costs. The prime costs of power plants are defined as the total effective costs to generate 1 kWh of electricity. Additionally, all the other results, financial or physical, of the modules are available. Changes in the physical models or financial schemes are limited to the related modules only and hence can be implemented fast and easily. Based on the experience which was gained at Soultz-sous-Forêts, two structures by this Euronaut software were created. The first one is a simplified two well (doublet) system where all properties are dependent of the reservoir depth, mainly the temperature of the fluid for heat extraction, the drilling costs and the permeability of the rocks. As a result, the depth dependent effective costs for running a plant are determined. The second one will be a model of the actual situation of the EGS at Soultz-sous-Forêts with the individual features of all four wells GPK1, 2, 3 and 4. This model can be used for all kinds of sensitivity analyses to clarify the impact of some components or to find an optimized operation scheme of the plant. In this paper, firstly the Euronaut software is explained briefly with a closer look at the distinct modules of an EGS plant. Then the financial characteristics of hypothetical doublet systems for different reservoir depths are calculated. Finally, the future model of the four well EGS plant at Soultz-sous-Forêts is presented.
2 The EGS structure
An integral EGS plant consists of some main components, which starts from its heart: the reservoir, then the boreholes, the pumps and the heat-to-power conversion unit. This general scheme is shown in Fig. 1. In order to get a list of all input parameters, dependencies and costs, not the structure itself is shown here, but the quantitative and qualitative behavior of the separated components as well as the individual rules of operation and financial characteristics are listed.
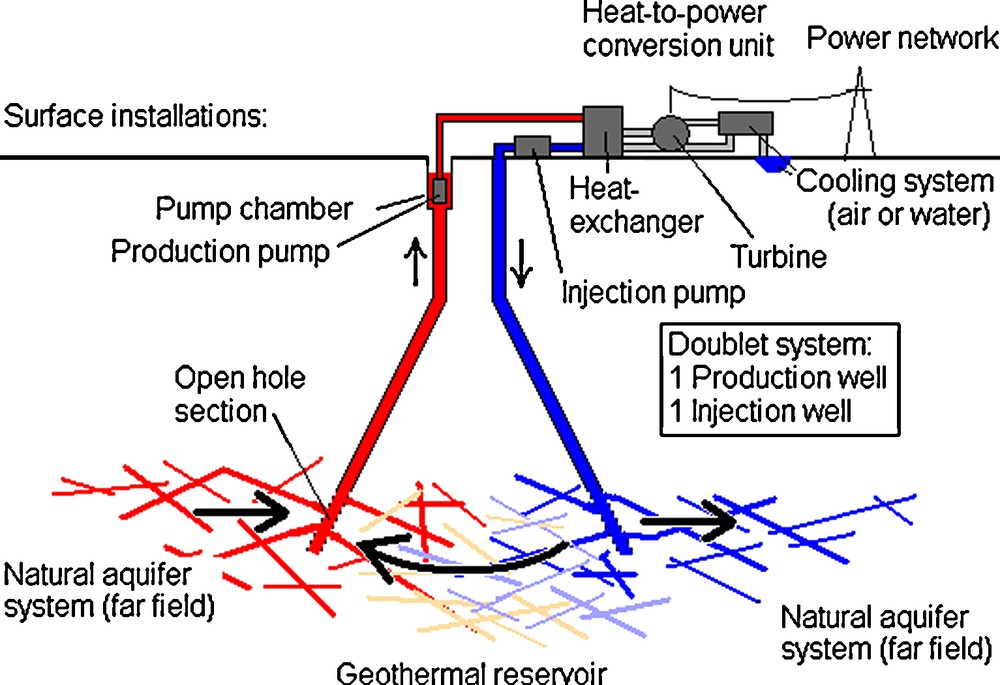
General scheme of an EGS plant: the reservoir, wells, pumps and the heat-to-power conversion unit.
Schéma général d’une centrale EGS : réservoir, puits, pompes et unité de conversion de chaleur en énergie.
2.1 Reservoir
The reservoir is an adaptable combination of the HDR model and an EGS. The fluids circulating between the re-injection well and the production well are cooling down the hot rock gradually. This depends on the thermal properties of the rocks and the fluid, the geometry of the flow paths and most dominant by the flow rate of the circulating fluid. The parts of the fluid which are not circulating but are produced from and re-injected into the far field of the aquifer system are not affected by this thermal drawdown. The equations describing the HDR model have been developed by Heuer (1988). The combination of HDR and EGS models to an enhanced analytical heat-exchanger are explained in detail by Heidinger et al. (2006). For the following calculations, the internal surface of the heat-exchanger hooked up by two wells was chosen to be 3.4 km2. This surface is modeled by three horizontal oriented “penny-shaped” fracs, each with a radius of 600 m. The fracs are coupled by conductive heat flow. This setting is derived from the stimulated volume between GPK2 and GPK3; see Fig. 2 and results from flow logs performed in the open-hole sections of these wells. The lateral distance between the open parts of the wells is 600 m; the connectivity to the far field is set to 50%. Tracer experiments indicate even connectivity to the far field up to 80% (Sanjuan et al., 2006). The small thermal drawdown for such a reservoir in 5 km depth at a low circulation rate of 25 L/s is shown in Fig. 3 (temperature at inlet of production well). For higher flow rates or lower connectivity values to the far field, the thermal drawdown can affect the production temperature significantly after relatively short times (∼ years). Hydraulic and chemical stimulation together with the reservoir are fixed costs of 1 M€. Dependent of the reservoir depth, the initial temperature of the reservoir is defined by the undisturbed temperature profile at Soultz-sous-Forêts; the profile was measured down to 5 km depth, below it is extrapolated, see Fig. 4.
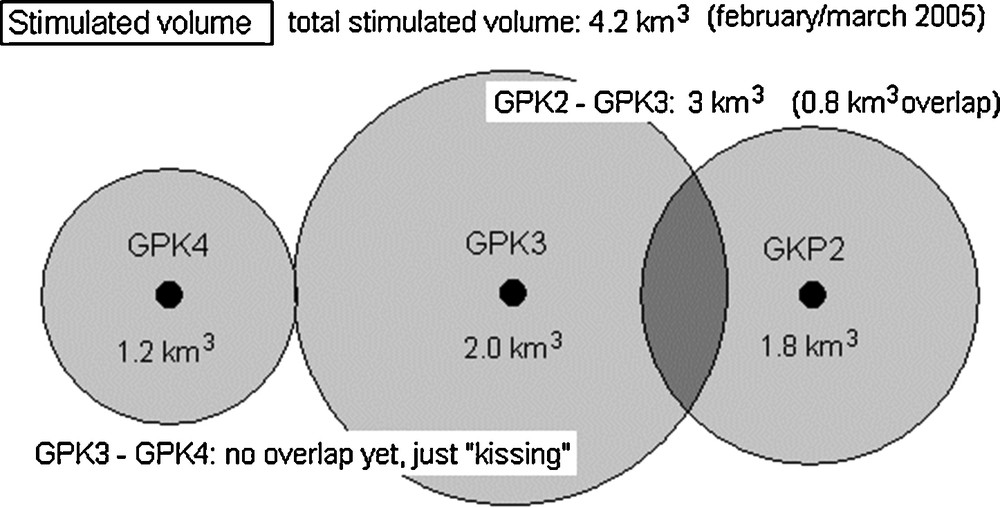
Enveloped volume of seismic events during stimulations of the wells GPK2, GPK3 and GPK4.
Volume enveloppé des éléments sismiques pendant les simulations des puits GPK2, GPK3, GPK4.
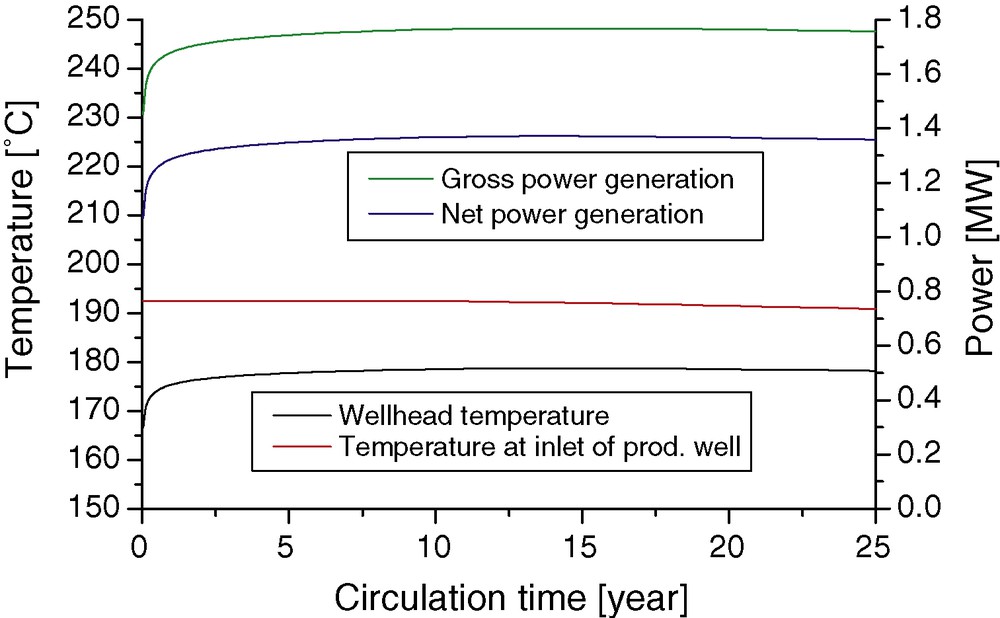
Actual situation of doublet system (GPK2, GPK3) at Soultz-sous-Forêts. Prediction of gross and net power generation of the plant and wellhead and inlet temperature of the production well for 25 years operation with a constant circulation rate of 25 L/s.
Situation actuelle du double système de puits (GPK2, GPK3) à Soultz-sous-Forêts. Prédiction de la génération d’énergie brute et nette de la centrale et température de tête de puits et d’admission du puits de production, sur une durée de 25 ans avec un flux de circulation constant de 25 l/s.

Temperature profile at Soultz-sous-Forêts. Above 5000 m depth, the formation temperature is known by measurements, below the temperature is extrapolated.
Profil de température à Soultz-sous-Forêts. Au-dessus de 5000 m de profondeur, la température de formation est connue par mesure, au-dessous, la température est extrapolée.
2.2 Drilling operation
The drilling costs of wells are rising exponentially with depth; this empirical behavior is described by Garnish (1987), and by Legarth and Wohlgemuth (2003). “Steel prices” and energy costs have boomed (drilling rigs are equipped with fuel oil generators) during the last years and the costs to drill a borehole to a specific depth increased significantly. Depth dependent costs for mobilizing a rig and to drill two boreholes with casing, used in the following calculations, are shown in Fig. 5. The costs for two wells to 5 km depths would be actually ∼ 17 M€, whereas to 3 km depth only ∼ 6 M€.
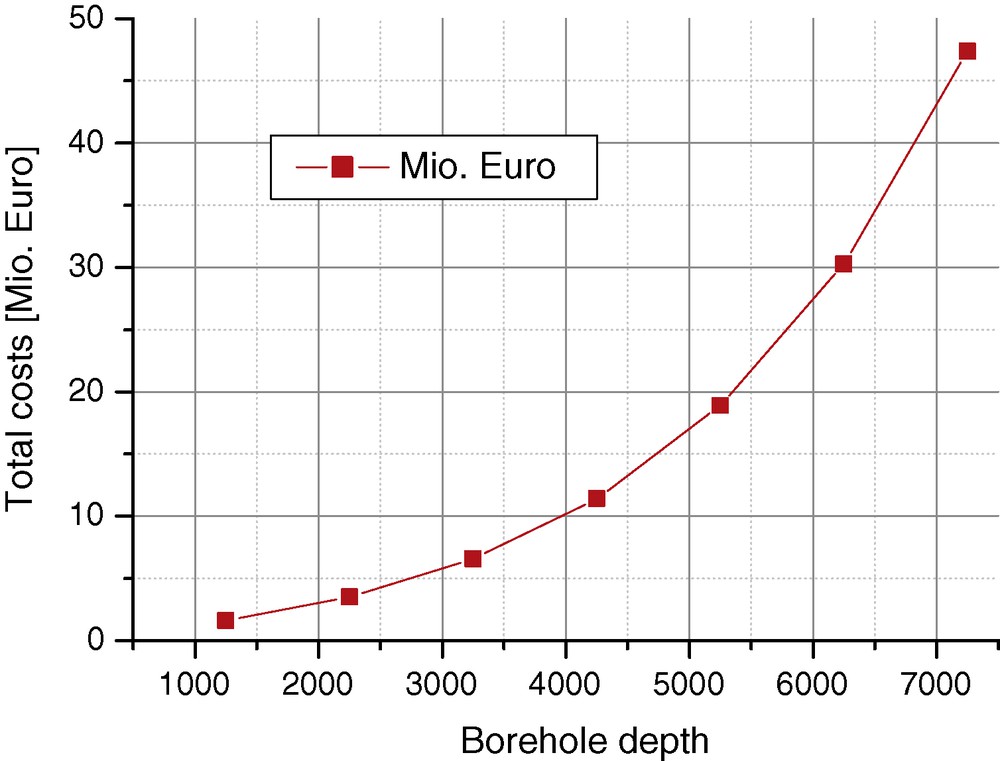
Depth dependent total drilling costs for a doublet well system (2 wells, mobilization and drilling costs, casing included).
Coûts du forage total dépendant de la profondeur pour un système double de puits (2 puits, coûts de mobilisation et de forage, tubage compris).
2.3 Pumps and wells
The power demand of pumps and the temperature change development of the fluid during its flow in the wells are a nice example of complex dependencies within the EGS. When the produced fluid ascends in the well, it is cooled down by the surrounding rocks; with time these rocks get heated itself and the cooling of the ascending fluid decreases. Thus, the temperature of the fluid at the wellhead increases with time. The “flow depending” temperature evolution of the geothermal fluid during its transit up and down the wells was described with an analytical approach by Ramey (1962). Together with a thermal drawdown of the reservoir, this leads in most calculations to a peak of energy production which is reached after several years. This temperature change does not only affect the energy production of the plant but also the “parasitic” power demand of the pumps (the energy demand of the pumps and the self-consumption of the heat-to-power unit are necessary to run the plant and are not a by-side effect, therefore this negative contribution to the energy balance of the plant is called parasitic). The electric power needed for the pumps to maintain the fluid circulation depends on several factors, these are: the flow rate, the efficiency of the pumps (different for production, here 50% and injection pumps, here 65%) and the total dynamic head (TDH) of the pump which itself again depends on: the flow rate, the productivity or injectivity index of the well, friction losses and the buoyancy effect. The buoyancy effect is driven by density differences between the water column responsible for the hydrostatic pressure in the reservoir and the water column in the well and supports the circulation. The density of the fluid is pressure, temperature and “chemical composition” dependent (Champel, 2006) and based on the database of ASPEN (1988) computations. Nevertheless, the “chemical composition” dependency is considered constant over the lifetime of the plant. The friction losses are calculated after Stelzer (1974). The fluid pressure in the surface piping system from the production pump outlet to the injection pump inlet is kept at 16 bars to prevent scaling, corrosion and pump cavitation by “degassing”. See evolution of power demand for GPK2 and GPK3 for actual characteristics at Soultz-sous-Forêts in Fig. 6. The pump chamber of the production pump is situated at 400 m depth; the pump can be either a line-shaft or a submersible pump; both types are difficult to maintain and lifetime is set to 10 years and investment costs are set to 800 000 €. The re-injection pump is located on the surface, easier to maintain than production pump but requires fine filtration to avoid erosion of injection pump impeller by mineral particles; there is no lifetime limitation and investment costs are set to 100 000 €.

Actual situation of GPK2 (productivity index 9.3 L/s/MPa) and GPK3 (injectivity index 3.6 L/s/MPa) at Soultz-sous-Forêts. Parasitic power demand of both pumps for the first two years calculated at a constant flow rate of 23.6 L/s; also shown, the temperature evolution at the wellhead of GPK2.
Situation actuelle de GPK2 (indice de productivité 9,3 l/s / Mpa) et de GPK3 (indice d’injectivité 3,6 l/s /Mpa) à Soultz-sous-Forêts. Demande d’énergie parasite des deux pompes pour les deux premières années, calculée à débit constant de 23,6 l ; l’évolution de la température en tête de puits, dans le cas de GPK2, est également montrée.
2.4 Heat-to-power conversion
For heat-to-power conversion, the temperature of the produced geothermal fluid is low and far from ideal. The maximum possible efficiency of an ideal heat-to-power conversion in the power station is defined by the Carnot efficiency, but in reality the efficiencies are lower. Due to the high mineralization of the formation water, a closed loop for circulation is required and binary systems for heat-to-power conversion are used. These are mainly organic-rankine-cycles (ORC) or Kalina-cycles. This module uses specific characteristics of the conversion (coolant temperature 20 °C, pinch-point temperature differences at condenser 15 °C and vaporizer 15 °C, efficiency of turbine 85%, re-injection temperature 70 °C) to calculate production temperature dependent efficiencies (Milora and Tester, 1976). This process can be adapted to the model of the conversion unit. With this implementation, a location-specific decision of the type and model of the power station type can be done. The costs of the unit are specific costs linked to the maximum producible electric gross power output; the value used for the following calculations is 1.5 M€/MWel. Inflow temperature dependent gross efficiencies for the above given set of characteristics are shown in Fig. 7. The self-consumption of the conversion unit amounts to 10% of the gross energy production. The load factor of the plant is set to 95%.
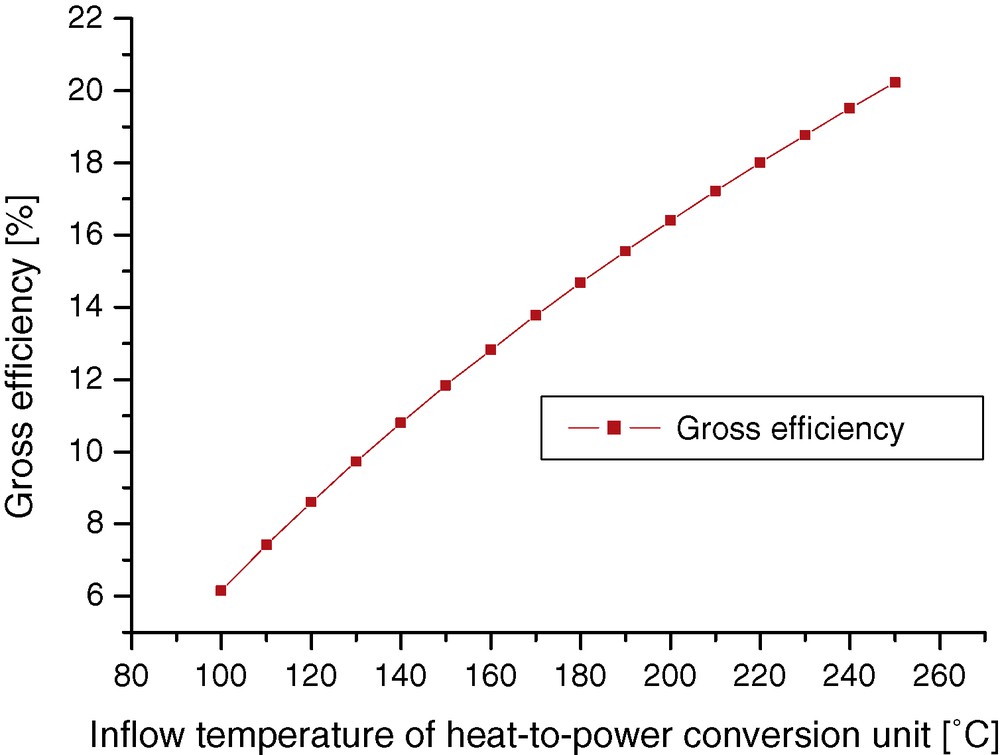
Gross efficiency of ORC heat-to-power conversion unit dependent on the wellhead temperatures of the produced fluid. Other parameters are re-injection temperature of fluid: 70 °C, coolant temperature: 20 °C, efficiency of turbine: 85%, pinch-point temperature difference at vaporizer: 15 °C and at condenser: 15 °C.
Efficacité brute de l’unité de conversion ORC chaleur–énergie, dépendant des températures en tête de puits, du fluide produit. D’autres paramètres sont : température de réinjection du fluide : 70 °C, température du fluide de refroidissement : 20 °C, efficacité de la turbine : 85 %, différence de température au point de pincement du vaporisateur : 15 °C et du condenseur : 15 °C.
2.5 Permeabilities
The rock permeability in each well determines the productivity and injectivity indexes of the well (PI and II). These indexes may exhibit great variations from one well to another, even when they are very close to each other. The individual characteristics of all wells define the maximum possible circulation rate as well as the energy consumption of pumps. The financial revenues are directly linked to both effects and the productivity and injectivity indexes easily decide about success or failure of a project. The indexes cover magnitudes, from nearly 0 to 30 L/s/MPa at the geothermal site at Landau, Germany (BMU, 2008), yielding circulation rates from 4 L/s to 70 L/s; in the Molasse of Bavaria even 150 L/s (BMU, 2008) was reached. The great range of these indexes is explained with the fractal characteristics of the fluid flow paths and no reliable predictions of the well indexes before drilling them are possible today. Generally permeability decreases with increasing pressure (Rummel, 1990). Extrapolating results from the upper (best value found in Evans et al., 2005) and lower reservoir (average of GPK2, GPK3 and GPK4, Nami et al. (2008) at Soultz-sous-Forêts, a depth dependent well index profile was compiled, see Fig. 8. Generally, the naturally found productivity/injectivity well index can be improved by artificial hydraulic and/or chemical stimulations. In the following, the stimulation process of the reservoir was set to fixed costs (independent from depth) of 1 M€.
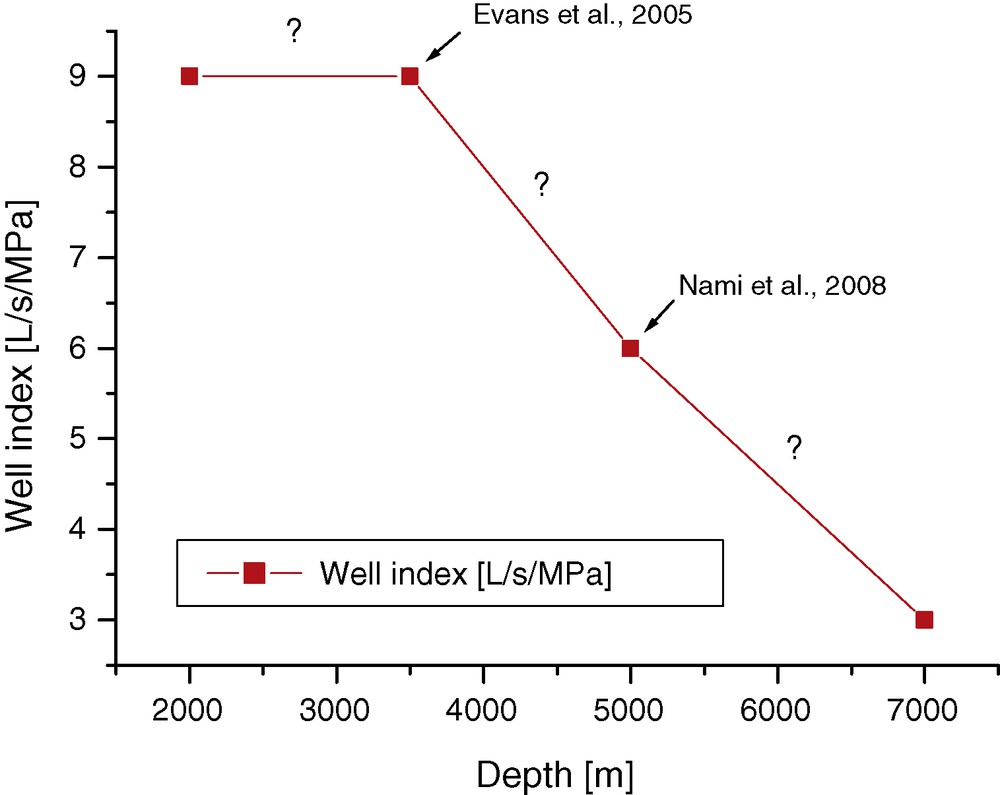
Assumed depth dependent well (productivity and injectivity) indices at Soultz-sous-Forêts.
Indice (productivité et injectivité) du puits dépendant de la profondeur assumée.
2.6 Feed-in tariffs in France and Germany
The revenue of the geothermal plant for the generated electric power differs in France and Germany and depends also on various other parameters: the size of the plant, when it was constructed, operation time or some bonus if thermal energy is sold too. Generally, the net present value (NPV), which is the sum of all discounted cash flows, is an indicator of how much value a project adds to an investment and is widely used throughout economics as criteria for evaluating projects. Here, it may not be the appropriate method, because the NPV is not related to the investment sum and the investment costs of a deep geothermal power plant vary strongly because of the depth dependent drilling costs. In this case, better criteria are the prime costs. These prime costs are the total effective costs to generate 1 kWh of electricity. These costs are composed by all costs, including the investment costs and are independent from the feed-in tariff. This sum in relation to the sum of the product (here the electricity, which can be sold), yields the total effective costs. But regulations defining the electricity, which can be feed-in, are different in France and Germany. In France, only the net resulting energy is sold (net scheme, generated energy minus parasitic energy consumption of plant). Whereas in Germany, all generated power is fed to the electric grid (gross scheme), the power to maintain the pumps and the heat-to-power conversion unit is bought in at lower prices. Therefore, effective costs are quite different for the same type of plants located in France and in Germany. This conclusion is only slightly dependent from an optional sale of heat.
2.7 Remaining input parameter
The most important remaining input parameters are listed here. A summary of all input parameters can be found in the Appendix A of this article.
| Financial | |
| Rate for discounting the cash flows | 3.8%/a |
| Investments | |
| Buy and explore land | 1 M€ |
| Commercial period | |
| Lifetime of commercial energy generation | 25 years |
| Production rate | 25 L/s |
| Operating costs (maintenance and salary) | 0.2 M€/a |
| Price to buy electricity (only gross scheme) | 0.06 €/kWh |
3 Sensitivity analysis of well and reservoir depth
All the described components of this structure are dependent on each other and changing one input parameter can influence all modules. The type of EGS plant and its components shown in Fig. 1 is represented in the configuration. All the dependencies and financial or physical rules described in the previous chapters are implemented. Thus, the complex sensitivity analysis of the drilling and reservoir depth of a new hypothetical deep geothermal power plant, with the geological features revealed at Soultz-sous-Forêts, is performed by varying only one parameter: the drilling depth; all described components are affected directly or indirectly by this value, the costs and time needed for drilling the wells, the reservoir temperature and behavior, the production temperature, the costs and efficiency of the heat-to-power unit, and so on. For each depth, an optimization cycle was performed to find the circulation rate minimizing electricity generation costs. To find a range of possible circulation rates, the maximum possible production rate was determined first. Surprisingly, the decreasing productivity index with depth had no effect to the maximum production rate. The reason for this behavior is the buoyancy effect, which gets stronger with depth and compensates the reduced productivity of the well. For the investigated depth range from 2000 to 7000 m depth, the maximum possible production rate amounts from 25 to 30 L/s. The parasitic power demand of pumps at these production rates is not yet strong enough to limit the circulation rate with the minimized electricity generation costs. Therefore, best economics results for this specific type of plant are accomplished at maximum possible circulation rates. For easier comparing and to focus on the impact of the parameter reservoir depth, a constant circulation rate of 25 L/s was chosen. Results calculated with an additional non-constant circulation rate (utilizing the maximum possible circulation rate for each depth) are only slightly different to the results presented here and do not affect the conclusions of this analysis. The effective costs (gross and net scheme), the total investment costs, averaged gross and net power generation of the plant are shown in Fig. 9. The economically most important factor; the effective costs are high for shallower depths; with increasing depth the costs are firstly decreasing and then start rising again. A minimum for both, the net and the gross feed-in financing schemes is found at about 5500 m depth, which is very close to the real well and reservoir depth at Soultz-sous-Forêts. The main part of the investment costs are the drilling costs; therefore the investment costs have a similar exponential behavior. The gross and net power generation is dependent on the temperature of the produced fluid which is time dependent. Therefore, shown is the averaged gross and net power output of the commercial period (25 years).
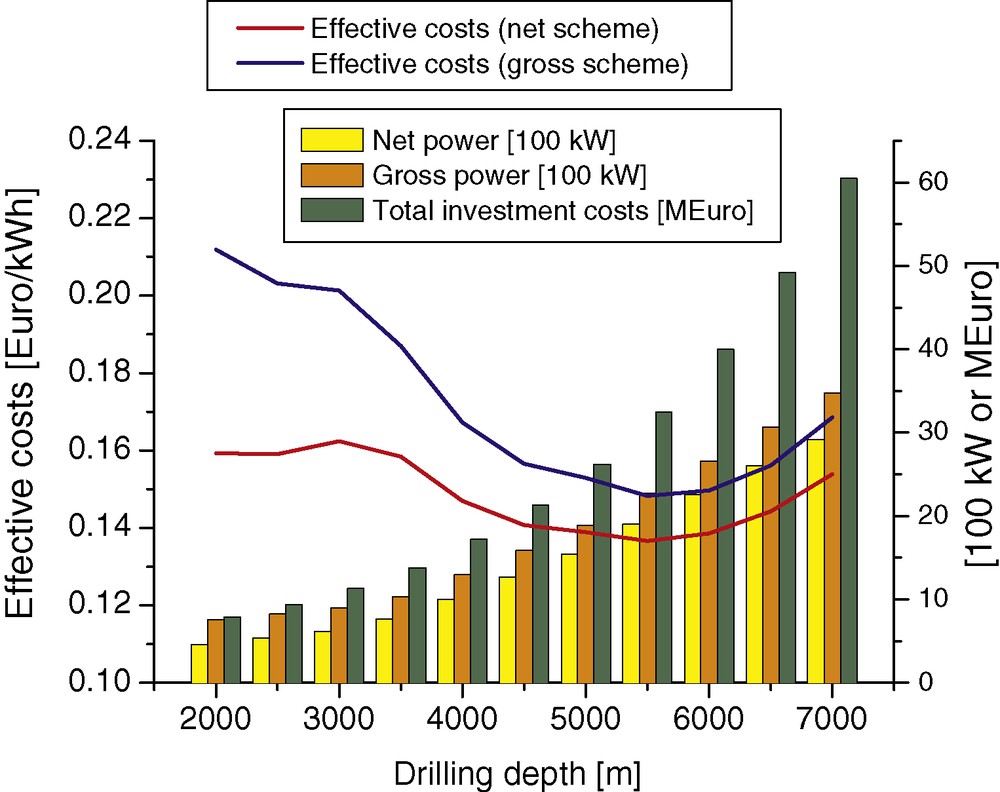
Major results of well and reservoir depth sensitivity analysis: effective costs (gross and net scheme), total investment costs, averaged gross and net power generation.
Principaux résultats de l’analyse de susceptibilité à la profondeur du puits et du réservoir : coûts effectifs (bruts et nets), coûts totaux d’investissement, génération d’énergie brute et nette moyennée.
The EGS structure implemented by this configuration reacts on other parameters as well. It is important to understand, that these economic and physical results are only valid for the given set of input parameters and cannot be generalized. Other input parameters (i.e. the productivity and injectivity indices) strongly affect the economic and physical results also and can shift the minimum of the effective costs dramatically.
4 Situation at Soultz-sous-Forêts, model results and predictions
The model used for the sensitivity analysis of the depth is only a slight modification of the real situation of the geothermal power plant at Soultz-sous-Forêts. The second configuration differs to the sensitivity model only in few elements:
- • The well diameters are not a fixed value for the entire depth and same for all wells, but the real geometry of each well is used (sizes and geometry can be found in e.g. Tischner et al. (2006)). TVD of the wells GPK2, GPK3 and GPK4 is 5026, 5021 and 4972 m, respectively; the open-hole length of wells range from 500 to 600 m;
- • The production pump is not installed in 400 m but in 350 m depth; this has only a small effect on the energy consumption but reduces the maximum production rate;
- • The productivity and injectivity indexes of the wells are not averaged, but have the individual values. Actual indexes are GPK1 10 L/s/MPa, GPK2 9.3 L/s/MPa, GPK3 3.6 L/s/MPa and GPK4 5 L/s/MPa;
- • The reservoir between GPK2 and GPK3 has the same characteristics as described in chapter “Reservoir” with a connectivity of 50%; the reservoir between GPK3 and GPK4 is smaller (internal surface of the heat-exchanger chosen to be 2.7 km2) but has a higher connectivity to the far field (80%), see sketch in Fig. 2;
- • Possible re-injection into the only 3500 m deep well GPK1 has no thermal effect to GPK2 or GPK4 because of unconnected aquifer systems.
The average temperature of the rocks opened up by the wells accounts to 192.5 °C. This value is used in the following calculations of the situation at Soultz-sous-Forêts as the temperature of the undisturbed reservoir and for the incoming fluids from the far field.
4.1 Power consumption of pumps and temperature change in the wells
The economics of a geothermal power plant are affected significantly by the parasitic power consumption of the pumps. The power consumption of such well pumps is in first approximation proportional to the square of the flow rate. The pumps are located on ground surface or close from it but the pressure for production and re-injection are needed at the intersection of the open hole to the reservoir. Therefore, the different densities between the water column in the well and the water column responsible for the hydrostatic pressure in the reservoir have to be accounted in the calculations. At production, the fluid is warmer and has a lower density, than the fluid column on the underground reservoir, which helps the pump; at injection, the fluid is soon colder than the fluid in the formation and has a relatively higher density, which again helps the pump. In both cases, the buoyancy effect supports the pump. In the beginning of the circulation, the temperature of the fluid changes much while flowing in the wells; by time the surroundings of the wells are influenced by the temperature of the fluid and this effect decreases. This temperature evolution again affects the density and therefore the buoyancy effect. Even more important is this effect for calculating the wellhead temperature of the production well. This temperature is the intake temperature to the heat-to-power conversion unit and directly affects the amount of produced electric energy. The evolution of the fluid temperature (and pressure) during their flow in the boreholes was well constrained by adaptation of the model (diffusivity value of 1.25 × 10–6 m2/s of the surrounding rocks) to the data from the injection experiment into GPK3 in June, 2007, where down hole measurement instruments have been installed.
The parasitic power demand of the pumps in Fig. 6 was calculated with a flow rate of 23.6 L/s. This is the only flow rate where the power consumption of the actual installed pumps at Soultz-sous-Forêts is known. Without further calibration, the results fit already quite well with the known values after ∼ 10 days of circulation: injection pump 110 kW and production pump 88.4 kW. Also shown is the temperature evolution at the wellhead of GPK2. During these first two years, the parasitic power demand of the pumps only amounts to ∼ 12.5% of the gross energy generation. Regarding the self-consumption of the heat-to-power unit also, the total parasitic power demand requires ∼ 22.5%; this is nearly one quarter of the gross energy generation. The results shown in Fig. 3 reveal that even after some years of production, a temperature difference from the reservoir to the production wellhead of ∼ 14 °C is remaining. Then after ∼ 12 years, the reservoir starts to cool down slowly; decreasing temperatures at the inlet and, with some delay, decreasing temperatures at the wellhead are the consequence. The gross and net power generation of the plant are closely related to the wellhead temperature, which can be seen in Fig. 3.
4.2 Doublet system GPK2 – GPK3
For this actual existing doublet system a flow rate dependent sensitivity analysis was performed. The flow rates are varying from 5 to 35 L/s; a higher flow rate is not possible because otherwise the pressure in the pump chamber of the production pump would be too low (< 16 bars). No investment costs at all are assumed, the maintenance costs are higher then in the previous calculations and set to 1 M€ per year due to reduced lifetime of pumps. The calculation system for the generated power is the net scheme, the feed-in tariff accounts to 12 Cents/kWh; both cash flows: the maintenance costs and the feed-in tariff are increasing by 1.5% per year. The lifetime of the project was shortened to 15 years. The heat-to-power conversion unit shall not be limited to a maximum power. The results of this calculation are shown in Fig. 10. For circulation rates lower than 20 L/s the system has a negative economical balance. At 20 L/s the system starts to make profit. Then, growing circulation rates increase not only the generated net energy of the plant, but have significant positive effects to the NPV. The conclusion of this analysis is clear: to operate the doublet system at highest possible production rate. In reality, the production rate is not only limited by the production pump, but also by the heat-to-power conversion unit and the behavior of GPK3 during re-injection to avoid seismic events.
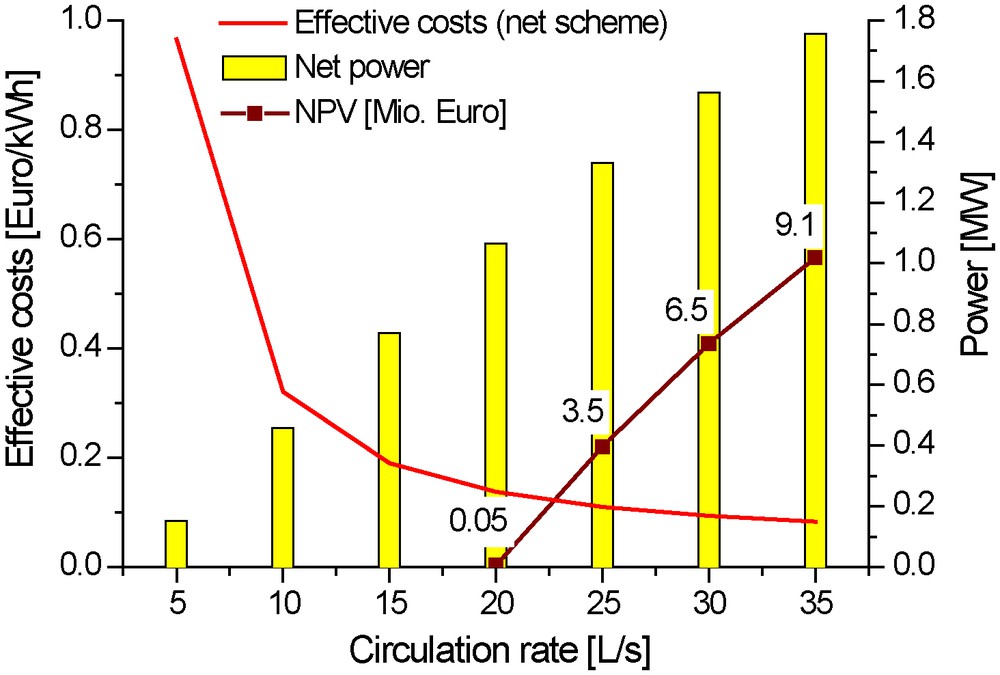
Circulation rate dependent financial (effective costs and NPV) and physical (net generated power) results of the doublet system GPK2 – GPK3 at Soultz-sous-Forêts. This calculation accounts only operating costs of the plant, no investments, for a period of 15 years.
Résultats financiers (coûts effectifs et NPV) et physiques (énergie nette générée) dépendant de la vitesse de circulation, obtenus sur le système des deux puits GPK2-GPK3 à Soultz-sous-Forêts. Ce calcul rend compte uniquement des coûts d’exploitation de la centrale, mais pas des investissements, et ce, pour une période de 15 ans.
4.3 Multi well system GPK1, GPK2, GPK3, GPK4
As a future development, the multi well system will be implemented as another configuration of modules within the Euronaut software. For this system, GPK2 and GPK4 will be used for production and GPK1 and GPK3 for re-injection. Actually, this task is not yet completed, but similar simplified calculations about the power balance of this multi well system were performed already with the antecessor program HDRec v6.2. In 2006, the idea was still to use only GPK2, GPK3 and GPK4 as a triplet system with GPK3 as the only re-injection well. But due to the low injectivity index of GPK3, the power demand for higher circulation rates would have been very high and seriously affecting the energy balance, also it would heighten the risk of seismic events. At that time, the idea emerged to use GPK1 as an additional re-injection well. The distribution of the re-injection in the calculations was chosen dependent on the individual injectivity indexes in order to get the lowest possible power consumption of both pumps. The additional use of GPK1 for re-injection allowed raising the production rate without excessive increase of the parasitic pumping power consumption. The effect to the energy balance and the generated electricity is significant. To get new qualitative and quantitative results, the calculations will be repeated with actual data of the multi well system at Soultz-sous-Forêts.
5 Conclusions
The Euronaut has proven its usability and performs absolute calculations as well as sensitivity analyses. The modules representing parts and components of a deep geothermal power plant can be combined in different ways and adapt doublet or multi well systems or different financing schemes easily. The results of the modules were constrained with data from Soultz-sous-Forêts. The software and the EGS structure can be used as a tool to plan and evaluate new deep geothermal power plants. This is valuable for the dimensioning of the physical components as well as the knowledge about the costs and revenues arising during the whole lifetime; the assessment is based on all parts of the system and the results can be used for making decisions. But results are only worth the input parameters, and some of the important ones are not predictable with sufficient accuracy prior to the drilling: temperatures, transmissivity and long-term behavior of geothermal reservoir. These factors and other critical points (success of drilling or stimulation, lifetime of pumps…) will create real sensitivity analyses rather long and difficult. Further studies should be done to confirm the flexibility of this new software to model dependencies and its use as a decision making tool.
The first configuration implemented by the Euronaut software represents an EGS Doublet well system. Most input parameters of this structure are data experienced by the project at Soultz-sous-Forêts; i.e. these are the costs for drilling, but also all the geologic underground properties. Whereas the costs for drilling are applicable for other plant sites too, the reservoir properties like fracture density, enveloped reservoir volume, connectivity to the far field, productivity/injectivity indices, rock properties are site dependent. Therefore, specific results of this reservoir depth analysis are limited to the vision of a “Soultz-type” geothermal power plant. The general result of a depth yielding the least effective costs for electricity generation is transferable because of two assumptions valid universally. At shallow depths, the temperature of the produced fluid is too low for economic heat-to-power conversion; also at a certain depth, the exponential rise of the drilling costs with depth dominate any other positive effect of greater depth and the effective costs begin to increase. Somewhere in between the optimum depth with the least effective costs can be found. For this specific depth analysis, the optimum reservoir depth of 5500 m is close to the existing reservoir depth at Soultz-sous-Forêts of ∼ 4750 m. Effective costs (net feed-in scheme) of ∼ 15.5 Cents/kWh for a newly constructed hypothetical power plant with a reservoir depth of 4750 m are valid for the chosen input parameter set only. Other parameters than reservoir depth are affecting the results significantly as well and were not analyzed here. Therefore, the results of this sensitivity analysis illustrate the influence of the reservoir depth only and are not a sensitivity analysis of an entire hypothetical “Soultz-type” plant.
Once a deep geothermal power plant is constructed and the modules constrained, the software will model and predict the integral behavior of the plant and its components: these are the thermal drawdown of the reservoirs, the power demands of the pumps or the power generation of the heat-to-power conversion unit. Sensitivity analyses of the system can help finding the best operating scheme of the plant and to rank the weight of different parameters. The comparison of predicted results from the constrained Soultz-sous-Forêts model with real data was not yet possible. This will require long term and constant observation of the running geothermal plant. To improve the reliability, energy balances of other geothermal power plants should be performed and compared with empirical data from these plants.
Generally, the composition of modules can be changed or extended easily, e.g. to sell heat additionally. An additional module for supplemental heating of the produced fluid by e.g. wood or other biomass is planned. This implementation then will evaluate so-called hybrid plants.
Acknowledgements
The author thanks the European Union and the Bundesministerium für Umwelt for funding this project (No.: 0329950D). This document was improved by comments of two unknown reviewers; they have been very helpful and well substantiated.
Appendix A
Input parameter of the reservoir depth sensitivity analysis.
| Financial Input Data | |
| Fraction of capital in bonds | 50% |
| Bond interest rate | 8% |
| Equity interest rate | 4% |
| Income tax rate | 55% |
| This data is leading to WACC (Weighted Average Cost of Capital) of | 6% |
| And a WACC after tax of | 3.8% |
| The German and French way to pay the Feed-In tariff is handled by two different calculations schemes: The gross calculation scheme for Germany and the net calculation scheme for France. Both schemes were performed in the calculations | |
| Gross calculation scheme | |
| All parasitic energy of the system (self-consumption of heat-power plant, injection pump, production pump) is bought in externally | |
| Price per kWh | 0.06 €/kWh |
| Rate of increase per year | 1.5%/year |
| Gross generated energy is sold at Feed-In tariff prices. Cost to buy energy is added to the cost of the prime cost | |
| Net calculation scheme | |
| All parasitic energy of the system (self-consumption of heat-power plant, injection pump, production pump) is subtracted from the gross generated energy. Only remaining net energy is sold and affects the prime cost | |
| Investments | |
| Buy and explore land | 1 Mio. € |
| Mobilization of drilling rig | 500 000 € |
| Diameter of well | 0.216 m |
| Scaling coefficient of cost | 8788 €/m3 |
| Scaling coefficient of depth | 3· × 10-4 m-1 |
| This data is leading to depth-dependent cost for a doublet system (2 wells) as shown in Fig. 5 | |
| Production pump | 800 000 € |
| Lifetime of pump | 10 years |
| This means every 10 years of production this investment has to be re-invested | |
| Rate of price increase for re-investment | 1.5%/year |
| Injection pump | 100 000 € |
| Lifetime of pump | not limited |
| Stimulation of reservoir | 1 Mio. € |
| Specific cost of Heat-power plant | 1.5 Mio. €/MW |
| (Investment cost dependent on maximum gross capacity of the plant) | |
| Commercial Period | |
| Duration of energy generation | 25 years |
| Salary of personnel | 200 000 €/year |
| Rate of increase per year | 1.5%/year |
| Heat-to-power plant | |
| Load factor of power plant | 95% |
| Re-injection temperature of fluid | 70 °C |
| Coolant temperature | 20 °C |
| Efficiency of turbine | 85% |
| Pinch-point temperature difference at vaporizer | 15 °C |
| Pinch-point temperature difference at condenser | 15 °C |
| This data is leading to a gross efficiency as shown in Fig. 7 | |
| Production rate | 25 L/s |
| Specific heat capacity of fluid | 4180 J/kg/K |
| Density of fluid | 1070 kg/m3 |
| Self consumption of plant as percentage from gross energy | 10% |
| Boreholes | |
| Diffusivity of the surroundings | 1.25· × 10-6 m2/s |
| (This value is used for calculation of the fluid temperature change during upward or downward flow in the boreholes) | |
| Geothermal reservoir | |
| Undisturbed reservoir temperature is depth-dependent as shown in Fig. 4 | |
| Connectivity to the far field (not influenced by thermal drawdown) | 50% |
| Density of reservoir rocks | 2500 kg/m3 |
| Specific heat capacity of rocks | 1100 J/kg/K |
| Number of fracs | 3 |
| Distance injection well – frac center | 300 m |
| Distance production well – frac center | 300 m |
| Aperture (width) of frac | 0.005 m |
| Radius of (penny-shaped) frac | 600 m |
| Distance between adjacent (parallel) fracs | 200 m |
| Injection pump | |
| Efficiency of pump | 65% |
| Injectivity of well is depth-dependent as shown in Fig. 8 | |
| Pressure difference due to buoyancy is calculated from density difference between the density of the hydrostatic water column on the reservoir and the (time-dependent) density of the water column in the borehole | |
| Density of the fluids is calculated for a fluid with a salinity of | 100 g/L |
| Temperature and pressure dependent density data values for such a fluid were obtained by ASPEN (1988) | |
| Pressure loss in the well due to friction is calculated after Stelzer (1988) | |
| Roughness of tubing | 0 m |
| Temperature dependent dynamic viscosity of the fluid is calculated after Faust and Mercer (1975) | |
| Pressure at inlet of pump | 1.6 MPa |
| Production pump | |
| Efficiency of pump | 50% |
| Productivity of well is depth-dependent as shown in Fig. 8 | |
| Pressure difference due to buoyancy is calculated from density difference between the density of the hydrostatic water column on the reservoir and the (time-dependent) density of the water column in the borehole | |
| Density of the fluids is calculated for a fluid with a salinity of | 100 g/L |
| Temperature and pressure dependent density data values for such a fluid were obtained by ASPEN (1988) | |
| Pressure loss in the well due to friction is calculated after Stelzer (1988) | |
| Roughness of tubing | 0 m |
| Temperature dependent dynamic viscosity of the fluid is calculated after Faust and Mercer (1975) | |
| Discharge pressure at wellhead | 1.6 MPa |
| Depth of pump chamber | 400 m |
| Minimum pressure allowed at inlet of pump | 1.5 MPa |
| Dismantling | |
| Cost to safe the boreholes | 100000 € |
| Benefit by selling the heat-power plant in percentage of its investment | 10% |


