1 Introduction
In the past, traditional spirit levelling has been used to obtain height information with very high accuracy. By its nature, spirit levelling is known to be a time consuming and difficult task. This is especially evident in large and topographically rough countries like Algeria, where the establishment of a high-resolution levelling network for all parts of the country would be impractical from the financial point of view. Furthermore, with regard to the national levelling network where the coverage is considered as good in the north and becomes poor in the south, the GPS/Levelling technique remains the only possible alternative to hope to cover, in the near future, the whole of Algeria by levelling points, in order to answer to the immediate needs of several potential users of this fundamental information. The combination of GPS heights with geoid ones can to provide an efficient alternative to derive orthometric heights. However, the crucial part of this method is the geoidal undulation, which normally is obtained with a lower accuracy than the ellipsoidal height and affects the accuracy of the orthometric one.
The main goal of this work is to determine the precision of the transformation of the geometrically ellipsoidal heights from the GPS technique into orthometric heights related to the Earth's gravity field in the north part of Algeria. In this context, 247 GPS levelled points collected from the TYRhenian GEOdynamical NETwork (TYRGEONET) project and some local networks, as well as a gravimetric geoid model have been used in this investigation.
Furthermore, and in this same context, we tried to test if the adopted methodology and the derived precision can be generalized for the altimetric auscultation of a storage reservoir situated at 40 km of Oran town (West of Algeria).
2 National levelling network
The origin of levelling in Algeria dates back to the French colonial period. It was confided to the Geographical Service of the army (GSA), then taken in charge by the National Geographical Institute – France. Provided with a similar material to that used by the Service of the General Levelling of France (NGF), its operators elaborated from 1887 a geometric levelling network of limited precision to first and second order. Between 1953 and 1954, the levelling works were led in parallel with the re-observation of the North parallel and the 1st order complementary of the coastline. The lines of spirit levelling executed since 1976 by the National Institute of Cartography and Remote Sensing (INCT) followed in parallel the works of the geodesy by the densification of the North parallel. Nowadays, the Algerian levelling network includes, 33,757 km levelled. This coverage remains insufficient for some areas, particularly in South of Algeria and where new measurements are needed to accomplish a homogeneous coverage.
3 The available data
3.1 Presentation of the gravimetric geoid model
The demand for a high-resolution geoid model has grown substantially during the last few decades especially after the inception of GPS. Many countries across the world have already developed their own geoidal model which serves as the means of deriving orthometric heights from GPS observations. The impact of GPS on surveying applications is undeniable. Moreover, this revolution has not been confined to the surveying community, but has extended into mapping, navigation and the Geographic information system (GIS) areas. During the last few years, we have been witnessing the wide spread adoption of GPS with an equivalently vibrant range of accuracy requirements. Many of these applications require accurate vertical positions. The task of transforming the ellipsoidal height obtained from the GPS technique to the orthometric height has prompted geodesists around the world to determine the high precision geoid undulations, for their region of interest. In this context, Algeria has recently focused a part of current research on the precise geoid determination to support Levelling by GPS using different methods. In this work, we have used the gravimetric geoid model computed by Geodetic Laboratory of the National Centre of Spatial Techniques. This model was computed from the following data: a geopotential model, OSU91A complete to degree and order 360 and developed by Ohio State University (Rapp et al., 1991), a set of 12,183 validated point free air gravity anomalies covering the region and a two elevation grids: 1 km × 1 km digital terrain model for the North of Algeria and the ETOPO5 for the remaining area.
3.1.1 Gravity anomalies
Gravity anomalies used in this work were supplied by the Bureau gravimétrique international (BGI). These measurements with an initial precision of 1 m Gal were expressed in the Geodetic Reference System GRS67 and were transformed into the GRS80 system. Moreover, we applied an atmospheric correction recommended by the International Association of Geodesy (IAG, 1971) in order to eliminate the influence of atmospheric masses. All data have been checked carefully to remove duplicate points, and validated for gross errors by applying the Least Square Collocation method. The error ratio detected using this technique represents 1.21%, which remains small with regard to the number of measures used, and proves that the gravity data measurements provided by BGI are of good quality and subsequently, can be used for the Algerian geoid computation. Fig. 1 shows the geographical distribution of the available gravity data. From this figure, it becomes clear that the coverage with gravity observations is not sufficient for some land areas and new measurements are needed to accomplish a homogeneous coverage.
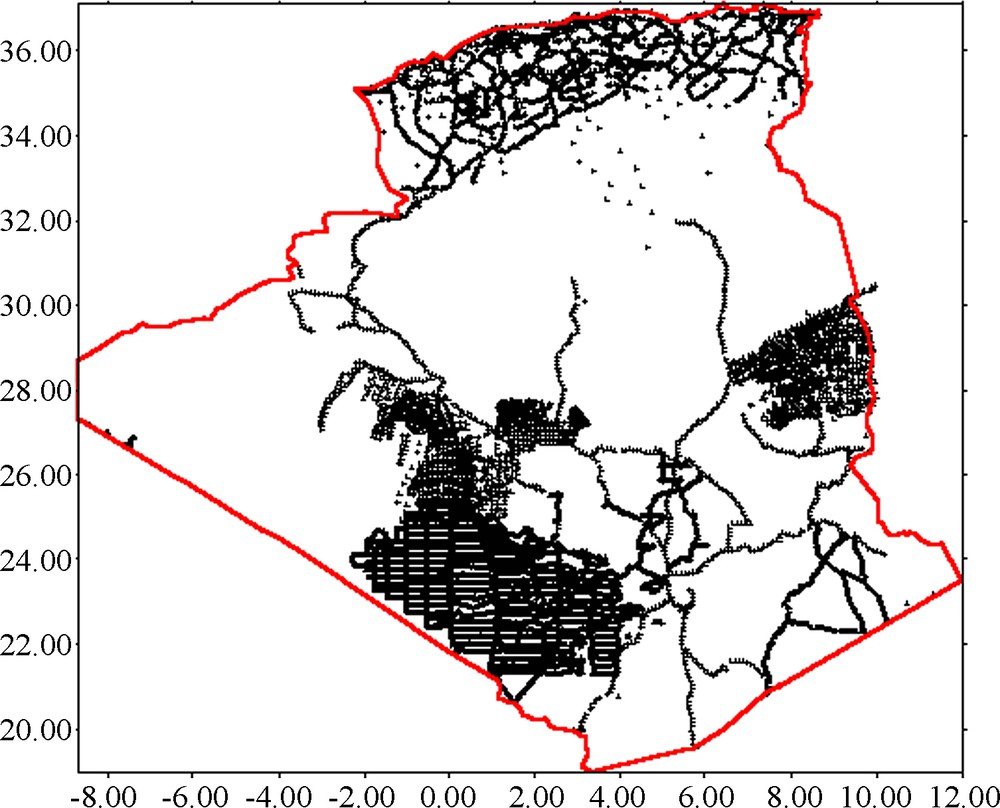
Geographical distribution of BGI gravity measurements
Répartition géographique des mesures de gravité fournies par le BGI.
3.1.2 Geopotential model
The choice of the best geopotential model is one of the critical steps in computing the geoid. Several studies have shown that the geopotential models tailored to regional or local gravity data are best suited for high precision geoid computations. So the problem of choosing a best geopotential model in Algeria to reduce geodetic data has not been solved definitely. In 2000, an analysis based only on the previous gravity data supplied by the BGI was carried out to select the best geopotential model in Algeria. Four global geopotential models were used in this study: GPM2, OSU81, OSU91A and the recently most accurate high degree geopotential model EGM96. The comparisons were made for all gravity data by computation of the residual data (i. e. observed data minus each model contribution). The statistical parameters considered in this work are the mean, the standard deviation of the differences between the geopotential models and tested data, and the smoothed covariance function necessary for all estimations by collocation technique. The most informative of these statistics is the standard deviation, because the mean of the differences is distorted by the exclusion of the zero-order term (Zhang and Featherstone, 1995). The result obtained for the geopotential model comparison has showed that the OSU91A model fits best the BGI gravity data in Algeria (Benahmed Daho and Kahlouche, 2000). This model, completed to degree and order 360 with about 55 km resolution was adopted as a reference to remove and restore the long wavelength components of the gravity and the geoid, respectively.
In spherical approximation, the gravity anomalies and geoid undulation can be computed from a geopotential coefficient given by:
| (1) |
| (2) |
3.1.3 Topographic data
The computation of the terrain effects on the geoid required a detailed DTM model. For this purpose and due to the lack of any high resolution photogrammetric based DTM in the Algeria region, two elevation grids of different resolution were used:
- • 10 km DTM covering the area 15° ≤ φ ≤ 40°, −10° ≤ λ ≤ 15° subtracted from ETOPO5;
- • 1 km DTM covering 33° ≤ φ ≤ 38°, −3° ≤ λ ≤ 9° derived from the GLOBE database.
3.1.4 Geoid computation
The computations were made using the “GRAVSOFT” package, developed during a number of years at the National Survey and Cadastre of the Copenhagen University. For the actual solution, the Fast collocation technique and the Remove–Restore procedure were used to compute the geoid heights. The procedure is summarised as follows:
- • Available free air gravity anomalies are reduced for the reference geopotential model and terrain effects , yielding smooth residual anomalies .
(3) - • Gridding of to produce a 5’ × 5’ grid of residual gravity anomalies and then converted it into residual geoid undulations by Fast Collocation method.
- • Restore the effects removed in the first step (Reference geopotential model and terrain effects) on the prediction grid to get the final geoid model.
| (4) |
The geopotential model OSU91A developed to degree and order 360 has been used as a reference to remove the long wavelength component of the gravity data. However, in order to smooth the anomalous gravity field of the test area, i.e. to remove the irregular variations of the topography, the Residual Terrain Model (RTM) reduction is applied, which takes into account only the short-wavelengths of the topography. The method employs a smooth reference surface which may be derived either from a spherical harmonic expansion of the global topography or by averaging the local elevation data. The computation of the effects of the topography according to the RTM reduction modelling method is based on two elevation grids: 1 km × 1 km digital terrain model for the North of Algeria; and a global topographic model ETOPO5 of 5’ × 5’ for the rest of the area which was used up to a distance of 200 km. The reference surface of 15’ × 15’ needed for the RTM reduction is formed from the 5’ × 5’ blocks of ETOPO5. This grid is smoothed further by taking moving averages over the 3 × 3 adjacent blocks. The statistics, in mGals, of the reduced gravity data are regrouped in Table 1.
Statistiques, dans la zone de calcul, des données de gravité réduites.
| Anomalies | Minimum | Maximum | Mean | Standard deviation |
| −82.59 | 136.20 | 4.89 | 26.84 | |
| −67.75 | 123.46 | 0.12 | 12.31 | |
| −34.17 | 110.38 | 3.09 | 13.00 |
From the results of Table 1, it is obvious that the OSU91A reference field fits well the gravity in the area under consideration, and the smoothing of the gravity data is considerable after the removal of the topographic effect if we take into account only the mean and standard deviation values. The standard deviation of data reduces from 26.84 mGals to 13.00 mGals (a reduction of 50%).
The gridding of to produce a 5’ × 5’ grid of residual gravity anomalies between the limits 18° ≤ φ ≤ 38° and −9° ≤ λ ≤ 11° was done with the GEOGRID program using a fast quadrant-search collocation algorithm. The prediction of the grid gravity value was computed from the five closest points in each quadrant around the prediction point, using a second-order Markov model covariance function fitted to local data (correlation length x1/2 = 25 km), and taking into account individual variance of the gravity data.
However, the first step in the use of the fast collocation for residual geoid heights estimates from the grid of residual gravity anomalies resides in the determination of the empirical covariance function and subsequently the selection of its corresponding analytic representation capable to describe the local behaviour of the gravity field.
The empirical covariance function of the BGI residual gravity anomalies was computed by EMPCOV program (Tscherning et al., 1992) using the following formula:
| (5) |
where M is the number of combinations, ψ is the spherical distance between Qi and Qj. δΔg is the BGI free-air residual gravity anomalies. The summation was made for all the combinations of the data points Qi and Qj where the interstation distances in the range between and , and denotes the sampling interval size.
These empirical values were used in order to estimate the parameter values of a local covariance function model. As a model of the covariance function, we have adopted, in our case, a classical analytic covariance function for the disturbing potential proposed by Tscherning and Rapp (1974), which is expressed by a sum of series of Legendre polynomials (Moritz, 1980):
| (6) |
The actual use of this model as a local covariance function requires the estimation of three parameters: the radius of the sphere of Bjerhammar (RB) and two scale factors α and A. These parameters are estimated by fitting this model to a number of empirical covariance values using the least square adjustment. The results of the adjustment of the empirical covariance function on the Tscherning & Rapp model were obtained by the program COVFIT8 (Knudsen, 1987). Fig. 2 shows the empirical and analytic covariance functions of the residual anomalies. The agreement is optimum between them up to a spherical distance of around 0.30° (∼ 30 km) which is much greater that the correlation distance..
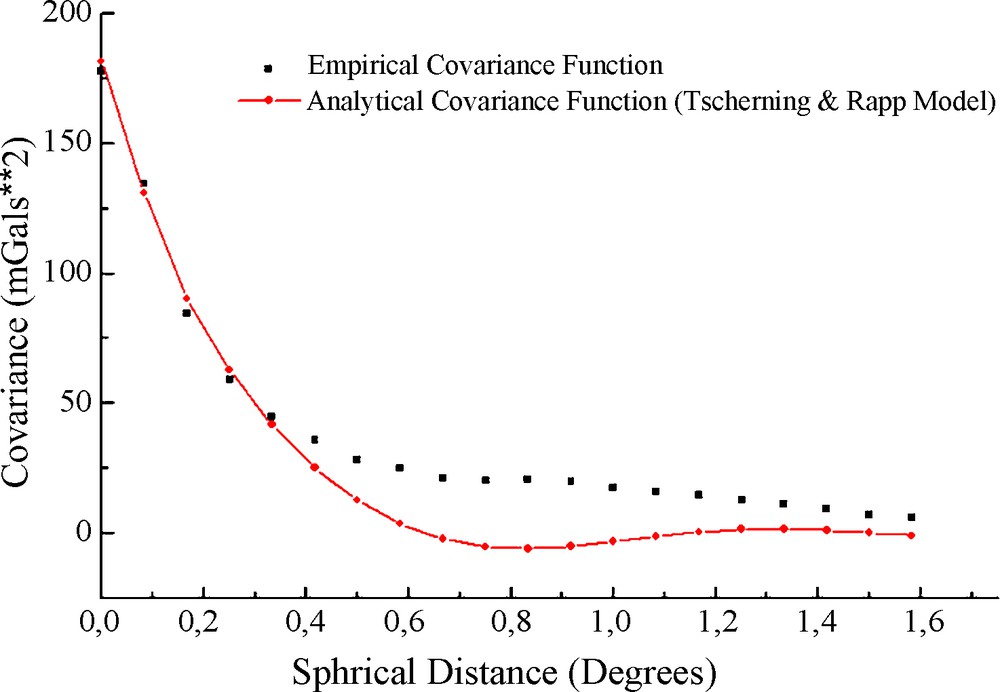
Covariance functions of residual gravity anomalies.
Fonctions de covariance des anomalies de gravité résiduelles.
The gridded residual gravity anomalies have subsequently been converted to geoid heights by using the Fast Collocation method (Bottoni and Barzaghi, 1993). The Collocation was carried out on a grid of 241 × 241 points. The final geoid was obtained by adding the geopotential model and the residual terrain effect on the 5’ × 5’ residual geoid grid. The major contributions to the final geoid are coming from the OSU91A geopotential model. Fig. 3 shows a map of the geoid solution in Algeria contoured with 1 m intervals.

Geoid solution in Algeria (Unit: [m]).
Géoïde gravimétrique sur le territoire algérien (en mètres).
3.2 GPS/Levelling data
Many GPS campaigns have been carried out in the past years in Algeria principally in the north part of the country. The distribution is fairly good but the total number of the GPS stations is too small in relation to northern part of Algerian's area. The GPS data used in this work are collected from the international TYRGEONET, ALGerian GEOdynamical NETwork (ALGEONET) projects and the some local GPS/Levelling surveys. Started in 1990, the TYRGEONET project, constituted of 50 points with some VLBI and SLR stations, was initiated by the Istituto Nazionale di Geofisica e Volcanologia (INGV) and the University of Bologna whose initial objective was the oceanographically study and the geodynamics control of the Italian peninsula.
The extension of the TYRGEONET project contributes to the setting up of the new ALGEONET project, composed of ten stations with two points TYRGEONET (Arzew and Algiers), has for essential objective the geodynamical and seismic control of active zones of the North of Algeria. A first GPS observing campaign of the ALGEONET network was conducted during 6 days in June 1998, simultaneously with the TYRGEONET campaign. The data of this campaign was processed with the Bernese GPS software version 4.2 developed at the Astronomical Institute of the University of Bern (Beutler et al., 2001). Code pseudo ranges were used to estimate receiver a priori co-ordinates and clock synchronisation with respect to GPS time. Precise satellite ephemerides and satellite clock file information provided by the International GPS Service (IGS) were used in the computation. The standard deviations of the computed ellipsoidal heights do not exceed 3 cm. This network has been used later for the densification, establishment of the new local geodetic networks and the determination a set of the transformation parameters between WGS84 and our local datum North-Sahara.
All GPS stations have been connected to the national levelling network, which consists of orthometric heights. The connection of the GPS stations to the levelling network has been carried out by traditional levelling. The accuracy of the levelling heights may be estimated to about 6 cm depending on the type of connection measurements, because some GPS points used in this work as benchmarks are located in mountainous regions in which spirit levelling would be impractical.
For this investigation, 247 precise GPS levelled points have been used, of which ten are benchmarks of the first order levelling network, and the others belong to the second order levelling network. All of these points are located in the North of Algeria. The geographical distribution of the available GPS/levelling data is shown in Fig. 4.
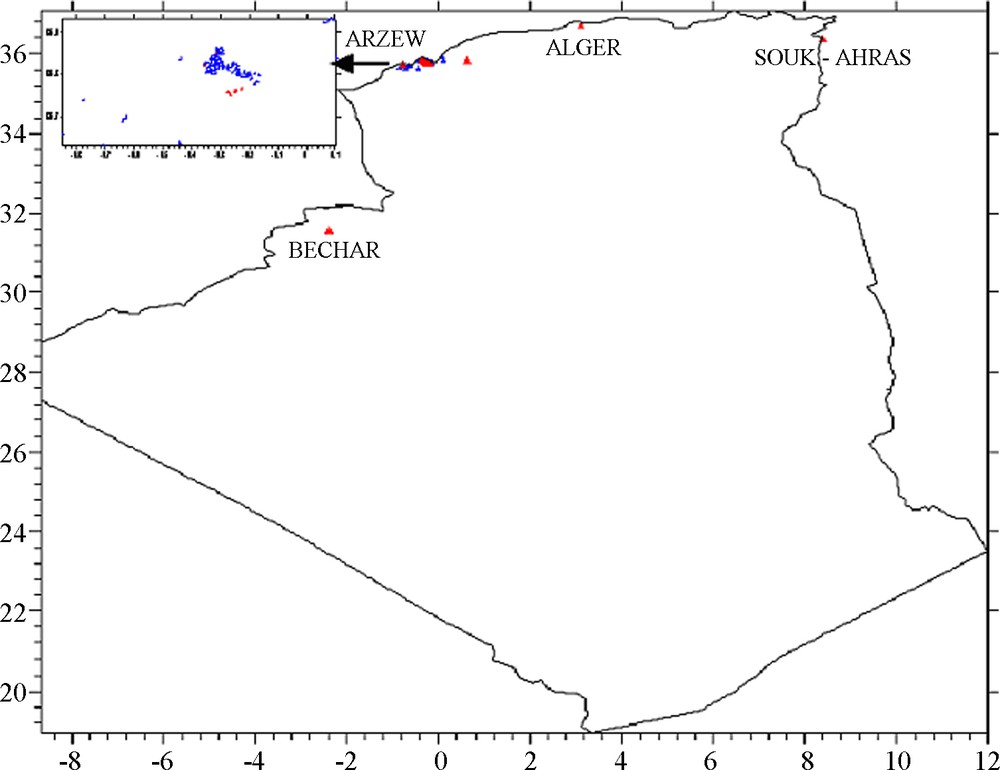
Geographical distribution of available GPS/Levelling stations in the North of Algeria (Δ: Benchmark point, Δ: Control point)
Répartition géographique des points GPS nivelés (Δ : point d’appui, Δ : point de contrôle).
4 Comparison of geoide model with GPS/levelling data
For our study and in order to assess the precision of the gravimetric geoid estimate, this model has been compared with 247 GPS/Levelling derived geoid undulations. All of these points are located in the North of Algeria and distributed as in Fig. 4 where most are close to the station of Arzew. The statistics of the absolute differences in benchmarks between the gravimetric geoid model and the GPS/Levelling derived geoid height are summarised in Table 2 and they indicate that the overall agreement between the gravimetric and GPS/Levelling derived geoid undulation is about 68 cm in terms of standard deviation and that there exist systematic biases between these two kinds of geoid representations with a mean value of about −1.481 m. These systematic biases are due to the datum inconsistencies inherent among the height types, each of which refers to a different reference surface and long wavelength systematic errors in N, distortions in the orthometric height datum due to an over-constrained adjustment of the levelling network, effect of various geodynamic effects, improper or non-existent terrain/density modelling in the geoid modelling and orthometric heights and negligence of the sea surface topography at the tide gauges, poorly modeled GPS errors (i.e. tropospheric effects), and assumptions and theoretical approximations made in processing observed data. The major part of these discrepancies is usually attributed to long wavelengths errors introduced by the use of a global model in gravimetric geoid computation that is not necessarily optimal in the area of interest, to the systematic errors and to datum inconsistencies inherent among the height types which can be reduced by the use a corrector surface model (Fotopoulous, 2003).
Résultats de comparaison avant ajustement entre le modèle du géoïde et les hauteurs du géoïde déterminées par GPS/nivellement (en mètres).
| Minimum | Maximum | Mean | Standard deviation | |
| −2.144 | 0.306 | −1.481 | 0.678 |
In practice, to minimize these deviations, we have tested a four and a third polynomial transformation models in order to find the best model able to represent the correction that should be applied to the gravimetric geoid.
The four-parameters model is the most commonly used in such adjustments and is given by the following formula (Heiskanen and Moritz, 1967):
| (7) |
The third order polynomial model may be adequate to absorb non-periodic large scale systematic errors, such as systematic levelling errors:
| (8) |
Among the 247 GPS levelled stations, only 16 well-distributed GPS points (see Fig. 2) are used as benchmarks in a least-squares adjustment to solve for the unknown parameters of the parametric model transformation, and the remaining points were excluded from the combined adjustment in order to estimate the real accuracy given by cross-validation. The fitting of the gravimetric geoid model to a set of levelled GPS reference points has been carried out by a program, called ADJ_GLG (Benahmed Daho, 2004) developed at Geodetic Laboratory of the National Centre of Space Techniques for combined adjustment between the gravimetric geoid model and GPS/Levelling data using the Hybrid approach (Kotsakis and Sideris, 1999). The statistics of the differences after fitting out the systematic biases and tilts between the gravimetric geoid and the GPS/Levelling data using the previous parameter models transformation are summarised in Table 3. These statistics in benchmarks show that a good fit between the Algerian geoid and GPS/Levelling has been reached when the third order polynomial was used as corrector surface. The standard deviation of these discrepancies between these two representations at benchmarks is about ± 1.4 cm after fitting. This discrepancy depends upon the quality and the density of data integrated in the combined adjustment, and represents the internal accuracy of the adjustment. In addition, and before any special tests are performed for checking particular features of the general adjustment model, some global statistical test must be used first. Levelled GPS points with global residual module larger that four times RMS were rejected. No outliers can be identified. This does not necessarily mean that outliers do not exist, but more exhaustive statistical means must be used to identify the possible blunders on the gravimetric geoid, levelling and GPS networks by using their individual component residuals. Since this is not the purpose of this work, it was assumed that all GPS/Levelling data points were valid. Furthermore, the Chi2 (χ2) test with significance level α = 1% was employed. This test is positive and indicates that the model is not problematic. The next step is to test if a parameter or set of parameters in the model are significant. The application of the Student test on the parameters values shows that the estimated parameters are statistically significant.
Résultats de comparaison, après ajustement, entre les hauteurs du géoïde gravimétrique et les hauteurs déterminées par GPS/nivellement (en mètres).
| Minimum | Maximum | Mean | RMS | |
| Third polynomial model | −0.020 | 0.022 | 0.000 | 0.014 |
| Four parameters transformation model | −0.029 | 0.056 | 0.000 | 0.022 |
However, the previous RMS value is not a real accuracy of the determined geoid; this provided proof that the combined adjustment can optimally fit the gravity geoid to the GPS levelling point in the least square sense. So, and in order to pronounce on the conclusion drawn on the parametric model choice and to assess the real accuracy of the adjustment, we have applied the cross-validation procedure. Its principal consists to compare the GPS/Levelling derived geoid undulations at control points with adjusted ones computed using the estimated parameters for the each model transformation. The statistics of these differences for tested parameter models are summarized in Table 4. We can see that the combination of the gravimetric geoid model with GPS/Levelling gives the best results in experimental area when the third order polynomial model was used as a corrector surface. The standard deviation of the differences between these two representations at control points is about ± 5.5 cm after fitting. In most points (89%), the differences are smaller than 5 cm. There are very few stations where really large differences occur. However, the obtained accuracy cannot be generalized for whole country, considering the number of GPS\Levelling points and their distribution.
Statistiques de la validation croisée (en mètres).
| Minimum | Maximum | Mean | RMS | |
| Third polynomial model | −0.100 | 0.587 | 0.006 | 0.055 |
| Four parameters transformation model | −0.144 | 0.615 | 0.025 | 0.062 |
5 Altimetric auscultation of a storage reservoir
One of the main goals of a combined adjustment between levelling, GPS and the geoid is to substitute expensive levelling through cheaper GPS measurements at least in regions where the highest accuracy is not necessary. In order to test the capability of GPS for height determination, a special GPS campaign was carried out in 2004 for the altimetric auscultation of an oil storage reservoir located at 40 km from Oran (in the West of Algeria). A total of about 132 new GPS stations, for which fifty points are considered as benchmarks, were established. The GPS observations were performed using ASHTECH Z-12 dual frequency receivers with a observation period between 15 mn and 45 mn and were processed with the Bernese GPS software version 4.2 using the precise ephemerides supplied by IGS and the TYRGEONET station (Arzew) as reference point. Code pseudo ranges were used to estimate receiver a priori co-ordinates and clock synchronisation with respect to GPS time. All GPS stations have been connected to the national height system through spirit levelling, which consists of orthometric heights. The comparisons between GPS and levelling were performed by transforming the GPS ellipsoidal heights into orthometric ones using the adjusted gravimetric geoid heights. These differences on the benchmarks and their statistics, after fitting out the systematic biases and tilts using the optimal four-parameter transformation model, are summarised in Tables 5 and 6, respectively. Their analysis permits us to conclude that the orthometric heights on benchmarks can be deducted from the GPS observations with a precision better that 2 cm. It is about 3 cm in the remaining points. We note that this precision remains not sufficient for GPS/Levelling purpose but it can be used in low accuracy scientific applications.
Écarts entre les altitudes observées et celles calculées aux points d’appuis (en mètres).
| Benchmarks | Observed height | Computed height | Discrepancies |
| R01 | 2.977 | 2.972 | −.005 |
| R02 | 2.930 | 2.924 | −.006 |
| R03 | 4.275 | 4.265 | −.010 |
| R04 | 4.490 | 4.482 | −.008 |
| R05 | 4.277 | 4.274 | −.003 |
| R06 | 3.105 | 3.102 | −.003 |
| R07 | 2.770 | 2.758 | −.012 |
| R08 | 3.963 | 3.961 | −.002 |
| R09 | 2.727 | 2.725 | −.002 |
| R10 | 3.366 | 3.360 | −.006 |
| R11 | 3.848 | 3.855 | .007 |
| R12 | 3.553 | 3.557 | .004 |
| R13 | 4.315 | 4.312 | −.003 |
| R14 | 3.235 | 3.236 | .001 |
| R15 | 4.284 | 4.286 | .002 |
Statistiques en mètres des différences aux points d’appuis.
| Minimum | Maximum | Mean | RMS |
| −0.012 | 0.007 | −0.003 | 0.006 |
6 Conclusion
A detailed study of the possibility of substituting classic spirit levelling by GPS/geoid derived orthometric heights was presented. The main goal of this work is to assess the precision of the transformation of the ellipsoidal heights from GPS into orthometric heights in the northern part of Algeria. The field experiment introduced above clearly proves that the combination of GPS/Levelling and gravimetric geoid model computed from the gravity data supplied by BGI is capable of producing orthometric heights with an acceptable accuracy for the low order levelling network densification with regard to the actual national levelling network status. The accuracy obtained is thought to be quite sufficient for many applications compared to the alternative method of spirit levelling, which is time consuming and impractical from the financial point of view. Unfortunately, the non-availability of GPS levelling data in the whole of the country, with a homogeneous distribution and sufficient density, does not allow a more reliable assessment at the national scale of the quality of the used gravimetric geoid model.
The analysis of the results shows that the third order polynomial model transformation used for modelling the deviations between the gravimetric geoid and the available GPS/Levelling points gives the best results in the experimental area. It also shows that the four-parameter transformation model usually employed in studies dealing with the combined adjustment of GPS, levelling and geoid data is not always sufficient for removing the systematic errors introduced by the datum differences of the three height data sets. Nevertheless, we note that these results remain dependent on the quality and the density of data used, particularly the levelled GPS data of which the present configuration is incomplete from the point of view of density and quality.
Finally, the obtained results were satisfactory, so in the near future, new solutions will be proposed and the additional comparisons should be made for a complete error assessment of the our local geoid model. These will include new gravity data, topographic information, and the new data of GPS/Levelling in order to reach an acceptable accuracy on all the country.
Nowadays, it does not seem to be possible to replace precise levelling by GPS/Levelling, at least not on short distances, but with refined observation and data analysis techniques, it will certainly be appropriate in the future.
Acknowledgements
The authors gratefully thank the many institutions and persons who provided data and software, making this work possible: The Professors R. Forsberg, C.C. Tscherning and P. Knudsen for the GRAVSOFT package, The Bureau gravimétrique international, for the gravity set on the Algerian territory.


