A pore-throat model based on grain-size distribution to quantify gravity-dominated DNAPL instabilities in a water-saturated homogeneous porous medium

Khalifa Nsir; Gerhard Schäfer

doi:10.1016/j.crte.2010.09.001

Hydrology, environment

A pore-throat model based on grain-size distribution to quantify gravity-dominated DNAPL instabilities in a water-saturated homogeneous porous medium
[Modèle de réseau de pores et de capillaires, basé sur la courbe granulométrique pour la quantification des instabilités gravitaires du déplacement d’un DNAPL dans un milieu poreux homogène saturé en eau]

Présenté par : Ghislain de Marsily

Khalifa Nsir ¹ ; Gerhard Schäfer ¹

¹ UMR 7517, Centre national de la recherche scientifique (CNRS), laboratoire d’hydrologie et de géochimie de Strasbourg (LHYGES), université de Strasbourg (UdS), 1, rue Blessig, 67084 Strasbourg cedex, France

Comptes Rendus. Géoscience, Volume 342 (2010) no. 12, pp. 881-891.

Résumés

Anglais
Français

A pore-scale network model based on spherical pore bodies and cylindrical pore throats was developed to describe the displacement of water by DNAPL. The pore body size and the pore throat size were given by statistical distributions with user-specified values for the minimum, mean and maximum sizes. The numerical model was applied to a laboratory experiment conducted on a sand-filled glass column. The parameters relative to pore body size and pore throat size that were used in the construction of the equivalent network were derived from the discrete grain-size distribution of the real porous medium. The calculated arrival times of the DNAPL front were compared with those measured using optic fibre sensors placed at different points on the control section of the experimental device. Furthermore, the model simulated DNAPL pressure measured at the entrance section of the system. In general, the numerical results obtained with the model were in good agreement with the actual measurements.

Un modèle type réseau de pores et de capillaires a été développé pour décrire le déplacement de l’eau par un DNAPL. Les tailles de pores et de capillaires sont obtenues à partir d’une distribution statistique basée sur l’introduction d’une taille minimale, moyenne et maximale, spécifiées pour les pores et les capillaires. Le modèle numérique développé est utilisé pour simuler des expériences de laboratoire conduites sur une colonne en verre. Le milieu poreux utilisé est un sable moyen de granulométrie uniforme. Les paramètres relatifs à la taille des pores et des capillaires utilisée pour générer un réseau équivalent au milieu poreux ont été dérivés de la courbe granulométrique discrète du sable. Les temps d’arrivée du front de DNAPL calculés ont été comparés avec ceux mesurés au moyen des fibres optiques placées à différents points dans une section de contrôle du dispositif expérimental. De plus, la pression moyenne du DNAPL mesurée pendant l’expérience dans la section d’entrée de la colonne a été confrontée à la pression transitoire prédite par le modèle développé. Les résultats numériques sont globalement en bon accord avec les observations expérimentales.

Métadonnées

Reçu le : 2010-04-21
Accepté le : 2010-09-13
Publié le : 2010-11-17

DOI : 10.1016/j.crte.2010.09.001

Keywords: Pore-throat model, Instabilities, Two-phase flow, Porous media, DNAPL, Size distribution
Mot clés : Modèle de pores et de capillaires, Instabilités, Écoulement diphasique, DNAPL, Distribution de la taille

Affiliations des auteurs :

Khalifa Nsir ¹ ; Gerhard Schäfer ¹

¹ UMR 7517, Centre national de la recherche scientifique (CNRS), laboratoire d’hydrologie et de géochimie de Strasbourg (LHYGES), université de Strasbourg (UdS), 1, rue Blessig, 67084 Strasbourg cedex, France

@article{CRGEOS_2010__342_12_881_0,
     author = {Khalifa Nsir and Gerhard Sch\"afer},
     title = {A pore-throat model based on grain-size distribution to quantify gravity-dominated {DNAPL} instabilities in a water-saturated homogeneous porous medium},
     journal = {Comptes Rendus. G\'eoscience},
     pages = {881--891},
     publisher = {Elsevier},
     volume = {342},
     number = {12},
     year = {2010},
     doi = {10.1016/j.crte.2010.09.001},
     language = {en},
}

TY  - JOUR
AU  - Khalifa Nsir
AU  - Gerhard Schäfer
TI  - A pore-throat model based on grain-size distribution to quantify gravity-dominated DNAPL instabilities in a water-saturated homogeneous porous medium
JO  - Comptes Rendus. Géoscience
PY  - 2010
SP  - 881
EP  - 891
VL  - 342
IS  - 12
PB  - Elsevier
DO  - 10.1016/j.crte.2010.09.001
LA  - en
ID  - CRGEOS_2010__342_12_881_0
ER  -

%0 Journal Article
%A Khalifa Nsir
%A Gerhard Schäfer
%T A pore-throat model based on grain-size distribution to quantify gravity-dominated DNAPL instabilities in a water-saturated homogeneous porous medium
%J Comptes Rendus. Géoscience
%D 2010
%P 881-891
%V 342
%N 12
%I Elsevier
%R 10.1016/j.crte.2010.09.001
%G en
%F CRGEOS_2010__342_12_881_0

Khalifa Nsir; Gerhard Schäfer. A pore-throat model based on grain-size distribution to quantify gravity-dominated DNAPL instabilities in a water-saturated homogeneous porous medium. Comptes Rendus. Géoscience, Volume 342 (2010) no. 12, pp. 881-891. doi : 10.1016/j.crte.2010.09.001. https://comptes-rendus.academie-sciences.fr/geoscience/articles/10.1016/j.crte.2010.09.001/

Version originale du texte intégral

1 Introduction

Two-phase flow is encountered widely in the field of hydrology because soil and groundwater pollution by dense non-aqueous phase liquids (DNAPLs), such as chlorinated solvents (e.g., trichloroethylene (TCE)), constitute a large and serious environmental problem (Bano et al., 2009; Bohy et al., 2004). When infiltrating through porous media, migration of DNAPLs can result in highly fingered fluid distributions. The occurrence of fingering is caused by flow instabilities due to differences in viscosity and density between DNAPL and water (Khataniar and Peters, 1992; Lindner and Wagner, 2009; Riaz and Tchelepia, 2006; Tehelepi et al., 1994). These fingers propagate rapidly, resulting in an early breakthrough compared to the displacement of a stable front. Generally, two approaches are used to study the displacement process through porous media. The first approach uses the continuum description of the porous medium associated with macroscopic laws (e.g., Muskat's law) to represent the volumetric flow vector for each fluid phase on the REV scale (Barenblatt and Patzek, 2003; Bear, 1972; Galusinski and Saad, 2009). The second approach is based on the microscopic description of the pore geometry and on the physical laws of flow and transport within the pores (Blunt and King, 1990; Laroche and Vizika, 2005; Lowry and Miller, 1995). One of the common tools that has been used to study the displacement process is pore-scale network modelling, which uses simple geometric shapes to represent the pore space. Many network models have been developed to study a wide range of displacement processes, including drainage and imbibitions (Hilpert and Miller, 2001; Joekar-Niasar et al., 2009; Nordhaug et al., 2003; Patzek, 2000; Singh and Mohenty, 2003). The most critical aspect of network model construction is the appropriate choice of the pore structure and its capacity to represent the real physical system (Celia et al., 1995; Raoof and Hassanizadeh, 2009). Generally, an equivalent network to the real porous medium is used. This network can be based on statistical distributions and correlations of basic morphologic parameters, such as pore bodies and pore throats. Typical parameters used for building an equivalent network include pore body size distribution, pore throat size distribution and throat length distribution. In the majority of models, the parameters are fictive and do not represent a realistic porous medium. Consequently, these models cannot effectively analyse and reproduce physical experiments.

Different approaches exist for identifying pore structures (Saad et al., 2010). One of the common approaches is the inverse method. Pressure-saturation curves measured in the laboratory for a given two-phase fluid system in a porous medium are fitted using theoretical relationships to obtain the equivalent geometric parameters of the network model. Other experimental approaches are direct methods, such as the use of mercury porosimeters to assess the pore-size distribution of the porous medium. Because direct measurements of pore space structure are generally costly and time consuming, recent conceptual approaches have been developed to derive the void size distribution (VSD) from the grain size distribution (GSD). The GSD is widely available for many soil types and can be routinely determined in the laboratory. A novel approach based on the geometric proprieties of the packing of spheres has been elaborated (Dodds, 1980; Geoffrey and Mellor, 1995). This approach computes the VSD resulting from a specific packing of spheres. The shape and size-distribution of the voids within a random packing of an array of spheres and the effect of GSD on the packing have received considerable attention (Rouault and Assouline, 1998).

In this article, we present a novel network model for simulating drainage processes in a homogeneous porous medium. The developed model is based on the same basic flow characteristics as the model introduced by Nordhaug et al. (2003). However, our model considers capillary effects at water-DNAPL interfaces. Capillary pressure is assumed to be located at the boundary between a pore body and a pore throat. To quantify the flow rate in a pore throat, which is connected to a pore body separated by a water-DNAPL interface, we used the Washburn equation. Furthermore, to obtain a predictive network model, the model parameters used to generate both a pore-body size distribution and pore-throat size distribution were quantified using a geometrical model of an array of spheres based on the grain-size distribution combined with a probabilistic approach. The numerical model was then applied to a laboratory drainage experiment (DNAPL/water) that was conducted on a sand-filled column under stable and unstable flow conditions. The pressure at the column entrance section and the arrival times distribution of the DNAPL front in a cross-section, measured during the displacement process, were compared to the numerical results. A sensitivity study of the size of pore throats and the size of the lattice was used to analyse the influence of these model parameters on the displacement of water by DNAPL.

2 Network model

Pore-scale network models typically represent the pore space of the medium using simplified geometries. Within these geometric representations, the models solve equations to explicitly track the location of all fluid–fluid interfaces within the network. We developed a pore-throat network model to simulate the drainage process in saturated porous media. Drainage occurs during an immiscible displacement of a wetting fluid (water) by a nonwetting fluid, such as trichloroethylene.

2.1 Geometry of the network

The pore network that is simulated in the model is a cubic lattice with constant node spacing. The pore bodies are represented by spheres. Similarly, pore throats are cylindrical with a circular cross-section (Fig. 1). The locations of fluid-fluid interfaces are restricted to the connections between the pore bodies and pore throats. The pore space is constructed by assigning radii to the lattice elements using a Weibull distribution (Weibull, 1951), which is frequently used to construct network analogs of porous media. The distribution is attractive due to its flexibility and to the fact that it is based on fixed parameters that describe the characteristics of the sizes of pore bodies and pore throats of the network. A minimum, mean and maximum radius (r_min, r_mean and r_max, respectively) specified for both pore bodies and pore throats are therefore required to randomly generate the pore body-size distribution and pore-throat size distribution in the network. The probability distribution that was used is given by:

g (x) = \{\begin{cases} \frac{x}{x_{2}^{2}} \exp (- \frac{x^{2}}{x_{2}^{2}}) for x \leq x_{3} \\ 0 for x > x_{3} \end{cases}

(1)

where x = r − r_min, x₂ = r_mean − r_min, and x₃ = r_max − r_min. Pore body radius and pore throat radius are represented by r. For a throat connecting pores i and j, the throat length is defined as L_ij = L − (r_pore, _i + r_pore, _j), where L is the distance between the centres of two adjacent pore bodies. L is constant in the chosen network. Pore body and pore throat radii are generated independently of each other. Therefore, there is no relationship between the radii of throats and the neighbouring radii of pores. However, radii of pore bodies are larger than those of pore throats to ensure the converging–diverging nature of pores. In section 3, we explain the model concept to quantify the ensemble of the pore body radius and the pore throat radius (r_min, r_mean, r_max), as well as the node spacing, L, needed to construct an equivalent network of a real porous medium.

Fig. 1
3D view of a pore-throat network with randomly distributed spherical pores and uniformly sized cylindrical throats.
Illustration 3D du réseau de pores et de capillaires avec une distribution aléatoire de la taille de pores sphériques et des capillaires cylindriques de taille uniforme.

The porosity of the equivalent porous medium is assumed to be equal to the areal porosity of a horizontal transect of the network model. The reason for using areal porosity is that volumes do not scale as the third power of the radius, whereas areas scale as second power of the radius. Assuming that the pore throat volumes are negligible compared to the total volume of pore bodies, the porosity ø[-]of the pore-throat network is given by:

ϕ = \frac{\sum_{i} A_{pore, i}}{n_{x} n_{y} n_{z} L^{2}}

(2)

where A_pore, _i [L²] is the area of pore body, and n_x, n_y and n_z are the number of pores in the x-, y- and z-directions, respectively. The index i runs over all the pore bodies of the network.

2.2 Governing flow equations of the pore-throat model

The developed network model makes the following assumptions: (i) the fluids used are Newtonian, incompressible and immiscible; (ii) the flow is laminar; and (iii) the local capillary pressure in the pore bodies is negligible, resulting in only one mean pressure within a pore body, independent of the phase saturation of that pore body. The mass balance equation for each pore is therefore written as follows:

\sum_{j} Q_{ij} = Q_{i}^{e}

(3)

where Q_ij [L³T⁻¹] denotes the flow rate through a pore throat connecting pore node i and pore j. Q^e_i [L³T⁻¹] is the external flow rate into pore i, which is zero unless the pore is located at the upstream flow boundary. The sum refers to all neighbouring pores of pore body i. The expression used for the flow rate Q_ij depends on the fluid present in the pore throat connecting pores i and j and on the presence of a meniscus at the boundaries between a pore body and a pore throat.

If no meniscus is present at pore throat entry, the flow rate Q_ij through the pore throat is given by Poiseuille's Law

Q_{i j} = \frac{π r_{i j}^{4}}{8 L μ_{α}} (P_{i} - P_{j} - (z_{i} - z_{j}) ρ_{α} g)

(4)

where μ_α [ML⁻¹T⁻¹] and ρ_α [ML⁻³] are the dynamic viscosity and the density of the fluid moving in the pore throat, respectively. P_i and P_j are the fluid pressures in pores i and j at vertical positions z_i and z_j, respectively.

If a meniscus is present at pore throat entry, the flow rate Q_ij through the pore-throat is expressed by the Washburn equation (Washburn, 1921):

Q_{i j} = H 〈P_{i} - P_{j} - (z_{i} - z_{j}) ρ_{α} g - P_{c} (r_{i j})〉 \frac{π r_{i j}^{4}}{8 L \bar{μ}} (P_{i} - P_{j} - (z_{i} - z_{j}) \bar{ρ} g)

(5)

P_c(r_ij) [ML⁻¹T⁻²] used in Eq. (5) denotes the capillary entry pressure assigned to pore throat connecting pore i and j that needs to be exceeded by the DNAPL to enter the water filled pore throat. The capillary entry pressure is given by Young Laplace's Law as follows:

P_{c} (r_{ij}) = \frac{2 σ c o s θ}{r_{i j}}

(6)

where θ is the contact angle (assumed zero in our case), and r_ij denotes the radius of the pore throat connecting pore i and pore j.

$H 〈X〉$ is a Heaviside function that stands for the displacement condition of the interface in a pore throat. The throat can be blocked by capillarity if the capillary entry pressure (P_c (r_ij)) has not yet been reached. The Heaviside function is defined as:

H 〈X〉 = \{\begin{array}{c} 1 for X > 0 \\ 0 for X \leq 0 \end{array}

(7)

In situations where a meniscus is present at boundaries between a pore body and a pore throat, the identity of the fluid flowing through the pore throat (DNAPL or water, or capillary blocked) can only be determined after computation of the pressure value of the whole network. Therefore, we use an “effective” viscosity $\bar{μ}$ and an “effective” density $\bar{ρ}$ for the displacing fluid in Eq. (5), which are defined by:

\begin{array}{l} \bar{μ} = μ_{n w} S_{ij} + (1 - S_{ij}) μ_{w} \\ \bar{ρ} = ρ_{nw} S_{ij} + (1 - S_{ij}) ρ_{w} \\ S_{ij} = (S_{i} + S_{j}) / 2 \end{array}

(8)

where the suffixes w and nw refer to the wetting and nonwetting fluid, respectively, and S_ij [-] is an average phase saturation between pore bodies i and j. This factor evolves as function of time and indirectly takes interface movement inside a pore throat into account.

Introducing the appropriate expression of flow rate Q_ij in Eq. (3) leads to a set of algebraic equations with the pore body pressures as unknowns. This set of equations is written in matrix form as follows:

AP = B

(9)

where A is the conductance matrix with elements that depend on the connection between different pore throats, P denotes the pressure vector, and the B vector contains the pressures and the flow rates at the boundaries and the capillary pressure term if a meniscus is present in such pore throat entry. For a given time step, the flow is assumed to be in steady state, with constant fluid properties. To control the nonlinearities under such displacement conditions, the system of Eq. (9) is solved for pressure P using the value of the saturation term of the previous time step (Singh and Mohenty, 2003).

The saturation field is updated after computation of the pressure terms by quantifying a characteristic minimum time (hereafter called T_min), which corresponds to a minimum filling time for each of the pore bodies. The calculated pressure field is used to quantify fluid fluxes through the pore throats. The ratio of free volume in a pore body (not invaded by displacing fluid) to the flow rate at a given interface location gives the filling time needed for that pore body to be invaded. The saturations in each pore body are then updated using:

S_{i}^{n + 1} = S_{i}^{n} + \frac{Q_{i} \times T_{\min}}{V_{i}}

(10)

where S_iⁿ and S_iⁿ⁺¹ denote the saturation at the previous time (n) and calculated at the new time (n + 1), respectively, Q_i [L³T⁻¹] represents the sum of flow rates in all pore throats connected to pore body i and contains a moving interface, V_i is the volume of pore body i, and T_min is the time step as defined above.

During one time step, only one pore body reaches full nonwetting phase saturation. This pore body generates the additional interfaces, which are located at all connecting pore throats that are filled with wetting fluid. Newly created interfaces are tested for stability, and appropriate expressions for flow rate Q_ij are then identified. This leads to a modified matrix of conductance terms that is reformulated for each time step in the set of equations (Eq. (9)). The field pressure is computed and the procedure for updating saturation in pore bodies is repeated; this provides a transient response for pressure and saturation fields.

In the case of a single-phase flow, the intrinsic permeability k [L²] of the equivalent porous medium can be furthermore computed using Darcy's Law as follows:

k = \frac{μ_{α} Q_{i,total}^{e} h}{A (Φ_{up} - Φ_{down})}

(11)

where Q^e_i,total [L³T⁻¹] is the sum of external flow rate into pores i, located at the upstream boundary of the network, A [L²] and h [L] are the cross-sectional area and the total height of the network, respectively. Φ_up [ML⁻¹T⁻²] and Φ_down [ML⁻¹T⁻²] denote the phase potential at the upstream and downstream boundary of the network, respectively. Here, the phase potential is defined as Φ = P + ρ_αgz, where P [ML⁻¹T⁻²] is the fluid pressure computed by the pore-throat model.

3 An approach based on grain-size distribution to derive the radii of pore bodies and pore throats

3.1 Theory

To generate a distribution of pore-body sizes and pore throat-sizes for the network, we used a statistical distribution that specifies values of the minimum, mean and maximum size (Section 2.1). Assessment of these network parameters is essential to deliver a quantitative model and to obtain reliable simulations of laboratory experiments. Our modelling concept is based on geometric properties of packing spheres, which are combined with a probability approach proposed by Rouault and Assouline (1998). Models using packing spheres represent the porous medium as a geometric system that can be described by tetrahedral subunits formed by groups of four touching spheres. The probability of occurrence of each subunit is expressed in terms of the volume of the spheres, their probability of being present and the probability that specific pairs of spheres in contact may exist. The pore space in a subunit can be approximated by a narrow throat in each of the four faces of the tetrahedral subunit that meet at a pore body, which occupies the central cavity of the tetrahedron. Fig. 2 shows an example of a tetrahedral subunit formed by four touching spheres and an approximation of the pore space structure. The size of the pore throat is evaluated by a cylinder with a diameter given by the sphere in between the three spheres in the face. The pore body-size is determined by the sphere created in between the four touching spheres. Formulas given in the Rouault and Assouline (1998) work for computing pore body size (r_p), pore throat size (r_ci) and their relative probability densities were used.

Fig. 2
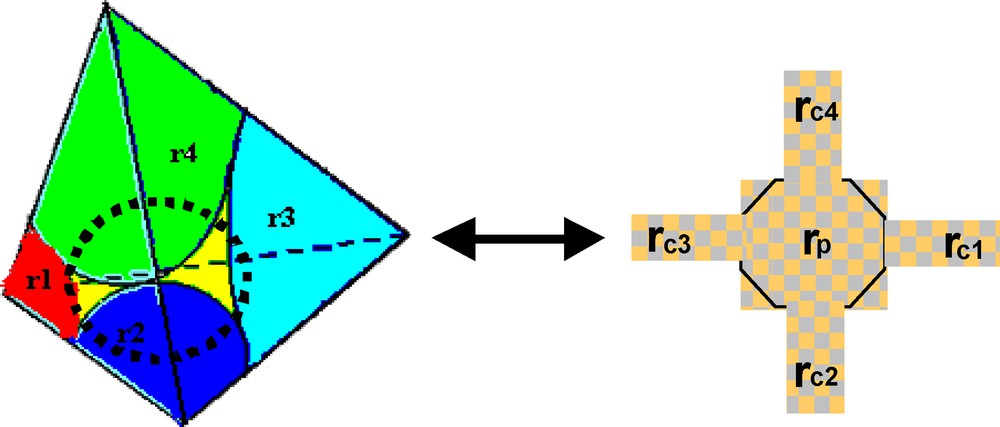
A tetrahedral subunit of four touching spheres with given radii r₁, r₂, r₃ and r₄ and its pore space approximation as four pore throats with computed radii r_c1, r_c2, r_c3 and r_c4 meeting at a cavity pore body with computed radius r_p.
Illustration d’un tétraèdre unité, formé par le chevauchement de quatre sphères de rayons r₁, r₂, r₃, et r₄ et approximation de l’espace poral, donnée par quatre capillaires de rayons calculés r_c1, r_c2, r_c3 r_c4 et un pore central de rayon calculé r_p.

The input data for sphere packing are in the form of a discrete sphere-size distribution, which can be derived from the GSD of the porous medium. We describe the GSD of a sand used in our laboratory experiment by a normal distribution, which is commonly used for an analytical description of grain-size distribution and can easily be applied in practice. The density probability function f(d) of this distribution is given by:

f (d) = \frac{1}{\sqrt{2 π σ_{g}}} \exp (- \frac{1}{2} {(\frac{d - d_{50}}{σ_{g}})}^{2})

(12)

where d is the grain-size diameter, d₅₀ is the mean grain size diameter, and σ_g is the standard deviation of the grain-size distribution deduced by graphical analysis.

For each set of four radii, the probability density of the tetrahedron subunits and the corresponding radius of the “kissing” sphere are obtained. The final result is one pore-size distribution curve and four throat-size distribution curves. Assuming that the generated pore body-sizes and pore throat-sizes are normally distributed, which is generally assumed for a large sampling number, the assessment of the mean value and the standard deviation of corresponding curves allows for calculation of various ranges of pore body radii and pore throat radii. These parameters are geometric input data of the pore-throat model.

3.2 Application to a medium-size sand

In this section, we use the conceptual approach described in Section 3.1 to parameterise the equivalent network of the H2F sand that was used in the physical experiment. H2F is a medium-size quartz sand with a hydraulic conductivity of about 8 × 10⁻⁴ m/s (k = 8 × 10⁻¹¹ m²), a total porosity of 40% and a low fraction of organic content (foc = 0.09%, based on NFT 31–109) (Bohy et al., 2006).

Fig. 3 shows the grain-size distribution curve of the H2F sand used in the experiment and its corresponding derived sphere-size distribution considered in the model of sphere packing. The mean value and the standard deviation of the sphere-size distribution allow positive values at each distance even at three standard deviations away from the mean value. Twenty-one spheres of different sizes were considered in the packing. This relatively high number of spheres ensured the reliability of statistics on the evaluation parameters as C⁴₂₁ (5985) possible sets of four radii might be formed. The radii of chosen spheres are equally spaced; this means that the radii are arithmetically related. The sizes of the radii vary between a minimum value of 0.05 mm and a maximum value of 0.34 mm. The ratio between the maximum and minimum sizes satisfies the packing condition mentioned in the work of Dodds (1980).

Fig. 3
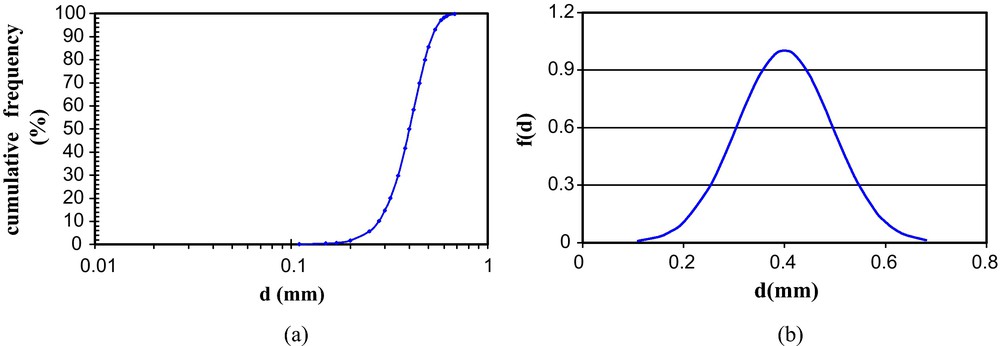
Medium-size H2F sand: (a) grain-size distribution; (b) derived sphere-size distribution.
Sable moyen H2F : (a) courbe granulométrique ; (b) distribution calculée de la taille des sphères.

The generated pore body and pore throat-size distributions are shown in Fig. 4. In contrast to the pore body-size distribution, the packing model allows us to compute four different distributions that can be used to describe the pore-throat size. The pore body-size distribution has a shape similar to the sphere-size distribution. The results agree well with the findings of Rouault and Assouline (1998). The forms of throat-size distributions vary and occupy a large range of radii. Based on the assumption that the volume of pore throats is negligible compared to that of pore bodies, we limited our analysis to the pore-throat distribution that presents the smallest mean radius (r_c1).

Fig. 4
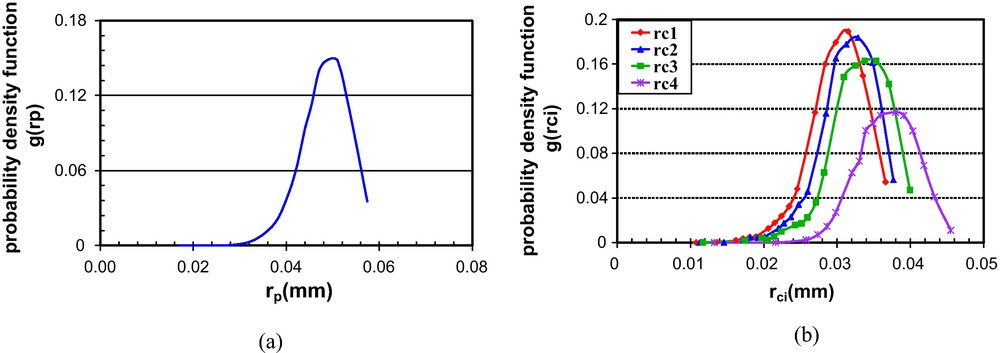
Medium-size H2F sand: (a) calculated pore-body size (r_p) distribution; (b) pore-throat size (r_ci) distributions.
Sable moyen H2F : (a) distribution calculée de la taille des pores (r_p) ; (b) distribution calculée de la taille des capillaires (r_ci).

Table 1 shows various values derived for both pore-body radii and pore-throat radii using the mean value and the standard deviation of the corresponding generated size distributions. For both size distributions, Case 1, Case 2 and Case 3 refer to the minimum and maximum radii derived from a size distribution as one time, two times and three times the standard deviation of the size distribution, respectively. For fixed distribution parameters of pore body radius and by combing the pore body radii with the pore throat radii given in Case 1, Case 2 and Case 3, we obtained at least nine possible realisations of the pore space geometry of our network model. To reduce the number of possible realisations of the geometry of the network model, we used the macroscopic properties of medium-size H2F sand, such as the intrinsic permeability (k = 8 × 10⁻¹¹ m²) and porosity (ø = 40%). For each of the nine possible combinations, we fixed the distance between pore-body centres at L = 0.14 mm, which is greater than two times the maximum radii of pore bodies. A single-phase water flow was simulated using the generated network model with given pressure boundaries. The intrinsic permeability and the porosity of the network, calculated with Eqs. (2) and (11), respectively, were then compared to the measured values of the sand used in the laboratory experiment (Table 2). The combination of Case 1 of the pore-body radii with Case 2 of the pore throat radii gave the best fit for the macroscopic properties of the sand. While the calculated permeability of 8.6 × 10⁻¹¹ m² was quite close to the experimental value, the porosity of our network model (ø = 47%) overestimated the porosity of our sand. The porosity might be better estimated by increasing the distance L between pore body centres. However, this would cause a decrease in the equivalent macroscopic permeability.

	Pore body radius	Pore throat radius
	r_min (mm)	r_mean (mm)	r_max (mm)	r_min (mm)	r_mean (mm)	r_max (mm)
Case 1	0.042	0.048	0.057	0.026	0.03	0.036
Case 2	0.036	0.048	0.061	0.022	0.03	0.04
Case 3	0.03	0.048	0.067	0.017	0.03	0.046

Pore body radius	Pore throat radius	Macroscopic proprieties
r_min (mm)	r_mean (mm)	r_max (mm)	r_min (mm)	r_mean (mm)	r_max (mm)	ø (%)	K (10⁻¹¹ m²)
0.042	0.048	0.057	0.026	0.03	0.036	47	12.87
0.042	0.048	0.057	0.022	0.03	0.040	47	8.6
0.042	0.048	0.057	0.017	0.03	0.046	47	13.2
0.036	0.048	0.061	0.026	0.03	0.036	49	12.84
0.036	0.048	0.061	0.022	0.03	0.040	49	7.64
0.36	0.048	0.061	0.017	0.03	0.046	49	13.42
0.30	0.048	0.067	0.026	0.03	0.036	53	11.73
0.30	0.048	0.067	0.022	0.03	0.040	53	11.83
0.30	0.048	0.067	0.017	0.03	0.046	53	12.05

4 Numerical simulation of a laboratory experiment

4.1 Model parameters

One of the objectives of our study was to use experimental results (Nsir, 2009) for verification of the network model developed. Experiments were conducted in a sand-filled glass column with a length of 70 cm and inner diameter of 10 cm. The DNAPL used was TCE, which was injected at a constant flow rate of 40 mL/min. The displacement was performed from bottom to top, which reproduced a stable displacement condition, and from top to bottom, which reproduced an unstable gravity condition. The experimental device was equipped with pressure transducers for monitoring pressure at the inlet and outlet sections of the glass column. The experimental programme also allowed the measurement of the arrival time of the DNAPL front at eight points on a control section equipped with optical fibre sensors (Nsir, 2009).

Simulation results reported here were carried out on a network of 7×7×4858 pore bodies. The spatial discretisation used reproduces the total height of the physical model but only a small fraction of the column section. We assumed that the chosen network is sufficiently large to be a representative elementary volume (REV) which may reproduce the macroscopic properties of the sand column such as intrinsic permeability and porosity. The pore-body and pore-throat radii considered in the simulations correspond to Case 1 for pore bodies and Case 2 for pore throats, as given in Table 1. The distance between pore-body centres was fixed at L = 0.14 mm.

The network model is initially water-saturated, and a constant flow rate of 29.6 × 10⁻⁴ mL/min of TCE was applied at the inlet section of the model. The injection rate was calculated by accounting for the ratio between the modelled section and the total section of the glass column. At the outlet section of the model, the observed water head was specified as a constant pressure boundary. The simulation stopped when the duration of the DNAPL injection that occurred in the experiment was reached.

4.2 Stable case of water displacement by DNAPL

To illustrate the case of stable displacement, the displacing fluid (TCE) was injected at the bottom of the network. The boundary pressure applied to the outlet section corresponded to a water height of 18 cm. Fig. 5a shows a comparison of calculated and measured inlet pressures as a function of time. According to the experimental observations, the value of the pressure in the whole domain increased with time. The water/DNAPL interface was stabilized by the gravity effect; the potentially destabilizing influence of the viscosity ratio on the front behaviour was not significant. The increase in pressure was therefore caused by the high density of the invading fluid, which overrides the decrease of viscous pressure during the displacement of the less viscous DNAPL.

Fig. 5
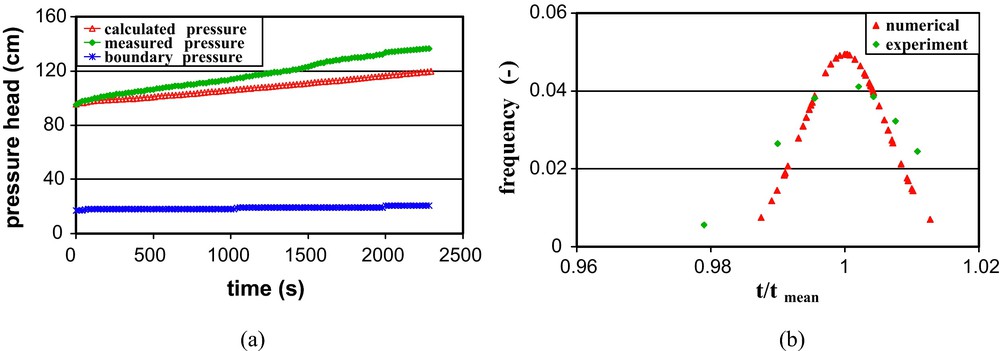
Stable displacement of water by DNAPL: (a) inlet pressure measured and simulated as functions of time; (b) distribution of calculated and measured dimensionless arrival times of the water/DNAPL front.
Déplacement stable de l’eau par du DNAPL : (a) pression mesurée à l’entrée de la colonne et simulée en fonction du temps ; (b) distribution des temps d’arrivée adimensionnels du front d’eau/DNAPL.

Even though the increasing pressure behaviour observed in the experiment was adequately reproduced, the measured pressure increases were stronger than what was calculated experimentally. This can be explained by the chosen arrangement of pore and throat sizes in the pore-throat model. The very narrow throats that exist in the real porous medium were not considered in the network and may require a higher displacement pressure to be invaded by the displacing fluid. Using a wider pore body-size distribution might also reduce this misfit of inlet pressure.

The curves representing the distributions of dimensionless arrival times of the water/DNAPL front in the experiment and the simulation were similar (Fig. 5b). The calculated standard deviations were very close to the measured values (14 s calculated compared to 9 s measured in the experiment). According to our experimental observations, the distribution of front arrival times at the control section is almost uniform. Due to the stabilizing effect of gravity, a flat piston-like front was observed moving through the network. Consequently, very little wetting fluid was left behind and a compact pattern of the invading fluid occurred. The network model adequately reproduced the stability mechanisms of displacement caused by the positive contribution of gravity.

4.3 Unstable case of water displacement by DNAPL

In the case of unstable water displacement, the DNAPL was injected at the top of the network using the same boundary and initial conditions as described in section 4.1. For this displacement, we expected a much more irregular front with possible gravity fingering. Fig. 6a shows the variation of displacement pressure measured and calculated by the model. Due to the constant injection rate, the pressure value in the domain decreased as the less viscous and denser fluid invaded the system. The sudden increase of pressure shown in Fig. 6a corresponds to the breakthrough of the invading fluid at the outlet section. Under these displacement conditions, gravity forces are destabilizing and dominate the movement, resulting in typical DNAPL fingers in the displaced fluid. The macroscopic water/DNAPL interface was no longer horizontal and many throats were blocked by the capillary effect. The number of active invasion paths was therefore low, and the flow section of DNAPL was reduced. The contribution of viscous pressure was also limited and was dominated by the contribution of the higher density of the invading fluid. This resulted in a decrease of the inlet pressure. The inlet pressure observed was reproduced by the numerical model, but the rate at which it decreased in the model was different from the measured one, the calculated pressure decrease was more substantial than that observed. In addition, we recorded an earlier breakthrough time than we observed. This result can be explained by the number of active invasion paths that were lower in the network model than in the real porous medium. This effect may be due to the narrow generated pore-throat size distribution that contains many large pore throats.

Fig. 6
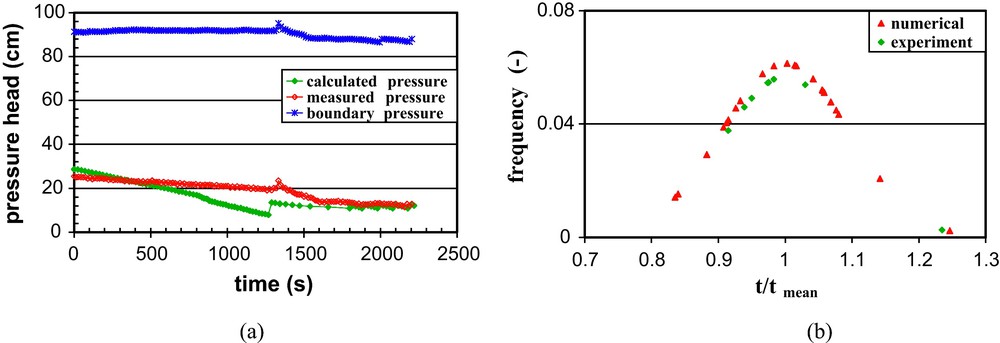
Unstable displacement of water by DNAPL: (a) inlet pressure measured and simulated as functions of time; (b) distribution of calculated and measured dimensionless arrival times of the DNAPL front.
Déplacement instable de l’eau par du DNAPL : (a) pression mesurée à l’entrée de la colonne et simulée en fonction du temps ; (b) distribution des temps d’arrivée adimensionnels du front d’eau/DNAPL.

Fig. 6b shows a comparison between the distribution of calculated arrival times of the front and those observed at the control section. The statistical data of both distributions are similar. They both illustrate highly non-uniform distributions of arrival times with significant standard deviations. The calculated standard deviation was 75 s, compared to 70 s measured in the laboratory experiment. Thus, gravity fingering was numerically confirmed by the distribution of arrival times of the front at the chosen cross-section of the network. However, the mean arrival time of the water/DNAPL front calculated at the control section was approximately 633 s, compared to the observed time of approximately 747 s. This finding directly confirms the earlier computed breakthrough of TCE at the downstream section (Fig. 6a).

4.4 Sensitivity study

A sensitivity study of specific model parameters, such as the size of the lattice and the size of pore throats, was undertaken to analyse the influence of these parameters on the displacement of water by DNAPL. Furthermore, we assessed whether a reasonable modification of their values might explain the differences between the simulated and measured DNAPL pressures at the inlet section, as well as the simulated and measured arrival times of the DNAPL front. Specifically, we analysed the unstable case of water displacement by DNAPL.

4.4.1 Effect of the lattice size

Using a larger section of network may be more valid for the appropriate representation of the real porous medium. However, larger networks suffer from computation times that can become, in some cases, very high, even with powerful computers. Fig. 7a shows the calculated inlet pressure obtained from simulations carried out on networks of two lattice sizes (5×5×4858 and 6×6×4858 pore bodies) that were smaller than the reference case and one lattice size (9×9×4858) that was larger than the reference case discussed in Section 4.3. The size of the reference case was 7×7×4858. On a Linux-computer with 3956 MB RAM and a Celeron processor running at 1998 MHz, the corresponding Central Processing Unit (CPU) times were very different; the times were one day, four days, thirteen days and twenty days for the two small lattices, the medium lattice and the large lattice, respectively. In all cases, the modelled inlet pressure behaviour was similar; it decreased with increasing time, particularly for the reference case and the case of the bigger lattice (the pressure profiles for those cases were almost the same). However, the breakthrough times calculated for the bigger lattice and the reference lattice were shorter than the times calculated for the two smaller lattice sizes. The smaller lattices were closer to the observed breakthrough time. Thus, developed displacement instabilities are more significant in bigger lattices than in smaller lattices. The arrival time distribution of the front water/DNAPL calculated and measured (Fig. 7b) in the same control section confirms this conclusion. The corresponding curves for both bigger lattices were almost the same and were more widely distributed than those computed using the smaller lattices. The standard deviation of the distribution of arrival times was 75 s and 79 s for lattice sizes 7×7×4858 and 9×9×4858, respectively. These values are very close to the measured standard deviation of 72 s. The standard deviation arrival times for the smaller lattices sizes (5×5×4858 and 6×6×4858) were 59 s and 64 s, respectively. A large lattice size leads to a spatial pore body size distribution and pore throat size distribution that is more heterogeneous than for a small lattice. Consequently, preferential pathways are more likely to occur during displacement. As a result, the water/DNAPL front arrives earlier at the downstream section of the model in the case of bigger lattice sizes. Thus, the distribution of arrival times of the water/DNAPL front is not uniform, as shown in Fig. 7b. In contrast, based on the numerical results obtained from the 7×7×4858 and 9×9×4858 lattices, which were quite similar, we concluded that a lattice size of 7×7×4858 adequately reproduces the unstable displacement process in the given porous medium.

Fig. 7
Influence of the lattice size on the unstable DNAPL displacement: (a) inlet pressure measured and simulated as functions of time; (b) the distribution of calculated and measured dimensionless arrival times of the water/DNAPL front.
Influence de la taille de réseau sur le déplacement instable de l’eau par du DNAPL : (a) pression mesurée et simulée en fonction du temps ; (b) distribution des temps d’arrivée, mesurés et calculés du front d’eau/DNAPL.

4.4.2 Effect of the variance in pore-throat size

In this study, we used the three distribution parameters for pore throat radius as given in Table 1 (Case 1, Case 2 and Case 3) to analyse the influence of the variance in the pore throat size on the unstable displacement of water by DNAPL. Case 1 has a pore throat size variation range smaller than Case 2, which is hereafter referred to as the reference case. Case 3 has pore throat size variation range larger than the reference case. The size of the network considered in our simulations was the same for each pore throat size distribution (with identical pore body size distribution). We chose the smallest lattice size (5×5×4858) because it required less computational time and memory.

Fig. 8a shows the calculated pressure for different network constructions that were compared to the measured pressure. We note that the inlet pressure increased with increasing variance of the pore throat distribution and was accompanied by a later breakthrough of the water/DNAPL front. Apparently, the pore-throat radius controls the dynamic displacement of the water/DNAPL interface in the network. Case 3 had the smallest pore-throat sizes. This resulted in an increase in pressure in the pore bodies at the upstream boundary of the model, which was required to maintain the prescribed constant mass flow rate for DNAPL. A higher local pressure field permitted the DNAPL to overcome the capillary entry pressure in the throats and therefore resulted in a more uniform invasion of the water-saturated pore bodies by DNAPL in the model transect. However, the pore-throat size distributions of Case 1 and Case 2 had much larger throats, resulting in preferential pathways that were more likely to occur. This made the overall invasion of the section harder. As a consequence, the model predicted earlier breakthrough times, and the pressure field decreased rapidly. This may explain why the computed breakthrough of the displacement front in Case 3 was later than in Cases 1 and 2. Furthermore, in analysing the calculated DNAPL saturation field (not presented here), the DNAPL front in Case 3 was characterised by several gravity-dominated fingers, whereas in Case 1, fewer fingers were formed.

Fig. 8
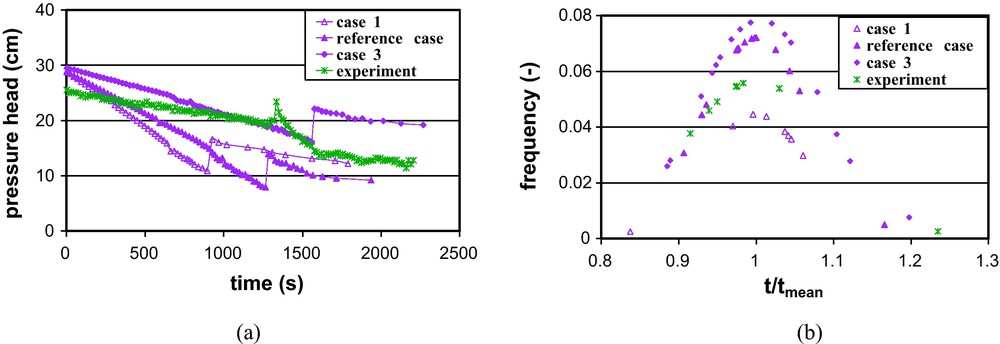
Influence of the variance of the pore-throat size on the unstable DNAPL displacement: (a) inlet pressure measured and simulated as functions of time; (b) distribution of calculated and measured dimensionless arrival times of the water/DNAPL front.
Influence de la variance de la taille de capillaires sur le déplacement instable de l’eau par du DNAPL : (a) pression mesurée et simulée en fonction du temps ; (b) distribution des temps d’arrivée, mesurés et calculés du front d’eau/DNAPL.

Fig. 8b shows a comparison between distributions of dimensionless arrival times of the water/DNAPL front calculated and measured at the control section. The prediction with a pore-throat size distribution as in Case 3 was quite close to the experimental data. The corresponding curve was more widely spread than those obtained with the narrow pore-throat size distributions of Case 1 and Case 2. The calculated standard deviation relative to the pore-throat distribution of Case 3 was approximately 69 s, which is quite close to the experimentally determined value of 72 s. However, the calculated standard deviation was only 49 s and 59 s for Case 1 and the reference case, respectively. Case 3 provides a wider pore-throat radius distribution. This may allow much invasion pathways to be formed, leading to a better reproduction of the displacement front observed in the laboratory experiment. Because the pore-throat size distribution variability was lower in Case 1 and Case 2, one may think that the number of accessible pore throats for the displacing fluid was reduced and therefore only a few fingers resulted.

5 Conclusions

We developed a pore-throat network model that adequately describes the dynamic drainage process. A geometric model of packing spheres combined with a probabilistic approach was used to obtain realistic pore sizes and throat sizes based on grain-size distribution. The pore-scale network model was tested using experimental data. The prediction of the temporal evolution of pressure at the inlet section and the distribution of arrival times of the water/DNAPL front in a given cross-section matched well with laboratory measurements. An important feature of the model is its capability to reproduce the observed pressure behaviour for stable and unstable displacement regimes. The sensitivity study indicated that the lower pore-throat size strongly influenced the instability of DNAPL displacement. However, additional numerical studies may be necessary to analyse the influence of pore body size on unstable DNAPL displacement. Furthermore, application of the developed numerical model to a drainage experiment recently conducted in a homogeneous fine sand may allow an additional verification step of the model to derive pore body sizes and pore throat sizes in the case of a low permeability porous medium.

The network model used in the present work considers the converging–diverging nature of pores and is based on the pore body size distribution and pore-throat size distribution. However, no correlation exists between pore throat sizes and neighbouring pore bodies. Besides, pore space asperities and roughness were not considered. Additional quantitative information about the degree of correlation between pore-body size and pore-throat size are needed to take into account more features of the pore space geometry of the porous medium. The lattice sizes used resulted in time consuming simulations. This prohibits application of the model to a larger part of the cross-section of the porous medium. One possible way to overcome this problem might be to develop a more efficient algorithm to solve the large set of equations.

Acknowledgements

Financial support for this research was received from the programme REALISE (REseau Alsace de Laboratoires en Ingénierie et Sciences pour l’Environnement). The Région Alsace, the GDR “Hydrodynamique et Transferts dans les Hydrosystèmes Souterrains” (INSU-CNRS), and the Conseil Scientifique de l’Université Louis-Pasteur Strasbourg are gratefully acknowledged. Furthermore, the authors would like to thank Professor Insa Neuweiler and the two other anonymous reviewers for their valuable comments and suggestions, which helped to improve the article significantly.

Bibliographie

[Bano et al., 2009] M. Bano; O. Loeffler; J.F. Girard Ground penetrating radar imaging and time-domain modelling of the infiltration of diesel fuel in a sandbox experiment, C. R. Geoscience, Volume 341 (2009), pp. 846-858

[Bear, 1972] J. Bear Dynamics of Fluids in Porous Media, Elsevier, New York, 1972

[Barenblatt and Patzek, 2003] G.I. Barenblatt; T.W. Patzek The mathematical model of nonequilibrium effects in water-oil displacement, SPE Reserv. Eng., Volume 8 (2003), pp. 409-416

[Blunt and King, 1990] M. Blunt; P. King Macroscopic parameters from simulations of pore scale flow, Phys. Rev. A, Volume 42 (1990), pp. 4780-4787

[Bohy et al., 2004] M. Bohy; G. Schäfer; O. Razakarisoa Caractérisation de zones sources de DNAPL à l’aide de traceurs bisolubles : mise en évidence d’une cinétique de partage, C. R. Geoscience, Volume 336 (2004), pp. 799-806

[Bohy et al., 2006] M. Bohy; L. Dridi; G. Schäfer; O. Razakarisoa Transport of a mixture of chlorinated solvent vapors in the vadose zone of a sandy aquifer, Vadose Zone J., Volume 5 (2006), pp. 539-553

[Celia et al., 1995] M.A. Celia; P.C. Reeves; L.A. Ferrand Recent advances in pore scale models for multiphase flow in porous media, Rev. Geophys., Volume 33 (1995), pp. 1049-1058

[Dodds, 1980] J.A. Dodds The porosity and contact points in multicomponent random sphere packings calculated by a simple statistical geometric model, J. Colloid Interface Sci., Volume 77 (1980), pp. 317-327

[Galusinski and Saad, 2009] C. Galusinski; M. Saad Weak solutions for immiscible compressible multi-fluid flows in porous media, C. R. Acad. Sci. Paris, Ser. I, Volume 347 (2009), pp. 249-254

[Geoffrey and Mellor, 1995] M. Geoffrey; M.D. Mellor Simulation of drainage and imbibition in a random packing of equal spheres, J. Colloid Interface Sci., Volume 176 (1995), pp. 214-225

[Hilpert and Miller, 2001] M. Hilpert; C.T. Miller Pore-morphology-based simulation of drainage in totally wetting porous media, Adv. Water Resour., Volume 24 (2001), pp. 243-255

[Joekar-Niasar et al., 2009] V. Joekar-Niasar; S.M. Hassanizadeh; L.J. Pyrak-Nolte; C. Berentsen Simulating drainage and imbibition experiments in a high porosity micro-model using an unstructured pore network model, Water Resour. Res., Volume 45 (2009), p. W02430 (doi:10.1029/2007WR006641)

[Khataniar and Peters, 1992] S. Khataniar; E.J. Peters The effect of reservoir heterogeneity on the performance of unstable displacements, SPE Reserv. Eng., Volume 7 (1992), pp. 263-281

[Laroche and Vizika, 2005] C. Laroche; O. Vizika Two-phase flow properties prediction from small-scale data using pore-network modeling, Transp. Porous Media, Volume 6 (2005), pp. 77-91

[Lindner and Wagner, 2009] A. Lindner; C. Wagner Viscoelastic surface instabilities, C. R. Physique, Volume 10 (2009), pp. 712-727

[Lowry and Miller, 1995] M.I. Lowry; C.T. Miller Pore-scale modeling of nonwetting-phase residual in porous media, Water Resour. Res, Volume 31 (1995), pp. 455-473

[Nordhaug et al., 2003] H.F. Nordhaug; M. Celia; H.K. Dahle A pore network model for calculation of interfacial velocities, Adv. Water Resour., Volume 26 (2003), pp. 1061-1074

[Nsir, 2009] Nsir, K., 2009. Étude expérimentale et numérique de la migration des polluants non miscibles à l’échelle de Darcy. PhD thesis, université de Strasbourg, France, 207 p.

[Patzek, 2000] T.W. Patzek Verification of a complete pore network simulator of drainage and imbibition, SPE Reserv. Eng., Volume 7 (2000), pp. 1-12

[Raoof and Hassanizadeh, 2009] A. Raoof; S.M. Hassanizadeh A new method for generating pore network models of porous media, Transp. Porous Media, Volume 81 (2009), pp. 391-407

[Riaz and Tchelepia, 2006] A. Riaz; H.A. Tchelepia Numerical simulation of immiscible two-phase flow in porous media, Phys. Fluids, Volume 18 (2006), p. 014104

[Rouault and Assouline, 1998] Y. Rouault; S. Assouline A probabilistic approach towards modelling the relationships between particle and pore size distributions: the multicomponent packed sphere case, Powder Technol., Volume 96 (1998), pp. 33-41

[Saad et al., 2010] A. Saad; S. Guédon; F. Martineau Microstructural weathering of sedimentary rocks by freeze–thaw cycles: experimental study of state and transfer parameters, C. R. Geoscience, Volume 342 (2010), pp. 197-203

[Singh and Mohenty, 2003] M. Singh; K. Mohenty Dynamic network for drainage through three dimensional porous materials, Chem. Eng. Sci., Volume 58 (2003), pp. 1-18

[Tehelepi et al., 1994] H.A. Tehelepi; F.M. Orr; U. Stanford Interaction of viscous fingering. Permeability heterogeneity, and gravity segregation in three dimensions, SPE Reserv. Eng., Volume 9 (1994), pp. 266-271

[Washburn, 1921] E.W. Washburn The dynamics of capillary flow, Phys. Rev., Volume 17 (1921), p. 273

[Weibull, 1951] W. Weibull A statistical distribution function of wide applicability, J. Appl. Mech., Volume 18 (1951), pp. 293-307

Commentaires - Politique