Analysis of physical quality of soil using the water retention curve: Validity of the <i>S</i>-index

Glenio Guimarães Santos; Euzebio Medrado da Silva; Robélio Leandro Marchão; Pedro Marques da Silveira; Ary Bruand; Francois James; Thierry Becquer

doi:10.1016/j.crte.2011.02.001

Hydrology, environment (Pedology)

Analysis of physical quality of soil using the water retention curve: Validity of the S-index
[Analyse de la qualité physique du sol à partir de la courbe de rétention de l’eau : validité de l’indice S]

Présenté par : Ghislain de Marsily

Glenio Guimarães Santos ¹ ; Euzebio Medrado da Silva ² ; Robélio Leandro Marchão ² ; Pedro Marques da Silveira ³ ; Ary Bruand ⁴ ; Francois James ⁵ ; Thierry Becquer ⁶

¹ Universidade Federal do Piauí, BR 135, km três, 64900-000, Bom Jesus, Piauí, Brazil
² Embrapa Cerrados, BR 020, Km 18, Caixa Postal 08223, Planaltina, Distrito Federal, Brazil
³ Embrapa Arroz e Feijão, GO-462, km 12, 75375-000, Santo Antônio de Goiás, Goiás, Brazil
⁴ CNRS/INSU, université d’Orléans, Institut des Sciences de la Terre d’Orléans (ISTO) UMR6113, 1A, rue de la Férolerie, 45071 Orléans cedex, France
⁵ CNRS, UMR 6628, université d’Orléans, mathématiques et applications, physique mathématique d’Orléans (MAPMO), rue de Chartres, BP 6759, 45100 Orléans, France
⁶ IRD, UMR 210 Eco&Sols (INRA-IRD-SupAgro), 2, place Viala, bâtiment 12, 34060 Montpellier cedex 1, France

Comptes Rendus. Géoscience, Volume 343 (2011) no. 4, pp. 295-301.

Résumés

Anglais
Français

Among the various soil indicators established in order to discuss physical properties of soils is the S-index, derived from the slope of the soil water retention curve at its inflection point, used by a number of authors. In this publication we discuss the value of the slope at the inflection point of the soil water retention curve according to the independent variable used to plot it. We show that a representation of the water content according to the arithmetic rather than logarithmic expression of the suction for the S-index yields a different result for the soil selected. More generally, our results show that examining the physical properties of soil using a water retention curve plotted with an arithmetic expression of suction offers greater potential than when plotted with its natural or decimal logarithm as is often found in the literature.

Parmi les différents indicateurs qui ont été proposés pour rendre compte des propriétés physiques du sol, l’indice S, qui correspond à la pente de la courbe de rétention en eau du sol à son point d’inflexion, a été largement utilisé. Dans cet article, nous discutons de la valeur de la pente au point d’inflexion de la courbe de rétention en eau du sol, en fonction de la variable indépendante qui est utilisée pour le déterminer. Nous montrons que la représentation de la teneur en eau en fonction de l’expression arithmétique de la succion au lieu de son expression logarithme, comme pour l’indice S, conduit à un résultat différent pour le sol sélectionné. Plus généralement, nos résultats montrent qu’une discussion des propriétés physiques du sol, en utilisant une représentation de la courbe de rétention d’eau en fonction de l’expression arithmétique de la succion, offre plus de possibilités que l’expression logarithmique naturelle ou décimale qui a été largement utilisée jusqu’alors.

Métadonnées

Reçu le : 2010-05-29
Accepté le : 2011-02-16
Publié le : 2011-04-01

DOI : 10.1016/j.crte.2011.02.001

Keywords: Soil compaction, Bulk density, Van Genuchten model, S-index
Mot clés : Compaction du sol, Densité apparente, Modèle de van Genuchten, Indice S

Affiliations des auteurs :

Glenio Guimarães Santos ¹ ; Euzebio Medrado da Silva ² ; Robélio Leandro Marchão ² ; Pedro Marques da Silveira ³ ; Ary Bruand ⁴ ; Francois James ⁵ ; Thierry Becquer ⁶

@article{CRGEOS_2011__343_4_295_0,
     author = {Glenio Guimar\~aes Santos and Euzebio Medrado da Silva and Rob\'elio Leandro March\~ao and Pedro Marques da Silveira and Ary Bruand and Francois James and Thierry Becquer},
     title = {Analysis of physical quality of soil using the water retention curve: {Validity} of the {\protect\emph{S}-index}},
     journal = {Comptes Rendus. G\'eoscience},
     pages = {295--301},
     publisher = {Elsevier},
     volume = {343},
     number = {4},
     year = {2011},
     doi = {10.1016/j.crte.2011.02.001},
     language = {en},
}

TY  - JOUR
AU  - Glenio Guimarães Santos
AU  - Euzebio Medrado da Silva
AU  - Robélio Leandro Marchão
AU  - Pedro Marques da Silveira
AU  - Ary Bruand
AU  - Francois James
AU  - Thierry Becquer
TI  - Analysis of physical quality of soil using the water retention curve: Validity of the S-index
JO  - Comptes Rendus. Géoscience
PY  - 2011
SP  - 295
EP  - 301
VL  - 343
IS  - 4
PB  - Elsevier
DO  - 10.1016/j.crte.2011.02.001
LA  - en
ID  - CRGEOS_2011__343_4_295_0
ER  -

%0 Journal Article
%A Glenio Guimarães Santos
%A Euzebio Medrado da Silva
%A Robélio Leandro Marchão
%A Pedro Marques da Silveira
%A Ary Bruand
%A Francois James
%A Thierry Becquer
%T Analysis of physical quality of soil using the water retention curve: Validity of the S-index
%J Comptes Rendus. Géoscience
%D 2011
%P 295-301
%V 343
%N 4
%I Elsevier
%R 10.1016/j.crte.2011.02.001
%G en
%F CRGEOS_2011__343_4_295_0

Glenio Guimarães Santos; Euzebio Medrado da Silva; Robélio Leandro Marchão; Pedro Marques da Silveira; Ary Bruand; Francois James; Thierry Becquer. Analysis of physical quality of soil using the water retention curve: Validity of the S-index. Comptes Rendus. Géoscience, Volume 343 (2011) no. 4, pp. 295-301. doi : 10.1016/j.crte.2011.02.001. https://comptes-rendus.academie-sciences.fr/geoscience/articles/10.1016/j.crte.2011.02.001/

Version originale du texte intégral

1 Introduction

Water movement in soils as described using hydrogeophysics (Cousin et al., 2009; Frangi et al., 2009) is related to their hydraulic properties which in turn are closely dependent on soil structure. Its high lateral and vertical variability in soils has led soil physicists to seek out physical indicators enabling the discussion of its characteristics, and more generally of the quality of physical properties (Dexter, 2004a, 2004b, 2004c; Dexter and Bird, 2001; Dexter and Czyz, 2007; Dexter et al., 2007; Reynolds et al., 2002). Among these indicators, the index proposed by Dexter and Bird (2001) and Dexter (2004a) enables the physical quality of soil (workability, permeability, structure stability, etc.) to be investigated and should be particularly effective for providing information on the soil hydric functioning. This index is the slope (S) of the soil-water retention curve (SWRC) at its inflection point. It is determined for the SWRC when the gravimetric water content (W), a function of soil-water suction (h) and expressed using the van Genuchten equation (Richard et al., 2001), is plotted with the natural logarithm of h. In this study we use W to denote the gravimetric water content, rather than θ, as in Dexter and Bird (2001), to be more consistent with the literature since θ usually represents the volumetric water content. As for the van Genuchten equation (van Genuchten, 1980) which was written for θ, it remains valid for W.

Dexter (2004a) derived the expression of the slope of the SWRC analytically to calculate the value of S, thus leading to the following expression:

S = - n (W_{s} - W_{r}) {[1 + \frac{1}{m}]}^{- (1 + m)}

(1)

with m and n the fitted dimensionless shape parameters of the van Genuchten equation (van Genuchten, 1980), and W_s and W_r, in g of water per g of oven-dried soil, and the saturated and residual gravimetric water contents of the van Genuchten equation, respectively. This characteristic of the SWRC was considered by Dexter (2004a) as a physical parameter (S-index) of the physical quality of soil. Dexter (2004a) showed that it was related to the texture, bulk density, organic matter content and root growth of soil. Since its early developments, the S-index has been used by many authors (Dexter, 2004c; Dexter and Czyz, 2007; Dexter and Richard, 2009; Dexter et al., 2005; Dexter at al., 2007; Han et al., 2008; Tormena et al., 2008).

Dexter and Bird (2001), however, noted that there were two possible inflection points depending on whether W is plotted against log(h) or against h. They reported that the two inflection points are in close proximity for soils with a narrow pore-size distribution. This explains why they used the inflection point of curves of W vs. log(h), believing this was an estimate of air entry into granular materials which were considered in their study. Another point not raised by Dexter and Bird (2001) concerned their choice for computing the slope in a graph W vs. ln(h) of the W curve as a function of h according to the van Genuchten equation (Dexter and Czyz, 2007; Dexter et al., 2007) instead of the slope of the W curve vs. ln(h) which would have been mathematically more consistent.

In this study we discuss the choice of Dexter and Bird (2001) and compare the S-index with the slope of the SWRC at its inflection point when it is expressed as a function of the independent variable h, ln(h) or log(h). The equations developed are applied to a non-compacted and compacted soil and the resulting values of the slope are compared to the S-index.

2 Theory

2.1 Expression of W according to h, ln(h) and log(h)

On the basis of the van Genuchten equation (van Genuchten, 1980), W can be expressed as:

W = (W_{s -} {\hat{W}}_{r}) {[1 + {(\hat{α} h)}^{\hat{n}}]}^{- \hat{m}} + {\hat{W}}_{r}

(2)

with W the gravimetric soil water content (g g⁻¹); W_s the measured gravimetric saturated soil water content (g g⁻¹);

{\hat{W}}_{r}

the fitted residual gravimetric soil water content (g g⁻¹);

\hat{α}

the fitted scaling parameter (kPa⁻¹); and

\hat{n}

and

\hat{m} = 1 - 1 / \hat{n}

(Mualem, 1976) dimensionless fitted shape parameters. In order to facilitate presentation, it can be admitted that Eq. (2) can be represented as:

W = g (h| W_{s}, {\hat{W}}_{r}, \hat{n}, \hat{α}, \hat{m})

(3)

with g being W as a function of h, given that parameters

W_{s} (g g^{- 1})

{\hat{W}}_{r} (g g^{- 1})

\hat{n}

(dimensionless),

\hat{α} (h p a^{- 1})

, and

\hat{m}

(dimensionless) are known. The circumflex on a letter is used to identify a fitted parameter value (

\hat{m}

can also be fitted but in this study it was forced to 1–1/n).

Similarly, W vs. ln(h), can be represented by f using Eq. (2) as:

W = f (\ln (h) |W_{s}, {\hat{W}}_{r 1}, {\hat{n}}_{1}, {\hat{α}}_{1}, {\hat{m}}_{1})

(4)

with the fitted parameters

{\hat{W}}_{r 1} (g g^{- 1})

{\hat{n}}_{1}

(dimensionless),

\hat{α} (h P a^{- 1})

and

{\hat{m}}_{1}

(dimensionless) and W vs. log(h), can be represented by k using Eq. (2) as:

W = k (\log (h) {|W_{s}, {\hat{W}}_{r 1}, n {}_{1}, \hat{α}}_{2}, {\hat{m}}_{1})

(5)

with

{\hat{α}}_{2}

the only new fitted parameter such as

{\hat{α}}_{2} = {\hat{α}}_{1} \ln 10

, the other fitted parameters being identical to those determined for f.

2.2 Derivation of the SWRC to obtain the inflection point

Taking Eqs. (3), (4), and (5) as general representations of the WRC and using Eq. (4), we can write the following derivatives:

\dot{g} = \frac{d W}{d h} = - \hat{m} \hat{n} ({\hat{α}}^{\hat{n}}) (W_{s} - {\hat{W}}_{r}) \{{[1 + {(\hat{α} h)}^{\hat{n}}]}^{- \hat{m} - 1}\} \ln (h^{\hat{n} - 1})

(6)

with ġ the first derivative of W in relation to h,

\dot{g} = \frac{d W}{d (\ln (h))} = {\hat{m}}_{1} {\hat{n}}_{1} ({\hat{α}}_{1}^{{\hat{n}}_{1}}) (W_{s} - {\hat{W}}_{r 1}) \{[1 + {({\hat{α}}_{1} \ln (h))}^{- \hat{m} - 1}]\} \log {(h)}^{{\hat{n}}_{1} - 1}

(7)

with

\dot{f}

the first derivative of W in relation to ln (h), and:

\dot{k} = \frac{d W}{d (\log (h))} = - {\hat{m}}_{1} {\hat{n}}_{1} ({\hat{α}}_{2}^{{\hat{n}}_{1}}) (W_{s} - {\hat{W}}_{r 1}) \{{[1 + ({\hat{α}}_{2} \log {(h)}^{{\hat{n}}_{1}})]}^{- {\hat{m}}_{1} - 1}\} \log {(h)}^{{\hat{n}}_{1} - 1}

(8)

with

\dot{k}

the first derivative of W in relation to log (h).

It is important to state that $\dot{f} = d W / d (\ln (h))$ cannot be computed by simply applying the chain rule from Eq. (3) because the parameters determined by fitting either g (Eq. (3)) or f (Eq. (4)), subjected to Eq. (2), are not necessarily the same. This can be also said for functions g (Eq. (3)) and k (Eq. (5)), except that here the only difference between $\dot{f}$ and $\dot{k}$ is the magnitude of the scaling parameters ${\hat{α}}_{1}$ and ${\hat{α}}_{2}$ .

It is known that any continuous and differentiable mathematical function has its inflection points located where the second derivative is null throughout its real domain. Thus, at the inflection points for function g, we can set:

\dot{g} = \frac{d^{2} W}{d h^{2}} = - \hat{m} \hat{n} ({\hat{α}}^{\hat{n}}) (W_{s} - {\hat{W}}_{r}) \{(- \hat{m} \hat{n} - \hat{n}) ({\hat{α}}^{\hat{n}}) {[1 + {(\hat{α} h)}^{\hat{n}}]}^{- \hat{m} - 2} h^{2 \hat{n} - 2} + (\hat{n} - 1) (h^{\hat{n} - 2}) {[1 + {(\hat{α} h)}^{\hat{n}}]}^{- \hat{m} - 1}\} = 0

(9)

with

\ddot{g}

, the second derivative of W in relation to h. After simplifying Eq. (9), we obtain:

(- \hat{m} \hat{n} - \hat{n}) ({\hat{α}}^{\hat{n}}) {[1 + (\hat{α} h) \hat{n}]}^{- \hat{m} - 2} (h^{2 \hat{n} - 2}) + (\hat{n} - 1) (h^{\hat{n} - 2}) {[1 + {(\hat{α} h)}^{\hat{n}}]}^{- \hat{m} - 1} = 0

(10)

Eq. (10) can be solved for h to obtain the precise location of its inflection point (h)_i as follows:

{(h)}_{i} = \frac{1}{\hat{α}} {(\hat{m})}^{\frac{1}{{\hat{n}}_{1}}}

(11)

Similarly, we can compute the second derivative of Eqs. (7) and (8) to obtain:

{(\ln (h))}_{i} = \frac{1}{{\hat{α}}_{1}} {({\hat{m}}_{1})}^{\frac{1}{{\hat{n}}_{1}}}

(12)

with (ln(h))_i, the inflection point of W vs. ln(h), and:

{(\log (h))}_{i} = \frac{1}{{\hat{α}}_{2}} {({\hat{m}}_{1})}^{\frac{1}{{\hat{n}}_{1}}}

(13)

with (log(h))_i, the inflection point of W vs. log(h).

2.3 Calculation of the slope at the inflection point of the SWRC

The slope, S_h, from function g (Eq. (3)) at its inflection point (Eq. (11)) is obtained by substituting Eq. (11) into Eq. (6), which yields:

S_{h} = - (\hat{α}) (\hat{n} - 1) (W_{s} - {\hat{W}}_{r}) {(\hat{m})}^{\hat{m}} {(1 + \hat{m})}^{- \hat{m} - 1}

(14)

Similarly, the slope, S_ln(h), from function f (Eq. (4)) at its inflection point (Eq. (12)), is obtained by substituting Eq. (12) into Eq. (7):

S_{\ln (h)} = - (\hat{α}) ({\hat{n}}_{1} - 1) (W_{s} - {\hat{W}}_{r 1}) {({\hat{m}}_{1})}^{{\hat{m}}_{1}} {(1 + {\hat{m}}_{1})}^{- {\hat{m}}_{1} - 1}

(15)

The slope, S_log(h), from function k (Eq. (5)) at its inflection point (Eq. (13)) is obtained by introducing Eq. (13) into Eq. (8):

S_{\log (h)} = - ({\hat{α}}_{2}) (\hat{n} - 1) (W_{s} - {\hat{W}}_{r 1}) {({\hat{m}}_{1})}^{{\hat{m}}_{1}} {(1 + {\hat{m}}_{1})}^{- {\hat{m}}_{1} - 1}

(16)

3 Application to a case study

3.1 The soil and methods used

The equations developed in this study were applied to samples from a cultivated soil where compacted layers were identified (Balbino et al., 2002). The soil studied was a clayey Oxisol (Typic Acrustox) (Soil Survey Staff, 1998), a Latossolo Vermelho according to the Brazilian Soil Classification (Santos et al., 2006) and a Ferralsol according to the IUSS-WRB (2006) soil classification. It was located on a private farm (latitude 16.493246 S, longitude 49.310337 W, and altitude 776 m), near the Embrapa Arroz e Feijão Agricultural Research Center, at Santo Antônio de Goiás, GO, Brazil. The native vegetation was a typical Cerrado until 1985. After clearing the land, the soil was occupied by annual crops with conventional tillage for two years and then by a pasture of Brachiaria decumbens cv. Basilisk stapf. The soil was managed according to intensive animal grazing without any addition of fertilizer. This management led to a compaction of the topsoil. In 2006, soil cores were collected with stainless steel 100 cm³ cylinders (diameter = 5.1 cm, height = 5.0 cm) in the compacted 0–5 cm and non-compacted 70–75 cm layers (Table 1). The higher bulk density found in the 0–5 cm layer is accounted for soil compaction since under native vegetation, this type of soil exhibits a uniform bulk density profile according to depth, with bulk density close to 1.0 g cm⁻³ (Balbino et al., 2002; Volland-Tuduri et al., 2005).

Soil	Particle size distribution^a	Organic carbon^a	Bulk density^b
Clay	Silt	Sand
Compacted	485	71	444	0.70	1.27
Non-compacted	549	72	380	0.16	1.03

^a g kg⁻¹.

^b g cm⁻³.

Gravimetric water contents (W in g g⁻¹) at −10, −30, −60, −100, −330, −800, −4000, −10 000, and −15 000 hPa were determined in triplicate for the two layers studied (Table 2) using the centrifuge method (Reatto et al., 2008; Silva et al., 2006). An SWRC was fitted using the van Genuchten equation (van Genuchten, 1980) (see Eq. (2)) to the different water contents measured for the compacted and non-compacted layers, using h, ln(h) or log(h) as independent variable. The Solver routine embedded in Microsoft Excel was used to obtain the fitting parameters ${\hat{W}}_{r}$ , $\hat{α}$ , $\hat{n}$ , and $\hat{m}$ (Table 3). During the fitting process, W_s was taken as the mean value of the three saturated water contents measured (Reatto et al., 2008): 0.367 g g⁻¹ and 0.544 g g⁻¹ for the compacted and non-compacted layer, respectively, and therefore was not adjusted.

Suction (hPa)	W – Compacted layer	W – Non-compacted layer
	Replicate 1	Replicate 2	Replicate 3	Replicate 1	Replicate 2	Replicate 3
0	0.366	0.356	0.380	0.558	0.549	0.523
10	0.356	0.346	0.355	0.540	0.542	0.516
30	0.332	0.324	0.306	0.456	0.455	0.432
60	0.297	0.290	0.281	0.337	0.360	0.333
100	0.277	0.287	0.271	0.287	0.278	0.277
330	0.237	0.242	0.237	0.240	0.231	0.227
800	0.222	0.230	0.226	0.218	0.213	0.214
4000	0.199	0.206	0.204	0.201	0.195	0.195
10 000	0.185	0.190	0.190	0.193	0.184	0.187
15 000	0.178	0.180	0.181	0.182	0.176	0.175

Variables	Independent variable^h			Dexter (2004a)
	h	ln(h)	log(h)
	C	NC	C	NC	C	NC	C	NC
W_s(g g⁻¹)	0.367 ± 0.012	0.544 ± 0.018	0.367 ± 0.012	0.544 ± 0.018	0.367 ± 0.012	0.544 ± 0.018	0.367 ± 0.012	0.544 ± 0.018
W_r (g g⁻¹)	0.160 ± 0.010	0.192 ± 0.004	0.147 ± 0.012	0.188 ± 0.004	0.147 ± 0.012	0.188 ± 0.006	0.147 ± 0.010	0.188 ± 0.004
n ^a	1.314 ± 0.045	2.057 ± 0.088	3.182 ± 0.254	6.396 ± 0.364	3.182 ± 0.254	6.396 ± 0.364	3.182 ± 0.045	6.396 ± 0.088
α ^b	0.057 ± 0.009	0.032 ± 0.002	0.227 ± 0.006	0.263 ± 0.003	0.524 ± 0.013	0.606 ± 0.008
m ^a	0.239 ± 0.025	0.514 ± 0.020	0.686 ± 0.023	0.844 ± 0.008	0.686 ± 0.023	0.844 ± 0.008	0.686± 0.025	0.844 ± 0.020
Suction at the inflection point^c	5.876	22.421	3.948	3.699	1.696	1.606	1.715	1.632
Slope at the inflection point^d	0.0020	0.0046	0.035	0.142	0.0805	0.3261	0.0816	0.329
Equivalent pore diameter at the inflection point^e	510	134	60	74	60	74	58	70
Water content at the inflection point^f	0.300	0.394	0.266	0.373	0.266	0.365	0.266	0.365
RMSE^g	0.0065	0.0114	0.0065	0.0106	0.0065	0.0106	0.0065	0.0114
R²	0.987	0.991	0.988	0.992	0.988	0.992	0.987	0.988

^a Dimensionless.

^b Units in hPa⁻¹ for h; ln hPa⁻¹for ln h; and log hPa⁻¹ for log h.

^c Units in hPa for h; ln hPa for ln h; and log hPa for log h.

^d Units for S_h (g g⁻¹ hPa⁻¹); S_{ln h} (g g⁻¹ ln hPa⁻¹); or S_{log h} (g g⁻¹ log hPa⁻¹).

^e Unit in μm.

^f ^g $R M S E = \sqrt{\frac{1}{N} \sum_{i = 1}^{N} {({\hat{W}}_{i} - W_{i})}^{2}} in g g^{- 1} .$

^h The standard errors for W_s were calculated directly from the measured values. Those for W_r, n, α, and m originated from the analysis of variance of errors due to regression when fitting these parameters.

3.2 Comparison of the different S-index values obtained

At this point, it should be remembered that Dexter and Bird (2001) and Dexter (2004a) derived the S-index formulation from the slope of SWRC plotted in an ln scale, and the result was transformed to a log scale by multiplying it by ln 10; this log scale was then used afterwards. In order to compare and discuss the location of the inflection point according to the independent variable used, we applied the equations developed here and those of Dexter and Bird (2001) and Dexter (2004a) to water retention properties found for compacted and non-compacted soils (Table 2).

The S-index computed using Eq. (1) and multiplied by ln 10 according to Dexter (2004a) was 0.082 and 0.329 for the compacted and non-compacted soils. Using Eq. (16), the slope at the inflection point of the SWRC expressed according to log(h) as independent variable was 0.081 and 0.326 for the compacted and non-compacted soils. These values are very close to the S-index computed as described by Dexter (2004a). Thus, using an equation of W fitted with h as independent variable and plotted with log(h) as abscissa, or an equation of W fitted with log(h) as independent variable and plotted according to log(h), the slopes of the two curves at the inflection point are very similar. This could be expected since the experimental points remain at the same place in the W – log(h) graph regardless of the independent variable used for the equation to describe the SWRC. Consequently, the slope at the inflection point of the SWRC computed according to Dexter (2004a) to lead to the S-index and used by many authors would have been similar using Eq. (16) instead of Eq. (1).

On the other hand, the location of the inflection point of the curve of W vs. h, and the slope of the curve at this point, have more physical meaning than the corresponding values computed by Dexter (2004a). The value of h at the inflection point can be considered as the “breakthrough” matrix potential at which air penetrates throughout the soil as discussed by White et al. (1972) and Dullien (1992). The slopes at the inflection point of the SWRC using Eq. (14) (using h as independent variable) were 0.0020 and 0.0046 for the compacted and non-compacted soil. These values are 41 and 72 times smaller than the corresponding S-index values (Table 3). Suction at the corresponding inflection point using Eq. (11) was 6 and 22 hPa for the compacted and non-compacted soil, while according to Dexter (2004a) it was 52 and 43 hPa (Table 3).

Using Jurin's law (Bruand and Prost, 1987), we computed the equivalent pore diameter corresponding to the suction at the inflection point of the SWRC (Table 3). The results showed a close equivalent pore diameter for compacted and non-compacted soil at the inflection point when the SWRC was plotted with ln(h) or log(h) as independent variable (60 and 74 μm) and according to Dexter (2004a) (58 and 70 μm). On the other hand, the equivalent pore diameter at the inflection point of the SWRC was about four times higher for compacted soil (510 μm) than for the non-compacted soil (134 μm) when the SWRC was plotted with h as independent variable (Table 3).

In contrast to what is indicated by the S-index, however, air would penetrate throughout the soil at a smaller suction, and consequently for a larger equivalent pore diameter for compacted than for non-compacted soil. This result may appear surprising since compaction leads to smaller porosity with a shift of the inflection point on the SWRC to larger suction (Bruand and Cousin, 1995; Cui et al., 2010; Richard et al., 2001). The effects of compaction on pore geometry are difficult to understand since they depend on the structure and related pore types prior to compaction, on soil composition and water content, and on the intensity of compaction.

Beneath native vegetation, the soil studied had a weak macrostructure and a pronounced granular structure at the micrometer scale (Balbino et al., 2002; Volland-Tuduri et al., 2005). Since the structure of non-compacted soil is considered as similar to the structure under native vegetation, its theoretical SWRC would be a bimodal curve with two inflection points:

• the first inflection point would correspond to pore draining resulting from the assemblage of the micro-aggregates and occurring for a very low suction of several hPa such as for coarse sandy soils;
• the second corresponding to pore draining resulting from the assemblage of elementary particles in micro-aggregates and occurring for values of several hundred hPa. Because of the difficulty to correctly measure water retention of the soils studied at several hPa, the second inflection point is the only one that is usually measured (Balbino et al., 2002).

When soil is compacted, the pores resulting from the assemblage of micro-aggregates are transformed into smaller pores (Bruand and Cousin, 1995; Richard et al., 2001). The resulting SWRC contains one inflection point, which is related to a continuous distribution of equivalent pore diameters from the smaller pores, which were distorted by compaction into those resulting from the assemblage of the elementary particles in micro-aggregates. Fig. 1, based on the results of several studies on similar soils (Balbino et al., 2001; Volland-Tuduri et al., 2004, 2005), illustrates how using such a transformation of porosity makes it possible to pass from a SWRC with a given inflection point and its related equivalent pore diameter for a non-compacted soil, to another SWRC with an inflection corresponding to a larger equivalent pore diameter for compacted soil.

Fig. 1
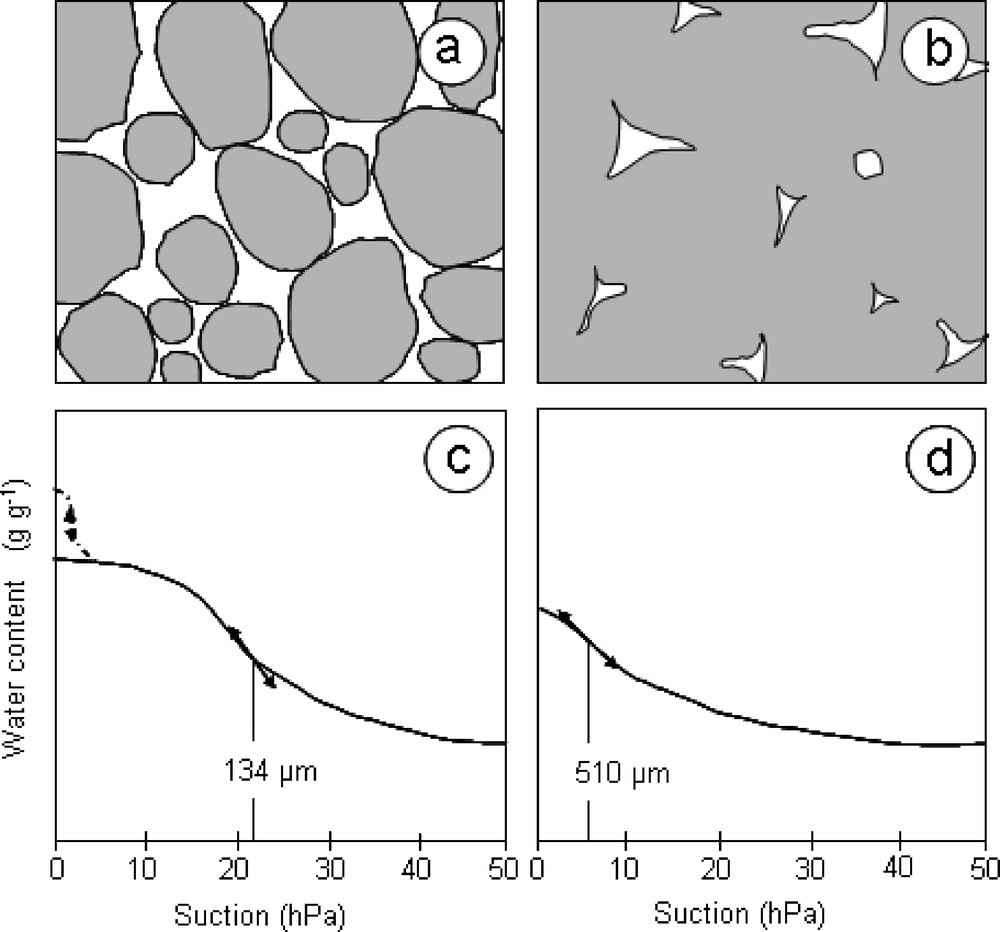
Schematic representation of the structure of the non-compacted (a) and compacted soil (b), and soil water retention curve corresponding to the non-compacted soil (c) with the part of the curve related to the pores resulting from the assemblage of the micro-aggregates (in white in (a) and dashed curve in (c)) which was not measured, and the soil water retention curve of the compacted soil (d) with the value of the equivalent pore diameter in μm at the inflection point.
Représentation schématique de la structure du sol non compacté (a) et compacté (b), de la courbe de rétention en eau du sol correspondant au sol non compacté (c), avec la partie de la courbe liée aux pores résultant de l’assemblage de micro-agrégats (en blanc dans (a) et courbe en pointillés dans (c)) qui n’a pas été mesurée, et la courbe de rétention en eau du sol correspondant au sol compacté (d), avec la valeur du diamètre équivalent des pores, en microns, au point d’inflexion.

Finally, our results question the value of S as a possible index to determine the physical quality of soil. The values of h at the inflection point determined for compacted and non-compacted soil are low, thus corresponding to a water content close to saturation which should not be optimal for soil tillage.

4 Conclusion

Our results show that the expression of the SWRC according to ln(h) or log(h) instead of h as independent variable leads to different values of the S-index. Computing the S-index when the SWRC is expressed with h as independent variable is both mathematically and physically consistent. We also show that independently of the consistency of the approach, the discussion of the physical properties of the soil can thus be limited according to the independent variable used. For the soil selected, our results in fact show that calculation of the S-index when it is expressed with h as independent variable significantly increases the relevance of the analysis compared to the range of the S-indices when it is expressed as proposed by Dexter (2004a). Further work will aim at determining in which proportion the S-index is affected for a large range of soils and verifying if the use of h as independent variable effectively increases sensitivity of the analysis.

Acknowledgments

This research is part of the project Embrapa Cerrados-IRD, No. 0203205 (Mapping of the Biome Cerrado Landscape and Functioning of Representative Soils). This work was supported by a grant awarded to G.G. Santos by the CNPq (Conselho Nacional de Desenvolvimento Científico e Tecnológico, Brazil)

Bibliographie

[Balbino et al., 2002] L.C. Balbino; A. Bruand; M. Brossard; M. Grimaldi; M. Hajnos; M.F. Guimarães Changes in porosity and microagregation in clayey Ferralsols of the Brazilian Cerrado on clearing for pasture, Eur. J. Soil Sci., Volume 53 (2002), pp. 219-230

[Balbino et al., 2001] L.C. Balbino; A. Bruand; M. Brossard; M.F. Guimarães Comportement de la phase argileuse lors de la dessiccation dans des Ferralsols microagrégés du Brésil : rôle de la microstructure et de la matière organique, C. R. Acad. Sci. Paris, Ser. IIa., Volume 332 (2001), pp. 673-680

[Bruand and Cousin, 1995] A. Bruand; I. Cousin Variation of textural porosity of a clay-loam soil during compaction, Eur. J. Soil Sci., Volume 46 (1995), pp. 377-385

[Bruand and Prost, 1987] A. Bruand; R. Prost Effect of water content on the fabric of a soil material: an experimental approach, J. Soil Sci., Volume 38 (1987), pp. 461-472

[Cousin et al., 2009] I. Cousin; A. Besson; H. Bourennane; C. Pasquier; B. Nicoullaud; D. King; G. Richard From spatial-continuous electrical resistivity measurements to the soil hydraulic functioning at the field scale, C. R. Geoscience, Volume 341 (2009), pp. 859-867

[Cui et al., 2010] K. Cui; P. Défossez; Y.J. Cui; G. Richard Soil compaction by wheeling : changes in soil suction caused by compression, Eur. J. Soil Sci., Volume 61 (2010) no. 61, pp. 599-608

[Dexter, 2004a] A.R. Dexter Soil physical quality: Part I, Theory, effects of soil texture density, and organic matter, and effects on root growth, Geoderma., Volume 120 (2004), pp. 201-214

[Dexter, 2004b] A.R. Dexter Soil physical quality: Part II, Friability, tillage, tilth and hard-setting, Geoderma., Volume 120 (2004), pp. 215-225

[Dexter, 2004c] A.R. Dexter Soil physical quality: Part III, Unsaturated hydraulic conductivity and general conclusions about S-theory, Geoderma., Volume 120 (2004), pp. 227-239

[Dexter and Bird, 2001] A.R. Dexter; N.R.A. Bird Methods for predicting the optimum and the range of soil water contents for tillage based on the water retention curve, Soil Till. Res., Volume 57 (2001), pp. 203-212

[Dexter et al., 2007] A.R. Dexter; E.A. Czyz et al. A method for prediction of soil penetration resistance, Soil Till. Res., Volume 93 (2007), pp. 412-419

[Dexter and Czyz, 2007] A.R. Dexter; E.A. Czyz Applications of S-theory in the study of soil physical degradation and its consequences, Land. Degrad. Dev., Volume 18 (2007), pp. 369-381

[Dexter and Richard, 2009] A.R. Dexter; G. Richard Tillage of soils in relation to their bi-modal pore-size distributions, Soil Till. Res., Volume 103 (2009), pp. 113-118

[Dexter et al., 2005] A.R. Dexter; E.A. Czyz; M. Birkas; E. Diaz-Pereira; E. Dumitru; R. Enache; H. Fleige; R. Horn; K. Rajkaj; D. de la Rosa; C. Simota SIDASS project Part 3, The optimum and the range of water content for tillage – further developments, Soil Till. Res., Volume 82 (2005), pp. 29-37

[Dullien, 1992] F.A.L. Dullien Porous media: fluid transport and pore structure, Academic Press, New York, 1992 (574 p)

[Frangi et al., 2009] J.-P. Frangi; D.-C. Richard; X. Chavanne; I. Bexi New in-situ techniques for the estimation of the dielectric properties and moisture content of soils, C. R. Geoscience, Volume 341 (2009), pp. 831-845

[Han et al., 2008] H. Han; D. Gimenez; A. Lilly Textural averages of saturated hydraulic conductivity predicted from water retention data, Geoderma., Volume 146 (2008), pp. 121-128

[IUSS-WRB, 2006] IUSS-WRB, 2006. World reference base for soil resources 2006: a framework for international classification, correlation and communication, 2nd ed. World Soil Resources Reports, 103, FAO, Roma, Italy, 145 p.

[Mualem, 1976] Y. Mualem A new model predicting the hydraulic conductivity of unsaturated porous media, Water. Resour. Res., Volume 12 (1976), pp. 513-522

[Reatto et al., 2008] A. Reatto; E.M. Silva; A. Bruand; E.S. Martins; J.E.F.W. Lima Validity of the centrifuge method for determining the water retention properties of tropical soils, Soil. Sci. Soc. Am. J., Volume 72 (2008), pp. 1547-1553

[Reynolds et al., 2002] W.D. Reynolds; B.T. Bowman; C.F. Drury; C.S. Tan; X. Lu Indicators of good soil physical quality: density and storage parameters, Geoderma, Volume 110 (2002), pp. 131-146

[Richard et al., 2001] G. Richard; I. Cousin; J.F. Sillon; A. Bruand; J. Guérif Effect of compaction on the porosity of a silty soil: consequences on unsaturated hydraulic properties, Eur. J. Soil Sci., Volume 52 (2001), pp. 49-58

[Santos et al., 2006] Sistema brasileiro de classificação de solos (H.G. Santos; P.K.T. Jacomine; L.H.C. Anjos; V.A. Oliveira; J.B. Oliveira; M.R. Coelho; J.F. Lumbreras; T.J.F. Cunha, eds.), Embrapa Solos, Rio de Janeiro, Brazil, 2006 (306 p)

[Silva et al., 2006] E.M. Silva; J.E.F.W. Lima; J.A. Azevedo; L.N. Rodrigues Valores de tensão na determinação da curva de retenção de água de solos do Cerrado, Pesq. Agropec. Bras., Volume 41 (2006), pp. 323-330

[Soil Survey Staff, 1998] Soil Survey Staff Keys to Soil Taxonomy, United States Department of Agriculture, Washington, USA, 1998 (326 p)

[Tormena et al., 2008] C.A. Tormena; A.P. Silva; S.D.C. Imhoff; A.R. Dexter Quantification of the soil physical quality of a tropical Oxisol using the S index, Sci. Agric., Volume 65 (2008), pp. 56-60

[van Genuchten, 1980] M.T. van Genuchten A closed-form equation for predicting the hydraulic conductivity of unsaturated soils, Soil Sci. Soc. Am. J., Volume 44 (1980), pp. 892-898

[Volland-Tuduri et al., 2004] N. Volland-Tuduri; M. Brossard; A. Bruand; H. Garreau Direct analysis of microaggregates shrinkage for drying: Application to microaggregates from a Brasilian clayey Ferralsol, C. R. Geoscience, Volume 336 (2004), pp. 1017-1024

[Volland-Tuduri et al., 2005] N. Volland-Tuduri; A. Bruand; M. Brossard; L.C. Balbino; M.I.L. Oliviera; E.S. Martins A relationship between mass proportion of microaggregates and bulk density in a Brazilian Clayey Oxisol, Soil. Sci. Soc. Am. J., Volume 69 (2005), pp. 1559-1564

[White et al., 1972] N.F. White; D.K. Sunada; H.R. Duke; A.T. Corey Boundary effects in desaturation of porous media, Soil. Sci., Volume 113 (1972), pp. 7-12

Commentaires - Politique

Ces articles pourraient vous intéresser

Modeling the soil–water retention curves while the soil is deforming

Eduardo Rojas; Hiram Arroyo; Jaime Horta; ...

C. R. Méca (2020)

Fully coupled hydromechanical model for compacted soils

Hiram Arroyo; Eduardo Rojas

C. R. Méca (2019)

Influence of suction cycles on the soil fabric of compacted swelling soil

Hossein Nowamooz; Farimah Masrouri

C. R. Géos (2010)