1 Introduction
Since the very beginning of tectonophysic studies in Russia, i.e., in about the second half of the 1950s, founders V.V. Beloussov (1954) and M.V. Gzovsky (1954a) formulated their goal: interpreting, from the physics point of view, the mechanism generating deformational structures in geological objects at different scales. Such deformational structural elements are, first of all, faults and folds, but also entail large deformational structures of the Earth's crust and sedimentary basins. Formation mechanisms comprise a large spectrum of physical parameters including rock properties, burial conditions, and stress fields, deformational and secondary small structural features which record the effect of deformation on the rocks.
These goals raised other fundamental problems: classification of, and research on, the various stress generation mechanisms in the lithosphere and rock mechanics. The large number of theoretical ideas concerning stress generation in the crust, such as the expanding or contracting Earth, the impact of Earth rotation, the vertical tectonics in geosynclines, the tectonics of oceanic lithospheric plates, etc. required developing special tectonophysic methods to study the stresses in rock massifs in natural conditions. M.V. Gzovsky made a great contribution developing tectonophysic modeling including laboratory experiments and mathematical solutions of boundary problems of the mechanics of tectonic processes. With respect to the genesis of stresses in the Earth, M.V. Gzovsky gave priority to field observational data obtained directly on natural objects (Gzovsky, 1954b). Our brief review will concentrate on two main topics: tectonophysic modeling and field methods for evaluating natural stresses.
2 Tectonophysic centers in Russia and the former USSR
Several large tectonophysics centers were created in the former USSR from the 1950s to the 1970s. The first tectonophysics laboratories were established in Moscow: in 1958 by V.V. Beloussov (whose head is presently M.A. Goncharov) in the Moscow State University (MSU), and in 1968 in the Institute of Physics of the Earth (IPE) by M.V. Gzovsky, replaced in 1974 by D.N. Osokina; its head is now Yu.L. Rebetsky. Tectonophysics laboratories were founded somewhat later by S.I. Sherman in the Institute of Earth's Crust in Irkutsk (its head now is K.Zh. Seminsky), by V.G. Guterman in the Institute of Geophysics in Kiev (now headed by Ya.I. Khazan), and I.V. Luchitsky in the Institute of Geology and Geophysics of RAS Siberian branch in Novosibirsk, where the laboratory of Structural Geology and Experimental Tectonophysics is now closed. In addition to these large centers in Russia, there are also smaller groups and individual researchers using tectonophysical methods: first of all, the group of physical experiment of structures at the lithosphere scale, e.g., modeling of subduction and rift regions, in the Geological Museum of MSU headed by A.I. Сhemenda; A.V. Lukyanov's group in the Geological Institute, which uses analogue modeling; A.N. Bokun's group in L’vov Geophysical Institute, using wet clays in modeling; Sh.D. Fatkhullaev, R.A. Umurzakov of the geological group in the Tashkent Geological Institute; and the geological group headed by E.I. Patalakha in the Geological Institute in Alma-Ata, developing mostly methods of deformational structures in field studies.
The common feature of most of these tectonophysics laboratories was the use of physical and mechanical modeling to study natural geological objects. Evaluation methods of natural stress state parameters, based on analysis of sets of faults, were intensively developed in the IPE, besides physical and mathematical modeling. In the MSU, methods of structural geology were largely used in addition to physical modeling when studying folds and flow structures. In the tectonophysics laboratory founded by S.I. Sherman in 1978 in the Institute of the Earth's Crust (IEC), the main study objects are large faults in the Earth's crust. Consequently, studies aiming at identifying the mechanical laws controlling fault zone development were attempted there.
3 Theoretical and experimental basis of modern tectonophysics
Results of experimental geomechanics (Byerlee, 1967, 1978; Mogi, 1964; Stavrogin and Protosenia, 1992) and use of modern apparatus of fault mechanics studies (Cherepanov, 1974; Panasuk, 1968) allowed one to understand in the 1970–1980s the main factors controlling brittle deformation and spacing during crack and fault development. The experiments proved the determining role of fluid pressure in rock pores (Rummel et al., 1978; Terzaghi, 1943) on the amount of deviatoric stresses that the rock can stand without undergoing brittle fracturing. The criterion of brittle fracturing is the Coulomb criterion, which takes into account the fluid pressure. It is found that when the ratio of deviatoric stresses to effective pressure in the rocks of the middle and upper crust reaches a certain value, then cataclastic flow occurs, involving cracks of macro and mega sizes, similar to plastic flow. From the mechanical point of view, the best models describing the deformation of fractured rocks are the Coulomb–Mohr and Drucker–Prager plastic bodies, which define as critical certain relationships between isotropic (i.e., pressure) and deviatoric components of the stress tensor. Cataclastic flow not only defines the instant reaction of rocks over the critical loading by formation of crack deformation, but also the slow creeping deformation, which is reflected by an increase of irreversible deformation due to the decrease of internal cohesion in rocks, i.e., the long-term stiffness. The characteristic feature of the cataclastic creeping is the dependence of the effective viscosity on Coulomb stresses, which makes the complete relaxation of deviatoric stresses impossible.
The deformation behavior of the upper crust, i.e., the first 10–15 km where the confining pressure is not yet large enough, is mostly conditioned by fault-and-block structure. Here, away from faults, viscosity in crystalline rocks is practically lacking (diffuse viscosity) due to the low level of deviatoric stresses, which are much lower than the elasticity limit, i.e., yielding. Viscosity in the fault zones is linked both to cataclastic flow and crystals and grains size decrease as in mylonite. The density of cracks grows as their size decreases with depth. Faults form narrow zones even when developed over large areas. Cataclastic flow in folded orogenic belts involves a great part of the middle crust. Because the lithostatic pressure is high in the lower crust, large cracks cannot exist for a long time there. Cataclastic flow in the lower crust is effected mainly through intragrain sliding planes. Regeneration of grains and crystals plays a great role in ductile and viscous flows like those which exist in the upper crustal fault zones. Increasing temperature and fluid pressure can locally initiate the mechanism of re-crystallization plasticity (Vernon, 1976). The real plasticity, i.e., ductility, due to dislocations in crystals possibly occurs below Moho (Nikolaevsky, 1979). Confining pressure in the upper mantle has only a small impact on rock flow, and the Mises's plastic body well describes the boundary state and deformation behavior.
Relationship between stress state and rock rheology in the crust and the lithosphere can be demonstrated on Mohr's diagram (Fig. 1). This figure shows how the stress ratio can be used to predict the occurrence of new ruptures and reactivation of preexisting features (the zone of a cataclastic flow). The domain of high level of isotrope pressure at low and middle levels of deviatoric stresses is a domain of plastic compaction. The area of a quasiplastic flow is also outlined in this figure. Here rocks which are dominantly in mylonite conditions record large irreversible deformations with high level deviatoric stresses at high level of isotropic pressure. Plastic strength limit can appear in the middle and lower crust where the increase in isotropic pressure is accompanied by a temperature increase. The bending of curvilinear boundary and friction line (dashed line) for the high level of deviatoric stresses is also connected with a decrease of the brittle strength because of a rise in temperature in the lowermost part of the crust. Below the ductile lower crust and the Moho, hardening is observed in the upper mantle, probably resulting from an increasing level of the deviatoric stresses.

Diagram of rock deformation regimes in Mohr's parametric space, i.e., the maximum shear stress and isotropic pressure, explaining interrelation of level of deviatoric and isotropic stresses with mechanisms of energy dissipation of elastic deformations.
Diagramme des régimes de déformation des roches dans l’espace paramétrique de Mohr, c’est-à-dire le maximum de contrainte de cisaillement et de pression isotrope expliquant l’inter-relation entre le niveau de contraintes isotropes et de déviation et les mécanismes de dissipation d’énergie des déformations élastiques.
4 Tectonophysic modeling
D.N. Osokina (IPE RAS, Moscow) collected data on stress distribution in vicinities of 2D plane shear crack with friction, first through experiments using optical active elastic materials (Osokina et al., 1960, 1979) then by analytical modeling (Osokina, 1988, 2000). His studies were an essential step forward in stress state knowledge in the vicinity of shear cracks after they are generated or activated, compared with well-known works by M.A. Chinnery (1963). D.N. Osokina (Osokina and Fridman, 1987) found important rules controlling stress state near cracks, which are now widely used by geologists and mining engineers when studying natural objects. First of all, a sharp change in the orientation of principal stress axes is observed when moving toward the tip of the crack, so that orientation of the principal stresses in adjacent sides becomes practically opposite, causing there generation of secondary faults of diverse morphology. Conjugate sectors of local maximum and minimum confining pressures occur at crack tips. Zones of low intensity of maximal shear stress are formed near the middle part of the crack whereas maximum values of this parameter are generated at crack tip. Depending on the angle of the maximum compression axis, the inclination of the initial (before crack activation) homogeneous stress field can be symmetrical (at 45°) to crack plane or be shifted toward the axis of maximal compression at various angles.
Research is now carried out in the IPE laboratory of tectonophysics by A.S. Lermontova (Rebetskii and Lermontova, 2010), who studied the modes of interaction among many shear cracks, by expanding the analytical approximation of crack mechanical problem. The advantage of the approximation used (Rebetsky et al., 2002) rests in the simplicity when solving the problem for a set of frictional shear cracks. A system of linear algebric equations for average stress drop values is solved here at each crack, instead of solving a system of integral equations for dislocation discontinuity (a classic solution for mechanical problems).
In the IPE tectonophysics laboratory, physical modeling of the Earth's crust deformation structures was based not only on elastic optical models and analytical methods of stress analysis (Grigoryev et al., 1988; Pogorelov et al., 2010; Rebetsky, 1988), but also on experiments using wet clays (Gzovsky and Chertkova, 1953; Mikhailova, 1989). Stress laws and strain distribution in sedimentary blanket over faults with various kinematics, e.g., thrust, normal fault, strike-slip fault and their combination, in a crystalline basement were evidenced during these experiments.
V.G. Guterman (1987) should be referenced, when presenting the results of tectonophysics groups using physical modeling of tectonic processes. V.G. Guterman used centrifuges, which make it possible for low viscous materials to model cases when gravitational forces play the main role (Ramberg, 1967). He developed unique models not only for sedimentary basins, but also for regional seismoactive structures, such as the Kuril–Kamchatka subduction zone. The Russian school of analogue modeling is also famous thanks to A.I. Chemenda, who studied deformation mechanism in subduction and rift zones (Shemenda, 1994; Shemenda and Groholskyi, 1986). He conducted experiments using low elastic modulus plastic materials, such as silicone putty and gels. Afterwards A.I. Chemenda left for Montpellier University, and then to Nice Univ.-Geo-Azur at Sophia-Antipolis in France, whereas his colleagues and students continued carrying out their researches in the MSU Geological Museum (Dubinin et al., 1999) using the special facilities he had built.
S.A. Borniakov (1980) and K.Zh. Seminsky (1986) in the IEC, after numerous physical experiments on wet clays, identified the laws controlling brittle structures in fault zones. Three formation stages were recognized: (1) an initial stage when small individual cracks are generated and spaced with a certain periodicity, but far from each other; (2) an intermediate stage when the crack density sharply increases and the cracks merge together; (3) a final stage, which is characterized by the localization of the deformation zones and the formation of the main crack. Based on laboratory and field studies, the term “zone of rupture dynamic impact” (Sherman et al., 1983) was suggested. It defines the area of the rupture impact on the nearest geological structures through a perturbation of stress state caused by the rupture. This group has always focused his studies on the Baikal rift and several physical experiments were devoted to its formation peculiarities (Logachev et al., 2000).
A.N. Bokun (2009) conducted highest quality and detailed physical experiments on plastic materials such as wet clays, sand, carborundum and oil. He separately studied the model material properties for each analogical experiment, allowing to understand the operating mechanism, and to define differences in modeling results under the same loading conditions (Fig. 2).

The material used for the experiment is made up of carborundum 70%, and oil 30%. a: rheological curve , b: photograph of model surface, system R and R’ ruptures; R’ ruptures are rotated during the deformation (Bokun, 2009).
Le matériau utilisé pour l’expérience est composé de 70 % de carborandum et de 30 % de pétrole. a : courbe rhéologique . b : photographie de la surface du modèle, système R et ruptures R’; on observe une rotation des ruptures R’ au cours de la déformation (Bokun, 2009).
5 On the role of numerical simulations in modern tectonophysics
The capabilities of physical experiments are limited because it is hard to maintain the similarity of the gravitational stress state (Rebetsky and Mikhailova, 2011), which requires the Poisson elastic coefficient to be the same in the model and in nature. The impossibility of satisfying this requirement for wet clays and different kinds of analogue materials often used in modelling, leads to the violation of similarity for the deviatoric component of the initial gravitational stress state (Rebetskii, 2008; Rebetsky, 2008). Reconstruction in tectonophysic experiments of a gravitational stress state similar to the natural one is crucial when studying the morphology of brittle failure and transcritical deformation. As it is known from the mechanics of elasto-plastic media, the final stress and strain state depends on the path of the loading process; therefore ignoring deviatoric component of initial stress state can deeply affect the result, the final stress state. Mechanism of formation of strike and shear failure structures above crystalline basement fault is discussed in Rebetsky and Mikhailova (2011), and takes into account the initial gravitational stress state and the deviatory component.
All the above discussion highlights the importance of numerical methods using finite-element and finite-difference calculation schemes. Modern numerical modeling methods make it possible to correctly maintain similarity conditions and to adequately take into account heterogeneities of rheological and mechanical properties of real rocks, which is practically impossible to handle by means of analogue modeling. Numerical modeling also allows inferring areas of large plastic deformation, lines and surfaces of localized strain and brittle failure cracks. To illustrate the capabilities of modern numerical modeling methods developing now in Russia (Makarov, 2007, 2008; Stefanov, 2002a, 2002b) we mention results of numerical calculations for shear fracture zones (Fig. 3). Initial loading in the calculations corresponded to homogeneous stress state and homogeneous properties of model material in which initial defects were absent. The resulting plastic deformation is localized in en echelon zones of large plastic deformations, i.e., localized strain line, which corresponds to the results of experiments with rocks (Rutter and Newmann, 1995). Recent knowledge on plastic and brittle failure is used in calculation algorithms and summarized on the diagram of Fig. 1.

Results of numerical calculations for homogeneous initial horizontal shear (Stefanov, 2002a, b). High intensity of shear deformations is locally observed.
Résultats des calculs numériques pour un cisaillement horizontal initial homogène (Stefanov, 2002a, b). Une forte intensité de déformations cisaillantes est localement observée.
6 Natural stress and deformation study methods
After M.V. Gzovsky's work, methods of stress and deformation reconstruction in nature were intensively developed in Russia based on discontinuous displacement data. Following historical chronology, one should first of all mention the methods of structural analysis of cracks: conjugate pairs of shear fractures by M.V. Gzovsky (1954b); fracture belts by V.N. Danilovich (1961) further developed by S.I. Sherman (1966); tectono-dynamic analysis of crack families by P.N. Nikolaev (1977); quasi-principal stresses by V.D. Parfenov (1981); microtectonic analysis of brittle structures by L.M. Rastvetaev (1987); morpho-kinematic analysis by O.B. Gintov (Gintov and Isai, 1984); structural-morphological analysis of fractures by L.A. Sim (1996); cross-cutting relationships of cracks by K.Zh. Seminsky (2002). All these methods were developed to replace that based on the erroneous hypothesis of G.F. Becker (1893), according to which the fault plane coincides with the circular section plane of the stress ellipsoid. Algorithms for determining the principal stress plane orientation were developed in the structural analysis methods, using experimental results on rock failure under uniaxial loading and in conditions of localized slip (e.g., experiments by H. Cloos, W. Riedel, etc.), which generated a given fracture. All these methods aimed at analysing geological data on fractures and faults formed in the vicinity of shear fracture plane. A.V. Vvedenskaya (1969) proposed a method of analysis of principal stress axis based on seismological data of earthquake source mechanisms. The method is based on the hypothesis that nodal planes coincide with conjugate planes of maximal shear stresses. Later it was demonstrated (Kostrov, 1975; Kostrov and Das, 1988) that this hypothesis does not satisfy the nature of brittle failure in rocks. The failure occurs, first of all, over planes oriented close to the internal friction plane (Obert, 1976). Note that L.-M. Zobak (1992), studying the largest earthquakes worldwide, uses an approach similar to that of A.V. Vvedenskaya. It should also be noted that M.V. Gzovsky's and E.M. Anderson's (Anderson, 1951) methods are similar. V.N. Danilovich's graphic method after development by S.I. Sherman is close to F. Arthaud's (1969) method of M-planes. Later V.D. Parfenov's method was also applied by Zhonghuai and collaborators (Zhonghuai et al., 1992).
The above-mentioned methods were based on brittle failure mechanics when developing algorithms of stress reconstruction. The methods developed thereafter used principles of plasticity mechanics, in particular the Batdorf–Budiansky's plasticity theory (Batdorf and Budiansky, 1949). Among such methods we can mention O.I. Gushchenko's kinematic analysis method of shear fracture families (Gustchenko, 1975), and S.L. Unga's method (Nikitin and Unga, 1978). These methods postulated the coincidence of the fault side slip direction with the shear stress direction on the fracture plane. Graphic (Gustchenko, 1979) and numerical (Nikitin and Unga, 1978) algorithms for calculating the principal stresses and evaluating the Lode–Nadai coefficient, determining the shape of the stress ellipsoid and the ratio of deviatoric components of principal stresses were developed on this assumption. In western Europe and USA, methods based on similar approaches were developed simultaneously, e.g. the postulate by R.E. Wallace (1951) and M.H.P. Bott (1959), and the methods of E. Carey (Carey and Brunier, 1974), J. Angelier (1975) (shear fracture inversion), Z. Reches (1983), J. Gephart (Gephart and Forsyth, 1984), A. Etchécopar (Etchécopar et al., 1981), R. Lisle (1987), A. Michael (1984). Yu.V. Riznichenko (1965, 1978), V.V. Stepanov (1979), S.L. Unga (Lukk and Unga, 1988; Unga, 1979) developed another line of approach based on the plasticity theory and aimed at assessing the irreversible faulting strain. Numerical algorithms were developed for calculating the principal axis and the Lode–Nadai coefficient of tensor increment of seismotectonic strains (deformations), generated because of dislocations along a set of shear faults. Simultaneously, J. Brune (1968) started research along the same line. The calculations in all the above-mentioned studies were based on seismological data on earthquake source mechanisms.
The most prospective method is now considered to be the method of cataclastic analysis of discontinuity dislocation (MCA) (Rebetsky, 1997, 1999, 2001, 2007, 2009, in press; Rebetskii, 2003, 2009; Rebetskii et al., 2001), which is developed in the tectonophysics laboratory in IPE. This method integrates the main principles for calculating stress parameters and irreversible deformations, and follows the plasticity theory. The method consists of four stages of reconstruction, and consequently assesses components of both complete stress and normalized tensors of seismotectonic strain increment. The method is based on energy preservation principles of the plasticity theory, which is used to assess stress tensor components, maximizing dissipation of internal elastic energy of the seismotectonic strain tensor. It requires simultaneous calculations of the stress tensor and of the irreversible strains, which was indeed missing in all the above-mentioned methods.
The possibility, with this method, to assess not only the orientation of the principal stress axis but also the stress magnitudes, is based on earthquake source mechanisms in addition to seismological data on stress-drop, geophysical data on topography and Earth's crust density together with general principles of geomechanics and theory of brittle failure.
Notice that the inter-dependence of deviatoric stresses and the effective confining pressure at shear fracture, which proceed from geomechanic experiments, were assumed in Angelier (1989), Govers et al. (1992), Michael (1984), and Reches (1983). When evaluating stresses, J. Hardebeck (Hardebeck and Hauksson, 2001) used additional seismological data on stress-drop in the source of the 1992 Landers earthquake. His assumption, that the vertical stresses are equal to the weight of the rock column used firstly by R.H. Sibson (1974), was also the basic assumption for evaluating the critical level of deviatoric stresses in the crust (Cloethingh and Burov, 1996; Govers et al., 1992).
The method discussed in Angelier (1989) is the closest to the MCA, which uses geological data on striation angles. The difference between the MCA's and J. Angelier's methods rests in the algorithm for assessing the cohesion strength in rocks, using data on stress drop, as well as the rejection of the postulate on hydrostatic law of fluid pressure distribution with depth. Note, that the latter hypothesis was used also in (Cloethingh and Burov, 1996; Govers et al., 1992; Sibson, 1974). Therefore, the MCA incorporates most of the previous algorithms linking them in one unique algorithm on the basis of the main principles of failure mechanics and the plasticity theory.
7 Achievements in natural stress studies
The methods of calculation of stress ellipsoid and assessment of seismotectonic strain increment played a very important role in evaluating both seismological and geological data on discontinuous displacement interpretation. The principal stress axis and the seismotectonic strain increment orientation make it possible to describe active tectonic provinces according to stress-state regime including the horizontal pressure or tension, the horizontal slip and the combination of both regimes. The data together with the ratio of stress tensor deviatoric components, i.e., the Lode–Nadai coefficient, were used when addressing tectonophysic modelling, when solving geodynamic problems for structures at different scales, and when solving practical tasks for mining and applied geology.
However, the most prospective results for geodynamic and applied geology problems were obtained after further development of reconstruction methods assessing stress magnitudes. Thus, assessment of average shear stresses in upper crust in the region of the Landers 1992 earthquake presented in Hardebeck and Hauksson (2001), resulted in values amounting to a few hundreds of bars. This result differs essentially from those values of tensor components reported in Cloethingh and Burov (1996), Govers et al. (1992), Sibson (1974) (a few kilobars at 10–15 km depth in the zones of horizontal pressure). Evaluation of stresses inferred through the MCA method for different seismically active regions (Rebetsky, 2007, 2009; Rebetskii and Marinin, 2006; Rebetsky and Marinin, 2006) demonstrated that a decrease of maximal shear stresses is due to an increased fluid pressure (Rebetsky, 2005; Rebetsky, 2006), which exceeds hydrostatic pressure.
Application of the MCA method for stress reconstruction in regions of catastrophic earthquakes allowed, for the first time, to observe peculiarities of tectonic stress distribution before a strong earthquake (Rebetskii and Marinin, 2006; Rebetsky and Marinin, 2006). Thus, for the Sumatra-Andaman earthquake of 2004 (Mw = 9.3), it was found that the region responsible for the rupture nucleation was located in the zone of maximum stress gradient, i.e., the bended sector along Sumatra (Fig. 4). A 400–500 km long low effective confining pressure p*, i.e., the tectonic pressure after subtraction of the fluid pressure, was located to the north, whereas a 300–400 km long area of maximal effective pressure was located to the south. Such stress distribution analysis from the geomechanics point of view shows that the brittle failure developed in regions characterized by high effective confining pressure. Most part of internal energy of elastic strain was used to overpass frictional forces over rupture (this energy was finally transformed in heating). On the other hand, brittle failure is developed most effectively in regions of low effective confining pressure. Strong earthquakes occur in regions of moderate to low level of effective pressure, in which, according to Coulomb's theory, maximal shear stresses are low. Note that J. Rice (1969) already predicted a higher efficiency of the brittle failure in zones of low deviatoric stresses. Such regularity allows to formulate criteria for detecting zones capable of generating anomalously large earthquakes in seismically active regions of Earth's crust (Rebetsky, 2001).
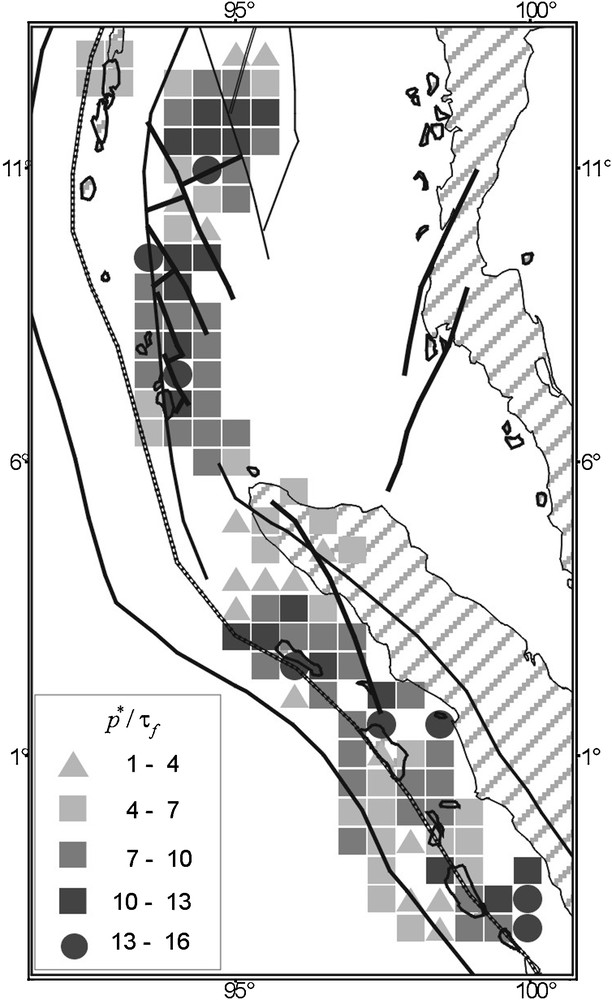
Distribution of relative effective isotropic pressure
Distribution de la pression isotrope effective relative
8 Remaining questions and perspective in tectonophysics
The analysis of only two directions in tectonophysic studies developed in the former USSR and Russia shows that an essential progress has been achieved in both directions. Laws of tectonic stress distribution have been derived from the study of natural objects supported by numerical modelling. These laws allow a new approach to solve other important tectonophysics problems.
Information on stress distribution in seismically active regions of the Earth's crust makes it possible to develop a physical theory of earthquake source from new standpoints. Efforts made on H.F. Reid's ideas (Reid, 1910), to build a concept considering an earthquake source zone as a zone of high deviatoric stresses, have failed. Experiments (Byerlee, 1967, 1978) demonstrated that when brittle failure of rocks occurs, the critical issue is not the stress, but stress state, i.e. certain relationship between deviatoric stress and confining pressure. Such a state is influenced by fluid pressure in rock pores, which creates zones favorable for brittle failure under low deviatoric stresses (Rebetskii, 2007; Rebetsky, 2007).
Natural stress reconstructions in intraplate orogens through MCA demonstrate the presence of many continental domains which are characterized by large intermountain valleys or depressions (Rebetsky, in press), and by horizontal tension where the maximum principal stress axis is sub-vertical. This observation corresponds with the data on in situ stress measurements (Brady and Bzown, 2004; Hast, 1969; Markov, 1977, 1984), which confirm that the zones of horizontal shortening correspond to crustal uplifts in intracontinental platform domains and intraplate orogens, and zones of horizontal stretching, which correspond to crustal subsidence. Such data on natural stress distribution requires a thorough revision of our understanding of the problem of high stresses in continents, which is usually related to the lateral push applied by the oceanic lithospheric plates in convergence zones. We are talking about a new stage in generation mechanism of stresses in the Earth's crust and the continental lithosphere. It is crucial to understand the relative impacts of deviatoric component of gravitation stress tensor, of the planetary stresses related to the Earth's rotation (Leibenzon, 1955; Stovas, 1975), and of the stresses due to plate tectonics (Bobrov and Trubitsyn, 2006; Trubitsyn, 2000; Trubitsyn and Rykov, 2000) on the overall stress state. Our studies demonstrate that the role of residual stresses generated by gravitational compaction was not correctly evaluated, and must be re-evaluated (Rebetskii, 2008; Rebetsky, 2008). The residual stresses in the upper crust last for up to tens and even hundreds of million years, and is best expressed in uplifted zones accompanied by erosion.
Another important problem is the genesis of rock flow in the middle and lower crust (Lisle, 1987; Luk’ianov, 1987), which generates periodicity of morphological structures (Ez, 1962; Leonov, 1993; Ollier, 1981). Manifestation of such structures in the crustal topography points towards certain similarities of their forming process with the process of mechanic stability loss. This problem is observed also in the genesis of some types of folds, as already mentioned by V.V. Beloussov (1958). Elastic contraction of rocks under gravitational stress conditions possibly influences greatly the instability process. Elastic contraction of rocks is usually ignored in comparison with irreversible deformations accumulated in the process of plastic flow. It is especially the case when calculating convection in the mantle. Rebetsky (2011) found that taking into account the elastic compaction of rocks together with their ability to flow determine a new type of rock instability, i.e., the instability of gravitational stress state. This form of instability is essentially linked to the denudation processes at the surface, and to deep processes contributing to maintaining the isostatic equilibrium. They are still waiting to be thoroughly analyzed. The new form of crustal instability identified here should be considered as another mechanism generating deviatoric stresses.
The study of crustal fault rheology should constitute a specific task. Faults must be assumed and modeled as a specific non-isometric medium characterized by its own set of natural phenomena and special inner structures (Chikov, 1992; Luk’ianov, 1987, 1991). It is probably not enough to study only fault plane structures, but it is necessary to also study in details the damaging of adjacent rock assemblages (Luk’ianova and Luk’ianova, 1987; Patalaha et al., 1987; Rebetsky, 2005), carefully taking into account stress distribution and metamorphic zonation. Laws of stress distribution observed in seismogenic zones of strong earthquakes should be used for this purpose (Rebetskii, 2007; Rebetskii and Marinin, 2006; Rebetsky and Marinin, 2006).


