1 Introduction
Characterizing the distribution of stress orientations and magnitudes in the crust is a major challenge in Earth Sciences. Motivation arises from applied purposes such as evaluation and mitigation of geological hazard, engineering activities and resource exploration, but also from academic purposes, such as understanding the mechanical behaviour of geological materials and deciphering tectonic mechanisms at various scales.
Stress is a concept of continuum mechanics; it is defined by the limit of the applied force divided by the area as the area goes to zero. Defining a stress tensor in a rock material requires theoretically that an elementary representative volume (ERV) may be identified, which is the smallest volume for which there is equivalence between the continuum material and the real rock, and which is the physical representation of the mathematical point. The ERV is sufficiently small for its mechanical properties to be considered homogeneous and constant. The local stress tensor is thus theoretically defined: at a point in a rock mass; and at a given, instantaneous time, in other words over a time span of virtually no duration.
Several techniques have been developed for measuring or estimating some or all of the component of the local stress tensor. These techniques rely upon different bases of measurement: fluid pressure for hydraulic fracturing, i.e., a quantity directly related to stress; geometry of finite deformation and/or reloading strains for borehole techniques; relief strains, evolution of relief strains, reloading strains, finite deformation state for techniques on cores; and seismic radiation for earthquakes. Theoretically, methods using hydraulic fractures, boreholes or rock cores all have the potential for the complete determination of the stress tensor from a set of measurements at a particular location but in practice this only applies when rock coring is undertaken. For a detailed review of techniques of stress measurements, see Amadei and Stephansson (1997); Cornet (1993); Engelder (1993); Harper and Szymanski (1991); Ljunggren et al. (2003). Noticeably, these various techniques do not yield the same information, so one may wonder whether the results obtained can really be compared.
On the other hand, methods of paleostress reconstructions based on mechanical interpretation of structural elements in natural rocks have been set out in order to decipher the past tectonic evolution. Most of them aim at determining the principal directions of the regional stress field from the analysis of the slip motions induced by this stress field on faults with various dip and strike (e.g., Angelier, 1975, 1984, 1990; Carey and Brunier, 1974; Delvaux and Sperner, 2003; Etchecopar et al., 1981; Gephart and Forsyth, 1984; Michael, 1984; Pfiffner and Burkhard, 1987). The orientation of the slip motion can be determined either from the direct observation of slickensides on faults or from the focal mechanisms of earthquakes. In these cases, the basic concept noticeably differs from that of a local stress tensor: for fault slip data inversion, the concept is instead that of a “mean (or common) paleostress tensor”, i.e., “averaged” over several thousands or even several millions years (the duration of a tectonic event) and over the rock volume investigated, assumed to be representative; for inversion of focal mechanisms of earthquakes, the concept is that of a “mean (or common) contemporary tensor”, i.e. “averaged” over a stress province within a tectonically active region.
Earth scientists determining contemporary stresses from in situ measurements or from earthquake focal mechanisms and those improving and using methods of paleostress reconstructions based on fault slip data do not seem to share similar underlying mechanical concepts. Despite few attempts at including paleostress determinations within recent rock formations in the compilation of the present-day global tectonic stress pattern (see Section 5), contemporary stress and paleostress determinations are generally carried out separately and results have rarely been critically compared (see Lacombe, 2007 for a comparison of paleostress and contemporary stress magnitudes). Only few studies have tried to compare the results of paleostress inversion in terms of orientations and regimes with contemporary stresses measured in situ or derived from earthquake focal mechanisms (e.g., Blenkinsop, 2006; Kao and Angelier, 2001; Lacombe et al., 2006; Shabanian et al., 2010). The ability of fault slip data inversion to yield a quantity that has a “paleostress meaning” has even been questioned (e.g., Twiss and Unruh, 1998): the debate on the dynamic vs the kinematic (e.g., Marrett and Allmendinger, 1990) interpretation of fault slip data is still open.
It is thus timely to summarize the state of the art in fault slip data inversions and their ability to yield a quantity – paleostresses – that can be compared with contemporary stresses. In this article, I do not intend to carry out a comparison of the results of stress measurements and paleostress reconstructions on a theoretical basis. I only aim at making a short point on our present knowledge about inversion of fault slip data, and at providing some clues for a suitable comparison of stresses and paleostresses in terms of orientations and distribution in time and space. As a hommage, most of the discussion is based on studies Jacques Angelier (1947–2010), my former Professor and a pioneer in the field of stress/paleostress determinations, had been involved in to some extent.
2 To what extent do fault slip data inversions yield “paleostresses”?
2.1 Principle of inversion of fault slip data for paleostresses
Since 1974, many works in brittle tectonics have focused on the development of inversion methods for, and on their application to, fault slip data (see review in Angelier and Hancock, 1994), and on the theoretical examination of the actual constraints brought by faults on the calculation of paleostress tensors (e.g., Célérier, 1988; Fry, 2001). Basically, fault slip inversion methods theoretically assume that:
- (1) the analyzed body of rock is physically homogeneous and isotropic and if prefractured, it is also mechanically isotropic, i.e., the orientation of fault planes on which slip accumulates is random. In practice, these methods were extensively and successfully applied to sedimentary rocks that are anisotropic because of bedding and fractures. They also yielded tectonically significant results when more recently applied to brittlely deformed anisotropic foliated metamorphic rocks (e.g., Mehl et al., 2005, 2007; Tricart et al., 2004); the influence of a strong pre-existing foliation anisotropy on later brittle faulting and on possible local re-orientation of related paleostress axes has been however poorly documented to date;
- (2) the rock behaves as a rheologically linear material; linear elasticity is commonly considered as a requirement for a reliable description of the local deformation surrounding individual slip discontinuities, even though the adaptation of the methods to ductile shear zones met some success (Srivastava et al., 1995);
- (3) the displacements on the fault planes are small with respect to their lengths – i.e., measurements are carried out on non-connected small-scale faults displaying low displacement and which therefore are associated with very few amounts of strain in the rock volume – and there is no ductile deformation of the material and thus no rotation of fault planes;
- (4) the global volume of rock from which the data are taken for the inversion is large compared to the scale of the local slip discontinuities that contribute to the deformation, and for a given faulting event, the stress tensor is homogeneous over this volume (i.e., the remote stress tensor is spatially uniform within the rock mass containing the faults related to this event and temporally constant during the faulting event), so the local slip direction on each individual shear plane reflects, on average, the characteristics of the homogeneous stress tensor. This assumption implies that although the local deformation can be described as a discontinuous slip on a discrete shear plane, a global stress can be inferred only if the local slip discontinuities integrate over a global volume to a homogeneous continuum deformation (Twiss and Unruh, 1998). Note that in case of superimposed faulting events (i.e., polyphase tectonics), one searches for subgroups of data that are compatible with successive common stress tensors that are also assumed to be homogeneous for each faulting episode.
A main issue is therefore whether the stress at the scale of individual faults remains sufficiently similar to the “bulk” stress at the investigated scale, which is favored by conditions (3) and (4).
- (5) The slip responsible for the striation occurs on each fault plane in the direction and the sense of the maximum resolved shear stress on each fault plane (Wallace (1951)-Bott (1959) principle). This means that the slips on the fault planes are independent on each other's.
The basic principle of computation of a paleostress tensor thus consists in finding the best fit between the observed directions and senses of slip on a large number of shear planes displaying a wide distribution of orientations and the theoretical shear stress induced on these planes by the tensor solution of the inverse problem. The numerical quality of the tensor resulting from inversion is quantified by an estimator of misfit between each observed fault slip datum and the closest shear stress orientation predicted theoretically from the tensor parameters. The results are the orientation (trend and plunge) of the three principal stress axes σ1, σ2, and σ3 (with σ1 ≥ σ2 ≥ σ3, pression considered positive) and a ratio between differential stress magnitudes which is a scalar invariant of the stress tensor that constrains the shape of the stress ellipsoid (e.g., ϕ = (σ2-σ3)/(σ1-σ3), with 0≤ϕ≤1, Angelier, 1984). These four parameters define the reduced stress tensor. The procedure for separating superimposed stress tensors and related subsets of fault slip data is based on both mechanical and kinematical compatibility and relative tectonic chronology data, such as superimposed striations on fault surfaces or crosscutting relationships between faults.
Because fault slip data inversion remains a popular tool for geologists (and inversion of earthquake focal mechanisms a popular tool for seismologists as well), and following the pioneering works cited above, new methods of inversion of fault slip data have recently been published, with the aim at improving either paleostress reconstructions from heterogeneous fault sets (e.g., Choi et al., 1996; Liesa and Lisle, 2004; Lisle et al., 2001; Nemcok and Lisle, 1995; Nemcok et al., 1999; Shan et al., 2004a, b, 2006; Yamaji, 2000; Yamaji et al., 2006; Žalohar and Vrabec, 2007, 2008) or stress determination based on earthquake focal mechanisms (Angelier, 2002; Hardebeck and Michael, 2006), and a wealth of new regional stress/paleostress results have been produced (e.g., Amrouch et al., 2010; Angelier et al., 2004; Choi et al., 2011; Delvaux and Barth, 2010; Liesa and Simón, 2009; Shabanian et al., 2010; Sippel et al., 2009; among others).
2.2 Theoretical objections and the need for caution when carrying out fault slip data inversion for regional paleostress
2.2.1 Are fault slip data inversions properly used in practice?
Criticisms of the wide and uncritical use of fault slip data inversion to derive paleostresses have been voiced. Some authors claim for more caution when inverting fault slip data for regional paleostresses (e.g., Hippolyte et al., 2012; Sperner and Zweigel, 2010). I find these “pleas for more caution” perfectly justified by the common misunderstanding and the uncritical use of stress inversion software that are still considered by (too) many people as “black boxes” requiring only a few fault slip data measured in a hurry (hence often of poor quality) as input and yielding an indisputable “bulk” paleostress tensor as output. The popularity of such “easy-to-use” computer-based inversion techniques has caused the oversight of the fundamental assumptions they rely upon. The separation of homogeneous fault sets from a heterogeneous population and the (relative) dating of these sets is not always carefully done as well.
2.2.2 Do fault slip data inversions actually yield “paleostresses”?
On the other hand, some authors have even questioned the reliability and the significance of results of inversion of fault slip data in terms of paleostresses. Among the most recent papers are Gapais et al. (2000), Twiss and Unruh (1998), and Kaven et al. (2011). The reliability of stress determination from earthquake focal mechanisms will not be discussed hereinafter; the reader can refer to the papers by Twiss and Unruh (1998) and by Angelier (2002). Only to mention the paper by Célérier (2010) in which are discussed in a renewed way the alternative lines of thoughts for the interpretation of P, B, and T axes of earthquake focal mechanisms. P, B, and T axes are either considered as approximations of the principal stress directions and used to infer the closest Andersonian (see Célérier, 2008 for a review of the Anderson theory in seismicity) tectonic regime, or as indicators of the rake of slip vector, hence used to classify data into categories of fault movements. Célérier concludes that in the case of reactivation of nearly optimally oriented fault planes with a vertical principal stress, Andersonian geometry prevails and the P, B, and T axes provide reasonable estimates of principal stress directions, whereas in other cases, the P, B, and T axes of a single event are better interpreted in terms of fault and slip geometry.
The measurement of stress almost always involves the direct measurement of some intermediate quantity and the implicit or explicit application of a constitutive relation that relates the intermediate quantity to the stress (Twiss and Unruh, 1998). The same principle applies to the inference of paleostresses from fault slip data, which are observations or records of local displacements. The fault slip inversion provides direct information about the orientations of the principal strain rates, and the stress tensor is related to these strain rates by a constitutive relationship between the deformation rate and the stress (Twiss and Unruh, 1998). The basis of the criticism by these authors is the fact that fault slip data are fundamentally displacement data and that the net result of many small displacements on faults of varying orientations integrated over a global-scale volume is just an increment in the global continuum deformation of the volume, which is best described as resulting from cataclastic flow. The inversion of a set of fault slip data thus gives direct information about the characteristics of the global deformation rate, not of the global stress. The characteristics of the global stress are related to the global deformation rate and thereby to the fault slip data through the rheologic behavior of the material, which is described by the constitutive equation for cataclastic flow. The stress interpretation and the kinematic interpretation of inversions of fault slip data are equivalent only if the directions of maximum resolved shear stress and maximum resolved rate of shear on any given plane are parallel, which requires that the material is mechanically isotropic (so the principal stress axes are parallel to those of the strain rate) and that the constitutive equation relating deviatoric stress to deviatoric strain rate is linear; in addition, the fault pattern should display a minimum characteristic symmetry. To illustrate the theoretical failure of fault slip data inversion to yield paleostresses, Twiss and Unruh (1998) use the case of a fault zone where deformation results from a multitude of brittle slip events smoothed over the volume of the fault zone and consists of cataclastic flow. Around the fault zone, however, the deformation results from a slip discontinuity on the fault and can be modeled as an elastic deformation. Because the fault slip data reflect a cataclastic flow within the fault zone, they argue that it is not, in general, correct to associate an elastic stress outside the fault zone with the cataclastic flow within that zone.
On a theoretical point of view, these authors are correct when they claim that because the stresses inside and outside the fault zone could have different orientations (and magnitudes), the linearity and isotropy of the elastic behaviour outside the fault zone cannot be used as a justification for inferring the stress from the inversion of fault slip data within the fault zone. The stress within the fault zone is therefore probably related to the strain rate by a non-linear anisotropic constitutive equation, and if this is true, then the stress could not accurately be inferred directly from the inversion of fault slip data. As they mention, the degree of inaccuracy would depend on the degrees of anisotropy and non-linearity, which at present remain unknown.
However, it should be noticed first that the framework of Twiss and Unruh (1998) supposes to first define a strain rate tensor, and then, with rather demanding assumptions, to relate it to stress. This is quite different from that used by those who developed stress inversion, which is based on the Wallace-Bott hypothesis that directly relates the observed displacement with shear stress. An arguable strength of the Wallace-Bott hypothesis is that it more or less bypasses any assumption on the constitutive relationship. This difference in basic hypotheses makes “classical” stress inversion and Twiss and Unruh (1998) approach difficult to directly compare. In addition, most incremental strain determinations involve a summation of elementary dislocations (Amelung and King, 1997; Bailey et al., 2009; Gauthier and Angelier, 1985; Jackson and McKenzie, 1988; Kostrov, 1974; Marrett and Allmendinger, 1990; Sipkin and Silver, 2003) rather than the slip vector–shear strain rate parallelism invoked by Twiss and Unruh (1998). Finally, if the incremental approximation breaks down, which may become possible if finite strain is significant, for instance when the time span for paleostress is large, then the summation needs to be replaced by a more complex composition (Cladouhos and Allmendinger, 1993). This last point indicates that block rotations associated with large strain, which is known to be an issue for stress inversion, also requires a different framework for strain computations.
Second, it has been well known for a long time by structural geologists that natural fault zones typically show concentrated and complex deformation and therefore that many of the assumptions necessary for the methods for determining paleostresses are not met therein. Non-coaxial deformation within fault zones is often associated with a strong rheological and/or mechanical anisotropy and with important displacements. In this context, infinitesimal strain principal axes or principal strain rates axes are not parallel to finite strain principal axes, displacements are parallel neither to stress axes nor to strain axis, and the stress field is very inhomogeneous in both orientation and magnitude, so that in order to sort out the regional paleostress field of interest, small-scale fault slip measurements have to be carried out away from major fault zones where the condition of coaxial deformation is fulfilled. In addition, a fault zone may also cause in its neighbourhood significant stress perturbations at the meter/centimeter scale (the scale of the measured striated faults); this local stress field is related to the proper rheology and/or kinematics of the fault zone and usually differs from the far-field stress of interest (see Section 6). To conclude, Twiss and Unruh strain versus stress argumentation is difficult to compare with the Wallace-Bott-based paleostress approach, and the limitations these authors report refer to particular situations; these objections should be taken into account by people using fault slip data inversion as a “black-box”, but in general they do not preclude the reliable use of inversion of fault slip data to derive a far-field stress of interest.
Pollard et al. (1993) and Dupin et al. (1993) investigated the extent to which local slip discontinuities and their interactions deviate principal stress orientations from the ideal homogeneous solution and the hypothesis of mutual independence of fault slips, respectively, and found that in most cases the assumptions made are justified. In their recent contribution, Kaven et al. (2011) again discussed the two basic assumptions – the stress field is spatially homogeneous and temporally constant, and the direction of slip and the direction of the maximum shear stress resolved on each would-be fault plane are coincident – and evaluated them by using a methodology similar to that employed in forward modeling that uses the equations of motion and explicitly includes the faults and their associated fields of stress and deformation. They show – but again this has been known for a long time by structural geologists – that when stress inversion methods are applied on isolated faults or on fault systems with limited ranges of orientations, the orientation of the remote stress may be determined more or less precisely (in the extreme case of a single plane, principal stress orientations are only confined to a quadrant, thus quite poorly constrained (McKenzie, 1969)), but the remote stress ratio is generally poorly constrained. They further test the effect of diversity of fault orientations and find that Wallace-Bott type inversions do not perform well for limited ranges of orientations. They finally propose a new method that incorporates the effects of mechanical interaction of the entire fault or fault system, and solves the complete mechanical problem instead of employing empirical relationships between slip and stress or strain (or strain rate). They conclude that stress inversion methods using fault slip data can be improved, significantly in some cases, by solving a mechanical boundary value problem that takes into account the actual geometry of faults or fault systems. Again, the criticisms raised by Kaven et al. are justified on a theoretical basis, but in practice, their work in fact validates the results of inversion in most cases because they show that Wallace-Bott-based inversions that assume that the striation on a fault plane is parallel to the resolved shear stress exerted by the regional stress tensor of interest fail only in a limited number of particular situations (e.g., fault tips), and in general yield a reasonable bulk tensor.
Among the several thousands of paleostress reconstructions carried out worldwide using fault slip data in various tectonic settings over the last 35 years, most have proved consistent with the orientations of major structures, with the statistics of microtectonic data such as stylolites and joints (e.g., Mattauer and Mercier, 1980; Pollard and Aydin, 1988), the significance of which as reliable stress indicators being beyond doubt, and even with paleostresses inferred from calcite twins (e.g., Lacombe et al., 1992; see also Lacombe, 2010 and references therein). Furthermore, the homogeneity of stress regimes throughout the investigated areas and the subsequent reliability of the results of tectonic studies are generally confirmed by the a posteriori consistency of tensors identified in neighbouring places, in spite of lithological variations. At the regional scale, inhomogeneities in the stress field can be analysed provided that the domain is divided into smaller more homogeneous sub-domains where conditions of isotropy and linearity are much more likely.
As a result, one can safely consider that, provided that the set of methodological/practical prescriptions mentioned above is carefully/thoughtfully followed, inversion of fault slip data reliably yields the paleostresses of interest. It thus sounds highly reasonable to compare results of inversion of fault slip data with contemporary stresses, and to try to combine both approaches to better constrain the mechanical behaviour of the continental crust.
3 Paleostress orientations from fault slip data versus contemporary stress orientations in tectonically active regions: examples from Taiwan and the Zagros
Following some earlier studies comparing independent data sets from seismology (e.g., earthquake focal mechanisms) or geodesy (displacements from GPS surveys) to recent geological deformations or to fault slip data (e.g., Bellier and Zoback, 1995; Blenkinsop, 2006; Kao and Angelier, 2001; Philip, 1987; Roberts and Ganas, 2000; Sbar and Sykes, 1973; Shabanian et al., 2010), I synthetize hereinafter the results of several studies conducted in tectonically active regions (Taiwan and Zagros) that illustrate the consistency between recent paleostresses derived from fault slip data and those derived from other indicators such as veins and pressure-solution seams (“stylolites”), contemporary stresses derived from borehole breakouts and/or from inversion of earthquake focal mechanisms, and from GPS measurements.
Fig. 1 illustrates the good consistency between the contemporary maximum horizontal principal stress orientation derived from borehole elongation (Suppe et al., 1985) and the Plio-Quaternary compressional trends derived from inversion of fault slip data and from veins and pressure-solution-like impact features (so-called “impressed pebbles”) in Pleistocene conglomerates in the central part of the active Taiwan orogen (data after Lacombe et al., 1996a; Mouthereau, 2000 and unpublished data). The N100-110°E trend of the maximal horizontal principal stress/paleostress is consistent with the Plio-Quaternary kinematics of major thrusts and with the results of the analysis of calcite twins (Lacombe et al., 1993a, 1996a). The figure also illustrates the good consistency with the seismotectonic compressional trend determined by inversion of 106 focal mechanisms of the Chichi crustal earthquake aftershock sequence (20 September 1999 to 16 September 2000) located in the hanging wall block of the Chelungpu fault and in the surrounding regions to the north and to the south (Angelier, 2002), which suggests that the overall regional state of stress remained unchanged.

A. Comparison between Plio-Quaternary compressional trends deduced from outcrop-scale fault patterns (a: σ1 axes) (Lacombe et al., 1996a; Mouthereau, 2000; unpublished data) and directions of the contemporary maximum horizontal principal stress determined from borehole breakouts (b; Suppe et al., 1985) in central Taiwan. Diagrams illustrating fault-slip data: thin curves represent fault planes and dots with double arrows (left- or right-lateral) or simple ones (centripetal-reverse) indicate striations. Stars indicate stress axes with five branches (σ1), four branches (σ2) and three branches (σ3) computed using Angelier's (1984, 1990) inversion method. Small grey squares represent poles to veins. Bedding planes shown as dashed lines. Large black arrows: direction of compression (convergent arrows) and extension (divergent arrows); diagrams with * show paleostress orientations deduced from the statistical interpretation of clustering of pressure-solution-like features related to pebble impression (black diamonds) and poles to veins. **: unfolded data. Lower hemisphere equal area projection. B. Topographic map of Taiwan showing active and Quaternary faults and epicenters (white stars) and focal mechanisms of recent earthquakes in western Taiwan including the Chi-Chi earthquake (after Mouthereau and Lacombe, 2006). White/black quadrants correspond to dilatational/compressional first motions. C. Compressional trend resulting from inversion for seismotectonic stress of focal mechanisms of earthquakes from the Chi-Chi sequence (modified after Angelier, 2002). The thick line on the map shows the rupture during the Chi-Chi earthquake.
A. Comparaison des directions de compression plio-quaternaires déduites des jeux de failles (a : axes σ1) (Lacombe et al., 1996a ; Mouthereau, 2000 ; données inédites) et des directions de la contrainte principale horizontale maximale actuelle, déduites des ovalisations de puits (b : Suppe et al., 1985) dans le centre de Taiwan. Diagrammes illustrant les jeux de failles (projection de Schmidt, hémisphère inférieur) : les traces cyclographiques représentent les plans de failles et les points assortis de flèches les stries. Les étoiles grises correspondent aux axes principaux de contraintes calculés (cinq branches : σ1 ; quatre branches : σ2 ; trois branches : σ3) par la méthode d’Angelier (1984, 1990). Les pôles des veines sont représentés par les carrés gris, la stratification par les tiretés. Les flèches noires correspondent aux directions de compression ou d’extension horizontales. Les diagrammes assortis de * montrent les orientations de contraintes déduites de l’interprétation statistique des pôles des veines et/ou des impressions de galets analogues à des figures de pression-dissolution orientée (diamants noirs). Les diagrammes assortis de ** ont été débasculés du pendage de la stratification locale. B. Carte topographique de Taiwan montrant les failles actives et quaternaires et les épicentres (étoiles blanches) et les mécanismes aux foyers des séismes récents dans l’avant-pays occidental de Taiwan, incluant le séisme de Chi-Chi (d’après Mouthereau et Lacombe, 2006). Les quadrants blancs/noirs correspondent aux secteurs de premier mouvement en dilatation/compression. C. Direction de compression résultant de l’inversion des mécanismes aux foyers des séismes de la séquence de Chi-Chi (modifié d’après Angelier, 2002). La ligne épaisse sur la carte montre la rupture lors du séisme.
Fig. 2 illustrates the results of reconstructions of Late Neogene paleostresses in the Simply Folded Belt of the Zagros in the western Fars. The 020° compressional trend of the most recent stress regime determined from fault slip data is in very good agreement with the results of inversion of earthquake focal mechanisms (small magnitudes: Tatar et al., 2004; moderate magnitudes: Talebian and Jackson, 2004) from both the basement and the cover as well as with the distribution of their P axes (Lacombe et al., 2006) and with principal axes of geodetic strain rate tensors (Walpersdorf et al., 2006). In Andersonian terms, this paleostress regime is either truly compressional (vertical σ3 axis) or strike-slip (vertical σ2 axis), without any obvious regional variation in the results, indicating that the values of the principal stresses σ2 and σ3 were nearly similar hence that σ2 and σ3 axes could easily switch between being vertical and horizontal. This close association of small-scale thrust and strike-slip regimes in the cover during the Late Cenozoic resembles the combination of reverse and strike-slip-type focal mechanisms of earthquakes, whatever their magnitudes and focal depths (Fig. 2). This is confirmed by low Φ ratios (close to 0) computed from both faults and focal mechanisms (Lacombe et al., 2006), allowing both regimes to exist coevally in the Zagros during the Late Neogene, in the cover and the basement. This overall compressional-strike-slip stress regime accounts well for the kinematics of the active major faults (Berberian, 1995). It is worth noting that the Hormuz decollement poorly decouples principal stress/strain orientations in the cover and the basement.
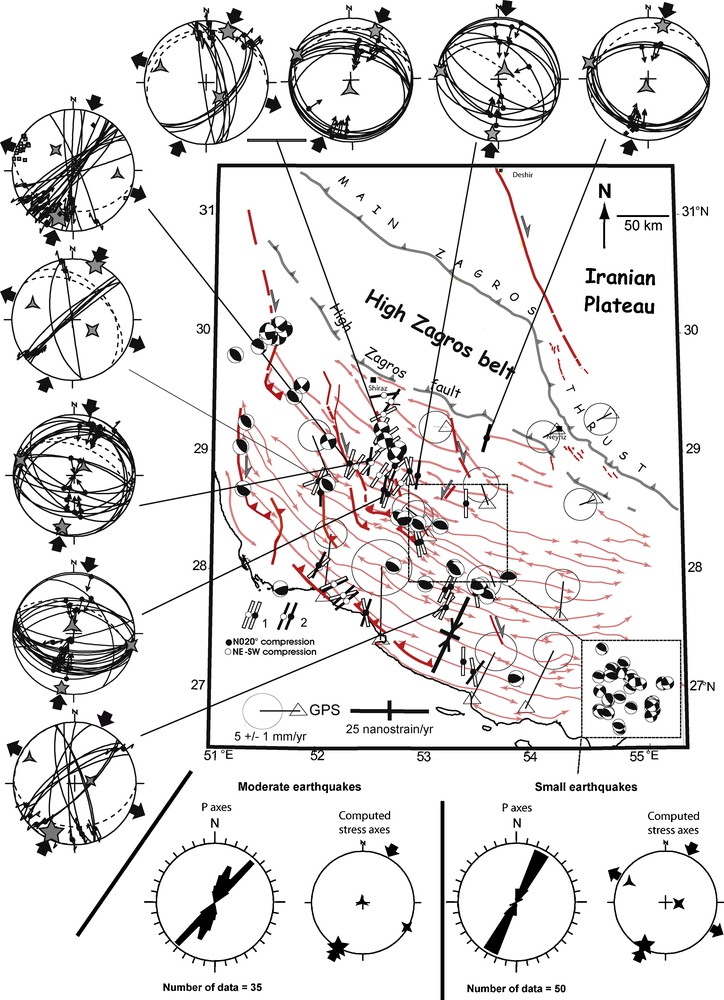
Comparison between Late Neogene compressional trends deduced from outcrop-scale fault patterns (small bars represent σ1 axes, white: strike-slip regime, black: compressional regime)(data after Lacombe et al., 2006, 2011), statistical orientations of P axes from small to moderate earthquakes from both cover and basement and modern stress orientations determined by inversion of their focal mechanisms (Lacombe et al., 2006) and principal axes of geodetic strain rate tensors (Walpersdorf et al., 2006) reported on a structural map of the western Fars province (Zagros, Iran) showing main faults and anticline axes. Fault slip data: same key as in Fig. 1.
Comparaison des directions de compression Néogène supérieur, déduites des jeux de failles (les barettes représentent les axes σ1, en blanc : régime décrochant, en noir : régime compressif) (données d’après Lacombe et al., 2006, 2011), l’orientation statistique des axes P des séismes de magnitudes faibles et modérées dans le socle et la couverture et des orientations des contraintes actuelles déduites de l’inversion de leurs mécanismes aux foyers (Lacombe et al., 2006) et des axes principaux du tenseur de taux de déformation géodésiques (Walpersdorf et al., 2006) reportés sur une carte structurale de la province occidentale du Fars (Zagros, Iran) montrant les principales failles et les axes des anticlinaux. Pour les diagrammes, même légende qu’en Fig. 1.
These two studies unambiguously demonstrate the high level of consistency between the “paleostresses” derived from inversion of fault slip data and from other geological indicators, modern stresses and even geodetic measurements, and therefore strongly support the reliability of paleostress reconstructions to reveal an orogenic stress field that remained stable with respect to time.
4 Is one principal (paleo)stress always vertical (and if yes, is its magnitude always equal to the overburden)?
In most in situ measurements of contemporary stresses, it is common to assume that one principal stress is vertical and that its magnitude is that of the overburden load. This assumption relies on the fact that the ground surface is a free surface with no shear stress so that one of the principal stress directions must be normal to it (Anderson, 1905). However, determinations of vertical stress are far less numerous than of horizontal stresses, so it is often not an easy matter to directly test the hypothesis of a principal stress being a function of integrated density. McGarr and Gay (1978) assessed the validity of the assumption of a vertical principal stress and concluded that it is basically valid although slight departures from this rule are common. In their compilations of different types of in situ stress indicators in North America, Zoback and Zoback (1980) made similar arguments which were later extended to the global compilation of in situ stress indicators (Zoback, 1992; Zoback et al., 1989). In the KTB site, Brudy et al. (1997) discussed hydrofracturing results where a principal stress direction is assumed to be vertical and its magnitude to equate overburden. Further indications for this assumption to be valid are given by the analysis of focal plane solutions (e.g., Angelier et al., 2004) at various sites that show that at depth one of the principal stresses is often within a few degrees of vertical.
On the other hand, Cornet (1993) argues that the assumption of verticality of one principal stress is often unjustified. In flat regions, the vertical direction is a principal direction, at least at the ground surface. However, in mountainous area or, more generally, anywhere the ground surface is not horizontal, the vertical direction is not a principal direction in the vicinity of the surface, and the deviation from the vertical direction may reach 15 to 20°. The question then arises of determining the depth up to which this non-verticality of one of the principal stresses may be observed. The answer to the question involves some considerations on the structure of the rock mass. In the simplest case the rock may be assumed to be homogeneous and isotropic and the effect of topography on the stress field may be supposed to reflect the elastic response of the domain to the load imposed by gravity alone or by combined gravitational and tectonic stresses. Thus, in mountainous areas where the vertical direction is not a principal direction, reliable sampling of stresses in the upper few km (i.e., < 2–3 km) requires direct measurements since the validity of the elastic hypothesis and that of the homogeneity hypothesis are always debatable. Because the principal directions are unknown, only stress determinations that do not only rely on the a priori knowledge of one of the principal directions may be applied and this strongly limits the methods available for such measurements. Note that even if the ground surface is horizontal, the vertical direction may not be a principal direction away from ground surface because of the influence of the structure of the formation (e.g., diapirs). Amadei and Stephansson (1997) mentioned the case of various laterally restrained anisotropic rock masses assumed to exhibit an elastic response to the effect of gravity forces. Their results suggest that for these conditions, the principal directions may strongly depart from the vertical direction.
In fact, there is no clear agreement on this topic; people “believing” in a vertical principal stress component usually discard stress measurements very close to the surface, only measurements made at greater depths (e.g., > 3 km) where the verticality of a principal stress is likely being considered in large-scale reconstructions for tectonic/geodynamic purposes (see Section 5). Note interestingly that the converse could be argued: shallow depth is close to the boundary condition of vertical stress (or of principal stress normal to topography), whereas at depth tectonic forces and decollements such as in thrust wedges could significantly rotate the stress field (e.g., Hafner, 1951).
On the other hand, the compilation by Lisle et al. (2006) showed a highly plunging principal stress axis in most paleostress reconstructions. A possible explanation of this (apparent) difference with contemporary stresses is that paleostresses are associated with tectonic deformation of rocks at depth, generally of larger magnitudes and of longer duration (the duration of a “tectonic event”) than present-day stresses. As put forward by Lacombe (2007), these paleostresses: are reconstructed from rocks now exhumed and observed at the surface but fractured and faulted at depth; and are “averaged” over several millions years, so they are controlled to the first order by the vertical (gravity) and the horizontal (tectonic forces) directions and do not reflect local and/or temporal sources of stress perturbation as for instance the evolving-with-time topography can be.
In low deformation environments, such as foreland environments, the verticality of one principal stress is strongly supported by widespread joint systems which are very close to vertical, a condition that is most likely if one of the principal stresses is vertical (Engelder and Geiser, 1980). In contrast, in regions of large deformation (e.g., fold-thrust belts), the assumption of a vertical principal stress must be considered with care, and may obviously be unjustified if principal stress directions rotated.
As emphasized by Sanz et al. (2008), stresses that develop during folding likely show a complex pattern and evolution in space and time since they are potentially affected by the interaction between deforming rock layers with different mechanical properties (e.g., Bourne, 2003; McConaughy and Engelder, 2001), the interfacial condition of the layer boundaries and the presence or absence of bed-parallel slip (e.g., Cooke and Underwood, 2001; Couples and Lewis, 2000; Guiton et al., 2003a, b; Johnson and Johnson, 2000). The stress distribution is expected to change over time due to fold amplification, bedding rotation (Engelder and Peacock, 2001; Fischer and Wilkerson, 2000), and even reactivation of early-formed structures. One could therefore expect some small-scale fault-slip data collected in fold limbs to have recorded such deviations of the principal stress axes from the vertical direction.
However, as mentioned above, paleostress reconstructions based on fault slip data in folded strata generally yield a highly plunging principal stress axis (Lisle et al., 2006), provided that the stress regime (extensional/compression/strike-slip) is well defined (i.e, Φ ratio not close to 0 or 1). This a posteriori finding of a vertical principal stress is not independent from the inferred chronology of faulting with respect to folding and on the a priori assumption of a governing Andersonian stress regime. There is no ambiguity with microstructures formed during late stage fold tightening (LSFT) (i.e., formed in the same stress regime that created the fold but after the end of strata tilting) or after folding possibly in a different stress field, and yielding a vertical paleostress axis since they are observed in their initial attitude. In contrast, microstructures that yield one stress axis perpendicular to bedding while the other two lie within the bedding plane (e.g., bed-perpendicular joints/veins or stylolites, or Layer-Parallel Shortening (LPS) – related microfaults) yield a sub-vertical paleostress axis only after backtilting to their prefolding attitude, which in turn implicitely leads to consider them as pre- or early-folding. However, it has been argued that such structures could have developed within tilted layers, hence possibly under a non vertical principal stress, if bedding anisotropy was able to significantly reorient stresses or if flexural slip occurred at very low friction so that the principal stresses rotated but remained either parallel or perpendicular to bedding (e.g., Tavani et al., 2006). Although this expectedly occurs for a very small range of bedding dips, this situation may not be simply ignored or dismissed; a careful comparison with neighbouring locations where similar features are recognized in still nearly horizontal strata may help overcome the ambiguity.
A kind of circular reasoning may thus be involved when chronology is based on an Andersonian assumption only. Note however that chronology can also be independent from that assumption. One typical such case is, when the microtectonic data collected across a fold yield after unfolding a more consistent stress solution than the folded data: the underlying assumption here is rather that a uniform tensor is preferred to a varying tensor, or, that a low misfit solution is preferred to a high misfit solution, in a way similar to the so-called “fold-test” for paleomagnetic data.
Ambiguity also arises when paleostress tensors with compression axes inclined consistently less than, but in the same direction as bedding dip, suggesting syn-folding faulting, are documented (e.g., Bergerat et al., 2007); in this case again, one can interpret the fault system either as formed under a non-vertical (rotated) principal stress, or as a system formed under a vertical principal stress when the strata were already tilted, then itself tilted with ongoing folding, so restoring the fault slips in their initial attitude does not require complete unfolding, or even resulting from both situations. Here again, the finding of a vertical principal stress does depend on the interpretation. However, such evidence remain also very few, suggesting that internal deformation of strata in fold limbs is mainly achieved during LPS when strata were still (sub)horizontal or during LSFT and remains limited during folding, being mainly accommodated by flexural slip (e.g., Amrouch et al., 2010; Sanz et al., 2008).
To conclude, the assumption of a governing perfectly vertical principal paleostress may be challenged in some cases, and one cannot preclude that the few data that could have supported actual stress rotation during folding (as predicted by numerical models) have either been missed by geologists because stress rotations were sufficiently small to keep one principal stress close enough to the vertical direction to be within the error range of stress axis determinations, or simply discarded from the whole data set as being noise. In most cases however, the statistical analysis of the results of inversion of fault-slip data from fold-thrust belts supports that paleostresses reconstructed away from perturbing features like major fault tips, diapirs or large volcanic centers correspond to a “long-term” Andersonian paleostress system, and in that sense are comparable with contemporary stresses determined at depth (e.g., Zagros, Lacombe et al., 2006; Fig. 2).
5 Homogeneity of stress vs paleostress patterns over large areas
The compilation of the successive World Stress Maps (Coblentz and Richardson, 1995; Heidbach et al., 2007, 2008; Zoback, 1992) allowed one to investigate the forces acting on the lithosphere, to better understand intraplate seismicity and to identify possible various wavelengths of modern stress patterns. Stress data used for the compilations come from earthquake focal mechanisms, deep stress measurements, borehole breakout orientations, and (few) inversions of fault-slip data. Only indicators of the stress field at depth were considered while all the data which may be influenced by topography effects or by human activity were excluded.
The modern intraplate stress field is generally in the compressive or wrench regimes (Zoback, 1992). Despite many causes for inhomogeneities, this stress field is characterized by nearly uniform stress orientations (Zoback, 1992; Zoback et al., 1989) over large regions. To a first order the maximum horizontal stress (SHmax) is sub-parallel to the direction of absolute plate motion in several plates, suggesting that these orientations are the result from far-field plate boundary forces that are transmitted throughout the intraplate region. For instance, the present-day ENE-WSW orientation of the maximum principal stress remains in that orientation up to 2500 km away in the center of cratonic North America (Zoback and Zoback, 1980).
SHmax orientations appear well correlated with convergence directions for plate boundary regions where the convergence direction is nearly orthogonal to the boundary, while the orientation of the stress field in other convergent boundaries is more directly related to the overall geometry of the plate. For instance, northward impingement of the Indian subcontinent acting as a rigid indentor into Eurasia produces a pattern of quasi-radial compression throughout much of eastern Eurasia. SHmax trajectories fan out away from the indentor, ultimately becoming nearly orthogonal to the plate convergence zones forming the eastern boundary of Eurasia. The stress field is roughly consistent over 1000 km into central Asia (Tapponnier et al., 1986). In this example, the midplate compression direction is dominantly controlled by the geometry of the eastern Eurasian plate. In a similar manner, NNW to northwest SHmax trajectories throughout western Europe can be explained as a result of relatively weak convergence of Africa from the south acting together with ridge push forces on the northern and western boundaries of the Eurasian plate (Müller et al., 1992).
However, density contrasts and active fault systems may also affect the regional stress pattern. Short wavelength stress patterns (< 200 km) were identified in several places such that western Europe, Alaska, the southern Rocky Mountains, Scandinavia, most of the Himalayas, and Indonesia (Heidbach et al., 2010). This does not rule out that long wavelength stress patterns prevail in the intraplate regions (e.g. Europe), but this could indicate that plate boundary forces may either act over shorter distances than previously thought on the basis of earlier compilations or that local and regional stress perturbations may sometimes be of the order of the magnitudes of the plate boundary forces.
Using fault slip data, Letouzey (1986) and Bergerat (1987) have sorted out a succession of fairly uniform paleo-states of stress during the Cenozoic in the West European platform; for instance, based on kinematic affinity of fault patterns, stratigraphic dating where possible and relative chronology criteria, an Eocene north-south to NNE-SSW compression has been identified. This north-south compression has been identified as far as 1300 km away from the present-day Pyrenean-Alpine front (e.g., Arthaud and Choukroune, 1972; Hibsch et al., 1995). This paleostress field likely reflects the transmission of orogenic stresses from the Pyreneo-Alpine paleo-plate boundaries during Eocene times (Lacombe, 2010; Lacombe et al., 1996b) and is related to the overall Africa-Eurasia convergence (Le Pichon et al., 1988). In contrast, the Miocene stress field related to the late stages of emplacement of nappes in the Alps rather show a fan-shape distribution of compressive stress trajectories, related either to late indentation tectonics or body forces (Bergerat, 1987), in a way similar to the stress pattern in the Himalaya region. Recently, Liesa and Simón (2009) conducted a nearly similar reconstruction of the evolution of intraplate stress fields in the Iberian Chain (NE Spain) during the Tertiary. The final proposed model includes three different, partially superposed first-order intraplate stress fields driven by genetically independent far-field tectonic forces related to the active Iberia plate margins, and showing second-order patterns of locally and regionally deflected stress trajectories.
As a result, paleostress patterns may be homogeneous over large domains from intraplate settings, and can therefore be compared with contemporary stress orientations in stress provinces as reported on World Stress Maps. For both types of data, this homogeneity depends however on the scale to which the stress distribution is considered; changing the scale of investigation to a more local one allows identification of stress/paleostress deviations related to lithological/rheological inhomogeneities or to fault kinematics.
6 Stress versus paleostress spatial perturbations related to major fault kinematics
A number of tectonic studies in the vicinity of fault zones have shown that the regional stress field is perturbed near these structures (e.g., Rispoli, 1981; Segall and Pollard, 1980; Xiaohan, 1983). In situ stress measurements as well as analyses of recent folds and of focal mechanisms of earthquakes demonstrate the reorientation of the maximum horizontal stress in the vicinity of major strike-slip faults, such as close to the San Andreas and Great Sumatran Faults where it tends to become perpendicular to the faults (e.g., Mount and Suppe, 1987, 1992). Extensive analysis of Neogene fracture patterns in the Zagros recently revealed varying palaeostress orientations through time in the different domains investigated that were related to the presence of basement faults with north-south and WNW trends, above which basement and cover were variably coupled during stress build-up and early deformation of the Arabian margin (Lacombe et al., 2011). At a more local scale, Lin et al. (2010) also reported from borehole breakouts analysis a localized rotation of the principal stresses close to the Chelungpu fault in Taiwan.
Experimental and numerical modeling allows a better characterization of these stress perturbations (in both orientation and magnitude) in the vicinity of faults, especially close to fault tips and in relay zones (e.g., Homberg et al., 1997, 2010; Sassi and Faure, 1997). These patterns and amounts of stress deviations may be slightly different depending on the amount of mechanical coupling, the amount of horizontal displacement, the rheology of the fault zone, or occurrence of strain partitioning (e.g., Teyssier et al., 1995).
Recognition of such perturbations of stress directions in the vicinity of strike-slip faults has led to pay close attention to, and therefore to consider with care, correlations based only on the homogeneity of stress directions without taking into account the structural grain of the domain, since successive different stress orientations may have only a local significance (see again Sperner and Zweigel, 2010). For example, field studies and reconstruction of Alpine paleostress patterns in the Jura mountains (Homberg et al., 1997, 2004) have shown that stress perturbations occur close to fault zones. These stress perturbations are either directly caused by the slip along the fault or undirectedly by the mechanical weakening of the fault zone compared to neighbouring areas. For the Pontarlier strike-slip fault, which was active during the Mio-Pliocene emplacement of the Jura mountains (Homberg et al., 2004) and the Rhine-Saône transform zone, which accommodated the Oligocene opening of the Rhine and Saône branches of the West European Rift (Lacombe and Angelier, 1993; Lacombe et al., 1993b) (Fig. 3A and B), the stress deviations are directly related to the kinematics and are well accounted for by simple elastic models (e.g., Homberg et al., 1997): the regional stress field causes slip along the fault, and this slip induces a local stress field close to the fault tips which is deviated with respect to the regional stress field. In a similar way, contemporary stress perturbations in wellbores indicated by breakout rotations have consistently been interpreted as due to small patches of slip on faults intersected by the well (e.g., Zoback et al., 2003).
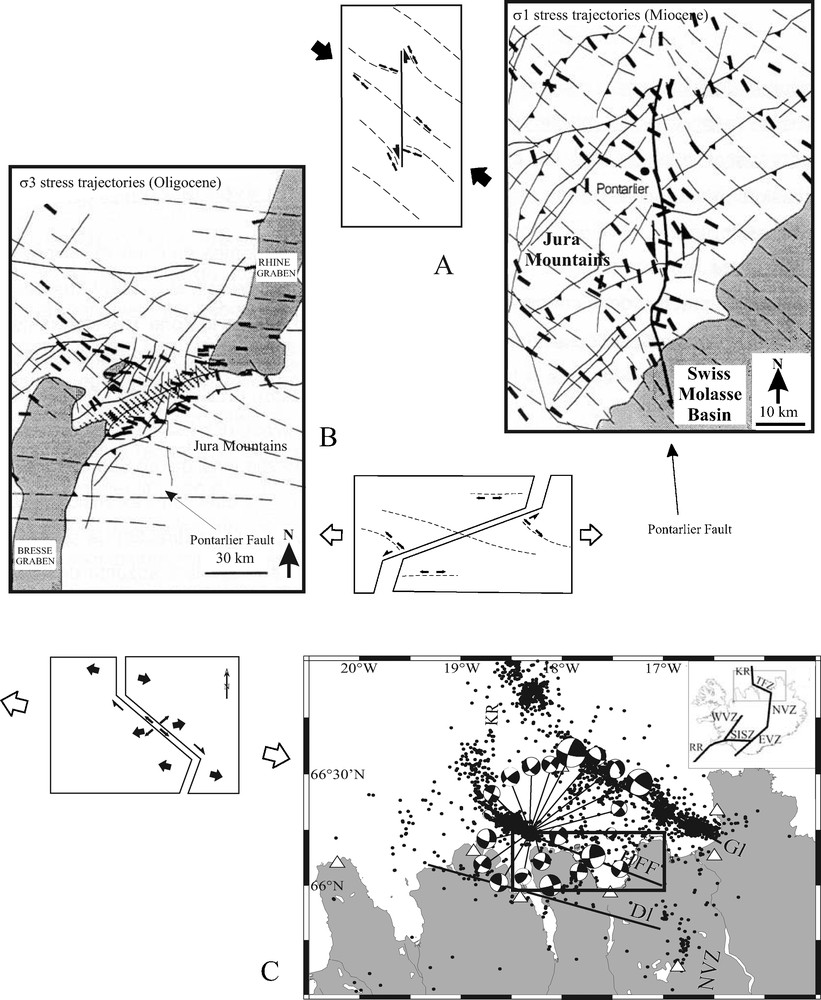
Examples of paleostress/stress perturbations in space (A, B) and time (C) in relation to fault kinematics. On each figure and corresponding idealized sketch, dashed lines represent paleostress trajectories interpolated from local paleostress determinations. A. First-order spatial perturbations of the Mio-Pliocene Alpine compressional stress trends in the Jura mountains (eastern France) related to the kinematics of the left-lateral Pontarlier strike-slip fault zone. Small black bars represent σ1 axes. Modified after Homberg et al., 2004. B. First-order spatial perturbations of the Oligocene extensional stress trends in the Burgundy platform (eastern France) and the Jura mountains related to the kinematics of the left-lateral Rhine-Saône transform zone. Small black bars represent σ3 axes. Modified after Lacombe and Angelier (1993) and Lacombe et al. (1993b). C. Inset: rift zone segments and transform faults in Iceland (EVZ: EastVolcanic Zone, WVZ: West Volcanic Zone, SISZ: South Iceland Seismic Zone, TFZ: Tjorrnes Fracture Zone, RR: Reykjanes Ridge). Temporal variations of stress directions derived from earthquake focal mechanisms in the vicinity of the Husavik-Flatey Fault in northern Iceland. The reported focal mechanisms (size proportional to magnitude) have been selected among those of the earthquakes used to carry out the study (frame) to illustrate the different faulting regimes encountered (Modified after Garcia et al., 2002). HFF: Husavik-Flatey Fault; NVZ: North Volcanic Zone; KR: Kolbeinsey Ridge; Dl: Dalvik lineament; Gl: Grimsey lineament. On the idealized sketch, large divergent black arrows correspond to the regional extensional trends while small black divergent arrows indicate local extensional stress trends.
Exemples de perturbations de contraintes/paléocontraintes dans l’espace (A, B) et dans le temps (C) en relation avec la cinématique des grandes failles. Sur chaque figure et schéma correspondant, les tiretés représentent les trajectoires de paléocontraintes interpolées à partir des déterminations locales. A. Perturbations spatiales de premier ordre des directions de compressions mio-pliocènes alpines dans le Jura, en relation avec la cinématique du décrochement sénestre de Pontarlier. Les petites barres représentent les axes σ1. Modifié d’après Homberg et al. (2004). B. Perturbations spatiales de premier ordre des directions d’extension oligocène dans la plate-forme bourguignonne et le Jura, en relation avec la cinématique de la Zone Transformante Rhin-Saône. Les petites barres représentent les axes σ3. Modifié d’après Lacombe et Angelier (1993) et Lacombe et al. (1993b). C. Encart : segments de rifts et failles transformantes en Islande (EVZ : EastVolcanic Zone, WVZ : West Volcanic Zone, SISZ : South Iceland Seismic Zone, TFZ : Tjorrnes Fracture Zone, RR : Reykjanes Ridge). Variations temporelles des directions de contraintes déduites des mécanismes aux foyers des séismes au voisinage de la faille de Husavik-Flatey dans le Nord de l’Islande. Les mécanismes aux foyers reportés (taille proportionnelle à la magnitude) ont été choisis parmi ceux des séismes utilisés dans l’étude (cadre) pour illustrer les différents régimes de failles rencontrés. HFF : Husavik-Flatey Fault ; NVZ : North Volcanic Zone ; KR : Kolbeinsey Ridge ; Dl : Dalvik lineament ; Gl : Grimsey lineament. Sur le schéma, les grandes flèches extensives représentent les directions régionales, alors que les petites flèches extensives représentent les directions locales. Modifié d’après Garcia et al. (2002).
Interestingly, despite the different time and spatial scales involved, both stress and paleostress distribution around strike-slip fault zones more or less fit the response predicted by simple elastic models of stress perturbations at the tips of a preexisting default loaded under mode II conditions and undergoing strike-slip propagation. For both contemporary stresses and paleostresses, these perturbations occur at different scales, from few centimeters (Rebai et al., 1992; Rispoli, 1981) to several hundreds kilometer scale, for instance along the Altyn Tagh strike-slip fault on the northwestern side of the Tibet plateau (e.g., Meyer et al., 1998). In this last example, the recent to present-day stress distribution derived from active fold-thrust systems in the vicinity of the major Altyn Tagh strike-slip fault supports the elastic behaviour of the crust (lithosphere?) over time scales of 10 Ma. This may indicate a first-order elastic-frictional behaviour of the continental crust (lithosphere?) over time scales ranging from the duration of the seismic cycle to several millions years.
7 Stress versus paleostress variations with time
Whatever the rock and whatever the location, stresses in a rock mass vary with time. In the absence of artificial disturbances (e.g., human activity), these variations are controlled by geologic processes like erosion, compaction, glacial rebound or any of the plate tectonics mechanisms. The time scale of these variations ranges from a few millions years for slow plate tectonic phenomena to a few seconds for the stress drop associated with earthquakes.
An example of rapid variations of Late Cenozoic and contemporary stresses in response to the geometric accommodation within a transform fault zone is provided by the Husavik-Flatey Fault (HFF) in Iceland (Garcia et al., 2002). The HFF is a dextral transform fault in northern Iceland that trends oblique to the mid-Atlantic Ridge. It is part of the Tjôrnes Fracture Zone (TFZ) that connects the North Volcanic Zone and the Kolbeinsey Ridge. Stress inversions were performed from both Late Cenozoic fault slip data collected in the field and earthquake focal mechanisms in order to reconstruct the paleostress fields and present-day stress fields along the fault. For both types of data, nearly coaxial normal and/or strike-slip faulting stress regimes were identified. The complex stress pattern is interpreted in terms of partitioning and geometric accommodation within the transform zone, in response to the obliquity of the HFF with respect to Eurasia-North America divergence (Garcia et al., 2002) (Fig. 3C). It is important to notice that the largest magnitude earthquakes reveal the regional stress field (dextral transtension along an ENE-WSW trend) tightly related to the transform motion whereas the lowest magnitude earthquakes depend on the local stress fields (fault-perpendicular and fault-parallel extensions: Fig. 3C).
An interesting point is that no chronological relationship for the three regimes (the dextral transtension, the HFF-perpendicular and the HFF-parallel movements) was clearly established using fault slip data. Moreover, during the 3-year period of focal mechanism recordings used in the study, the three regimes occurred without any clear spatial and temporal trend. The authors propose that the three stress regimes do not occur as a definite succession of tectonic events, but rather as random local tectonic successions. If their conclusion is correct, for a given time span, one should not expect to find the same succession at different locations in the transform zone, since this succession is geographically distributed as the moving patches within the deformed area. This example illustrates consistent but complex Late Cenozoic and contemporary stress changes related to fault slip over very short time spans, emphasizing the role of fault slip in locally perturbing the regional stress field. An alternate explanation that should be tested by further studies could be that all three stresses are approximately equal in magnitudes and/or that deformation is largely driven by high pore pressure. This example draws attention on the likelihood of such rapid changes of the local stress field in the past, that may have induced local fault sets inconsistent with the “average” smoothed long-term fault pattern, thus increasing the apparent scattering of data, and the possible loss of information if these uncorrelated fault sets are discarded as being either measurement errors or noise in regional paleostress reconstructions.
8 Conclusions
The aim of this article has been to discuss whether there is an adequate basis for a reliable comparison of contemporary stresses and paleostresses (especially inferred from fault slip data) in terms of orientations, patterns and meaning at different scales.
Several conclusions can be drawn from this short review:
- • the methods of determination of contemporary stresses and paleostresses and their results may differ, but not the physical definition of stress and the underlying mechanical concepts;
- • both types of stress data do not have strictly the same geological meaning: contemporary stresses measured in situ reflect instantaneous, ambient crustal stresses, while reconstructed paleostresses reflect ancient crustal stresses at the particular time of tectonic deformation, averaged over the duration of a tectonic event;
- • both quantities can interestingly be compared in terms of patterns, at the scale of plate interiors or at more local scale;
- • there may be more variability between different methods to infer contemporary stresses than between similar methods used to infer contemporary stresses and paleostresses in term of space. Within contemporary stress methods, borehole or stress relief techniques are local whereas focal mechanism inversion may involve a very large volume. Within paleostress stress methods, tension cracks or stylolites or calcite twinning are very local whereas fault slip inversion involves a volume that depends on the outcrop size. The main issue is thus how to combine up or down scale results obtained from different methods, and this applies both to contemporary stresses and to paleostresses;
- • on a tectonic point of view, the similarity of stress and paleostress regimes (as highlighted for instance in the Zagros) may allow to go back into the past to determine over which time span the overall pattern of orogenic stresses has remained nearly unchanged, hence the regional tectonic regime and the plate kinematics remained more or less stable. On a mechanical point of view, spatial and temporal stress/paleostress perturbations related to fault kinematics, when combined with mechanical modelling, may help constrain the rheological behaviour of the upper continental crust over time scales of up to tens of Ma.
Acknowledgements
The author would like to thank F. Bergerat and N. Bellahsen for their suggestions on a first draft of this manuscript, as well as B. Célérier and an anonymous reviewer for their thorough and very constructive comments.


