1 Introduction
In order to better understand the interactions between climate, erosion and tectonics (e.g. Bonnet, 2009; Whipple, 2009) and more generally, the dynamics of mass transfers at the Earth's surface, it is important to understand the erosion rates and patterns in mountain belts as well as their climatic controls. Among the existing methods for measuring erosion rates, the measurement of sediment loads in rivers may be the most straightforward solution for estimating erosion. In fact, sediment loads have been studied for this purpose and to constrain how erosion rates vary according to their potential controlling factors (e.g. Ahnert, 1970; Dadson et al., 2003; Milliman and Syvitski, 1992; Pinet and Souriau, 1988; Summerfield and Hulton, 1994; Wolman and Miller, 1960). However, the interpretation of sediment load measurements is not straightforward for several reasons. First of all, numerous studies have documented discrepancies between short-term erosion rates derived from suspended sediment data and millennial- to geological-scale ones (e.g. Dadson et al., 2003; Kirchner et al., 2001; Meyer et al., 2010; Schaller et al., 2001). Several reasons for this are usually given, including the quality of the suspended sediment record itself (e.g. sampling frequency and length of record compared to the timescale for the occurrence of events), the impact of internal storage within drainage basins, the effect of anthropogenic influences, etc. Second, the use of sediment load measurements to derive erosion rates needs to account for the sediment transfer mechanisms from hillslopes to the rivers, as well as within the rivers themselves (e.g. Benda and Dunne, 1997). Fuller et al. (2003) demonstrated that the interpretation of the suspended sediment record in Taiwan must at least distinguish between the transport-limited conditions (sediments are available and variations in the sediment flux depends only on the transport capacity of the river) and the supply-limited conditions (variations in the sediment flux depend on the supply of sediments to the river from the hillslopes).
In this article, we analyze daily water discharge and sediment flux measurements covering a period of several years for the three main drainage basins in Nepal, on the basis of results obtained by Andermann et al. (2011, 2012a, 2012b). We first show how precipitation-discharge data can be used to highlight the impact of groundwater storage on the annual hydrological cycle of Himalayan rivers. Then, we show how the concentration of suspended sediment in rivers varies at the year scale depending on the river discharge cycle, as well as how the release of groundwater impacts the concentration of materials in rivers. Finally, we propose a new conceptual model for the mobilization and transportation of material within the monsoonal discharge cycle in the central Himalayas.
2 Setting and data
We consider here the drainage basins of the Sapta Koshi, Narayani and Karnali Rivers (Fig. 1), which represent the three main drainage basins in Nepal. In the southern front of the central Himalayas, climate is characterized by a strong seasonality, with two very distinct climatic periods (Hannah et al., 2005): an extremely wet season, the Indian Summer Monsoon (ISM, from June to September), and a very dry season, from October to May (Fig. 2a). The dry season can be subdivided into the pre-ISM (March–May), post-ISM (October–November) and winter season (December–February). Up to 80% of the annual amount of precipitation falls during the ISM season (Andermann et al., 2011; Bookhagen and Burbank, 2006; Shrestha, 2000), whereas the spatial distribution of the precipitation is highly influenced by orographic effects, resulting in a maximum of precipitation at an elevation of ∼4000 m asl (Andermann et al., 2011; Anders et al., 2006; Bookhagen and Burbank, 2006): Fig. 2b. Among the three studied basins, the mean annual precipitation is comparable in the Karnali and Sapta Koshi catchments, ∼920 mm/yr, which is significantly lower than in the Narayani catchment (∼1400 mm/yr), which drains the Annapurna massif where very high precipitation intensities are observed. The annual river hydrograph of these rivers (Fig. 2a) clearly highlights the control of the ISM on water discharge, causing a one to two magnitude increase. Among the three studied basins, the glacial cover is the largest in the Narayani catchment (∼10% of the catchment surface, Andermann et al., 2012a) when compared to the Karnali and Sapta Koshi catchments (respectively 4.7 and 7.3%: Andermann et al. (2012a)). In contrast to the rivers in the western (e.g. Indus and Sutlej) and eastern Himalayas (e.g. Tsangpo-Brahmaputra), the contribution of snow and glacier melt runoff to the hydrological cycle is minor in the central Himalayas (Andermann et al., 2012a; Bookhagen and Burbank, 2010).
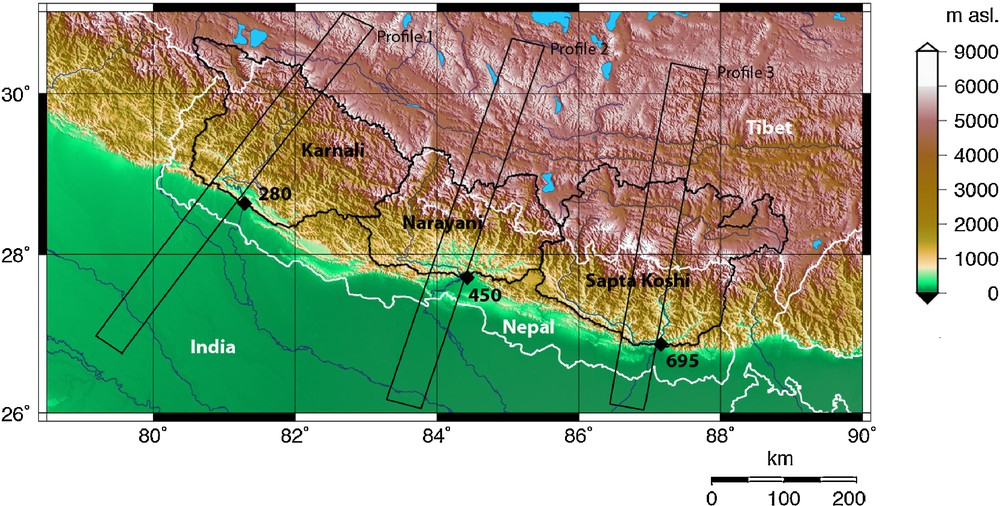
DEM of the central Himalayas (SRTM3) showing the three main drainage basins of Nepal studied here: the Karnali, Narayani and Sapta Koshi drainage basins. Diamonds indicate the location of the hydrological stations, from where we analyzed data in this work, with their respective station number.
Modèle numérique de terrain de l’Himalaya central (SRTM3) présentant les trois principaux bassins versants du Népal, étudiés ici : les bassins versants du Karnali, du Narayani et du Sapta Koshi. Les losanges indiquent la localisation des stations hydrologiques, à partir desquelles les données ont été acquises, avec le numéro respectif de chaque station.
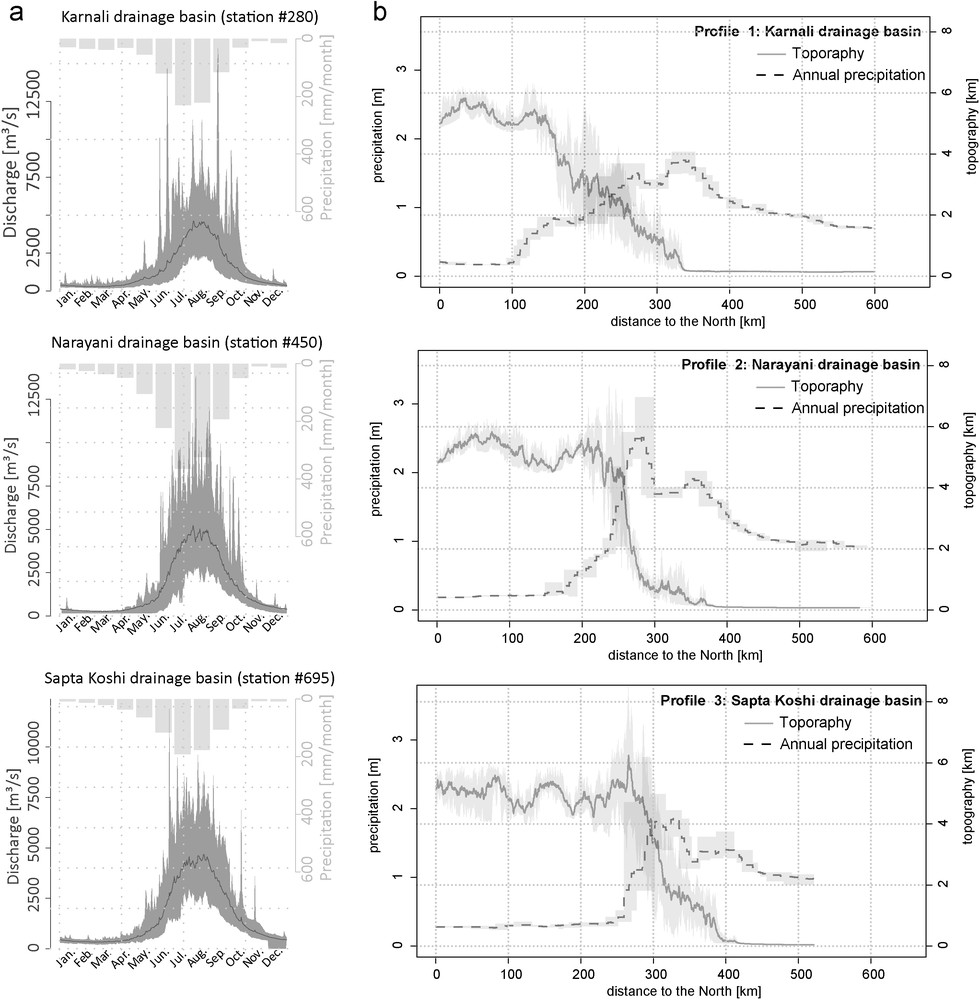
a: mean basin-wide monthly (1951–2006) and mean, maximum and minimum daily discharge over the years of data availability (Table 1) for the Karnali, Narayani and Sapta Koshi drainage basins (modified from Andermann et al. (2012a). Precipitation data is taken from the APHRODITE database (see Yatagai et al. (2009) and Andermann et al., 2011); b: precipitation swath profile across the three studied drainage basins (see location on Fig. 1), plotted against elevation from north to south. Precipitation data is taken from the APHRODITE database (see Yatagai et al. (2009) and Andermann et al. (2011)) and topography from SRTM3. Shading represents the mean, maximum and minimum values along each swath profile.
a : débit moyen mensuel mesuré sur la largeur du bassin (1951–2006) et débit journalier moyen, maximum et minimum sur les années pour lesquelles les données sont disponibles (Tableau 1) pour les bassins versants du Karnali, du Narayani et du Sapta Koshi (modifié selon Andermann et al., 2012a). Les données de précipitations proviennent de la base de données APHRODITE (voir Yatagai et al., 2009 et Andermann et al., 2011) ; b : profils moyens Nord-Sud de précipitations et de topographie des trois bassins versants étudiés (voir la Figure 1 pour la localisation des fenêtres de moyennage). Les précipitations sont issues de la base de données APHRODITE (voir Yatagai et al. (2009) et Andermann et al. (2011)) et la topographie de la base de données SRTM3. Les valeurs moyennes de topographie et de précipitations sont encadrées des valeurs minimums et maximums, représentées par la bande grisée.
The studied basins drain the entire Himalayan range, from the Tibetan Plateau to the Lesser Himalayas (Fig. 1). Most of their headwaters are located on the arid Tibetan Plateau where the influence of the ISM is weak. This is particularly important for the Sapta Koshi catchment because a large part of its area (∼55%: Andermann et al. (2012b)) drains the plateau (Fig. 1). The rivers in the studied basins incise bedrock and comprise, from north to south, the low-grade Paleozoic-Mesozoic Tethyan Sedimentary Series, high-grade metamorphic gneisses and migmatites of the High Himalayan Crystalline Series and low-grade Proterozoic sediments of the Lesser Himalayas. Most of the data considered here come from outlet stations located to the north of the Siwalik foreland (Fig. 1).
Here, we used three datasets in order to characterize the links between sediment transport and the hydrological cycle of the Himalayan rivers. We considered daily precipitation data from the Asian Precipitation Highly Resolved Observational Data Integration Towards Evaluation of Water Resources (APHRODITE) (precipitation dataset (Yatagai et al., 2009). The data are an interpolated rain gauge product, comprising orographic corrections, and as we have already demonstrated, it is currently the best available dataset for the Himalayan region in terms of temporal resolution and absolute accuracy (Andermann et al., 2011). Data are available from 1951 until 2007, in daily temporal resolution and 0.25° (∼30 km) spatial resolution. We also considered daily river discharge and suspended sediment concentration data acquired by the Department of Hydrology and Meteorology Nepal DHM (DHM, His Majesty's Government, 2003; DHM/FFS, 2004): Fig. 3 C. All of the records span several years between 1973 and 2006 (Table 1). Importantly, days of missing data are randomly distributed over the available time series and do not cluster preferentially in one season (e.g. monsoon season).

Perspective view of the topography of the Narayani drainage basins showing the high peaks of the High Himaylayas and views of the Kali Gandaki River (A at Kalopani and B near Mirimi) and Narayani (C at Bhâratpur) River. The Kali Gandaki River is a tributary of the Narayani River. The picture shown in (C) was taken at the Department of Hydrology and Meteorology Nepal's gauging station (station 450 on Fig. 1).
Vue en perspective de la topographie du bassin versants du Narayani montrant les pics élevés du Haut Himalaya et vues des rivières Kali Gandaki (A à Kalopani et B près de Mirimi) et Narayani (C à Bhârapur). La rivière Kali Gandaki est un tributaire de la rivière Narayani. La photo C a été prise à la Station de jaugeage du Département d’Hydrologie et Météorologie du Népal (station 450 de la Fig. 1).
Principales caractéristiques des bassins de drainage étudiés et périodes de disponibilité des données relatives à l’eau et au sédiment en suspension.
| Drainage basin | Drainage area (km3) | Mean basin relief (km) | Annual rainfall (mm) | Annual discharge (km3) | Water discharge availability | Suspended sediment availability |
| Karnali | 45,967 | 2.1 | 920 | 44 | 1973–2006 | 1973, 1974, 1977–1979 |
| Narayani | 32,002 | 2.3 | 1396 | 49.5 | 1973–2006 | 1976–1977, 1979, 1985–1986, 1996, 2001–2003 |
| Sapta Koshi | 54,024 | 2.2 | 920 | 49 | 1977–2006 | 1987, 1999, 2001–2003 |
3 Results
3.1 River discharge versus precipitation rate
Plots of the mean basin-wide precipitation versus the daily specific water discharge (water discharge normalized to the area of the drainage basin located upstream from the gauging station) highlight a considerable scatter within the ∼30-year datasets for all of the catchments we considered (Fig. 4). However, the same general pattern is observed in all of the studied basins, showing a well-defined annual cycle when the chronology of the data is considered. They show an increase in discharge with increasing precipitation from the pre-ISM to the ISM and a decrease during the post-ISM. However, a striking feature is that for a given precipitation rate, the river discharge is systematically higher during the post-ISM compared with the pre-ISM. Thus the data display annual anticlockwise hysteresis loops, which are very similar in all of the studied catchments, implying that part of the precipitation is temporarily stored within the catchments and not transferred directly to the river during the pre-ISM and ISM seasons, whereas the storage compartment is drained during the post-ISM season. This behavior has also been observed in the sub-catchments within these large drainage basins, irrespective of the geological units, or the presence of glacier and snow cover (Andermann et al., 2012a).
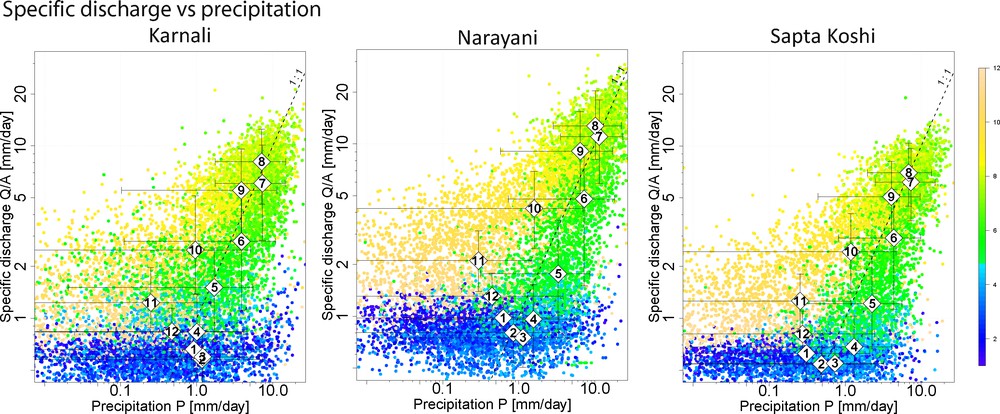
Bi-logarithmic plots of the specific discharge (discharge normalized by drainage area) vs. the mean basin daily precipitation for the studied drainage basins over the years of data availability (Table 1), modified from Andermann et al. (2012a). Note that discharge was not plotted when the precipitation is zero. The color bar is scaled for the calendar age (1 = January,…, 12 = December). The white filled circles represent the mean monthly values, where the months are indicated by numbers. The error bars represent the 5% and 95% quantiles of the daily data distribution for each month.
Diagramme bi-logarithmique représentant les valeurs de débit spécifique (débit normalisé par l’aire drainée) en fonction des précipitations journalières moyennes, pour les bassins de drainage étudiés sur les années de disponibilité des données (Tableau 1), modifié d’après Andermann et al., 2012a. À noter que le débit n’a pas été représenté quand les précipitations étaient nulles. La barre d’échelle de couleur correspond à l’âge calendaire (1 = janvier, …, 12 = décembre). Les cercles blancs représentent les valeurs moyennes mensuelles, où les mois sont indiqués par des numéros. Les barres d’erreur représentent les quantiles 5 % et 95 % de la distribution des données journalières pour chaque mois.
3.2 Suspended sediment concentration versus discharge
Plots of the daily-suspended sediment concentration versus the daily specific water also show considerable scatter for all of the catchments when we consider the existing data (Fig. 5a). However, when the chronology during the year is considered, a consistency of the data emerges. Actually, the data show an increase in concentration with increasing discharge from the pre-ISM to the ISM and then a decrease during the post-ISM, but again, the data describe a hysteresis loop albeit a clockwise loop: for a given discharge, the suspended sediment concentration is systematically higher during the pre-ISM compared with the post-ISM. Such hysteresis prevents the use of a simple rating model to evaluate the sediment flux from the water discharge chronicle, as is classically done (e.g. Morehead, 2003). The fact that sediment concentrations versus river discharge display a hysteresis behavior through the seasons has already been observed (Gabet et al., 2008; Hasnain and Thayyen, 1999; Wulf et al., 2010) and suggests that material supply and/or water sources vary temporally between the seasons. In the mainly glaciated hinterland of the Annapurna massif, Gabet et al. (2008) proposed that the seasonal hysteresis loop they observed is driven by variations in the glacial sediment supply. Similarly, Hasnain and Thayyen (1999) observed increased concentrations during the onset of the monsoon in an almost exclusively glaciated catchment of the upper Ganges headwaters in India. The most obvious explanation for this phenomenon is the depletion of a sediment stock within the glacier and at its ablation front. In other words, hysteresis loops between sediment concentrations versus river discharge are classically related to a problem of sediment supply, since the sediment supply in the contributing areas is exhausted during the course of monsoon, leading to higher concentrations in the pre-ISM compared to the post-ISM.

a: bi-logarithmic plots of the suspended sediment concentration vs. the total daily water discharge for the studied drainage basins over the years of data availability (Table 1). The color bar is scaled for the calendar age (1 = January, …, 12 = December). The white filled circles represent the mean monthly values, where the months are indicated by numbers. The error bars represent the 5% and 95% quantiles of the monthly data distribution; the dashed lines represent the direct linearity between concentration and discharge; b: same as a, except that the suspended sediment concentration is plotted only against the runoff fraction of the total discharge (direct discharge). Modified from Andermann et al., 2012b.
a : diagramme bi-logarithmique représentant les valeurs de concentration de sédiment en suspension, en fonction du débit quotidien total d’eau pour les bassins versants étudiés sur les années de disponibilité des données (Tableau 1). La barre d’échelle de couleur correspond à l’âge calendaire (1 = janvier,…, 12 = décembre). Les cercles blancs représentent les valeurs mensuelles moyennes, où les mois sont indiqués par des numéros. Les barres d’erreur représentent les quantiles 5 % et 95 % de la distribution des données mensuelles ; les lignes tiretées montrent la linéarité directe entre concentration et débit ; b : identique à a, excepté le fait que la concentration de sédiment en suspension est représentée en fonction de la seule fraction d’eau issue du ruissellement (débit direct). Modifié d’après Andermann et al., 2012b.
3.3 Suspended sediment concentration versus direct discharge
The annual anticlockwise hysteresis loops we observed between precipitation and discharge may provide an alternative clue to interpret the observed hysteresis loops between sediment concentrations versus river discharge. Actually, the storage and release of water in a storage compartment could control the concentration of the sediment stock transported within the rivers because of differential dilution. To test this hypothesis, we performed a classic hydrograph separation analysis (see Lim et al., 2010) in order to separate river discharge into a low-frequency baseflow component and a high-frequency component. This high-frequency component, hereafter referred to as direct runoff, corresponds to the fraction of river discharge characterized by a short transfer time, resulting in a short response (< 1 day) of the discharge hydrograph following a rainfall event. For this purpose, we applied the generic digital filtering method proposed by Lim et al. (2010) to the discharge datasets (see Andermann et al. (2012b) for details). For all of the studied catchments, the plot of the sediment concentration versus the direct discharge reveals a linear relationship with a slope of one between the two variables, and a hysteresis effect is no longer observed (Fig. 5b). These data illustrate that the direct discharge is at a minimum during the post-ISM and winter seasons, as the suspended sediment concentration is low, whereas high direct discharge and concentration are observed during the pre-ISM and ISM seasons.
4 Interpretation and discussion
4.1 Transfer of precipitation into river discharge: influence of groundwater storage and release
The anticlockwise hysteresis loops we observed between discharge and precipitation imply that part of the precipitation water is temporarily stored in a reservoir during its course into rivers. In the studied area, glacier and snow melt runoff principally occur during the pre-ISM and ISM seasons (Bookhagen and Burbank, 2010; Immerzeel et al., 2009), therefore the storage of water in glaciers cannot explain the observations. In fact, the effect of melting glaciers and snow would drive a clockwise hysteresis, not an anticlockwise one. Moreover, Andermann et al. (2012a) also observed such hysteresis in unglaciated catchments, demonstrating that the glacier is not the main driver of this phenomenon. Conversely, evapotranspiration in the Himalayas reaches a maximum during the pre-ISM, between April and May (e.g. Lambert and Chitrakar, 1989), which could qualitatively explain the observed hysteresis loops when only the timing is considered. However, because the magnitude of the evapotranspiration rapidly decreases with elevation (Lambert and Chitrakar, 1989) and because of the high elevation reached by the studied catchments (Fig. 2b), this is estimated to account for less than 10% of the overall hydrological budget (Bookhagen and Burbank, 2010) so this effect alone is not able to drive the observed hysteresis. Consequently, the main mechanism explaining the hysteresis effect is probably a transient storage of water in a groundwater unit during the rising ISM and its release during the post-ISM season (Andermann et al., 2012a). Andermann et al. (2012a) discussed the nature of this groundwater unit by modeling the data using a conceptual hydrological model. By solving the water balance at the catchment scale, they attempted to discriminate the time response distribution in the discharge data and to relate it to the storage compartments through modeling. Their model simulated the catchment response to precipitation and incorporated three main components: a snow module, a rain-to-discharge flow related to quick runoff processes, and a slow-flow component representing groundwater contribution while the model was forced by precipitation, temperature and potential evapotransipration (see Andermann et al. (2012a) for details). In all of the catchments they studied, including the three catchments discussed here, they very confidently reproduced all of the hysteresis loops through significant water storage within the slow-flow reservoir, with a long characteristic response-time of about 45 days. Using this type of a long response-time and baseflow recession analysis, they demonstrated the significant contribution of a hard-rock aquifer to river discharge. They also demonstrated that the annual volume of water flowing through this groundwater system is very large, representing ∼2/3 of the annual river discharge. In the Himalayas, the major increase in precipitation during the ISM is consequently responsible for the recharge of basement aquifers, which are refilled during the ISM and then purged in the post-ISM, leading to the observed annual hysteresis effect (Fig. 4).
4.2 Post-ISM dilution of suspended sediment concentrations by groundwater release
The direct dependency of sediment concentration on direct discharge (Fig. 5b) demonstrates that the suspended sediment concentration is not dependent on the amount of water in the rivers but depends on the amount of water draining the near surface into the rivers, characterized by a short residence time. It implies that the suspended sediment concentration depends on the supply of material from the hillslopes and that the observed hysteresis loops between the concentrations and total river discharge is not the result of differences in the availability of sediment supply from there, between the pre- and post-ISM seasons, as has been classically proposed (Gabet et al., 2008; Hasnain and Thayyen, 1999; Wulf et al., 2010). Consequently, hillslopes as a contributing sediment source are in a transport-limited state: sediments are always available for transportation and variations in the sediment flux only depend on variations in the transport capacity. Another main finding is that groundwater release during the falling limb of the ISM appears to be the main driver of the observed hysteresis loops between the concentrations and total river discharge (Fig. 5a), which consequently appears as a dilution effect (Andermann et al., 2012b).
5 Conclusion: annual Himalayan hydro-sedimentary cycle
Our analysis of hydro-sedimentary data for the Himalayan rivers in Nepal can be used to propose a new cyclic conceptual model for erosion and sediment transport linked to the annual occurrence of the ISM (Fig. 6). During the pre-ISM, water availability is low and groundwater is almost completely purged; however, it starts to refill during this period. In fact, during rainfall events, a significant part of water infiltrates and is going to refill the deep groundwater system, thus the concentration of suspended material in rivers is low. During the ISM, precipitation intensity and frequency reach their maximum and therefore the runoff on the hillslopes provides a large amount of eroded material to the rivers because of their transport-limited state. The high transport capacity of the rivers is due to the contribution of runoff to the discharge as well as to the groundwater input into the rivers. During the ISM, water storage in groundwater is fully replenished and pore pressure in the subsurface material is high, probably inducing landslides. In our model, most of the erosion consequently takes place during the ISM. During the post-ISM, only a few precipitation events occur and the erosion on hillslopes is low. However, water discharge into rivers remains high because of a large amount of water released from groundwater storage into the rivers, resulting in the dilution of the suspended load. Finally, in winter, few precipitation events take place, mainly as snow at high elevation; water availability and sediment transport are at a minimum.

Schematic sketch illustrating how deep groundwater storage during the pre-monsoon season and release during the post-monsoon season control the concentration of suspended sediments in rivers.
Schéma illustrant comment le stockage d’eau dans les aquifères profonds durant la période pré-mousson et son relargage en post-mousson contrôle la concentration en sédiments en suspension dans les fleuves du Népal.
Our study shows how erosion and sediment transportation in the Himalayas are intimately linked to the water cycle with a main characteristic due to the strong seasonality of the climate because of the ISM. We show that groundwater has a major impact on the annual hydrological cycle and in the modulation of the concentration of suspended sediment in rivers. Finally, we show that because of annual fluctuations in groundwater release, the total river discharge cannot be used as a proxy for estimating sediment transport through the establishment of a rating curve, as is usually done.


