Determination of transfer time for sediments in alluvial plains using 238U-234U-230Th disequilibria: The case of the Ganges river system

François Chabaux; Estelle Blaes; Mathieu Granet; Raphaël di Chiara Roupert; Peter Stille

doi:10.1016/j.crte.2012.10.013

Hydrology, environment

Determination of transfer time for sediments in alluvial plains using ²³⁸U-²³⁴U-²³⁰Th disequilibria: The case of the Ganges river system
[Détermination des temps de transfert des sédiments dans les plaines alluviales par la méthodologie des déséquilibres radioctifs ²³⁸U-²³⁴U-²³⁰Th : le cas du Ganges et de ses affluents]

Présenté par : Written on invitation of the Editorial Board

François Chabaux ¹ ; Estelle Blaes ¹ ; Mathieu Granet ¹ ; Raphaël di Chiara Roupert ¹ ; Peter Stille ¹

¹ Laboratoire d’hydrologie et de géochimie de Strasbourg (LHyGES), EOST, université de Strasbourg et CNRS, 1, rue Blessig, 67084 Strasbourg cedex, France

Comptes Rendus. Géoscience, Volume 344 (2012) no. 11-12, pp. 688-703.

Résumés

Anglais
Français

An approach to deriving the transfer time of sediments within alluvial plains by using the variation of the U-series nuclides in sediments collected along rivers is presented in this article and discussed in the light of new data from samples from different locations within the Ganges watershed and its outlet. These data indicate that the upstream-downstream variation of ²³⁸U-²³⁴U-²³⁰Th disequilibria in the sediments, with different variation trends for suspended and coarse-grained sediments, is probably a general feature of all Himalayan rivers flowing across the Indo-Gangetic plain. The data therefore confirm the occurrence of very different transfer times within the plain, depending on the sediments granulometry, with much shorter transfer time for the fine-grained (a few ky or less) than for the coarse-grained sediments (100 ky or more). A new solving approach, using a parallel stochastic Quantum-behaved Particle Swarm Optimization (p-QPSO), has been developed for identifying the unknown parameters of the model necessary for the determination of the transfer time. The data of sediments collected at the Ganges outlet show significant variations of the ²³⁴U/²³⁰Th activity ratios for the fine-grained sediment end-member collected in 2004 and 2008. Such variations indicate that the fine-grained sediments transit quickly (a year or less) within the plain. The highly variable activity ratios might be the result of quickly changing weathering intensities. Conversely, the U-Th variations observed for the 2004 and 2008 bedload from the Ganges basin cannot result from a short sedimentary transfer time. They probably result from the dredge sampling procedure, which might be influenced by local placer effects controlling the abundance of U and Th carrying minerals. Dredging may not allow the sampling of a representative bedload, hence it may cause an artificial mineralogical and, therefore, an U-Th variability for bedload sediments collected at different periods. At this stage, the transfer time uncertainty induced by this variability is difficult to assess.

L’approche proposée pour déterminer les temps de transferts des sédiments dans les plaines alluviales à partir de la variation des nucléides des séries de l’U, mesurés dans les sédiments collectés le long des fleuves est présentée dans ce papier et discutée à la lumière de nouvelles données obtenues sur des sédiments collectés à différents endroits de la plaine du Ganges et à son exutoire. Ces données indiquent que la variation amont-aval des déséquilibres ²³⁸U-²³⁴U-²³⁰Th dans les sédiments, avec des tendances de variations différentes pour les sédiments en suspension et les sédiments à grains grossiers, est probablement une caractéristique générale des rivières himalayennes dans la plaine Indo-gangétique. Ces données confirment donc l’existence de temps de transfert très différents des sédiments dans la plaine du Ganges, selon leur granulométrie, avec des temps beaucoup plus courts pour les sédiments fins (quelques ka ou moins) que pour les sédiments grossiers (100 ka ou plus). Une nouvelle approche de résolution intégrant l’utilisation d’une optimisation stochastique par agrégat particulaire quantique (version parallèle) (p-QPSO en anglais) fut développée pour caractériser les paramètres du modèle utilisé pour déterminer les temps de transferts. Les données collectées à l’exutoire du Ganges montrent, quant à elles, des variations significatives des rapports d’activité (²³⁴U/²³⁰Th) pour le pôle fin des sédiments collectés en 2004 et 2008. De telles variations indiquent que ces sédiments à grains fins transitent rapidement (de l’ordre de l’année ou moins) dans la plaine. Ces variations rapides des rapports d’activités des sédiments fins pourraient provenir d’un changement de l’intensité des processus d’altération dans la plaine du Ganges d’une année sur l’autre. En revanche, les variations U-Th observées dans les sédiments de fond de rivières collectés en 2004 et 2008, ne peuvent pas s’expliquer par des temps de transferts rapides de ces sédiments. Elles sont certainement liées à la procédure d’échantillonnage par dragage, qui pourrait être influencée par des effets de concentration locaux de minéraux portant l’U et le Th. Le dragage ne permettrait pas de collecter un échantillon représentatif en Th et en U, ce qui conduirait à une variabilité minéralogique et en U-Th artificielle, lorsque sont comparés entre eux des sédiments collectés à différentes périodes. L’incertitude qu’induit une telle variabilité sur le temps de transfert calculé est difficile à évaluer à ce stade.

Métadonnées

Reçu le : 2012-06-01
Accepté le : 2012-10-26
Publié le : 2012-11-01

DOI : 10.1016/j.crte.2012.10.013

Keywords: Sedimentary transfer time, U-series nuclides, Ganges river, Modeling
Mot clés : Temps de transfert sédimentaire, Nucléides des séries de l’U, Ganges, Modélisation

Affiliations des auteurs :

François Chabaux ¹ ; Estelle Blaes ¹ ; Mathieu Granet ¹ ; Raphaël di Chiara Roupert ¹ ; Peter Stille ¹

¹ Laboratoire d’hydrologie et de géochimie de Strasbourg (LHyGES), EOST, université de Strasbourg et CNRS, 1, rue Blessig, 67084 Strasbourg cedex, France

@article{CRGEOS_2012__344_11-12_688_0,
     author = {Fran\c{c}ois Chabaux and Estelle Blaes and Mathieu Granet and Rapha\"el di Chiara Roupert and Peter Stille},
     title = {Determination of transfer time for sediments in alluvial plains using {\protect\textsuperscript{238}U-\protect\textsuperscript{234}U-\protect\textsuperscript{230}Th} disequilibria: {The} case of the {Ganges} river system},
     journal = {Comptes Rendus. G\'eoscience},
     pages = {688--703},
     publisher = {Elsevier},
     volume = {344},
     number = {11-12},
     year = {2012},
     doi = {10.1016/j.crte.2012.10.013},
     language = {en},
}

TY  - JOUR
AU  - François Chabaux
AU  - Estelle Blaes
AU  - Mathieu Granet
AU  - Raphaël di Chiara Roupert
AU  - Peter Stille
TI  - Determination of transfer time for sediments in alluvial plains using 238U-234U-230Th disequilibria: The case of the Ganges river system
JO  - Comptes Rendus. Géoscience
PY  - 2012
SP  - 688
EP  - 703
VL  - 344
IS  - 11-12
PB  - Elsevier
DO  - 10.1016/j.crte.2012.10.013
LA  - en
ID  - CRGEOS_2012__344_11-12_688_0
ER  -

%0 Journal Article
%A François Chabaux
%A Estelle Blaes
%A Mathieu Granet
%A Raphaël di Chiara Roupert
%A Peter Stille
%T Determination of transfer time for sediments in alluvial plains using 238U-234U-230Th disequilibria: The case of the Ganges river system
%J Comptes Rendus. Géoscience
%D 2012
%P 688-703
%V 344
%N 11-12
%I Elsevier
%R 10.1016/j.crte.2012.10.013
%G en
%F CRGEOS_2012__344_11-12_688_0

François Chabaux; Estelle Blaes; Mathieu Granet; Raphaël di Chiara Roupert; Peter Stille. Determination of transfer time for sediments in alluvial plains using ²³⁸U-²³⁴U-²³⁰Th disequilibria: The case of the Ganges river system. Comptes Rendus. Géoscience, Volume 344 (2012) no. 11-12, pp. 688-703. doi : 10.1016/j.crte.2012.10.013. https://comptes-rendus.academie-sciences.fr/geoscience/articles/10.1016/j.crte.2012.10.013/

Version originale du texte intégral

1 Introduction

The sediment transfer time in alluvial plains is a key parameter for the understanding and modelling of the evolution of the continental surface and its response to external forcing factors i.e. climate changes, tectonic events or human activities. Besides modelling, experimental and tracing approaches have been developed to estimate more or less directly these time-dependent sediment parameters, including the sediment basin response time to external perturbations (e.g., Castelltort and Van Den Driessche, 2003; Castelltort et al., 2004; Davy and Lague, 2009; Liébault et al., 2012; Métivier and Gaudemer, 1999; Paola et al., 1992; Sear et al., 2000). A more accurate estimate of these parameters can be obtained by using radiochronometers. The application of cosmonuclides would undoubtedly open new horizons in this field of research (Wittmann et al., 2011); however, so far, their sediment analysis has mainly been devoted to the estimation of denudation rates at the watershed scale (e.g., von Blanckenburg, 2005, 2006). On the other hand, an effort has been made in recent years to develop and use radioactive U-series disequilibria (i.e., ²³⁸U-²³⁴U-²³⁰Th). DePaolo et al. (2006, this issue and references therein), developed the concept of the comminution age based on the analysis of the (²³⁴U/²³⁸U) activity ratio which allows one to constrain the time “elapsed subsequent to bedrock being reduced by physical weathering to small grains”. Several other studies underline the potential of such an approach (e.g., Dosseto et al., 2010; Lee et al., 2010; Maher et al., 2006). At the same time, it has been proposed to use the variation of the U-series nuclides in sediments along rivers to recover the time constant of the sediment transfer within alluvial plains (Chabaux et al., 2006; Dosseto et al., 2006; Granet et al., 2007, 2010). The potential of these latter approaches has been emphasized in the study of the sediments from the Ganges river system (Granet et al., 2007, 2010), one of the world's largest purveyor of Quaternary alluvial sediments shed from the largest orogen, i.e., Himalaya. The analysis of sediments collected along the Ganges river and two of its Himalayan tributaries allowed one to define a transfer scenario with time constants for the sediment transfer which vary strongly in function of the sediments granulometry.

The aim of this article is to present the principles of this approach and to discuss some possible limits in the light of new data from samples collected at different locations within the Ganges watershed and its outlet.

2 Principle of the approach

The potential of U-series nuclides to provide information on the transfer time of sediments in alluvial plains is a consequence of the dual property of these nuclides: (1) to be fractionated during water-rock interactions and hence during chemical weathering processes; and (2) to have radioactive decay periods of the same order of magnitude as the time-scales of these processes (e.g. Chabaux et al., 2003a, 2008; Dosseto et al., 2008a). The approach, illustrated in the study of sediments from the Ganges river basin (Granet et al., 2007, 2010), mainly relies on the principle that in large alluvial plains sediments are only transferred along the streams and not affected by additional inputs of new weathering products from fresh bedrocks; in such a case, the intensity of ²³⁸U-²³⁴U-²³⁰Th disequilibria in river sediments will only depend on two parameters: (a) the duration of the transfer including the time spent in soils and in the river; and (b) the nature and the intensity of U-Th fractionations occurring in sediments during their transfer into alluvial plains. In the limiting case of a pure transport regime, without secondary U-Th fractionations, Th activity ratios of the sediments collected along the stream are only affected by radioactive decay. In this simple case, the determination of the sediments Th activity ratios along the river yields directly the “age”, which corresponds to the residence time of the sediment in the plain. If secondary U-Th fractionation occurred during the transit of the sediments within the alluvial plain, then the time information derived from the variation of U-Th disequilibria in sediments along the alluvial plain requires the identification of the origin of these secondary U-Th fractionations and their modelling by using realistic mathematical laws. For the sediments of the Ganges river system (Granet et al., 2007, 2010) it has been shown that the main U-Th fractionations are related to sediment weathering during their transit and storage in the plain. The interpretation of U-Th data relies in this case on a time evolution law of the U-series nuclides, which is the classical law used to account for the variations of the radioactive disequilibria during weathering, namely a loss and gain model (e.g., Chabaux et al., 2003b, 2011, 2012; Dequincey et al., 2002; Dosseto et al., 2008b; Ma et al., 2010, 2012). In the frame of such a scenario the temporal evolution of the number of the atoms of the four ²³⁸U-²³⁴U-²³⁰Th-²³²Th nuclides per gram of sample is described by the four following equations:

\frac{\partial {}^{238}U}{\partial t} = f_{238} {}^{238}U_{0} - k_{238} {}^{238}U - λ_{238} {}^{238}U

(1)

\frac{\partial {}^{234}U}{\partial t} = f_{234} {}^{234}U_{0} - k_{234} {}^{234}U - λ_{234} {}^{234}U + λ_{238} {}^{238}U

(2)

\frac{\partial {}^{230}{Th}}{\partial t} = f_{230} {}^{230}T h_{0} - k_{230} {}^{230}{Th} - λ_{230} {}^{230}{Th} + λ_{234} {}^{234}U

(3)

\frac{\partial {}^{232}{Th}}{\partial t} = f_{232} {}^{232}T h_{0} - k_{232} {}^{232}{Th} - λ_{232} {}^{232}{Th}

(4)

λ_i is the decay constant (in y⁻¹) of nuclide i (here ²³⁸U, ²³⁴U, ²³⁰Th, and ²³²Th), k_i is the first-order rate constant (in y⁻¹) for leaching of nuclide i and f_i is the input flux (in y⁻¹) of nuclide i gained by the sample. For simplification, the input fluxes are expressed as the proportion of the number of atoms of nuclides added per year to the initial sample (expressed as λ_i N₀).

Solving the above equation system allows one to calculate the theoretical activities of the various nuclides in the sample at time t and the three independent activity ratios (²³⁴U/²³⁸U), (²³⁰Th/²³⁸U), and (²³⁰Th/²³²Th). The nuclide activities and the activity ratios are a function of the mobility parameters (k_i, f_i) of the model, the initial activities of the different nuclides and the time t. The time t corresponds to the time span between the initial state of the sample at t = 0 and its present state. Thus, the time t corresponds to the time duration elapsed for a sample to move from the starting position to its current position. Usually the reference sample is collected at a locality upstream in the plain, which corresponds to the starting or reference position. It is important to note that such an approach implies that the transfer of sediments within the plain works at steady state.

The mobility parameters (k_i, f_i) are usually unknown. The approach retained to solve this problem is to collect a series of samples along the alluvial plain and to consider the mobility parameters as constant for the whole plain. The determined radioactive disequilibria of these samples are then used to determine: (1) the mobility parameters of the different radionuclides; and (2) the age of the different samples relative to the reference sample; this age corresponds to the mean residence time of the sample in the alluvial plain and defines the time span necessary to move from the reference position to its current position.

In the studies of the Ganges sediments and its tributaries, this mathematical approach allowed one to derive a long sediment transfer time of 100 ky or more for coarse-grained sediments; the fine-grained material, however, has a much shorter transfer time of a few ky (Granet et al., 2007, 2010).

3 Sampling locations and mineralogical and geochemical characteristics of sediments

In order to complement the first results obtained on the Ganges river system and to validate the previous conclusions concerning the transfer time of sediments within the alluvial Gangetic plains (Granet et al., 2007, 2010), additional sediments have been sampled in three other areas during several field campaigns (between 2004 and 2009) and analyzed. They come: (1) from Rishikesh and Kanpur situated at the upstream portion of the Ganges river; (2) from Harding Bridge at the outlet of the Ganges river just before the confluence with the Brahmaputra river; and (3) from the Kosi river, with one sample collected at the outlet of the Range and another one just before the confluence with the Ganges River (Fig. 1).

Fig. 1
Map of the Ganges River basin and locations of river sampling, modified from Chabaux et al. (2001). MCT: Main Central Thrust; MFT: Main Frontal Thrust. Location numbers are those given in Table 1. Stars give the location of samples studied by Granet et al. (2010), whose results are given in insert of Fig. 2.
Carte du bassin du Ganges avec la localisation des échantillons (d’après Chabaux et al. (2001)). MCT : « Main Central Thrust » ; MFT : « Main Frontal Thrust ». Les numéros des positions sont ceux indiqués dans le Tableau 1. Les étoiles correspondent aux lieux de prélèvement des échantillons étudiés par Granet et al. (2010), dont les données sont représentées en encart de la Fig. 2.

For each sampling location, both suspended and bedload or bank river sediments (Table 1) were collected and analyzed. Bedload sediments were dredged in the center of the channel, whereas bank sediments, which correspond to the most recent deposits, were sampled in the active part of the channel. River bank sediments, which actually are rather bar sediments, have been collected at several places in the same sampling location, in order to integrate a total surface of about a few square meters. Suspended materials were collected at different depths of the water column by using a polypropylene bottle, ballasted and equipped with a depth probe. The sampling depth given in Table 1 corresponds to the average depth recorded during the filling of the bottle and may fluctuate by ± 0.5 m. Suspended sediments are collected by filtration of water samples through a 0.22 μm with a diameter of 99 mm PES filter in pressurized teflon coated filtration units within 12 to 48 h of collection (Galy et al., 2008; Granet et al., 2010; Lupker et al., 2011). To assess the temporal variability of U-Th series nuclides of the sediments during the monsoon season when 70–80% of the total annual rainfall occurs (Singh et al., 2007), the Ganges river at its outlet (Harding Bridge) was sampled four times (once in July 2004 and three times in 2008).

	Type	Sampling date	Depth m	U ppm	Th ppm	(²³⁴U/²³⁸U)	(²³⁰Th/²³²Th)	(²³⁸U/²³²Th)	(²³⁰Th/²³⁸U)	Th/Nd
Ganges
Rishikesh (#1, 30°7.60′ N, 78°19.82′ E)
BR922	SL	Aug. 2009	0.2	4.58	15.7	1.004	0.988	0.883	1.12	0.60
BR920	SL	Aug. 2009	6	4.38	15.3	0.997	1.030	0.868	1.19	0.57
BR924	Bank	Aug. 2009		2.91	12.5	1.003	0.754	0.704	1.07	0.56
Kanpur (#2, 26°36.78′ N, 80°16.55′ E)
BR907	SL	Aug. 2009	0	3.85	17.8	1.001	0.998	0.655	1.53	0.59
BR945	SL	Aug. 2009	3	2.77	12.7	1.001	0.901	0.659	1.37	0.57
BR905	Bedload	Aug. 2009	–	1.87	10.7	1.007	0.628	0.530	1.19	0.55
Harding Bridge (#3, 24°3.17′ N, 89°1.48′ E)
BR415	SL	July 2004	0	3.78	19.2	1.018	0.773	0.596	1.30
BR413	SL	July 2004	4	3.43	18.5	1.010	0.703	0.564	1.25
BR412	SL	July 2004	6.5	3.15	17.2	1.014	0.716	0.555	1.29
BR418	Bedload	July 2004	10	6.03	44.1	0.998	0.446	0.415	1.07
BR8218	SL	1st Sept. 2008	2	2.77	17.4	1.016	0.658	0.482	1.37
BR8217	SL	1st Sept. 2008	4	2.72	17.4	1.010	0.633	0.476	1.33
BR8216	SL	1st Sept. 2008	7	2.69	17.6	1.009	0.612	0.462	1.33
BR8221	Bedload	1st Sept. 2008	12	5.11	41.7	1.004	0.397	0.372	1.07
BR8253	SL	10th Sept. 2008	0	2.86	18.0	1.018	0.702	0.483	1.45
BR8251	SL	10th Sept. 2008	5	2.63	17.2	1.012	0.623	0.464	1.34
BR8281	SL	22th Sept. 2008	0	3.02	18.8	1.015	0.753	0.488	1.54
BR8280	SL	22th Sept. 2008	6	2.97	18.9	1.015	0.657	0.476	1.38
BR8283	Bedload	22th Sept. 2008	12.5	2.38	16.4	1.007	0.485	0.442	1.10

Ganges tributaries
Chambal (#4, 26°39.45′ N, 77°54.15′ E)
BR938	Bank	Aug. 2009	–	1.24	8.47	1.010	0.524	0.446	1.18
Gomti (#5, 25°34.66′ N, 83°59.92′ E)
BR8126	SL	Aug. 2008	0	4.00	19.6	0.993	0.747	0.619	1.21
Kosi Upstream (#6, 26°50.89′ N, 87°9.08′ E)
PB68	SL	July 2005	0	4.37	23.0	1.005	0.630	0.576	1.09	0.52
PB65	SL	July 2005	3	4.26	21.8	1.003	0.635	0.594	1.07	0.54
PB70	Bank	July 2005	–	2.68	14.9	0.994	0.560	0.547	1.02	0.51
Kosi Downstream (#7, 25°25.12′ N, 87°13.66′ E)
BR103	Bedload	Aug. 2001	–	3.44	25.0	1.008	0.475	0.418	1.14	0.55

The bedload or bank sediments (grain size of ∼200–500 μm) are mainly composed of quartz, feldspar, mica and heavy minerals (zircons, xenotimes, monazites and garnet) (Garzanti et al., 2010; Singh, 2009; Singh et al., 1993, 2007). Suspended sediments (grain size of ∼0–50 μm) are enriched in mica, contain some calcite, dolomite and fewer amounts of epidote, amphibole and garnet (details in Garzanti et al., 2011; see also Singh et al., 2007).

Sedimentological analysis of the river sediments collected in the Ganges basin from the Himalayan front downstream to the Ganges mainstream in Bangladesh suggests that mineral sorting strongly controls the chemical composition of the sediments (Lupker et al., 2011, 2012a). Grain size, shape and density of the sediment suspension are defined by the hydro-dynamical conditions of the water column. This results in a mineralogical and thus chemical differentiation of sediments at the scale of the water column; it is illustrated through the variations of major elements at the scale of the water column (for example, decrease of Al₂O₃ and increase of SiO₂ with increasing depth). Major element data further indicate that sediments from Gangetic plain rivers (Ganges river, Himlayan rivers in the downstream part of the plain) suffered a higher degree of chemical weathering than the sediments from the Himalayan rivers at the outlet of the High Range (Lupker et al., 2011, 2012a).

4 Analytical techniques

U, Th concentrations and U, Th isotopic ratios were analyzed in Strasbourg (LHyGeS) by Thermal Ionisation Mass Spectrometry (TIMS) on a Thermo Scientific Triton. To improve the digestion of sediments, samples were crushed by using first an agate disk mill and then an agate ball mill. The grain size of the sample is < 100 μm with the first crushing step and decreases to < 50 μm after the second step. This is of prime importance in order to get a full digestion of the samples, in particular of the minerals such as zircons, xenotimes and monazites which are U and Th-rich.

For U and Th analyses, 100 mg of crushed powder were spiked with a mixed ²³³U-²²⁹Th tracer. The U-Th tracer was regularly calibrated by TIMS with the AThO rock standard. The sample-spike mix was then dissolved using a three-step procedure with HNO₃-HF acids, HClO₄ and HCl–H₃BO₃ acids (Granet et al., 2007, 2010; Pelt et al., 2008). Separation and purification of the U and Th fractions were achieved by using conventional anion exchange chromatography (Granet et al., 2007; Pelt et al., 2008). The accuracy and reproducibility of (²³⁴U/²³⁸U) activity ratio were controlled by analyzing the HU1 secular equilibrium standard solution. During the period of data acquisition (2008–2010), the mean (²³⁴U/²³⁸U) ratio of the HU1-standard was 0.999 ± 0.005 (n = 45; 2σ), which is in agreement with the value of 1 for a rock in secular equilibrium. During the course of this study, the accuracy of Th isotopic ratio measurements was assessed by analysing the BRGM Th105 standard solution (Innocent, 2008): ²³²Th/²³⁰Th =220316 ± 4480 (n = 27, 2σ). The reproducibility of U concentration and activity ratios was better than 2 and 0.5%, respectively. For Th, the reproducibility of concentration and activity ratios was better than 2%. The total procedure blanks were < 50 pg for U and < 500 pg for Th. This is negligible (< 2‰) compared to the amounts of elements analysed in the studied samples (at least 100 ng and 1000 ng of U and Th, respectively).

5 Results and discussion

5.1 Variations of U and Th nuclides in the upstream part of the Ganges and Kosi rivers

The U and Th isotope systematics in the sediments of the Kosi and of the upstream Ganges rivers are very consistent with those obtained previously, for the Ganges main stream, and two of its tributaries, the Gandak and Ghaghara rivers (Granet, 2007; Granet et al., 2007, 2010). Similar to previous studies, the data points of each sampling site define trends in the isochron diagram (Fig. 2) that can be interpreted in terms of mixing of coarse- and fine-grained sediments. In addition, the data imply a systematic upstream to downstream variation of the ²³⁸U-²³⁴U-²³⁰Th disequilibria in the sediments with different variation trends for the two sediment end-members: both the (²³⁰Th/²³²Th) and (²³⁸U/²³²Th) activity ratios decrease from upstream to downstream in the coarse-grained sediments, whereas only the (²³⁸U/²³²Th) ratio decreases significantly in the fine-grained suspended sediment (Fig. 2). This indicates that the upstream-downstream variation of ²³⁸U-²³⁴U-²³⁰Th disequilibria in the sediments along the rivers, with different variation trends for suspended and coarse-grained sediments, is probably a general feature of all Himalayan rivers flowing across the Indo-Gangetic plain. Therefore, using the new Ganges and Kosi river data, one might expect to arrive at interpretations and conclusions similar to those of Granet et al. (2007, 2010): sediment transfer time within the watershed varies as a function of the sediment grain size, with much shorter transfer time for the fine-grained than for the coarse-grained sediment.

Fig. 2
Plot of the sediment data points in the (²³⁰Th/²³²Th) vs (²³⁸U/²³²Th) diagram for the sediment samples from Rishikesh (black squares), Kanpur (white triangles), Kosi downstream (grey triangles) and Kosi upstream (grey squares) rivers. Larger symbols are used to indicate bedload and bank river sediments, whereas the same but smaller symbols are used to indicate suspended river materials. Insert: data from Granet et al. (2010) for the Narayani-Gandak river sediments.
Représentation des données dans le diagramme (²³⁰Th/²³²Th) vs (²³⁸U/²³²Th) pour les sédiments de rivière collectés à Rishikesh (carrés noirs), Kanpur (triangles blancs), la Kosi aval (triangles gris), la Kosi amont (carrés gris). Les symboles plus gros indiquent les sédiments de fond/sédiments de berge, les mêmes symboles mais plus petits sont utilisés pour les sédiments en suspension. Encart : données de Granet et al., 2010 pour les sédiments de la Gandak et du Ganges.

5.1.1 Sediment transfer time calculation

A more quantitative estimate of the sediment transfer time can be made by using the loss and gain model, detailed in section 2, and already applied in the previous studies on Ganges plain sediments (Granet et al., 2007, 2010). This approach is basically similar to those developed for interpreting the variations of U series disequilibrium in weathering profiles (e.g. Chabaux et al., 2003b, 2011, 2012; Dequincey et al., 2002; Dosseto et al., 2008b, 2012; Ma et al., 2010, 2012). Such approaches allow for solving systems of significantly under-constrained equations, which is the general situation for all these studies. Thus, in the case of the Kosi and the Upper Ganges, the U-Th analysis of only two sediment samples per river, yields three independent activity ratios, namely (²³⁸U/²³²Th), (²³⁴U/²³⁸U) and (²³⁰Th/²³²Th) activity ratios, which is obviously insufficient to precisely determine the age of the downstream sample relative to the upstream one, and the eight mobility parameters of the model. The solving approach, developed for solving such under-constrained problem, aims to find a set of plausible parameters (here the mobility parameters k_i, f_i of the four nuclides ²³⁸U, ²³⁴U, ²³⁰Th, ²³²Th) and the age of the downstream sediment relative to the upstream one) from an a priori set of parameters, which fits best the activity ratios in a least square frame work. In the present study, the solving approach developed to perform the determination of these unknown parameters is a parallel stochastic Quantum-behaved Particle Swarm Optimization (Mikki and Kishk, 2005; Sun et al., 2004). To our knowledge, it is probably the first time that such an approach is used for this kind of problem in geochemistry. Such a method is well-adapted: (1) for situations where large numbers of parameters and low numbers of data are available (present case); and (2) for cases where an a priori relationship can be proposed for the different parameters, or at least some of them (more detail in Appendix A). For modelling the Ganges and the Kosi river data, some a priori information can be indeed provided on the values of the U and Th mobility parameters. The Th/Nd elemental ratios (Nd can be seen as a relatively immobile element) of the coarse-grained and fine-grained sediments are relatively invariant from upstream to downstream locations (Fig. 3). This implies that sediment weathering during their transfer and residence within the alluvial plain does not significantly mobilize Th, which is clearly not the case for U. This therefore justifies considering Th to be immobile (k_Th and f_Th ≈ 0). Furthermore, from the literature data it can be seen that the k_U parameters range from 10⁻⁷ to 10⁻⁴ y⁻¹ (e.g., Andersen et al., 2009; Dequincey et al., 2002; Dosseto et al., 2008b; Vigier et al., 2001). In the present study, we expanded the a priori interval of variations for k_U to the interval 10⁻⁹–10⁻³ y⁻¹. In addition, as in the Ganges system, the U activity ratios of waters are > 1 and < 1.5 (Chabaux et al., 2001; Granet et al., 2007), the k₂₃₄/k₂₃₈ ratios and f₂₃₄/f₂₃₈ ratios (with k and f the model mobility parameters) are also suggested to be in range between 1 and 1.5. Thus f₂₃₄/f₂₃₈ ratios can indeed be assimilated to the activity ratios of the incoming U input whereas k₂₃₄/k₂₃₈ ratios represent the differential removal of ²³⁴U relative to ²³⁸U for leaching processes. Therefore, both ratios should have values close to those of river water of the studied region.

Fig. 3
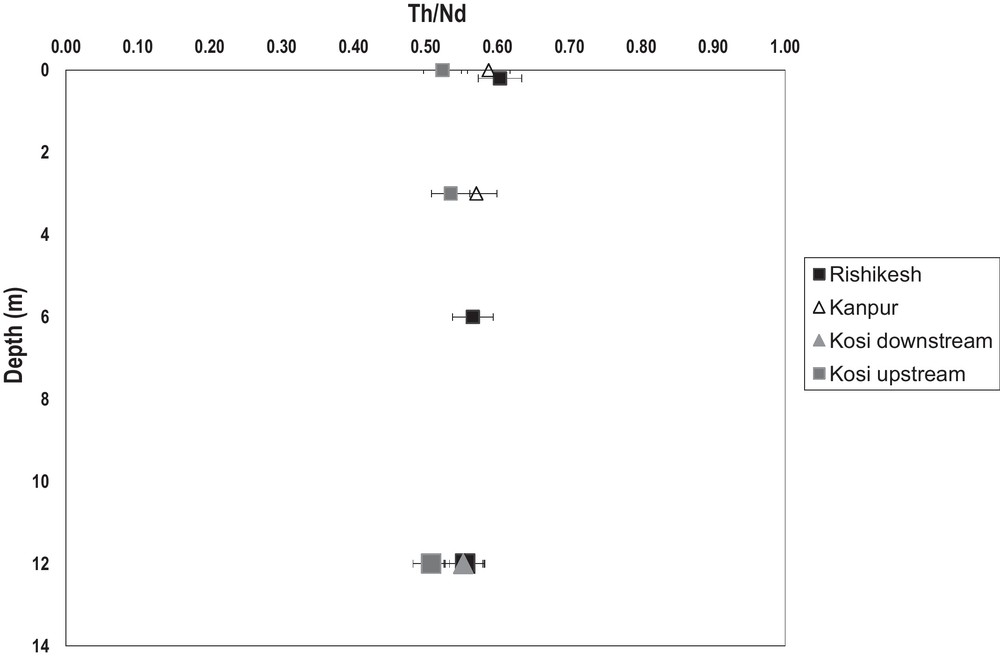
Depth-variations of Th/Nd ratios for the sediments of the Rishikesh (black squares), Kanpur (white triangles), Kosi downstream (grey triangles) and Kosi upstream (grey squares) sampling locations. As no depth has been allocated to the bedload, these latter and bank samples were defined for this graphic at a depth of 12 m.
Variations des rapports Th/Nd en fonction de la profondeur pour les sédiments de rivière collectés à Rishikesh (carrés noirs), Kanpur (triangles blancs), Kosi aval (triangles gris) et Kosi amont (carrés gris). Comme les profondeurs des sédiments de berge et de certains sédiments de fond ne sont pas définies, une valeur arbitraire de 12 m a été utilisée.

Solving Eqs. (1)–(4) with the above intervals of a priori values for the mobility parameters leads to transfer times of 90 ky to 170 ky for bedload sediments collected between Rishikesh and Kanpur (with k₂₃₈ leaching coefficients ranging from 10.3 × 10⁻⁵ y⁻¹ to 0.66 × 10⁻⁵ y⁻¹) (Fig. 4, Table 2a), and from 100 to 170 ky for the Kosi river (with a k₂₃₈ parameter ranging from 4.3 × 10⁻⁵ y⁻¹ to 1.3 × 10⁻⁵ y⁻¹) (Fig. 4, Table 2b). The results of the model also suggest that the different mobility parameters depend on each other and on the transfer time. Thus, the above values of sediment transfer time for both Ganges and Kosi rivers are linked to the value of the k₂₃₈ leaching parameters (Fig. 5a), whereas the ratios k₂₃₈/f₂₃₈ and k₂₃₄/f₂₃₄ are correlated with each other (Fig. 5b).

Fig. 4
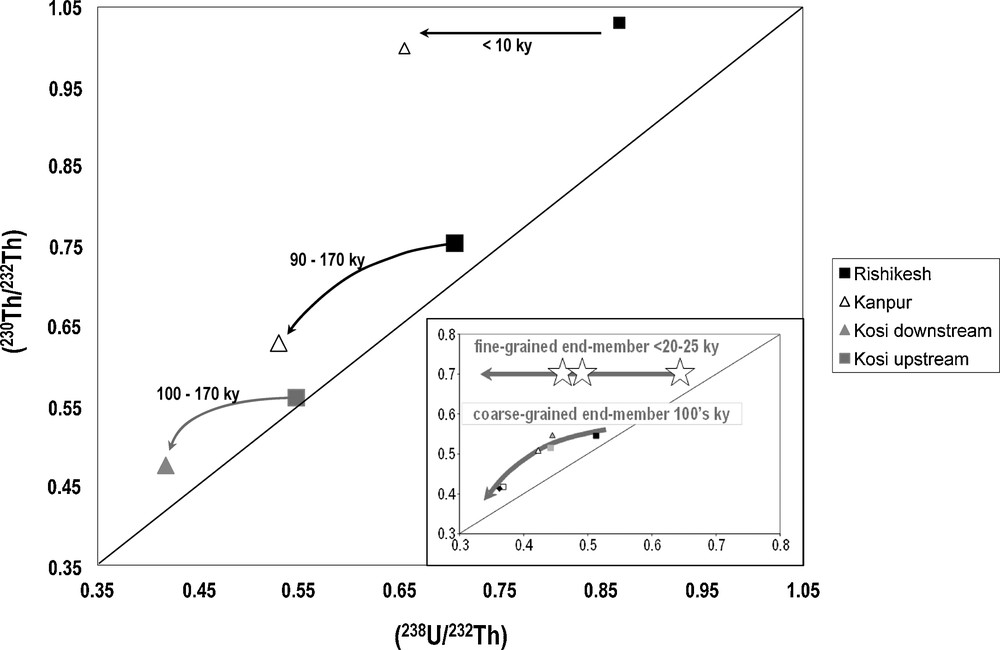
Time interpretation for the U-Th variations of river sediments in the (²³⁰Th/²³²Th) vs (²³⁸U/²³²Th) diagram. Insert: previous estimates based on U-Th data from Gandak and Ganges sediments (Granet et al., 2010).
Interprétation en terme de temps de transfert des variations U-Th des sédiments dans le diagramme (²³⁰Th/²³²Th) versus (²³⁸U/²³²Th). Encart: estimations faites à partir des données U-Th des sédiments de la Gandak et du Ganges (Granet et al., 2010).

Time (ky)	k₂₃₈ (10⁻⁵ y⁻¹)	k₂₃₄ (10⁻⁵ y⁻¹)	f ₂₃₈	f ₂₃₄	k₂₃₄/k₂₃₈	f₂₃₄/f₂₃₈
Upper Ganges between Risikesh and Kanpur (coarse-grained sediments)
93	10.3	11.4	7.70	8.60	1.1	1.1
169	0.66	0.87	0.42	0.60	1.3	1.4

Kosi (Upstream-Downstream) (coarse-grained sediments)
104	4.3	6.0	3.2	4.6	1.4	1.4
167	1.3	1.3	0.94	1.0	1.0	1.1

Upper Ganges between Risikesh and Kanpur (fine-grained sediments)
0.38	71.9	72.8	1 × 10⁻⁸	1 × 10⁻⁸	1.0	1.0
5.4	14.3	18.6	7.50	11.0	1.3	1.5

Fig. 5
(a) Plot of the k₂₃₈ parameter against transfer time for the 7500 plausible solutions derived for the model applied to the coarse-grained sediments of the Upper Ganges. (b) Plot of the k₂₃₄/f₂₃₄ ratio against the k₂₃₈/f₂₃₈ ratio for the 7500 plausible solutions derived for the model applied to the coarse-grained sediments of the Upper Ganges.
(a) Variation du paramètre k₂₃₈ en fonction du temps de transfert pour les 7500 solutions plausibles obtenues à partir du modèle appliqué sur les sédiments grossiers du Ganges amont. (b) Variation du rapport k₂₃₄/f₂₃₄ en fonction du rapport k₂₃₈/f₂₃₈ pour les 7500 solutions plausibles obtenues à partir du modèle appliqué sur les sédiments grossiers du Ganges en amont.

Even if it is clear that supplementary sediment samples would be required to get a better precision of the coarse-grained sediment transfer time, the important point to stress here, is that the new data obtained for the Upper Ganges and Kosi rivers confirm the long transfer time of bank sediments within alluvial plains of the Ganges river system (Granet et al., 2007, 2010). This result might be surprising in the light of ¹⁰Be data for instance (Lupker et al., 2012b), which indicates that the denudation rates are one order of magnitude shorter than the above U/Th transfer times. A specific study comparing the results of the U-Th and ¹⁰Be methods is certainly required to constrain the origin of such an apparent discrepancy. This, however, is beyond the scope of this study.

The same solving approach applied to the fine-grained sediment end-member from the upstream part of the Ganges, between Rishikesh and Kanpur, gives a residence time < 10 ky, with a k₂₃₈ leaching coefficient of about 10⁻⁶ y⁻¹ (Table 2, Fig. 4). Once again, this is very similar to the maximum residence time proposed for the fine-grained sediments at the scale of the Narayani-Gandak river (in Granet et al., 2010). It can, however, be noticed that the above calculation has been performed with sediments which are not totally similar in terms of grain size, and hence that this maximum value could be underestimated. This is nevertheless not really important, as it will be shown in section 5.2 that the fine-grained sediment transfer time can be constrained independently.

5.1.2 Origin of the upstream–downstream U and Th variations

In the frame of the above scenario, which assumes that the budget of U and Th nuclides in the sediments of the Indo-Gangetic plain rivers is controlled by both the secondary weathering processes modifying the sediments during their transfer across the plain and the duration of this transfer, the new data imply that: (a) the (²³⁰Th/²³²Th) and (²³⁸U/²³²Th) activity ratios of sediments eroded along the Himalayan range and carried by the rivers can be different from one river to another when entering the plain; and (b) that Th and (²³⁸U/²³²Th) activity ratios of the fine-grained and coarse-grained sediments can also differ within a single river, when entering the plain. If these activity ratios record those of the source rocks, from where the sediments originate, then the data indicate that the lithologies controlling the U-Th budget of the sediments have variable (²³⁸U/²³²Th) and hence (²³⁰Th/²³²Th) activity ratios at the scale of the Himalayan Range. The Sr isotope ratios of the sediments at the outlet of the Himalayan range show much stronger variations than those of Nd (Lupker, 2011; Lupker et al., submitted), and are most likely the result of variable contributions of a “Lesser Himalaya” (LH) component to these sediments, as these rocks are known to be characterized by high Sr isotopic ratios (Singh et al., 2008, and references therein). However, it has been shown that the (²³⁸U/²³²Th) activity ratios of the three main Himalayan structural units (i.e. the High Himalayan Crystalline, the Lesser Himalaya and the Tethys Sedimentary Series) are quite similar (Granet et al., 2007). This implies similar average U/Th and hence Th activity ratios for the source of Himalayan sediments, and hence does not favor the above scenario which assumes that the variations of the Th and U/Th ratios of the sediment at the outlet of the Himalayan Range reflect the U-Th variations of the sediments source rocks. Nevertheless, it is worth noting that the rock database used for constraining the mean U/Th ratios of the three main Himalayan lithologies is probably not entirely representative of the whole Himalayan Range, as it mainly comprises rocks from the Central Nepal Himalaya. In addition, it is not perfectly adapted to estimate the U/Th ratios of these units, as the budget of U and Th in sediments could be significantly affected by the presence of minor lithologies such as leucogranites and black shales, which are U and Th-rich (Chabaux et al., 2001; Singh et al., 2003). The geographical repartition of such specific lithologies is not perfectly known. Their occurrence along the High Range might control the variations of the (²³⁸U/²³²Th) and (²³⁰Th/²³²Th) activity ratios in the river sediments at the outlet of the Range. The analysis of pebbles collected in different Himalayan rivers, as done for the Narayani-Gandak river (Granet et al., 2010), could provide additional information to test this hypothesis. But at this stage and keeping in mind the above limitations, the data base for estimating the average U/Th ratio of the Himalayan structural units rather excludes a scenario that considers the variations of the (²³⁸U/²³²Th) and (²³⁰Th/²³²Th) activity ratios in the Himalayan sediments at the outlet of the High Range to be the result of the variabilities of the U-Th signatures of the source rocks.

Therefore, as an alternative, we propose that the sediments, which arrive in the Indian plain, have been weathered sufficiently long time to allow for a modification of their U-Th values. It has been shown that the sediments carried by the Kali Gandaki river, one of the main Nepalese streams flowing within the Himalayan range, have been weathered for a relatively long period (up to 100 ky) before their removal and transport by the rivers (Granet et al., 2007). These weathering processes can fractionate U and Th and produce sediments with (²³⁸U/²³²Th) and (²³⁰Th/²³²Th) activity ratios different from those of the unaltered Himalayan rocks. In this case, variations in the intensity of these weathering processes along the High Range might explain why the sediments of the different Himalayan rivers have different U/Th ratios when they enter the Indian plain. The difference observed in the U-Th systematics of fine-grained sediments and coarse-grained sediments in the Himalayan rivers at the outlet of the range would then indicate that in function of the granulometry: (1) the sediments originate from different geographical areas or from different pedological horizons; or (2) the sediments are transported over different time-scales. In order to better constrain these hypotheses, it is now of prime importance to study in detail the U-Th systematics of the sediments from the High Range of the Himalaya.

5.2 Variations of the U and Th isotopes ratios in the fine-grained sediments at the outlet of the Ganges river

As for sediments of the two other sampling locations, the Ganges sediments collected at its outlet, before the confluence with the Brahmaputra, display a relatively wide range of variations in their (²³⁸U/²³²Th) and (²³⁰Th/²³²Th) activity ratios, with low values in bedload sediments and high values in the suspended sediments (Table 1, Fig. 6a). In the isochron diagram (Fig. 6a), the data points also define linear trends, which again might reflect mixing (or sorting) relationships between a coarse-grained and a fine-grained sediment end-member. In detail, however, the data points plot along different mixing trends, relatively close to each other for all the suspended sediments collected in 2008, whereas the 2004 data points plot clearly along a different trend. Such a difference suggests that the U-Th characteristic of the fine-grained sediment end-members can vary significantly from one year to another and probably also within a year; significant variations of the (²³⁸U/²³²Th) and (²³⁴U/²³⁰Th) ratios are observable, whereas the Th and U activity ratios remain more or less invariant for the different sampling periods (2004 and 2008). If the U-Th variations between sediments collected in 2008 and 2004 do not result from a sampling bias, they imply that the transfer of sediments for the Ganges is not stationary over a few years, or even a few months. The immediate corollary is that the transfer time of the fine-grained end-member of the Ganges sediments or at least of one of its components is much shorter than 10 to 20 ky (Granet et al., 2010; previous section), probably of the order of the year or less.

Fig. 6
(a) Plot of the sediment data points in the (²³⁰Th/²³²Th) versus (²³⁸U/²³²Th) diagram for Harding bridge samples. Larger symbols are used to indicate bedload and bank river sediments, whereas the same but smaller symbols are used to indicate suspended river materials. (b) Comparison with data points of suspended sediments collected in the Chambal river, the Himalayan rivers at the outlet of the Himalaya range, and the Himalayan river in the plain.
(a) Représentation dans le diagramme (²³⁰Th/²³²Th) versus (²³⁸U/²³²Th) des données des sédiments collectés à Harding Bridge. Les symboles plus gros indiquent les sédiments de fond/sédiments de berge, les mêmes symboles mais plus petits sont utilisés pour les sédiments en suspension. (b) Comparaison avec les données des sédiments en suspension pour la Chambal, les rivières himalayennes en sortie de chaine, et les rivières himalayennes dans la plaine.
Data source: this study–Granet et al., 2010.

The geochemical variations in the fine-grained sediment end-member are not only reflected by the U/Th ratios but also by major element concentrations and deuterium isotope ratios in sediments regularly collected at the outlet of the Ganges over the 2002–2010 years/period (Lupker et al., 2012a). These latter are assumed to be the result of changes in the proportion of sediment contributions from the South Ganges tributaries (mainly the Chambal river) and the Himalayan rivers. Although the number of Chambal sediments analyzed for U and Th is small (this study; Sarin et al., 1990), the position of these sediment data points in the isochron diagram and in the (²³⁴U/²³⁸U) versus (²³⁰Th/²³⁸U) diagram (not shown) indicates that this assumption cannot be upheld as an explanation for the U-Th variations in the Ganges sediment end-member. In the isochron diagram for instance, the data points representative of the Chambal suspended sediments plot between the suspended 2008 and 2004 sediments and, therefore, cannot be a mixing end-member (Fig. 6b). An alternative mixing scenario, which could be proposed to explain the difference between 2004 and 2008 suspended sediments (Fig. 6b), would be to interpret the particular U-Th characteristics of the 2004 sediments by a stronger sediment contribution from upstream Ganges tributaries relative to plain sediments (sediments from Gandak and Ghaghara river on the Indian plain for instance). However, again, this scenario fails when looking at the position of the data in the (²³⁴U/²³⁸U) vs (²³⁰Th/²³⁸U) diagram (not shown).

Not only for these reasons, but also because the temporal variations are observed for the (²³⁸U/²³²Th) activity ratios (and ²³⁰Th/²³⁸U ratios) and not for the (²³⁰Th/²³²Th) (nor the (²³⁴U/²³⁸U) ratios) at the outlet of the Ganges, we suggest that these variations may reflect annual changes in the degree of weathering of the Ganges suspended sediments. In such a scenario the lower U/Th ratios of the 2004 suspended sediments point to a smaller U loss and hence a smaller degree of weathering than in the case of the 2008 suspended sediments. Such an explanation is consistent with the observation that the amount of carbonates in the 2004 sediments (6 to 8%) is higher than in the 2008 sediments (3–4%) (carbonate concentrations in Lupker et al., 2012a). It may be related to the fact that in 2004 the monsoon was much less intense across the whole Indo-Gangetic plain than in 2008 (data from the India Meteorological Department, http://imd.gov.in/section/hydro/distrainfall/districtrain.html). Such a relation between the weathering intensity of sediments and the rainfall intensity is quite possible in view of the relationships between weathering fluxes carried by rivers and the river discharge observed at both regional or local scale (Millot et al., 2002; Olivia et al., 2003; Viville et al., 2012 and references therein).

5.3 U-Th disequilibrium in the bedload sediments of the Ganges outlet

As observed in the isochron diagram (Fig. 6), the (²³⁸U/²³²Th) and (²³⁰Th/²³²Th) activity ratios of the bedload sediments collected at the outlet of the Ganges basin vary significantly over the 2004–2008 period. The range of variation is smaller than observed for the upstream and dowstream sediments of the Upper Ganges or the Kosi river. It is, however, very similar to the upstream-downstream variation in the Gandak river sediments (Granet et al., 2007). Such annual variations within a single location are unexpected for a scenario of long sediment transfer time (≈ 100 ky or more) within the plain and might question the reliability of such estimates.

Looking in more details at the data, one observes that the two samples with the lowest (²³⁸U/²³²Th) and (²³⁰Th/²³²Th) activity ratios are the most enriched in U and Th (Table 1). In addition, these two samples have relatively high Zr and Hf concentrations, whereas the sample with the highest (²³⁰Th/²³²Th) activity ratio has lower Zr content (unpublished data, France-Lanord personal communication). This certainly indicates that the observed variations result from variation in the proportion of minor heavy minerals within the sediments; Garzanti et al. (2010) have indeed shown that Th and U in bedload sediments are mainly contained in minor minerals (zircon, monazite, allanite and xenotime), whereas in the suspended sediments they are mainly carried by clay minerals. The rock dissolution and grinding procedure was modified a few years ago to avoid the existence of residual and undissolved minerals (Granet et al., 2010) and, thus, also applied in this study. It allows for a complete dissolution of minerals; this is validated by U and Th concentration reproducibility tests of Ganges river sediments, but also by the good consistency obtained in this study between the Th concentrations determined by TIMS and by ICP-MS (Fig. 7); the ICP-MS determinations have been performed after a complete digestion of the sample by Li metaborate fusion. We therefore consider that the observed variation of the Th and U/Th activity ratios in the Ganges sediments over the 2004–2008 period is real and not a consequence of analytical bias. Such a variation might point to a very fast transfer of the coarse sediments (or at least a part of it) within the Ganges basin as already proposed for the fine-grained sediment end-member. In this case, the upstream-downstream variation reported for the (²³⁰Th/²³²Th) and (²³⁸U/²³²Th) activity ratios in sediments of the Ganges tributaries (Kosi river, Ghaghara river, Gandak river, Upper Ganges river) can no longer be interpreted in terms of long transfer time. They should rather be interpreted in terms of mineral sorting along the rivers flow path (with logically preferential upstream depositions of heavy minerals). Th and U/Th activity ratio variations in the sediments at the Ganges outlet suggest that the heavy minerals have low (²³⁰Th/²³²Th) and (²³⁸U/²³²Th) ratios. This would imply, in contrast to what is expected, that sediments in the alluvial plain are more enriched in heavy minerals than the upstream sediments. In addition, the Sr and Nd isotopic data in the sediments of the Gandak river do not point to any upstream-downsteam mineral sorting (Granet et al., 2007). Similarly, the REE patterns normalized to Upper Continental Crust values in the sediments of the Ganges tributaries do not really change from upstream to downstream, whereas it should vary if there was mineral sorting involving heavy minerals such as zircon (Fig. 8). Thus, all these observations and reasonings suggest that the (²³⁰Th/²³²Th) and (²³⁸U/²³²Th) activity ratio variations in the sediments from the Ganges tributaries cannot be interpreted in terms of mineral sorting, and hence reflect long transfer time for the sediments within the plain. It is therefore a priori difficult to involve short sedimentary transfer time to account for the U-Th variations observed in the bedload collected at the Ganges basin outlet over the period 2004–2008. We propose for this reason that such variations might simply be linked to the sampling procedure of the bedload by dredging, which would not allow for the collection of a representative sediment sample especially with respect to the amount of minor minerals. The difference in the mineral densities, combined with the local dynamics of stream waters might cause local redistributions of sediments and minerals on the river bottom with formations of “placer” enriched in heavy minerals and “anti-placer” zones depleted in heavy minerals (Garzanti et al., 2010). Thus, dredging might imperfectly sample all these different sediment types and result in an artificial mineralogical and, hence, U-Th variability when different bedload sediments have been collected at different periods. The real impact of such a sampling bias is, however, difficult to correctly assess on the basis of our data alone. It obviously creates an additional uncertainty on the estimated sediment transfer time. However, it seems that estimates based on bank sediment analysis and not on dredged bedloads, as done for the Gandak and Ghaghara rivers, are probably more reliable. Indeed such samples are composite samples (see Section 3), which probably allow one to get a more representative coarse-grained sediment than by dredging.

Fig. 7
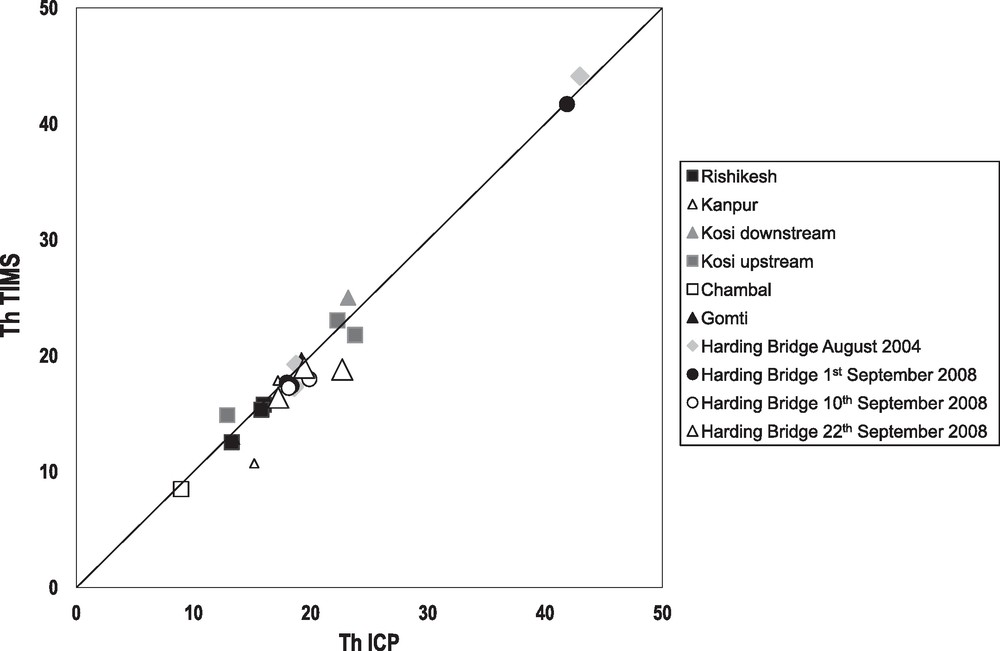
Comparison of the Th concentration measurements of bank and bedload sediments by TIMS and ICP-Ms. TIMS data were obtained by isotope dilution and acid dissolution in Strasbourg (this study). ICP-Ms data were analyzed at Centre de Recherches Pétrographiques et Géochimiques (CRPG) in Nancy (France) after complete digestion of the sample by Li metaborate fusion. (France-Lanord, pers. com.)
Comparaison des concentrations en Th dans les sédiments grossiers mesurées par TIMS et par ICP-MS. Les données par TIMS ont été obtenues après dilution isotopique et dissolution acide à Strasbourg (cette étude). Les données par ICP-MS ont été obtenues au Centre de Recherche Pétrologique et Géochimique (CRPG) à Nancy (France) après fusion au métaborate de Li (France-Lanord, com. pers.).

Fig. 8
REE variations normalized to Upper Continental Crust values for the bedload or bank sediments from Rishikesh (black squares), Kanpur (white triangles), Kosi downstream (grey triangles) and Kosi upstream (grey squares) rivers. (REE data: France-Lanord, pers. com.)
Variations des terres rares normalisées aux valeurs de la croûte continentale supérieure pour les sédiments grossiers collectés à Rishikesh (carrés noirs), Kanpur (triangles blancs), Kosi aval (triangles gris) et Kosi amont (carrés gris) (données : France-Lanord, com. pers.).

6 Conclusions

The new U and Th data presented in this study for suspended and coarse-grained sediments (bedload and bank sediments) from the Upper Ganges and the Kosi rivers are entirely consistent with the ²³⁸U-²³⁴U-²³⁰Th-²³²Th systematics obtained previously for the Ganges main stream and two of its tributaries (Granet et al., 2007, 2010): an upstream–downstream variation of the ²³⁸U-²³⁴U-²³⁰Th disequilibria in the sediments along the rivers within the Ganges plain, with different variation trends for suspended and coarse-grained sediments. Assuming that such trends result from the combination of both radioactive decay and U-Th fractionations associated to the sediment weathering during its transit and storage in the plain, the above data confirm the occurrence of very different sediment transfer times which strongly depend on their grain size: much shorter transfer time for the fine-grained sediment (a few ky or less) than for the coarse-grained sediment (100 ky or more).

The fine-grained sediment end-members collected at the Ganges outlet in 2004 and 2008, however, show significantly different ²³⁴U/²³⁰Th activity ratios. This difference is most probably an indication of a quick transit for the fine-grained sediment end-member (of the order of the year or less) within the plain. It is proposed that the variation of the U/Th ratio in this sediment end-member results from a significant difference in the intensity of weathering of these sediments during their transfer in the rivers from one year to another. Conversely, the U-Th variations observed in the bedload collected at the Ganges basin outlet over the period 2004-2008 cannot result from short sediment transfer time. They probably are the result of dredging; this kind of sampling might not allow for the collection of a representative sediment sample, especially with respect to minor minerals that carry U and Th. It results in an artificial U-Th variability in the different bedload sediments collected at different periods and certainly induces an uncertainty on the estimated sediment transfer time. This uncertainty, however, could be reduced when bank sediments can be studied instead of bedload sediments.

Acknowledgments

The financial support by the INSU/CNRS, the REALISE network and the University of Strasbourg over the 2001-2010 period has allowed the development of the study of ²³⁸U-series disequilibria in sediments and more generally on environmental samples in Strasbourg laboratory. All these French research organizations are warmly thanked for their support. The Simone and Cino Del Duca Foundation is also thanked for support to FC in 2005. Estelle Blaes acknowledges the Region Alsace and the CNRS (BDI), France, for the funding of her Ph.D. scholarship, and the University of Strasbourg for a temporary lecturer (ATER) position in 2010. A part of this study has been performed in the frame of the “Calimero” ANR project. M. Lupker and C. France-Lanord are thanked for the samples provided for this study. Discussions with P. Ackerer, C. France-Lanord and M. Lupker during the course of this study were very appreciated. We are also very grateful to F. Delay for his insightful comments on the manuscript. Review by M. Lupker helped to improve the manuscript. This is a EOST-LHyGeS contribution.

Appendix A Solving approach for model equations

The gain and loss model used to interpret the radioactive disequilibrium variations along the river stream is described by the ordinary differential equation system given in section 2 (Eqs. (1) to (4)), whose analytical solutions can be found in Chabaux et al. (2012). A stochastic bound constrained optimization algorithm based on a particle swarm technique has been constructed and used to perform the calculation of the leaching rate and input flux constants (k₂₃₈, f₂₃₈ coefficients) of each nuclide and the transfer time. The optimization algorithm uses the measured (²³⁴U/²³⁸U), (²³⁰Th/²³⁸U), (²³⁸U/²³²Th) and (²³⁰Th/²³²Th) activity ratios of each sample as constrains for the model.

A.1 Particle Swarm Optimization (PSO) algorithm

Classical techniques using population-based evolutionary systems such as particle Swarm Optimization (PSO, e.g., Kennedy and Eberhart, 1995) are intended to mimic the evolution of a social organism, in which individuals (also called “particles” or “bees”) describe the candidate solution to a designed problem. Each particle flies through a prescribed and bounded multidimensional space to find the optimal solution. Each individual evaluates its current position with reference to a goal (the objective function at each iteration). Particles are allowed to share memories of their best position in a prescribed local neighborhood. These positions are then used to update particle velocities and positions (see the following Eqs. (5) and (6)). Let M be the swarm size and D the size of the search domain (number of parameters). In the original PSO version, each M-particle moves inside the D-dimensional search space according to:

ν_{i j}^{n + 1} = ν_{i j}^{n} + c_{1} r a n d_{1} (P_{i j}^{n} - x_{i j}^{n}) + c_{2} r a n d_{2} (P_{g i}^{n} - x_{i j}^{n})

(5)

x_{i j}^{n + 1} = x_{i j}^{n} + Δ t_{n} ν_{i j}^{n + 1}

(6)

where

x_{i j} (t_{n}) = x_{i j}^{n}

is the position vector of the ith-particle for the jth-parameter at the time iteration t_n and Δt_n is the time step,

P_{g} (t) = (P_{g 1} (t), P_{g 2} (t), ..., P_{g D} (t))

is the global best swarm position vector i.e. the best sought position among the whole set of individuals and over all the times steps between 0 and t_n and

P_{i} (t) = (P_{i 1} (t), P_{i 2} (t), ..., P_{i D} (t))

is the best position experienced by particle i over all the time steps between 0 and t_n. Each particle can be represented by the position vector

x_{i} (t) = (x_{i 1} (t), x_{i 2} (t), ..., x_{i D} (t))

and the velocity vector

ν_{i} (t) = (ν_{i 1} (t), ν_{i 2} (t), ..., ν_{i D} (t))

for i = 1,…,M and j = 1,…,D. The parameters c₁ and c₂ are called the acceleration coefficients and rand₁, rand₂ are random numbers distributed uniformly between 0 to 1. The downside of PSO is that global convergence cannot be guaranteed. Classical PSO systems must be bound states (or conditioned states) to guarantee collectiveness of the swarm. Therefore quantum PSO (QPSO) technique has been developed by Sun et al. (2004). In traditional PSO, particles move “freely” in a finite zone whereas in QPSO, particles, bounds or more exactly prescribed probability density functions rule the particle motion at any position in the whole feasible search space.Quantum-behaved Particle Swarm Optimization (QPSO) algorithm

In QPSO approach, all particles move under quantum-mechanical rules rather than classical Newtonian random motion. In quantum mechanics, the governing equation is the well-known time-dependent Schrödinger equation

j ℏ \frac{\partial}{\partial t} Ψ (x, t) = \hat{H} Ψ (x, t)

(7)

where

\hat{H} = - \frac{ℏ^{2}}{2m} \nabla^{2} + V (x)

is a time-independent Hamiltonian operator, ℏ is Planck's constant, m is the mass of the particle and V(x) is the potential energy of the particle at the vector position x.

The unknown in the previous Schrödinger equation is the wave function $Ψ (x, t)$ . In the QPSO approach, the wave function is a spatially distributed function measuring the probability of a particle motion and obeying to the norm ${|Ψ (x, t)|}^{2}$ . Clerc and Kennedy, 2002 showed that convergence of the algorithm might be achieved if each i-particle moves toward its local attractor. During the optimization procedure, all “bees” are flying towards the optimum location defined by vector p(t).

Let the ith-particle local attractor be a vector p_i with coordinates in the D-dimensional parameter space $p_{i j} (j = 1,..., D)$ with:

p_{i j} (t) = ϕ P_{i j} (t) (1 - ϕ) P_{g j} (t), ϕ = \frac{c_{1} r a n d_{1}}{c_{1} r a n d_{1} + c_{2} r a n d_{2}},1 \leq j \leq D

(8)

Equation (8) requires only two random numbers and can be seen as a stochastic local attractor of the ith-particle. Here, c₁ is called the cognitive parameter and c₂ is called the social parameter. The random scalar φ is uniformly distributed between 0 to 1. In the QPSO approach, the original PSO system is considered as a quantum-like system, making that each particle has a quantum behavior with motions ruled by the wave probability density function (pdf). Different attractive potential field functions have been tested. A “reasonable” potential field selection is intended to attract particles towards the center of the potential field. However, such convergence speed is achieved while sacrificing an even search activity over the whole space of parameters.

For the sake of simplicity let us take particles moving in a one-dimensional parameter space and let us define r as r = x-p, where x is the current particle position and p is the average best position. We present here the simplest potential, the so-called delta-well function given by $V (x) = - γ δ (x - p) = - γ δ (r)$ where γ is proportional to the depth of the well. In QPSO optimization, we are only interested in bounds states given by the stationary states i.e. the wave envelope function (Mikky and Kishk, 2005). Assuming the principle of separation for time and space variables in the wave function, the time-independent solution of the Schrödinger equation, i.e., the so-called wave envelope function is given by:

ψ (r) = \frac{1}{\sqrt{L}} e^{- |r| / L}

(9)

where E represents the particle energy,

ψ (r)

the wave envelope, L = ℏ²/mγ is the characteristic length of the potential well, m the mass particle, γ the intensity (depth) of the potential well and |r| = |x-p|. We note that this solution is very similar to the classical solution to a homogeneous diffusion problem with a delta-Dirac function as sink-source term.

It can be shown that following this potential field, we have an analytical expression for the probability density function (pdf) of the particle's motion. The probability density function Q is thus given by

Q (r) = {(ψ (r))}^{2} = \frac{1}{L} e^{- 2 |r| / L}

(10)

and the corresponding probability distribution function F is

F (r) = 1 - e^{- 2 |r| / L}

(11)

Now, one needs to link the above quantum description provided by the wave function (Eqs. (10) and (11)) and a Newtonian description of the particle motion. The next step is therefore to measure the position of the particle i.e. “collapsing the quantum state to the classical state”. A classical Monte Carlo method is used to simulate the process of measurement. The procedure of simulation is described as follows. Let v be the random number uniformly distributed in the interval (0, 1). Substituting v for F(r) leads to $1 - v = e^{- 2 |r| / L}$ and because u = 1–v is also a random number of uniform distribution between 0 and 1, it becomes obvious that $r = \pm L / 2 \ln (1 / u)$ .

For time dependent Lⁿ (iterative procedure), i.e. $L^{n} = L (t_{n})$ and using $r (t_{n}) = x (t_{n}) - p (t_{n})$ , one can obtain the random sequence of the position as,

x (t_{n + 1}) = p (t_{n}) \pm \frac{L (t_{n})}{2} ln (1 / u)

(12)

For the D-dimensional search space, the particle position is updated at each iteration step by using:

x_{i j}^{n + 1} = p_{i j}^{n} \pm \frac{L_{i j}^{n}}{2} ln (1 / u), u \sim U (0,1)

(13)

where u is a random number with uniform distribution between 0 and 1 and

p_{i j}^{n}

is the ith-particle local attractor for its coordinate j in the D-dimensional parameter space at time iteration t_n. In QPSO, a global point named mainstream vector or mean best position of the population is introduced. The global point, denoted μ, is defined as the mean of the individual best positions among all particles,

μ (t_{n}) = (μ_{1}^{n}, ... μ_{D}^{n}) = (\frac{1}{M} \sum_{1}^{M} P_{i 1}^{n}, ..., \frac{1}{M} \sum_{1}^{M} P_{i D}^{n})

(14)

where M is the population size and P_i is the personal best position of particle i. To guarantee the convergence of the QPSO algorithm, the crucial condition, L(t)→0 when t→+∞ must be satisfied (more details in Sun et al. (2004)). Yielding to a possible expression of L(t) in the form

L_{i j}^{n} = 2 α (μ_{j}^{n} - x_{i j}^{n})

Hence, one has

x_{i j}^{n + 1} = p_{i j}^{n} \pm α (μ_{j}^{n} - x_{i j}^{n}) \ln (1 / u)

(15)

where the parameter α is known as the contraction–expansion coefficient. The latter can be tuned to control the convergence speed of the algorithms. Other attractive potential fields have been investigated in the present study such as Harmonic Oscillator or Square Well potential. In essence, all other potential field distributions are compatible with the notion of convengence beard by QPSO algorithms (Yukawa potential, Woods-Saxon potential, etc.) but they do not lead to analytical solutions to the particle motion pdfs which are a crux point to obtain QPSO procedures easy to implement and rapid to calculate. The simplest way of improving QPSO without changing the potential field (and the pdf of particle motion) discussed above is to select and control the coefficient α.

With exceptions of the swarm size (Number of bees), the number of maximum iterations and the problem dimension D, the most important parameter is the contraction-expansion coefficient which is crucial to the dynamical behavior of each individual and the convergence speed. Results from several stochastic simulations reported in Sun et al. (2004) showed that the particle position either converges to its local optimum when α < 1.78 or diverges when α > 1.8. Tο prevent blowing the swarm apart, we set the contraction-expansion factor to e^γ₀ ≈ 1.781 where γ₀ ≈ 0.577 is the Euler-Mascheroni constant. For practical consideration, the Euler-Maclaurin method is used to generate α. Values for the cognitive parameter c₁ and the social parameters c₂ are better to be chosen even at c₁ = c₂ = 2 (see Mikki and Kishk, 2005).

A.2 Optimization of the determination of time-scales of sedimentary transfer using QPSO

For weathering optimization problem solved by QPSO-based method, our objective function is the relative squared error RSE defined by:

R S E = \sum_{k = 1, N p t, l = 1, N a c t} {(\frac{F (l, k) - F^{exp} (l, k)}{σ (l, k)})}^{2}

(16)

where F (l, k) is the l-activity ratio at experimental point k defined in the “assemble section” of the input file, F^exp (l, k) is the measured ratio and σ (l, k) the corresponding error bar at the given point. The optimization process using QPSO is outlined below.

Choose a suitable potential well (Delta well, Harmonic well, Square well). Solve the Schrödinger equation to get the envelope wave function ψ (r) and then the pdf function of the particle position.

“Collapse” wave function into the bounded region (absolute/relative bounds) using Monte Carlo procedure.

Initialize the swarm of size MaxBee:

fort = 1 to MaxIter until convergence
- Compute the fitness value of each particle with the objective function defined as RSE
- Update the particle best position P_i
- Update the global best position of the swarm P_g
- Compute the mean best position μ of the swarm
for each particle in the swarm
- Update each component of the particle's position and adjust the component x_i
- end for
- Rescale solutions within absolute and relative bounds
- Evaluate convergence
end for

Bibliographie

[Andersen et al., 2009] M.B. Andersen; Y. Erel; B. Bourdon Experimental evidence for ²³⁴U-²³⁸U fractionation during granite weathering with implications for ²³⁴U/²³⁸U in natural waters, Geochim. Cosmochim. Acta, Volume 73 (2009), pp. 4124-4141

[Castelltort and Van Den Driessche, 2003] S. Castelltort; J. Van Den Driessche How plausible are high-frequency sediment supply-driven cycles in the stratigraphic record?, Sediment. Geol, Volume 157 (2003), pp. 3-13

[Castelltort et al., 2004] S. Castelltort; J. Van Den Driessche; J.P. Davy Reply to comment on “How plausible are high-frequency sediment supply-driven cycles in the stratigraphic record? By Jasper”, Sediment. Geol., Volume 164 (2004), pp. 331-334

[Chabaux et al., 2001] F. Chabaux; J. Riotte; N. Clauer; C. France-Lanord Isotopic tracing of the dissolved U fluxes of Himalayan rivers: implications for present and past U budgets of the Ganges-Brahmaputra system, Geochim. Cosmochim. Acta, Volume 65 (2001), pp. 3201-3217

[Chabaux et al., 2003a] F. Chabaux; J. Riotte; O. Dequincey U-Th-Ra fractionation during weathering and river transport, Rev. Mineral. Geochem., Volume 52 (2003), pp. 533-576

[Chabaux et al., 2003b] F. Chabaux; O. Dequincey; J. Lévèque; J. Leprun; N. Clauer; J. Riotte; H. Paquet Tracing and dating recent chemical transfers in weathering profiles by trace-element geochemistry and ²³⁸U-²³⁴U-²³⁰Th disequilibria: the example of the Kaya lateritic toposequence (Burkina-Faso), C. R. Geoscience, Volume 335 (2003), pp. 1219-1231

[Chabaux et al., 2006] F. Chabaux; M. Granet; E. Pelt; C. France-Lanord; V. Galy ²³⁸U-²³⁴U-²³⁰Th disequilibria and timescale of sedimentary transfers in rivers: Clues from the Gangetic plain rivers, J. Geochem. Explor., Volume 88 (2006), pp. 373-375

[Chabaux et al., 2008] F. Chabaux; B. Bourdon; J. Riotte U-Series Geochemistry in Weathering Profiles, River Waters and Lakes, U-Th Series Nuclides in Aquatic Systems, Elsevier, 2008 pp. 49–104 (Chapter 3)

[Chabaux et al., 2011] F. Chabaux; L. Ma; P. Stille; E. Pelt; M. Granet; D. Lemarchand; R. di Chiara Roupert; S.L. Brantley Determination of chemical weathering rates from U series nuclides in soils and weathering profiles: Principles, applications and limitations, Appl. Geochem, Volume 26 (2011), pp. 20-23

[Chabaux et al., 2012] Chabaux, F., Blaes, E., Stille, P., di Chiara Roupert, R., Dosseto, A., Pelt, E., Ma, L., Buss, H.L., Brantley, S.L. Regolith formation rate from U-series nuclides: Implications from the study of a spheroidal weathering profile in the Rio Icacos watershed. Geochimica et Cosmochimica Acta (2012), . | DOI

[Clerc and Kennedy, 2002] M. Clerc; J. Kennedy The particle swarm: explosion, stability, and convergence in a multi-dimensional complex space, IEEE Trans. Evolutionary Computation, Volume 6 (2002), pp. 58-73

[Davy and Lague, 2009] P. Davy; D. Lague Fluvial erosion/transport equation of landscape evolution models revisited, J. Geophys. Res., Volume 114 (2009)

[DePaolo et al., 2006] D.J. DePaolo; K. Maher; J.N. Christensen; J. McManus Sediment transport time measured with U-series isotopes: Results from ODP North Atlantic drift site 984, Earth Planet. Sci. Lett., Volume 248 (2006), pp. 394-410

[Dequincey et al., 2002] O. Dequincey; F. Chabaux; N. Clauer; O. Sigmarsson; N. Liewig; J. Leprun Chemical mobilizations in laterites: evidence from trace elements and ²³⁸U-²³⁴U-²³⁰Th disequilibria, Geochim. Cosmochim. Acta, Volume 66 (2002), pp. 1197-1210

[Dosseto et al., 2006] A. Dosseto; B. Bourdon; J. Gaillardet; L. Maurice-Bourgoin; C. Allègre Weathering and transport of sediments in the Bolivian Andes: time constraints from uranium-series isotopes, Earth Planet. Sci. Lett., Volume 248 (2006), pp. 759-771

[Dosseto et al., 2008a] A. Dosseto; B. Bourdon; S.P. Turner Uranium-series isotopes in river materials: insights into the timescales of erosion and sediment transport, Earth Planet. Sci. Lett., Volume 265 (2008), pp. 1-17

[Dosseto et al., 2008b] A. Dosseto; S.P. Turner; J. Chappell The evolution of weathering profiles through time: new insights from uranium-series isotopes, Earth Planet. Sci. Lett., Volume 274 (2008), pp. 359-371

[Dosseto et al., 2010] A. Dosseto; P.P. Hesse; K. Maher; K. Fryirs; S. Turner Climatic and vegetation control on sediment dynamics during the last glacial cycle, Geology, Volume 38 (2010), pp. 395-398

[Dosseto et al., 2012] A. Dosseto; H.L. Buss; P.O. Suresh Rapid regolith formation over volcanic bed rock and implications for landscape evolution, Earth Planet. Sci. Lett., Volume 337–338 (2012), pp. 47-55

[Galy et al., 2008] V. Galy; C. France-Lanord; B. Lartiges Loading and fate of particulate organic carbon from the Himalaya to the Ganga–Brahmaputra delta, Geochim. Cosmochim. Acta, Volume 72 (2008), pp. 1767-1787

[Garzanti et al., 2010] E. Garzanti; S. Andò; C. France-Lanord; P. Censi; P. Vignola; V. Galy; Y. Najman Mineralogical and chemical variability of fluvial sediments, 1: Bedload sand (Ganga-Brahmaputra, Bangladesh), Earth Planet. Sci. Lett., Volume 299 (2010), pp. 368-381

[Garzanti et al., 2011] E. Garzanti; S. Andò; C. France-Lanord; P. Censi; P. Vignola; V. Galy; M. Lupker Mineralogical and chemical variability of fluvial sediments, 2: Suspended-load silt (Ganga-Brahmaputra, Bangladesh), Earth Planet. Sci. Lett., Volume 302 (2011), pp. 107-120

[Granet, 2007] Granet, M., 2007. Constantes de temps des processus d’érosion et d’altération dans le système himalayen: approche géochimique élémentaire et isotopique par les séries de l’Uranium. Thèse, Université Louis-Pasteur, Strasbourg.

[Granet et al., 2007] M. Granet; F. Chabaux; P. Stille; C. France-Lanord; E. Pelt Time-scales of sedimentary transfer and weathering processes from U-series nuclides: Clues from the Himalayan rivers, Earth Planet. Sci. Lett., Volume 261 (2007), pp. 389-406

[Granet et al., 2010] M. Granet; F. Chabaux; P. Stille; A. Dosseto; C. France-Lanord; E. Blaes U-series disequilibria in suspended river sediments and implication for sediment transfer time in alluvial plains: the case of the Himalayan rivers, Geochim. Cosmochim. Acta, Volume 74 (2010), pp. 2851-2865

[Innocent, 2008] Innocent, C., 2008. Intercomparaison de quatre standards isotopiques de Th synthétisés au BRGM. Premiers résultats. Rapport BRGM/RP-56066-FR. 36 p., (7 ill.).

[Kennedy and Eberhart, 1995] Kennedy J., Eberhart, R.C., 1995. Particle swarm optimization. in Proc. IEEE Conf. Neural Networks IV, Piscataway, NJ.

[Lee et al., 2010] V.E. Lee; D.J. DePaolo; J.N. Christensen Uranium-series comminution ages of continental sediments: case study of a Pleistocene alluvial fan, Earth Planet. Sci. Lett., Volume 296 (2010), pp. 244-254

[Liébault et al., 2012] F. Liébault; H. Bellot; M. Chapuis; S. Klotz; M. Deschatres Bedload tracing in a high-sediment-load mountain stream, Earth Surf. Process. Landforms, Volume 37 (2012), pp. 385-399

[Lupker, 2011] Lupker, M., 2011. Dynamique sédimentaire, érosion physique et altération. chimique dans le système himalayen. Thèse, l’Institut National. Polytechnique de Lorraine, Nancy.

[Lupker et al., 2011] M. Lupker; C. France-Lanord; J. Lavé; J. Bouchez; V. Galy; F. Métivier; J. Gaillardet; B. Lartiges; J.-L. Mugnier A Rouse-based method to integrate the chemical composition of river sediments: application to the Ganga Basin, J. Geophys. Res. Earth Surface, Volume 116 (2011), pp. 1-24

[Lupker et al., 2012a] M. Lupker; C. France-Lanord; V. Galy; J. Lavé; J. Gaillardet; A.P. Gajurel; C. Guilmette; M. Rahman; S.K. Singh; R. Sinha Predominant floodplain over mountain weathering of Himalayan sediments (Ganga basin), Geochim. Cosmochim. Acta, Volume 84 (2012), pp. 410-432

[Lupker et al., 2012b] M. Lupker; P.H. Blard; J. Lavé; C. France-Lanord; L. Leanni; N. Puchol; J. Charreau; D. Bourlès ¹⁰Be-derived Himalayan denudation rates and sediment budgets in the Ganga basin, Earth Planet. Sci. Lett., Volume 333–334 (2012), pp. 146-156

[Lupker et al., submitted] Lupker, M., France-Lanord, C., Galy, V., Lavé, J., Kudrass, H. Increasing chemical weathering in the Himalayan system since the Last Glacial Maximum. Earth Planet. Sci. Lett. (submitted).

[Ma et al., 2010] L. Ma; F. Chabaux; E. Pelt; E. Blaes; L. Jin; S.L. Brantley Regolith production rates calculated with uranium-series isotopes at Susquehanna/Shale Hills Critical Zone Observatory, Earth Planet. Sci. Lett., Volume 297 (2010), pp. 211-225

[Ma et al., 2012] L. Ma; F. Chabaux; E. Pelt; M. Granet; P.S. Sak; J. Gaillardet; M. Lebedeva; S.L. Brantley The effect of curvature on weathering rind formation: evidence from Uranium-series isotopes in basaltic andesite weathering clasts in Guadeloupe, Geochim. Cosmochim. Acta, Volume 80 (2012), pp. 92-107

[Maher et al., 2006] K. Maher; C.I. Steefel; D.J. DePaolo; B.E. Viani The mineral dissolution rate conundrum: insights from reactive transport modeling of U isotopes and pore fluid chemistry in marine sediments, Geochim. Cosmochim. Acta, Volume 70 (2006), pp. 337-363

[Métivier and Gaudemer, 1999] F. Métivier; Y. Gaudemer Stability of output fluxes of large rivers in South and East Asia during the last 2 million years: implications on floodplain processes, Basin Res., Volume 11 (1999), pp. 293-303

[Mikki and Kishk, 2005] Mikki, S., Kishk, A., 2005. Investigation of the quantum particle swarm optimization technique for electromagnetic applications. Antennas and Propagation Society International Symposium, IEEE 2A, 45-48.

[Millot et al., 2002] R. Millot; J. Gaillardet; B. Dupré; C.J. Allègre The global control of silicate weathering rates and the coupling with physical erosion: new insights from rivers of the Canadian Shield, Earth Planet. Sci. Lett., Volume 6095 (2002), pp. 1-16

[Olivia et al., 2003] P. Olivia; J. Viers; B. Dupré Chemical weathering in granitic environments, Chem. Geol., Volume 202 (2003), pp. 225-256

[Paola et al., 1992] C. Paola; P. Heller; C. Angevine The large-scale dynamics of grain-size variation in alluvial basins, 1: theory, Basin Res., Volume 4 (1992), pp. 73-90

[Pelt et al., 2008] E. Pelt; F. Chabaux; C. Innocent; A. Navarre-Sitchler; P. Sak; S. Brantley Uranium-thorium chronometry of weathering rinds: Rock alteration rate and paleo-isotopic record of weathering fluids, Earth Planet Sci. Lett., Volume 276 (2008), pp. 98-105

[Sarin et al., 1990] M. Sarin; S. Krishnaswami; B. Somayajulu; W. Moore Chemistry of uranium, thorium, and radium isotopes in the Ganga-Brahmaputra river system: Weathering processes and fluxes to the Bay of Bengal, Geochim. Cosmochim. Acta, Volume 54 (1990), pp. 1387-1396

[Sear et al., 2000] Sear, D.A., Lee, M.W. E., Oakley, R.J., Carling, P.A., Collins, M.B., 2000. Coarse sediment tracing technology in littoral and fluvial environments: a review. In: Tracers in the Environment edited by F. I, pp. 21–55.

[Singh, 2009] P. Singh Major, trace and REE geochemistry of the Ganga River sediments: Influence of provenance and sedimentary processes, Chem. Geol., Volume 266 (2009), pp. 242-255

[Singh et al., 1993] A. Singh; B.D. Bhardwaj; A.H.M. Ahmad Tectonic setting and sedimentology of Ganga. River sediments, India, Boreas, Volume 22 (1993), pp. 38-46

[Singh et al., 2003] S.K. Singh; T.K. Dalai; S. Krishnaswami ²³⁸U series isotopes and ²³²Th in carbonates and black shales from the Lesser Himalaya: implications to dissolved uranium abundances in Ganga-Indus source waters, J. Environ. Radioact., Volume 67 (2003), pp. 69-90

[Singh et al., 2007] M. Singh; I.B. Singh; G. Muller Sediment characteristics and transportation dynamics of the Ganga River, Geomorphology, Volume 86 (2007), pp. 144-175

[Singh et al., 2008] S.K. Singh; S.K. Rai; S. Krishnaswami Sr and Nd isotopes in river sediments from the Ganga Basin: sediment provenance and spatial variability in physical erosion, J. Geophys. Res., Volume 113 (2008), p. 18p

[Sun et al., 2004] Sun J., Xu W., Feng B., 2004. A global search strategy of quantum-behaved particle swarm optimization. Cybernetics and Intelligent Systems, IEEE Conference, vol. 1, pp. 111–116.

[Vigier et al., 2001] N. Vigier; B. Bourdon; S. Turner; C.J. Allègre Erosion timescales derived from U-decay series measurements in rivers, Earth Planet. Sci. Lett., Volume 193 (2001), pp. 549-563

[Viville et al., 2012] D. Viville; F. Chabaux; P. Stille; M.-C. Pierret; S. Gangloff Erosion and weathering Fluxes in granitic basins: the example of the Strengbach catchment (Vosges massif, eastern France), Catena, Volume 92 (2012), pp. 122-129

[von Blanckenburg, 2005] F. von Blanckenburg The control mechanisms of erosion and weathering at basin scale from cosmogenic nuclides in river sediment, Earth Planet. Sci. Lett., Volume 237 (2005), pp. 462-479

[von Blanckenburg, 2006] F. von Blanckenburg The control mechanisms of erosion and weathering at basin scale from cosmogenic nuclides in river sediment, Earth Planet. Sci. Lett., Volume 242 (2006), pp. 224-239

[Wittmann et al., 2011] H. Wittmann; F. von Blanckenburg; L. Maurice; J.L. Guyot; P. Kubik Recycling of Amazon floodplain sediment quantified by cosmogenic ²⁶Al and ¹⁰Be, Geology, Volume 39 (2011), pp. 467-470

Commentaires - Politique

Ces articles pourraient vous intéresser

Tracing and dating recent chemical transfers in weathering profiles by trace-element geochemistry and ²³⁸U²³⁴U²³⁰Th disequilibria: the example of the Kaya lateritic toposequence (Burkina-Faso)

François Chabaux; Olivier Dequincey; Jean-Jacques Lévèque; ...

C. R. Géos (2003)

Uranium comminution ages: Sediment transport and deposition time scales

Donald J. DePaolo; Victoria E. Lee; John N. Christensen; ...

C. R. Géos (2012)