1 Introduction
There are now a large number of approaches to isotopic geochronology – the use of radioactive decay or other natural nuclear processes to measure the ages of geologic rock formations and features. When applied to sediments and sedimentary rocks, however, isotopic geochronology is typically ineffective, or at least challenging (e.g., Dickin, 1995, Rasmussen, 2005). The more successful approaches to dating sedimentary formations depend on the presence of intercalated volcanic ash layers that are more amenable to common geochronologic methods, or correlation between fossil assemblages that have been dated using volcanic materials. Sedimentary formations that contain neither fossils nor volcanic interbeds are usually not dateable. One of the difficulties with dating clastic sediments is that the rock and mineral grains that comprise them had a prior existence, potentially for a long time, as parts of other rock formations before they were broken down by erosion, transported, and deposited as a sedimentary formation. The challenge for dating is in finding a physical or chemical change that happens at or near the time of sediment deposition, and that expresses itself as a disruption to a radioactive decay system.
Recent attempts at dating clastic sedimentary rocks involve the uranium and thorium radioactive decay series or cosmogenic nuclides. In both cases, there are difficulties in establishing when the isotopic clocks are set, and this difficulty, as well as analytical limitations, translates into considerable uncertainty in the determined age. For the use of U-Th isotopic disequilibrium (e.g. Chabaux and Riotte, 2003; Dosseto et al., 2008; Granet et al., 2007, 2010; Vigier et al., 2001), the assumption is that U and Th are chemically separated (fractionated) during weathering in soils where the sediment originates. For cosmogenic nuclides, which are sensitive to exposure of rock material to the cosmic ray-produced neutrons at the Earth's surface, the exposure age measured in sediments is a combination of the time since deposition and time spent close to the Earth's surface in a soil or regolith before or during transport (Phillips et al., 1997; Bierman and Nichols, 2004).
This article summarizes recent research using the U radioactive decay series, but with a specific approach referred to as the “U comminution age”. The comminution age method (DePaolo et al., 2006) is designed to measure the time that elapses subsequent to bedrock being reduced by physical weathering to small grains–small being defined functionally as less than about 50 μm in diameter. The U radioactive decay series is sensitive to the size of the particles in which the U is contained, as described below. The term comminution refers to any process that accomplishes the reduction of rock material to silty-sand, silt, or clay-sized mineral grains. A key conceptual problem is to determine (or define) when sand and silt-size particles are produced from bedrock. Glacial erosion represents one geologic situation where this time may be well defined.
2 Comminution age model
The decay of 238U to 206Pb occurs in several steps (cf. Dickin, 1995; Ku, 2000). The first few steps in the sequence produce 234U via an intermediate daughter isotope 234Th. In most rocks and minerals that are older than a million years, and even in many that are younger, the 234U/238U ratio is almost exactly equal to the inverse ratio of the decay constants (λ) for these two U isotopes. This condition is referred to as radioactive equilibrium, and implies that the rate of production of 234U by the decay of 238U is equal to the rate of decay of 234U, so that the ratio of 234U/238U is constant and equal to λ238/λ234. The equilibrium condition can also be described in terms of the activity ratio (234U/238U)AR being equal to unity.
In a small sediment grain with diameter of order 10 μm or less, it is impossible for the 234U/238U ratio to be maintained at the equilibrium ratio. The failure to maintain equilibrium is due to the fact that in the process of radioactive decay of 238U, during which a high-energy alpha particle is ejected from the 238U nucleus, the radioactive decay product nucleus 234Th is propelled through the mineral crystal lattice a distance of about 0.034 μm as a result of “recoil” from the ejection of the alpha particle (Fig. 1; cf. Maher et al., 2006a). Consequently, the outermost 0.034 μm layer of the mineral grain will accumulate 234U at a slower rate because some of the 238U-decays will result in the 234Th (eventually to become 234U), being ejected from the mineral grain entirely. The smaller the grain radius, the larger will be the fraction of “missing” 234U.
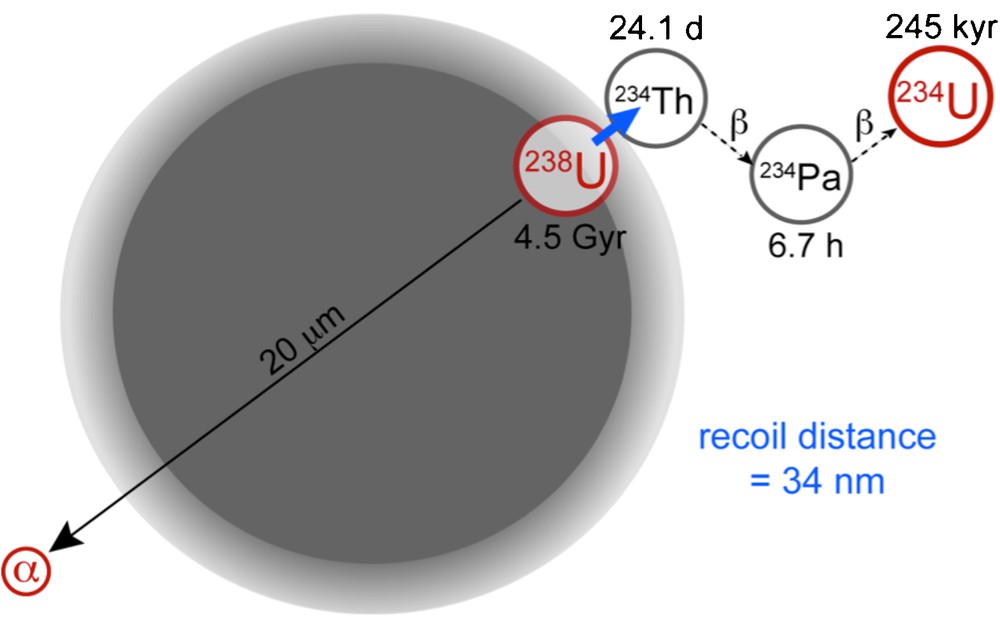
Conceptual model of recoil effects associated with the alpha decay of 238U contained in a spherical mineral grain having a diameter of about 15 μm. The emission of the alpha particle during 238U-decay causes the 234Th daughter nucleus to recoil a distance of about 34 nanometers (0.034 μm). If the 238U atom resides close enough to the grain boundary it can be ejected from the grain. The subsequent β decay to 234Pa and 234U occurs outside the grain, usually in pore fluids, which tend to be enriched in 234U relative to 238U because of this process. The net effect on the grain is that the bulk 234U/238U ratio tends toward a value less than the radioactive equilibrium value due to the 234U loss near the grain boundaries. The fractional loss rate of 234U is a function of the surface/volume ratio of the mineral grain. This loss is negligible for large grains (≥ 100 μm diameter), but can be 10 to 30% for grains less than 10 μm in diameter.
Modèle conceptuel d’effets recul associés à la désintégration alpha de l’238U contenu dans un grain minéral sphérique de diamètre d’environ 15 μm. L’émission de la particule alpha pendant la désintégration de l’238U provoque le recul du noyau fils 238U d’une distance d’environ 34 nanomètres (0,034 μm). Si l’atome d’238 U est suffisamment proche de la limite du grain, il peut être éjecté du grain. La désintégration ultérieure β en 234Pa et 234U se produit en dehors du grain, en général dans les fluides des pores, qui tendent à être enrichis en 234U par rapport à 238U en raison de ce processus.
If one imagines a U-bearing mineral grain with radius large compared to 0.034 μm and having the equilibrium 234U/238U ratio, and then breaking this large grain into much smaller grains of a few μm diameter each, these small grains will at first still have the equilibrium 234U/238U ratio. As the “comminuted” grains age, the decay of 234U will be faster than the accumulation of 234U from 238U-decay because of the recoil losses from the grains. Hence, the 234U/238U ratio of the small grains will decrease with time until a steady state ratio of 234U/238U is reached, with this steady state ratio being substantially lower than the equilibrium ratio. The time required to reach this steady state ratio is > 500,000 years, and therefore, during this time, the 234U/238U ratio is acting as a clock, measuring the time since the original large grain was crushed (or comminuted) to much smaller grains.
The evolution of the 234U/238U activity ratio with time is described by the following equation (graphed in Fig. 2):
| (1) |
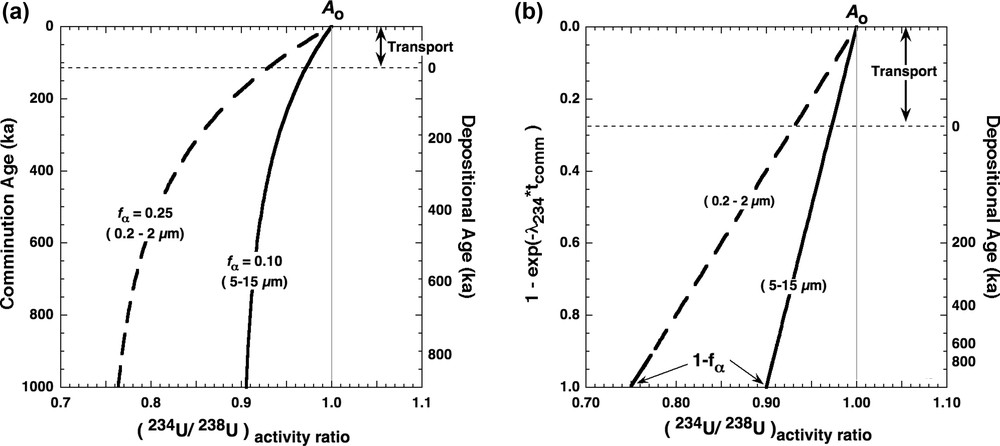
Model isotope ratio evolution curves for small sediment grains comminuted from larger rock fragments at time zero. (a) 234U/238U activity ratio versus age, showing hypothetical transport time of about 110,000 years followed by deposition and burial. The curves are based on the fα value shown, and the correspondence with grain size follows approximately from the data in Fig. 3. (b) Equivalent to 2a but with age plotted so that the isotopic ratio changes linearly (see Eq. (1)). If sediment ages are known, this plot can be used to extrapolate data from a continuous sedimentary section to estimate both the transport time and the recoil loss factors (cf. DePaolo et al., 2006).
Modèle de courbes d’évolution du rapport isotopique de grains de sédiment de petite taille, comminutés à partir de plus grands fragments de roche au temps zéro. (a) rapport d’activité 234U/238U en fonction de l’âge; (b) équivalent à (a), mais avec les chiffres d’âge reportés de manière à ce que la valeur isotopique change linéairement (voir Éq. (1)).
This model, although simple, could be a reasonably good representation of the formation of fine-grained sediment, especially by glacial erosion. The implication is that recently-produced fine sediment grains contain, in their 234U/238U ratios, a measure of how long they have been in existence as small grains. In the case of glacial sediment, the 234U/238U ratio could measure the time elapsed since the production of the grains by glacial grinding of bedrock.
For any sediment, the age of the grains must be equal to the age of the sediment (the elapsed time since the sediment was deposited), plus the time that elapsed while the sediment was being transported from the site of its glacial origin to the site of deposition. So the “comminution age” is the sum of the transport time and the sediment age. Consequently, in situations where the sediment age is known, the comminution age and the sediment age can be used to estimate the transport time (e.g., Dosseto et al., 2010). In situations where the transport time is known, or known to be very short, the comminution age can be interpreted as the age of sediment deposition. The comminution age clock is useful for a little more than 500,000 years, so this method is mainly for study of relatively recent (Late Pleistocene) sedimentary systems.
3 Issues and complications
3.1 The recoil loss factor
The model described above and encompassed in Eq. (1) is dependent on obtaining knowledge of the value of the recoil loss parameter fα. Although this is a geometric factor, it is difficult to estimate accurately for natural mineral grains because the shapes and surfaces of such grains are complex (Anbeek, 1992; Brantley and Mellott, 2000). Relative to a simple sphere of radius r, the effective surface area of mineral grains for recoil loss exceeds 4πr2 by a factor of between about 2 and 20 based on recent measurements (Fig. 3). This excess loss factor can be expressed crudely as “roughness” of the mineral surface. The data in Fig. 3 show that the roughness factor tends to be larger for larger grain sizes (Lee et al., 2010). Furthermore, the surface area measured for minerals is dependent on the method used for the measurement. Gas adsorption techniques (such as BET), sense roughness at the scale of a few Angströms (10−10 m) and hence tend to overestimate the surface area that applies to recoil loss, which is only sensitive to roughness at the larger scale of the recoil length (L), about 3 × 10−8 m. Methods have been devised to scale BET measurements to provide useful surface area measurements for recoil (Bourdon et al., 2009), according to the following equation:
| (2) |
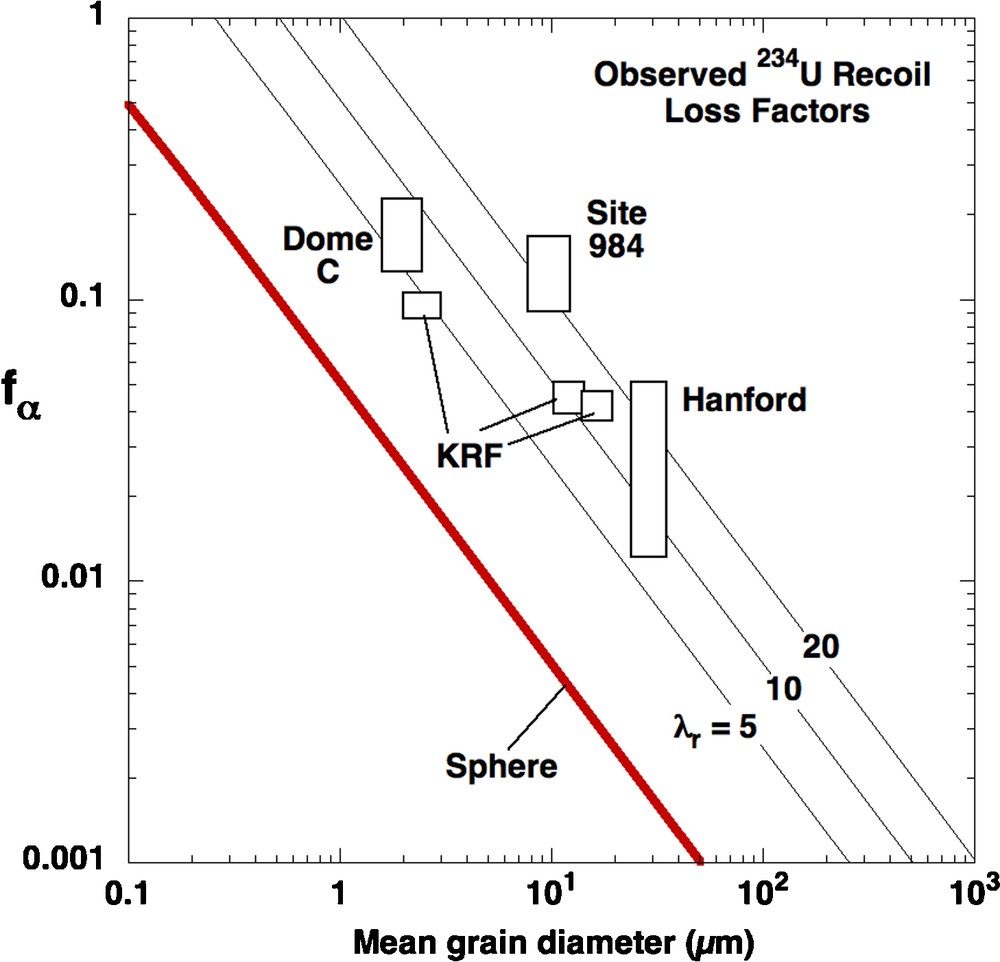
Measured or estimated fα values for samples of sand, silt and clay. Hanford data are from Maher et al. (2006a). Site 984 data from DePaolo et al. (2006). Dome C dust data from Aciego et al. (2011). King's River Fan (KRF) data are from Lee et al. (2010). The parameter λr is a roughness factor that accounts for both grain shape and surface roughness relative to a spherical grain.
Valeurs f ά mesurées ou estimées pour des échantillons de sable, de silt et d’argile. Données sur Hanford (Maher et al., 2006a), sur le site 984 (DePaolo et al., 2006), sur le Dome C (Aciego et al., 2011), sur King's River Fan (KRF) (Lee et al., 2010). Le paramètre λr est un facteur de rugosité qui tient compte à la fois de la forme du grain et de la rugosité de surface relatives à un grain sphérique.
A promising approach to measuring fα by geochemical means, but one that has not yet been adequately tested, is the use of measurements of 226Ra and 230Th. The ratio of these two isotopes, if measured on the same population of sediment grains measured for 234U/238U, should theoretically give the value of fα that is applicable to the 234U/238U ratios according to:
| (3) |
Dosseto et al. (2010) used an efficient approach to the problem of estimating fα. Instead of using grain size separates they used bulk < 50 μm fractions and then determined the particle size distribution. This information was used in concert with a geometric model with estimates of grain aspect ratios and surface roughness to arrive at a value of fα.
3.2 Weathering, partial dissolution, or coating of mineral grains
The U isotope ratio of small mineral grains measures age only if the surfaces of the mineral grains do not change significantly with time as a result of dissolution into pore fluids, or by acquiring coatings of secondary minerals. Dissolution could cause removal of the outer 234U-depleted region of the grains, which would cause the grains to appear younger, but could also increase surface roughness and enhance recoil loss, making the grains appear older.
The effect of dissolution on the 234U/238U of sediment grains can be evaluated by comparing the time necessary to achieve 234U depletion in the outer rind of a mineral grain as a result of recoil effects (the mean life of 234U = 354 kyr), to the time scale for removing a layer of thickness L from the surface of a grain by dissolution. This ratio is (DePaolo et al., 2006):
| (4) |
The parameter R is the specific mineral dissolution rate, which has been estimated for silicate soils and some sediments to be of order 2.5 × 10−18 mol/m2/sec (2 × 10−11 kg/m2/yr, assuming that the primary dissolving mineral is plagioclase feldspar; cf. Maher et al., 2006b). Using L = 3 × 10−8 m and ρ = 2700 kg/m3 yields a value for this dimensionless number of about 0.1, which suggests that dissolution is a second order effect in many cases. However, there are complications because the dissolution rate of the U-bearing minerals determines the size of the effect, and those rates could be larger or smaller than the value used above. In addition, dissolution rates also vary with environment (Maher, 2010) and time (e.g. Maher et al., 2004; White and Brantley, 2003).
Secondary mineral precipitation generally is a concern, and necessitates leaching natural samples before analysis (Dosseto et al., 2010; Lee et al., 2010; Maher et al., 2004). Leaching can be difficult and there is not yet an established best practice for the U comminution age method. In general, if leaching is too weak, high 234U/238U authigenic phases are likely to be included in the analysis, which will bias the results to young or even negative ages (Fig. 4). If leaching is too strong, it could possibly preferentially remove the 234U-depleted surface layer of the grains, which would also bias the results toward high 234U/238U and younger ages. In preliminary tests of multiple leaching procedures, Lee et al. (2010) determined that sequential leaching approaches similar to that of Tessier et al. (1979) yield the most useful results. However, DePaolo et al. (2006) used only a single weak HCl leach and also achieved consistent results on deep-sea sediments. Dosseto et al. (2010) used a procedure that starts with ashing of the samples to remove organic material followed by leaching with 1.5 N HCl while monitoring the Ca, Fe, U and Th concentrations in the leachate. This procedure is followed with a second leaching step to remove residual Fe-oxides.
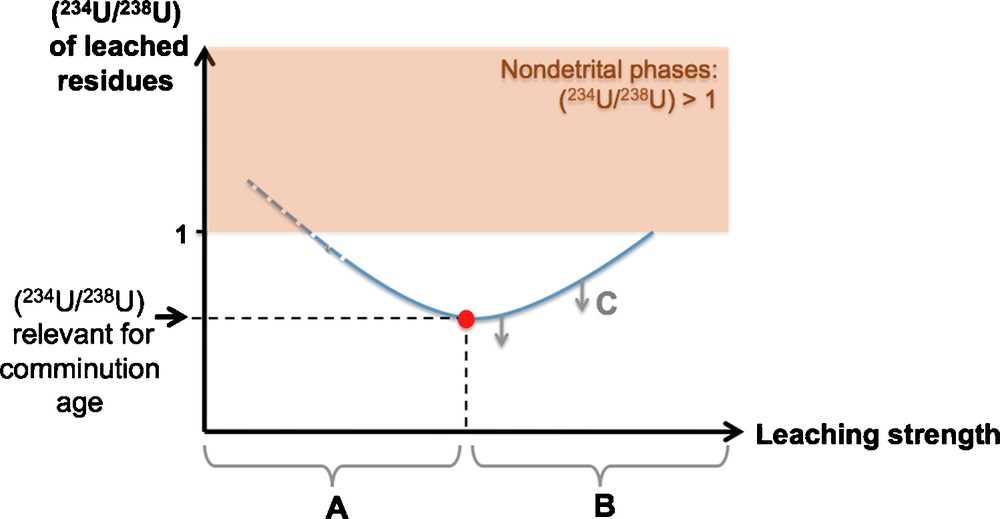
Schematic of the expected effects of leaching treatments on the 234U/238U activity ratio of sediment samples. If samples are not leached, they tend to include secondary (non-detrital) phases that precipitated from pore fluids and have (234U/238)AR > 1. Leaching should initially remove these secondary minerals resulting in lowering of (234U/238)AR as depicted for line segment “A.” If leaching treatments are too strong (“B”), however, the outer 234U-depleted parts of the grains could be dissolved, causing (234U/238)AR to increase. The optimal leaching procedure should presumably give the minimum value for (234U/238)AR.
Schéma des effets attendus des traitements de lessivage sur le rapport d’activité 234U/238U d’échantillons de sédiment, sachant que, si les échantillons ne sont pas lessivés, ils tendent à inclure les phases secondaires (non détritiques) formées à partir des fluides poreux, et que s’ils sont lessivés, les minéraux secondaires sont alors évacués.
3.3 Initial 234U/238U ratio
It is expected that comminuted glacially-derived sediment of near-zero age will have a 234U/238U activity ratio close to unity. However, there are data in the literature that suggest that bedrock samples do not always conform to this expectation (Gascoyne et al., 2002). To further address the issue, which is critical to interpretation of U comminution ages, we analyzed samples of glacial outwash from several alpine glaciers around the world to assess the variability of the initial 234U/238U activity ratio. The results are summarized in Fig. 5. These data, which will be more completely described in a separate publication, suggest that glacial outwash generally has (234U/238U)AR of 1.00 ±0.01. This result appears to be independent of bedrock lithology; the metasedimentary rocks of the New Zealand Alps are not significantly different from the granitic rocks of the Swiss Alps. It is possible that the values that are slightly greater than unity are significant, but additional work would need to be done to confirm this observation.
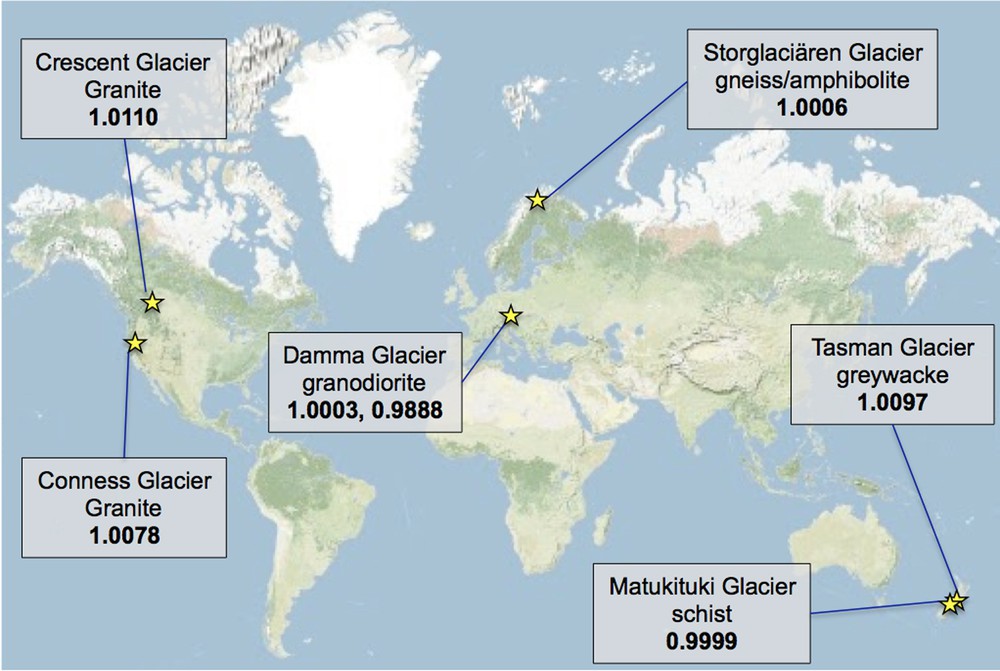
Measured 234U/238U activity ratio for silt and sand from glacial outwash. Glacier name and bedrock lithology is indicated. Locations and samples are: Crescent Glacier, British Columbia, outwash at glacier toe, silt; Conness Glacier Sierra Nevada, California, Little Ice Age moraine, sand/gravel; Damma Glacier, Switzerland, bedrock (1st number) and steam sediment 1km below glacier, sand plus fines (2nd number); Storglaciaren, Sweden, subglacial till, very fine silt; Tasman glacier, New Zealand Alps, stream suspended load, fine silt; Matukituki Glacier, New Zealand Fiordland, clayey stream sediment. Uncertainty on measured ratios is generally ± 0.0017; analytical procedures including leaching methods are described in Lee et al. (2010).
Rapport d’activité 234U/238U mesuré sur des silts et des sables provenant de dépôts glaciaires. Le nom des glaciers, leur localisation et la lithologie de la roche mère sont indiqués.
4 Sediment age versus transport time
The application of U comminution ages to sedimentary sections is best done using multiple measurements on a continuous stratigraphic section or independently dated samples so that self-consistency can be evaluated. Available data for isotopic ratio and comminution age versus stratigraphic position or age are illustrated in Figs. 6 and 7, with two examples showing variable and relatively long transport time and one showing a section where transport time is most likely small.
Measured 234U/238U on leached bulk sediment samples from Site 984A (DePaolo et al., 2006), grain size separates from the King's River Fan (Lee et al., 2010), and < 50 μm sediment fractions from the Murrumbidgee River basin (Dosseto et al., 2010). In (a) and (b), the dashed lines represent model curves that would correspond to a constant sedimentation rate. (a) Site 984 has cyclical variation in 234U/238U. The data are approximately bounded by the two curves shown, both assuming initial 234U/238U = 1.000, one for pre-deposition transport of about 350,000 years and the other for a transport time of zero. The variations in transport time correlate roughly with glacial cycles and with changes in sediment provenance. (b) King's River Fan data show relatively systematic changes in 234U/238U with depth. The dashed curves are fit through the deepest samples from the core, which are almost 800,000 years old and hence should be close to steady state with respect to 234U/238U. The 234U/238U of the ≤ 6 μm fraction decreases monotonically with depth, but imply an increasing sedimentation rate with decreasing age. The 10 to 15 μm and 15 to 20 μm fractions are nearly identical in U isotopes. The complications in 234U/238U could be expected for an alluvial fan due to changes in transport time correlated with Pleistocene glaciation cycles, redistribution of older fan sediment at younger times, and admixtures of aeolian sediment. In the uppermost sample the 10 to 20 μm fractions have lower 234U/238U than the < 6 μm fraction. This could be an indication that coarser material has a different transport time than finer materials, or that the fine fraction is more affected by weathering. (c) Sediment samples (< 50 μm fraction) from paleochannels in the Murrumbidgee River basin show systematically increasing 234U/238U during the latest Pleistocene glacial period and then a shift to lower values in the Holocene.
Rapports 234U/238U mesurés sur des échantillons de sédiment grossier lessivés, en provenance du site 984A (DePaolo et al., 2006), des fractions granulométriques variées du King's River Fan (Lee et al., 2010) et des fractions < 50 μm du bassin de la rivière Murrumbidgee (Dosseto et al., 2010), respectivement, Fig. 6a, b et c. En a et b, les lignes tiretées représentent les courbes du modèle qui correspondraient à un taux de sédimentation constant.
Calculated U comminution ages and estimated uncertainties for King's River Fan samples reported in Lee et al. (2010) and Murrumbidgee River basin samples reported in Dosseto et al. (2010). For the King's River Fan, uncertainties are estimated as twice the analytical uncertainty on the measured (234U/238U)AR plus an additional uncertainty of ± 0.01 in fα (see Lee et al., 2010 for additional details). An average value of fα of 0.047 was used for both the 10 to 15 μm and the 15 to 20 μm size fractions (see Fig. 6b). For the Murrumbidgee River samples, uncertainty estimates are described in the original reference and attempt to capture all aspects of the analysis, although the uncertainty in fα that is due to leaching is still likely to be approximate.
Ages de comminution d’uranium calculés et incertitudes estimées pour les échantillons de King's River Fan (Lee et al., 2010) et du bassin de la rivière Murrumbidgee (Dosseto et al., 2010), respectivement Fig. 7a et 7b.
Site 984A in the North Atlantic Ocean is a drift site; the sediments are deposited from ocean bottom currents and hence are transported several hundred kilometers along the ocean floor after first being deposited into the oceans by streams (DePaolo et al., 2006). These sediments represent a case where transport times could be relatively long. The second example is from the Kings River Fan (KRF), a large Pleistocene age alluvial fan in central California. The sediments in the Kings River Fan are glacially-derived from the neighboring Sierra Nevada, transported a relatively short distance by streams and deposited in a non-marine environment (Weissmann et al., 2002). This alluvial fan environment is one in which it might be inferred that transport times are small enough that the comminution age should correspond to the depositional age of the sediment. The third example is from a moderately large drainage basin in Southeast Australia (900 km long, 106 km2; Dosseto et al., 2010) that was not glaciated in the Pleistocene and which gives indications of a wide variation in sediment transport time through the basin (or residence time in the basin) over the past 100,000 years.
For the Site 984A deep-sea sediments, the samples that suggest long transport times also tend to have low 143Nd/144Nd and high 87Sr/86Sr (DePaolo et al., 2006). These sediments are derived from the Fennoscandian Shield and then transported by bottom currents westward in the North Atlantic south of Iceland. The samples with higher 234U/238U and corresponding short transport times have high 143Nd/144Nd and low 87Sr/86Sr and are presumably derived from Iceland and transported a short distance to the site of deposition. The record of transport time, combined with the provenance information, yield information that probably relates to extent of sea ice in the North Atlantic over the last 400,000 years. When Iceland is ice-locked, there is likely to be little sediment input from Iceland to Site 984A area, whereas when the surrounding sea is ice-free there is a larger flux of Icelandic volcanic sediment.
Fig. 6c shows data from the Murrumbidgee River basin in southeastern Australia (Dosseto et al., 2010). In this case the sediments, which were collected from paleochannels in the middle and lower part of the basin, have been dated independently using luminescence methods. The measured 234U/238U ratios, even without consideration of the fα values, show a substantial variation. Shown for reference in the figure is a curve corresponding to fα = 0.1 (close to the average measured) and for zero transport time. The data suggest that sediment residence time in the basin became systematically shorter through the last Pleistocene glacial cycle, was near zero at the last glacial maximum, and then became long again during the present interglacial. Fig. 7b shows the calculated comminution ages, which mirror the measured 234U/238U ratios because the measured fα values are not highly variable. For the zero age samples, the comminution age equals the residence time (300 kyr to almost 500 kyr), whereas for the older samples the residence time is the comminution age minus the depositional age. This case shows that quite long sediment residence times are possible in continental basins.
The Site 984A and the Murrumbidgee River basin data are an indication of the type of information that can be derived from sediment 234U/238U using the comminution age approach. The sediments in these cases can be independently dated, so the 234U/238U can be used to infer transport or residence time. In both cases the transport time is large enough that it can be determined with useful precision. The Kings River Fan data are significant because the U comminution age approach could be useful for absolute dating of continental sediments, which generally do not contain index fossils and hence are difficult to date. The KRF 234U/238U data show some of the expected character required for age determinations, but also some complications. One important issue is that the age cannot be estimated without a reliable value for fα. The simplest model for fα, uses the fact that the deepest samples are known to have reversed magnetic polarity (older than 780,000 years), and hence must be close to steady state with respect to 234U/238U. The KRF core has not been independently dated, but there are inferred approximate ages for the units represented in the shallower portions of the core, derived from correlations with other nearby alluvial deposits and ultimately based on K-Ar ages that are not especially reliable (Lee et al., 2010). Using the oldest measured sample to estimate fα, Fig. 7a shows the calculated U comminution ages for the size-separated samples shown in Fig. 6b, and a comparison curve that represents the inferred age profile based on geologic correlations. The comminution ages suggest that the sediments are considerably younger than has been inferred from stratigraphic inferences, and that there may in addition be variations in residence time that could relate to glacial cycles as in the Murrumbidgee basin.
5 Relationship to cosmogenic nuclide- and U,Th-series methods
Cosmogenic radionuclide (CRN), concentrations in sediments (such as 10Be and 26Al; Bierman et al., 1995; Phillips et al., 1997; Gosse and Phillips, 2001) are also used in the study of sediment transport and age, and this approach has some similarities and interesting differences relative to the U isotope comminution age approach. For CRN's, the isotopes accumulate in the sediment grains and in bedrock (no dependence on grain size) due to cosmic ray neutron bombardment, and only when the grains are situated within about 1 meter of the Earth's surface, not when they are more deeply buried. After burial, the radionuclides decay and the concentrations decrease. The CRN signal in sediments therefore reflects the time of residence of the grains in soils, the erosion rate of the bedrock, the transport time, and the burial time (related to the time since deposition). CRN production rates also depend on the elevation and latitude at which the sediment originated and was deposited. The concentration of cosmogenic nuclides in freshly eroded sediment has been shown to be inversely proportional to the erosion rate, and independent of grain size (Heimsath et al., 1999). The U comminution clock starts only when the grains become quite small. The CRN method generally requires quartz, or quartz-rich sediment; the U isotope technique by contrast is insensitive to the presence of quartz, because of the low U content of quartz, and instead relates to the history of the grains that are composed of minerals other than quartz.
The differences between the CRN methods and U comminution ages make the two approaches complementary and potentially powerful probes of sediment generation and transport processes. The in situ produced cosmogenic nuclide content of fresh sediment should be a direct indicator of the rate at which the catchment containing the sediment is eroding (e.g., Bierman and Nichols, 2004; Matmon et al., 2012), and this information could be valuable for interpreting the U isotope effects. Once incorporated into a sedimentary deposit, such as a floodplain, fan, or terrace, and buried by more than 1 meter, the 10Be and 26Al concentrations decrease as the result of radioactive decay. During transport it is not clear whether or to what extent the grains get more cosmic ray irradiation. However, the U isotope effects continually accumulate during soil residence, transport, storage and after final deposition. By measuring two CRNs, correction can be made for the effects of erosion on absolute production rates, and sediment ages can be determined if the pre-deposition irradiation is sufficient. Comparison of U isotope and CRNs could be an exciting new approach, leading to new insights about U isotopes and CRNs, as well as erosion and sediment transport.
Other applications of U series isotopes to sediment transport processes involve the combined U and Th decay series (Dosseto et al., 2008; Granet et al., 2007, 2010). The U-Th approach relies on the likelihood that during soil formation, there is chemical separation of U from Th, since U is generally more soluble than Th. The U-Th method is also potentially complementary to the U comminution age approach. The U-Th method is inferred to be independent of grain size, so in general measurements made with the U-Th method have not been done on grain size characterized samples, which impedes direct comparison of the two methods. Concurrent application of the U-Th chemical fractionation method and the comminution age method, employing grain size separated fractions of the sediment involved, could be a fruitful way to improve confidence in the interpretations of sediment transport history.
6 Summary and conclusions
The time scales of U-series isotopes, which are in the range of a few thousand to a few hundred thousand years, are applicable to study of sediment transport and deposition processes. These isotope systems can be applied to Late Pleistocene or active sedimentary systems to help estimate the rates at which sediment is generated by weathering and erosion and transported to the sites of deposition. In many circumstances the U comminution ages can yield the time since deposition, i.e. depositional age of the sediment. The specific approach of using the U comminution age, which involves measuring the depletion of 234U relative to 238U, is not dependent on chemical fractionation as in the case of the U-Th isotopic disequilibrium approach, but rather on the physical shape and size of sand grains. The U comminution age method is complementary to the U-Th approach, as well as to cosmogenic nuclide methods.
The primary source of uncertainty in the application of U comminution ages is in determining the effective 234U loss rate due to recoil effects in small sediment grains (fraction of 238U-decays leading to loss of 234U is denoted as fα). The 234U loss rate is related to the surface/volume ratio of the grains, which is difficult to estimate precisely due to uncertainty in the surface area stemming from roughness of natural mineral grain surfaces. Multiple approaches have been proposed for estimating surface area of mineral grains, the most promising results have come from combining gas adsorption methods with estimates of the fractal dimension of the grain surfaces (Bourdon et al., 2009; Oster et al., 2012). It may also be possible to use measurements of 226Ra/230Th to directly measure fα, but this approach has not been tested. In situations where a continuous sediment section can be measured, it is possible to use the data to infer both the transport time and fα.
Recent studies of the (234U/238U)AR of modern glacial outwash and stream sediments suggest that the initial (234U/238U)AR of silt and fine silt-sized sediment grains is typically equal to the radioactive equilibrium ratio (activity ratio = 1.00 ± 0.01). There is no obvious correlation of this ratio with bedrock lithology, although there are small deviations from the equilibrium value that are larger than the analytical uncertainties. The effects of mineral grain dissolution on the U comminution age systematics can be small, but no study has specifically addressed this issue. Secondary authigenic minerals can disturb the U isotope systematics, and need to be leached away prior to analysis. Leaching procedures can affect the results and more robust protocols for sample preparation need to be established.
The available data suggest that the U comminution age method has substantial potential to aid in quantifying sediment transport times, especially for ocean sediments that are redistributed on the ocean floor by bottom currents, and for dating alluvial and other types of terrestrial sediments that are up to or slightly more than 500,000 years old. The comminution age method may also be useful for understanding the formation of cataclastic material such as fault gouge in active fault zones.
Acknowledgements
The research carried out by the authors at U.C. Berkeley and the Lawrence Berkeley National Laboratory was supported by the Director, Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231, and by a grant from the U.S. National Science Foundation (EAR-0617704), Surface Earth Processes Section.