The postperovskite (PPv) phase transition of bridgmanite (Brg), which is the most abundant lower mantle mineral (Poirier, 1991; Wang et al., 2015), occurs at the pressure (P), temperature (T) conditions (Murakami et al., 2004; Tsuchiya et al., 2004) close to the Earth's D″ layer located between the silicate lower mantle and the metallic outer core. Therefore, it is quite likely that PPv is the most dominant mineral in the D″ layer and that the PPv phase transition of Brg is responsible for the discontinuous increase in shear wave velocity in this region (Garnero and McNamara, 2008; Hutko et al., 2008; Lay, 2008; Lay et al., 1998; van der Hilst et al., 2007). In the lower mantle, Brg forms a solid solution with Fe2+SiO3, Fe3+Fe3+O3, Fe3+Al3+O3, and Al3+Al3+O3 (Kesson et al., 1998; McCammon, 1997). This produces the Brg + PPv two-phase coexistence (TPC) domain, whose width changes depending on the type and amount of solute. To understand the relationship between the PPv phase transition and the D″ seismic discontinuities, it is critical to clarify the effects of solutes on the TPC domain of the PPv phase transition. However, precise experimental determinations of the multicomponent phase transition boundaries at the core-mantle boundary (CMB) P,T (∼ 136 GPa and 2500 ∼ 4000 K) (Poirier, 1991) are still challenging (Andrault et al., 2010; Catalli et al., 2009; Grocholski et al., 2012; Hirose and Sinmyo, 2006; Mao et al., 2004; Nishio-Hamane et al., 2007; Sun et al., 2018; Tateno et al., 2005). Previous results, not only on the phase transition pressures but on the width of TPC domains, are largely controversial, e.g., at ∼ 2500 K, Brg with ∼ 10 mol% Fe2+SiO3 was reported to have a TPC domain from 99 GPa to 118 GPa with a ∼ 19 GPa width (Mao et al., 2004), while higher transition pressures with a broader TPC domain from 110 GPa to 134 GPa with a ∼ 24 GPa width (Catalli et al., 2009) were also proposed. Furthermore, the phase transitions of 10 mol% and 15 mol% Fe3+Al3+O3-bearing Brg under 2500 K were reported to 111 GPa and 147 GPa with TPC widths of ∼ 22 GPa and ∼ 26 GPa, respectively (Catalli et al., 2009; Nishio-Hamane et al., 2007). A similar controversy can also be seen in experiments on more complicated multi-phase aggregates (Grocholski et al., 2012; Murakami et al., 2005). Generally, experimental measurements presented broad TPC domains notably larger than the typical seismic detection limit of 5 GPa (∼ 80 km in depth) (Lay and Garnero, 2007), since the seismic body waves with a typical frequency of ∼ 1 Hz have this scale of wavelengths. Also, in some experiments, the PPv transition was detected to start at pressures higher than the CMB pressure of 136 GPa (Tateno et al., 2005). These indicate that the discontinuities in the D″ layer might not arise from the PPv phase transition of Brg.
Computational simulations based on the first-principles method, which can theoretically explore the material properties relying only on basic physical laws, were also carried out to investigate the PPv phase transition behaviors of Fe and Al-bearing Brg (Akber-Knutson et al., 2005; Caracas and Cohen, 2005, 2008; Metsue and Tsuchiya, 2012; Tsuchiya and Tsuchiya, 2008; Zhang and Oganov, 2006). The general conclusion drawn from these previous studies is that the Fe and Al incorporations decrease and increase the transition pressure, respectively. However, theoretical simulations carried out at static condition ignoring the lattice thermal effects (Akber-Knutson et al., 2005; Caracas and Cohen, 2005, 2008; Zhang and Oganov, 2006) give unreasonable TPC ranges. In addition, the strongly correlated interactions among the Fe 3d orbitals that must be treated correctly for the Fe-bearing cases were not considered (Akber-Knutson et al., 2005; Caracas and Cohen, 2008; Zhang and Oganov, 2006). By means of the method we developed (Metsue and Tsuchiya, 2012; Tsuchiya and Wang, 2013; Wang et al., 2015), the high-P,T properties of Brg containing geophysically relevant solute elements can be directly simulated with an appropriate treatment by the internally consistent Hubbard U correction. Based on the thermoelasticity of Fe and Al-bearing Brg investigated by this technique, it was recently reported that the pyrolite model containing ∼ 80 vol% Brg and ∼ 20 vol% ferropericlase (Fe-bearing MgO) is reasonable for the average lower mantle composition (Wang et al., 2015). Also using the same technique, it was suggested that at ∼ 2500 K, the PPv phase transition with 6.25 mol% Fe2+SiO3 and Al3+Al3+O3 acquires relatively narrow TPC ranges (Caracas and Cohen, 2008; Metsue and Tsuchiya, 2012). However, effects of the Fe3+, which are also expected to be important in the lower mantle (Kesson et al., 1998; McCammon, 1997), on the TPC domain still remain unexplored. In this work, we systematically study the effects of Fe2+SiO3, Fe3+Fe3+O3, Fe3+Al3+O3, and Al3+Al3+O3 incorporations on the PPv phase transition boundary under high T.
We reported the structures, spin states, and thermodynamic properties of Fe2+SiO3, Fe3+Fe3+O3, Fe3+Al3+O3, and Al3+Al3+O3-bearing Brg in our previous works (Metsue and Tsuchiya, 2012; Tsuchiya and Tsuchiya, 2008; Tsuchiya and Wang, 2013; Wang et al., 2015). For PPv, previous results showed that 12.5 mol% Fe substituted at the Mg and the Si site have the high spin (HS) and the low spin (LS) state in its thermodynamic stability pressure range, respectively (Tsuchiya and Wang, 2013). We studied the stable spin configuration of 6.25 mol% Fe using a PPv supercell containing 80 atoms (fig. S1B), and our results agree with that of 12.5 mol% Fe-bearing cases (Tsuchiya and Wang, 2013) under the high-P range (from 50 GPa to 180 GPa). Therefore, we can conclude that within the Fe concentration smaller than ∼ 12.5 mol%, the spin configuration of Fe-bearing PPv is independent of iron concentration (Supplementary Material and Fig. S2). Therefore, phonons of the configurations of (
Phonon dispersions are calculated up to 210 GPa, and no imaginary frequency is observed above 70 GPa (fig. S3), indicating that 6.25 mol% Fe and Al-bearing PPv are vibrationally stable from the middle to deep lower mantle, even though thermodynamically unstable. Phonon dispersions and vibrational density of states (VDoS) of (
Including the zero-point vibrational energy, the calculated phase transition pressure of pure MgSiO3 at 0 K is 95.4 GPa, and it increases up to 115.8 GPa, 121.4 GPa, and 127.0 GPa at 2000 K, 2500 K, and 3000 K, respectively, because of the positive Clapeyron slope of the PPv phase boundary (Murakami et al., 2004; Tsuchiya et al., 2004). As shown in Table S2 at 0 K, the presence of 6.25 mol% Fe2+SiO3 and Fe3+Fe3+O3 decreases the PPv phase transition pressures by 2.5 GPa and 4.3 GPa, respectively. Moreover, the transition pressure of 6.25 mol% Fe3+Al3+O3 (Al3+Al3+O3)-bearing Brg is by 0.5 GPa (3.4 GPa) higher than that of pure MgSiO3. The results indicate that at 0 K, the incorporation of a small amount of Fe and Al, respectively, decreases and increases the transition pressure, which is consistent with previous theoretical works (Akber-Knutson et al., 2005; Caracas and Cohen, 2005, 2008; Tsuchiya et al., 2004; Zhang and Oganov, 2006).
The high-T (from 2000 K to 3000 K) TPC domains determined by finite-temperature free energies (supplementary materials) are shown in Fig. 1 and Table S2 with previous estimations (Akber-Knutson et al., 2005; Andrault et al., 2010; Caracas and Cohen, 2005, 2008; Catalli et al., 2009; Grocholski et al., 2012; Hirose and Sinmyo, 2006; Lay and Garnero, 2007; Metsue and Tsuchiya, 2012; Murakami et al., 2005; Nishio-Hamane et al., 2007; Sun et al., 2018; Tateno et al., 2005; Tsuchiya and Tsuchiya, 2008; Zhang and Oganov, 2006). It can be seen that at 2500 K, the incorporation of 6.25 mol% Fe2+SiO3 slightly decreases the phase transition pressure with a quite narrow TPC domain of ∼ 0.8 GPa. This pressure variation corresponds to a thickness of ∼ 20 km, which is sufficiently smaller than the typical seismological detection limit of 5 GPa (Lay and Garnero, 2007). The previous simulations also gave a narrow TPC domain of ∼ 3.8 GPa for the case of 6.25 mol% Fe2+-bearing MgSiO3 (Caracas and Cohen, 2008), as shown in Table S2. Similarly, a narrow TPC domain of ∼ 2.3 GPa is found in the case of 6.25 mol% Al3+Al3+O3-bearing Brg, which is well consistent with our previous work (Tsuchiya and Tsuchiya, 2008). Compared to 0 K, the transition pressure at high-T slightly decreases due to phonon effects (Tsuchiya and Tsuchiya, 2008). In contrast to Fe2+SiO3- and Al3+Al3+O3-bearing cases, results in Fig. 1C and D, demonstrate that the 6.25 mol% Fe3+Fe3+O3 and Fe3+Al3+O3 incorporations expand the Brg + PPv TPC domain significantly in addition to a lowering of the transition pressure. At 2500 K, the coexistence domains of 6.25 mol% Fe3+Fe3+O3- and Fe3+Al3+O3-bearing Brg are 8.8 GPa and 16.8 GPa, respectively, which are much broader than the seismological detection limit. Please note that the key process of the PPv phase transition is the octahedral tilting and that the octahedral tilting is easier when a smaller ion occupies the Mg site, resulting in a lower phase transition pressure. Therefore, the large differences in the thickness of the TPC domain between Fe2+ and Fe3+-bearing Brg are mainly due to the fact that Fe2+(92 pm) has larger ionic radius than Fe3+(78.5 pm), as discussed in the supplementary materials.
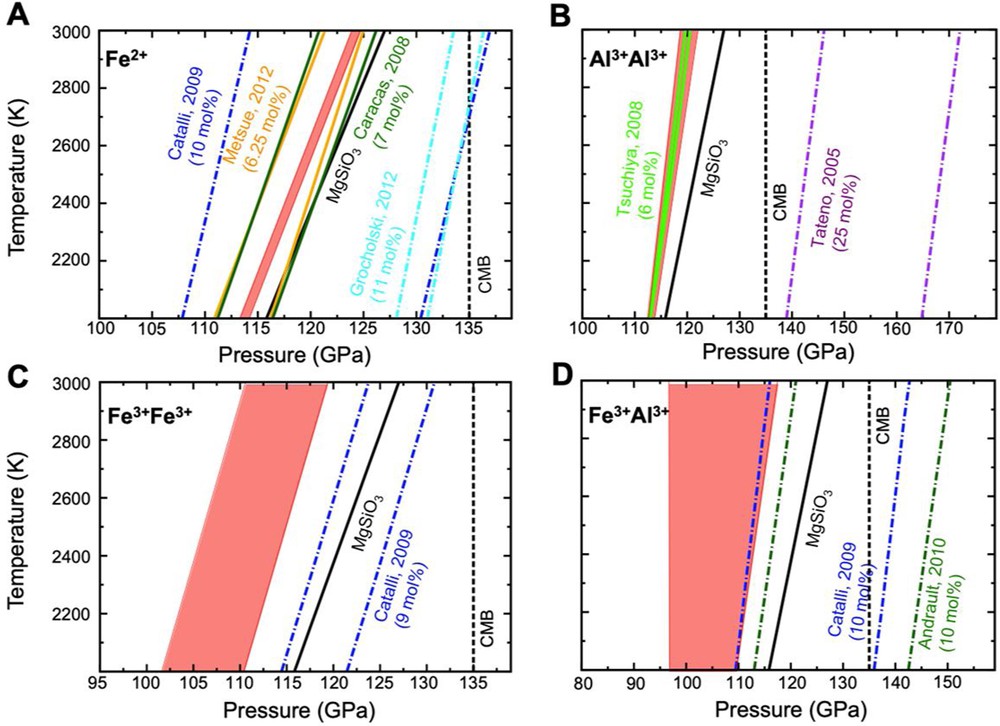
Two-phase coexistence (TPC) domains of Fe and Al-bearing MgSiO3 at ∼ 2500 K. A–D. The TPC domain of MgSiO3 containing 6.25 mol% Fe2+SiO3 (A), Al3+Al3+O3 (B), Fe3+Fe3+O3 (C), and Fe3+Al3+O3 (D). The TPC domains are represented by the red-shaded areas. Vertical black dashed lines indicate the P condition of the CMB, and the phase boundary of pristine MgSiO3 is represented by the black solid line. Experimentally reported TPC domains are shown by colored dotted dashed lines, purple for Tateno et al. (2005), blue for Catalli et al. (2009), dark-green for Andrault et al. (2010), and light-blue for Grocholski et al. (2012). Previous theoretical estimations of TPC domains are shown by solid colored lines, dark-green for Caracas and Cohen (2008), light-green for Tsuchiya and Tsuchiya (2008), and orange for Metsue and Tsuchiya (2012). Masquer
Two-phase coexistence (TPC) domains of Fe and Al-bearing MgSiO3 at ∼ 2500 K. A–D. The TPC domain of MgSiO3 containing 6.25 mol% Fe2+SiO3 (A), Al3+Al3+O3 (B), Fe3+Fe3+O3 (C), and Fe3+Al3+O3 (D). The TPC domains are represented by the red-shaded areas. Vertical black dashed ... Lire la suite
In Fig. 2, the TPC domains are shown as a function of solute concentration. At 2500 K, the width of the TPC domain in (

Phase diagrams of Fe and Al-bearing MgSiO3 at 2500 K. A. Phase diagram of the MgSiO3–Fe2+SiO3 binary system. B. Phase diagram of the MgSiO3-Al3+Al3+O3 binary system. C. Phase diagram of the MgSiO3–Fe3+Fe3+O3 binary system. D. Phase diagram of the MgSiO3-Fe3+Al3+O3 binary system. The two-phase coexistence (TPC) domains are shown by red mesh areas. The blue arrows indicate the pressure width of TPC domains equal to 5 GPa.
Our simulations, however, clearly show that the PPv phase transition in Fe2+-bearing Brg accompanies the narrow TPC domain, which may can be detected by seismological observations. Al-free or poor Brg is rather known to be produced in depleted peridotite such as harzburgite, which composes the most part of the subducted slabs (Irifune and Ringwood, 1987). It is therefore strongly suggested that places beneath circum-Pacific, where the positive shear wave discontinuities are observed, have a high concentration in depleted materials. This is consistent with the fact that the circum-Pacific comprises the most active subduction zones. Also, there would be another possibility that these regions are related to geochemically assumed early depleted reservoir (Boyet and Carlson, 2005, 2006). In contrast, the D″ discontinuities are not so distinct beneath central Pacific and Africa, where the large low-S velocity (LLSV) anomalies are observed instead (Lay and Garnero, 2007). In the edges of LLSV provinces, there are some ultra-low-velocity zones (ULVZs), where the compressional and shear wave velocities are 5–10% and 10–30% smaller than that of surrounding minerals. The low-VS bodies are often discussed associated with accumulations of subducted basaltic materials (McNamara and Zhong, 2005). Since they are expected to contain a large amount of Fe3+, Brg in those regions hardly produces a sharp PPv transition. This view is highly consistent with no or rare observations of the D″ discontinuity in the LLSV provinces (Lay and Garnero, 2007). The present large scale ab initio computations integrating several advanced techniques of direct lattice dynamics, quasi-harmonic approximation, and internally consistent LDA + U therefore suggest a heterogenous distribution of depleted and fertile materials in the D″ layer, which would be formed as a result of the global mantle circulation.
Acknowledgements
We thank D.Y. Sun for helpful comments and S. Whitaker for support to the preparation of the manuscript. This research was supported by the NSFC under Grant 11674329 and U1230202 (NSAF) and MEXT/JSPS KAKENHI JP20001005, JP21740379, and JP15H05834.


