1 Introduction
The deep mantle water cycle has been discussed with regard to various implications on the properties of silicate materials, which can host water at high pressures and temperatures (e.g., Karato, 2011), and the amount of water that the mantle from the early to the present Earth can contain has been examined (Rüpke et al., 2004; Sandu et al., 2011). A series of our studies on hydrous mantle convection models have focused on the mantle water cycle, including the dehydration reactions associated with water solubility in mantle minerals (Nakagawa and Spiegelman, 2017; Nakagawa et al. (2015)) and the effects of the occurrence of surface plate motions and water absorption in the mantle transition zone (Nakagawa and Iwamori, 2017). These studies also noted that heat transfer during hydrous mantle convection might be enhanced by approximately 30% compared with that during dry mantle convection due to viscosity reduction and enhancement of surface plate motion associated with water dependence of viscosity. In a coupled core–mantle evolution modeling, this has been mainly done in dry mantle convection simulations (e.g., Nakagawa and Tackley, 2010), but not in hydrous mantle convection simulations. The question is how the material properties of the hydrous mantle (e.g., water-dependent viscosity) affect the coupled core–mantle evolution.
Regarding hydrous mantle convection modeling, several parameterized models of mantle heat transfer with water migration have been investigated assuming coupled ocean–plate–mantle evolution (Korenaga, 2011; Rüpke et al., 2004; Sandu et al., 2011), which suggested that water in the planetary system (both in the exosphere and in the deep interior) may contain several times the present-day amount of surface seawater (1.4 × 1021 kg; e.g., Genda, 2016); however, those studies did not discuss the impacts on core evolution, the effects of dehydration reactions on mantle water migration, and the dynamical effects of mantle convection. Without core evolution effects, it seems that a planetary system assuming water solubility effects during hydrous mantle convection may contain at least 6 to 12 ocean masses of water at maximum (Nakagawa et al., 2018), which seems to be consistent with petrological estimates of 8 to 12 ocean masses (Iwamori, 2007). Note that this estimate is the maximum value, but, due to geological and geochemical constraints for water in the Earth's mantle, it seems that the mantle may contain less water than indicated in the above statements because only small sea level change would be expected (Korenaga et al., 2017; Parai and Mukhopadhyay, 2012) and because of the evolution of the D/H ratio (Kurokawa et al., 2018), which would be 1 to 2 ocean masses in the mantle. This question remains controversial.
The effects of the thermal evolution of the planetary core in a hydrous mantle convection system must still be discussed to give a better understanding of the evolution of the deep planetary interior. It would be worth to investigate how hydrous mantle convection affects the thermal and chemical evolution of the core–mantle boundary (CMB) to reveal the physical and chemical processes involved in the core–mantle–plate–ocean system; this means that we may add constraint, that is, the present-day amount of surface seawater, into the previous core–mantle evolution model. Here, we introduce a new successful scenario of the thermal and chemical evolution of the deep planetary interior and ocean in hydrous mantle convection. Moreover, as a consequence of our modeling results, the hydrogen cycle across the deep Earth's interior could be implied with the core–mantle chemical interactions by the metal–silicate partitioning of hydrogen (Okuchi, 1997), because recent accomplishments in high P-T experiments suggest that iron and water-bearing minerals might be stable at lower mantle conditions (Nishi et al., 2017) and that hydrogen might also be generated by the chemical reactions of such minerals (Hu et al., 2016) and could be partitioned into bridgmanite-post-perovskite (Townend et al., 2016).
1.1 Model description
In this study, we use a modified version of the coupled core–mantle evolution model used in Nakagawa and Tackley (2010). The modified core–mantle evolution model includes the effects of water migration and the partitioning of water into the molten mantle, as described in Nakagawa et al. (2015) and Nakagawa and Spiegelman (2017). A more detailed formulation of the model is given in the Appendices A1 to A3. Here, we briefly introduce these points.
For the modeled mantle, we assumed a compressible and truncated anelastic approximation with temperature-, pressure-, and water-dependent viscosity given as follows:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
To compute the thermo-chemical mantle convection, we use the StagYY numerical code for simulating thermo-chemical mantle convection (Trackley, 2008). Detailed information on the mantle convection simulations and water migration can be found in a series of our previous studies (Nakagawa and Iwamori, 2017; Nakagawa and Spiegelman, 2017; Nakagawa et al., 2015, 2018) and in the Appendix. The water solubility of hydrous mantle silicates is applied as in Nakagawa et al. (2018), including the water solubility of dense hydrous magnesium silicate (DHMS), as shown in Fig. 1, which is based on experimental data (Nishi et al., 2014; Ohira et al., 2014). Briefly described, when the water in the mantle material exceeds the assigned water solubility, the excess water can be generated from the difference between the actual water content in the mantle silicate and the water solubility of the hydrous mantle mineral. We also include a reduction of the solidus temperature of the mantle silicate according to the similar scaling law provided by Katz et al. (2003), and the partitioning of water into the molten mantle is assumed with a partition coefficient of 0.01 between the solid and molten mantle, which means that 99% of water is partitioned into the molten material. The numerical resolution of the mantle convection model is 1024 × 128 with 4 million tracers for tracking the chemical composition, melt fraction, and water content.
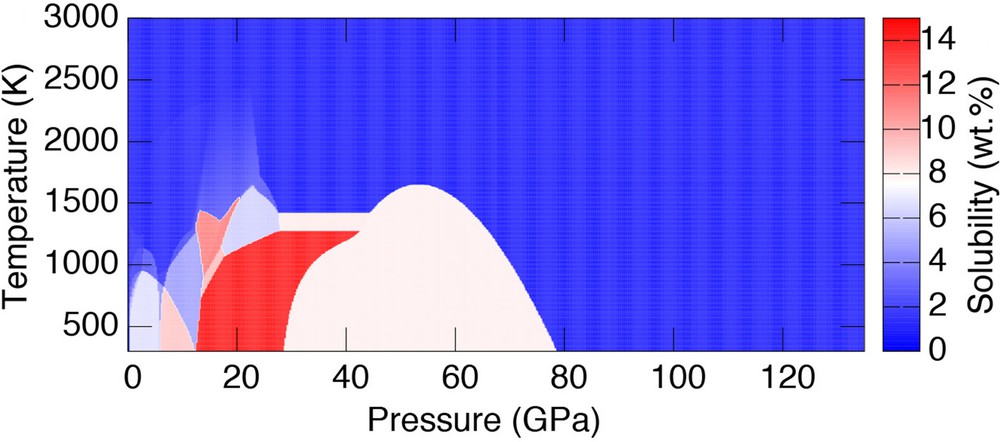
Water solubility map of the ambient mantle material in the whole mantle pressure and temperature range. For the water solubility of the oceanic crust, we use the same solubility in the upper mantle as that proposed by Iwamori (2007), and we use that of the ambient mantle material in the lower mantle because of the similar mineral phases expected.
For the initial conditions of the mantle, the initial temperature profile is set with an adiabatic temperature of 2000 K at the surface, the mantle composition is uniform (20% basaltic material and 80% depleted harzburgitic material), and the water content is zero. The surface boundary condition is fixed as 300 K, but we use the energy of the core evolution described below at the CMB. For the boundary condition of mantle water circulation, a finite reservoir of surface seawater with a box model assumption is used. The mass of the water reservoir can be computed as
| (6) |
| (7) |
With regard to the core evolution incorporated into the mantle convection simulations, the temperature at the CMB is computed from an energetic formulation based on Buffett et al. (1992) and Buffett et al. (1996) for the global heat balance and Lister (2003) for the entropy balance, which is similar to the implementation of Nakagawa and Tackley (2010), whose detailed formulation of core evolution is given in Appendix A3. A simplified and analytical formulation of the heat balance is assumed across the core, with uniform composition and an isentropic temperature due to well-mixed convective conditions for the core evolution. The initial CMB temperature is considered to be 5000 K, which is ∼1500 K higher than the solidus temperature of silicates found in high-P–T experiments (e.g., Andrault et al., 2014; Nomura et al., 2014). This initial condition of the CMB temperature would be observed for a partial melting region in the deep mantle coincident with a basal magma ocean (Labrosse et al., 2007).
All physical parameters used in this study are listed in Table 1 for the mantle and Table 2 for core evolution.
Mantle model physical parameters.
| Symbol | Meaning | Value |
| η 0 | Reference viscosity | 1 × 1021 Pa s |
| ρ 0 | Surface density | 3300 kg m−3 |
| g | Surface gravity | 9.8 m·s−2 |
| α 0 | Surface thermal expansivity | 5 × 10−5 K−1 |
| κ0 | Surface thermal diffusivity | 7 × 10−7 m2 s−1 |
| ΔTsa | Temperature scale | 2500 K |
| T s | Surface temperature | 300 K |
| C p | Heat capacity | 1250 J kg−1 K−1 |
| L m | Latent heat | 6.25 × 105 J kg−1 |
| H | Present-day internal heating rate | 5 × 10−12 W kg−1 |
| λ | Half-life of radioactive elements | 2.43 × 109 yr |
| C Y | Cohesion stress | 10 MPa |
| E d | Activation energy of the dry mantle | 290 kJ mol−1 |
| V d | Activation volume of dry mantle | 2.4 × 10−6 m3 mol−1 |
| E w | Activation energy of wet mantle | 380 kJ mol−1 |
| V w | Activation volume of wet mantle | 4 × 10−6 m3 mol−1 |
Physical parameters for the core evolution model. The theoretical model of core evolution energies is based on Buffett et al. (1992) and Buffett et al. (1996), with some modifications for computing the latent heat release caused by inner core growth.
| Symbol | Meaning | Value |
| ρ 0 | Density at the center | 12491 kg m−3 |
| cp | Heat capacity | 750 J kg−1 K−1 |
| T m,0 | Melting temperature at the center | 4900 K |
| g | Gravity | 9.8 m s−2 |
| G | Gravitational constant | 6.67 × 10−11 m3 kg−1 s2 |
| (∂TL/∂P)X | Pressure derivative | 9 × 10−9 K Pa−1 |
| (∂TL/∂X)P | Composition derivative | −2.04 × 104 K |
| k c | Thermal conductivity | 100 W m−1 K−1 |
| γ | Grüneisen parameter | 1.4 |
| ΔS | Entropy change | 118 J kg−1 |
| ΔρIC | Density change due to inner core growth | 580 kg m−3 |
| R | Gas constant | 8.314 J K−1 mol−1 |
| X m,0 | Initial concentration of light elements | 0.05 |
2 Results
A total of six cases are examined to investigate how hydrous mantle convection affects core evolution. The total amount of water in the entire planetary system is assumed as the control parameter of this study, which varies from 3 to 15 ocean masses (i.e. with a present-day ocean mass of 1.4 × 1021 kg). All cases are set for a friction coefficient of 0.3. This friction coefficient is a nearly lower-bound value of the observational constraints on the strength of the oceanic lithosphere, and is in the range from 0.2 to 0.7 (Zhong and Watts, 2013).
2.1 Dry vs. hydrous
First, to discuss how hydrous mantle convection affects the core–mantle evolution system, Fig. 2 shows the chemical-viscous-hydrous structure taken at 4.6 billion years from the initial conditions. For the case of hydrous mantle convection, we use six ocean masses as a total water mass in the planetary system. The dry mantle model seems to exhibit episodic plate-like behavior; as a result, flat layering above the CMB region can be found. Meanwhile, vigorous plate-like behavior is observed for the hydrous mantle convection model owing to the water-weakening effect, and the model contains four large subduction regions with small-scale compositional anomalies in the deep mantle. This means that the water-weakening effect may enhance surface plate motions, as was noted by Nakagawa and Iwamori (2017). Also, the high-water-content region in subducting slabs can penetrate the uppermost lower mantle corresponding to the substantial water solubility associated with DHMS (e.g., phase D).

Viscous-chemical-hydrous structure taken at 4.6 billion years for the dry (left) and hydrous (right) mantle convection simulations.
Fig. 3 shows comparisons of the core evolution diagnostics between the dry and hydrous mantle models. The heat flow across the CMB is higher for hydrous mantle convection than for dry mantle convection, which is attributable to a difference in the mode of surface plate motion. As a result, the CMB heat flux seems to be very small for the dry mantle model, but it reaches 10 TW for hydrous mantle convection.
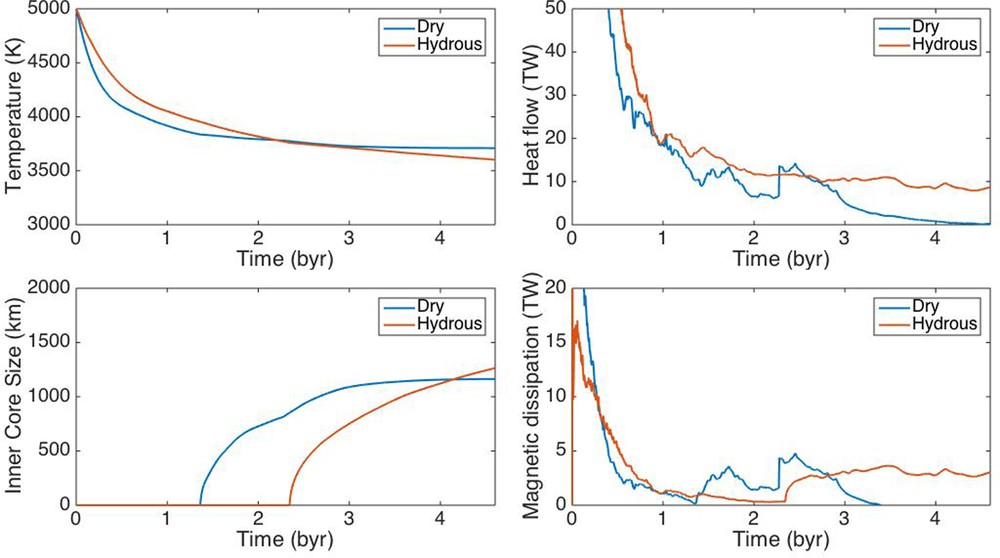
Evolution diagnostics (temperature at the CMB, heat flow across the CMB, inner core size and magnetic dissipation) of the core for the dry and hydrous mantle convection cases.
2.2 Sensitivity of the total water amount in the planetary system
Fig. 4 shows the chemical-viscous-hydrous structure taken at 4.6 billion years for a total water amount of 6 and 15 ocean masses in the planetary system. Compared to the hydrous mantle convection model (left of Fig. 4; 6 ocean masses with stronger oceanic lithosphere) with that shown in the right side of Fig. 2 (6 ocean masses with weak oceanic lithosphere), the plate-like behavior displayed in the left side of Fig. 4 is slightly less vigorous because of the high friction coefficient used in those cases. As a result of the less vigorous plate-like behavior, compositional anomalies at larger scales in the deep mantle are likely to be preserved. Concerning the mantle water content, large amounts of water are found in the uppermost lower mantle region beneath cold subduction regions. Again, as suggested by Nakagawa et al. (2018), this is caused by the appearance and dissolution reaction of phase D.
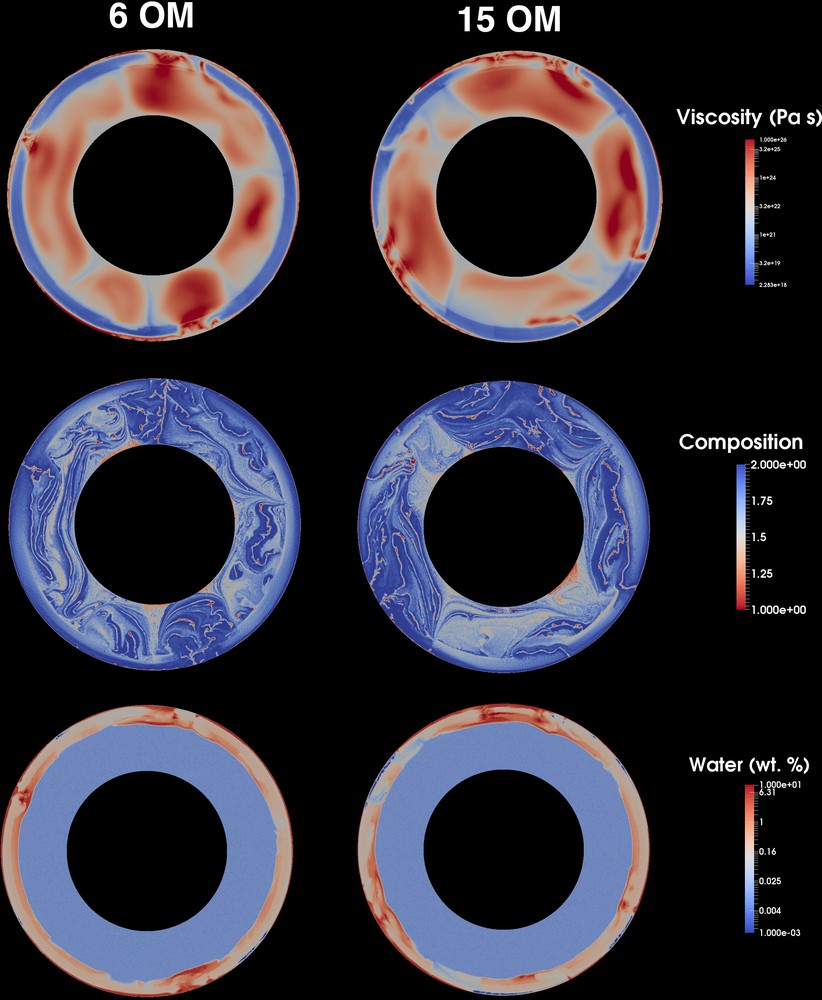
Viscous-chemical-hydrous structure taken at 4.6 billion years for total water amounts of 6 OM in the planetary system (left) and 15 OM (right).
Fig. 5 plots the amounts of surface seawater and mantle water and the mass-averaged mantle temperature as a function of time for all hydrous mantle convection cases, and the 1-D horizontally-averaged water content and temperature taken at 4.6 billion years for a total water amount of 15 ocean masses. Up to the case of 12 ocean masses, the surface ocean is completely transported into the deep mantle within 4.6 billion years; for the case with 15 ocean masses, the surface ocean may survive over 4.6 billion years. Therefore, for the cases between 12 and 15 ocean masses, the present-day Earth could have one ocean mass at the surface. Note that this is a maximum estimate. Regarding the estimates of the total water mass in the mantle reported by Iwamori (2007), the mantle may have absorbed approximately ∼12 ocean masses at the maximum estimate, which is consistent with the ocean masses expected in this study. However, note that this maximum estimate of the water mass of the mantle is computed in the saturated situation for oceanic lithosphere, but an experimental constraint on the water content of oceanic crust suggests that the oceanic crust would be in the undersaturated condition (e.g., Carlson, 2003). Preferably, the mantle water mass would be ∼6 to 7 ocean masses indicated in the averaged value of mantle water mass (Table 3 in Iwamori, 2007). Theoretical model on partitioning of hydrogen in the mantle silicate at lower mantle condition is also indicated as the similar value (Table 2 in Merli et al., 2016). In Fig. 5b, the mantle water contents at depths above the first 200 km and between the depths of 700 km and 900 km are computed as approximately 4.2 and two ocean masses, respectively. For understanding why a large amount of water can be transported into such regions, the relationship of mantle temperature and water solubility is a key. Fig. 5c shows the 1-D horizontally-averaged mantle temperature. Since the cold geotherm may pass through below the choke-point of water solubility maps (see Fig. 1), a large amount of water can be transported into the mantle transition zone as well as into the uppermost lower mantle associated with the high-solubility region caused by DHMS. This suggests that the cold downwelling flow can work for the main host of water transporting into the deep mantle. Again, note that an actual water mass absorbed in the mantle would be less than this estimate, because the hydrous condition in the oceanic lithosphere would be undersaturated to give a value of the water mass of the mantle consistent with the expected averaged values of Iwamori (2007) and Merli et al. (2016).
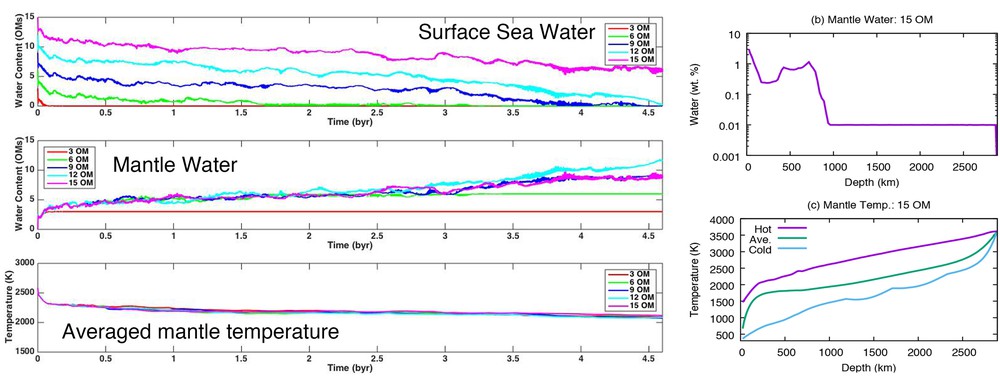
(a) Evolution diagnostics of the surface water mass (top), mantle water mass (middle), and mantle temperature (bottom) for each value of the total water amount in the planetary system. (b) 1-D horizontally-averaged profile of the mantle water content for 15 OM and (c) 1-D horizontally-averaged profile of the mantle temperature for 15 OM.
Fig. 6 shows the mantle water fluxes (ingassing, dehydration and degassing) as a function of time for the cases with six ocean masses (all surface water is transported into the deep interior) and 15 ocean masses (surface water remains on the surface). The computing procedures are found in Nakagawa and Spiegelman (2017) and Nakagawa et al. (2018). The detailed description can be found in Appendix A2.
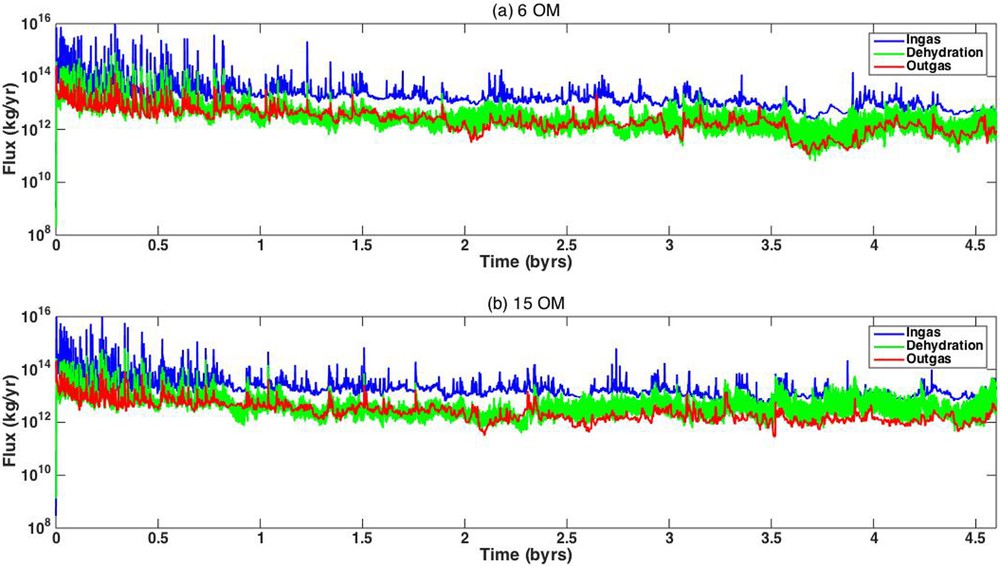
Diagnostics of the water fluxes (ingassing: blue, degassing: red and dehydration: green) for (a) 6 OM and (b) 15 OM.
Fig. 7 shows the sensitivity of core evolution for all cases of convection of the hydrous mantle. There is less sensitivity in core evolution with different choices of the total amount of water in the planetary system. On the present-day Earth, the temperature at the CMB is estimated to be ∼3600 K, and the heat flow across the CMB is 10 TW; the inner core is 2 billion years old, and continuous dynamo activity has lasted over 4 billion years, as obtained from this numerical model. These values seem to be similar to a series of previous studies for dry mantle convection with weaker plate cases (e.g., Nakagawa et al., 2010). For the CMB heat flow, it would be in the range 5–15 TW (e.g., Lay et al., 2008). For the age of the inner core, it would be older than recent results that evidence a much younger inner core (e.g., Biggin et al., 2009), but it would be still very controversial because the paleomagnetic data for constraining the age of the inner core would suffer a huge discrepancy. As discussed in the previous sections, hydrous mantle convection would be more promising for revealing the evolution of the core–mantle–plate–ocean system that matches various observational constraints (i.e. the geomagnetic field, the size of the inner core, and the current amount of surface seawater).
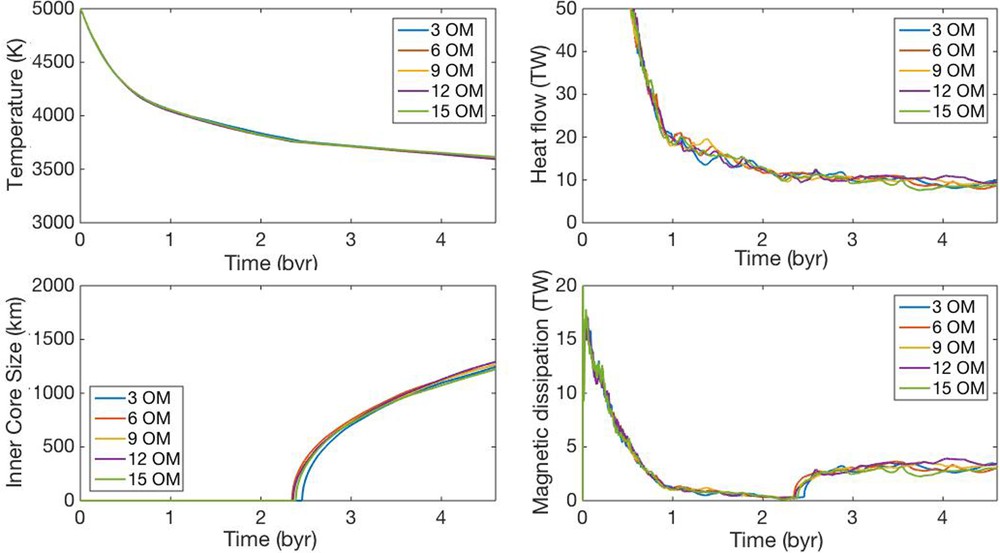
Model sensitivities of the core evolution diagnostics to each amount of the total water in the planetary system.
Regarding the heat flow across the CMB and the age of the inner core, various theoretical studies on core evolution and paleomagnetism suggested much higher heat flow values and younger inner core ages (Biggin et al., 2009; Davies, 2015; Labrosse, 2015). However, in particular, the paleomagnetic data that could be utilized to imply the age of the inner core still seems to be controversial due to uncertainties in the data (Biggin et al., 2009).
3 Discussion and summary
3.1 Findings
Here, we investigate the effects of hydrous mantle convection on the evolution of the core. Moreover, we also discuss the evolution of surface seawater by providing a constraint on the amount of water that has been delivered since the early planetary formation. The main findings in this study are as follows.
Hydrous mantle convection is a crucial process for understanding the cooling processes of the core–mantle system caused by the viscosity reductions occurring under the effect of water-dependent viscosity.
To accommodate one ocean mass for the present-day Earth, the total amount of water in the planetary system was between 12 and 15 ocean masses at the maximum. This seems to be consistent with the maximum water mass in the mantle found from a realistic geotherm (Iwamori, 2007). However, more preferably, the mantle water mass could be absorbed in ∼6 to 7 ocean masses (averaged value in Table 3 in Iwamori, 2007; Table 2 in Merli et al., 2016). This suggests that the hydration condition of the oceanic lithosphere would not be saturated, which is pointed out by an experimental constraint of water content in the oceanic crust (e.g., Carlson, 2003). As discussed in the Appendix A4, the hydration condition of the oceanic crust may not be very sensitive, and the storage capacity of water in the mantle mineral may be determined for the hydration situation in the deep mantle. In the subduction-scale modeling, the minimum water content of oceanic lithosphere may be around two wt. percent to generate the volcanic activities beneath the island arc (Horiuchi and Iwamori, 2016). Therefore, this modeling result seems to be somewhat robust to discuss the Earth-like features of the mantle water cycle.
This is the first attempt to develop a coupled evolutionary model for the core–mantle–plate–ocean system. Although core evolution in hydrous mantle convection is not very sensitive to the total amount of water in the planetary system, the hydrous models explain the heat flux across CMB better compared to the dry model.
3.2 A total amount of water in the planetary system
As discussed in the previous section, the mantle water mass studied here is consistent with the maximum estimate of the water mass of the mantle using the realistic geotherm (Iwamori, 2007). However, more preferably, the mantle water mass could be absorbed in ∼6 to 7 ocean masses with water solubility and partitioning of hydrogen (averaged value shown in Table 3 of Iwamori (2007); Table 2 of Merli et al. (2016)). For estimating the maximum amount of mantle water mass, this is based on the saturated condition in the oceanic lithosphere and uppermost lower mantle. As shown in Fig. 5b and c, the oceanic lithosphere seems to be the water-saturated situation. Therefore, our estimate of the absorbed water in the mantle is similar to the maximum one proposed by Iwamori (2007). However, the water content in the oceanic crust ranging from 0.5 to 6 wt. % is found from experimental estimates (Aubaud et al., 2008; Carlson, 2003), which is considerably uncertain, but suggests that the hydrous situation of oceanic crust may be undersaturated for the water.
Moreover, the heterogeneous condition of hydration of oceanic crust caused by thermal cracking phenomena (Korenaga, 2007) and serpentinization in the outer-rise fault (Hatakeyama et al., 2017) should be incorporated for further understanding of the transport of water into the deep mantle and of the hydrous structure in the deep mantle. Again, in our model, the boundary condition of mantle water transport is assumed with the water-saturated condition of oceanic crust. To check how the hydrous situation of oceanic crust affects the results, as indicated in Appendix A4, we evaluate the sensitivity of the water content of oceanic lithosphere to water evolution. As a result, the evolution diagnostics of water in both mantle and surface are not strongly sensitive to the hydration condition of the oceanic lithosphere, even though it is the undersaturated condition. As a result, the storage capacity of water in mantle minerals could play a more key role in the hydration condition in the deep mantle than the hydration condition of oceanic crust. Any hydration mechanism could result in a similar evolution scenario. However, again, we note that this estimate of water evolution is still the maximum one; the result might be changed if the water solubility limit of hydrous mantle minerals were revised, but the current understanding of the storage capacity of water suggests that the results shown in this study are still robust. Also, the sensitivity of the power-law index of the water-dependent viscosity should be tested because a recent experimental investigation suggested that this index should be r = 0.3 (Fei et al., 2013), which is much lower than that used in this study (r = 1.0).
There are several caveats before interpreting numerical results. For the evolution of surface seawater, other studies would indicate a different scenario provided from geochemical and geological accomplishments, that is, ‘continental freeboard’ (Korenaga et al., 2017; Parai and Mukhopadhyay, 2012) and D/H ratio evolution of the Archean seawater (Kurokawa et al., 2018). In these authors’ implications, the mantle water mass would not be very large, likely 1 to 2 ocean masses. However, these studies have not incorporated the effects of water solubility of each mantle minerals for evaluating the evolution of the water mass of the mantle. Hence, the present-day mantle water mass would be still controversial. For resolving this issue, it would be required to check the numerical model of hydrous mantle convection rather than to use a simple mass flux computation without assuming the solubility of water in each mantle mineral.
Regarding the sea level change inferred from the continental freeboard hypothesis, this would not be changed over a time scale of a few billion years (∼500 m; Korenaga et al., 2017; Parai and Mukhopadhyay, 2012). This implies that the water budget between the deep Earth and the exosphere would have been balanced for over a few billion years. As pointed out by the potential water mass in the deep mantle inferred from the water solubility limit of mantle minerals, the mantle may have 6 to 8 ocean masses (Iwamori, 2007). This suggests that the mantle may have a huge amount of water in the early state of the Earth. To have a huge amount of water in deep mantle, looking at Fig. 1, the temperature in the early mantle of the Earth should be much colder than assumed in this study, because the water content in the mantle is strongly regulated by the water solubility limits (Nakagawa and Spiegelman, 2017). For the thermal state from the early mantle to the present-day mantle, a situation similar to that proposed by Korenaga (2011) would be somewhat expected, which may start with colder temperatures in the mantle, which would be heated up by a heat-producing element, then cooled down by vigorous mantle convection. However, note that, in this study, the continental lithosphere is not included in the numerical model; this argument is still quite speculative. To tackle the issue on the free-board hypothesis and other important processes such as the formation of sediments, it is a crucial issue that should be addressed more systematically in numerical modeling of mantle convection, which has been initiated for the generation of the precursor material of the continental crust (Rozel et al., 2017). In this study, we have started with the development of the thermal and chemical history of hydrous mantle convection, then addressing the formation of continental crust for discussing the free-board hypothesis in the future study.
Moreover, regarding estimates of water flux associated with subduction, it would be less by a few orders of magnitude than our estimate shown in Fig. 6 (Bodnar et al., 2013; Jarrard, 2003). In Fig. 6, we computed the ingassing flux across the surface. Assuming the effects of the choke-point of solubility of the water content in the mantle, the ingassing flux associated with subduction would be reduced up to three orders of magnitude of the ingassing flux across the surface (Nakagawa et al., 2015). This means that the actual water flux transported into deep mantle would be an amount similar to the recent estimate of the water flux. Therefore, simplified arguments on mantle water flux are still very controversial, but the actual water mass in the mantle could not be estimated from the mass balance assumption.
3.3 Implications for water transport across the core–mantle boundary: hydrogen partitioning
As suggested from high-temperature and high-pressure mineral physics, hydrogen may be generated by the reaction of water with iron-bearing minerals during lower mantle convection (Hu et al., 2016; Nishi et al., 2017). Since hydrogen seems to be one of the most important light elements in core alloys (Poirier, 1994), understanding the amount of hydrogen that can be transported via the metal–silicate partitioning of hydrogen into metallic iron seems to be significant. Unfortunately, there has been quite few publications that addressed the metal–silicate partitioning of hydrogen into metallic iron, and this partitioning occurred at relatively lower pressure and temperature (e.g., Okuchi, 1997). An implication of the partitioning of hydrogen in core alloys suggests, when extrapolating such an experimental constraint to the conditions in the deep mantle, that hydrogen seems to be partitioned into metallic iron and that it never returns to the silicate mantle. This suggests that hydrogen is generated at the lower mantle condition associated with the water absorbed in the lower mantle. The metal–silicate partitioning of hydrogen can result in hydrogen transportation into the metallic core. Therefore, the hydration state of the lower mantle plays a key role for the partitioning of hydrogen into the metallic core caused by metal–silicate partitioning. However, recent investigations on metal–silicate partitioning of hydrogen between metallic core and silicate mantle indicate that hydrogen is likely to be partitioned into the silicate mantle (Clesi et al., 2018). The hydrogen in the Earth's core might be trapped as a result of metal–silicate partitioning due to core formation in the early Earth (Iizuka-Oku et al., 2017). This may suggest that the hydrous conditions in the deep mantle could be expected as the large-scale anomalies caused by thermal and chemical effects.
To further clarify that, investigations of the metal–silicate partitioning of hydrogen should be conducted in greater detail to integrate the water cycle into the core–mantle–plate–ocean system completely, which may reveal the hydration state in the lower mantle. It has to be noted that this type of metal–silicate partitioning could occur through the interaction with the silicate melt. The melting temperature of the silicate mantle ranges from 3500 K to 3800 K (Andrault et al., 2014; Nomura et al., 2014). Compared with the temperature at the CMB found in this study, that is, a present-day temperature of ∼3600 K, the metal–silicate partitioning of hydrogen could have occurred from a few billion years ago to the present day (when the melting temperature would be at a minimum). However, it would have stopped in a couple of billion years at a maximum value of the melting temperature at the CMB (see Fig. 7). This suggests that the survival time of a basal magma ocean would play a key role in operating such a metal–silicate partitioning process. However, again, the hydrogen of the Earth's core is still quite a controversial issue. For resolving that, more investigations are needed.
4 Conclusion
In this study, we developed a core–mantle–plate–ocean evolution model through a numerical mantle convection simulation. The findings can be summarized as follows.
To understand the long-term evolution of the Earth and of the planetary system, hydrous mantle convection is an essential process for a successful scenario describing core evolution, because hydrous mantle convection may enhance the heat transfer associated with mantle convection, with viscosity reductions caused by water-dependent viscosity.
The present-day amount of surface seawater within the mantle dynamics system would require between 12 and 15 ocean masses in the total planetary system. This means that the deep planetary interior may contain more than ten ocean masses. This also constitutes an enormous amount of water that has been absorbed into the mantle compared to values from a series of previous modeling studies on the mantle water cycle (Rüpke et al., 2004; Sandu et al., 2011). As incorporated into the water solubility map in the numerical mantle convection simulation, the water transported into the deep mantle seems to be mainly absorbed into the mantle transition zone and DHMS phases that have a solubility of ∼10%. However, considering a realistic geotherm with a temperature that is higher by a few hundred kelvins than the thermal structure in this study, this may suggest that DHMS solubility would not be significant for a contribution to the mantle water mass. Therefore, the mantle water mass is likely reduced to 6–7 ocean masses (Iwamori, 2007; Merli et al., 2016). However, since there is another hypothesis on the effects of the buoyancy of continental lithosphere that is not incorporated into this study, the amount of water in the deep mantle is still controversial.
Our findings imply that the partitioning of hydrogen could supply the partitioning of hydrogen associated with water absorbed into lower mantle minerals caused by metal–silicate partitioning into metallic iron. However, as suggested from experimental constraints (Clesi et al., 2018; Iizuka-Oku et al., 2017), partitioned hydrogen seems to be difficult to occur over the Earth's history, which might result in the differentiation of the core formation process in the early Earth. For more clarifying the hydrogen cycle in the whole planetary system, it would be worth to integrate the global-scale water cycle into the core–mantle–plate–ocean system based on the numerical model used in this study.
Acknowledgments
The authors thank Atsushi Nakao for the water solubility of the DHMS phases incorporated into the numerical mantle convection simulations and Paul Tackley for providing his numerical mantle convection code (StagYY). They also thank two anonymous reviewers for improving the original manuscript significantly. All of the simulation data are available from the corresponding author (TN) upon request, but the numerical simulation program is the property of the developer (Paul Tackley), and the water solubility data are the property of HI and are not available to the public. JSPS-MEXT Kakenhi financially supports TN through the ‘Core–mantle Co-evolution’ (15H05834), JSPS Kahenhi (JP16K05547), the FLAGSHIP2020 project, and MEXT within the CBSM2 project “Structure and Properties of Materials in the Deep Earth and Planets.” All numerical simulations were performed under the JAMSTEC Data Analyzer system.


