1. Introduction
The Little Ice Age (LIA) was a multi-secular cold period, lasting approximately from 1350 to 1850 AD, during which glaciers advanced worldwide [e.g., Solomina et al. 2015, 2016]. The magnitude and timing of the glacial advances was not synchronous worldwide [Grove 1988; Rabatel et al. 2008; Neukom et al. 2014; Solomina et al. 2015, 2016]. The evolution of glaciers since the Little Ice Age has been most frequently studied in mid-latitudes. For example, in the French Alps glaciers reached their maximum extent around the first half of the 17th century, and their front oscillated in a position slightly up-valley before re-advancing close to their maximum extent throughout the first half of the 19th century [e.g., Grove 1988; Vincent et al. 2004, 2005; Solomina et al. 2015, 2016]. [Paul and Bolch 2019] reviewed a number of studies of the evolution of Alpine glaciers since the LIA and concluded that it could be summarized by a km scale retreat, a rise in the equilibrium-line altitude (ELA) of 100–200 m, and an up-valley retreat of several hundred meters in glacier terminus positions. In Pyrenean glaciers, Campos et al. [2021] reported ELA rises of 220 m.
On the other hand, the evolution of glaciers in Tropical South America since the LIA has been the subject of few studies. The majority of glaciers reached their maximum extent between 1630 and 1720 and have been retreating ever since; their retreat has been interrupted several times by minor advances [Rabatel 2005; Rabatel et al. 2005, 2008; Jomelli et al. 2009, 2011]. Based on the dating of 15 Bolivian glaciers using lichenometry, radiocarbon or 10Be techniques, Rabatel et al. [2008] estimated that their ELA rose by 285 ± 50 m since the LIA while, based on the Telata Glacier also in Bolivia, Jomelli et al. [2011] estimated that the ELA rose by 320 m.
Understanding past glacier variations is key to better insights into future changes. In the case of tropical glaciers, this is of particular interest as they represent an important water resource for Andean populations [e.g., Soruco et al. 2015]. Tropical glaciers react rapidly to climate perturbations [by advancing or retreating, e.g., Kaser 2001; Thompson et al. 2006] making them suitable paleoclimate proxies to evaluate past climate scenarios.
Over tropical South America, paleoclimate proxies such as ice cores, sediments, tree rings or speleothems [e.g., Thompson et al. 2006; Ledru et al. 2013; Apaéstegui et al. 2018; Campos et al. 2019; Bird et al. 2011; Morales et al. 2012] and glacier sensitivity analyses [e.g., Rabatel et al. 2005, 2008; Malone et al. 2015] provide valuable temperature and precipitation data on the LIA. The main drawback of these methods is the temporal scale (annual to decadal). For example, glacier studies usually use simple approaches [e.g. simplified energy balance methods, Hastenrath and Ames 1995] which only allow comparison of glacier steady state conditions at two different periods, but do not provide detailed insights into seasonal changes in climatic forcing on the glacier mass balance.
The annual mass balance of South American tropical glaciers depends primarily on the timing and length of the wet season during the austral summer [Sicart et al. 2011] and they are highly sensitive to the temporal distribution of precipitation between September and the onset of the wet season [Autin et al. 2022]. Several studies suggest that the onset and length of the wet season may have changed during the Little Ice Age [e.g. Dıaz and Vera 2018], a feature that cannot be captured by models using annual temperature and precipitation amounts. Hence, such models may largely underestimate past mass balance variability [Sicart et al. 2011]. In addition, sub-annual precipitation records are rare over low latitude mountains and precipitation predictions are unreliable, making reconstruction of past glacier advances and estimating future retreat challenging in these regions.
In this study, we used the distributed energy balance model [DEBAM, Hock and Holmgren 2005] which had been adapted to tropical glaciers by Sicart et al. [2011]. This model is based on equations of mass and energy conservation and, in theory, the physical interpretation of the parameters can be linked to measurable quantities [Beven 1989]. However, because natural sub-grid heterogeneities can lead to a mismatch of scales between measured and modeled variables, the calibration process is often complicated [Klemes 1983; Seibert 1999]. Thus, to limit the risk of using a model calibration that makes the model subject to the three rules of classical tragedy: unity of place, unity of action and unity of time [De Marsily 1994], a parsimonious approach was chosen to minimize the number of parameters with the aim of matching model complexity to the availability of field observations. In this way, we expect that even if the models represent more fiction than reality, the fiction nevertheless helps understand reality [Seibert 1999].
We chose to apply the model to the tropical Zongo Glacier (16° S, Bolivia) because this glacier’s present-day climate controls have already been well studied [e.g., Rabatel et al. 2013; Autin et al. 2022] and its LIA maximum reconstructed [Rabatel 2005]. Run at an hourly time step, this model makes it possible to investigate the effect of changes in seasonal precipitation patterns on the surface mass balance at the LIA maximum extent of the glacier.
For this purpose, we created scenarios that differ in precipitation amounts and seasonality but where the physical consistency between measured meteorological variables is retained (i.e. physically-coherent scenarios). The scenarios that resulted in an equilibrium state (surface mass balance close to zero) were considered plausible LIA scenarios.
2. Study site and background on the LIA in the tropical Andes
2.1. Study site and present climate
Zongo Glacier (16° 15′ S, 68° 10′ W, Cordillera Real, Bolivia) is a valley-type glacier extending from ∼6000 m a.s.l. down to ∼4950 m a.s.l. A glacier monitoring program began in 1991 through collaboration between a Bolivian university (Universidad Mayor de San Andrés) and IRD [French Research Institute for Development, Francou et al. 1995; Ribstein et al. 1995]. Rabatel et al. [2013] and Sicart et al. [2015] provide a detailed overview of the monitoring network, which includes three automatic weather stations (AWS), one on the glacier, and two off-glacier, along with a discharge gauging station, and several ablation stakes and snow pits (Figure 1).
Zongo Glacier (16° 15′ S, 68° 10′ W) showing its monitoring network. The red outline represents the maximum extent of the LIA and the corresponding digital elevation model, the black line shows the extent of the glacier in 2012. The map in the top inset is a 3D view of the extent of the glacier at its LIA maximum extent. SAMA (5050 m a.s.l.), ORE (5050 m a.s.l.) and PLATAFORMA (4750 m a.s.l.) are the three automatic weather stations (AWS) installed on and around the glacier, TUBO is a discharge gauging station located at 4830 m a.s.l. The red star shows the position at which the measurements are used to force the model in LIA simulations. Source of the background image: Pleiades satellite in 2013, © CNES—Airbus D&S. Digital Elevation Model: Rabatel [2005].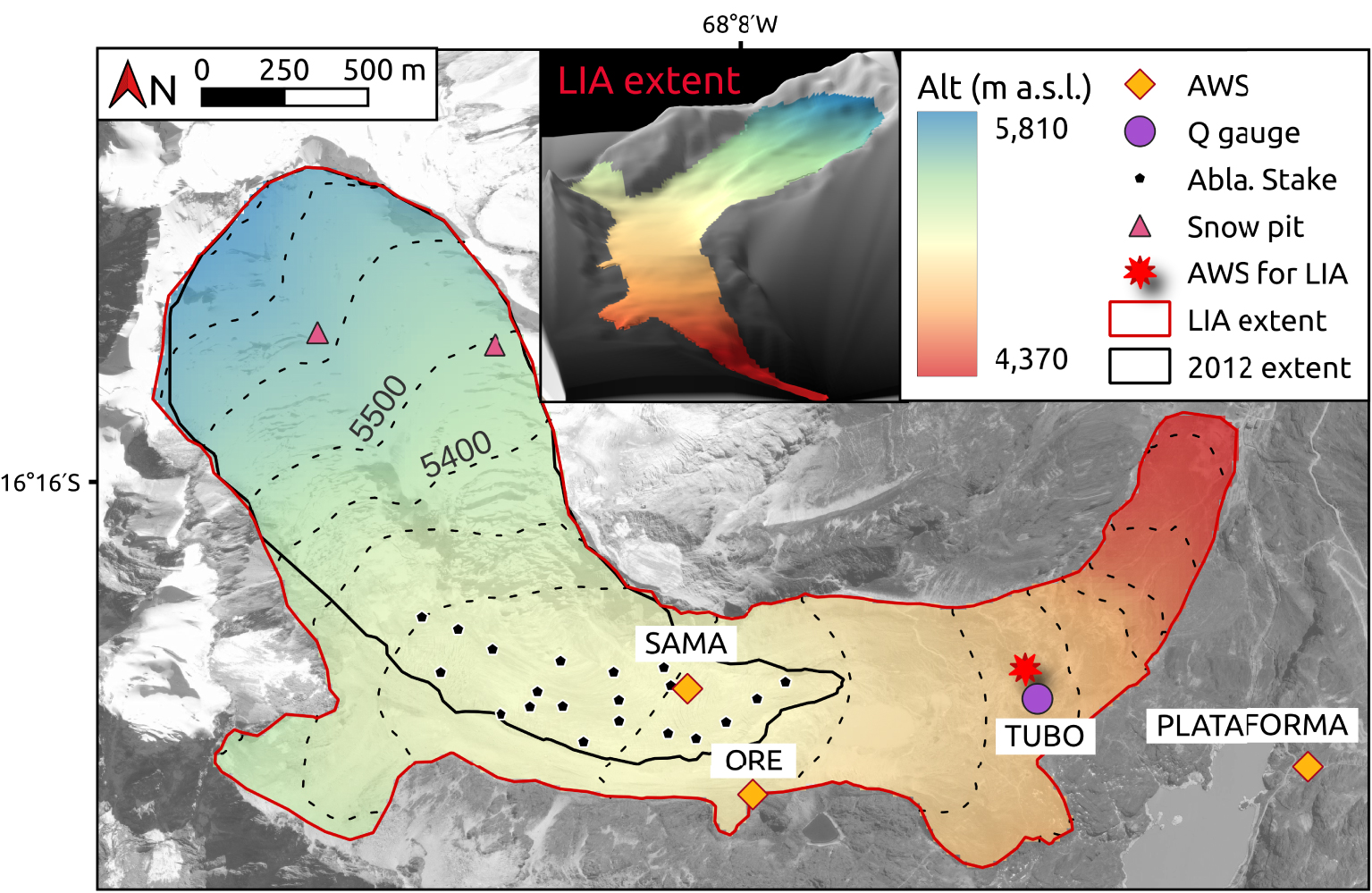
Being in the outer tropics, the climate over the glacier is characterized by marked precipitation and cloud cover seasonality, with a single wet season in austral summer and a pronounced dry season in austral winter [Troll 1941]. A number of authors have identified and described three seasons with distinct melt mechanisms over this tropical glacier where the hydrological year starts on the first of September [e.g., Sicart et al. 2011; Rabatel et al. 2012; Autin et al. 2022].
The transition season (September to November) is characterized by increasing melt rates due to limited precipitation [around 20% of the annual amount, Ramallo 2013] and increasing solar radiation as the top of atmosphere radiation approaches its maximum annual value reached at the austral summer solstice [Sicart et al. 2011]. Autin et al. [2022] simulated nine years of distributed surface energy balance over Zongo Glacier using DEBAM and showed that this period plays a key role in controlling annual mass losses and that the timing of precipitation events in the season is a key driver of melt.
The wet season (December to March) is linked to the mature phase of the South American monsoon system (SAMS). During the SAMS, a strong anticyclonic system in the upper troposphere [the Bolivian High, Lenters and Cook 1997] coupled with the southward displacement of the South American low-level jet (SALLJ) result in strong easterly winds on the eastern slopes of the Cordillera Real. This leads to moisture transport over the Cordillera Real, which, coupled with solar heating of the surface, results in frequent afternoon/early evening convection events over Zongo [e.g., Garreaud et al. 2003]. This season is characterized by decreasing melt rates due to the strong cloud cover and albedo feedback effect. Over this period, little ice mass loss is observed as most of the melt comes from large snowfall events [70% of the annual amounts, Ramallo 2013]. In addition, it is the glacier accumulation season.
April–May is a second transition period, from the end of the wet season to the onset of the dry season (June to August). During this period, the precipitation amounts and distribution are highly variable due to the interannual variability of the demise of the wet season (based on 18 years of measurements, the amount of precipitation received over this period is 50 ± 27 mm w.e.).
The dry season is characterized by low melt rates and rare precipitation events. The absence of clouds in the dry season creates an incoming longwave radiation deficit leaving little energy available for melt [Sicart et al. 2011]. In addition, the dry and cold air coupled with high wind speeds favors sublimation over melt [Wagnon et al. 1999; Sicart et al. 2005], limiting mass loss through this period.
A number of studies [e.g., Sicart et al. 2005; Wagnon et al. 1999] identified the net all-wave radiation flux as the main driver of melt at seasonal and interannual time scales, more specifically, the incoming shortwave radiation flux. Sicart et al. [2005, 2016] showed that the marked cloud and precipitation seasonality is an important factor in controlling seasonal mass balance variability. Building on this, Autin et al. [2022] showed that melt energy is highest during the transition season and that the interannual variability of the surface mass balance is mostly driven by the temporal distribution of precipitation events and their amounts and, to a lesser extent, by the cloud cover throughout this season.
2.2. LIA climate reconstructions in the tropical Andes
Ice cores are paleoclimate proxies that provide valuable information at seasonal and annual scales over the last 1000 years as well as information at a coarser temporal scale over the last 20,000 years [Vimeux et al. 2009; Hurley et al. 2019]. Using an ice core drilled in the Quelccaya ice cap (QIC, southern Peru), Thompson et al. [1986, 2006] showed a significant decrease in both δ18O and dust concentration during the LIA (1500–1800 AD) were associated with a decrease in temperatures. More recently, Hurley et al. [2019] showed that changes in δ18O are primarily linked with ENSO activity which, in turn, is related to changes in the activity of the South American monsoon system (SAMS) rather than temperature changes. Thus, in agreement with Hurley et al. [2019], we consider that the lower δ18O observed during the LIA is associated with increased precipitation rather than with colder temperatures.
Morales et al. [2012] analyzed Polylepis Tarapacana tree rings across the Altiplano to reconstruct the climate between 1300 and 2000 AD and found that sustained wet conditions prevailed between 1600 and 1750 AD leading to precipitation positive anomalies (up to 40% at its highest with respect to the average measurement for the period 1982–2000).
Speleothems [Campos et al. 2019; Apaéstegui et al. 2018; Vuille et al. 2012] and sediments of diverse origin [Ledru et al. 2013; Bird et al. 2011; Sachs et al. 2009; Haug et al. 2001] provide information on changes in temperature and precipitation patterns over the past 2000 years. Their wide spatial availability across tropical South America enables a 2000-year reconstruction of the SAMS. These studies suggest that a southern shift of the Inter Tropical Convergence Zone (ITCZ) linked to decreased radiative forcing [Maunder minimum, 1645–1715 AD, Lean 2000] caused colder North Atlantic Sea Surface Temperatures during the LIA, resulting in an intensification of SAMS that led to unprecedented moisture levels over the Eastern Cordillera.
Dıaz and Vera [2018] assessed four Paleoclimate Model Intercomparison Project 3/Climate Model Intercomparison Project 5 [PMIP3/CMIP5, Braconnot et al. 2011] model ensemble runs between 850 and 2005 AD over South America. These authors found that the models can correctly reproduce temperature variations over the past millennium (with respect to paleoclimate proxy information) but cannot represent the associated changes in precipitation. Similarly, we considered temperature and precipitation time series of two ensemble runs with paleoclimate proxy information from Michel [2020] and Tardif et al. [2019] thereby corroborating the findings of Dıaz and Vera [2018].
Dıaz and Vera [2018] also analyzed large-scale atmospheric conditions (250 hPa and 800 hPa zonal winds) of PMIP3/CMIP5 ensemble runs and showed an equatorial shift of the southern branch of the Hadley cell during the LIA that resulted in a wetter tropical South America [Lu and Vecchi 2014]. However, because the simulated precipitation amounts do not match proxy information, these models cannot be used to compare past precipitation amounts and present conditions.
Glacier modeling can be used to assess climate conditions which lead to a known past glacier extent. Based on a synthesis of sensitivity studies of tropical South American glaciers, Kaser [1999] attributed two thirds of the glacier retreat in the Cordillera Blanca since the LIA to a decrease in vapor pressure, and the remaining third to an increase in air temperature. Malone et al. [2015] applied a coupled ice-flow mass balance model on the QIC to reconstruct annual climate conditions during the LIA and concluded that the glacier is more sensitive to temperature than to precipitation. Finally, Rabatel et al. [2005, 2008] applied the Kaser [2001] model and Hastenrath [1984] approach to Bolivian tropical glaciers and found that for the glaciers to have reached their maximum extent during the LIA, a 20–30% increase in precipitation (that goes hand-to-hand with an increase in cloudiness) and cooler temperatures (∼−1 to −1.2 K) with respect to today’s climate conditions would have been required.
These different studies suggest that during the LIA, precipitation amounts were between 20 and 40% higher than today and that the temperature was 1 to 1.5 °C lower. However, uncertainties on how this extra precipitation was distributed within the year remain, which is just what our study aims to clarify, as using an energy balance model is the only way to investigate the effect of seasonal precipitation patterns on the annual surface mass balance.
3. Method
We used the distributed surface energy balance model [DEBAM, Hock and Holmgren 2005] to simulate the glacier surface mass balance of Zongo Glacier over the reconstructed surface area of the glacier during the LIA. The model is forced by hourly time series of meteorological data based on measurements recorded by an automatic weather station for nine years distributed between 1999 and 2017. The observations are used to construct four climate scenarios that are then assessed based on their ability to yield a near-balanced mass budget. Further details are given below.
3.1. Mass balance model
3.1.1. Model description
DEBAM simulates the glacier surface mass balance and melt discharge at hourly intervals over the grid cells of a digital elevation model (20 × 20 m cells) using an energy-balance approach [Hock and Holmgren 2005]. In this study, we use the multi-year calibration of Zongo by Autin et al. [2022]. The model requires seven input meteorological variables (air temperature and relative humidity, wind speed, precipitation, incoming short and longwave radiation and outgoing longwave radiation) and solves the following surface energy balance equation:
| (1) |
Incoming shortwave radiation was extrapolated across the glacier by splitting it into its direct and diffuse components. The albedo was modeled using a version of Oerlemans and Knap [1998]’s albedo parameterization adapted to tropical glaciers. This parameterization accounts for the rapid alternation (a few days) of accumulation and melt in the wet season, and the impact of ice on the albedo over shallow snow depths [Sicart 2002]. The incoming longwave radiation flux was assumed to be spatially constant.
Surface temperature was calculated at the AWS from the outgoing longwave radiation measurements and an altitudinal gradient of −0.1 K∕100 m was applied to extrapolate surface temperatures across the glacier (with an upper limit of 273.15 K). The subsurface snow module [Hock and Tijm-Reijmer 2012] was not used to evaluate spatial changes in the surface temperature due to lack of data to constrain the model (i.e. subsurface temperature and density profiles). This implies that we neglected the sub-surface heat flux in our simulations.
The sensible and latent turbulent heat fluxes were calculated according to the aerodynamic profile method between the glacier surface and the measurement height (wind speed, air temperature and relative humidity) based on the Monin–Obukhov similarity theory [see Hock and Holmgren 2005 for more details]. The stability functions were based on Beljaars and Holtslag [1991] for stable conditions and on the Businger–Dyer expressions from Paulson [1970] for unstable conditions. Relative humidity and wind speed were considered spatially constant across the glacier.
Discharge at the glacier terminus was simulated using a runoff module that routes glacier melt and rain water through the glacier using three linear reservoirs representing firn, snow and ice [storage constants of 350, 30 and 16 h, respectively, taken from Sicart et al. 2011]. In addition, for non-glacierized surfaces (30% of the catchment in the recent climate), a runoff coefficient of 0.8 was considered [based on Ribstein et al. 1995].
3.1.2. Model calibration and validation
We used the model parameter values from Autin et al. [2022], who calibrated and validated the model over Zongo Glacier over nine years distributed between 1999 and 2017. This calibration, summarized on Table 1, was a trade-off between years with high and low mass losses where particular emphasis was placed on accurately representing the transition and the wet season, as they play a key role both in the annual surface mass balance and in year-to-year variability. The transition season is the period when the glacier loses on average half its annual mass in the ablation zone, while the wet season is the accumulation period. Because their calibration did not include the multi-layer snow model, melt is overestimated during the dry season (JJA) which contributes to most of the average annual net mass loss overestimation [based on the 9 simulated years, the mass loss overestimation is 0.18 m w.e., when the average mass loss is −0.88 m w.e., Autin et al. 2022].
Summary of the main parameter values used for the DEBAM simulations
| Parameter | Value |
|---|---|
| Fresh snow albedo | 𝛼fresh‐snow = 0.85 |
| Firn albedo | 𝛼firn = 0.6 |
| Ice albedo | 𝛼ice = 0.3 |
| Clear sky transmissivity for solar radiation | 𝜏clear‐sky = 0.8 |
| Roughness height of momentum over ice | z0ice = 0.026 m |
| Roughness heights of temperature, humidity and momentum over snow | z0snow = z0T = z0q = 0.0026 m |
| Precipitation gradient from 4370 to 5200 m asl | |
| Glacier surface temperature gradient |
Analysis of 19 years of daily discharge and precipitation data provided by Ramallo [2013] showed that only 9% of the annual volume passes through the weir at TUBO (Figure 1) during the dry season. Not all of this discharge is a result of glacier mass loss, as an average of 4.3% of the annual precipitation occurred over the same period. Nonetheless, most of the discharge observed at TUBO comes from the glacier meltwater as its catchment is 70% glacierized and the snow on the moraines melts completely in a few days [e.g. Lejeune 2009]. This low dry season discharge highlights the limited mass loss that occurs at this time of the year [see also Autin et al. 2022; Sicart et al. 2011].
Therefore, the dry season is generally a period of low ablation whereas the high variability of the mass balance in the transition and wet seasons mostly controls the interannual ablation and accumulation variability. As model uncertainties are high during the dry season (importance of poorly known turbulent fluxes plus we disregard the subsurface heat flux), we end the simulations on May 31.
To achieve a 1 K cooling representative of the climate in the late 17th century, the AWS measurements were applied to a grid cell at 4850 m a.s.l. instead of at 5050 m a.s.l. (the method is detailed in Section 3.2.1). To avoid unrealistically high precipitation amounts at the top of the glacier caused by lowering the elevation of the forcing data, we applied the precipitation gradient of +10%/100 m used by Autin et al. [2022] from the glacier front up to 5200 m a.s.l. [instead of up to 5400 m a.s.l. in Autin et al. 2022].
3.2. Input datasets
3.2.1. Glacier extent at the LIA maximum extent and model initialization
Using lichenometry techniques, the LIA maximum extent of the glacier was dated to 1680 ± 28 AD [Rabatel et al. 2008]. A digital elevation model (DEM) of Zongo Glacier was reconstructed by redrawing contour lines so that the glacier fills the moraines [Rabatel 2005]. Between the LIA maximum extent and 2012, the glacier retreated 1.5 km, the terminus elevation rose by 550 m and the glacier lost 43% of its surface area and 0.16 ± 0.01 km3 of ice (see the red and black lines outlining the glacier on Figure 1).
We hypothesize that since tropical glaciers react rapidly to climate perturbations [Kaser 1999; Rabatel 2005], a hydrological year for which the glacier is close to equilibrium (B ≈ 0 m w.e.) in the current climate or during the LIA is representative of their respective steady state climate.
To obtain information on potential LIA glacier equilibrium characteristics (to serve as comparison for the simulation results), we evaluated the LIA steady state equilibrium-line altitude (ELA0) considering the frequently used constant area accumulation ratio (AAR) method [e.g. Rabatel 2005; Jomelli et al. 2009]. We evaluated the current climate ELA0 (5233 m a.s.l.) by linearly interpolating 25 observed annual ELAs as a function of surface mass balance. We then defined the corresponding AAR (0.68) based on the mean AAR value obtained from the existing glacier digital elevation models [DEM, Autin et al. 2022]. Considering a constant AAR, we derived the LIA ELA0 (ELA0,LIA = 5078 m a.s.l., i.e. 155 m lower).
The equilibrium snow line altitude (SLA0) for the LIA maximum extent was considered to have shifted by the same elevation as the ELA0 putting it at an altitude of 4883 m a.s.l considering the recent climate SLA0 = 5037 m a.s.l. [based on data from Rabatel et al. 2012]. The SLA0 defined this way was considered as the limit of the firn for model initialization.
3.2.2. LIA climate scenarios
We created four LIA climate scenarios based on nine years of available meteorological data between 1999 and 2017 [Autin et al. 2022]. All four scenarios assume a 1 K reduction in air temperature compared to the current climate. Three scenarios assume a 19–22% increase in annual precipitation based on paleoclimate proxy information and glacier climate studies of the past (Section 2.2), but differ in the way the additional precipitation is distributed across the year:
- Reference scenario: no difference in precipitation compared to the current climate
- Scenario 1: an earlier onset and longer wet season
- Scenario 2: a wetter wet season (December to March)
- Scenario 3: a wetter transition season (September–November) and April–May (the second transition period).
The reference scenario (hydrological year 2011/12) was selected from the nine years of glacier observations so that the precipitation seasonality most closely matched the average monthly variations observed in the 23 years of precipitation from PLATAFORMA, which we assumed to represent current climate precipitation seasonality (Figures 2a, 3a). We use precipitation data from this AWS, rather than the on-glacier SAMA AWS to define average seasonality due to the much longer record (the annual amounts are well correlated: R2 = 0.74). In addition, when the model is applied to the 2012 geometry, the surface mass balance up to June for 2011/12 is close to 0 m w.e. making it an ideal candidate to assess the impact of cooling on the glacier LIA extent mass balance (Figure 2b).
(a) Proportion of annual precipitation for each month at the on-glacier AWS SAMA (2011/12) and off-glacier AWS PLATAFORMA (average of 23 years between 1991 and 2015). (b) Simulated cumulative surface mass balance for the 9-year average (1999–2017) and 2011/2012 (reference scenario) over the current glacier geometry. The dashed part of the cumulative surface mass balance lines represent the period for which the model systematically overestimates melt since the subsurface heat flux is neglected.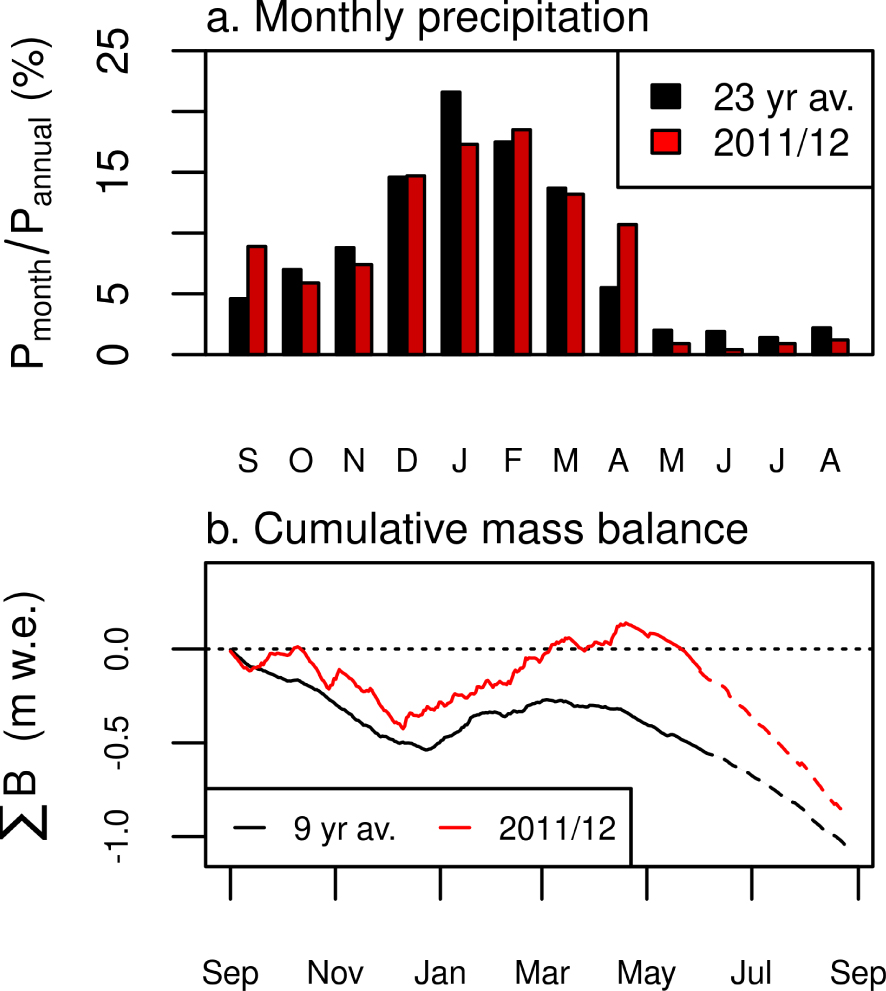
Scenarios 1 to 3 were obtained by replacing selected months in 2011/12 by the same month’s data from other years in the 9-year data set, chosen to yield an increase of ∼20% in annual precipitation compared to the long term average. We chose this procedure in preference to artificially adjusting precipitation amounts to preserve consistency between all meteorological variables for each month. In detail, we constructed the three precipitation scenarios as follows:
Scenario 1 (an earlier and longer wet season) was obtained by replacing the 2011/12 October and November data by the data from the same month of another year chosen among the two wettest months in the dataset (Figure 3b). Scenario 2 (a more intense wet season) was obtained by replacing the months of December to March by those in the dataset that had the highest number of events ⩾2 mm⋅d−1 (Figure 3c). Finally, scenario 3 (wetter September, October, November, April and May), was obtained by selecting the months in the transition seasons that had above average precipitation compared to the long term on-glacier average (Figure 3d). For all the scenarios, we used a trial-and-error procedure to determine which year’s monthly data to use to replace corresponding data in the 2011/2012 dataset, to achieve the targeted ∼20% increase in annual precipitation amounts.
Daily precipitation in the four LIA climate scenarios analyzed in this study. The modifications applied to the reference scenario (2011/2012) are in red. The precipitation distribution after the end of May is not accounted for in the simulations.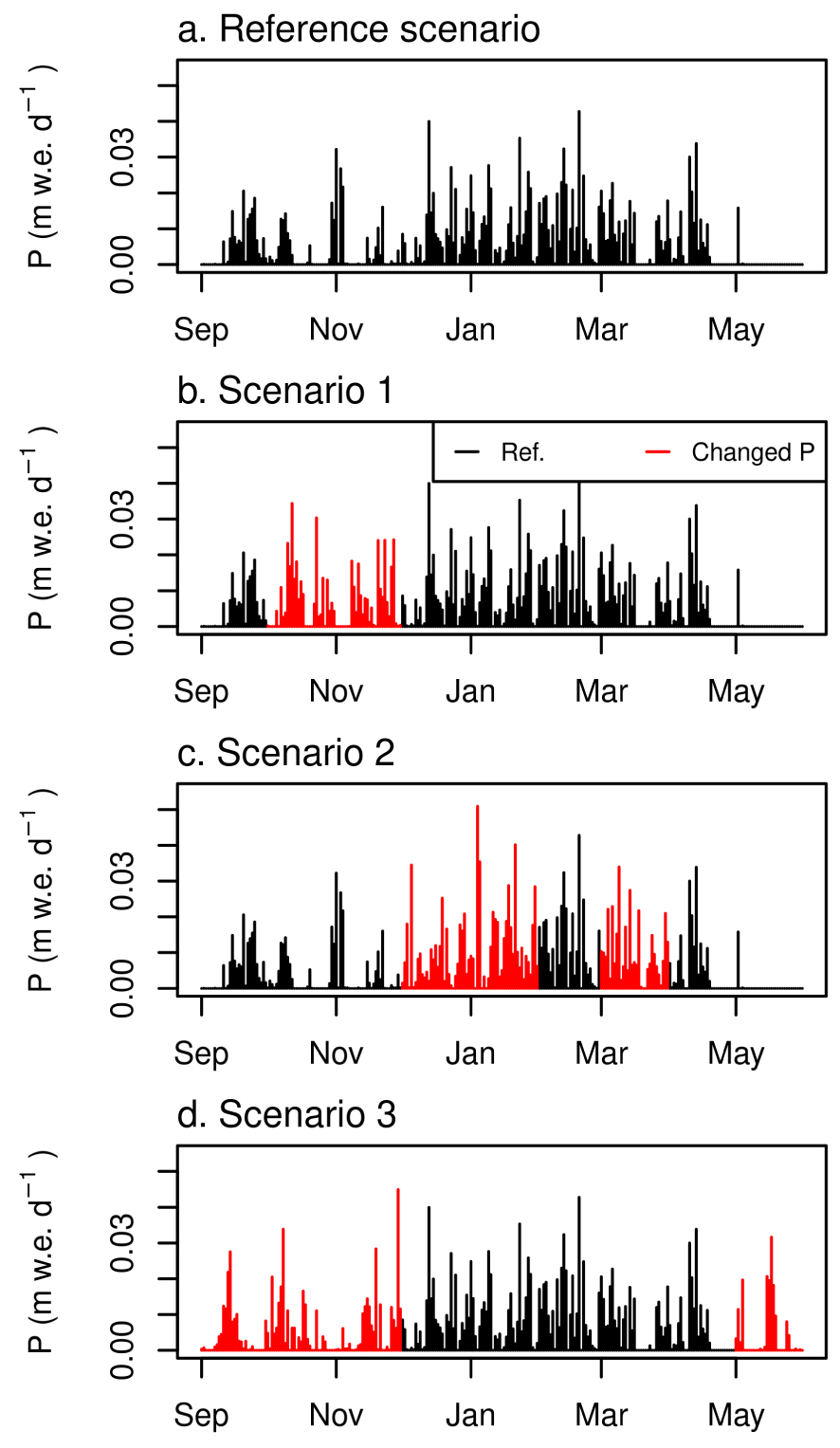
The reference scenario has 1.70 m w.e. of annual precipitation while scenarios 1 to 3 have 1.92, 1.92 and 1.97 m w.e., respectively, which represents a 6% increase in precipitation for the reference scenario, of 19% for scenarios 1 and 2, and a 22% increase for scenario 3, compared to the average of the nine years of the current climate (1.61 m w.e.).
Comparing the scenarios with the 9-year average (up to May 31) revealed that all the scenarios have less incoming shortwave radiation (Figure 4a) and increased longwave radiation (Figure 4b). The latter is due to increased cloud radiative forcing that summarizes the impact of the clouds on the incoming radiation fluxes (Figure 4c). This is a direct result of selecting/creating years with above-average precipitation (Figure 4d). All scenarios are colder than the measured 9-year average (Figure 4e), a result of the increased cloudiness and associated reduced incoming radiation. Finally, all the scenarios have annual scale glacier surface temperatures close to the nine-year average (illustrated by the mean outgoing longwave radiation in Figure 4f).
Annual scale differences between the scenarios and the 9-year average (XSce − XRT) of (a) incoming shortwave and (b) longwave radiation, (c) cloud radiative forcing, (d) precipitation, (e) air temperature and (f) outgoing longwave radiation used to derive the glacier surface temperature.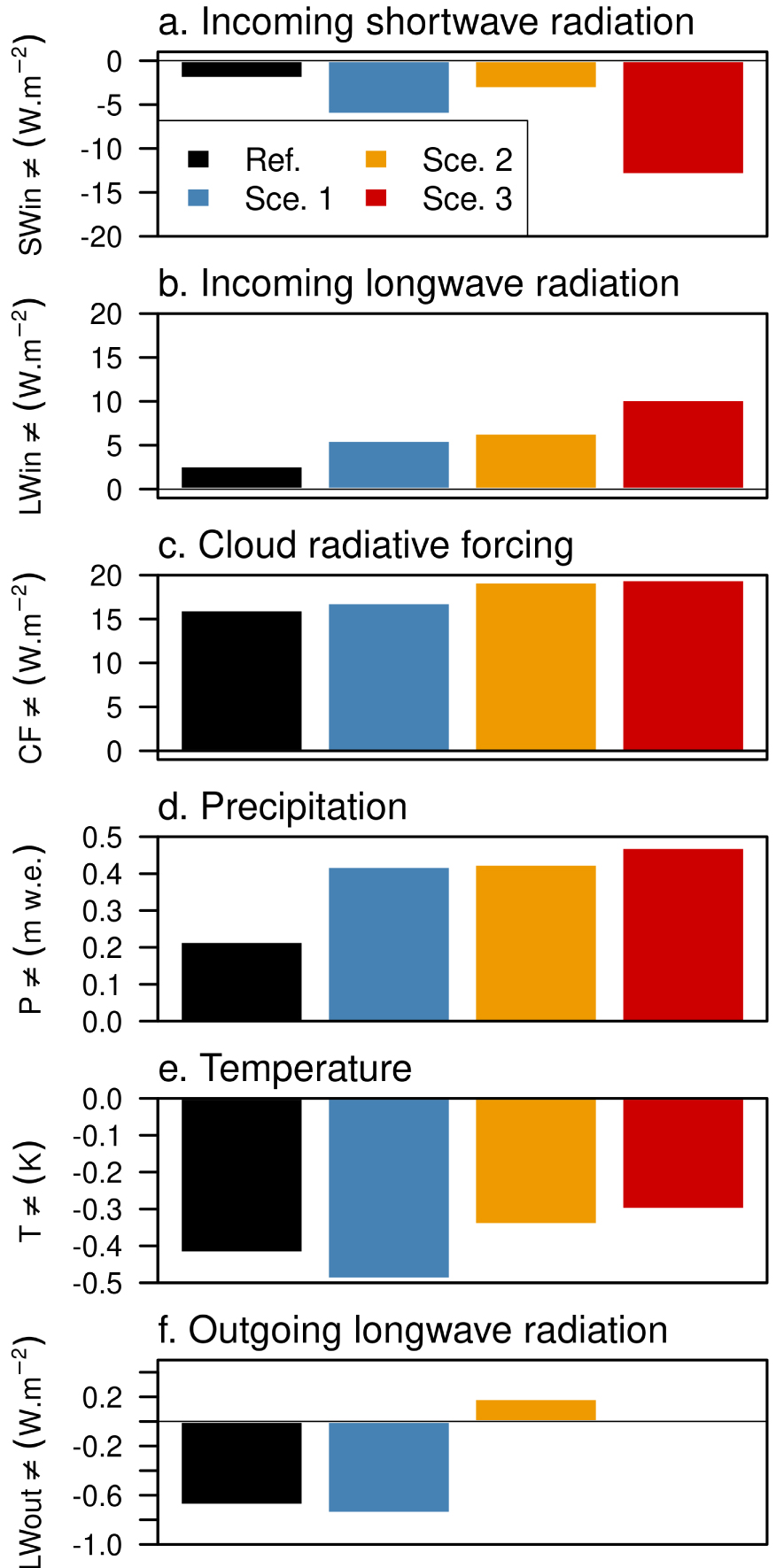
4. Results and discussion
4.1. Surface mass balance for the LIA glacier geometry
Figure 5 shows the impact of the scenarios on the cumulative surface mass balance between September 1 and May 31. At the glacier scale, the reference scenario yields a highly negative surface mass balance (Figure 5a, B = −0.52 m w.e.), scenario 1 results in close to equilibrium conditions (Figure 5b, B = −0.15 m w.e.). Scenario 2 results in a slightly more negative mass balance (Figure 5c, B = −0.26 m w.e.). Finally, scenario 3 results in a slightly positive surface mass balance (Figure 5d, B = 0.08 m w.e.).
Annual surface mass balance maps for the four LIA scenarios. The dashed lines represent the simulated ELA.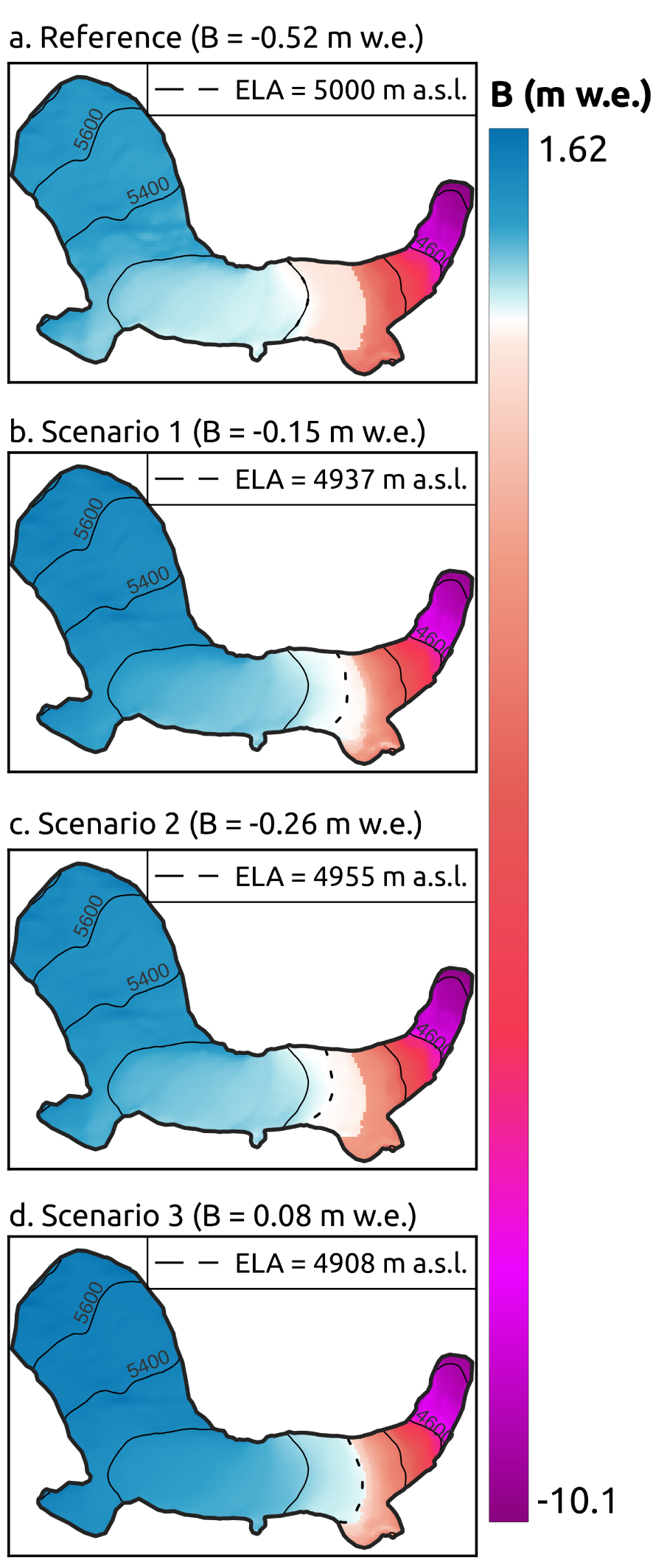
In scenario 3, the surface mass balance reaches 1.62 m w.e. in the upper reaches of the glacier (Figure 5d). Considering that melt can be disregarded over this part of the glacier (at about 5800 m a.s.l.), it is a reasonable value because the annual precipitation amounts received at the AWS (close to 2 m w.e. for all scenarios) which, via the precipitation gradient applied in the simulations (+10%/100 m up to 5200 m a.s.l.), implies that over 2.56 m w.e. reaches the upper part of the glacier.
At the glacier terminus, the cumulative mass loss, which ranges between 9.0 and 10.1 m w.e. depending on the scenario (Figure 5), is significantly higher than that observed in recent times, when the glacier wide mass balance has been close to zero (for example, measurements over the year 2000/2001 show BGlacier‐wide = 0.49 m w.e. and BGlacier terminus = −6.24 m w.e.). This difference can be explained by the larger accumulation zone in the LIA configuration (2.50 km2 versus 1.55 km2 in 2000/2001) and similar annual precipitation amounts (2000/2001 is one of the wettest year in the current climate dataset) leading to a larger accumulation volume (an extra 1.8 × 106 m3). As a result, the down-glacier ice flux is strengthened during the LIA, allowing the glacier front to reach low altitudes where melt rates are high (especially since in the lower reaches of the LIA glacier extent, the slope of the bedrock is steep and the width of the tongue is constrained by the topography, top inset in Figure 1).
The ablation area of tropical glaciers is characterized by steep altitudinal mass balance gradients due to marked variations in albedo [Sicart et al. 2011]. The simulations give similar mass balance gradients during the LIA as under the current climate (around 2 m w.e./100 m, Figure 6a) probably because this gradient is mostly controlled by atmospheric variables and the LIA scenarios were built using shuffled present-day meteorological forcing data.
Surface mass balance as a function of altitude (a) and corresponding changes in mass (b) in the four scenarios. The shaded area highlights the altitudinal range for the simulated equilibrium-line altitudes (4908–5000 m a.s.l.).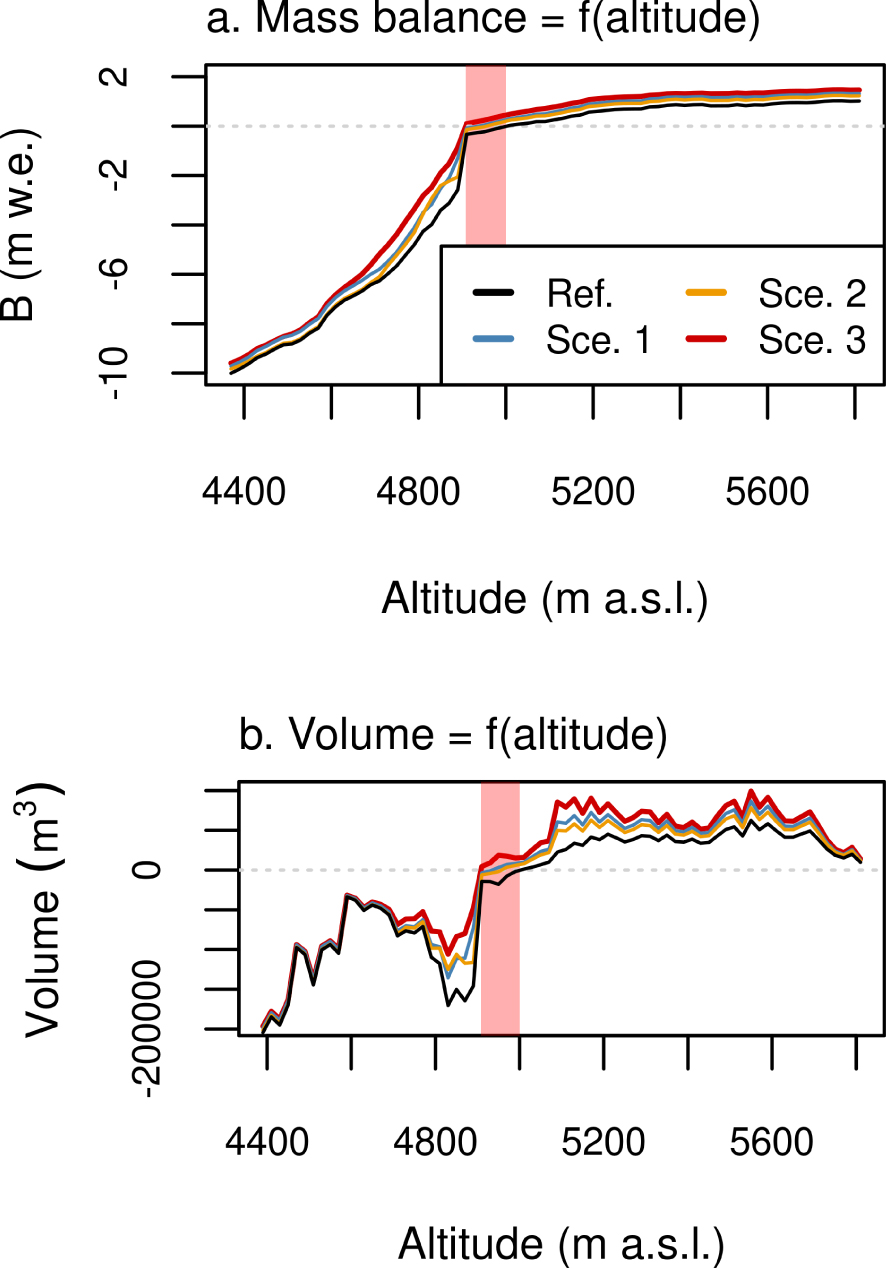
For the LIA scenarios, the specific mass turnover 𝜏 [Equation (2), e.g., Ohmura et al. 1992] was larger than for recent climatic conditions (𝜏LIA, all scenarios > 2 m w.e. whereas 𝜏2000∕01 = 0.98 m w.e., Table 2) emphasizing the role of the ice flux in compensating for the melt rates in the ablation zone.
| (2) |
where 𝜏 is the specific mass turnover, c the specific mass gain (in the accumulation zone) and a is the specific mass loss (in the ablation zone).
Summary of simulated glacier-wide surface mass balance B, specific ablation a, accumulation c, and mass turnover 𝜏 in the four LIA scenarios along with the differences in a and c between the reference scenario and scenarios 1–3
| Scenarios | B (m w.e.) | a (m w.e.) | c (m w.e.) | 𝜏 (m w.e.) | 𝛥a (m w.e.) | 𝛥c (m w.e.) |
|---|---|---|---|---|---|---|
| Reference | −0.52 | −3.31 | 0.96 | 2.13 | 0 | 0 |
| 1 | −0.15 | −4.28 | 0.90 | 2.59 | 0.97 | 0.06 |
| 2 | −0.26 | −3.78 | 0.93 | 2.35 | 0.47 | 0.03 |
| 3 | 0.08 | −4.69 | 1.04 | 2.86 | 1.38 | −0.07 |
Considering a constant AAR method to define the ELA0 is not valid here as this method yields a value that is much higher than our simulations show (ELA0,LIA = 5078 m a.s.l. with the AAR method versus 4908 to 5000 m a.s.l. depending on the scenario). Indeed, the AAR obtained with the LIA simulations is ∼0.8, whereas the AAR0 for the current climate is 0.68. Based on the analysis of the specific mass turnover and altitudinal mass balance gradients, this method is not valid primarily because of the topographic conditions (narrow and steep but because of the long ablation zone with a small surface area). This topographical setting coupled with the strong down-glacier ice flux enabled the glacier terminus to reach ∼500 m below the ELA0 during the LIA, as opposed to ∼250 m in current climate conditions.
Other methods exist to reconstruct past ELA0, for example, based on the altitude of lateral moraines, Rabatel [2005] estimated the ELA0 during the LIA to be at 5090 m a.s.l. Based on our results, this altitude is overestimated by ∼150 m, suggesting that the lateral moraine method can only give a maximum ELA due to uncertainties linked to moraine accretion from the glacier fluctuations between the LIA maximum extent and now, or by moraine erosion since the glacier retreat.
Mass balance (Figure 6a) and changes in volume (Figure 6b) by altitude make it possible to assess the variability of the spatial mass balance induced by the LIA scenarios. The mass balance profiles show high variability in the ablation zone. Analysis of changes in simulated snow heights, albedo and mass balance in the ablation zone (4400–4850 m a.s.l.) showed that this variability is driven by albedo feedback effects (not shown). At the annual scale, the increased variation in albedo with altitude is due to the increased influence of snow temporarily covering the ice (from ±0.002 at 4400 m a.s.l. to ±0.04 at 4850 m a.s.l.). Hence, via an albedo feedback effect, the timing and intensity of the precipitation play an important role in controlling melt rates in the upper reaches of the ablation zone.
Above ∼4600 m a.s.l., scenarios 1 and 3 (Figure 6a, blue and red lines, respectively) diverge, with a less negative mass balance gradient in scenario 1 because in scenario 3, the precipitation events are more evenly distributed, resulting in higher albedo values. Similarly, above ∼4700 m a.s.l., scenario 2 shows a shallower mass balance profile than the reference scenario (orange and black lines, respectively), because intense precipitation events throughout the wet season enable a thicker snowpack, thereby increasing the albedo and reducing annual mass loss.
Table 2 shows that the more positive the glacier-wide surface mass balance, the more negative the specific ablation and, in some cases, the lower the specific accumulation (observed in scenarios 1 and 2). Considering the mean differences between the reference scenario and in the three scenarios with changes in precipitation patterns, the variability of the specific ablation rate is higher than that of the accumulation rate (whereas w.e. w.e., Table 2) because of the effect of albedo feedback on the melt rate.
Considering the two most extreme scenarios in terms of surface mass balance value (the reference scenario and scenario 3), despite higher variability of the surface mass balance profile in the lower reaches of the glacier (below the ELA, Figure 6a), the biggest differences in volume occur in the upper reaches (above the ELA, Figure 6b), suggesting that accumulation processes play an important role in the glacier-wide surface mass balance. Compared to the reference scenario, scenario 3 generates an excess in volume of 0.55 × 106 m3 (1.1 × 106 m3) in the lower (upper) reaches of the glacier.
4.2. Impact of the climate scenarios on the surface energy fluxes
Scenarios 1 and 3 yield close to equilibrium annual glacier-wide surface mass balances whereas the reference scenario and scenario 2 result in negative mass balance conditions. The main differences in melt rates between these two groups occur between September and November (Figure 7a). As mentioned in Section 2.1, the transition season is characterized by increased solar radiation at the top of atmosphere and a low surface albedo, leading to large net shortwave energy fluxes that are responsible for the highest melt rates of the year, meaning this period plays a key role in controlling the annual surface mass balance [Sicart et al. 2011]. As a result, the two scenarios that are the most efficient at limiting mass loss are those with increased precipitation amounts and frequencies during the transition season (scenarios 1 and 3). Indeed, clouds reduce the incoming shortwave radiation fluxes and snowfall increases the glacier albedo, thereby reducing melt energy compared to the other two scenarios (Figure 7b).
Cumulative glacier-wide surface mass balance (a), net shortwave (b) and longwave (c) energy budgets along with the sensible (d) and latent (e) heat fluxes in the four LIA scenarios. The gray areas represent the transition (T.S.) and wet (W.S.) seasons.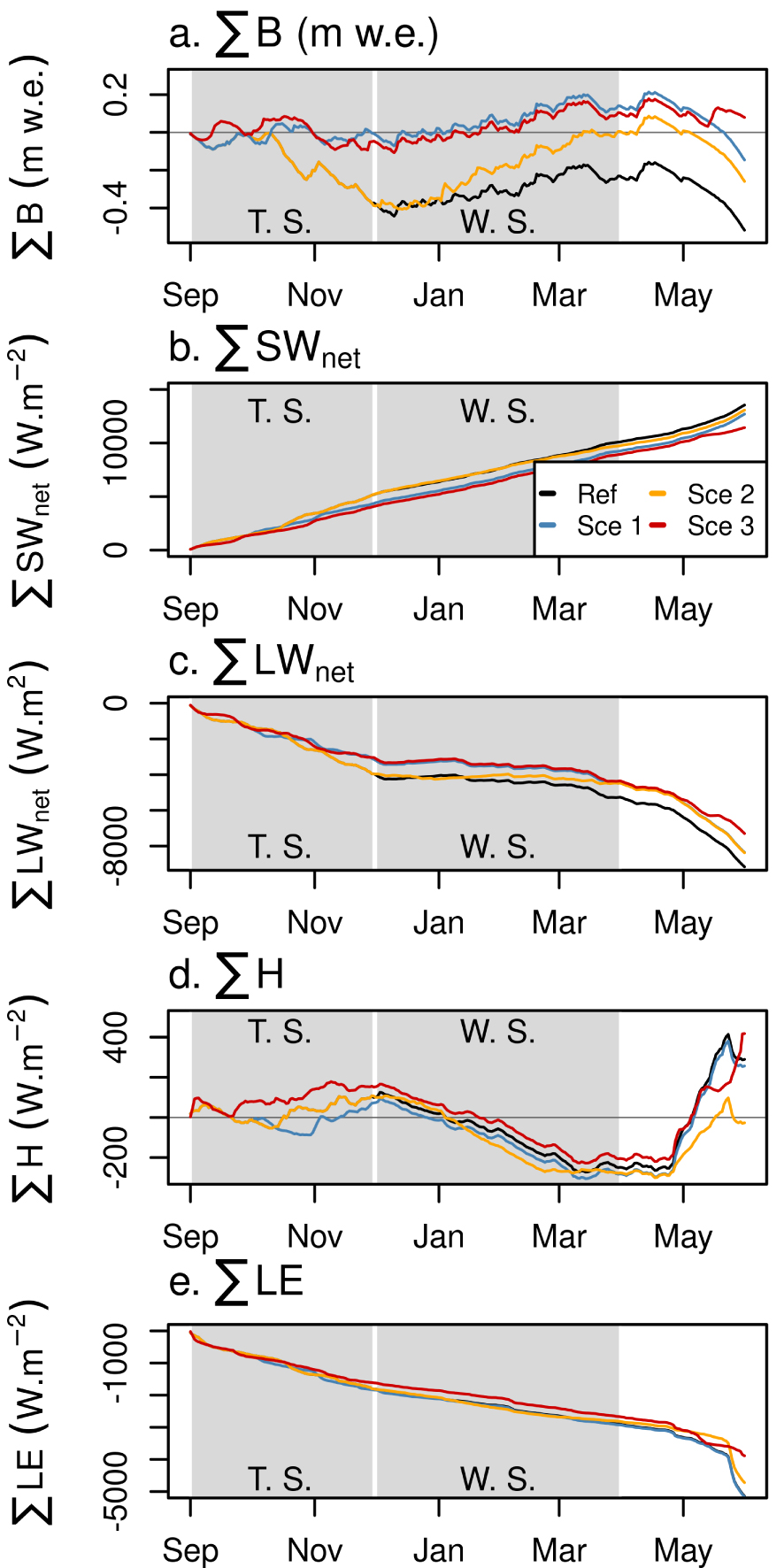
During the wet season, scenario 2 differs from scenarios 1 and 3 because it was constructed to maximize the number of large-scale precipitation events (Section 3.2.2). It reduces the amount of melt energy because the combined effect of clouds and precipitation reduces the net shortwave energy fluxes more than the clouds increase the net longwave energy budget (Figures 7b and c, respectively). This reduction, combined with the large precipitation amounts in this scenario explain the rapid mass gains observed in Figure 7a.
An early and longer wet season (scenario 1) is more efficient at reducing mass loss than a more intense wet season (scenario 2) because it reduces the incoming shortwave radiation (cloud cover) and increases the albedo (snowfall events) during the period of maximum potential solar radiation (summer solstice), which limits the mass loss over the transition season. During the core wet season, increased precipitation intensity and frequency (scenario 2) increases the mass gain but does not compensate for the losses during the transition season (Figure 7a).
During the core wet season, the glacier-wide averaged cumulative sensible heat flux is negative in all the scenarios, showing that the temperature of the glacier surface remains higher than the temperature of the air (Figure 7d). The higher temperature in the simulations is probably because in the model, the air temperature is extrapolated using a stronger altitudinal gradient than the surface temperatures (−0.55 K∕100 m versus −0.1 K∕100 m), resulting in a large part of the glacier where the simulated surface temperature is warmer than the air. However, considering the small cumulative sums of these fluxes over the year (−200 and 200 W⋅m−2), the impact on the melt rate is limited. Finally, in all the scenarios, the latent heat fluxes act as an energy sink (sublimation) whose annual amount is about half the sum of the net longwave energy flux (Figure 7e). Because more energy is lost via the latent heat flux than the energy provided by the sensible heat flux, the sum of the turbulent fluxes is negative (energy sink), a feature observed under the current climate [e.g., Sicart et al. 2011].
4.3. Sources of modeling errors
An important source of error is that we neglect the subsurface heat flux in the simulations, implying errors in the surface temperature. Although under the current climate, the subsurface heat flux only plays a significant role in reducing melt rates via nighttime cooling over the glacier’s accumulation zone and over the whole surface of the glacier in the dry season [e.g., Sicart et al. 2011], this heat flux may be significant during a large part of the year in the cooler LIA climate, particularly over the upper reaches of the glacier. Errors in the simulated surface temperature are partly offset by the surface temperature altitudinal gradient applied in the simulations. As the accumulation area is larger during the LIA than under the current climate (AAR = 0.8 versus 0.68), the model may overestimate the glacier-wide melt rates.
The model may also underestimate the turbulent fluxes. This is due to a number of reasons including the fact that a uniform wind speed is considered across the glacier, or the fact that errors in the simulated albedo impact the type of surface simulated (snow/firn/ice) via imprecise melt rates. Overestimation of the simulated surface temperatures in the accumulation zone also influences the turbulent fluxes via a reduced surface-air temperature gradient. Another source of error is that the model considers constant stability functions throughout the year whereas in reality, these vary with the meteorological conditions [Sicart et al. 2011]. As a result, the glacier wide latent heat flux is underestimated making the turbulent fluxes a smaller energy sink than they should be, thereby contributing to overestimating the melt rates.
Other sources of errors that impact the simulations are the air temperature and precipitation gradients which are poorly known under current climate conditions (and may have been different in the LIA climate). Considering these sources of errors in the modeling, the most important ones being that the subsurface heat flux is neglected and potential erroneous albedo simulations, it is likely that the model overestimates the melt rates and hence, the annual mass losses.
5. Concluding remarks
This study assessed the seasonal climate changes that occurred in tropical South America during the Little Ice Age (late 17th century) using a distributed surface energy balance applied to the tropical Zongo glacier (16° S, Bolivia) and scenarios that maintain physical coherence between the measured meteorological variables.
Using information provided by paleoclimate proxies, global climate model simulations and glacier-climate sensitivity studies of past glacier extents over tropical South America, we constructed three scenarios that focus on the distribution of precipitation over time. One scenario considered a wetter year (above average precipitation in September, October, November, April and May) and the other two others tested different wet season configurations: one considered an early onset of the wet season and the other a more intensive wet season. To ensure physical coherence between the measured variables, the scenarios were obtained by shuffling months of measurements of the current climate based on 9 years of continuous hourly measurements. The three scenarios were compared to a reference scenario in which the monthly precipitation is representative of the current climate and a 1.1 K decrease in temperature. The climate scenarios were assessed based on the resulting surface mass balance of the glacier’s LIA maximum extent. They were considered plausible if close to equilibrium conditions were evaluated (B ≃ 0 m w.e.).
The reference scenario was the one that resulted in the highest mass loss (B = −0.52 m w.e.) suggesting that, by itself, 1.1 K cooling cannot explain the glacier’s maximum extent during the LIA. Spreading precipitation out over the year, and more specifically, including more frequent precipitation events during the transition periods, via an albedo feedback effect, is key to reproducing a glacier that is close to equilibrium at its maximum extent during the LIA. In addition, a longer wet season (scenario 1, B = −0.15 m w.e.) is more efficient in reducing mass loss than a more intense one (scenario 2, −0.26 m w.e.), as the former shortens the transition period and hence limits the otherwise large mass losses that occur in the wet season. This confirms recent findings concerning the important role of the distribution of precipitation over the transition season in controlling the annual mass loss [e.g., Autin et al. 2022].
Thus, the simulations indicate that the LIA climate was likely 1.1 K cooler with ∼20% extra precipitation at the annual scale, in rough agreement with Rabatel et al. [2008]. However, our method also allowed us to investigate the effects of changes in the seasonal distribution of precipitation on the mass balance. Our results suggest that the 20% annual increase in precipitation is in agreement with the LIA glacier extent only if increased precipitation occurs in the transition season (period of highest melt rates) that precede the core wet season (December–March).
The simulations also reveal a significant change in the AAR of the glacier from around 0.68 for the current climate versus 0.80 for the LIA climate, mostly due to topographic conditions (the ablation area was steep and narrow during the LIA). This suggests that methods based on constant AAR to reconstruct the LIA climate result in overestimation of the past ELA0 of about 120 m. Indeed, we hypothesize that this topographic setting coupled with the large accumulation volumes favored a strong down-glacier ice flux that allowed the glacier to extend farther below the ELA during the LIA than what is observed under the current climate.
Applying the model to other glaciers in the tropical Andes with different morpho-topographic variables would provide further insights into which LIA scenarios are most plausible and an in-depth understanding of the limits of the AAR method. Another possible further study includes coupling DEBAM to a model of glacier dynamics to better quantify the role of the ice flux and mass turnover in reaching glacier steady-state conditions.
Acknowledgements
This study was conducted in the framework of the International Joint Laboratory LMI GREAT-ICE, the International Research Network Andes-C2H (IRD and Andean partners) and the French Service National d’Observation GLACIOCLIM (www.glacioclim.osug.fr, UGA-OSUG, CNRS-INSU, IRD, IPEV, INRAE). GLACIOCLIM is coordinated in La Paz by Dr. Alvaro Soruco (UMSA/IGEMA) who organizes the follow-up of the glaciological measurements on Zongo Glacier. The authors are grateful to everyone involved in the long-term in-situ monitoring of Zongo Glacier and acknowledge the support of LabEx OSUG@2020 (Investissements d’Avenir—ANR-10-LABX-0056).




 CC-BY 4.0
CC-BY 4.0