1. Introduction
Since the late 1980s, research has been conducted in France to understand the influence of water management infrastructure, such as arterial and subsurface drainage in rural catchments, on floods and on surface water quality. This became an important concern during a period (1980–1990) in which a national program of subsurface drainage investments was supported by the French government [Lesaffre and Penel 1990]. During this period, pollution of surface and groundwater progressively became an issue, linked to the intensification of agriculture, to which drainage contributed.
In France, many rural areas face seasonal waterlogging in the humid winter period [Lagacherie and Favrot 1987]. This is particularly the case in shallow loamy soils where an impervious barrier has developed due to clay leaching and enrichment in the deeper layers. Waterlogging is detrimental to root growth and reduces crop yield, particularly of winter cereals. To increase the flexibility of their crop rotations, many farmers were at that time eager to implement subsurface drainage in response to the competitive and volatile market context in Europe due to intermittent surpluses of various commodities (butter, milk, meat, etc.) that impacted farmer revenues.
The combination of subsurface drainage installation (plastic pipes at 10–25-m spacing and an average depth of 1 m) and of arterial drainage recalibration (often following land consolidation measures) has had an obvious influence on the transfer of water from the field to the rivers: more rainfall water flows through the soil into the pipe network, and less through surface runoff. The transfer from arterial drainage channels to the rivers may also be accelerated [Lesaffre and Zimmer 1988, and more recently King et al. 2014 or Valayamkunnath et al. 2022]. But how important are these changes, particularly in periods of floods or for the quality of the drainage water?
At that time, the scientific approach to subsurface drainage was based on a hydraulic method relating drain flow rates to the elevation of the water table mid-way between drains [Van Schilfgaarde 1963; Dumm 1964; Guyon 1964]. The saturated zone of the soil only was taken into consideration and two extreme conditions were classically considered: (i) the tail recession phase, after a rainfall event when a univocal relationship between water elevation and drain flow rate was observed; and (ii) the steady-state situation, when the rainfall recharge of the water table is equal to the drain flow rate. However, this approach was unable to predict the dynamic process of transient rainfall events inducing a non-univocal relationship between water table elevation and drain flow rate [Hervé 1980]. In particular, it was unable to predict the peaky response of drainage systems during rainfall events that were a growing concern regarding the influence of subsurface drainage on floods. As observed in several field experiments, the drain flow rates during rainfall events could be 3–10 times higher than predicted by classic equations linking drain flow rate to water table elevation [Lesaffre 1989].
Since the late 1930s [Flodkvist in Russel 1934], this observation has resulted in a debate about the water flow pattern generating these peak flows. If there is no simple correlation between water table elevation and drain flow rate, could it be that other mechanisms are at play? The debate continues today and several authors [Schneider et al. 2022; Bjerre et al. 2022; Williams and McAfee 2021] argue that surface runoff or water flowing in the plough layer could infiltrate through macropores into the drainage trench and contribute to these peak flows.
The approach implemented in France combined detailed field experiments [Zimmer 1989] with revisiting of the theoretical approach to subsurface drainage functioning based on the Boussinesq equation [Lesaffre 1989]. This resulted in the development of the basic blocks of a drainage model (SIDRA), as explained below. This model was validated against experimental results and was then combined with a number of other processes to assess various impacts of the changing agricultural water management on solute and particle transport, on plant growth and development and on the hydrology of wetlands and rural catchments.
This paper follows the rationale of the scientific developments during the period 1986–2020, which can be presented as a general theory of land drainage systems translated into the SIDRA model development. It summarizes the initial results based on experimental observations and on an extension of the classic Boussinesq equation. It then describes in a synthetic way some of the applications obtained by the coupling of the SIDRA model with other tools.
2. Initial experimental results
Among the experimental sites used to analyse the field drainage design and its impacts on winter crop yields, the experimental site of Arrou (France, Eure-et-Loir) was intensively studied for hydrological purposes from 1978 to 1995 [Lesaffre and Zimmer 1988; Tournebize et al. 2004]. In particular, water table levels and drain flow rates were monitored at an hourly time step throughout this period. During the winter season of 1985–1986 monitoring was completed by tensiometers installed at different distances (0, 0.5, 1 and 5 m, i.e. until mid-drain spacing) from a drain pipe and between the soil surface and a depth of 1 m [Zimmer 1989]. The purpose was to measure precisely the water potential inside the water table and in the unsaturated zone above it, as well as to analyse the water transfer patterns, with a particular focus on rainfall events.
The following observations were critical for the theoretical developments presented hereafter. During rainfall events, a unit hydraulic gradient is observed in the unsaturated zone of the soil as soon as a threshold pore water pressure of approx. −15 hPa is reached, meaning that for pore water pressures in the range of (−15, 0 hPa), the flow is purely vertical, equal to the soil hydraulic conductivity, and driven by gravity. Detailed observations reveal that the pore water pressure in the unsaturated zone during rainfall events is not correlated with the rainfall intensity in a simple way. Lower pressure values are observed for a similar rainfall intensity when the event occurs after previous rainfall events. These empirical findings were theoretically studied and generalized by Kao et al. [2001] and confirmed through a laboratory experiment by Kao [2002].
Furthermore, as soon as the soil becomes saturated (water pressure becoming positive), the vertical hydraulic gradients decrease to 0, i.e. the water flow inside the water table is horizontal. This behaviour is well known as the Dupuit–Forchheimer (DF) assumption and is largely referred to in hydrogeology since it enables a simplification of the solution to the Boussinesq equation.
Similar observations were obtained in other field experiments, except in some heavy clay soils [Zimmer 1989]. The interpretation of these observations is that, except in these soils, peak flows can be predicted by the water table behaviour only, without specific horizontal water transfer disconnected from it. If the macroporosity of the soil played a role, it would seem to be through the establishment of a downward gravity flow (vertical gradient equal to 1) as soon as the pore water pressure reaches a threshold of approx. −15–−20 hPa. These findings were also recently reported in other contexts [Jacobsen and Kjær 2007].
3. Model development
3.1. The Boussinesq approach, associated assumptions and solutions developed
Based on these observations, the classic Boussinesq approach [Boussinesq 1904] that describes water transfers generated by a drained water table was revisited. In this approach, and for the specific case of shallow soils where the drain pipe rests on an impervious barrier, the system is represented (Figure 1) by a transect section of the soil bounded at the bottom by a shallow impervious barrier. A drain that can be a pipe or an open ditch imposes atmospheric pressure at the depth of the impervious barrier. At the soil surface, assumed to be horizontal, a transient rainfall intensity is applied and is assumed to be transferred in a homogeneous way to the water table in the case that the water table remains below soil surface. When the water table reaches the soil surface, a certain fraction of the rainfall generates surface runoff. Finally, at a certain distance to the drain, generally midway between drains, it is assumed that no lateral flow occurs, dividing the pipe space into a symmetric system. This latter assumption can easily be changed.
Sketch of a drained transept from pipe to mid-drain spacing with Q(t), drain discharge, R(t) recharge generated by precipitations, h(x,t) and H(t) water table elevation above the impervious layer and WT water table surface.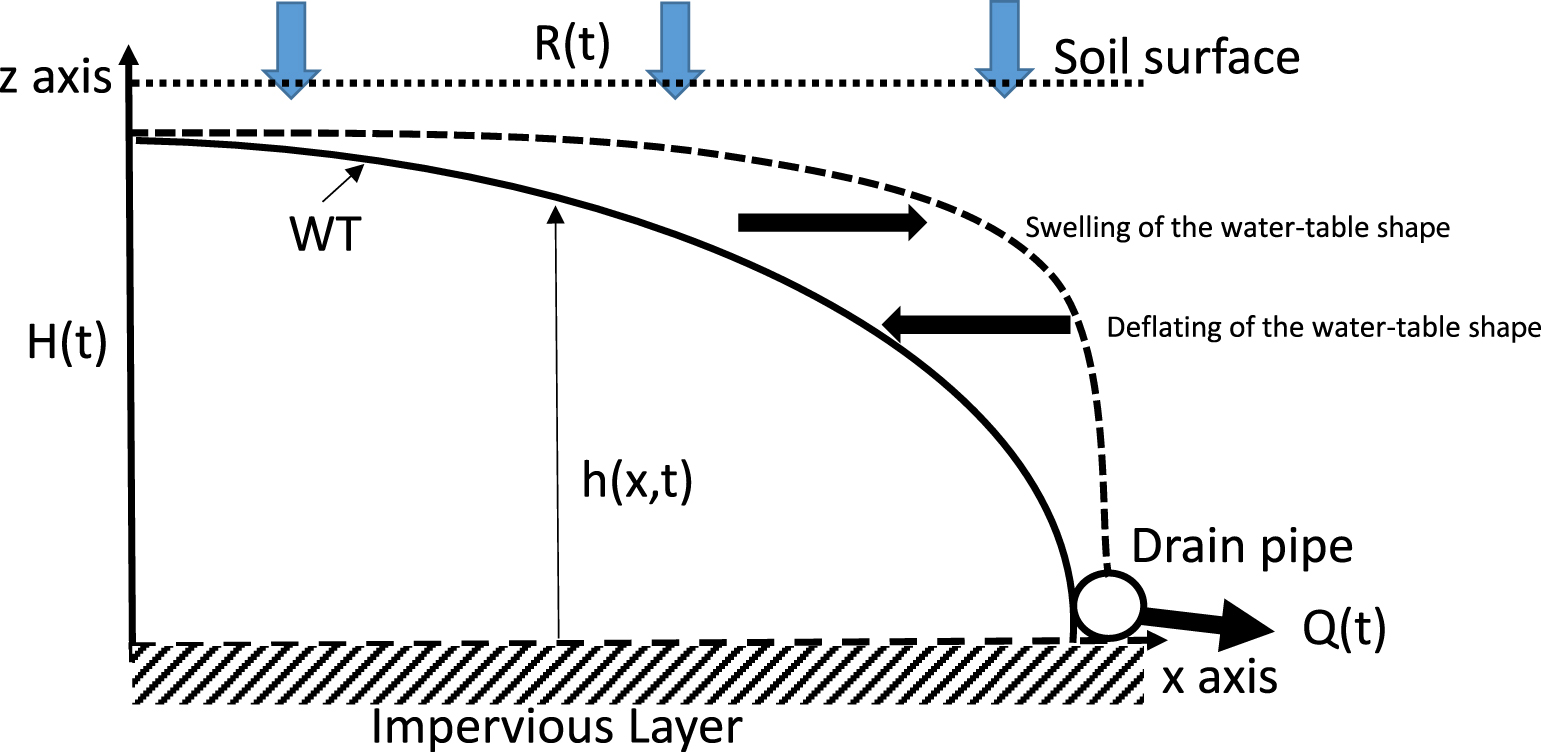
The Boussinesq approach rests on the combination of two basic equations. First, a motion equation (Equation (1)) describes the horizontal flow in the water table at a given abscissa x, q(x,t); this equation results from Darcy’s law integrated in the saturated zone between the drain level and water table surface. Second, a continuity equation (Equation (2)) describes the water balance, i.e. the variation of that horizontal flow when the water table elevation h(x,t) changes.
| (1) |
| (2) |
Two important assumptions are associated with the Boussinesq approach.
The drainable porosity parameter (f) has been the subject of considerable debate [see, e.g. in Vachaud 1968]. Drainable porosity also called “specific water yield” corresponds to the amount of water which could be drained from the soil [Moriasi et al. 2013]. The value depends on the soil–water dynamics and on the water table depth. The associated assumption is that this parameter is independent of the status (pressure, water content) of the unsaturated zone above the water table and that a similar value applies across the system and during recharge and drawdown of the water table. This assumption is a simplification of the reality, as it can be derived from more complete models such as those provided by the Richards equation including the concepts of dual porosity or dual permeability [Vauclin et al. 1976; Akay et al. 2008; Varvaris et al. 2021]. But our experimental data highlight the importance of macropores in which gravity water transfers occur during rainfall events. We therefore assumed that these macropores played a role during both recharge and drawdown of the water table and that the drainable porosity value was identical in these two phases.
The second important assumption is the Dupuit–Forchheimer (DF) assumption introduced earlier and derived from our field observations. This allows us to replace the total hydraulic head 𝜑(x,z,t) by the water table elevation h(x,t) in Equation (1), which simplifies its analytical integration. As shown below, the assumption is only required at mid-drain spacing (L), and the errors associated with this assumption can be assessed and corrected [Lesaffre 1989].
A third important assumption, introduced by Guyon [1964] on the basis of Boussinesq’s theoretical work, is that water table shapes during the recession and steady-state phases are very similar, so that the water table shape during the transient phase can be well approximated by the one under steady recharge. This leads to a relatively simple calculation of water table shapes.
The integration of Equations (1) and (2) was initially performed during tail recession, i.e. when the recharge rate of the water table R(t) = 0. The approach was later extended to the case of a positive recharge rate R(t) [Lesaffre 1989]. The approach rests on two separate integrations of Equations (1) and (2). Equation (1) can be integrated against x using the discharge potential function introduced by Tcharny [1951], who noted that q(x,t) can be expressed as:
| (3) |
| (4) |
| (5) |
| (6) |
The approach can be extended to the general case of deep impervious barriers and to the case of heterogeneous soils. F(0,t) − F(L,t) can be written in this general case as:
| (7) |
| (8) |
The next step is to integrate Equation (2) twice against x to obtain a second expression of . This is achieved through assumptions on the water table shape. Guyon [1964] initially assumed that h(x,t) can be written as W(X) ⋅ H(t) (separation of variables), where W(X) represents the non-dimensional water table elevation (h(x,t)∕H(t)) at abscissa X = x∕L.
Recognizing that the water table shape W(X) could change over time, particularly during recharge events (as occasionally observed in the field), Lesaffre [1989] extended the approach to the case of a time-dependent water table shape, i.e. where h(x,t) can be written as W(X,t) ⋅ H(t), which was further developed by Bouarfa and Zimmer [2000].
This successively yields three equations:
| (9) |
| (10) |
| (11) |
Combining Equations (5), (7) and (11) finally yields:
| (12) |
| (13) |
The drain flow described by Equation (12) has three components:
- the first term on the right-hand side of the equation represents a water table contribution that is the classic expression of the flow during tail recession;
- the second term represents a proportion of the recharge rate reaching the water table which contributes directly to the drain flow; this proportion is determined by the water table coefficient A, of the order of 0.87 when the pipe rests on the barrier in homogeneous soils, meaning that this proportion is of the order of 13% of the recharge rate;
- the third term is the contribution of water shape changes that occur mostly during recharge events; this contribution is due to the swelling or deflation of the water table (Figure 1); at the beginning of a rainfall event, coefficient A increases; the swelling of the water table shape mitigates the contribution of the recharge rate, thus creating a buffer.
The second and third terms are called “peak flow term” and “water table deformation”, respectively, by Lesaffre [1989]. According to Bouarfa and Zimmer [2000], these terms provide a physical explanation to the relative disconnection between drain flow and water table elevation during peak flow events and a possible answer to the debated issue of the origin of the peak flows observed during rainfall events. These terms also contribute towards explaining the preferential flow, as described by several authors [Akay et al. 2008].
3.2. The critical driver of subsurface drain flows
Investigations on the sensitivity of the system behaviour to the different parameters showed that factors of water table shape are the most sensitive parameters [Zimmer et al. 1995] and demonstrated that parameters K and f were interdependent for the prediction of drain flow rates [Favier et al. 1990], i.e. that identical drain flow rates could be generated by several couples of K and f values. This observation led us to revisit the Boussinesq equation by introducing the variable g(X,t) = f ⋅ h(X,t), which represents the drainable water content stored inside the saturated zone of the soil at a given abscissa x. Combining Equations (1) and (2) and introducing the non-dimensional abscissa X = x∕L yields the following in homogeneous soils:
| (14) |
| (15) |
Solving Equation (14) by a finite element scheme allowed us to examine in detail the water table shape changes for different values of 𝜎. “Fast-response” systems (𝜎> 1 m−1⋅h−1) generate high peak flows because of quick inflating/deflating processes of the water table shape W(X). In such systems, peak flow values largely exceed the transient recession stage A(t)J(t) component. Besides, at an hourly time step, the water table shape changes are fast enough to be neglected in the computations so that drain flow rates can be evaluated by the two first terms of Equation (12). In this case, the numerical solution of the Boussinesq equation can be simplified: the use of a simple Runge–Kutta method is sufficient for integrating the equations.
“Slow-response” systems (𝜎< 1 m−1⋅h−1) do not generate high peak flow rates. The water table recharge contributes towards inflating the water table shape W(X), which mitigates its effects on the drain flow rate. As a result, for these systems, accurate drain flow rate predictions require the computation of the three terms of Equation (12) through the complete solution to the Boussinesq equation.
For drainage simulation at a daily time step, water table shape changes have a lower impact on peak flow simulations. In the majority of French subsurface drainage systems, 𝜎 ranges between 0.05 and 1.25 m−1⋅h−1. Tournebize et al. [2004] tested the errors due to the simplified approach that ignores the water table shape changes in the drain flow rate predictions. The authors showed that even for very slow systems (𝜎 = 0.05 m−1⋅h−1), the simplification error was negligible for daily flow predictions (Figure 2). This result was particularly useful when coupling the drainage simulation with other models running at a daily time step.
Evolution of Nash performance criterion versus time step to compare simplified equations of drainage modelling in the case of “fast” and “slow” drained soil systems [adapted from Tournebize et al. 2004].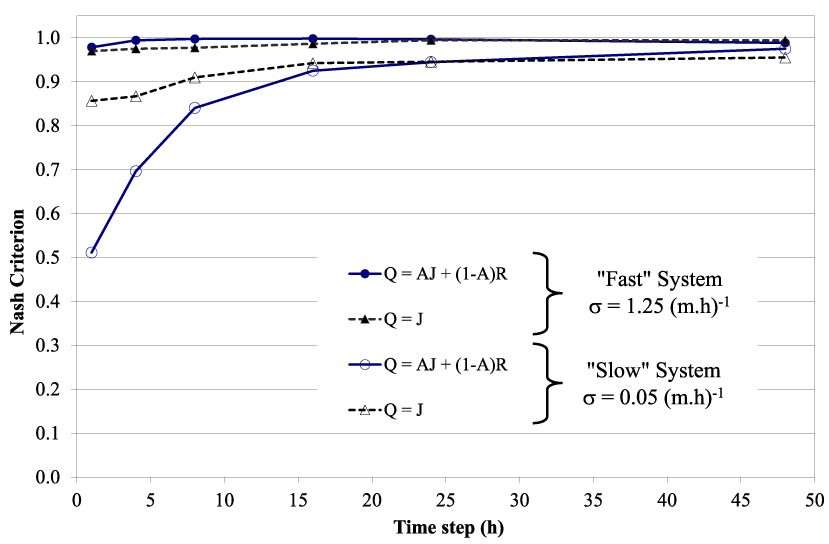
3.3. The SIDRA simulation tool
On the basis of the experimental and theoretical considerations above, a simulation tool of drainage systems, named “SIDRA” (Simulation of Drainage), was developed. The development of SIDRA, based on the above equations, followed different paths aimed at: (i) testing the quality of peak flow prediction; (ii) predicting surface runoff and its relative proportion versus subsurface drain flow; and (iii) coupling the drainage simulation with other tools simulating the effect of improved drainage or crop growth or the integrated hydrologic functioning of rural catchments. These different paths are summarized below together with the comparison against measured experimental results.
3.3.1. Experimental sites
Several experiments have contributed to the validation of the simulation tool (Table 1). These experiments have been equipped since the 1980s and monitored for at least 10 years.
Experimental sites with the corresponding SIDRA developments
| Experiment | Main purposes | Monitored data | References |
|---|---|---|---|
| Arrou (1 ha) 48° 05′ 50.42 N 1° 07′ 17.87 E Luvisol (Silty-Clayey) |
Develop drainage theory, measure impacts on crop development and nitrate leaching | Precipitations, drain flow rates, water table elevations, water pressure, crop development, nitrate absorption and leaching | Zimmer [1989] Brisson et al. [2002] Tournebize et al. [2004] |
| La Jaillière (1 ha) 47° 27′ 25.51 N 0° 51′ 16.83 W Stagnic Luvisol (Silty-Clayey) |
Impacts of drainage on crop development, on surface runoff and nitrate and pesticides transfers, impact and design of buffer zones | Precipitations, subsurface drain flow rates, surface runoff, water table elevations, solute and pesticides transfers | Kao et al. [1998] Henine et al. [2022] Branger et al. [2009] Jeantet et al. [2022] Kao [1994] |
| Chantemerle (36 ha) 48° 50′ 32.01 N 3° 06′ 41.82 E Luvisol (Silt) |
Impact of drainage on water quality (nitrogen, carbon, pesticides). Hydrological question of calibration (using data assimilation) | Precipitations, discharges, high-frequency monitoring of nitrogen, seasonal exportation of pesticides | Chelil et al. [2022a] |
| Rampillon (355 ha) 48° 32′ 19.66 N 3° 03′ 43.91 E Luvisol (Silt) |
Impact of drainage on water quality and remediation. Development of nitrate modelling | Precipitations, discharges, high-frequency monitoring of nitrogen, seasonal exportation of pesticides | Chelil et al. [2022b] |
| Merlachez (700 ha) 48° 52′ 01.74 N 3° 11′ 28.47 E Luvisol (Silt) |
Impact of land drainage on flood dynamics | Precipitations, discharges | Henine et al. [2014] |
3.3.2. Peak flow rate prediction in “fast” drainage systems
The Arrou site made it possible to analyse the seasonal functioning of drainage systems and to delineate precisely the periods of classic drainage functioning, termed “intense drainage seasons” [Lesaffre and Morel 1986]. The initial validation work of SIDRA was carried out for the intense drainage seasons of the period 1985–1995.
The value of 𝜎 in Arrou is equal to 3.3 (m⋅h)−1 (K = 0.41 m∕d and f = 0.014) for a drain spacing of 10 m, which makes this drainage system a “fast system” in which the water table shape changes are fleeting and can be neglected when simulating at a 1-h time step. The initial version of SIDRA did not consider these changes in water table shape. The management of the unsaturated zone was also very simple: a reservoir transfers the water table recharge instantly when full and is depleted by evapotranspiration between recharge events. During a rainy period, the reservoir is initially replenished before generating recharge. The simulation starts at the beginning of the intense drainage season during a rainfall event when the reservoir is assumed to be full.
In these conditions, and using the soil parameters K and f measured by Guyon’s pumping test [Guyon 1976; Lesaffre 1990], the drainage discharges, the water table elevations and the peak flow rates are well predicted [Lesaffre and Zimmer 1988]. These results validated that, in the absence of significant surface runoff, the simple initial modelling of the system has a very good predictive capacity when the soil reaches its saturated status in winter. In such systems, an average of 13% of the rainfall intensity generates, together with the water table contribution, the peak flow rates observed. Outside of the intense drainage season, when the soil is not saturated, sporadic drainage discharges may be observed that cannot be predicted by the model.
3.4. Water balance of drained versus non-drained hydromorphic soils
A global understanding of hydrological processes occurring at the agricultural plot scale in subsurface-drained watersheds is essential for the improvement of management practices to control water pollution, soil erosion and flood genesis. The hydrological studies dealing with water balance in subsurface-drained areas received considerable attention in the second part of the 20th century [see Kao 2008, for a review].
Among the various hydrological effects of subsurface drainage, a reduction in saturation excess surface runoff has been highlighted through the reduction of erosion [Skaggs et al. 1982]. Subsurface drainage lowers the shallow water table, increases the storage volume prior to rainfall events and then reduces surface runoff [Lowery et al. 1982; Enright and Madramootoo 1994; Kao et al. 1998].
Long-term experiments to record surface runoff rates in experimental subsurface-drained fields were performed in some locations in France [see, e.g. Kao et al. 1998; Augeard et al. 2005], in particular at the “La Jaillière” experimental site. The field experiment of La Jaillière is located in Maine et Loire [Henine et al. 2022; Jeantet et al. 2021, 2022] and was equipped since the early 1990s to monitor the functioning of drainage systems as well as their impacts on water quality. For this purpose, it was equipped to measure both subsurface drainage and surface runoff, since their relative proportions have important consequences on the transport of: (i) solute products such as nitrates, mostly transferred by subsurface flows, and (ii) non-solute products associated with soil particles such as most pesticides, mostly transferred by surface runoff.
In these experimental fields, observed surface runoff volumes are usually small (from 5% to 10% of the rainfall amount), which confirms the high infiltration capacity of such soils. After autumn harrowing, surface runoff is mainly generated midway between drains when rainfall intensity has exceeded the soil infiltration capacity controlled by the water table depth. Surface runoff propagation over the area above the drain depends on the drainage efficiency (depth, spacing, possibly plugging).
Modelling the distribution of surface runoff and subsurface drain discharges was managed by coupling the SIDRA model with a reservoir-based model (SIRUP) aiming to generate three types of flows: (i) classic Hortonian surface runoff generated by heavy rainfall intensity before complete water replenishment of the upper soil horizon; (ii) Dunne surface runoff generated by the saturation of the soil mid-way between drains; and (iii) water table recharge rate [see a review and the development of the SIRUP model by Kao et al. 1998 and Branger et al. 2009].
The SIRUP model consists of three separate conceptual reservoirs, respectively, accounting for (Figure 3):
- water storage in the superficial soil layer, and infiltration/runoff distribution depending on the water table depth (Reservoir 1 with three parameters);
- storage of infiltrated water and moisture distribution in deeper soil layers, evapotranspiration and recharge to the water table (Reservoir 2 with one parameter);
- lamination of surface runoff (Reservoir 3 with one parameter).
Reservoir 1 has a maximum water level R1 (L) and represents the rainfall water storage on the soil surface. Water flows from Reservoir 1 to 2 according to the emptying equation:
| (16) |
SIRUP module structure. I1, l2 and l3 are the water levels in the reservoirs; R1 and R2 are the volumes of Reservoirs 1 and Reservoir 2; T, M and B are the parameters of the emptying laws for R1 and R2; PET is the potential evapotranspiration, adapted from Branger et al. [2009], and Kao et al. [1998].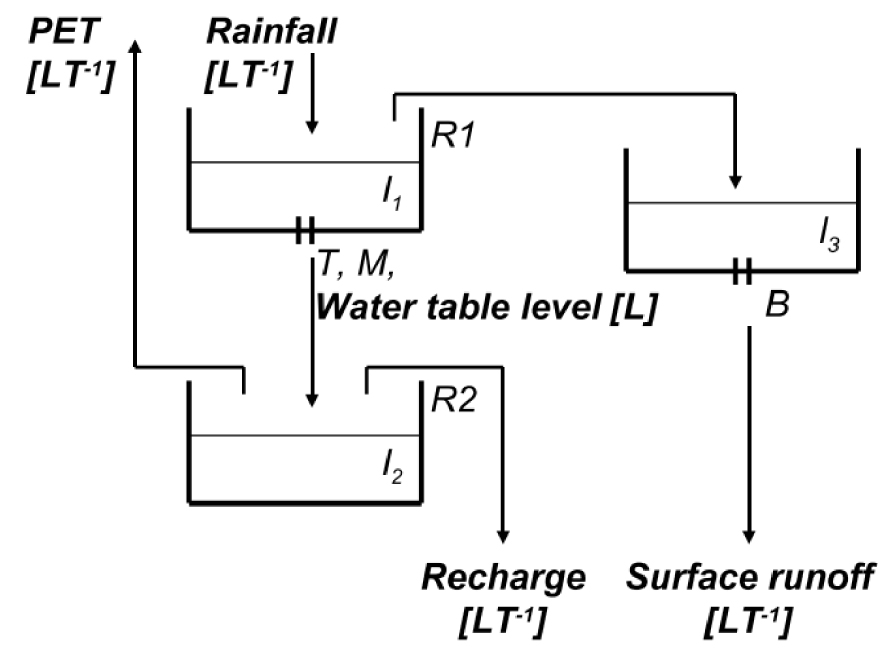
Equation (16) accounts very simply for the influence of the water table level on soil infiltration: a high water table level implies a reduced infiltration flow. When Reservoir 1 overflows, excess water flows to Reservoir 3 and is changed into surface runoff, according to:
| (17) |
Reservoir 2 receives infiltration flow from Reservoir 1 and is emptied by evapotranspiration. It has a maximum water level R2 (L). The overflowing water constitutes the recharge to the water table.
Based on the knowledge gained in La Jaillière, and in order to extend the use of SIDRA to other sites and to the different stages of replenishment of the soil water reserves across the year, a simplified version of the surface module SIRUP was developed and named “SIDRA-RU” [Henine et al. 2022; Figure 4]. Three stages were defined: (i) when the soil is unsaturated during late spring and summer, the water table recharge term is 0; (ii) during the fall, as water reserves are being replenished, one-third of the net rainfall replenishes the water table and two-thirds replenish the soil water reserves until soil saturation is reached; this required that the three parameters of SIRUP be replaced by two new parameters, Sinter and Smax; (iii) after saturation is reached, during winter, water table recharge R(t) is the full net rainfall. The Sinter and Smax parameters represent two soil water depth thresholds. Sinter (L) is an intermediate level of replenishment allowing for initial discharges in subsurface-drained soils. It is of the order of 85% of the total water holding capacity. Smax (L) corresponds to the full water replenishment of the soil profile, allowing for a conventional water table to be present in the soils.
Coupling of SIDRA-RU and comparison between yearly cumulative observation and simulation results with SIDRA-RU for plot T04, using the parameter set of calibration period P1 (T04_P1): rainfall, simulated and observed drainage discharge and surface runoff (mm/year) [adapted from Henine et al. 2022].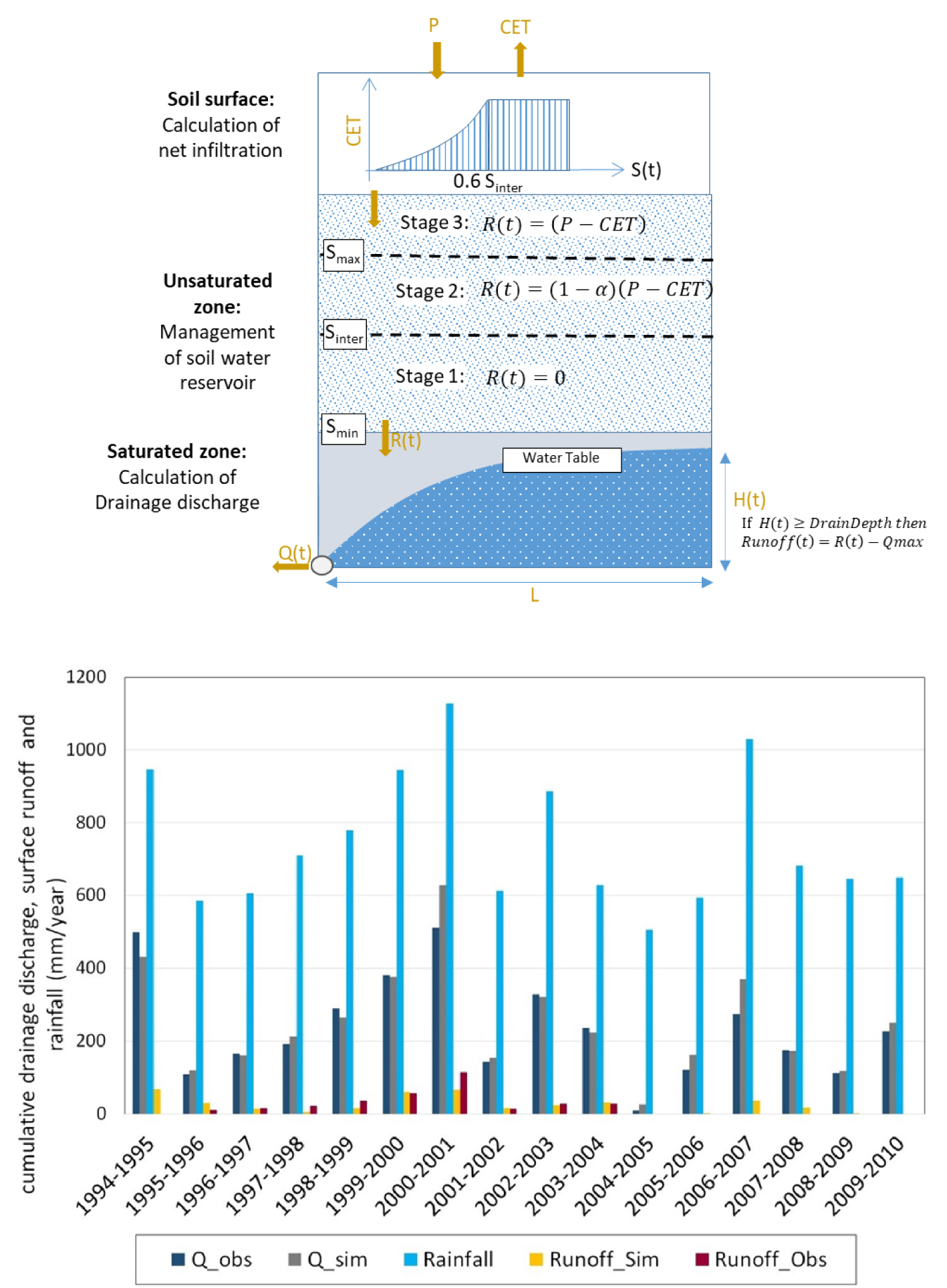
The simulated total runoff during the intense drainage season (i.e. when the soil water reserves have been replenished) was comparable to observations (35 mm/year) and represented 5% of total annual rainfall, congruent with the results of Moriasi et al. [2013]. Note that subsurface-drained discharges were estimated at 40% of annual rainfall, as reported by Moriasi et al. [2013], and surface runoff volumes in drained plots remain below 10% of the drained volume [Kao et al. 1998; Henine et al. 2022].
3.5. Robustness of SIDRA approach
The SIDRA model, initially developed and validated on two specific sites (Arrou and La Jaillière), was subsequently shown to predict drain flow rates and water table elevations on other sites. Its robustness was tested on 23 experimental sites in France with contrasting soil and climatic contexts [Jeantet et al. 2021]. These sites were monitored from 1969 to 2017. Their areas range from plot scale of ca. 1 ha to catchments of ca. 700 ha. The modelling was performed for a total of 170 years. SIDRA-RU requires few parameters as compared to other drainage models such as MACRO [Jarvis et al. 1997; Larsbo and Jarvis 2003] or DRAINMOD [Skaggs et al. 2012]. To obtain these parameters, two methods were used: regional delineation from calibrated values of the observed discharges on the 23 sites and using the split-sample test on nine of these 23 sites [Jeantet et al. 2021], or directly from on-site measurements through pumping tests such as Guyon’s test [Lesaffre 1990].
The performance criterion used in Figure 5 is the Kling–Gupta efficiency (KGE) [Gupta et al. 2009], defined as the combination of linear correlation, relative variability and bias between observed and simulated values. Values above 0.5–0.6–0.7 thresholds for hydrological models showed, respectively, acceptable, good and very good simulation quality [Moriasi et al. 2015]. The results showed congruent comparisons in simulations versus observations (KG2 > 0.5) especially in loamy soils, representing 80% of drained soils in France [Lagacherie and Favrot 1987]. The worst simulations were encountered in swelling clay soils (KGE < 0.5), due to probable mis-alignment of the assumptions used in the model (depth to the impervious layer, important role of soil cracks and macropores) such as Courcival (only point with KGE < 0.5 in Figure 5). Some regions with significant drained areas in the centre of France (Auvergne, Burgundy) were not tested due to a lack of experimental data.
Experimental sites used for assessment of the SIDRA-RU model in France and related performance with the Kling–Gupta efficiency (KGE) criterion. The map also displays the main regions where subsurface drainage has been implemented [adapted from Jeantet et al. 2021].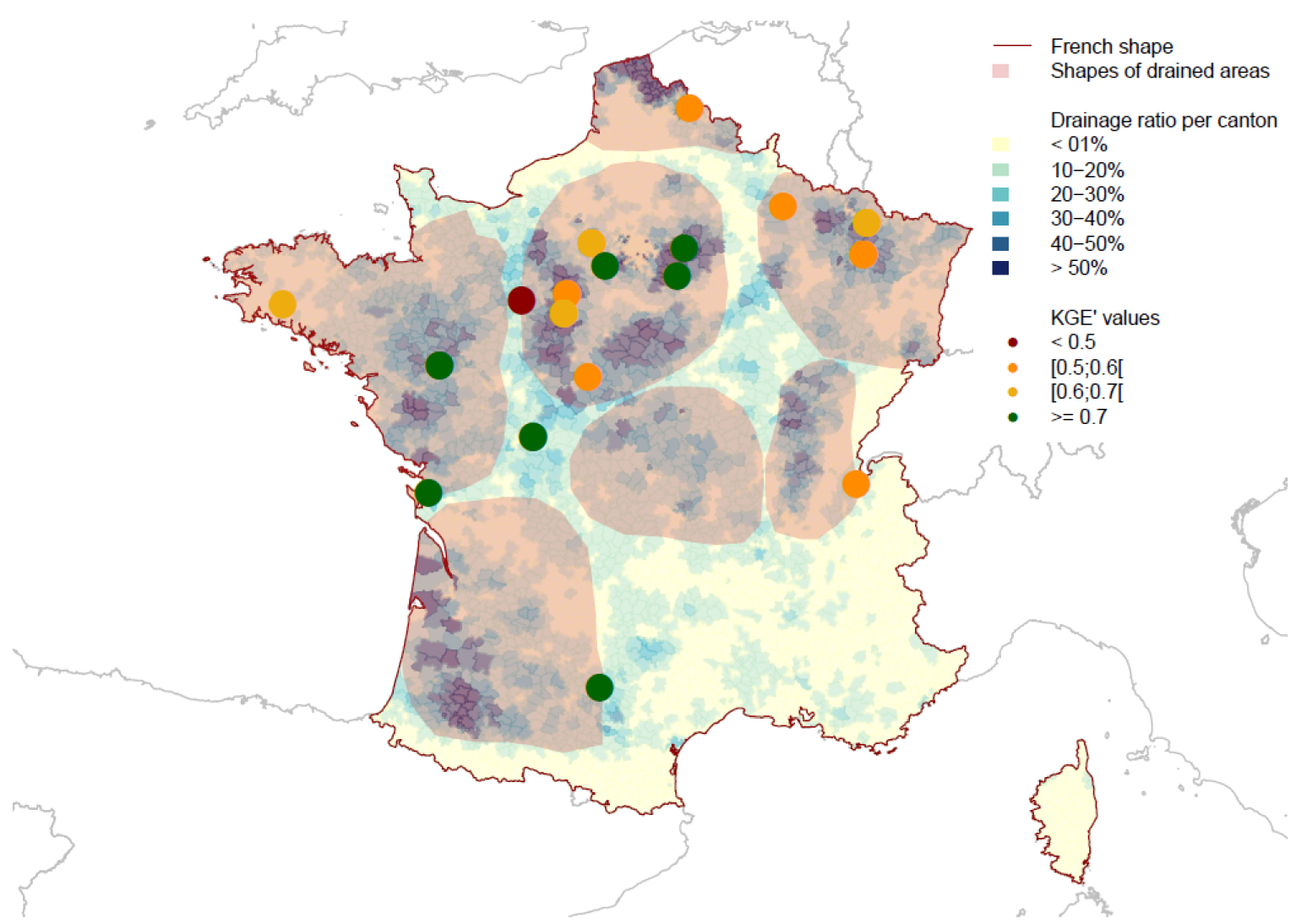
4. Impact of land drainage on flood generation and control
Research aiming to understand the consequences of subsurface drainage expanded from this experimental and modelling approach. This was achieved from plot scale to catchments or marshlands with large field drainage intensities such as the Melarchez, part of the Orgeval catchment on the Seine basin (upstream of Paris), or the Moëze marshland, a 22-km2 polder in western France. The SIDRA model was used to generate the distributed production functions of hydraulic models solving the classic Saint-Venant equations [Giraud et al. 1997].
The effect of subsurface drainage on floods is a matter of debate. Does subsurface drainage increase or decrease flooding? A modelling approach was used by Henine et al. [2012, 2014] to represent the complex interactions between pipe networks and groundwater flows during flood events. In this case, free-surface flow conditions in pipe drains are no longer respected and may flow under pressurized conditions due to high water levels in open channels at the drainage outlets. The approach consisted in coupling subsurface drainage processes through a 2D Boussinesq equation with a 1D Saint-Venant network model to take into account the interactions between subsurface drainage and open-channel flows. This model was used to investigate the effects of pressurization during flood events as compared with non-pressurization at the pipe outlet and compared with experimental observations. The simulation results were in good agreement with experimental observations [Henine et al. 2014]. The contribution of subsurface drainage flow to floods could be limited during peak events by redesigning the pipe outlet diameter (reducing the diameter of the collector into the ditch). This would be equivalent to an increase in the field buffer capacity of a few millimetres of rainfall.
In general, the arterial drainage function is the most influential and its storage and laminating capacity is essential. This capacity is to a great extent controlled by the number and position of hydraulic structures: reduced cross sections (e.g. culverts in road crossovers) or of a network of small gullies that has been built over time in wet areas.
In large marshlands (e.g. polders), the key buffer capacity is related to the large number of small gullies that store water in a decentralized way. Reducing this number to create large field plots, as is often implemented in the intensification process of agriculture, has been shown to have the greatest impact on wetland hydrology [Giraud et al. 1997]. By comparison, the influence of field drainage on the buffering capacity of the marshland is much smaller. In this application, controlled drainage, as largely studied in the United States, could be an option [DRAINMOD model application of drainage water management such as controlled drainage, i.e. Sloan et al. 2016].
Similar results can be deduced from observations and simulations carried out in the Orgeval basin (east of Paris). In this catchment that is representative of the French context, the retention capacity of the ditches determined by the number of culverts and the capacity to store water upstream of these is critical for the flood laminating capacity. More precisely, the number of retention structures along the network is more critical than their total storage capacity, which is explained by the dynamic storage (i.e. the fact that a given quantity of water is slowed down several times successively during its downstream transfer) provided by these structures.
Beyond these generic conclusions, the consolidated impacts of land drainage (i.e. the combination of field and arterial drainage) on hydrological regimes of rural catchments depend on the return periods of floods (Figure 6):
- Stage 1: increase in flood intensity for return periods aligned with the design of the subsurface drainage network (1–2 years); in that case, subsurface drainage has a negative impact on hydrological regimes by accelerating the propagation of the flood;
- Stage 2: self-limitation and storage in the network or in the field, for floods with a return period between 5 and 10 years; in that case, drainage has a positive impact by attenuating the propagation of the flood;
- Stage 3: beyond a return period of 10 years, in the hydro-system being saturated, drainage no longer shows any impact.
Flood return periods of hourly specific discharges measured at Melarchez Station (Orgeval Observatory https://gisoracle.inrae.fr/) during a 20-year period (1995–2015). Stages 1, 2, 3 correspond to increasing impacts, self-limitation, and no additional impacts of drainage on flooding, respectively [adapted from Henine et al. 2012].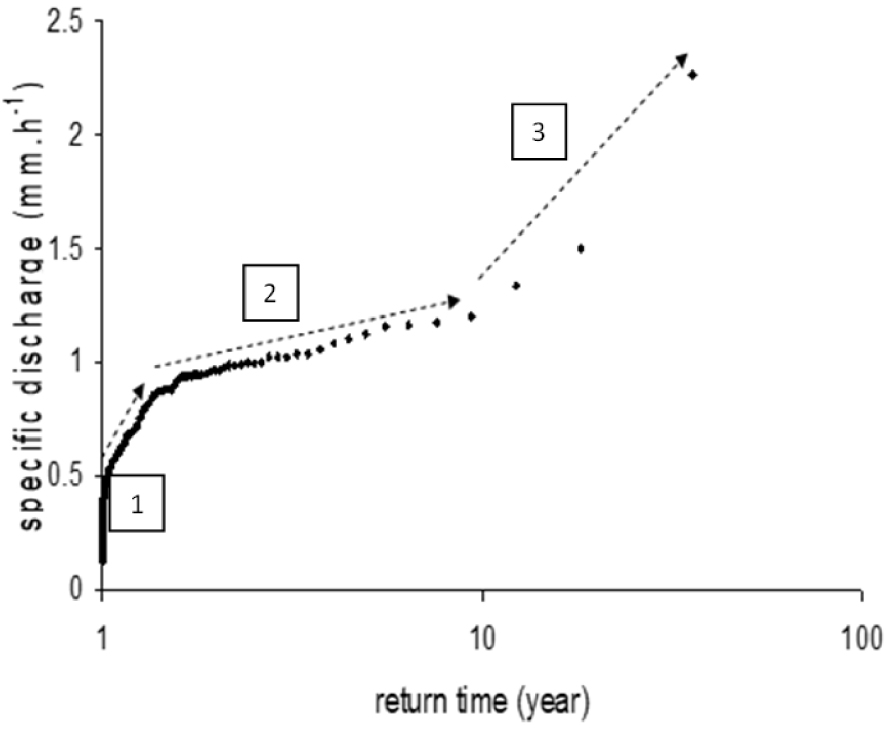
5. Solute transfer highlights hydrological functioning
Drain flow dynamics were studied by several authors [Jacobsen and Kjær 2007; Dairon et al. 2017; Kao 2002; Gatel et al. 2019] using in situ tracer experiments or model results. Since nitrate and some pesticides are highly soluble, the specific studies of their transfer dynamics at the drainage outlet stressed the preferential flow above the pipe and the matrix contribution from the area between the pipe and the mid-drain space. This duality of behaviour corresponds to the fast and slow transfers. The C-Q relationships shift during peak events exhibiting hysteresis patterns due to a high variability of the flushing/dilution effect [Liu et al. 2020]. From this state, a conceptual approach based on compartments was developed and coupled with the SIDRA model. Branger et al. [2009] proposed PESTDRAIN based on coupling of the SIDRA–SIRUP–SILASOL modules (Figure 7). The originality of this approach is the simplified choice of hydrological process for solute transfer by using transfer functions [Jury and Roth 1990]. An exponential formula [Magesan et al. 1994] is applied for two distinct artificial compartments (fast and slow). The calibration procedure led to quantification of the volume of soil reservoirs at 2 mm for fast transfers above the drain and at 200 mm for slow transfers between the drain and mid-drain space, thereby successfully reproducing pesticide transfer at the plot scale. The interesting point is the surface contribution of the two distinct compartments to the exported fluxes: 13% for fast transfers (area above the drain) and 87% for slow transfers (between the drain and mid-drain space), corresponding to the hydrological contribution (1-A) and A from SIDRA Equation (12).
Solute transfer in drained soil: PESTDRAIN version [left side, Branger et al. 2009] considering two reservoirs and the Magesan transfer function; NITDRAIN version [right side, Chelil et al. 2022a, b] considering three reservoirs and the Burns and Magesan transfer functions. Drain flow rates are simulated by the SIDRA model.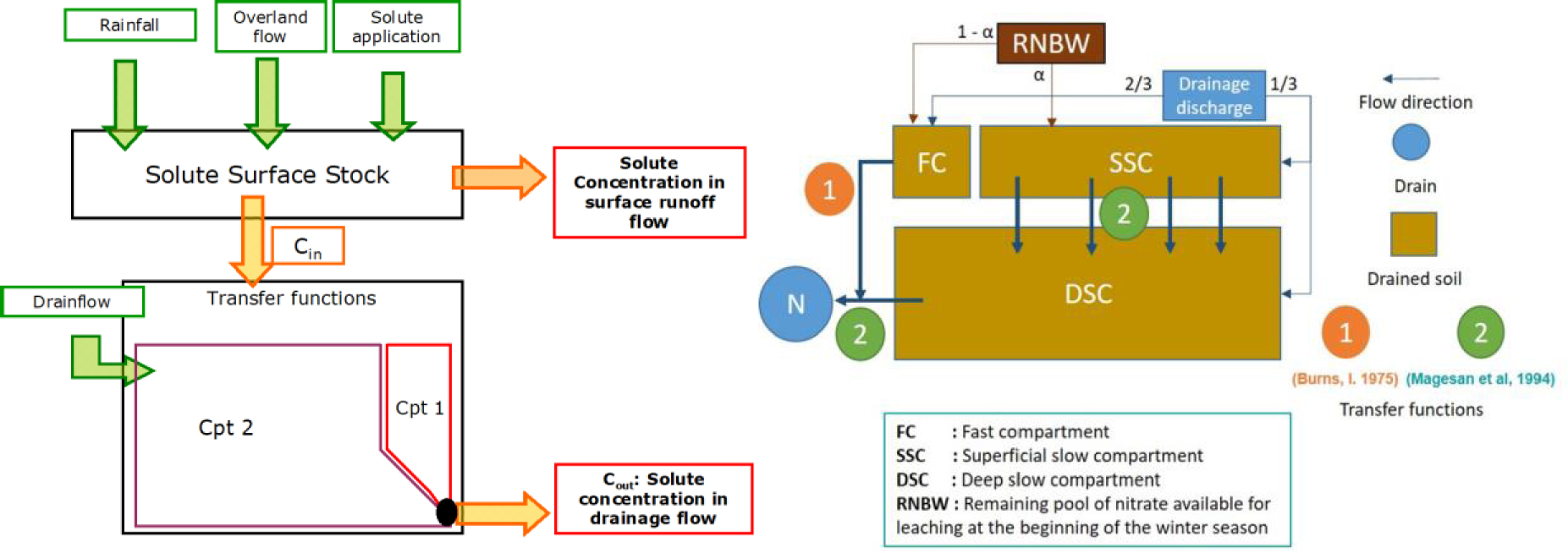
High-frequency monitoring of nitrate concentrations (hourly observation at the drainage outlet) provides clues to improve the conceptual approach of solute modelling based on hydrological drainage functioning. Thus, a new model for nitrate, NITDRAIN [Chelil et al. 2022a, b], considers three compartments and two distinct transfer functions (Figures 7 and 8): (1) the Burns equation for preferential vertical transfer [Burns 1975], and (2) the Magesan exponential equation for matrix lateral flow for upper and deeper slow reservoirs. The model succeeds in reproducing the flushing and dilution typical of nitrate concentration behaviour in subsurface-drained soil (Figure 8a and b). The mixing water at the outlet of the drained plot is composed of fast and slow flows, as presented in Figure 8. The fast compartment (FC) contributes directly to the flow outlet above the drain pipe. The surface slow compartment (SSC) transfers solute to the deep slow compartment (DSC), which is connected to the flow outlet (Figure 8c). The model provides a temporal evolution of solute stock in all compartments (Figure 8d). The results obtained with this model also help to improve our understanding of hydrological drainage processes. The switch between nitrate flushing and nitrate dilution concentration behaviour at the pipe outlet (Figure 8d) occurred specifically when the hydrological status of the drained soil switches from the beginning stage (unsaturated soil profile) to the intensive drainage season (saturated soil profile).
Simulation of nitrate concentrations with NITDRAIN on Rampillon watershed (Seine et Marne) showing the time of switching between flushing and dilution processed (dashed line): (a) time series of simulated and observed nitrate concentrations, (b) simulated vs observed concentrations, (c) simulated contribution fluxes of fast compartment (FC) and deep slow compartment (DSC), (d) evolution of nitrate storage in FC, DSC and SSC (surface slow compartment) [adapted from Chelil et al. 2022b].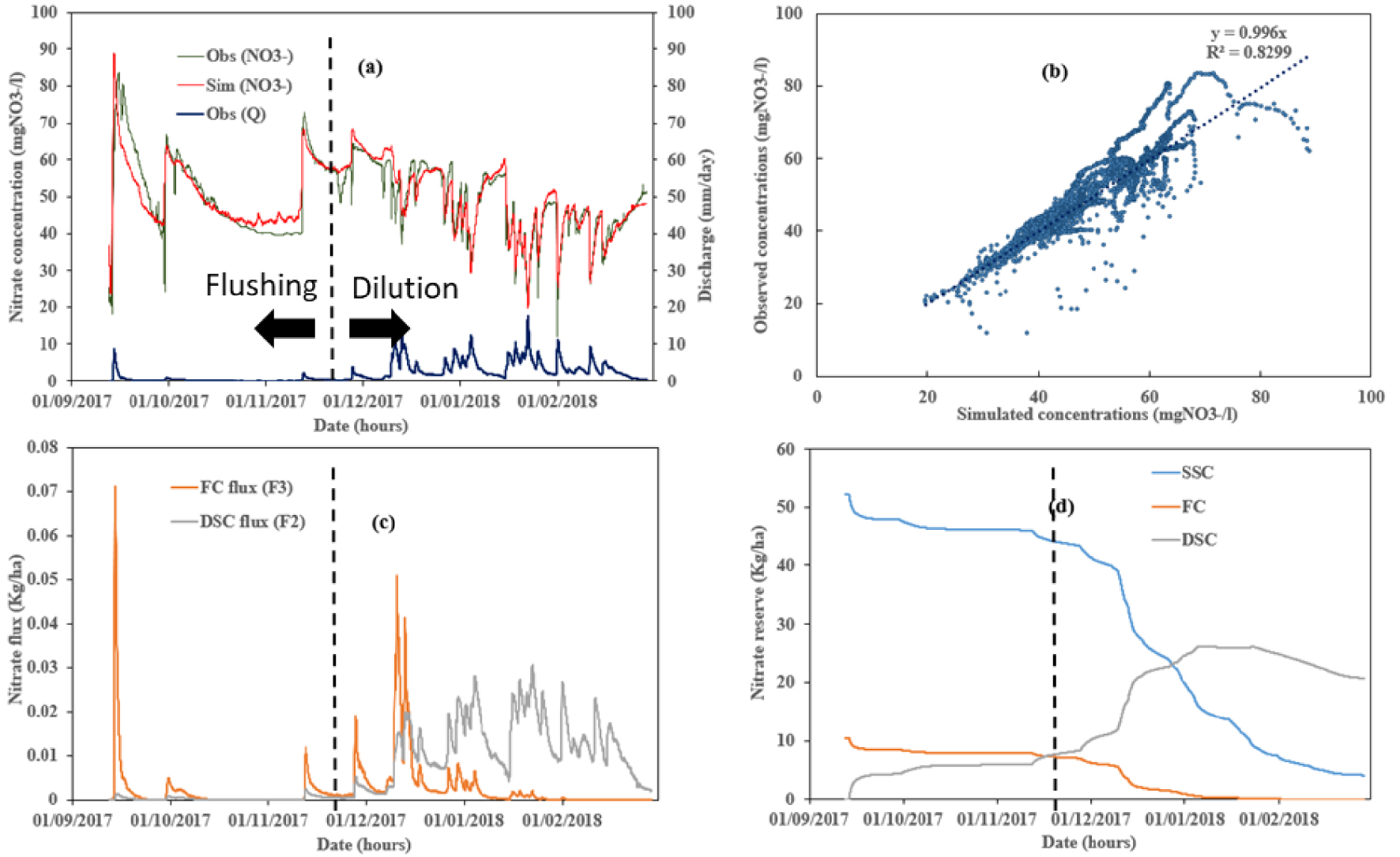
Both examples of solute modelling confirm the dual processes between preferential flow above the drain pipe and the water table slow contribution from the rest of the transect, as the hydraulic approach showed. The understanding of hydrological processes in subsurface-drained soils is thus supported by the analysis of solute transfer.
6. Conclusions
During 30 years of research on the functioning of subsurface drainage, we could demonstrate that relatively simple modelling tools based on a few equations and a limited number of parameters provide important insights into the functioning of drainage systems. In particular, the semi-analytical solution to the Boussinesq equation offers a simple way to describe the functioning of a majority of drainage systems in the French context as well as very important insights explaining their functioning. Specifically:
- It provides an explanation of the experimental results and confirms that, in most subsurface-drained soils, there is no need to advocate preferential flow in the plough layer or in the trench backfill to explain the peak drain flow rates at the outlet of these systems. This result was shown to be relatively robust in many soils except for heavy clay soils where the modelling approach did not reproduce the drain flow rates accurately.
- It provides a correct description of the relative disconnection between water table elevations and subsurface drain flow rates observed in experimental fields. Drain flow rates depend not only on the water table position in the soil but also on the recharge rate reaching that water table. The theory provides a good order of magnitude of the proportion (around 13%) of that recharge rate that contributes to the drain flow.
- It goes even further and adds to the water table elevation and the recharge rate a third component, i.e. the drain flow rate related to the swelling or deflating of the water table shape during recharge events. The reparameterization of the equation also demonstrates that drain flow rates can be fully predicted by a single parameter (𝜎), a combination of two soil parameters (saturated hydraulic conductivity and drainable porosity) and of the drainage system dimension (drain spacing). With high values of 𝜎, the swelling–deflating process is very brief and can be ignored in the modelling process. With low 𝜎 values, the process cannot be ignored and has a mitigation effect on the peak flow rate.
These theoretical results developed at field level have predictive capacity for other drainage systems such as water tables drained by water channels or rivers. They could also be extended to the generic case of deep impervious barriers. They explain in particular the steep increase of the flow rates during recharge periods in such systems and as such may have practical importance for the prediction of peak flows in such systems.
On the basis of these results, a series of modelling tools were developed, starting with the simple model SIDRA, based on a small number of parameters (4), which has demonstrated its capacity to predict subsurface drain flows—and particularly peak flows—in various regions of France during the winter drainage season. Papers dealing with the SIDRA model from 1987 comprised about 48 documents: 18 publications in peer-reviewed journals, 20 as conference presentations, and 10 as technical publications. In 2022, Scopus identified more than 235 citations of the SIDRA model in publications. As SIDRA is modular and can run independently, its insertion in different modelling tools is easier. For instance, the agronomic model STICS [Brisson et al. 2002] simulating crop production as well as environmental data below the soil root zone (water balance and nitrogen leaching) proposes a “subsurface drainage” option including SIDRA’s concept.
SIDRA was subsequently enriched and coupled with several other modelling tools to analyse the impact of subsurface drainage on the hydrology of rural catchments.
- A surface runoff module (SIRUP) was developed and validated against experimental data to predict the share of surface runoff and subsurface drainage.
- Coupling SIDRA with hydraulic models solving the Saint-Venant equations in the ditches and channels of the arterial drainage network was also used to analyse the impacts of land drainage at catchment level [Branger et al. 2010]. Results from a polder and from a more classic catchment demonstrated the predominant role of the retention in the channel system often reduced by the removal of the network of small gullies (e.g. after land consolidation programmes), and the recalibration of the ditch network combined with culverts and cross-overs designed for 10-year return flows (to avoid road degradation during floods). The field subsurface drainage instead has a mitigating effect on floods for average return periods (>10 years).
- Finally, SIDRA was coupled with solute transfer models to understand the impacts of drainage on pesticide and nitrate transfers in relation to surface and subsurface flow patterns. The hydrological understanding and modelling conceptualization of SIDRA helped and supported the compartmental approach leading to a simplified modelling structure (PESTDRAIN and NITDRAIN). Results confirmed the duality of solute behaviour in drained soil with a fast transfer from soil surface above the pipe area during peak flow and a slow transfer for the rest of the transect mid-drain space, especially during the water table tail recession.
Conflicts of interest
Authors have no conflict of interest to declare.
Dedication
The authors would like to dedicate the SIDRA model story to Ghislain de Marsily from Sorbonne University and a member of the Académie des Sciences, for his scientific support (participating directly in the PhD supervision or as a PhD jury member).
Acknowledgments
The authors would like to thank Bernard Vincent (1952–2022) for his relentless contribution to the improvement of drainage practices in France.




 CC-BY 4.0
CC-BY 4.0