1 Introduction and geological setting
Low-Ca amphibolites, which include cordierite–orthoamphibole rocks, are useful as they generally contain a large variety of mineral assemblages and complex reaction textures that can be used to constrain the P–T paths of metamorphic terrains [21,25]. Lensoid bodies of this kind of rock have been studied in the Guilleries Massif, located in the Catalan Coastal Ranges, in the northeastern part of the Iberian Peninsula (Fig. 1). This massif constitutes an outcrop of Palaeozoic basement rocks that were subsequently deformed and metamorphosed during the Variscan orogeny (Upper Carboniferous). The nearest outcrops of similar rock types were found in western Corsica, where they were suggested to belong to a Proterozoic basement [4].
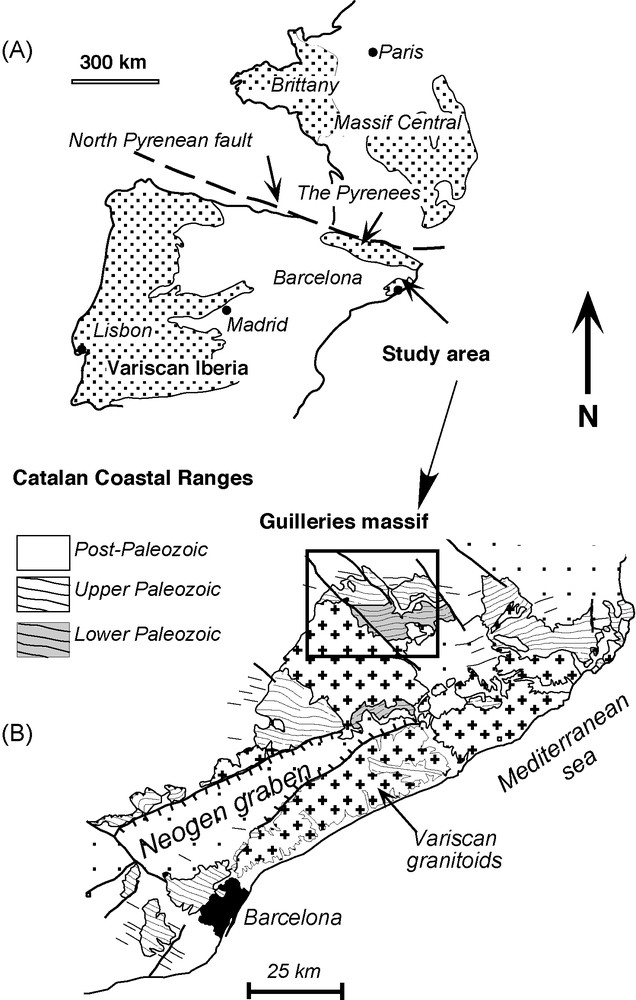
Geological setting of the Guilleries massif, showing its location (A) with respect to other Variscan terrains, such as the Iberian massif, the Pyrenees, and the Massif Central. The Osor complex forms part of the Lower Palaeozoic unit and contains the highest Variscan metamorphic grade outcrops in the Catalan coastal ranges. (B) The direction of the main Variscan foliation (S2) in the area is also shown.
Fig. 1. Situation géologique du massif de Guilleries, montrant sa situation (A) par rapport à des terrains varisques tels que le massif Ibérique, les Pyrénées ou le Massif central français. Le complexe d’Osor appartient aux unités du Paléozoïque inférieur, dans lesquelles l’on trouve les affleurements ayant le plus haut degré métamorphique de la chaîne côtière Catalane (B). La disposition de la foliation varisque majeure (S2) dans la région est également montrée.
The geology of the massif has been studied in detail [3,11]. The Palaeozoic stratigraphic record goes from a probable Cambrian to the Devonian. The Lower Infra-Caradocian sequence is divided into the Osor and the Susqueda metamorphic complexes. The metapelitic–metapsammitic Osor complex is similar in composition and setting to the Pyrenean Canavelles–Jujols series [2] and contains the interlayered amphibolite levels reported in this study. The metamorphic evolution of the Osor complex shows an LP–HT prograde P–T evolution (to 660 °C–5 kbar) during thickening, due to two D1 and D2 compressive deformation events followed by an anticlockwise evolution with isobaric cooling and by final decompression and cooling, probably related to a D3 fini-Variscan extensional event [19].
2 Bulk composition and petrography
The bulk-rock chemistry of the most representative cordierite–orthoamphibole, low-Ca amphibolites found in the Osor complex is shown in Fig. 2. The diagrams show the bulk compositional peculiarity of these amphibolites with respect to the major elements Al, K, Ca, Fe, and Mg when compared with common amphibolites and metapelites. Samples always plot near the AFM plane of the full AKCFM compositional space.
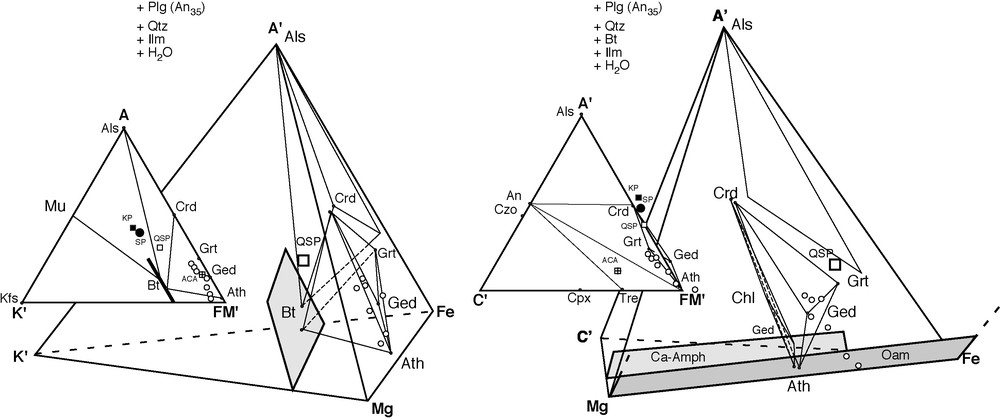
Chemographic analysis of the low-Ca amphibolites using tetrahedral and triangular projections of the full system NCKFMASH (Na2O, CaO, K2O, FeO, MgO, Al2O3, SiO2, H2O), depicting the position of the low-Ca amphibolite samples in this study (open, with circles). The apexes are A′: Al2O3–K2O–2.0769 Na2O, K′: KalO2, C′: CaO–1.076 Na2O, Fe: FeO–TiO2, Mg: MgO, FM′: FeO + MgO + MnO–TiO2. The projections are always from a plagioclase of intermediate composition (Plg An35), quartz (Qtz), ilmenite (Ilm), water, and biotite (only in the ACFM subsystem projection). Bulk composition averages for the pelites (KP: black square) and the semipelites (QSP: large with square) of the Osor complex, as well as the average pelites [22], (SP: black circle) and the average common amphibolites of [13,14] (ACA: crossed square) are plotted for comparison purposes. The low-Ca amphibolite samples always plot near the A′–Mg–Fe face in all projections, show a K′ and A′ depletion with respect to metapelites (that normally plot inside the Mu–Als–Bt triangle in A′K′FM′), show a C′ depletion with respect to common metabasites (that normally plot inside the An–Tre–FM′ triangle in A′C′FM′) and always plot inside the Crd–Bt–FM′ (in A′K′FM′) or inside the An–Crd–FM′ (in A′C′FM′) triangles, as shown by other authors [9]. Some samples even plot negatively (as do gedrite and the metapelites) with respect to the C′ apex, due to the low-Ca content. F/FM ≈ 0.7, as shown in the A′C′MgFe tetrahedron. Symbols for the minerals are as in [12]: Als, aluminium silicates; Mu, muscovite; Crd, cordierite; Grt, garnet; Ged, gedrite; Ath, anthophyllite; Bt, biotite; Kfs, K-feldspar; An, anorthite; Czo, clinozoisite; Tre, tremolite; Ca-Amph, Ca-amphibole; Oam, Orthoamphibole; Chl, chlorite; Cpx, clinopyroxene; Plg, plagioclase; Qtz, quartz; Ilm, ilmenite.
Fig. 2. Analyse chémographique des amphibolites pauvres en Ca avec des projections triangulaires et tétraédriques du système total NCKFMASH (Na2O, CaO, K2O, FeO, MgO, Al2O3, SiO2, H2O), montrant la position des échantillons des amphibolites de cette étude (cercles ouverts). Les paramètres des apex sont A′ : Al2O3–K2O–2,0769 Na2O, K′ : KalO2, C′ : CaO–1,076 Na2O, Fe : FeO–TiO2, Mg : MgO, FM′ : FeO + MgO + MnO–TiO2. Les diagrammes utilisent toujours comme point de projection le plagioclase de composition intermédiaire (Plg An35), le quartz (Qtz), l’ilménite (Ilm), l’eau et la biotite (seulement dans le sous-système ACFM). Les compositions globales des métapélites (KP : carré noir) et des semipélites (QSP : gros carré blanc) du complexe d’Osor aussi, tout comme la composition moyenne des pélites [22] (SP : cercle noir) et des amphibolites communes [13,14] (ACA : carré avec une croix) y sont dessinées, au cas où l’on voudrait établir des comparaisons. Les échantillons d’amphibolites pauvres en calcium se représentent toujours près de la face A′–Mg–Fe dans toutes les projections et montrent un appauvrissement en K′ et en A′ si on les compare avec les métapélites (qui se représentent toujours dans le triangle Mu–Als–Bt dans A′K′FM′). Ils montrent un appauvrissement en C′ si on les compare avec les métabasites communes (qui se représentent toujours dans le triangle An–Tre–FM′ dans A′C′FM′) et se représentent toujours dans les triangles Crd–Bt–FM′ (en A′K′FM′) ou An–Crd–FM′ (en A′C′FM′), comme d’autres auteurs l’ont déjà signalé [9]. Quelques échantillons sont représentés de façon négative (comme la gédrite et les métapélites) par rapport à l’apex C′, en raison des bas niveaux de calcium. F/FM ≈ 0,7, comme on le voit dans le tétraèdre A′C′MgFe. La symbolique utilisée pour le minéraux est la même qu’en [12] : Als, silicates d’aluminium ; Mu, muscovite ; Crd, cordiérite ; Grt, grenat ; Ged, gédrite ; Ath, antophyllite ; Bt, biotite ; Kfs, feldspath potassique ; An, anorthite ; Czo, clinozoïsite ; Tre, trémolite ; Ca–Amph, Ca–amphibole ; Oam, orthoamphibole ; Chl, chlorite ; Cpx, clinopyroxène ; Plg, plagioclase ; Qtz, quartz ; Ilm, ilménite.
Various authors have indicated significant alteration mechanisms to explain the genesis of the low-Ca amphibolite bulk composition by depletion in alkalis and Ca. The mechanisms involving extensive hydrothermal alteration of basic igneous rocks prior to metamorphism [10,21,27] are among the most plausible, although potassium depletion during HT metamorphism of pelites cannot be ruled out for some Osor samples [1]. The most frequent mineral assemblage (Fig. 3B and C) is garnet–cordierite–gedrite–antophyllite–plagioclase–ilmenite–biotite–quartz ± chlorite. Small garnet porphyroblasts (from less than 1 mm to 3 mm in size) contain some quartz, ilmenite, and plagioclase inclusions, sometimes arranged along an internal foliation (S1) discordant with the dominant external foliation (S2), which corresponds to an evolved crenulation outlined by matrix gedrites. Garnets show variable degrees of resorption, with cordierite being the most abundant mineral found in the reaction rims, although plagioclase, quartz, biotite, and orthoamphiboles are also found as inclusions in cordierite. Two orthoamphiboles are found: a green-blue gedrite is found predominantly in the matrix as the most abundant mineral with plagioclase. Orthoamphiboles that are included in cordierite moats around garnets and in matrix cordierite-rich domains are normally composite grains of light non-pleochroic, sub-idioblastic anthophyllite overgrowths over gedrite cores, but also small idioblastic, acicular anthophyllites with no gedritic cores. In most cases, the anthophyllite overgrowths do not surround completely the gedritic core.

Petrography of the low-Ca amphibolite samples. (A) Cordierite-free subassemblage garnet–orthoamphibole (gedrite)–plagioclase–quartz. Samples contain garnet porphyroblasts in a granonematoblastic gedrite–plagioclase-rich matrix. Gedrites are preferentially oriented along the dominant regional foliation S2. (B, C) Garnet–cordierite–gedrite–anthophyllite samples. Cordierite is present as moats rimming garnet porphyroblasts. The orthoamphibole matrix is gedrite. Where the orthoamphibole is in contact with or surrounded by cordierite, it has a gedritic core, is partially wrapped by anthophyllite, or is anthophyllite without a gedritic core. Cordierite-rich domains in these rocks contain allotriomorphic garnets at different stages of resorption, or no garnets at all. (D) Garnet-free subassemblage cordierite–gedrite–anthophyllite–chlorite. The orthoamphiboles are needle-like anthophyllites; gedrite is present only in small, allotriomorphic core domains of the biggest anthophyllites. Symbols for the minerals are as in [12].
Fig. 3. Pétrographie des échantillons d’amphibolites pauvres en calcium. (A) Paragenèse sans cordiérite, grenat–orthoamphibolite (gédrite)–plagioclase–quartz. Les échantillons contiennent des porphyroblastes de grenat dans une matrice granonématoblastique riche en gédrite et plagioclase. Les gédrites sont orientées préférentiellement dans le sens de la foliation régionale dominante, S2. (B, C) Échantillons à grenat–cordiérite–gédrite–anthophyllite. La cordiérite est présente sous forme de douves autour des porphyroblastes de grenat. Dans les sites où l’orthoamphibole est en contact ou enveloppée par la cordiérite, elle possède un cœur gédritique, partiellement enveloppé par de l’antophyllite, ou d’antophyllite, sans cœur gédritique. La plupart des domaines riches en cordiérite contiennent des grenats allotriomorphiques montrant différents niveaux de résorption. (D) Paragenèse sans grenat, cordiérite–gédrite–antophyllite–chlorite. Les orthoamphiboles sont principalement des antophyllites aciculaires, la gédrite étant réduite à de petites régions allotriomorphiques situées au cœur de plus gros cristaux d’antophyllite. La symbolique utilisée pour les minéraux est la même que celle utilisée dans la référence [12].
Other samples were found to contain the garnet free sub-assemblage (Fig. 3D) cordierite–gedrite–anthophyllite–plagioclase–biotite–quartz ± chlorite or the cordierite free sub-assemblage (Fig. 3A) garnet–orthoamphibole(gedrite)–plagioclase–biotite–quartz ± chlorite.
3 Mineral chemistry
Mineral analyses where performed with the Cameca Microprobe by the Hofman Laboratory of Earth Sciences at Harvard University under 15-kV accelerating potential, 10-nA image current.
Garnet has high values of the almandine and pyrope components. Grossular values are around 10% and spessartite reaches a maximum of 7%. The Fe/ (Fe + Mg) (F/FM) ratio evolves from flat-like profiles and low values (0.81) near the cores to high values (0.88) near the rims. In a few cases, F/FM decreases to a minimum (0.80) at some distance from the core, before sharply increasing towards the rim. The F/FM and Ca–Fe–Mg patterns imply diffusional profiles with remains of prograde growth imprints near the cores (Fig. 4A and C).

Mineral chemistry of the most important phases in the garnet–cordierite–gedrite–anthophyllite assemblage. Analyzed garnets always show a segment of Ca drop at a constant or slightly decreasing F/FM near the core (A), followed by a segment of increasing F/FM near rims in the triangular CaFeMg plot. Cordierite next to garnet shows the opposite tendencies (B), showing the importance of late FeMg-1 exchange between both minerals during cooling. In (C), a profile along a composite orthoamphibole grain shows the abrupt step in composition between the Al-rich gedritic core and the Al-poor anthophyllite envelope. The orthoamphiboles in the composite grains do not have appreciable zoning. The composite grains have been detected optically and through Al X-ray mapping (lighter shades of grey indicate increased Al content). 1 and 10 are EMPA analysis points given as references in the inset photograph as well as in the compositional profile.
Fig. 4. Composition des plus importantes phases de la paragenèse grenat–cordiérite–gédrite–antophyllite. Les grenats analysés sont caractérisés dans des diagrammes triangulaires CaFeMg, par une diminution du calcium et par une relation F/FM constante ou légèrement décroissante près du cœur (A), ainsi que par une augmentation de la relation F/FM près des bordures des cristaux. La cordiérite proche du grenat montre des tendances contraires (B), montrant ainsi l’importance de l’échange tardif en FeMg-1 entre les deux minéraux lors du refroidissement. (C) est une coupe d’une orthoamphibole. Elle montre une diminution brusque de l’aluminium entre le cœur gédritique et la couronne antophyllitique. Aucune des orthoamphiboles des grains composites (détectés optiquement et par cartographie de RX) n’a de zonation significative. 1, 10 et 14 sont des points de référence qui permettent relier l’encart photographique, la carte de RX et la coupe d’analyse quantitative par EMPA. Les tons clairs dans la carte de RX indiquent une proportion supérieure d’aluminium.
Cordierite shows small amounts of zoning in F/FM (0.36–0.38). In traverses going from cordierite towards garnet, a slight increase is followed by a sharp decrease in the F/FM relation. Analysis totals are always around 98%, which suggests the presence of water (0.5–0.6%).
Orthoamphiboles (gedrite and anthophyllite) were standardized using the RECAMP algorithm [24]. The lowest Fe3+ limit obtained corresponds to the ‘All Fe2+’ or the ‘Sum Ca = 15’ recalculations. The upper limit is always the recalculation ‘Sum Na = 15’, but this was discarded as it produces null values of Na in the A position and Na values in the octahedral M4 position that are vastly greater than the value of 0.08 stated in the literature [21] for orthoamphiboles coexisting with plagioclase. The ‘Medium Fe3+’ standard was taken in all the cases to be the upper limit. Fig. 4C shows the zoning profile pattern of a composite gedrite–anthophyllite grain.
Plagioclase compositions range between values of An30 (cores) and An39 (rims). Analyses of plagioclase inclusions located at different depths in garnets or orthoamphiboles also show a tendency toward variation in anorthite content, the plagioclase inclusions located near the rim of the minerals being always more anorthite rich than the inclusions located near the cores. Only in the cordierite-free assemblage is the zoning pattern in plagioclase detected as being the reverse, from An48 (cores) to An35 (rims).
Biotite has an F/FM ∼ 0.53, with a TiO2 content from 0.06 to 0.12. AlVI and Ti both show a slight inverse correlation with an M/MF ratio, and AlVI also shows an inverse correlation with Ti. Opaque phases are ilmenite, which contains a very high concentration of the FeTiO3 (ilmenite) component; the MnTiO3 pyrophanite component is always very low (around 0.008%).
4 Geothermobarometric constraints and pseudosection modelling
4.1 Geothermobarometry
Prograde and retrograde P–T paths followed by the Osor complex during the Variscan [20] are indicated in Fig. 5A and B. The evolution was constrained using classical thermobarometry and optimal multiequilibrium average P–T methods [16] as well as the pseudosection approach applied to semipelites and pelites [18]. The peak P–T was found to be around 5 ± 1 kbar and 640 ± 40 °C using a combination of multiequilibrium AvgPT methods [16] and classic garnet–muscovite/biotite–aluminosilicate–quartz (GMAQ and GMBAQ) thermobarometers. If dehydration melting of primary muscovite has taken place, this can increase peak T to around 680 °C. A P–T path with a first segment of isobaric cooling from the peak to around 620 °C followed by progressively decompressional cooling was found in these conditions. The retrograde closure conditions of around 560 °C and 3 kbar were obtained by applying AvgPT methods, garnet–biotite (GB) conventional thermometry, garnet–muscovite–aluminosilicate–quartz (GMAQ) and garnet–plagioclase–muscovite ± biotite/aluminosilicate–quartz (GPAQ, GPBQ, GPMQ and GPMBQ) conventional barometry. Garnet–biotite and garnet–cordierite geothermometry in the low-Ca amphibolites gave similar results.
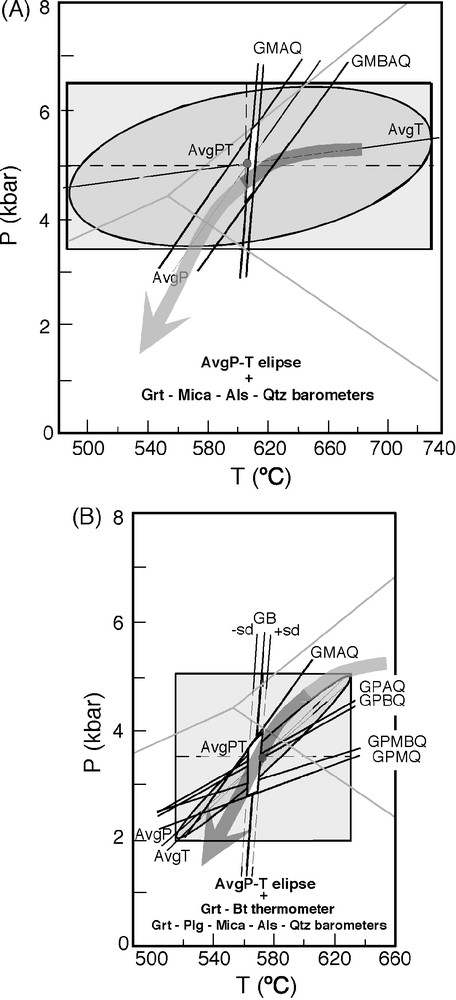
Geothermobarometric constraints in the evolution of the Osor metamorphic complex, obtained from enclosing metapelites and semipelites [19]. (A) Peak P–T conditions. (B) Retrograde closure conditions.
Fig. 5. Géothermobarométrie dans le complexe métamorphique d’Osor, obtenue à partir de l’étude des métapélites et semipélites encaissantes [19]. (A) conditions P–T du pic métamorphique. (B) Conditions de fermeture rétrograde.
4.2 Pseudosection modelling
MnNCFMASH (MnO–Na2O–CaO–FeO–MgO–Al2O3–SiO2–H2O) P–T pseudosections were generated using THERMOCALC [18] and the DS5 thermodynamic dataset [8] on the P–T window of 420–700 °C and 0–6 kbar. The mineral phases taken into consideration are: orthoamphiboles anthophyllite (Ath) and gedrite (Ged), cordierite (Crd), chlorite (Chl), staurolite (St), garnet (Grt), plagioclase (Plg), quartz (Qtz), and water (H2O). Quartz and water are considered in-excess phases. Biotite is considered a non-reactive phase and is not included in the models because it is the only phase with appreciable amounts of K. Its modelling would require modelling K as an ionic species in fluid, and probably in the orthoamphibole A site; these models are still not well constrained.
4.2.1 Formulae and mixing models
The solid solutions for the mineral phases used follow those already used by different authors, except for orthoamphiboles, in which Na-bearing end-members were also taken into consideration [20]. Although it is a simplification, given that metamorphic peak conditions are known to be well above the orthoamphibole solvus [23], a scheme considering two subsolvus phases, anthophyllite and gedrite, was used for the entire P–T range. For both orthoamphiboles, we used the ‘simple ideal mixing on sites’ scheme. The DQF corrections on the end-members nant (Na-antophyllite), hant (high-Al antophyllite), and lged (low-Al gedrite) were found using an iterative process that led to the invariant points in the NCFMASH petrogenetic grid being forced as much as possible to fit the classic invariants published previously in [25]. The abbreviations for names of phases and/or end-members follow, in general, those in the thermodynamic dataset [8]. Exceptions are indicated by asterisks. The model parameters are:
Ath: anthophyllite (NFMASH). End member formulae: antophyllite (anth): VMg7Si8O22(OH)2, ferro-antophyllite (fanth): VFe7Si8O22(OH)2, Na-antophyllite (nant*): NaMg7AlSi7O22(OH)2 and high-Al antophyllite (hant*): VMg6Al2Si7O22(OH)2. Thermodynamic data for the end-members nant and hant are not contained in the DS5 database, and so were generated by combining other end-members that are present. Thus: nant = 3/2 anth + 2/2 parg ± 2/2 tr ± 1/2 ged and hant = 1/2 anth + 1/2 ged. In the orthoamphiboles, the model was constructed so that the independent compositional variables (a, fa and na) equal the proportions (p) of the end-members, so: a(atf) = p(anth); fa(atf) = p (fanth) and na(atf) = p(nant) and p(hant) = 1–a–fa–na). Site fractions in terms of the compositional variables are: x(v,A) = 1 − na; x(Na,A) = na; x(Mg,M134) = 1 − fa; x(Fe,M134) = fa; x(Al,M2) = 1/2 − 1/2 a − 1/2 fa − 1/2 na; x(Fe,M2) = fa; x(Mg,M2) = 1/2 + 1/2 a − 1/2 fa + 1/2 na; x(Al,T1) = 1/4 − 1/4 a − 1/4 fa; x(Si,T1) = 3/4 + 1/4 a + 1/4 fa. The ideal activities for the phase components are expressed as: anth = x(v,A) x(Mg,M134)5 x(Mg,M2)2 x(Si,T1)2; fanth = x(v,A) x(Fe,M134)5 x(Fe,M2)2 x(Si,T1)2; nant = 3.079 x(Na,A) x(Mg,M134)5 x(Mg,M2)2 x(Al,T1)(1/2) x(Si,T1)(3/2) and hant = 12.317 x(v,A) x(Mg,M134)5 x(Mg,M2) x(Al,M2) x(Al,T1)(1/2) x(Si,T1)(3/2). DQF increments were taken into account in nant = 28.00 and hant = 20.00.
Ged: gedrite (NFMASH). End-member formulae: gedrite (ged): VMg5Al4Si6O22(OH)2, ferro-gedrite (fged*): VFe5Al4Si6O22(OH)2, Na-gedrite (nged*): NaMg6Al3Si6O22(OH)2, and low-Al gedrite (lged*): VMg6Al2Si7O22(OH)2. Thermodynamic data for the end-members fged, nged and lged are not contained in the DS5 database, and were generated by combining other end-members. Thus: fged = 5/7 fanth + 7/7ged ± 5/7 anth; nged = 1 anth + 1 parg − 1 tr and lged = 1/2 anth + 1/2 ged. In the orthoamphiboles, the model is constructed so that the independent compositional variables equal the proportions of the end-members, so: g(ged) = p(ged); fg(ged) = p(fged) and ng(ged) = p(nged) and p(lged) = 1 − g − fg − ng). Site fractions in terms of the compositional variables are: x(v,A) = 1 − ng; x(Na,A) = ng; x(Mg,M134) = 1 − fg; x(Fe,M134) = fg; x(Al,M2) = 1/2 + 1/2 g + 1/2 fg; x(Mg,M2) = 1/2 − 1/2 g − 1/2 fg; x(Al,T1) = 1/4 + 1/4 g + 1/4 fg + 1/4 ng; x(Si,T1) = 3/4 − 1/4 g − 1/4 fg − 1/4 ng. The ideal activities for the phase components are expressed as: ged = 4 x(v,A) x(Mg,M134)5 x(Al,M2)2 x(Al,T1) x(Si,T1); fged = 4 x(v,A) x(Fe,M134)5 x(Al,M2)2 x(Al,T1) x(Si,T1); nged = 16 x(Na,A) x(Mg,M134)5 x(Al,M2) x(Mg,M2) x(Al,T1) x(Si,T1), and lged = 12.317 x(v,A) x(Mg,M134)5 x(Al,M2) x(Mg,M2) x(Al,T1)(1/2) x(Si,T1)(3/2). DQF increments, were taken into account in lged = 20.00
Crd: cordierite (MnFMASH). Follows an ideal mixing on sites model (Roger Powell, pers. comm.). End-member formulae: cordierite (crd): Mg2(Al)4Si5O18, ferro-cordierite (fcrd): Fe2(Al)4Si5O18, manganese–cordierite (mncrd): Mn2(Al)4Si5O18 and hydrous cordierite (hcrd): Mg2(Al)4Si5O18·H2O. The compositional variables considered in cordierite are: x(cd) = Fe/(Fe + Mg); m(cd) = Mn/(Fe + Mg + Mn) and h(cd) = H2O. The proportions of the end-members are expressed as: crd = 1 − m − h + (–x) (1 − m); fcrd = x (1 − m); mncrd = m and hcrd = h. The site fractions in terms of the compositional variables are: x(Mg) = (1 − x) (1 − m); x(Fe) = x (1 − m); x(Mn) = m; h = h and noth = 1 − h. The ideal activities for the phase components are expressed as: crd = x(Mg)2 noth; fcrd = x(Fe)2 noth; mncrd = x(Mn)2 noth and hcrd = x(Mg)2 h.
Plg: plagioclase (NCAS). This phase was modelled with an ideal binary albite–anorthite solution model, but using a simple DQF correction in the anorthite end-member [6]. End-member formulae: albite (ab): Na2[AlSi3]O8, anortite (an): Ca2[AlSi3]O8. The compositional variable considered in plagioclase is: ca(C1pl) = an (proportion of anortite). The proportions of the end-members are expressed as: ab = 1 − ca; an = ca. The site fractions in terms of the compositional variables are: x(Na) = 1 − ca and x(Ca) = ca. The ideal activities for the phase components are expressed as: ab = x(Na); an = x(Ca). DQF increments were taken into account as: an = 6.01 − 0.004 T. For the rest of the minerals, the non-ideal contributions were considered using the symmetric formalism method outlined in [7,15,17].
Chl: chlorite (MnFMASH). The model uses an extension to MnFMASH (Roger Powell pers.com.) of the MASH a-X relations for this mineral given by [5]. End-member formulae: clinochlore (clin): Mg4[MgAl]Si2[AlSi]O10(OH)8, daphnite (daph): Fe4[FeAl]Si2[AlSi]O10(OH)8, amesite (ames): Mg4[AlAl]Si2[AlAl]O10(OH)8 and Mn-bearing chlorite (mnchl): Mn4[MnAl]Si2[AlSi]O10(OH)8. The compositional variables considered in chlorite are: x(chl) = Fe/(Fe + Mg); y(chl) = (1 − (XAl,M1))/2, assuming x(Al,M4) = 1 and m(chl) = x(Mn,M23) = x(Mn,M1). The proportions of the end-members are expressed as: clin = 2 − 2y − m + (−2/5 x) (3 − y − m); daph = 2/5 x (3 − y − m); ames = –1 + 2y and mnchl = m. The site fractions in terms of the compositional variables are: x(Fe,M23) = x (1 − m); x(Mg,M23) = (1 − x) (1 − m); x(Mn,M23) = m; x(Al,M1) = –1 + 2y; x(Fe,M1) = x (2 − 2y − m); x(Mg,M1) = (1 − x) (2 − 2y − m); x(Mn,M1) = m; x(Al,T2) = y and x(Si,T2) = 1 − y. The ideal activities for the phase components are expressed as: clin = 4 x(Mg,M23)4 x(Mg,M1) x(Al,T2) x(Si,T2); daph = 4 x(Fe,M23)4 x(Fe,M1) x(Al,T2) x(Si,T2); ames = x(Mg,M23)4 x(Al,M1) x(Al,T2)2 and mnchl = 4 x(Mn,M23)4 x(Mn,M1) x(Al,T2) x(Si,T2). The non-ideality Margules parameters, by symmetric formalism, are: W(clin,daph) = 2.5; W(clin,ames) = 18.0, and W(daph,ames) = 13.5.
St: staurolite (MnFMASH). It is modelled using the non-ideal model given in [28]. The effect of possible Zn and Ti substitution is considered by reducing the activity of the Fe-staurolite end-member so it is always 0.754 × x4, where x = Fe/ (Fe + Mg) in staurolite. End-member formulae: Mg-staurolite (mst): Mg4(Al)18Si7.5O48(H)4, Fe-staurolite (fst): Fe4(Al)18Si7.5O48(H)4, Mn-staurolite (mnst): Mn4(Al)18Si7.5O48(H)4. The compositional variables considered in staurolite are: x(st) = Fe/(Fe + Mg); m(st) = Mn/(Fe + Mg + Mn). The proportions of the end-members are expressed as: mst = (1 − x) (1 − m); fst = x (1 − m) and mnst = m. The site fractions in terms of the compositional variables are: x(Mg) = (1 − x) (1 − m); x(Fe) = x (1 − m) and x(Mn) = m. The ideal activities for the phase components are expressed as: mst = x(Mg)4; fst = (0.75)4 x(Fe)4 and mnst = x(Mn)4. Non-ideality by symmetric formalism is taken into account by taking W(mst,fst) = –8.0.
Grt: garnet (MnCFMAS). Is considered a quaternary regular solution using the symmetric formalism. Non-ideality is considered only to exist between grossular and pyrope and between almandine and pyrope (Roger Powell, pers. comm.). End-member formulae: grossular (gr): Ca3(Al)2Si3O12, almandine (alm): Fe3(Al)2Si3O12, pyrope (py): Mg3(Al)2Si3O12 and spessartine (spss). The compositional variables considered in garnet are: x(g) = Fe/(Fe + Mg); z(g) = Ca/(Fe + Mg + Ca + Mn) and m(g) = Mn/(Fe + Mg + Ca + Mn). The proportions of the end-members are expressed as: gr = z; alm = (1 − z − m) x; py = (1 − z − m) (1 − x) and spss = m. The site fractions in terms of the compositional variables are: xFeM1 = (1 − z − m) x; xMgM1 = (1 − z − m) (1 − x); xCaM1 = z and xMnM1 = m. The ideal activities for the phase components are expressed as: gr = xCaM13; alm = xFeM13; py = xMgM13 and spss = xMnM13. Non-ideality by symmetric formalism is taken into account by taking W(gr,py) = 33.0 and W(alm,py) = 2.5.
4.2.2 Pseudosection for the average bulk composition
Initially, the constant bulk composition corresponding to that of the average garnet–cordierite–gedrite–anthophyllite–plagioclase–quartz samples was used. The results are shown in Fig. 6A. If the P–T path obtained from metapelites is superimposed onto this model diagram, the garnet + orthoamphibole assemblage (followed by garnet + gedrite + anthophyllite in orthoamphibole subsolvus conditions) is maintained stable and neither cordierite nor chlorite is generated until P–T reaches unrealistically low values along the P–T path. This observation strongly indicates the probable existence of whole-rock disequilibrium and suggests that equilibration restrictions could apply on much smaller scales than the whole sample during the retrograde evolution. This model prediction is only matched by petrographic observations in samples containing the garnet–gedrite subassemblage (Fig. 6A).
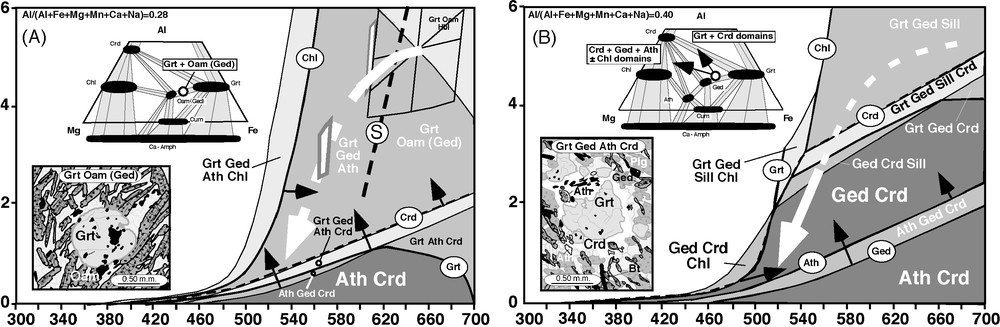
(A) MnNCFMASH P–T pseudosection constructed with THERMOCALC [18] for the average bulk composition of the garnet–cordierite–gedrite–anthophyllite low-Ca amphibolites from Osor. The values of the component oxides are shown as the percentage molar weight: Al2O3, 28.00; CaO, 10.54; MgO, 16.15; FeO, 37.16; Na2O, 7.83; MnO, 0.26. F/FM = 0.7 and Al/(Al + Fe + Mg + Mn + Ca + Na) = 0.28. The superimposition of the P–T path obtained from the Osor metapelites shows the stability of the garnet–orthoamphibole, cordierite-free subassemblage if the bulk composition remains unaltered. The orthoamphibole solvus crest (S) crossing towards lower temperatures, as in [23], enables the stabilization of two discrete orthoamphibole gedrite and antophyllite phases. The lower inset shows the peak garnet-orthoamphibole (gedrite) assemblage as being coherent with the first stages of retrogression. The upper inset shows a qualitative AFM phase diagram with the most important phase fields and the location of the bulk composition modelled. To construct the pseudosection in (B), the bulk composition was modified by increasing the Al/(Al + Fe + Mg + Mn + Ca + Na) ratio to a value of 0.40 and decreasing the F/FM ratio to 0.5. The movement of the gedrite/anthophyllite, cordierite and garnet stability fields (see labels enclosed in ovals as well as associated black arrows) up-P and of the chlorite bearing fields up-T accounts for the textural observations (lower inset) and the phase assemblage evolution (upper inset) during the main part of the retrograde evolution. Symbols for the mineral phases are as in [12].
Fig. 6 (A) Pseudosection MnNCFMASH construite avec le logiciel THERMOCALC [18] par la composition chimique moyenne des amphibolites pauvres en calcium d’Osor, avec la paragenèse grenat–cordiérite–gédrite–antophyllite. Les valeurs des oxydes composants, en pourcentage molaire en poids, sont : Al2O3, 28,00 ; CaO, 10,54 ; MgO, 16,15 ; FeO, 37,16 ; Na2O, 7.83 ; MnO, 0,26. F/FM = 0,7 et Al/(Al + Fe + Mg + Mn + Ca + Na) = 0,28. La superposition de la trajectoire obtenue avec les métapélites d’Osor dans la pseudosection montre la stabilité de la paragenèse grenat–orthoamphibole si on ne modifie pas la composition chimique de la roche. Dès que la trajectoire P–T croise le solvus des orthoamphiboles (S), comme en [23], vers les T décroissantes, deux orthoamphiboles (antophyllite et gédrite) sont possibles. Le dessin inférieur montre la paragenèse la plus probable du pic et des premiers étages de la décompression, avec du grenat–orthoamphibole (gédrite). Le dessin supérieur montre un diagramme qualitatif AFM avec les paragenèses les plus importantes et la position de la composition chimique globale. Pour construire la pseudosection (B), la composition chimique globale a été modifiée de telle façon que le rapport Al/(Al + Fe + Mg + Mn + Ca + Na) s’élève jusqu’à 0,40 et que le rapport F/FM diminue jusqu’à 0,5. Les mouvements des champs de stabilité des orthoamphiboles, de la cordiérite et du grenat (voir étiquettes dans des ovales) vers les plus hautes valeurs de P et des champs de stabilité de la chlorite vers les plus hautes T sont cohérents avec les observations texturales (encart supérieur) et avec l’évolution des paragenèses (schématisée par le dessin AFM) pendant l’essentiel de l’évolution rétrograde. Les symboles utilisés pour les phases minérales sont les mêmes qu’en [12].
4.2.3 Pseudosection restricted to aluminous microdomains
Otherwise, if a P–T pseudosection for the same bulk composition but with an increased Al/(Al + Fe + Mg + Mn + Ca + Na) ratio is drawn (Fig. 6B), then the P–T path effectively intersects the garnet-out and cordierite-in boundaries. It also approaches the gedrite-out boundary and the cordierite–gedrite–anthophyllite, gedrite–cordierite–chlorite and anthophyllite–cordierite fields. An intersection between the chlorite-in and anthophyllite-in boundaries will develop a chlorite–gedrite–anthophyllite–cordierite field (see trends marked with black arrows in Fig. 6A and B) when the Al/(Al + Fe + Mg + Mn + Ca + Na) ratio is increased further and the Fe/Fe + Mg of the bulk composition is decreased moderately.
5 Discussion and conclusions
The above-described trends in effective bulk composition are interpreted as occurring while the less aluminous garnet and gedrite phases are being progressively segregated from the reaction domains and substituted with a more aluminous and magnesian effective system dominated by cordierite. The black arrows in the AFM diagram inserts in Fig. 6B depict the qualitative evolution of the two segregated effective bulk domains. Note that, once relict garnet is overgrown with cordierite moats, the effective system in these domains becomes unreactive, except for iron–magnesium exchange (see Fig. 4B). The garnet-absent cordierite–gedrite–anthophyllite–cordierite ± chlorite domains can continue to evolve texturally by net transfer reactions, giving cordierite and chlorite, and destroying orthoamphibole (gedrite). Given that garnets show different stages of resorption, it follows that there must have been an episode characterized by the balanced coexistence of garnet–gedrite–anthophyllite–cordierite, in which net transfer reactions were also possible, prior to the segregation of the garnet–cordierite and cordierite–gedrite–anthophyllite domains. Mineral modes can change in the garnet-absent subdomains, involving cordierite growth, because net transfer reactions that do not necessarily involve garnet-phase components can also be written between orthoamphibole and cordierite phase components. At the same time that cordierite is produced, gedrite is destroyed, and anthophyllite grows. This prediction agrees with the observed allotriomorphic gedritic cores, surrounded by anthophyllite rims. The exact P–T conditions in which the subsystem garnet–cordierite became independent and closed from its surroundings is extremely difficult to determine. The persistence of samples containing the garnet–gedrite sub-assemblage (Fig. 3A) without any cordierite, which have probably remained metastable during retrogression, is perhaps due to the non-availability of fluids in restricted rock domains. This would also be coherent with the inverse zoning pattern found in plagioclase in this cordierite-absent assemblage. The enrichment in albite towards the rim in this case will be relict and due to plagioclase resorption during the prograde increase in P–T. The study shows how a set of samples of low-Ca amphibolites found in the Osor complex, in the Guilleries massif (NE Iberia), can be used to confirm the Late-Variscan P–T evolution, which was constrained previously using metapelite equilibria [19]. Again, a P–T path of cooling and decompression is confirmed during the final stages of Variscan deformation (sin-D3 to post D3). At the same time, it shows the importance of considering the bulk compositional effects on smaller scales than the thin section, as suggested earlier by other authors [26], when attempting to model the textural evolution observed on these scales.
Acknowledgements
The authors gratefully acknowledge support from Research Project CGL20065–09509/BTE. J. Reche also acknowledges help from R. Powell during the THERMOCALC course in Bellaterra, (Barcelona), from J. Schumacher during a stay in Kiel (Germany) and from F.S. Spear during a stay at Rensselaer Polytechnic Institute, Troy, NY (USA). We also acknowledge the comments made by J. Touret and by an anonymous referee, which helped us to improve our manuscript.


