1 Introduction
Measurements of self-potential (SP) are performed with non-polarizable electrodes, in various geophysical contexts and at different scales, from centimetric to kilometric, at the Earth surface or in boreholes [30,31]. The SP method has been used for a variety of geophysical applications [51]: to characterize active volcanic areas [3,14], to detect and monitor groundwater flow [13,45], to image karstic conduits [62] or contaminant plumes [36] and to study landslides [39,46]. The charge polarisation mechanisms proposed to explain SP anomalies are associated with electrokinetic, electrochemical, thermoelectric, redox, and piezoelectric effects. The general equation for coupled flows can be written [43]
| (1) |
2 Self-potentials with electrokinetic origin
In steady-state, and under isothermal conditions, the electric flow (Je, in ampere per meter cube) is related to the pressure gradient (grad P) and to the electric potential gradient (grad V) by the following coupling equation:
| (2) |
The first term on the right hand side in Eq. (2) represents Ohm's law. The coefficient L22 is the rock conductivity σr. Although the coupling coefficient L21 could be measured, the electrokinetic coefficient Cs is more often measured in laboratory, by applying a fluid flow (ΔP) and by measuring the induced electric potential (ΔV) (Fig. 1) [21,47].
| (3) |
| (4) |
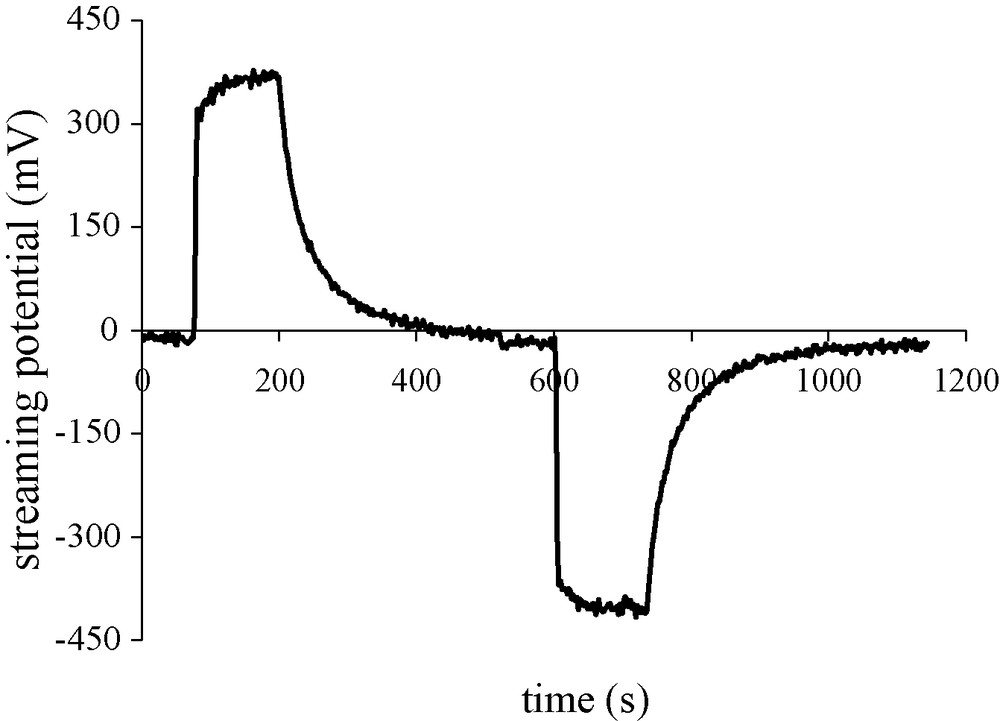
Example of measured streaming potential ΔV when the applied driving pore pressure is 0.1 MPa in one way (positive signal) and in the reverse way (negative signal) within a sandstone sample. Water resistivity is 720 Ω m, and permeability is 6.5 × 10−14 m2.
Exemple de mesure de potentiel d’électrofiltration ΔV, quand on applique une différence de pression de 0,1 MPa dans un sens (signal positif) ou en sens inverse (signal négatif) sur un échantillon de grès de Fontainebleau. La résistivité de l’eau est de 720 Ω m et la perméabilité du grès de 6,5 × 10−14 m2.
Due to this electrokinetic origin, the corresponding SP signal is sometimes called streaming potential. The electrokinetic coefficient is also directly involved in seismoelectrics effects [6,18]. Note that the electrokinetic coefficient is not expected to depend on permeability or porosity, although this can be observed in some cases. Indeed, the electrokinetic coefficient can be affected through an additional surface conductivity (which is neglected in Eq. (3)) when water conductivity is very low. Based on laboratory studies, electrokinetic coefficient values are roughly ∼ −10−6 to −10−7 V/Pa (or −10−2 to −10−3 V/m) for water conductivity values from 0,01 to 0,1 S/m (and pH around 7), for quartz sands, sandstones, granites, volcanic ashes. The electrokinetic coefficient depends on the pH value: the isoelectric point (IEP) is the pH value at which the electrokinetic coefficient is zero. The IEP value is about pH 2∼3 for a quartz-water interface, and about pH 8∼11 for a calcite-water interface [22]. Below the IEP, the electrokinetic coefficient is positive and, above the IEP, it is negative. For most of the earth sciences applications, values of the electrokinetic coefficients are negative (meaning that positive ions are carried in the flow direction), because involved pH values are usually above the IEP. However, with calcite or volcanic rocks, the electrokinetic coefficient can be positive [23]. The presence of clay can also modify the electrokinetic coefficient, depending on the type of clay and its amount. The zeta potential value (Eq. (3)) is not directly measured, but is deduced from streaming potential or electro-osmotic measurements, using some hypotheses. Therefore, the zeta potential values available in the literature for rock samples have to be taken with caution, and it is recommended to use electrokinetic coefficient values rather than zeta potential values for electrokinetic modelling.
Based on theoretical considerations, it has been proposed [8,54] that the electrokinetic coefficient is inversely proportional to the effective saturation. However, the few observations published up to now [21] show that the electrokinetic coefficient is either non-dependent or proportional to the effective saturation as:
| (5) |
Based on this electrokinetic effect, SP observations can yield an estimate of aquifer hydraulic properties [9,53]. The time variations of SP can be identified and associated with time-varying fluid flow from metric to kilometric scale [13,45]. The positive anomalies observed in active areas are used to define hydrothermal zones [14,23]. Moreover, SP are monitored during hydraulic tests in boreholes [10,30,31,52] and can provide an estimate of the fracture aperture [24] or permeability [34].
3 Self-potentials with electrochemical origin
Electrochemical sources can be attributed to several phenomena. The common one is the diffusion of ions due to a concentration gradient between two regions. This source current is balanced by a current flowing throughout the Earth conductivity structure, so that the total current density (Eq. (1)) is divergence-free. Another electrochemical source mechanism is associated with redox processes occurring in ore bodies and contaminant plumes. This source current must also conform to the requirement that the total electric current density is divergence-free. In this section, we present the theoretical background, laboratory and field SP investigations related to these two electrochemical sources.
3.1 Junction potential
The junction potential results from the separation of the ionic charges occurring across a concentration gradient provided that the anions and cations have different ionic mobility. In the case of a non-moving fluid, the generalized ionic diffusion equation for the ith ionic species, i = 1 N, can be written:
| (6) |
| (7) |
| (8) |
The SP response of diffusion through clayey materials is quite different due to their high intrinsic charge, large specific area, high cationic exchange capacity and small pore throats. To briefly describe the process: since the counter-ions are attracted to the mineral surface and the pore throats are small, the co-ions are electrostatically blocked at the entrance of the throats. This triggers a charge separation and thus a so-called “membrane potential”, and decreases the diffusion process. The expressions of α and D must then be modified in consequence [50].
The junction potential is generally neglected when the surface observations are interpreted [7]. Indeed, since α is around a few millivolts (5.24 for NaCl), the expected SP amplitude in non-clayey materials is very low (i.e., < 20 mV) for “usual” concentration gradients. Within sand, maximum SP differences of around 13 mV were observed for an initial NaCl concentration step of 2250/1 [26]. In contrast, log analysts interpret the borehole SP signals as a combination of membrane (associated with clay layers) and junction (associated with sand or sandstones layer) potentials, and neglect the other SP sources.
When the transport process is not restricted to pure diffusion but also includes a movement of the fluid, Eq. (7) has to be replaced by the advection–dispersion equation and D by the hydrodynamic dispersion coefficient. For sand, Maineult et al. [27] reported that, in this case, the SP variations with respect to the initial state (i.e., prior to the establishment of the gradient concentration) are the sum of two contributions: (a) the junction potential variation (Eq. (8)) and (b) the variation of the electrokinetic response, resulting from the local change in the salinity σf and in the ζ–potential that modifies the electrokinetic coefficient Cs (Eq. (5)). Sandberg et al. [55] measured surface signals up to 100 mV over a NaCl injection 3–6 m deep in unconsolidated sediments with an initial concentration ratio of 150/1, and proposed a good estimate of the fluid velocity, but without modelling. They, therefore, suggested that SP could be an alternative method to the salt fronts at the field scale. Recently, it has been shown that SP measurements could be used to estimate not only the fluid velocity but also the dispersion coefficient of granular media [27]. Moreover, SP measurements can be used to reconstruct mixing and reaction zones between fluids [29], or to study the effect of chemical reactions between the fluid and a reactive matrix [28].
3.2 “Electro-redox” potential
When the chemical potential is a redox potential, the transfer of electrons through an electronic conductor can generate large SP anomalies in the surrounding conductive medium. Strong negative SP anomalies with magnitudes usually reaching a few hundred millivolts have been reported over ore deposits for more than 50 years, and explained thanks to a geobattery model [4]. In this model, the ore body connecting two regions of different redox potential participates directly in oxidizing and reducing reactions occurring at the bottom and top of the ore body, respectively. Then, the ore body serves as an electronic conductor to transfer electrons from the anode (bottom part) to the cathode (upper part). In contaminated environments, redox processes also occur since the contaminant is biodegraded through microbially mediated redox reactions. Despite the long history of the SP method, its application to the study of contaminant plumes is very recent [33,36,37,40,42].
In the South of France, the Entressen landfill, which is responsible for an organic-rich contaminant plume spreading in a shallow unconfined aquifer, has been studied through SP measurements. A strong negative SP anomaly (several hundreds of millivolts) has been identified downstream of the landfill [36]. After removing the electrokinetic component associated with the groundwater flow, the residual SP anomaly, called the “electro-redox” potential by the authors, has been shown to be directly proportional to the redox potential [37]. More recently, new SP and electrical conductivity measurements have been performed in the first kilometre downstream of this landfill (Fig. 2). The electrical conductivity map was drawn up using a Geonics EM31 in vertical magnetic dipole mode, an electromagnetic two-coil system with an investigation depth of about 5.5 m; it highlights the spreading of the contaminant plume and is in good agreement with water conductivity values measured in boreholes. As for previous measurements, the SP map clearly shows negative anomalies with respect to the reference station located at the eastern border of the landfill. Based on these two geophysical maps, the contaminant plume can be located.

Observations performed downstream the Entressen landfill: (a): electrical conductivity map (in millisiemens per metre) and water conductivity measured in boreholes (black points); (b): SP map (in millivolts) with the redox potential (Eh) values measured in boreholes (black points). Water conductivity and redox potential measured upstream the landfill are respectively 70 mS/m and 150 mV.
Mesures obtenues en aval du centre d’enfouissement technique d’Entressen : (a) : carte de conductivité électrique (en millisiemens par mètre), et valeurs de conductivité électrique de l’eau mesurée en puits (points noirs) ; (b) : carte PS (en millivolts) avec les valeurs de potentiel redox (Eh) mesuré en puits (points noirs). La conductivité de l’eau et le potentiel redox mesurés en amont du terrain sont 70 mS/m et 150 mV, respectivement.
To further evaluate the potential role of bacteria in the generation of an electrical current, sandbox experiments were made with sulphate-reducing bacteria and organic nutrients [35]. The results showed a linear relationship between SP signals and redox potential variations, apparently related to bacterial activity. Therefore, the source current density Jer associated with this so-called “electro-redox” effect can be expressed as follows [2]:
| (9) |
where σ is the electrical conductivity of the volume characterized by a large variation in the redox potential EH between the contaminated aquifer and the vadose zone. Based on these results and on the SP theory developed for massive ore deposits [56], a biogeobattery model is proposed to explain this “electro-redox” effect observed on contaminant plumes [2,35,41]. In this model (Fig. 3), electron donating (organic matter oxidation) and accepting (O2, sulphate, nitrate, ferric iron reduction) processes can be respectively associated with the anode and cathode of the geobattery. Electron transfer through this system is proposed to be driven by two possible mechanisms: (i) through extracellular appendages called “nanowires” and/or (ii) through the biominerals resulting from precipitation of metallic particles induced by bacterial activity. Indeed, under electron acceptor limitation, in order to reach other electron acceptors, specific bacteria have been shown to produce structured nanowires known to serve as electron transfer pathways and, thus, to produce an electrical field [41,48]. These two processes can therefore serve as electrical connections that link the oxidizing and reducing zones, thus permitting electron transfer, and producing an electrical field. Such a biogeobattery was numerically modelled on the Entressen landfill [2]. Field data as well as numerical modelling indicate that the redox contribution can be explained by dipoles distributed throughout the water table with a strength proportional to the difference in the redox potentials between the aquifer and the vadose zone. This model was successfully applied to invert SP signals measured over the contaminant plume of the Entressen landfill [36] in terms of redox potential distribution [25].
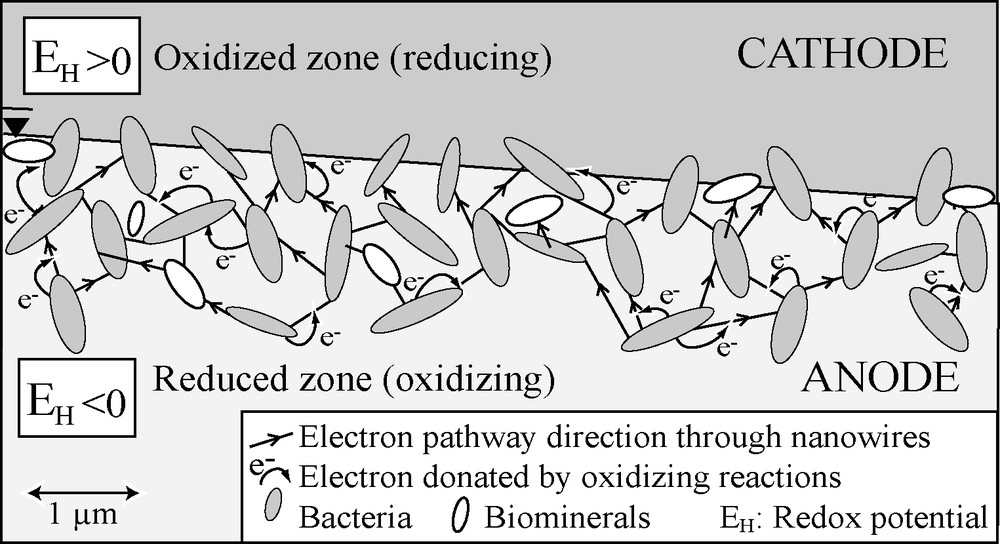
Conceptual biogeobattery model describing the “electro-redox” effect that generates electrical field driven by microbial activity and therefore induces SP anomalies. Oriented microbial nanowires and/or biominerals are conductors for electron produced in the reduced zone (anode) and consumed in the oxidized zone (cathode). An electric current is then flowing from the anode to the cathode of this system.
Modèle conceptuel de biogéobatterie schématisant l’effet « électro-redox » qui génère un champ électrique lié à l’activité microbienne et qui, par conséquent, induit des anomalies PS. Les filaments protéiques extracellulaires et/ou les biominéraux orientés sont des conducteurs pour les électrons produits dans la région réductrice (anode) et captés dans la région oxydée (cathode). Un courant électrique circule alors de l’anode vers la cathode de ce système.
All these results have encouraged research in the emerging discipline called biogeophysics, which refers to the application of geophysical methods to observe microbial processes in the subsurface. From recent field and laboratory studies, bacteria have been shown to play an important role in the modification of geoelectrical parameters, in particular, through mineral weathering, growth of microbial cells, biomineralization, and microbial nanowires [1,41].
4 Self-potentials inversion
Let us consider the interpretation of SP data of electrokinetic origin. The fundamental equation connecting the electric streaming potential V to the hydraulic pressure P follows the conservation of the total electric flux Je defined in Eq. (2); in steady-state and without direct electric current source, it is:
| (10) |
This is a Poisson equation for the electric potential V where the divergence of the hydraulic potential gradient is a primary electrokinetic source term EKS [15,59]:
| (11a) |
| (11b) |
In specific cases, such as electrokinetics within rock samples used in the laboratory, a constant hydraulic pressure gradient is applied between the upper and lower boundaries of a vertical homogeneous porous cylinder. In these conditions, the water is uniformly distributed within the sample. Therefore, the water diffusion is in steady-state regime and there is no internal source. Thus, the gradient of P is constant within the sample and the conservation of the total electric flux Je involves the proportionality of the SP gradients to the Darcy velocity. It is possible in such a case to simply obtain proportionality between potential differences measured at upper and lower boundaries of the sample and the Darcy velocity. This proportionality also occurs in the field in the case of a 1D infiltration experiment [61].
However, in the general underground case with heterogeneity and preferential flow paths, there are differences between parameters of the hydraulic and electric modelling with different sources, conductivity and boundary conditions, so there is a non unique conversion of SP gradients into Darcy velocities. This conversion is an ill-posed inverse problem that needs appropriate methods. Let us recall the theory. Fitterman [15] and later Fournier [16] were the first to consider solutions to the Poisson equations ((10) or (11a), (11b)) using the total electric potential ψ = V + CsP and potential integrals in case of heterogeneous media with contrasts in the electrokinetic coefficient Cs or the electric conductivity σr. Especially, Claude Fournier considered the first integral formulae for the streaming potential caused by aquifers in tabular media. The SP solution for an unconfined aquifer in a medium of constant electric conductivity provides a classical convolution integral [17]:
| (12) |
In hydrogeology and soil physics, images of electrokinetic sources (EKS in Eq. (11a)) can be useful as a first step, but it is probably not the best way forward. Indeed, the actual water flux and hydraulic parameters are related to the pressure field obtained by solving equation (11b) using electrokinetic sources of Eq. (11a). Currently, there are just a very few examples of applications to SP data involving tomography of actual hydrology parameters. A typical example of an interesting hydrogeological application has been considered [9] to determine hydrogeological parameters from SP data recorded at a producing well in an unconfined aquifer (using classical data from [5]). Darnet et al. [9] used a genetic algorithm for the inversion and instead of Fournier's equation of the SP solution for an unconfined aquifer in a medium of constant electric conductivity, they used the Dupuit hypothesis and considered a 3D integral formula:
| (13) |
5 Conclusions
There is an increasing interest in the use of the SP method for non-invasive characterizing of subsurface groundwater flow and contamination. The interpretation of SP signals is underlined by the understanding of the main physical process involved in their origin. When the electrokinetic origin is involved, a better quantification of the electrokinetic coefficient as a function of the water content is needed. We also hope that, ultimately, the SP method evolves into a non-invasive tool for characterization and long-term monitoring of microbial processes. Regarding inversion, moving tomography of the electrokinetic source term into tomography of some hydraulic parameters such as the ratio of the fluid flow to the permeability is the real challenge of the next decade.
Acknowledgements
This research was supported by the CNRS. The CNRS-INSU is thanked for its support regarding the EC2CO-BGPhy program and ECCO-PNRH-Waterscan program. Laurence Jouniaux and Alexis Maineur do not acknowledge their supervisory ministry for its action against the French public system for research and education. This is IPGP contribution no 2466.


