1 Introduction
Over the past 25 years, many studies have been published on biogeochemical nutrients cycles (C, N, P) in aquatic ecosystems. These studies emphasize the importance of the sediment compartment to particulate material and seawater interactions (Oelkers et al., 2012) and to nutrient budgets (Boström et al., 1988; Sundby et al., 1992). Indeed, lacustrine, lagoonal or estuarine sediment compartments receive organic matter coming from the watershed, allowing sediment to act as a sink for nutrients. According to the environmental dynamic pressures (waves, flood), the water column's oxygenation (Dedieu et al., 2007), and the biogeochemistry of the sediment interface as pH, redox conditions, or bioturbation (Malcom and Sivyer, 1997), solutes can be subsequently released into the water column, and sediment may become a source of nutrients.
The measurements of nutrients profiles remain difficult because the sediment interface is very fluid (containing more than 75% to 90% of water, depending on the considered environment). Even though these measurements are very difficult, study of the sediment compartment is crucial to evaluating aquatic ecosystem eutrophication budgets.
The literature on porewater sampling methods shows two main approaches:
- • a laboratory one, which involves sediment coring, followed by vertical sectioning. Then porewater is extracted by centrifugation under a nitrogen atmosphere (Brinkman et al., 1982; Jahnke, 1988). These methods, requiring physical pressure onto sediments, overestimate the nutrient concentrations by desorbing the ions fixed onto the particles;
- • an in-situ approach which uses devices introduced in sediment, which after an equilibration time allows sampling of porewater. The dialyser technique (Hesslein, 1976), DET (Diffusive equilibration in thin films, Davison et al., 2000) or DGT (diffusive gradients in thin films, Zhang and Davison, 1995) are the most common methods for sampling porewater at the sediment–water interface.
The advantage of dialyser methods is that they sample the interstitial water according to a continuous gradient between sediment and the water column, over 30-cm depth. Otherwise, it allows one to obtain nutrient concentration gradients useful for nutrient fluxes determination at the sediment–water interface. The necessary equilibration time of several weeks, which appeared firstly as a limit, is in fact an advantage, because it can include several tidal cycles, hydrodynamical pressure, natural conditions considering estuaries’ environment (Sakho et al., 2013).
It is useful to practice an in situ equilibration experiment because the porewater's physicochemical composition fluctuates over the time, with a time step ranging from the hour to the month. These variations can be explained by environmental conditions as bio-irrigation, bioturbation, deposit erosion cycles, water salinity. Otherwise, the use of a numerical diffusion model is necessary to fit experimental data sets and to estimate nutrients profiles. Nutrient exchanges modeling equations have been used to calculate the time at which nutrient concentrations are the same inside and outside the dialysis-sampler chambers (Webster and Teasdale, 1998).
Our work consisted in the construction and the deployment of dialysers into estuarine sediments of a temperate zone, the Seine Estuary (France, Bally et al., 2004), and of a tropical zone, the Somone Estuary (Senegal, Sakho, 2011; Sakho et al., 2011). The in situ experiments have been combined with one-dimensional numerical modeling. It appeared that the initial model has to be improved considering physical parameters such as convection and adsorption to get a better equilibration time (Bally et al., 2005). Then, the aim of this study is to improve the physical diffusion model, calibrate it using real data sets of the two studied estuaries under different conditions.
2 Material and methods
2.1 Study sites
2.1.1 The Seine estuary (Normandy, France)
The Seine estuary, recently studied from a hydrodynamic point of view (Bonneton et al., 2012), lies within a temperate climatic zone, is a macrotidal estuary with high turbidity linked to tidal and river flow conditions. Its catchment's area is 78,000 km2, in which 40% of the French population and economic activity are situated. Since the 19th century, the Seine estuary has suffered from human modifications, leading to a decrease of 80% of intertidal areas. These intertidal lateral mudflats are preferential sites for the accumulation and/or remobilization of organic material (OM), and thus serve as traps and/or sources of nutrients following the degradation of the OM (Bally et al., 2004). Thus, the mineralization of OM, in oxic or anoxic conditions, results in the release of nutrients, which are found in the dissolved phase in interstitial water (Bally et al., 2005).
2.1.2 The Somone estuarine mangrove (Senegal)
The Somone region lies within the Atlantic Soudanian climatic zone that is characterized by two contrasted seasons. The dry season lasts approximately eight months — from November to June — and is characterized by warm and dry winds, while the short rainy season — three to four months, from June/July to October — mainly features monsoonal flows. The Somone estuarine mangrove ecosystem located on the Petite Côte in Senegal is a 7 km2 tropical ecosystem. It extends at the end of a 350 m length sand spit, stretching parallel to the coast. The hydrographic network of the Somone region drains a 420 km2 watershed and it is formed by the confluence of two ephemeral streams that meet at the Bandia reserve. The maximum discharge has never exceeded 10 m3·s−1 with an annual average of 4 m3·s−1. The mangrove forest is located in a microtidal zone – tidal range < 2 m at its mouth. In this ecosystem, salinity is highly correlated with rainfall, with rather important seasonal variations. Seventy percent of the time, salinity increases when going upstream and in doing so characterizes a reverse estuary. This ecosystem is comprised of habitats, including mangroves (Rhizophora and Avicennia), intertidal mudflats, barren area (tannes), sand banks, sand spit. They are submerged by exceptional tides and/or rainfall during the wet season (June to October).
2.2 The dialysis porewater sampler, type Hesslein: design, preparation and deployment
The porewater sampling was performed using diffusion samplers (Hesslein, 1976), with an inert polysulfone membrane of 0.2 μm porosity (Millipore, Durapore). The diffusion sampler design employed consists of a 51.5/22/3 cm Plexiglas sheet in which fixed-volume (5.6 cm3) chambers are spaced out 1 cm apart. Each diffusion sampler has two series of 40 chambers. The samplers are inserted, at low tide, vertically into sediment, leaving six or seven chambers above sediment surface and 33 or 34 below. In order to avoid oxygen contamination in the chambers, the diffusion samplers were bubbled with nitrogen in a de-ionized water bath before their insertion. The equilibration time required for the diffusion sampler is three weeks (Bally et al., 2005; Mesnage et al., 2007). Porewater samplers were removed using plastic syringes. Samples were acidified with 1 N HCl and stored in conditioned 5 mL hemolysis tubes which were frozen until analyzed for dissolved species determination.
2.3 Numerical modeling of diffusion
We construct a 1-D diffusion model (Lecoq et al., 2013) to simulate the equilibration of a dialyser embedded in sediment with a uniform porewater concentration.
We used the following assumptions:
- • the problem is treated as a 1-dimensional one, i.e. diffusion occurs only along the horizontal direction. This assumption could be validated by the estimate of the gradient of concentration along the vertical direction;
- • no convection is considered in the analysis; the Péclet number is assumed to be negligible, because convection is assumed to be very small. Also, in the model, only the diffusion of the major elements has been studied;
- • in the far field (far from the dialyser), a uniform porewater concentration is assumed;
- • in the porous media, due to the presence of particles of different sizes and orientation, the diffusivity is lowered in comparison to the one in homogeneous fluid. An effective diffusivity Deff is then used, which takes into account a random distribution of pores in the heterogeneous media.
The effective diffusivity into sediment is estimated by dividing the free-water value of diffusivity D0 by the tortuosity squared τ2 (Bally et al., 2005). The tortuosity is evaluated empirically from the porosity ϕ by Boudreau (Boudreau, 1996):
| (1) |
Diffusion is orientation-dependent, so that the diffusion coefficient Deff can be replaced by a tensor which should be diagonal with coefficient along the y-direction lower than the one in the x-direction (Boisse et al., 2007; Lecoq et al., 2011). In this study, the simplest case of a constant coefficient (isotropic case) is used.
Taking into account the definition of this effective diffusivity, the following time-dependent differential equations for diffusion in sediment (domain Ω1) and in the dialyser (domain Ω2) are obtained, respectively:
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
3 Results and discussion
3.1 Physical parameters used in the model
The model sensibility was tested under several conditions allowing the impact of fluctuations of the modeled variables to be emphasized. Furthermore, these variables should be integrated into the numerical model in order to fit with the measured solutes’ profiles within sediment. The final objective is to evaluate the dialyser optimal equilibration time for a given kind of sediment.
In order to adjust the numerical model with the best solute diffusion computing, the physical parameter values controlling the diffusion within the porous media, e.g. sediment, such as coefficients of diffusion and porosities are taken from the literature (Boudreau, 1996; Li and Gregory, 1974). The diffusion coefficients of ions in water are obtained at the nominal temperature T = 25 °C. The diffusion coefficients of ions in water at the experimental temperature of the Seine or the Somone estuaries are estimated from the well-known Stokes–Einstein relation. Other parameters such as temperature, permeation speed of the membrane are chosen from experimental field data. The input parameters are summarized in Table 1.
Physical parameters used in the model for both studied systems.
| Parameters | Values used into the model | Units |
| Average sediment grain size | ||
| Seine | 0.04 | mm |
| Somone | 0.07 | mm |
| Tortuosity τ2 | ||
| Seine | 1.96 | |
| Somone | 2.25 | |
| Permeation speed | ||
| km | 0.43 | m·s−1 |
| Diffusion coefficients | ||
| D0(NH4+) (T = 25 °C) | 19.8 | 10−6 cm2·s−1 |
| D0(H2PO4–) (T = 25 °C) | 8.46 | 10−6 cm2·s−1 |
| D0(HPO42–) (T = 25 °C) | 7.34 | 10−6 cm2·s−1 |
| D0(SO42–) (T = 25 °C) | 10.7 | 10−6 cm2·s−1 |
| Temperature | ||
| Seine | 11 | °C |
| Somone | 28 | °C |
3.2 Modeling calibration in-situ data sets
The results of the numerical model presented above is compared with the ammonium (Fig. 1) and phosphate (Fig. 2) porewater data set from the Seine estuary (Bally et al., 2005). We choose specifically these two ions because the concentrations and diffusion coefficients are quite different (Table 1). Nevertheless, the dialyser concentration follows the same dynamics; this indicates that the convection is negligible, as it was assumed previously.
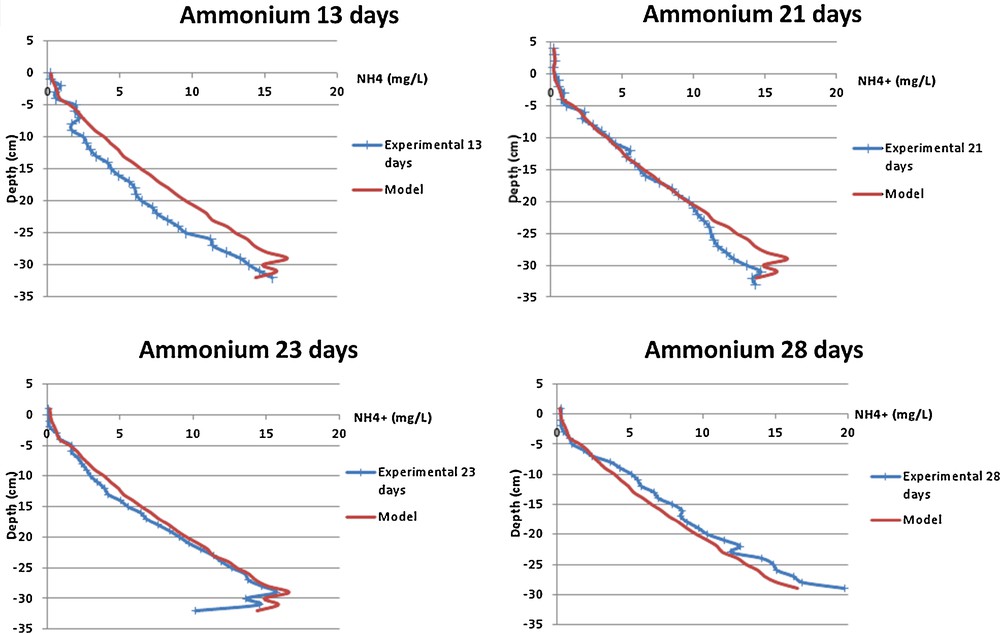
(Color online.) Comparison of the ammonium concentration profiles obtained with the 1-D diffusion model and in situ kinetics after 13, 21, 23 and 28 days in the Seine estuary.
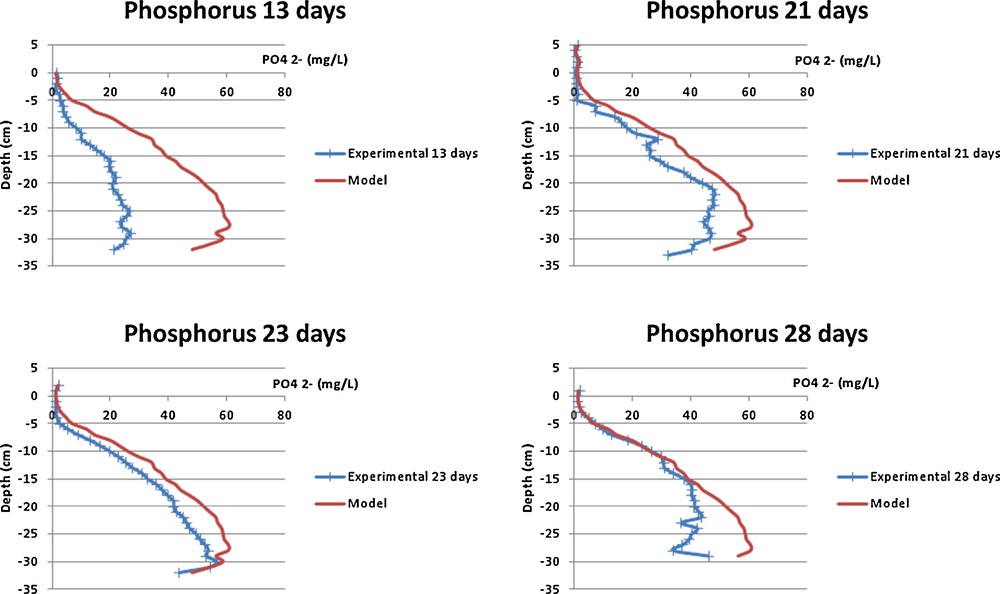
(Color online.) Comparison of the phosphate concentration profiles obtained with the 1-D diffusion model and in situ kinetics after 13, 21, 23 and 28 days in the Seine estuary.
The results of the numerical model tests highlighted that the peeper equilibration is not homogeneous within the 30 cm of investigated sediments. Indeed, for the ammonium ion, the model showed an equilibration for the first five sediment centimeters achieved in 13 days, then achieved in 10 days more (peeper achieved the equilibration in 23 days). Considering 5 days more (28 days), the theoretical and experimental curves separate; this may be due to the degradation of the membrane – Fig. 1.
However, as is observed in Fig. 2, the experimental phosphate data and the numerical modeling data are not well superimposed. Indeed, the behavior of phosphate ion is not the same as that of ammonium; as phosphate ions can be easily adsorbed onto sediments (Anschutz et al., 1999; Slomp and Van Capellen, 2006). This adsorption effect delays this ion diffusion process, and consequently the dialyser's equilibration time. It appears that an adsorption/desorption term must be included in the numerical model – see Eqs. (2–7).
3.3 Comparison between the Seine and the Somone systems
The previous model has been applied to two different data sets from the Seine and Somone estuaries, within the objective to optimize the use of the dialyser, i.e. to determine its time equilibration.
The effects of temperature and tortuosity with two different experimental data sets in regard to their environmentally contrasting conditions are first discussed. The temperate and tropical dry climates systems are contrasted in temperature, but the porosity of sediment (linked with the average sediment particles size) may also play an important role in diffusion and equilibration (cf. Table 1).
For a better understanding of both effects, a theoretical study is presented in Fig. 3. The normalized concentration of sulfate into the dialyser is plotted versus the time (expressed in days) for two sets of parameters: the tortuosity (obtained from the porosity using Boudreau formulation given by Eq. (1) and the temperature. The first parameter controls the mean path of ions into the porous medium, the second one controls the diffusion speed of ions into the interstitial fluid.
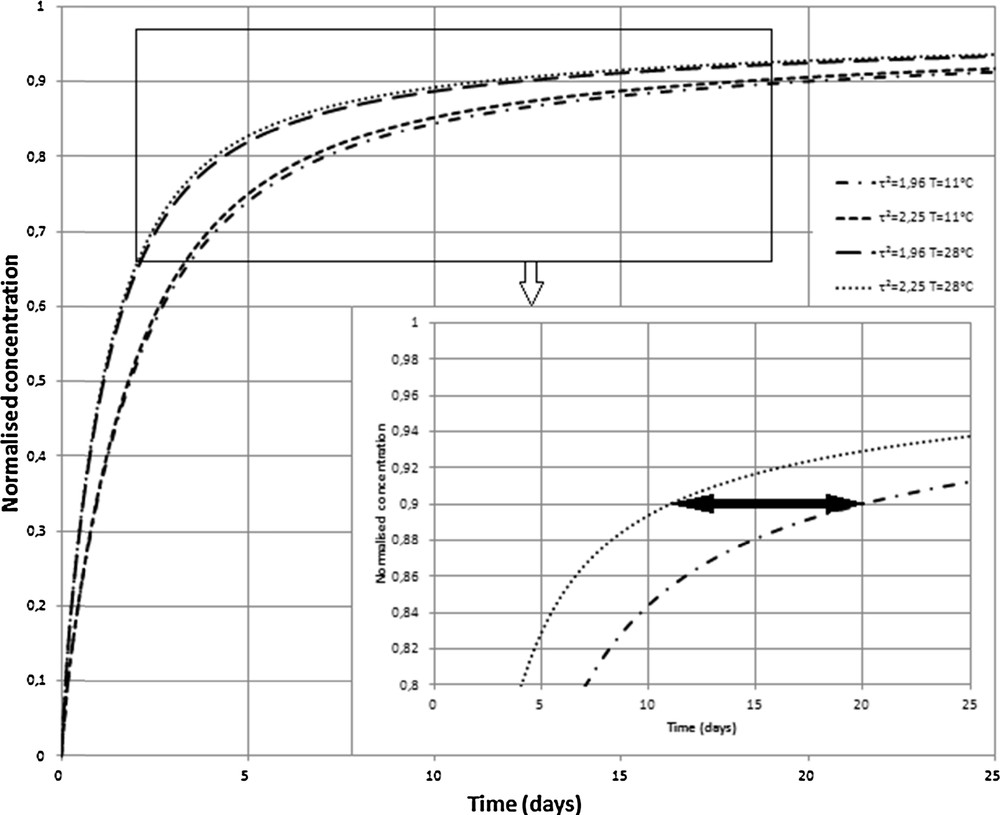
Theoretical time evolution of the normalized concentration of SO42–in both systems, Seine and Somone, using experimental evaluations of the temperatures and tortuosity of sediments. An enlargement shows the influence of temperature, which is the dominant effect.
It can be seen from Eq. (2) and with the definition of the effective diffusion coefficient that an increase of tortuosity decreases this coefficient for the considered ion. Nevertheless, the equilibrium in the dialyser is slightly faster when tortuosity increases, as shown in Fig. 3; this may be explained by the presence of a higher gradient of concentration close to the dialyser, and then the flux increases.
The second less surprising effect is that diffusion is faster when temperature increases. The horizontal arrow in the enlargement in Fig. 3 shows clearly that the same normalized concentration is obtained in the Seine environment around eight days later than in the Somone estuary.
The results of the numerical model have been compared with the porewater sulfate concentration of the Seine estuary after 13 days (Fig. 4a) and 23 days of equilibration (Fig. 4c); and those of the Somone estuary after 11 days (Fig. 4b) and 20 days of equilibration (Fig. 4d). Then, experimental data sets and modeling ones are summarized in Fig. 4 according to different equilibration time. Whatever the location and equilibration time, the agreement between the experimental profiles and the modeled ones is quite good, except for the surficial layer of sediment.
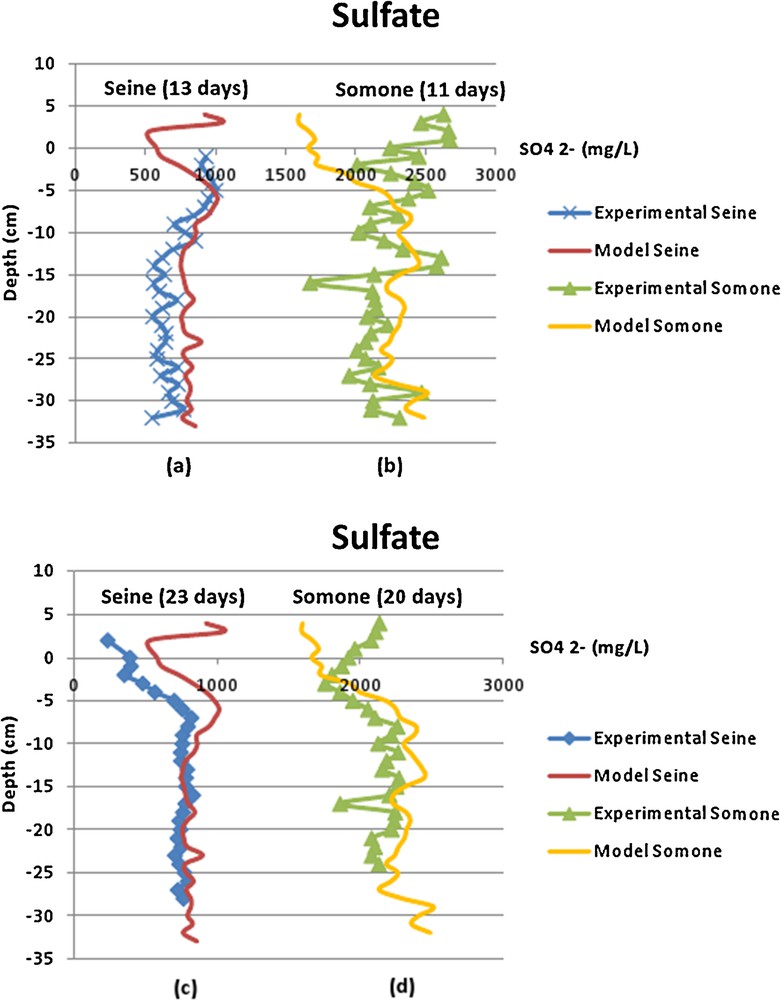
(Color online.) Sulfate (SO42−) in situ profiles in the total depth: (a) Seine 13 days, (b) Somone 11 days, (c) Seine 23 days and (d) Somone 20 days; the continuous lines correspond to the model, and the crossed-squared-triangular lines correspond to measurements.
Indeed, in the first 5 cm of the sediment column, the profiles are not well superimposed. This can be explained by the main dynamic property of an estuary ecosystem. The surficial sediments are mixed at each tide, involving variations in redox conditions due to mixing. Indeed, the dissolved oxygen of the water column entered the surficial sediment. Sulfate ions concentrations varied because of the diagenesis process; sulfate ions are reduced by bacterial activity.
4 Conclusion and perspectives
The numerical model fits with experimental data sets, except for the surficial layer of sediment. Indeed, the surficial sediment is subject to environmental impact especially in dynamic estuaries ecosystems. Then, it seems that the model should consider other environmental conditions such as sediment compaction which increased over the depth, sediment porosity and diffusion velocity (temperature dependent). Therefore, the model should be improved to allow the integration of three different porosity parameters, from 0 to 5 cm, from 15 to 20 cm and 25 to 30 cm depth. Furthermore, the model should take into account the surface sediment bioturbation and the microorganism density and/or activity, microorganisms which settle the membrane and consume the solutes. Therefore, it appears that parameters such as “bioturbation rate” or “bacteria density” should be integrated into the diffusion model in order to approach more precisely the environmental conditions.
Acknowledgements
The authors thank the referees for their remarks and useful comments. We would like to thank Gilles Morel, computer engineer at Rouen University, for providing computer facilities and David Moussa, chemical engineer at Rouen University, for providing chemical analysis data.


