1. Introduction
Rheological behavior of silicate melts and magmas are of high importance to understand how they form, travel, and emplace into and on the Earth’s surface. A special role in the magmatic evolution is exerted by the melt/magma undercooling degree(s); it is defined as the difference between the system temperature and the temperature at which a phase saturates in the given liquid [Kirkpatrick 1981; Giuliani et al. 2021]. From a thermodynamic point of View, the appearance of solid phases from a magma is driven by the undercooling degree. However, the nucleation and crystals growth of a mineral phase is also governed by kinetics processes [Lofgren 1980; Dowty 1980; Hammer 2008; Iezzi et al. 2008, 2009; Vetere et al. 2013, 2015; Giuliani et al. 2020a, b]. The overall variation in nucleation rate spans many orders of magnitude, while growth rates variation is more limited [Swanson 1977; Kirkpatrick 1981; Lasaga 1997; Cashman 1988; Hammer and Rutherford 2002; Zhang 2008; Iezzi et al. 2009; Mollo and Hammer 2017; Giuliani et al. 2020a]. For a similar bulk magmatic composition, a low nucleation rate produces few crystals that will became large, while a high nucleation rate will result in a large number of tiny crystals [Hammer 2008; Iezzi et al. 2009; Higgins 2006; Mollo and Hammer 2017]. Nucleation is favored in silicate liquids with a high chemical diffusion, i.e., poor in SiO2 and rich in H2O, whereas SiO2- and H2O-poor liquids are reluctant to nucleate and prone to vitrify [Iezzi et al. 2009; Vetere et al. 2015].
Nucleation and crystallization processes have profound implications for the rheology of magmas and lavas, which depends on the volumetric amount of solid phases as well as on their size and shape [Gonnermann and Manga 2007]. Hence, a clear knowledge of nucleation and crystallization processes driven by solidification, either by cooling or by degassing-induced depressurization, is the key to understand magma rheology and its evolution before turning into a solid rock.
The eruptive style of volcanoes is strongly affected by magma viscoelastic properties [Dingwell 1996; Gonnermann and Manga 2007; Cassidy et al. 2018, and reference therein] and, as shown by Petrelli et al. [2018], their associated timescales. Indeed, the P–T–fO2 path(s) for a starting magmatic composition (X) governs its solidification behavior and rheological pathway [Lanzafame et al. 2013, 2017].
Crystallization under kinetic conditions imposed by 𝛥T∕𝛥t and/or 𝛥P∕𝛥t was experimentally studied and investigated mainly for mafic compositions so far [Arzilli et al. 2019; Polacci et al. 2018; Hammer 2008; Conte et al. 2006; Fiege et al. 2015, and reference therein], while highly evolved melts are harsher to experimental investigation (time consuming), especially in a dry context [Vetere et al. 2013, 2015]. Nowadays, it is recognized that disequilibrium conditions often occur in natural processes [Kolzenburg et al. 2018; Vetere et al. 2019, 2021, and reference therein]. Moreover, ambiguities persist in our understanding of the interplay between crystal nucleation and growth on magma rheological variation (bulk viscosity and density) as it evolves from liquidus temperature down to the glass transition temperature, Tg. The cooling rate and degassing rate induced by depressurization of magmatic batches influence textural, petrological, and geochemical features, as well as volcanic behavior, i.e., from mildly lava effusion to violent explosive paroxysm [Armienti 2008; Hammer 2008; Applegarth et al. 2013; Shea and Hammer 2013; Fiege et al. 2015; Mollo and Hammer 2017; Arzilli et al. 2019, and references therein].
Due to the changes in residual melt chemistry and solid phase growth (as melt solidifies below the liquidus temperature, TL), it is expected that properties such as the apparent viscosity and density will vary, with significant impact on the magma’s ability to move [Giuliani et al. 2021]. To have an overview of this natural scenario and because of the paucity of direct field data [Chevrel et al. 2019, 2018, 2015], experimental approach is of paramount importance to further understand how magma behaves as it moves into and on the Earth.
In this review, after a general discussion on the nucleation and growth of minerals in silicate melts and magmas and on the general and most used laws and models governing magma rheology, we will focus both on recent experimental data on natural/synthetic systems and numerical approach with the aim to examine equilibrium versus disequilibrium conditions on the solidification of mafic compositions and its impact on rheological behavior. Specifically, we will constrain and model the rheological changes induced by cooling and also by shear stresses. Results point to the complex interactions between crystallization processes and rheological behavior as the key for understanding how magmas behave in natural systems. We will also emphasize the possible future experimental approaches in order to shed new light on these important natural processes that could be applicable to solidification induced by depressurization for volatile-rich magmas.
2. The state of the art
Petrological processes and scenarios are interpreted and reconstructed mainly by studying crystal-chemical attributes of phases [Giuliani et al. 2021, 2022]. This approach commonly assumes thermodynamic equilibrium between magmatic liquid and their mineral/volatile phases. From thermodynamically derived laws, intensive variables of magmatic systems can be obtained by crystal-chemistry of minerals and coexisting liquids, such as to track evolution of magmas [e.g., Putirka 2008, and references therein]. However, we now have clear evidence of disequilibrium features in both intrusive and especially volcanic rocks [e.g., De Paolo and Getty 1996; Roselle et al. 1997; Müller et al. 2004; Nabelek 2007; Baker 2008; Mollo and Hammer 2017; Giuliani et al. 2021]. Hence, the scientific community is aware that compositional changes of minerals in volcanic rocks are not necessarily related to equilibrium conditions, but rather and frequently to a disequilibrium state [e.g., Baker and Grove 1985; Hammer 2006, 2008; Iezzi et al. 2008, 2011; Del Gaudio et al. 2010; Mollo et al. 2010, 2011a, b]. For a bulk chemical composition of a magmatic batch, the increase of undercooling degree and deformation rate (i.e., stretching and folding mechanisms) progressively induces and facilitates nucleation and crystallization processes [Swanson and Ottino 1990; Perugini et al. 2008; Rossi et al. 2019; Tripoli et al. 2019]; in turn, they strongly affect rheological behavior of magmas that eventually rise from depth and emplace on the Earth’s surface. Deformations occurring in dynamic magmas enhance the nucleation and crystal growth; the movement of a magma furnishes continuous and fresh “feeding ingredients” around early formed crystals [Vetere et al. 2020; Vetere and Holtz 2020] when compared to a static condition. Also, in order to better understand the rheology of complex systems, another important aspect is related to the delay in crystal nucleation and growth that became progressively higher at low undercooling degree, i.e., close to liquidus temperature [Rusiecka et al. 2020; Giuliani et al. 2020b].
Rheology is defined as the science studying the deformation of materials under well-defined conditions. As defined in Mezner [2014], the term rheology (i.e., the flow science) derives from the Greek word “rhein” that is equivalent to the word “flow.” When applied to volcanology, the rheology of magmas essentially studies melt or magma flows as they are subjected to different stress, in magma chambers, along the way to the surface or when flowing on the Earth’s surface or other planetary surface (Mercury or Mars, for example). Starting from the definition of magma, it also implies that the rheological behavior depends mainly on phases present in a system (fluid ± crystals ± exsolved and dissolved volatiles), which depend on a variety of parameters such as pressure, temperature, and fO2 for a well-defined chemical system. In addition, it is now clear that such a behavior can change if phases are subjected to certain stress [e.g., shear rate dependence; Vetere and Holtz 2020 and reference therein]. In the conventional description of rheological data, in order to parameterize any suspension, there is a need to clearly define the relationship between the imposed shear stress (𝜎 in Pa) and the shear strain-rate ( in s−1; i.e., deformation rate). This relationship can be used to characterize the flow behavior and related flow curve. The flow regime is usually defined as Newtonian when there is a simple proportionality between stress and strain:
| (1) |
Newtonian and non-Newtonian behavior [Lenk 1967]. 𝜏y is the yield stress that is to be overcome in order to initiate flow; n is the flow index describing the degree of non-Newtonian behavior. For Newtonian materials 𝜏y = 0, n = 1, and the flow consistency K =𝜂; shear-thickening and shear-thinning materials are defined by n > 1 and n < 1, respectively.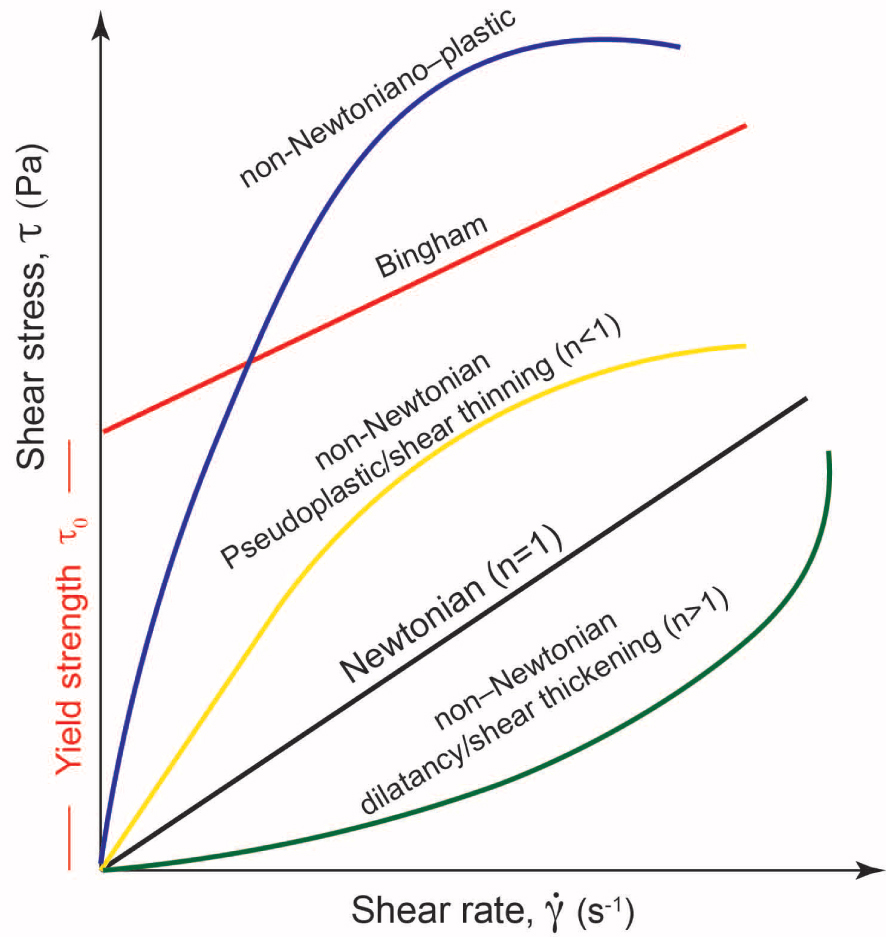
However, in multiphase and complex systems, such as magma, deviation from Newtonian behavior is observed and shear stress is not simply proportional to strain rate and the following cases are common: (1) a minimum stress is required before viscous flow initiates (also called the Bingham regime) or (2) both the above behaviors are combined, which is expressed by the Herschel–Bulkley model [Herschel and Bulkley 1926]:
| (2) |
The onset of non-Newtonian rheology in silicate melts has been investigated by Webb and Dingwell [1990a, b] using fiber elongation techniques. The chosen melt compositions were a high silica rhyolite, an andesite, a tholeiitic basalt, and a nephelinite. Viscosity was determined as the ratio of the applied tensile stress to the observed strain rate. As reported by the authors, “before experiments, each fiber was initially annealed at a temperature for a period of 104 s. This equilibration time is greater than both the shear and volume relaxation times of a melt with 𝜂v =𝜂 s = 1012 Pa⋅s and G∞ (shear modulus) ≈ K∞ (bulk modulus) 10 GPa (tV = tS = 100 s).” However, the measurements had no in situ monitoring of the sample temperature and did not consider viscous heating effects. Figure 2 illustrates the apparent viscosity reduction due to viscous heating effect. As reported by Cordonnier et al. [2012], “fluids with a temperature-dependent viscosity are affected by viscous heating once this heat source overcomes the heat loss (i.e., heat transfer by conduction, convection, and/or radiation).” This effect, despite increasing shear rates, will move magmas away from the glass transition [Gonnermann and Manga 2007]. Yue and Bruckner [1996] have re-analyzed the fiber elongation observations and formulated a correction for the strain-rate dependence of viscosity that includes viscous heating effects explicitly. The question as to whether viscous heating may have had a measurable effect on previous determinations of the onset of non-Newtonian viscosity remains unsolved.
Results of viscosity measurements using the Parallel plate viscometry on NIST-certified starting glass as reported in Cordonnier et al. [2012]. (A) Load applied to the sample; (B) Due to the applied load (when it is high enough), the temperature in the sample increases; (C) As temperature increases (B) viscosity drops. This viscosity drop is explained from the temperature increase and can also be predicted by the Vogel–Tamann–Fulcher equation [Hess et al. 2007].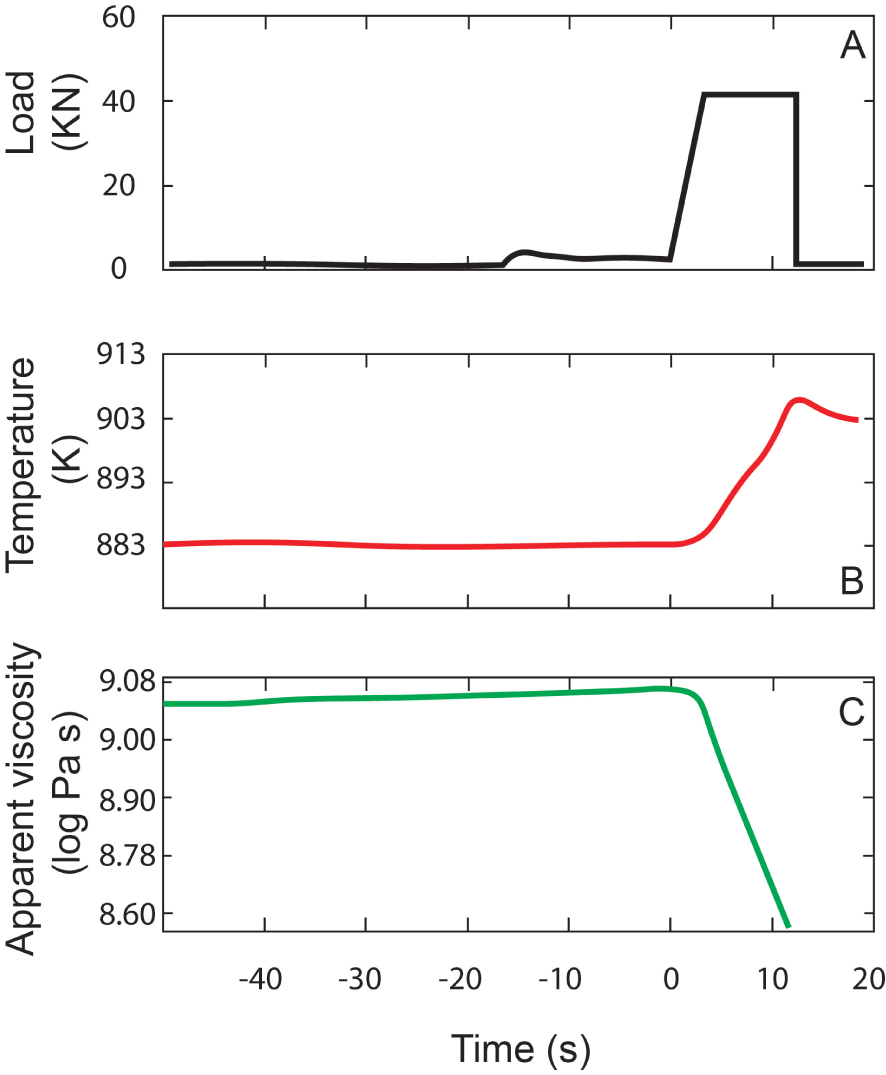
Because magmatic suspensions are strain rate dependent, thus sensitive to the applied shear stress, it is common to define the relative viscosity 𝜂r as:
| (3) |
Vona et al. [2011] provided a methodology to follow for the evolution of the apparent viscosity as crystallization processes proceed. Figure 3a shows an S-shape curve where relaxing, incubation, nucleation times, and crystallization processes with a final plateau (denoting the end of the crystallization process) are highlighted. This cartoon is confirmed by experimental data for different compositions (as those presented in the following paragraph). The steepness of the curve is related to the response of the melt when temperature is below the liquidus. In other words, the curve shows the time that is needed for a melt to relax and eventually to start to nucleate a solid phase. As expected, very fluid systems react much faster than more viscous ones and this is clearly evidenced in Figures 3b–d where three different melts with compositions varying from andesite (typical intermediate composition between basalt and rhyolite) to basalt and to pyroxenite (an ultramafic igneous rock consisting essentially of minerals of the pyroxene group) are compared. Obviously, considering the red curves in Figure 3 (e.g., experiments performed at shearrate = 0.1 s−1) the most depolymerized pyroxenite composition (Figure 3d) reacts faster (ca. 1800 s) when compared to basalt (ca. 2 × 104 s; Figure 3c) and basalt reacts faster when compared to andesitic composition (ca. 3 × 104 s; Figure 3b).
Note: Apparent viscosity variation versus time; (a) redraw from Vona et al. [2011] while (b–d) are redrawn from Vetere and Holtz [2020] and refer to (b) andesite from Calbuco 2015 eruptions, (c) Etna basalt from 122 A.C eruption, and (d) pyroxenite from Theo’s Flow which is a proxy for Martian lava flow samples. Blue and red curves refer to experiments performed at shear rate of 1 and 0.1 s−1, respectively. Note the shear-thinning behavior (apparent viscosity decreases as shear rate increases) with nucleation and crystallization processes related to the applied deformation rates (see text for details).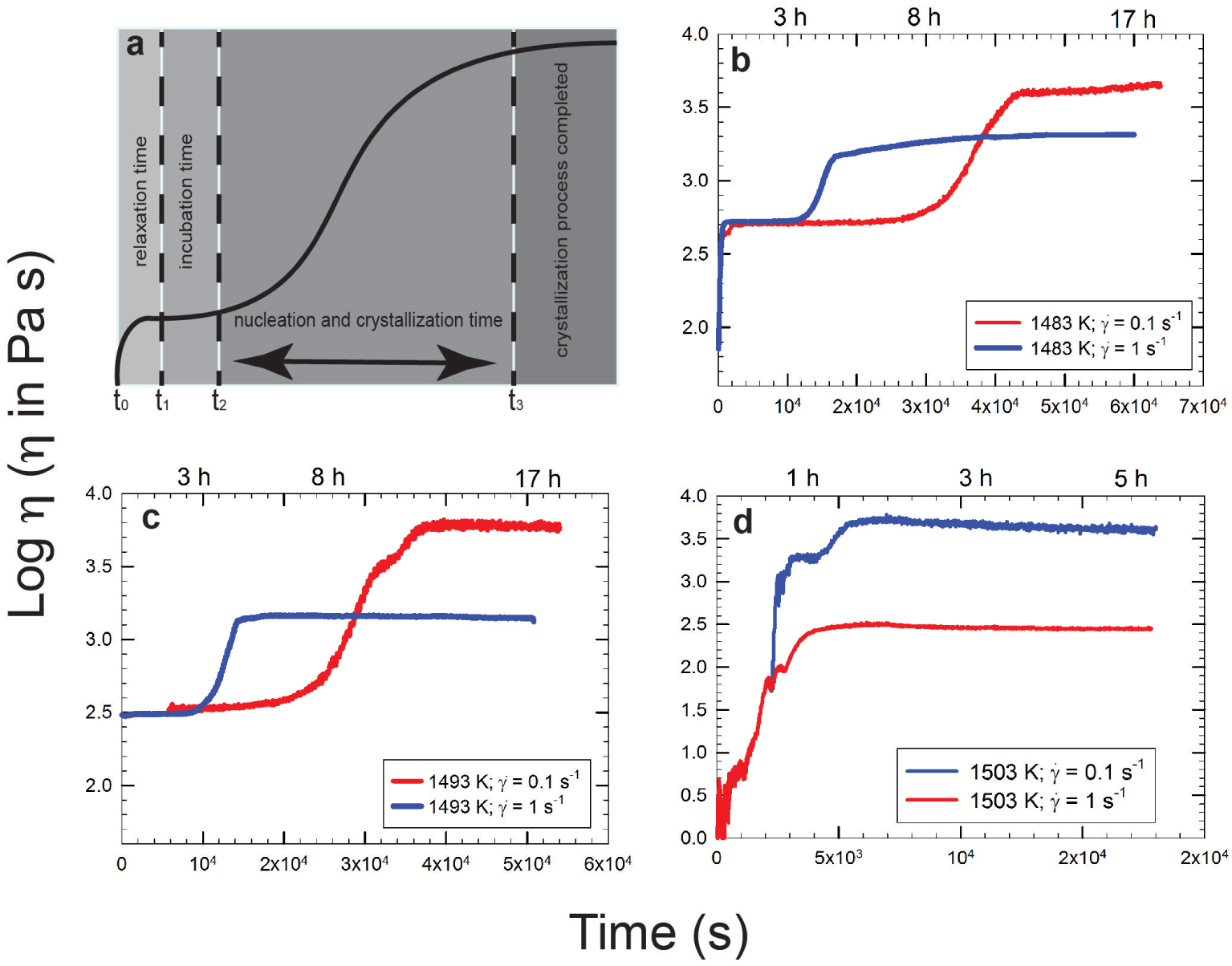
The last consideration on partly crystallized system concerns the approach to the so-called maximum packing fraction (𝛷m) where the viscosity of a suspension (thus, the ability of a melt plus crystal system to flow) tends to infinity and the transition from viscous to elastic behavior might occur. 𝛷m depends on particle sizes, shapes, and distributions and its value during a flow may change due to possible crystal alignment along the flow directions [see the concept of rheological critical melt percentage, RCMP as discussed in Arzi 1978 and reviewed by Rosenberg and Handy 2005].
3. Investigated compositions
The bulk compositions reconsidered and used in this review are reported in Figure 4 (Supplementary Appendix 1), on which both kinetics-controlled crystallization events, rheological test, and/or numerical modeling have been performed.
Note: Total alkalis versus silica diagram for the investigated starting compositions. VH20 refers to Vetere and Holtz [2020]; V20, 19 and 17 refer to Vetere et al. [2020, 2019, 2017, respectively]; M20 refers to Morrison et al. [2020]; K20, 19 and 18 as in Kolzenburg et al. [2020, 2019, 2018, respectively]; SW20 and 15 refer to Sehlke and Whittington [2020, 2015]; C16 refers to Campagnola et al. [2016]; S14 refers to Sehlke et al. [2014]; Vo11 refers to Vona et al. [2011]; I09 to Ishibashi [2009] and IS07 to Ishibashi and Sato [2007].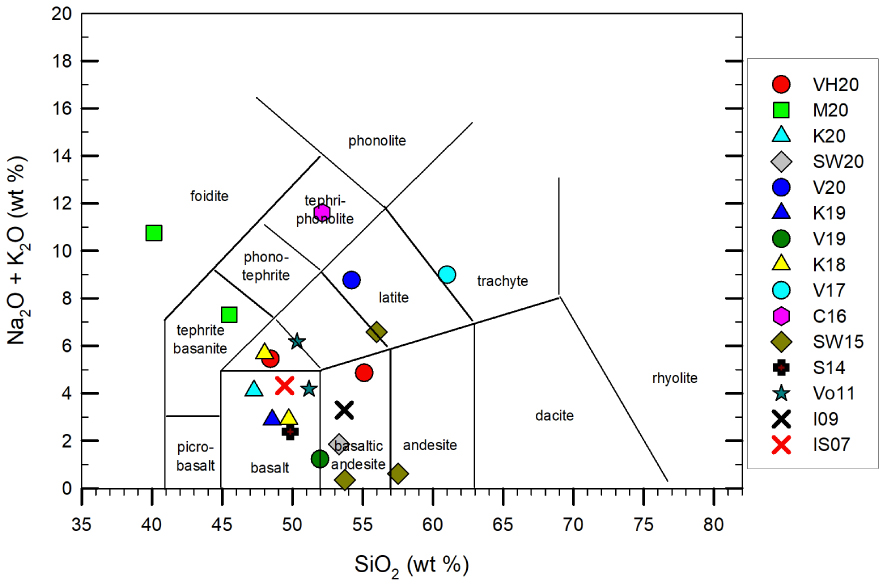
A first compositional dataset comprises rheological experimental data in which shear stress vary at isothermal conditions, ideally at a fixed undercooling degree [Morrison et al. 2020; Sehlke and Whittington 2020, 2015; Vetere and Holtz 2020; Vetere et al. 2020, 2017; Campagnola et al. 2016; Sehlke et al. 2014; Vona et al. 2011; Ishibashi 2009; Ishibashi and Sato 2007]. However, it is important to state that magmatic suspensions are complex chemical systems, where crystallizing phases have different compositions from the parental liquids [Iezzi et al. 2020]. Thereby, also at isothermal condition, the crystallization trough time determines a change in composition of both crystalline and liquid phases. The second dataset, although very limited, comprises rheological data derived upon shearing and cooling events acting on silicate liquids, and represent the closest to natural scenarios [Vetere et al. 2019; Kolzenburg et al. 2020, 2019, 2018].
These two experimental datasets were obtained with the identical methodology (i.e., concentric cylinder) and mirrors a viscosity range of 101–106 Pa⋅s, thus, partly crystallized silicate melts, where the magma dynamic regime is dictated by crystallinity (𝛷). Usually this regime varies from dilute (where 𝛷 varies between 0.05 and 0.25 and particles have low to moderate interaction mainly depending on the particle aspect ratio) to semi dilute regime (∼0.25〈𝛷〉∼0.6) where particles strongly interact with each other with a possible alignment with the flow direction [Figure 5; Hoover et al. 2001; Saar et al. 2001; Vetere and Holtz 2020]. Both regimes define non-Newtonian systems with shear thinning behavior (small or strong, depending on 𝛷) with a possible evolution of the apparent yield stress (Figure 1). Those data reveal the importance of dynamic applied to silicate melts under cooling as will be discussed below.
Concentric cylinder experimental results on Calbuco andesite at shear rate of 1 s−1 and temperature of 1483 K as in Vetere and Holtz [2020]. Phases are Fe–Ti oxides, plagioclase (plg), and glass. Note the plagioclase (plg) alignment along the flow direction.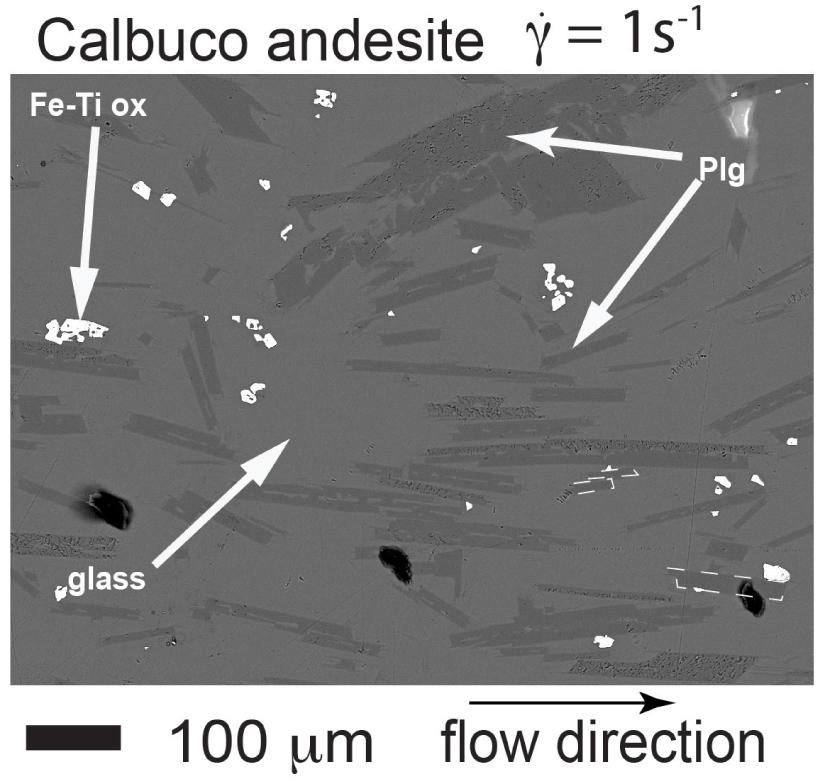
4. Numerical simulation
AlphaMELTS code was used to track the phase evolution path for compositions presented in Figure 4 as temperature cools from the liquidus to subliquidus conditions. The alphaMELTS (V. 1.9) software provide a simple text-based interface to subroutine versions of the algorithms MELTS, pMELTS, and pHMELTS [Asimow and Ghiorso 1998; Smith and Asimow 2005; Ghiorso et al. 2002; Ghiorso and Sack 1995]. Suitable for multi-component systems, it allows to calculate equilibrium assemblages along a thermodynamic path set by the user (for details on the software, see the following address: http://melts.ofm-research.org/ and https://magmasource.caltech.edu/forum/).
The evolution of residual melt compositions is reported in Figure 6a and the evolution of melt proportion versus temperature is shown in Figure 6b (as vol%). In both cases, a direct comparison with literature data is provided. The calculated liquidus temperature are also available in Supplementary Appendix 1 for all the studied compositions. In general, it shows progressively lower values as the chemistry of the systems evolves to more silicic ones (higher SiO2 content), as expected, to equilibrium conditions for the modeled melts. The evolution of SiO2 predicted in Figure 6a for samples I09, Vo11Stromboli, and Vo11Etna, as for sample M20NYI and SW15NVP–Na, shows higher values than experimental data, while the opposite is observed for sample S14, M20NYA, and, in both cases, the differences become important at lower temperatures. In general, predictions of the Al2O3 evolutions are more accurate as those for CaO and MgO oxides, while FeOtot is overestimated for M20NYA, C16 and underestimated for Vo11Stromboli, SW15NVP, and M20NYI samples, respectively. The difference between experimental data and data predicted by alphaMELTS are particularly large for M20NYI and M20NYA compositions. As reported by Morrison et al. [2020], this is related to differences in oxygen fugacities (experimental data are obtained at more reduced conditions). Thus, we will focus only on rheological data for these compositions. The observed differences can be attributed to two aspects: (i) the inherited accuracy of the thermodynamic calculations and (ii) the occurrence of disequilibrium conditions experienced by the analyzed run-products (Figure 6a).
SiO2, Al2O3, FeOt, MgO, and CaO evolution of melts with temperature as systems cool down starting from liquidus temperatures. Symbols refer to experimental data while dotted lines refer to prediction obtained by using alphaMELTS 1.9. The label on each plot refers to chemical compositions as those reported in Figure 4.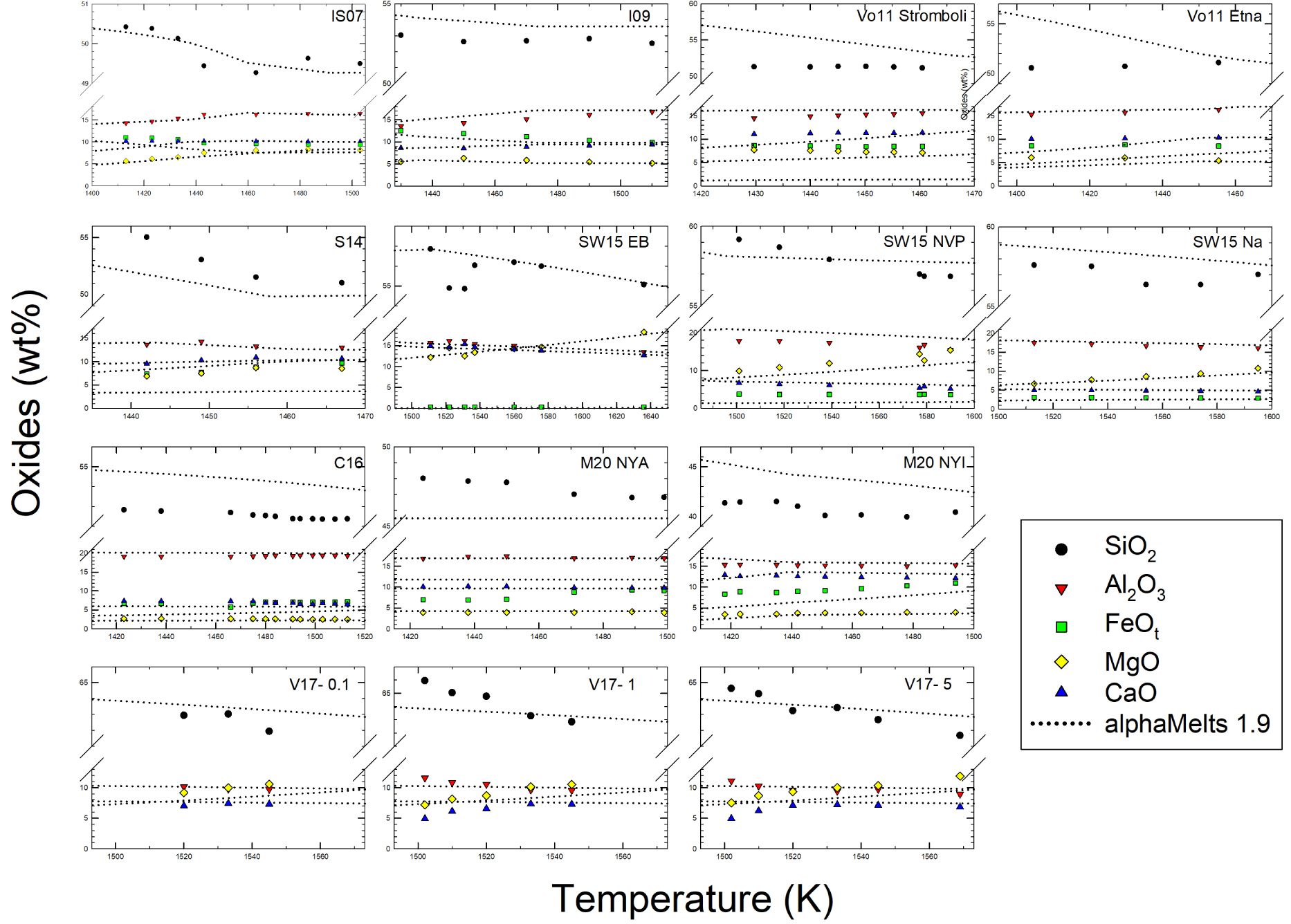
Comparison of the volume of residual melt (vol%) derived from modeling and experimental data. The label in each plot corresponds to the sample numbers provided in Figures 4 and 6a. Red curves refer to experimental data while black ones are those derived from alphaMELTS 1.9 results. The red curves fitted through the experimental data sometimes show S-shapes because the curves were drawn to fit exactly the determined melt fractions. However, such a behavior is not realistic and reflects the large uncertainty in the determination of melt/crystals ratio. Data refer to ambient pressure.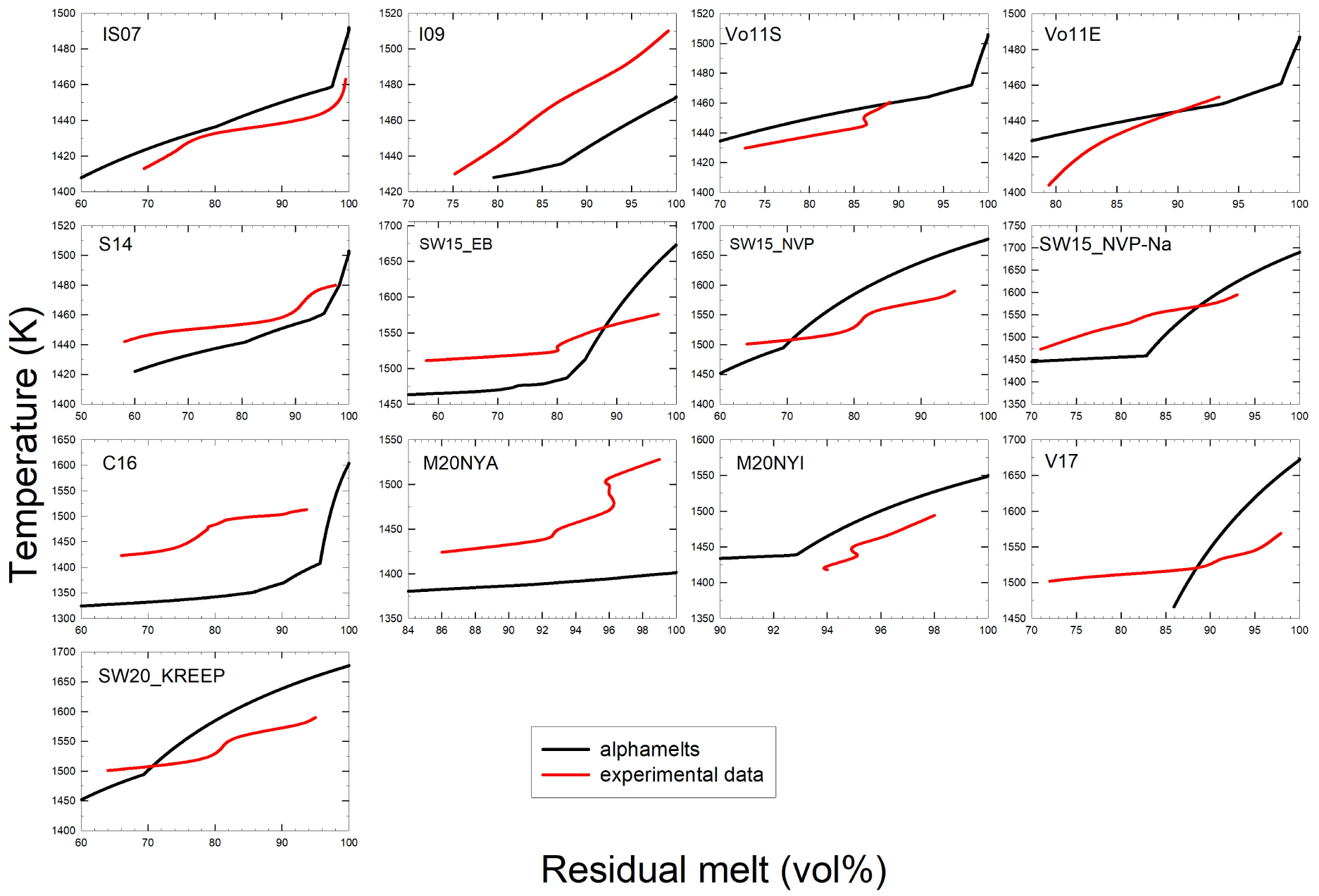
(A) Plagioclase, (B) pyroxene, and (C) olivine compositions for some of the magmatic systems studied. Note the similar compositional range of experimental data and modeling.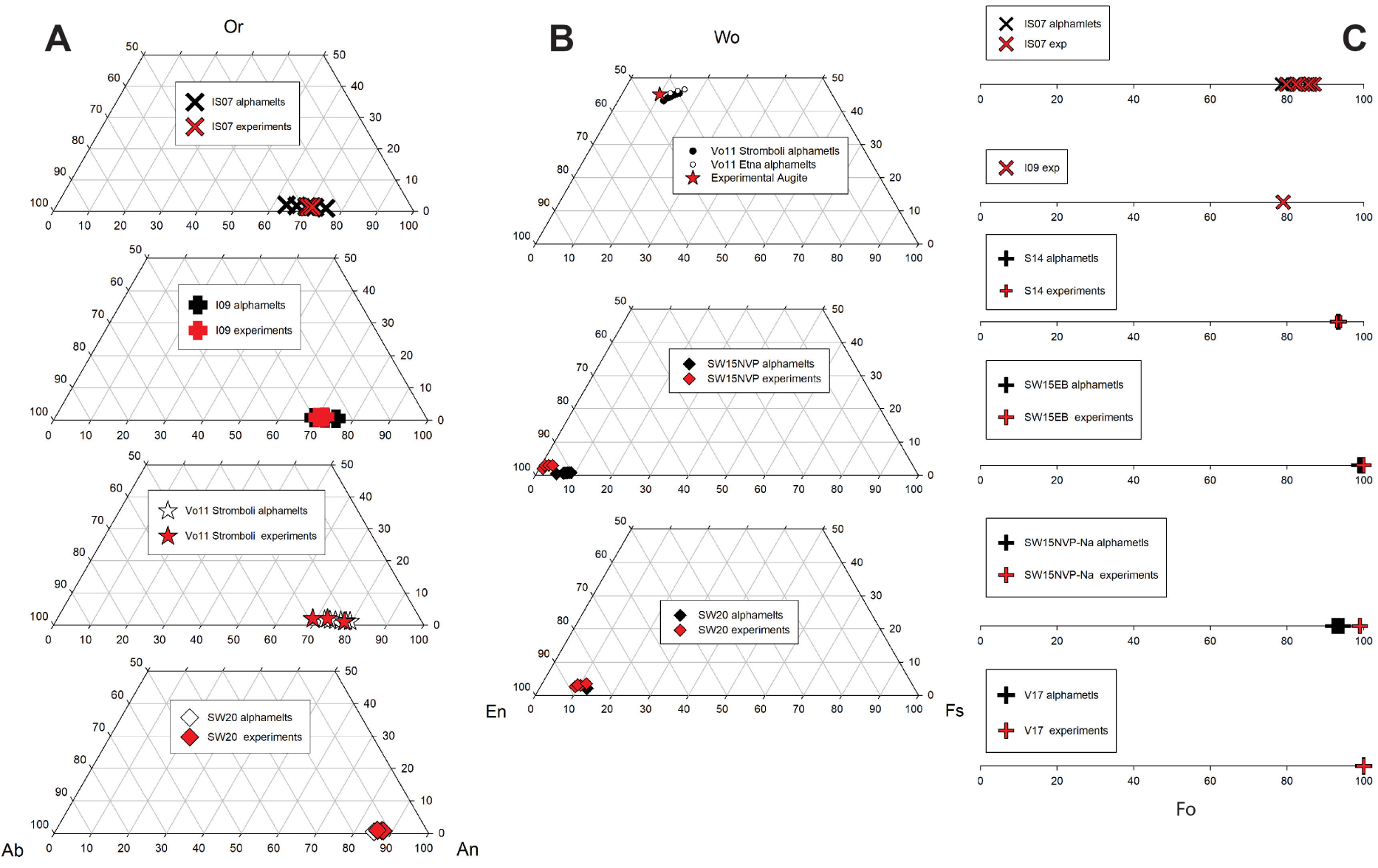
Crystallinity versus temperature for the compositions reported in Figure 4.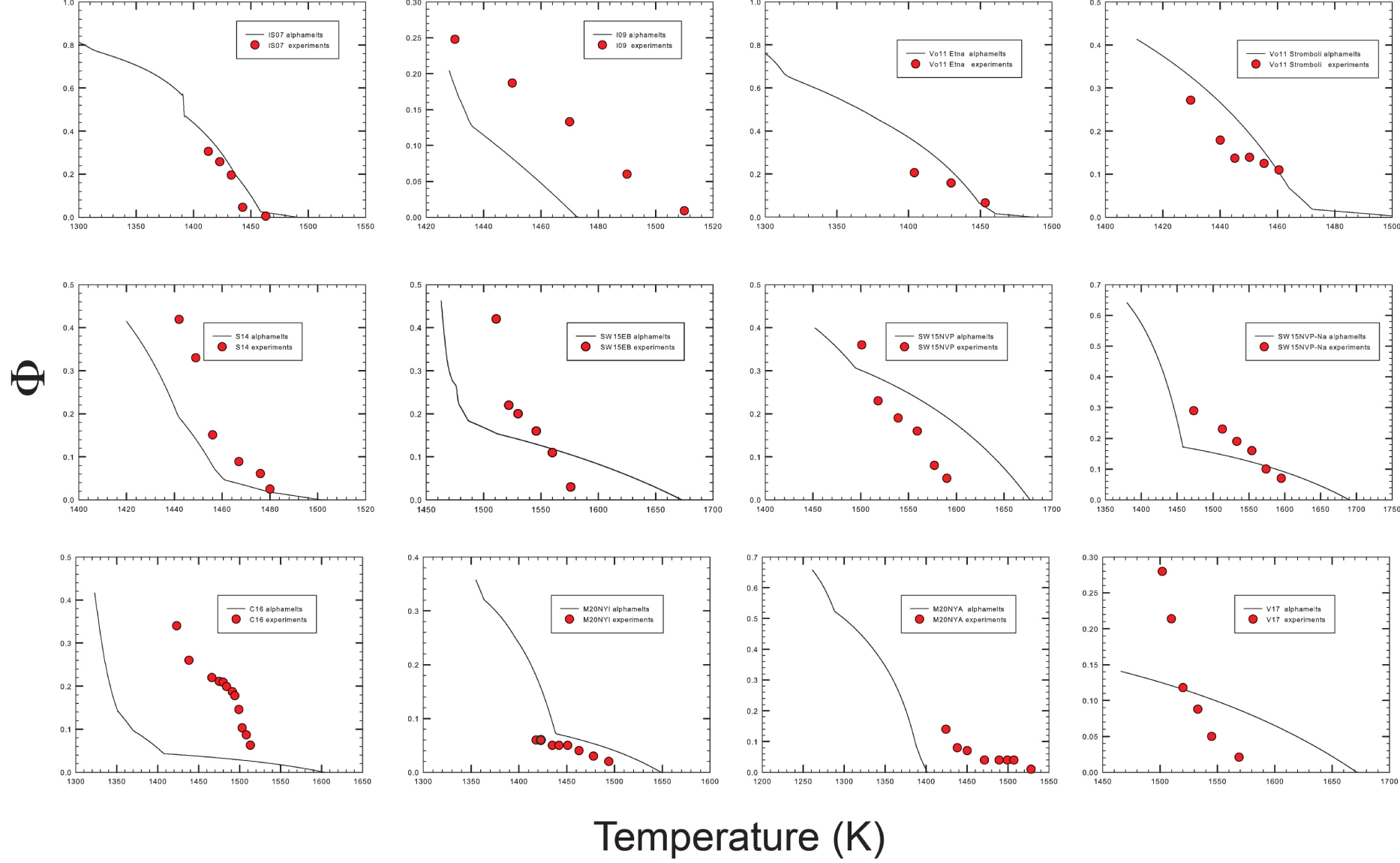
Experimental and thermodynamic calculations show that melt fraction decreases with temperature, as expected. In general, the very low effect of temperature on crystallinity predicted by to alphaMELTS 1.9 in the high temperature range is not reproduced by the experimental data (in particular, for M20NYA, V17, C16, SW15NVP–Na, SW15_EB, S14, and I09 compositions). In most cases, the volume of residual melt is much lower that the predicted volumes and the liquidus temperatures extrapolated from the experimental data are lower than predicted liquidus temperatures. As a result, the effect of temperature on the crystallinity in the experimental products is more pronounced than predicted (see also Figure 6d with the crystallinity of the individual experiments).
The composition of solid phases was compiled from the literature data and are reported in Figure 6c(A–C). The compositions of plagioclase (plg), pyroxene (px), and olivine (ol) that crystallized in the experiments are compared to predicted compositions with alphaMELTS 1.9. Predicted and experimental compositions are in general good agreement. This indicates that alphaMELTS 1.9 is successful in predicting equilibrium mineral compositions but that the prediction of phase proportions is more problematic, which may be due to calibration of the model from static experiments. Applying a shear stress to crystallization experiments is expected to promote the crystallization and reduce the delay time preceding nucleation [Rusiecka et al. 2020; Vetere et al. 2021]. Thus, the possible mechanisms to explain this difference in crystallinity might be related to the continuous stirring of the melts at high shear rate in dynamic experiments which is bringing the necessary “feed growth ingredients” (elements necessary to build a crystalline structure) close to individual crystal surfaces and which facilitates crystal growth (see below).
5. Modeling experimental data by varying shear rate and crystal content
Due to the intrinsic difficulties in performing experiments, the available experimental dataset on crystallization processes under dynamic conditions are still relatively scarce, as aforementioned. Moreover, the paucity of experimental data on more evolved systems is resulting from the limitations of the experimental technique (Figures 6a–6d). In particular, the range of viscosity that can be investigated with the most common apparatus to reach high stress and higher viscosity values (e.g., 𝜂 > 106 Pa⋅s) does not cover that of silicic melts at moderate temperature and even with low amounts of crystals. We collected 415 literature experimental viscosity data (see Supplementary Appendices 1 and 2) on different mafic to intermediate compositions at different temperature, shear rate, volume of crystals, and 2D aspect ratio. All data were obtained with the identical methodology by using concentric cylinder apparatus and the majority show a decrease in the apparent viscosity (at isothermal conditions) as deformation rate increases, pointing to the well-known effect of shear thinning as discussed above.
Apart from viscosity data, one general outcome for most of the investigated systems is that increasing of the strain rate promotes a fast crystal growth rate. Experiments with dynamic crystallization show that only ca. 6000 s are necessary to produce ca. 22 area % of crystals having plagioclase crystal lengths of ca. 300 mm, mirroring a growth rate value of 5 × 10−6 cm/s [Vetere and Holtz 2020], much faster than those reported in literature [i.e., 10−8–10−9 cm/s; Pupier et al. 2008].
Considering that water and other volatiles affect the rheology of silicate melts [Fiege et al. 2015, and reference therein], the crystals’ growth rate might also be dependent on strain rates in dynamic hydrous magmas. Literature provides different general models able to reproduce apparent or relative viscosity behaviors as a function of crystal content, shear rate, and aspect ratio of the solid phases. Most of them use melt viscosity in order to retrieve the relative viscosity of the suspensions (melt + crystals; see (3)), adopting general viscosity models such as proposed by Hui and Zhang [2007] or Giordano et al. [2008]. A list of the most used models is provided in Table 1.
Figure 7 provides an overview of the relative viscosity data and some of the models provided in Table 1 are plotted for comparison. All the experimental data processed at different deformation rates show a shear thinning behavior (note identical symbols with same crystal content but different 𝜂r in Figure 7) and relative viscosity differences increase with increasing the gap between low and high shear rate. For example, Sehlke and Whittington [2015] show that NVP–Na viscosity vary from 7500 to 1500 Pa⋅s as shear rate vary from 0.01 to 5 s−1 at 1473 K with crystal content 29 vol%. Vetere et al. [2017] show a decrease of 𝜂app from ca. 10200 to 1100 Pa⋅s at 1502 K and ca. 28 vol% of crystal as shear rate vary from 0.1 to 5 s−1 in synthetic silicate melt compositions analogue for Mercury (for details, please refer to Supplementary Appendix 2).
Relative viscosity evolution versus crystal content in vol%. (A, B) reproduce identical dataset with different scale in order to better appreciate difference in relative viscosity induced by different shear rate. Also, note in (B) a modified KD equation [Krieger and Dougherty 1959] able to reproduce relative viscosity for early departing systems such as those deformed at relatively low shear rate.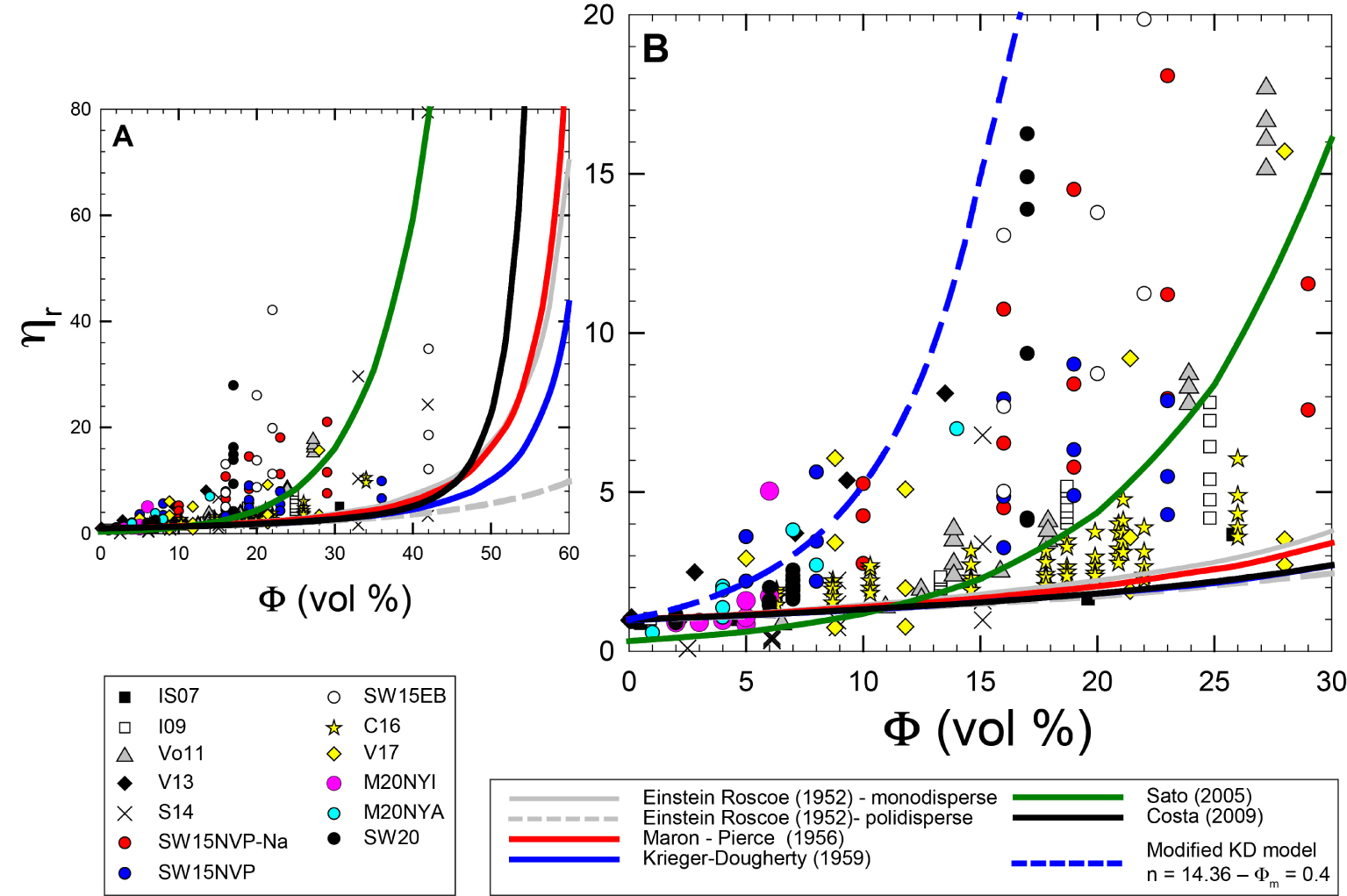
None of the models presented here are successful for predicting the whole experimental dataset. Reasons reside on the different parameters used for modeling. For example, the fact that 𝛷m can vary during deformation due to possible particle alignment will obviously change the rheological behavior. And this, up to now, is not predictable. Also, the use of image analysis to retrieve solid phase proportions can lead to some uncertainties and a statistically representative dataset of BSEs images selected along different orientations of the investigated sample is necessary. Thus, when using few BSEs images, AS (AS = crystals long axis/short axis), and the average volume proportions could be influenced by the orientation of the 2D section in a sample with a strong 3D crystal fabric [Lanzafame et al. 2017]. Ideally, analytical data based on tomographic approaches [Polacci et al. 2018; Arzilli et al. 2019] would give the solution to this problem but, up to now, especially when using concentric cylinder apparatus, it is highly difficult and techniques need improvements. Figure 7 shows also that it is possible to modify some of the parameters used in an equation in order to get a best fit with experimental data. This is the case, for instance, for the model proposed by Krieger and Dougherty [1959] which could better reproduce experimental data by varying the parameter B and 𝛷m as done in Figure 7B and Table 1. However, a more exhaustive rheological model has to engulf rheological transitions from a low viscosity, where flow regime is mainly those of the suspending liquids to a high viscosity regime, where parameters such as particle shape, orientation, and volume dominate.
Most common relative viscosity models
| Model | Literature reference | |
|---|---|---|
| 1 | 𝜂r = (1 + B𝜙) | Einstein [1906]; Dilute system (𝛷< 0.25) B = 2.5 |
| 2 | 𝜂r = 1 + B𝛷 + B1𝛷2 | Guth and Gold [1938]; Dilute system (𝛷< 0.25) and spherical particles B = 2.5, B1 = 14.1 |
| 3 | Eilers [1941, 1943] | |
| 4 | Vand [1948] | |
| 5 | 𝜂r = 1 −𝛼𝛷−B | Roscoe [1952]; 𝛼 = 0.135, B = 2.5 |
| 6 | Maron and Pierce [1956] | |
| 7 | Krieger and Dougherty [1959] | |
| 8 | Krieger and Dougherty [1959]; B = 2.5 for spherical particles; for elongated particles B could be modified | |
| 9 | Gay et al. [1969]; 𝛼 = 0.48 |
|
| 10 | Chong et al. [1971]; 𝛼 = 0.75 |
|
| 11 | Wildemuth and Williams [1984] | |
| 12 | Shapiro and Probstein [1992]; |
|
| 13 | Costa [2005]; |
|
| 14 |
|
Caricchi et al. [2007] on Costa [2005] with variable strain rate |
| 15 |
where: and |
Costa et al. [2009]; |
| 16 | Cordonnier et al. [2009]; 𝜎 is the differential stress, 𝜎crit is the limiting stress (109 Pa), and (0.06 exp(6∗𝜙)) is the crystal stress dependency relation with 𝜙 the crystal fraction. | |
| 17 | Ishibashi [2009] | |
| 18 | Vona et al. [2011] | |
| 19 | Moitra and Gonnermann [2015]; 𝛼 = 1.92 |
|
| 20 | Faroughi and Huber [2015] | |
| 21 | Liu et al. [2017]; 𝜂r(max) is value for 𝛷 = 1. k and n are adjustable parameters |
Please refer to the provided literature for details.
We performed diverse test on the dataset provided in Supplementary Appendix 2 for constraining a possible comprehensive apparent/relative viscosity model. The best solution was given by a polynomial approach, although it doesn’t provide excellent results. We propose an empirical approach to retrieve the apparent viscosity from (1) shear rate and volume of solid phases or (2) AS and volume of crystals in silicate melt suspensions. Results are based on the 415 experimental data presented in Supplementary Appendix 2, interpolated by a simple polynomial approach able to build a 3D surface on which log viscosity, shear rate, and volume of crystals in one case and log viscosity, AS, and volume of crystals in the other case are taken into account (Figure 8). The apparent viscosity can be estimated using the following expressions:
| (4) |
| (5) |
Surface modeling of apparent viscosity with respect of shear rate (𝛾 in s−1) and crystal content (𝛷; A) and aspect ratio (AS) and crystal content (𝛷; B). The model is based on 415 experimental data provided in Supplementary Appendix 2 derived from chem composition as in Figure 4 and Supplementary Appendix 1. Polynomial approaches (giving the best results in terms of R2) are provided in Table 1 together with best fit parameters and R2.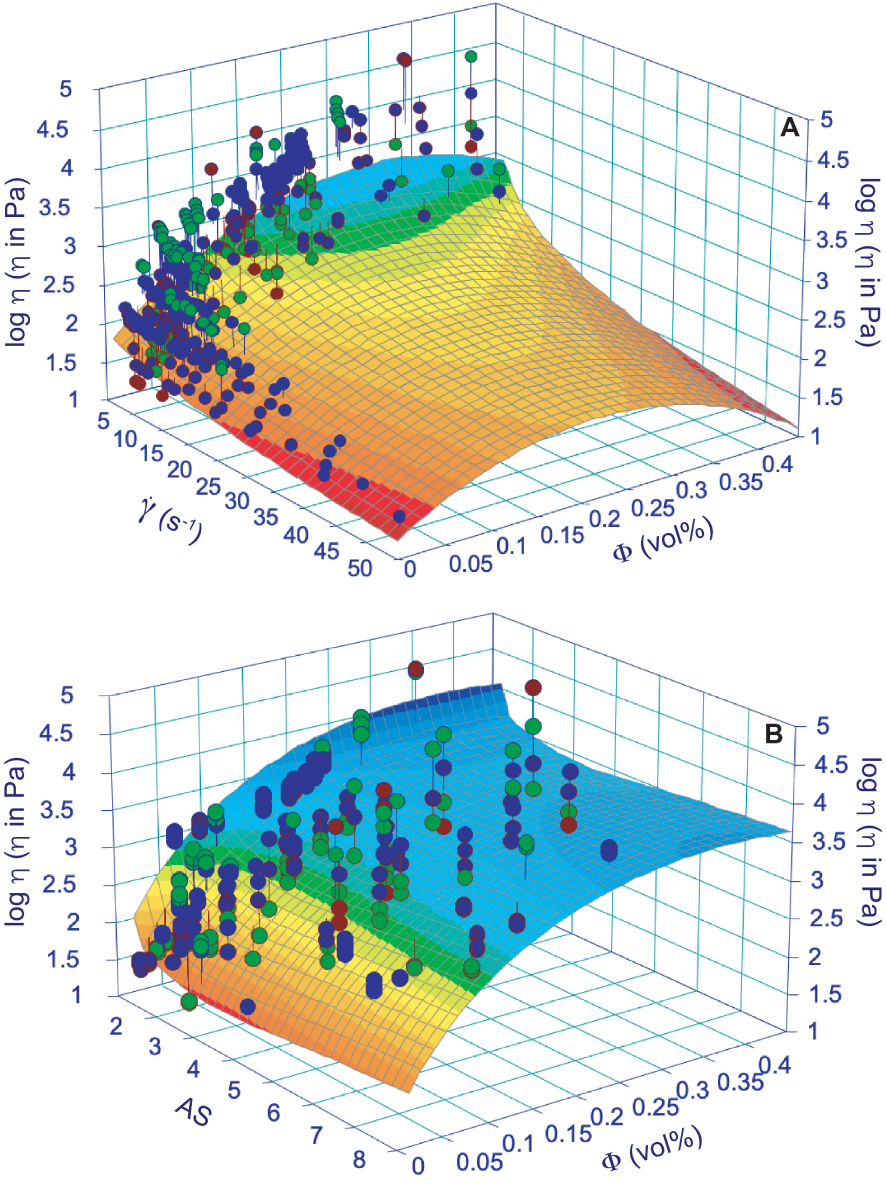
log𝜂 observed versus predicted from (4) and (5). (A) refers to (4) with R2 = 0.80 while (B) refers to (5) with R2 = 0.75.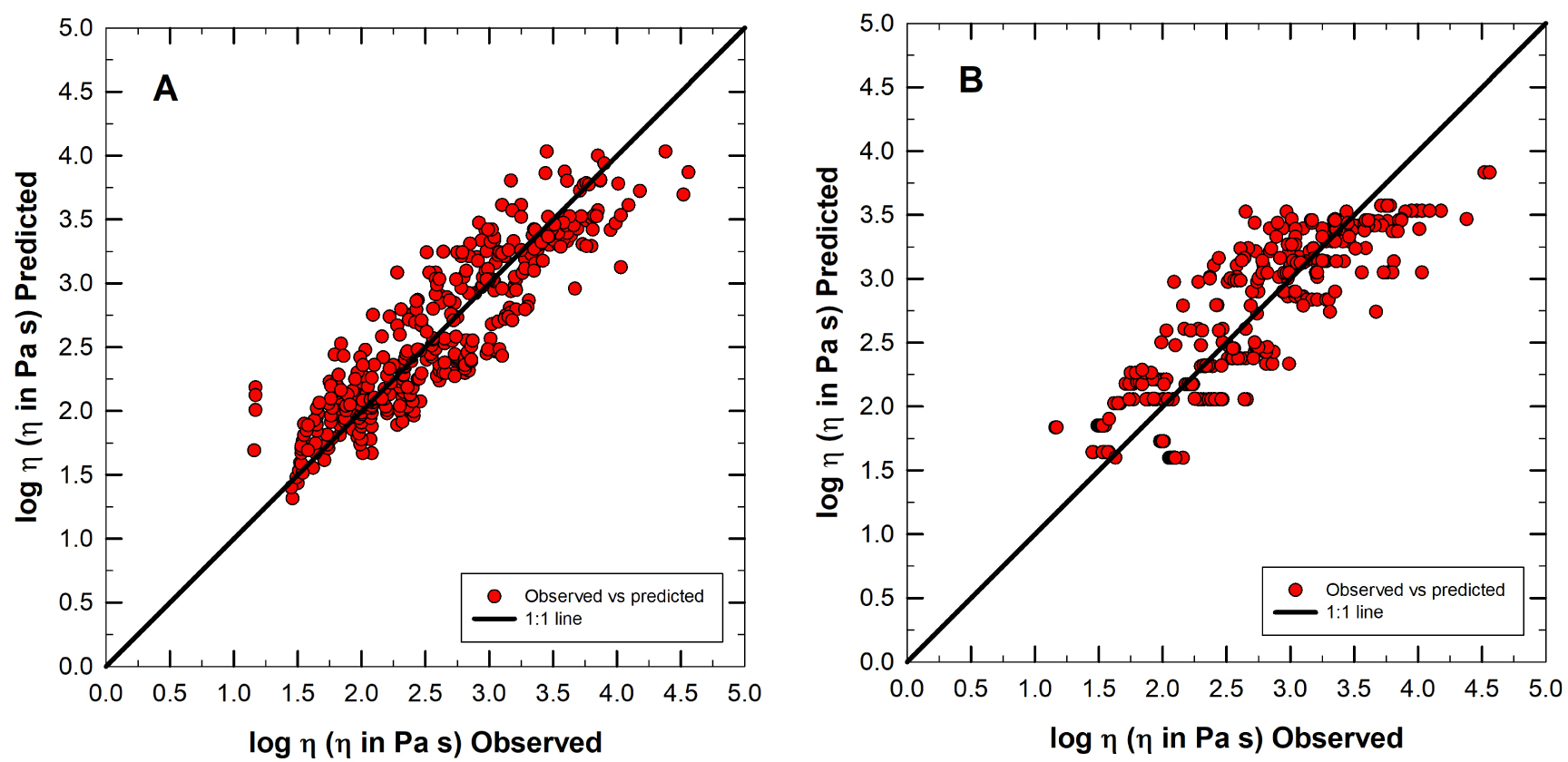
6. The effect of shear rate, crystal content, and cooling rates
The concomitant effect of shear rate and cooling on crystallinity and rheology can be retrieved from experimental data at one atmosphere pressure, mainly obtained for mafic composition. However, the rheology of systems crystallizing as a result of degassing-induced decompression as a function of decompression-rate and shear rate was never investigated experimentally. Such experiments would simulate the nearest approach to geological relevant conditions, specifically the ascent of magmas in conduits and dikes.
Vetere et al. [2020, 2019] and Kolzenburg et al. [2020, 2019, 2018, 2017] have performed experiments at one atmosphere pressure. Due to the progressive increase in crystallinity with time during cooling (contrasting to the classical isothermal viscosity experiments presented in paragraphs 4 and 5), the apparent viscosity will never reach a steady value because of the non-equilibrium conditions of the liquid plus crystal suspensions. As shown in Kolzenburg et al. [2018], crystal growth is progressively limited and potentially impeded in static systems (e.g., no shear) because the surrounding (residual intra-crystalline) melt is depleted in the compatible elements (already incorporated by the early growth events) required for further crystal growth. Also, the cooling and the first crystallizing phases enrich the residual and intra-crystalline melts in slow diffusion components (SiO2 and Al2O3), while the drop of temperature determines a progressive slowdown of chemical elements. Dendritic growth is the consequence of such situations, when the movement of chemical species is limited in a solidifying silicate liquid; if the diffusion is so sluggish compared to kinetic condition, nucleation is suppressed and a glass forms [Kirkpatrick 1981; Lofgren 1980; Shea and Hammer 2013; Vetere et al. 2013, 2015]. Shear or any other deformation acting on magmas and silicate liquids enhance the diffusion of elements by mass transfer.
As reported in Kolzenburg et al. [2017], systems cooled in the same thermal range crystallize faster (at low 𝛥T and high-T) and more abundantly with progressively increasing shear rates. This observation was also reported for isothermal experiments at sub-liquidus conditions by Kouchi et al. [1986], Vona and Romano [2013], Chevrel et al. [2015], and Vetere et al. [2017] and it is now widely accepted that increasing of shear rate increases the crystal growth rate. Also, Vetere et al. [2019, 2020] have shown that the shear rate during cooling influences the growth rate of solid phases. In particular, the growth rate of olivine, in pyroxenite melt at cooling rate of 10 K/h is ca. 5.3 × 10−6 cm/s. Clinopyroxene crystal in shoshonitic melts shows growth rates between 1.2 and 2.1 × 10−6 cm/s as cooling rates vary from 10 to 100 K/h, respectively, under a deformation rate of 1 s−1.
As shown in a simulation for magmatic conditions [Petrelli et al. 2016], mechanisms invoked as responsible for this fast crystal growth rate could be a continuous “fresh feeding ingredient” on individual crystal surfaces. The fast stirring also enhances the formation of new crystal nuclei, as suggested by Emerson [1926], Cashman et al. [1999], and Vona and Romano [2013]. Finally, oxygen fugacity also plays an important role on crystallization processes and related rheological changes [Kolzenburg et al. 2020]. For example, increasing of fO2 in magmas reaching the Earth’s surface can lead to a progressive shift of the equilibrium crystallization temperatures.
An example for the evolution of apparent viscosity with decreasing temperature and concomitant crystallization is given in Figure 10 for three different mafic magmas: pyroxenite, basalt, and shoshonite. Experimental conditions in Figure 10 are identical for pyroxenite and shoshonite (cooling rate of 10 K/h and shear rate of 1 s−1), while for basalt the applied cooling rate is slightly higher (30 K/h) and shear rate slightly lower (0.77 s−1). These differences are somewhat minimal, but in terms of reactivity to the cooling event, pyroxenite is the fastest. The kinks in the evolution of viscosity with temperature decrease are related to the onset of crystallization of mineral phases. Pyroxenite, basalt, and shoshonite compositions (composition reported in Figure 4 and Supplementary Appendix 1) have a liquidus temperature, computed by using alphaMELTS of 1543, 1444, and 1452 K, respectively. Obviously, crystallization occurs very quickly after reaching the liquidus temperature for the pyroxenite. The temperature (and time) interval between liquidus and crystallization temperature is larger for the basalt, and even larger for shoshonite. In structural terms, the chemical variability of silicate liquids might be described by the number of non-bridging oxygens (NBO) per tetrahedrally coordinated cation (T) [Mysen and Richet 2005]:
| (6) |
Finally, it has recently become evident that the formation of Fe-oxide nanolites can affect the composition of the residual melt and induce change in crystal nucleation and growth processes and thus, on the magma rheological response [Vetere et al. 2015; Di Genova et al. 2020, and reference therein]. While these phases are too small to be analytically quantified with most of the classical techniques applied to characterize the presented dataset, the potential occurrence of these phases might influence the data in some experimental charges.
Log apparent viscosity (Pa⋅s) versus temperature (K) evolution for basaltic, pyroxenite, and shoshonite melt compositions as in Figure 4 and Supplementary Appendix 1. Note the decrease of viscosity as melts cool down and crystallize.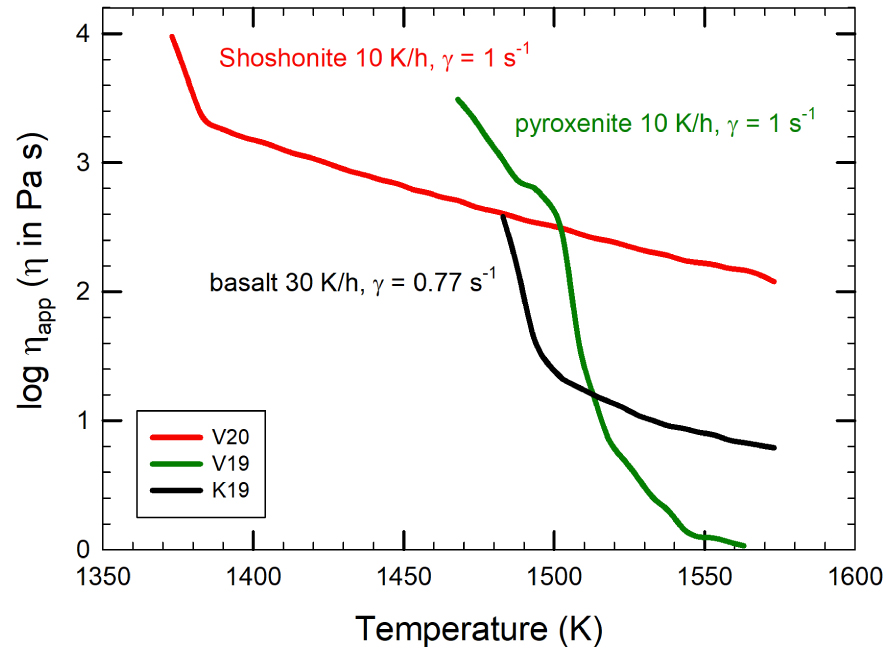
7. Conclusion and future challenges
This review shows that silicate melts subjected to different deformation rates show shear thinning behavior both on pure melts as well as on partly crystallized systems, where crystal content does not exceed ca. 40 vol%. It is obvious that there is still a need for experiments aimed at increasing the available dataset simulating viscosity evolution in crystallizing dynamic systems. Future studies need also to address the effect of pressure, degassing, and related crystallization to expand disequilibrium rheology models to crustal magmatic conditions. A common and rationale strategy is required to study magma rheology by using a common and systematic experimental protocol and this is particularly true for the concentric cylinder approach. From a general point of view, deformation applied to silicate melts enhances nucleation and growth rates of phases when compared to static conditions. This point needs to be considered in modeling magmatic and volcanic behaviors, since rheological behavior could drastically deviate from that predicted based on static experimental approaches and equilibrium modeling.
Conflicts of interest
Authors have no conflict of interest to declare.
Acknowledgements
This study was funded by the “Fondi Ateneo of the University G. D’Annunzio,” PRIN (2009PZ47NA_003) project “Experimental determination of the glass-forming ability (GFA), nucleation and crystallization of natural silicate melts,” and PRIN (2017J277S9_003) project “Time scales of solidification in magmas: Application to Volcanic Eruptions, Silicate Melts, Glasses, Glass-Ceramics” awarded to GI. Alexander von Humbold foundation senior research grant to FV is acknowledged.




 CC-BY 4.0
CC-BY 4.0